Discrete Bidirectional Associative Memory Neural Networks of the Cohen–Grossberg Type for Engineering Design Symmetry Related Problems: Practical Stability of Sets Analysis
Abstract
:1. Introduction
- (1)
- The practical stability concept is introduced to discrete-time BAM neural networks of the Cohen–Grossberg type that can be applied in numerical simulations and the practical realization of engineering design problems;
- (2)
- The practical stability notion is extended to the practical stability with respect to sets case, which is more appropriate in the presence of more constraints and initiates the development of the practical stability theory for the considered class of neural networks;
- (3)
- New practical stability, practical asymptotic stability, and global practical exponential stability results with respect to sets of a very general nature are established;
- (4)
- An extended Lyapunov function approach is applied, which allows representing the obtained results in terms of the model’s parameters.
- (5)
- Three examples are presented to illustrate the feasibility of the proposed practical stability with respect to sets results.
2. The Discrete BAM Cohen–Grossberg Neural Network Model
3. Practical Stability with Respect to Sets Definitions
- (a)
- -practically stable with respect to the BAM neural network model of the Cohen–Grossberg type (4) if for any pair with , we have implies , for some ;
- (b)
- -practically attractive with respect to the BAM neural network model of the Cohen–Grossberg type (4) if for any pair with , there exists such that implies for some ;
- (c)
- -practically asymptotically stable with respect to the BAM neural network model of the Cohen–Grossberg type (4) if it is -practically stable and -practically attractive;
- (d)
- -globally practically exponentially stable with respect to the BAM neural network model of the Cohen–Grossberg type (4) if there exist constants and such that for any , we havefor , .
4. Lyapunov Functions Method for Discrete Models
5. Practical Stability of Sets Analysis
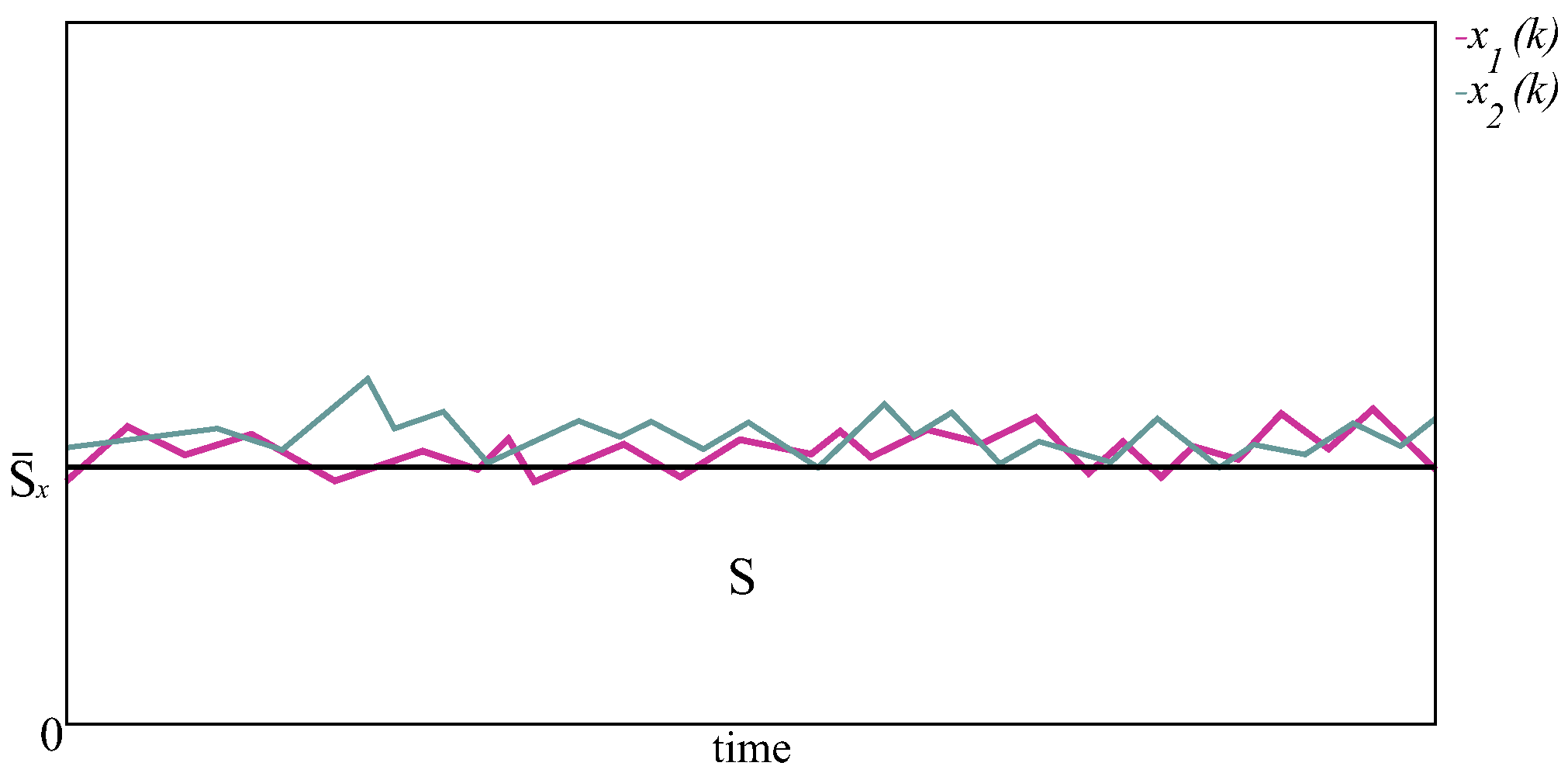
6. Examples and Numerical Simulations
7. Discussion
8. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer: Cham, Switzerland, 2018; ISBN 3319944622/978-3319944623. [Google Scholar]
- Alanis, A.Y.; Arana-Daniel, N.; López-Franco, C. (Eds.) Artificial Neural Networks for Engineering Applications; Academic Press: St. Louis, MO, USA, 2019; ISSN 978-0-12-818247-5. [Google Scholar]
- Arbib, M. Brains, Machines, and Mathematics; Springer: New York, NY, USA, 1987; ISBN 978-0387965390/978-0387965390. [Google Scholar]
- Kusiak, A. (Ed.) Intelligent Design and Manufacturing; Wiley: New York, NY, USA, 1992; ISBN 978-0471534730. [Google Scholar]
- Wang, J.; Takefuji, Y. (Eds.) Neural Networks in Design and Manufacturing; World Scientific: Singapore, 1993; ISBN 981021281X/9789810212810. [Google Scholar]
- Zha, X.F.; Howlett, R.J. (Eds.) Integrated Intelligent Systems in Engineering Design; IOS Press: Amsterdam, The Netherlands, 2006; ISBN 978-1586036751. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999; ISBN 0132733501/9780132733502. [Google Scholar]
- Nabian, M.A.; Meidani, H. Physics-driven regularization of deep neural networks for enhanced engineering design and analysis. J. Comput. Inf. Sci. Eng. (ASME) 2020, 20, 011006. [Google Scholar] [CrossRef] [Green Version]
- Stamov, T. On the applications of neural networks in industrial design: A survey of the state of the art. J. Eng. Appl. Sci. 2020, 15, 1797–1804. [Google Scholar]
- Wang, H.-H.; Chen, C.-P. A case study on evolution of car styling and brand consistency using deep learning. Symmetry 2020, 12, 2074. [Google Scholar] [CrossRef]
- Wu, D.; Wang, G.G. Causal artificial neural network and its applications in engineering design. Eng. Appl. Artif. Intell. 2021, 97, 104089. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Chen, Y. Hybrid teaching–learning-based optimization and neural network algorithm for engineering design optimization problems. Knowl. Based Syst. 2020, 187, 104836. [Google Scholar] [CrossRef]
- Cakar, T.; Cil, I. Artificial neural networks for design of manufacturing systems and selection of priority rules. Int. J. Comput. Integr. Manuf. 2007, 17, 195–211. [Google Scholar] [CrossRef]
- Hsu, Y.; Wang, S.; Yu, C. A sequential approximation method using neural networks for engineering design optimization problems. Eng. Optim. 2003, 35, 489–511. [Google Scholar] [CrossRef]
- Kanwal, K.; Ahmad, K.T.; Khan, R.; Abbasi, A.T.; Li, J. Deep learning using symmetry, FAST scores, shape-based filtering and spatial mapping integrated with CNN for large scale image retrieval. Symmetry 2020, 12, 612. [Google Scholar] [CrossRef]
- Lai, H.-H.; Lin, Y.-C.; Yeh, C.-H. Form design of product image using grey relational analysis and neural network models. Comput. Oper. Res. 2005, 32, 2689–2711. [Google Scholar] [CrossRef]
- Rafiq, M.Y.; Bugmann, G.; Easterbrook, D.J. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Shieh, M.-D.; Yeh, Y.-E. Developing a design support system for the exterior form of running shoes using partial least squares and neural networks. Comput. Ind. Eng. 2013, 65, 704–718. [Google Scholar] [CrossRef]
- Van Nguyen, N.; Lee, J.-W. Repetitively enhanced neural networks method for complex engineering design optimisation problem. Aeronaut. J. 2015, 119, 1253–1270. [Google Scholar] [CrossRef]
- Wu, B.; Han, S.; Shin, K.G.; Lu, W. Application of artificial neural networks in design of lithium-ion batteries. J. Power Sources 2018, 395, 128–136. [Google Scholar] [CrossRef]
- Brachmann, A.; Redies, C. Using convolutional neural network filters to measure left-right mirror symmetry in images. Symmetry 2016, 8, 144. [Google Scholar] [CrossRef] [Green Version]
- Krippendorf, S.; Syvaeri, M. Detecting symmetries with neural networks. Mach. Learn. Sci. Technol. 2021, 2, 015010. [Google Scholar] [CrossRef]
- Kosko, B. Adaptive bidirectional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef] [Green Version]
- Kosko, B. Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Xie, Q.; Yuan, Q.; Huang, H.; Li, Y. Research on a real-time monitoring method for the wear state of a tool based on a convolutional bidirectional LSTM model. Symmetry 2019, 11, 1233. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.M.; Watanobe, Y.; Nakamura, K. A bidirectional LSTM language model for code evaluation and repair. Symmetry 2021, 13, 247. [Google Scholar] [CrossRef]
- Acevedo-Mosqueda, M.E.; Yáñez-Márquez, C.; Acevedo-Mosqueda, M.A. Bidirectional associative memories: Different approaches. ACM Comput. Surv. 2013, 45, 18. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Li, J.; Duan, S.; Wang, L.; Guo, M. A reconfigurable bidirectional associative memory network with memristor bridge. Neurocomputing 2021, 454, 382–391. [Google Scholar] [CrossRef]
- Shi, J.; Zeng, Z. Design of In-Situ learning bidirectional associative memory neural network circuit with memristor synapse. IEEE Trans. Emerg. Top. Comput. 2021, 5, 743–754. [Google Scholar] [CrossRef]
- Cohen, M.A.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 1983, 13, 815–826. [Google Scholar] [CrossRef]
- Ozcan, N. Stability analysis of Cohen–Grossberg neural networks of neutral-type: Multiple delays case. Neural Netw. 2019, 113, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Li, X.; Aouiti, C.; Miaadi, F. Finite-time synchronization for Cohen–Grossberg neural networks with mixed time-delays. Neurocomputing 2018, 294, 39–47. [Google Scholar] [CrossRef]
- Pratap, K.A.; Raja, R.; Cao, J.; Lim, C.P.; Bagdasar, O. Stability and pinning synchronization analysis of fractional order delayed Cohen–Grossberg neural networks with discontinuous activations. Appl. Math. Comput. 2019, 359, 241–260. [Google Scholar] [CrossRef]
- Ali, M.S.; Saravanan, S.; Rani, M.E.; Elakkia, S.; Cao, J.; Alsaedi, A.; Hayat, T. Asymptotic stability of Cohen–Grossberg BAM neutral type neural networks with distributed time varying delays. Neural Process. Lett. 2017, 46, 991–1007. [Google Scholar] [CrossRef]
- Cao, J.; Song, Q. Stability in Cohen–Grossberg type bidirectional associative memory neural networks with time-varying delays. Nonlinearity 2006, 19, 1601–1617. [Google Scholar] [CrossRef]
- Li, X. Exponential stability of Cohen–Grossberg-type BAM neural networks with time-varying delays via impulsive control. Neurocomputing 2009, 73, 525–530. [Google Scholar] [CrossRef]
- Li, X. Existence and global exponential stability of periodic solution for impulsive Cohen–Grossberg-type BAM neural networks with continuously distributed delays. Appl. Math. Comput. 2009, 215, 292–307. [Google Scholar] [CrossRef]
- Wang, J.; Tian, L.; Zhen, Z. Global Lagrange stability for Takagi-Sugeno fuzzy Cohen–Grossberg BAM neural networks with time-varying delays. Int. J. Control Autom. 2018, 16, 1603–1614. [Google Scholar] [CrossRef]
- Ge, S.S.; Hang, C.C.; Lee, T.H.; Zhang, T. Stable Adaptive Neural Network Control; Kluwer Academic Publishers: Boston, MA, USA, 2001; ISBN 978-1-4757-6577-9. [Google Scholar]
- Haber, E.; Ruthotto, L. Stable architectures for deep neural networks. Inverse Probl. 2018, 34, 014004. [Google Scholar] [CrossRef] [Green Version]
- Stamov, T. Stability analysis of neural network models in engineering design. Int. J. Eng. Adv. Technol. 2020, 9, 1862–1866. [Google Scholar] [CrossRef]
- Stamova, I.M.; Stamov, T.; Simeonova, N. Impulsive control on global exponential stability for cellular neural networks with supremums. J. Vib. Control 2013, 19, 483–490. [Google Scholar] [CrossRef]
- Tan, M.-C.; Zhang, Y.; Su, W.-L.; Zhang, Y.-N. Exponential stability analysis of neural networks with variable delays. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2010, 20, 1551–1565. [Google Scholar] [CrossRef]
- Moller, A.P.; Swaddle, J.P. Asymmetry, Developmental Stability and Evolution; Oxford University Press: Oxford, UK, 1997; ISBN 019854894X/978-0198548942. [Google Scholar]
- Cao, J.; Wan, Y. Matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays. Neural Netw. 2014, 53, 165–172. [Google Scholar] [CrossRef]
- Muhammadhaji, A.; Teng, Z. Synchronization stability on the BAM neural networks with mixed time delays. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 99–109. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, J. Global stabilization of fractional-order bidirectional associative memory neural networks with mixed time delays via adaptive feedback control. Int. J. Appl. Comput. Math. 2020, 97, 2074–2090. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Ho, D.W.C. Discrete-time bidirectional associative memory networks with delays. Phys. Lett. A 2005, 335, 226–234. [Google Scholar] [CrossRef]
- Mohamad, S. Global exponential stability in continuous-time and discrete-time delayed bidirectional neural networks. Physica D 2001, 159, 233–251. [Google Scholar] [CrossRef]
- Shu, Y.; Liu, X.; Wang, F.; Qiu, S. Further results on exponential stability of discrete-time BAM neural networks with time-varying delays. Math. Methods Appl. Sci. 2017, 40, 4014–4027. [Google Scholar] [CrossRef]
- Cong, E.-Y.; Han, X.; Zhang, X. New stabilization method for delayed discrete-time Cohen–Grossberg BAM neural networks. IEEE Access 2020, 8, 99327–99336. [Google Scholar] [CrossRef]
- Liu, Q. Bifurcation of a discrete-time Cohen–Grossberg-type BAM neural network with delays. In Advances in Neural Networks–ISNN 2013, Proceedings of the 10th International Conference on Advances in Neural Networks, Dalian, China, 4–6 July 2013; Guo, C., Hou, Z.-G., Zeng, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 109–116. [Google Scholar]
- Lakshmikantham, V.; Leela, S.; Martynyuk, A.A. Practical Stability Analysis of Nonlinear Systems; World Scientific: Singapore, 1990; ISBN 978-981-02-0351-1. [Google Scholar]
- Sathananthan, S.; Keel, L.H. Optimal practical stabilization and controllability of systems with Markovian jumps. Nonlinear Anal. 2003, 54, 1011–1027. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, Q.; Zhou, L. Practical stabilization and controllability of descriptor systems. Int. J. Syst. Sci. 2005, 1, 455–465. [Google Scholar]
- Ballinger, G.; Liu, X. Practical stability of impulsive delay differential equations and applications to control problems. In Optimization Methods and Applications. Applied Optimization; Yang, Y., Teo, K.L., Caccetta, L., Eds.; Kluwer: Dordrecht, The Netherlands, 2001; Volume 52, pp. 3–21. [Google Scholar]
- Kaslik, E.; Sivasundaram, S. Multistability in impulsive hybrid Hopfield neural networks with distributed delays. Nonlinear Anal. 2011, 12, 1640–1649. [Google Scholar] [CrossRef]
- Stamov, T. Neural networks in engineering design: Robust practical stability analysis. Cybern. Inf. Technol. 2021, 21, 3–14. [Google Scholar] [CrossRef]
- Sun, L.; Liu, C.; Li, X. Practical stability of impulsive discrete systems with time delays. Abstr. Appl. Anal. 2014, 2014, 954121. [Google Scholar] [CrossRef] [Green Version]
- Wangrat, S.; Niamsup, P. Exponentially practical stability of impulsive discrete time system with delay. Adv. Differ. Equ. 2016, 2016, 277. [Google Scholar] [CrossRef] [Green Version]
- Wangrat, S.; Niamsup, P. Exponentially practical stability of discrete time singular system with delay and disturbance. Adv. Differ. Equ. 2018, 2018, 130. [Google Scholar] [CrossRef]
- Athanassov, Z.S. Total stability of sets for nonautonomous differential systems. Trans. Am. Math. Soc. 1986, 295, 649–663. [Google Scholar] [CrossRef]
- Bernfeld, S.R.; Corduneanu, C.; Ignatyev, A.O. On the stability of invariant sets of functional differential equations. Nonlinear Anal. 2003, 55, 641–656. [Google Scholar] [CrossRef]
- Stamova, I.; Stamov, G. On the stability of sets for reaction-diffusion Cohen–Grossberg delayed neural networks. Discret. Contin. Dynam. Syst.-S 2021, 14, 1429–1446. [Google Scholar] [CrossRef]
- Xie, S. Stability of sets of functional differential equations with impulse effect. Appl. Math. Comput. 2011, 218, 592–597. [Google Scholar] [CrossRef]
- Chaperon, M. Stable manifolds and the Perron–Irwin method. Ergod. Theory Dyn. Syst. 2004, 24, 1359–1394. [Google Scholar] [CrossRef]
- Rebennack, S. Stable set problem: Branch & cut algorithms. In Encyclopedia of Optimization; Floudas, C., Pardalos, P., Eds.; Springer: Boston, MA, USA, 2008; pp. 32–36. [Google Scholar]
- Sritharan, S.S. Invariant Manifold Theory for Hydrodynamic Transition; John Wiley & Sons: New York, NY, USA, 1990; ISBN 0-582-06781-2. [Google Scholar]
- Skjetne, R.; Fossen, T.I.; Kokotovic, P.V. Adaptive output maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; ISBN 978-0130673893. [Google Scholar]
- Kalman, R.; Bertram, J. Control system analysis and design via the second method of Lyapunov II: Discrete-time systems. J. Basic Eng. (ASME) 1960, 82, 394–400. [Google Scholar] [CrossRef]
- Bobiti, R.; Lazar, M. A sampling approach to finding Lyapunov functions for nonlinear discrete-time systems. In Proceedings of the 15th European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 561–566. [Google Scholar]
- Dai, H.; Landry, B.; Yang, L.; Pavone, M.; Tedrake, R. Lyapunov-stable neural-network control. arXiv 2021, arXiv:2109.14152. [Google Scholar]
- Giesl, P.; Hafstein, S. Review on computational methods for Lyapunov functions. Discret. Contin. Dyn. Syst. Ser. B 2016, 20, 2291–2331. [Google Scholar]
- Wei, J.; Dong, G.; Chen, Z. Lyapunov-based state of charge diagnosis and health prognosis for lithium-ion batteries. J. Power Sources 2018, 397, 352–360. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamov, T. Discrete Bidirectional Associative Memory Neural Networks of the Cohen–Grossberg Type for Engineering Design Symmetry Related Problems: Practical Stability of Sets Analysis. Symmetry 2022, 14, 216. https://doi.org/10.3390/sym14020216
Stamov T. Discrete Bidirectional Associative Memory Neural Networks of the Cohen–Grossberg Type for Engineering Design Symmetry Related Problems: Practical Stability of Sets Analysis. Symmetry. 2022; 14(2):216. https://doi.org/10.3390/sym14020216
Chicago/Turabian StyleStamov, Trayan. 2022. "Discrete Bidirectional Associative Memory Neural Networks of the Cohen–Grossberg Type for Engineering Design Symmetry Related Problems: Practical Stability of Sets Analysis" Symmetry 14, no. 2: 216. https://doi.org/10.3390/sym14020216
APA StyleStamov, T. (2022). Discrete Bidirectional Associative Memory Neural Networks of the Cohen–Grossberg Type for Engineering Design Symmetry Related Problems: Practical Stability of Sets Analysis. Symmetry, 14(2), 216. https://doi.org/10.3390/sym14020216




