Thermal Modal Performance of Composite Laminates Embedded with Anti-Symmetric Oblique Coupling Gradient Pre-Strained SMA Wires for Suppressing Resonance
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Anti-Symmetric Oblique Coupling Gradient Model
2.2. Internal Forces Due to Pre-Strain and Thermal Expansion
2.3. Dynamics Formulation
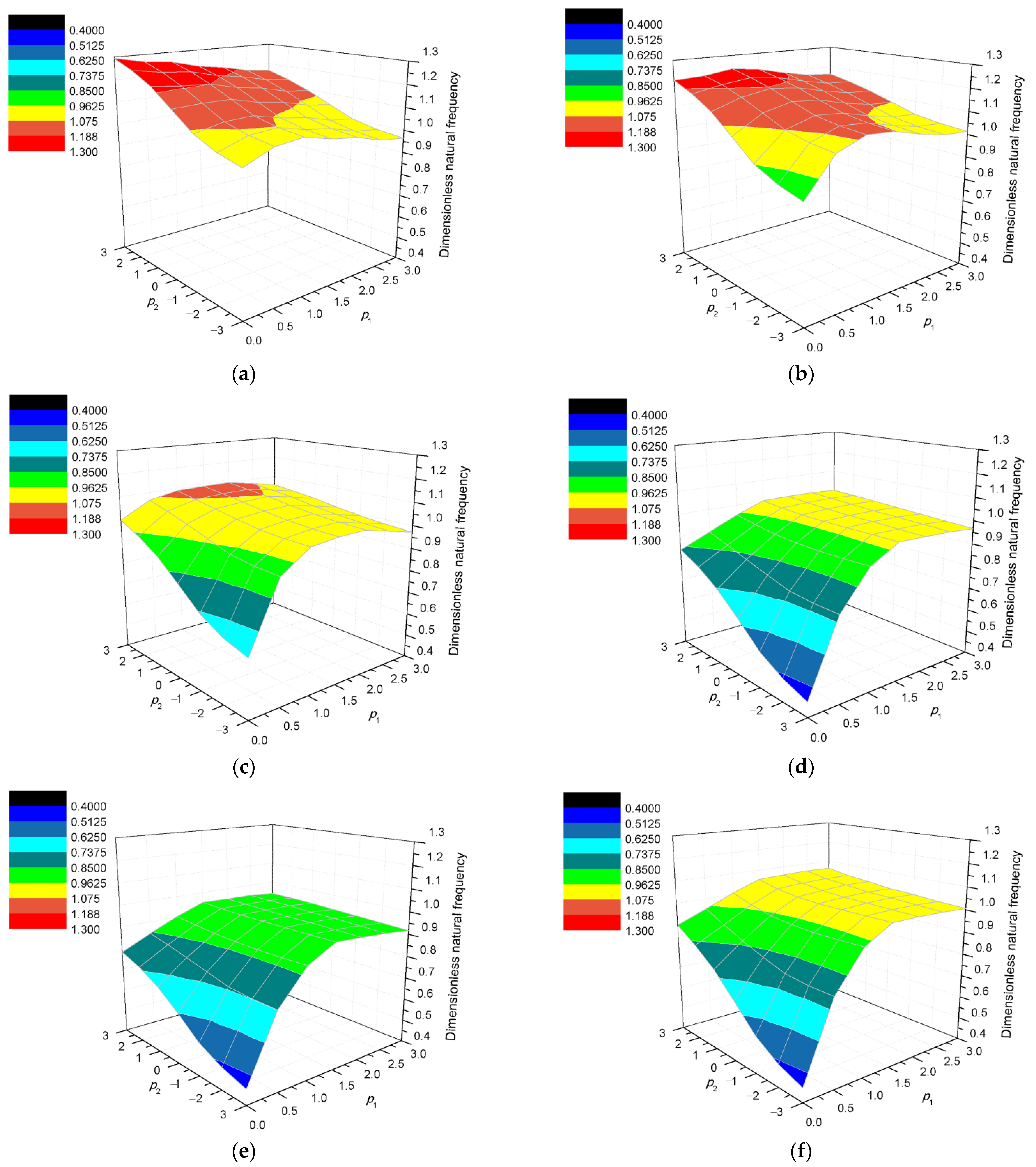
3. Numerical Results and Discussion
3.1. Materials Properties
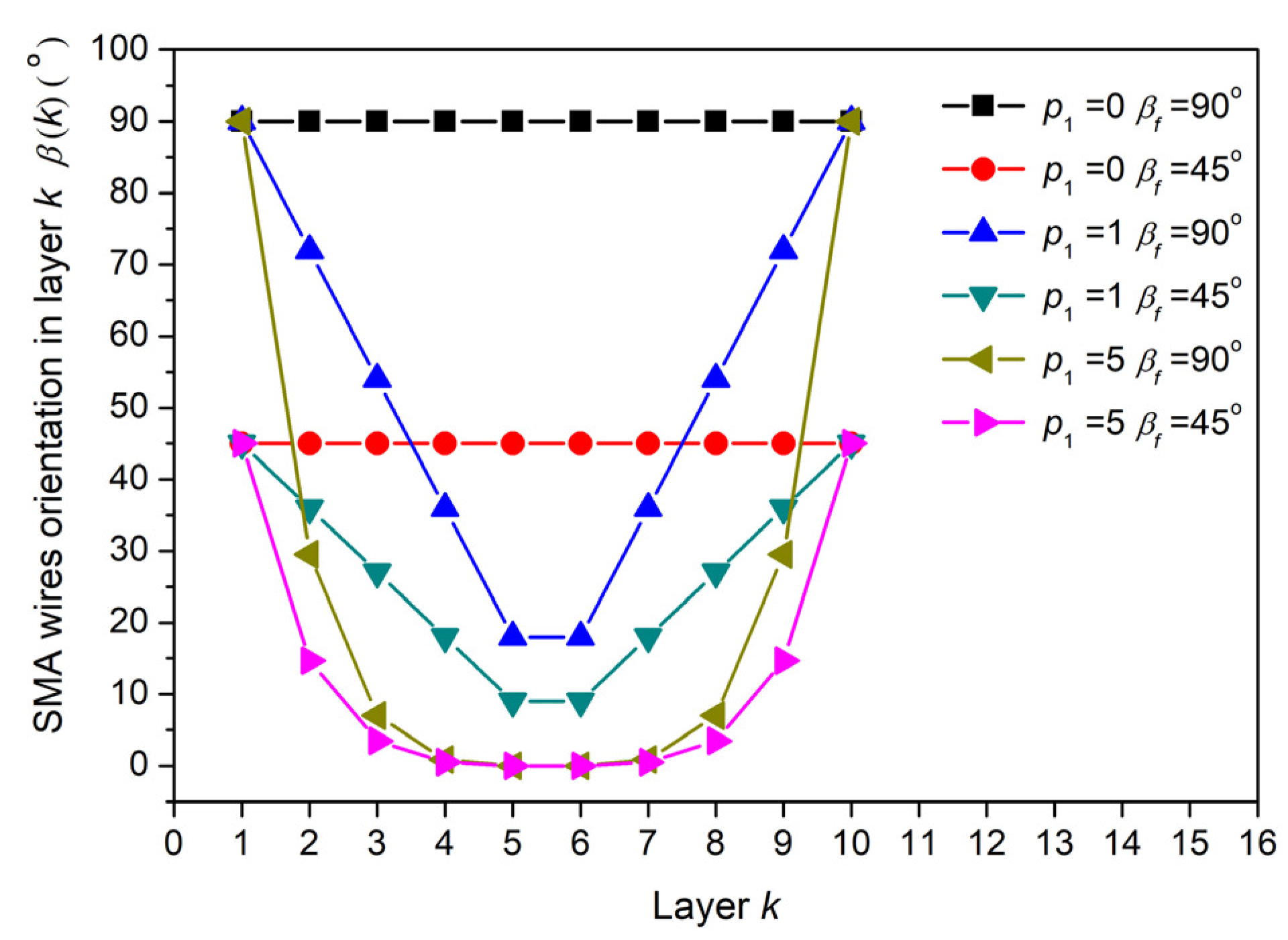
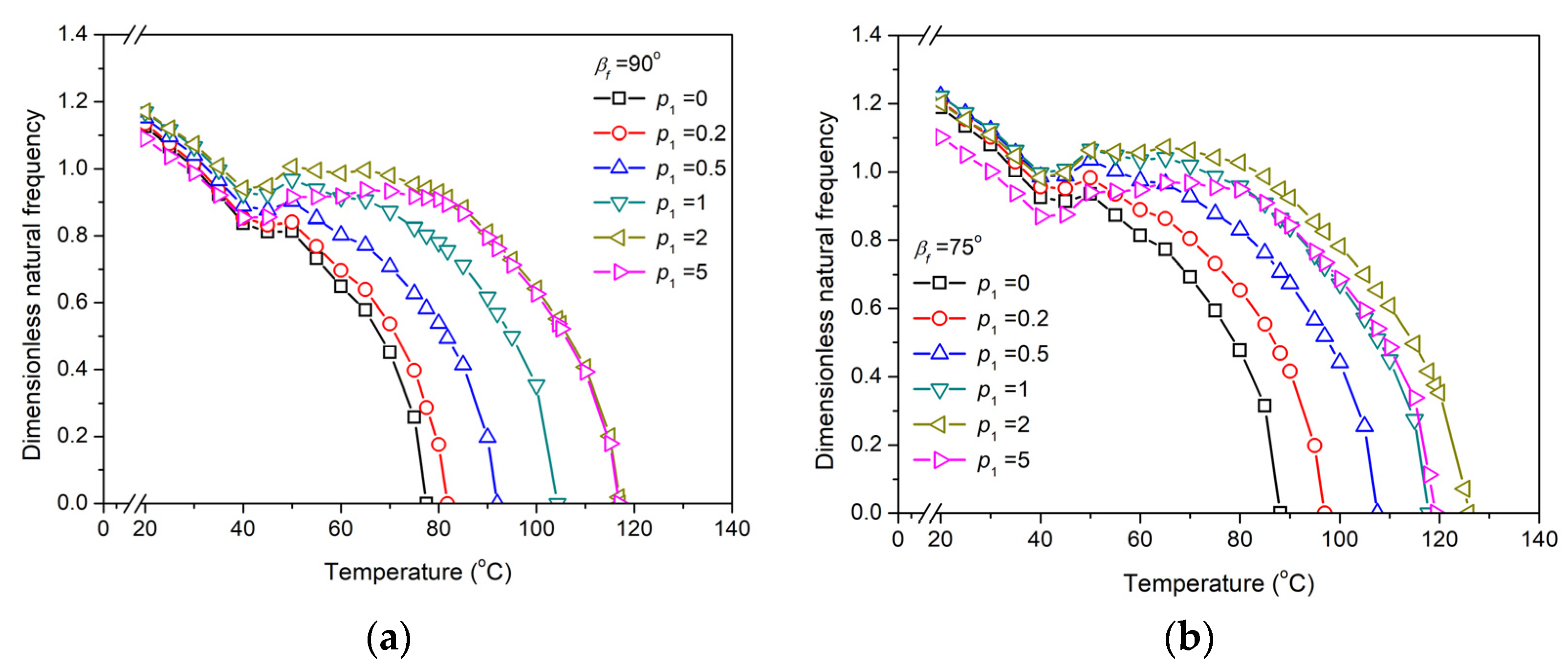
3.2. Influence of Anti-Symmetric Oblique Gradient Distribution Parameter of SMA Wires Orientation
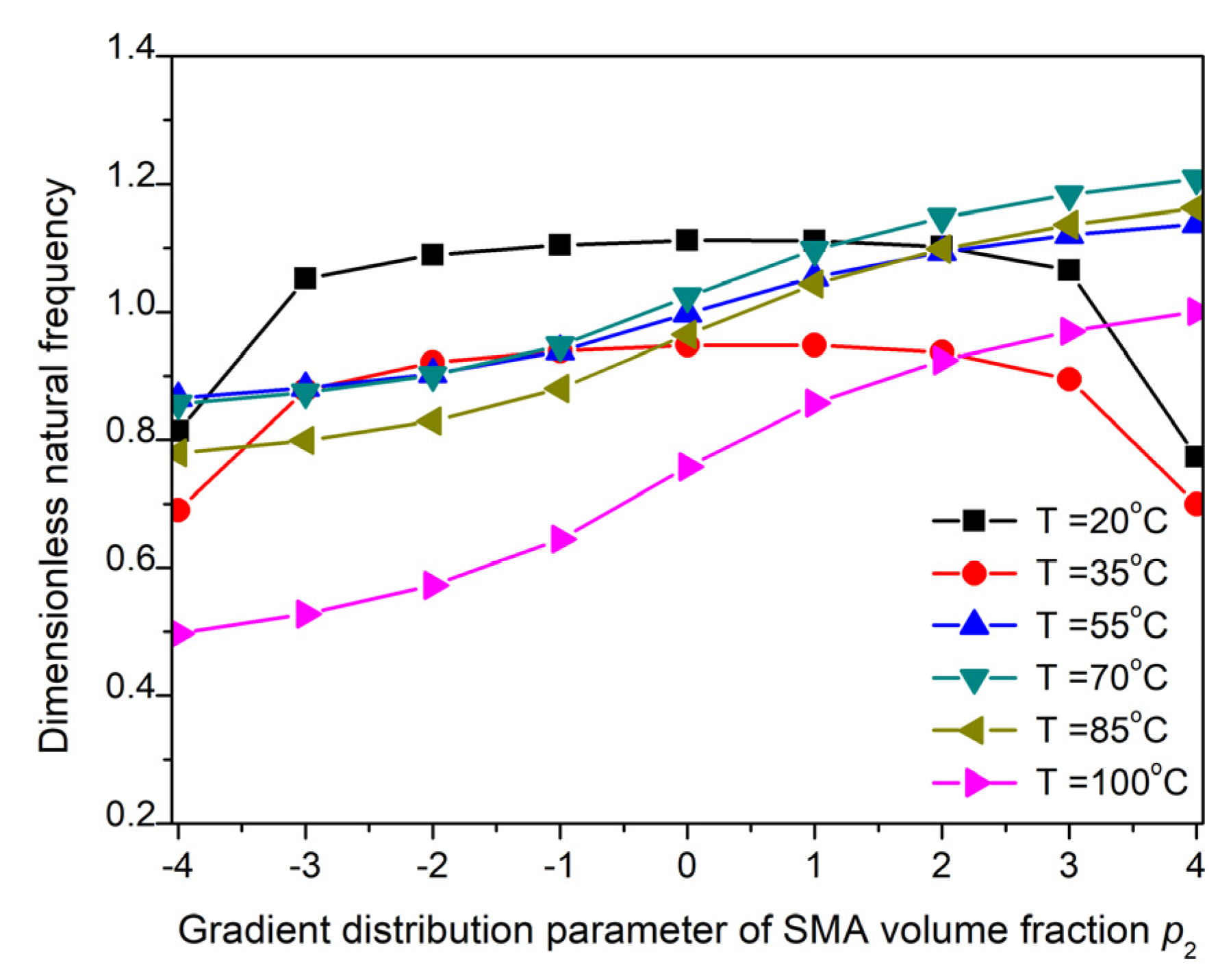
3.3. Influence of Gradient Distribution Parameter of SMA Volume Fraction
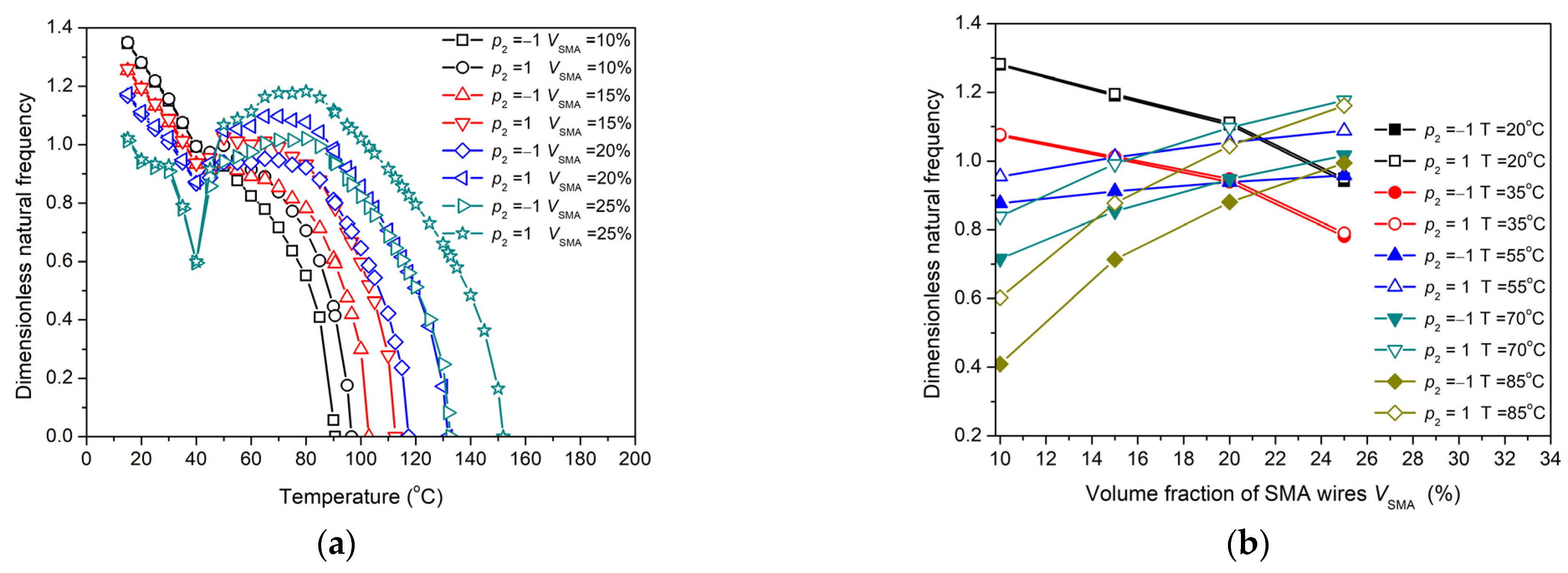
3.4. Influence of Anti-Symmetric Oblique Coupling Gradient Distribution of SMA
4. Experiment Validation
4.1. Prepared Experimental Samples
4.2. Experimental Equipment and Testing
5. Conclusions
- During the heating process, the SMA wires distributed in the form of anti-symmetric oblique positive gradient can fully exert the recovery stress generated by SMA tensile pre-strain, i.e., effectively improve the stiffness of the composite laminates.
- The natural frequency and the critical buckling temperature of SMA composite laminates with anti-symmetric oblique positive gradient distribution are higher than that of composite laminates with anti-symmetric oblique uniform/negative gradient distribution and symmetric orthogonal gradient distribution.
- Coupling gradient composite laminates embedded with SMA wires have the coupling design ability of gradient structure and material components, mainly from two aspects: gradient distribution of SMA wires orientation and gradient distribution of SMA volume fraction. The proposed structure effectively broadens the frequency modulation range, which makes the fine regulation of the natural frequency and critical buckling temperature feasible.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ro, J.; Baz, A. Nitinol-reinforced plates: Part I. Thermal characteristics. Compos. Eng. 1995, 5, 61–106. [Google Scholar] [CrossRef]
- Mohd Jani, J.; Learya, M.; Subica, A.; Gibsonc, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Dauksher, R.; Patterson, Z.; Majidi, C. Characterization and analysis of a flexural shape memory alloy actuator. Actuators 2021, 10, 202. [Google Scholar] [CrossRef]
- Fallah, A.; Dehkordi, M.B. A new nonlinear finite element model for transient dynamic response of a micro composite plate embedded with micro SMA wires considering the size effects. Mech. Adv. Mater. Struc. 2021, 10, 1–22. [Google Scholar] [CrossRef]
- Amiri, A.; Mohammadimehr, M.; Irani Rahaghi, M. Vibration analysis of a micro-cylindrical sandwich panel with reinforced shape-memory alloys face sheets and porous core. Eur. Phys. J. Plus 2020, 136, 20. [Google Scholar] [CrossRef]
- Chiker, Y.; Mourad, B.; Bouaziz, S.; Mouloud, G.; Amar, M.B.; Haddar, M. Free vibration analysis of hybrid laminated plates containing multilayer functionally graded carbon nanotube-reinforced composite plies using a layer-wise formulation. Arch. Appl. Mech. 2020, 91, 463–485. [Google Scholar] [CrossRef]
- Mehar, K.; Mishra, P.K.; Panda, S.K. Numerical investigation of thermal frequency responses of graded hybrid smart nanocomposite (CNT-SMA-Epoxy) structure. Mech. Adv. Mater. Struc. 2021, 28, 2242–2254. [Google Scholar] [CrossRef]
- Karimimahabadi, R.; Daneshpazhooh, M.; Shakeri, M. On the free vibration and design optimization of a shape memory alloy hybrid laminated composite plate. Acta Mech. 2021, 232, 1–21. [Google Scholar] [CrossRef]
- Rogers, C.A. Active vibration and structural acoustic control of shape memory alloy hybrid composites: Experimental results. J. Acoust. Soc. Am. 1990, 88, 2803. [Google Scholar] [CrossRef] [Green Version]
- Rogers, C.A.; Liang, C.; Jia, J. Structural modification of simply-supported laminated plates using embedded shape memory alloy fibers. Comput. Struct. 1991, 38, 569–580. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Krawczuk, M.; Zak, A. Natural frequencies of a multilayer composite plate with shape memory alloy wires. Finite Elem. Anal. Des. 1999, 32, 71–83. [Google Scholar] [CrossRef]
- Mahabadi, R.K.; Shakeri, M.; Danesh, P.M. Free vibration of laminated composite plate with shape memory alloy fibers. Lat. Am. J. Solids Struct. 2016, 13, 314–330. [Google Scholar] [CrossRef] [Green Version]
- Malekzadeh, K.; Mozafari, A.; Ghasemi, F.A. Free vibration response of a multilayer smart hybrid composite plate with embedded SMA wires. Lat. Am. J. Solids Struct. 2014, 11, 279–298. [Google Scholar] [CrossRef] [Green Version]
- Lal, A.; Markad, K. Thermal post buckling analysis of smart SMA hybrid sandwich composite plate. Polym. Polym. Compos. 2021, 29, 344–360. [Google Scholar] [CrossRef]
- Yas, M.H.; Basati, F.; Kamarian, S. Thermal buckling of trapezoidal composite laminated plates with embedded shape memory alloys. Polym. Compos. 2021, 42, 3349–3362. [Google Scholar] [CrossRef]
- Kuo, S.Y.; Shiau, L.C.; Chen, K.H. Buckling analysis of shape memory alloy reinforced composite laminates. Compos. Struct. 2009, 90, 188–195. [Google Scholar] [CrossRef]
- Rostamijavanani, A.; Ebrahimi, M.R.; Jahedi, S. Thermal post-buckling analysis of laminated composite plates embedded with shape memory alloy fibers using semi-analytical finite strip method. J. Fail. Anal. Prev. 2020, 21, 290–301. [Google Scholar] [CrossRef]
- Fani, M.; Taheri-Behrooz, F. Analytical study of thermal buckling and post-buckling behavior of composite beams reinforced with SMA by Reddy Bickford theory. J. Intell. Mater. Syst. Str. 2020, 33, 121–135. [Google Scholar] [CrossRef]
- Kamarian, S.; Shakeri, M. Thermal buckling analysis and stacking sequence optimization of rectangular and skew shape memory alloy hybrid composite plates. Compos. Part. B -Eng. 2017, 115, 137–152. [Google Scholar] [CrossRef]
- Asadi, H.; Kiani, Y.; Aghdam, M.; Shakeri, M. Enhanced thermal buckling of laminated composite cylindrical shells with shape memory alloy. J. Compos. Mater. 2015, 50, 243–256. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Z.; Li, C.; Mao, K.; Huang, Q. Modal Performance of Two-Fiber Orthogonal Gradient Composite Laminates Embedded with SMA. Materials 2020, 13, 1102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Li, L.; Xu, Z.; Li, C.; Mao, K. Free Vibration Analysis of Functionally Gradient Sandwich Composite Plate Embedded SMA Wires in Surface Layer. Appl. Sci. 2020, 10, 3921. [Google Scholar] [CrossRef]
- Shariyat, M.; Hosseini, S.H. Accurate eccentric impact analysis of the preloaded SMA composite plates based on a novel mixed-order hyperbolic global-local theory. Compos. Struct. 2015, 124, 140–151. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Z.; Yang, B. Experimental investigation of GF/epoxy laminates with different SMAs positions subjected to low-velocity impact. Compos. Struct. 2017, 171, 170–184. [Google Scholar] [CrossRef]
- Asadi, H.; Akbarzadeh, A.; Wang, Q. Nonlinear thermo-inertial instability of functionally graded shape memory alloy sandwich plates. Compos. Struct. 2015, 120, 496–508. [Google Scholar] [CrossRef]
- Miyazaki, E.; Watanabe, Y. Development of Shape Memory Alloy Fiber Reinforced Smart FGMs. Mater. Sci. Forum. 2003, 423, 107–112. [Google Scholar] [CrossRef]
- Xue, L. Theoretical Analysis of Functionally Graded Shape Memory Alloy Beam Subjected to Pure Bending. Chin. J. Mech. Eng. 2012, 48, 40. [Google Scholar] [CrossRef]
- Shariat, B.S.; Meng, Q.; Mahmud, A.S. Functionally graded shape memory alloys: Design, fabrication and experimental evaluation. Mater. Des. 2017, 124, 225–237. [Google Scholar] [CrossRef]
- Viet, N.; Zaki, W.; Umer, R. Analytical model of functionally graded material/shape memory alloy composite cantilever beam under bending. Compos. Struct. 2018, 203, 764–776. [Google Scholar] [CrossRef]











| SMA | From Figure 2 | - | 0.3 | 6450 | 10.26 × 10−6 |
| Graphite | 275.6 | 114.8 | 0.2 | 1900 | 24.40 × 10−6 |
| Epoxy | 3.43 | 1.27 | 0.35 | 1250 | 64.80 × 10−6 |
| Layer k | SMA Wire Length l | SMA Wires Nos n | Laying Spacing l/mm | SMA Volume Fraction Vs/% |
|---|---|---|---|---|
| 1 | 400 | 13 | 27.64 | 6.85 |
| 2 | 300 | 13 | 20.05 | 5.13 |
| 3 | 400 | 6 | 56.28 | 3.08 |
| 4 | 300 | 7 | 36.63 | 2.72 |
| 5 | 400 | 10 | 35.45 | 5.17 |
| 6 | 300 | 18 | 14.84 | 7.05 |
| Layer k | SMA Wires Nos n | SMA Volume Fraction Vs/% |
|---|---|---|
| 1 | 23 | 6.95 |
| 2 | 15 | 5.15 |
| 3 | 9 | 2.90 |
| 4 | 9 | 2.90 |
| 5 | 15 | 5.15 |
| 6 | 23 | 6.95 |
| Distribution Form | Mode Order | |||||
|---|---|---|---|---|---|---|
| (1,1) | (2,1) | (1,2) | (3,1) | (2,2) | ||
| symmetric orthogonal | Experimental results | 168.7 | 389.7 | 479.8 | 632 | 730.2 |
| Theoretical predictions | 174.6 | 364.5 | 507.6 | 667.7 | 745.5 | |
| Error | 3.49% | 6.47% | 5.79% | 5.65% | 2.10% | |
| antisymmetric oblique | Experimental results | 172.2 | 385.6 | 524.6 | 707.9 | 789 |
| Theoretical predictions | 182.4 | 406.3 | 556.2 | 718.9 | 793.1 | |
| Error | 5.92% | 5.37% | 6.02% | 1.55% | 5.19% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Shi, Y. Thermal Modal Performance of Composite Laminates Embedded with Anti-Symmetric Oblique Coupling Gradient Pre-Strained SMA Wires for Suppressing Resonance. Symmetry 2022, 14, 361. https://doi.org/10.3390/sym14020361
Huang Y, Shi Y. Thermal Modal Performance of Composite Laminates Embedded with Anti-Symmetric Oblique Coupling Gradient Pre-Strained SMA Wires for Suppressing Resonance. Symmetry. 2022; 14(2):361. https://doi.org/10.3390/sym14020361
Chicago/Turabian StyleHuang, Yizhe, and Yuanyuan Shi. 2022. "Thermal Modal Performance of Composite Laminates Embedded with Anti-Symmetric Oblique Coupling Gradient Pre-Strained SMA Wires for Suppressing Resonance" Symmetry 14, no. 2: 361. https://doi.org/10.3390/sym14020361
APA StyleHuang, Y., & Shi, Y. (2022). Thermal Modal Performance of Composite Laminates Embedded with Anti-Symmetric Oblique Coupling Gradient Pre-Strained SMA Wires for Suppressing Resonance. Symmetry, 14(2), 361. https://doi.org/10.3390/sym14020361





