First-Order Sign-Invariants and Exact Solutions of the Radially Symmetric Nonlinear Diffusion Equations with Gradient-Dependent Diffusivities
Abstract
:1. Introduction
2. Non-Stationary Sign-Invariant of Nonlinear Diffusion Equation
3. Non-Autonomous Sign-Invariant of Nonlinear Diffusion Equation
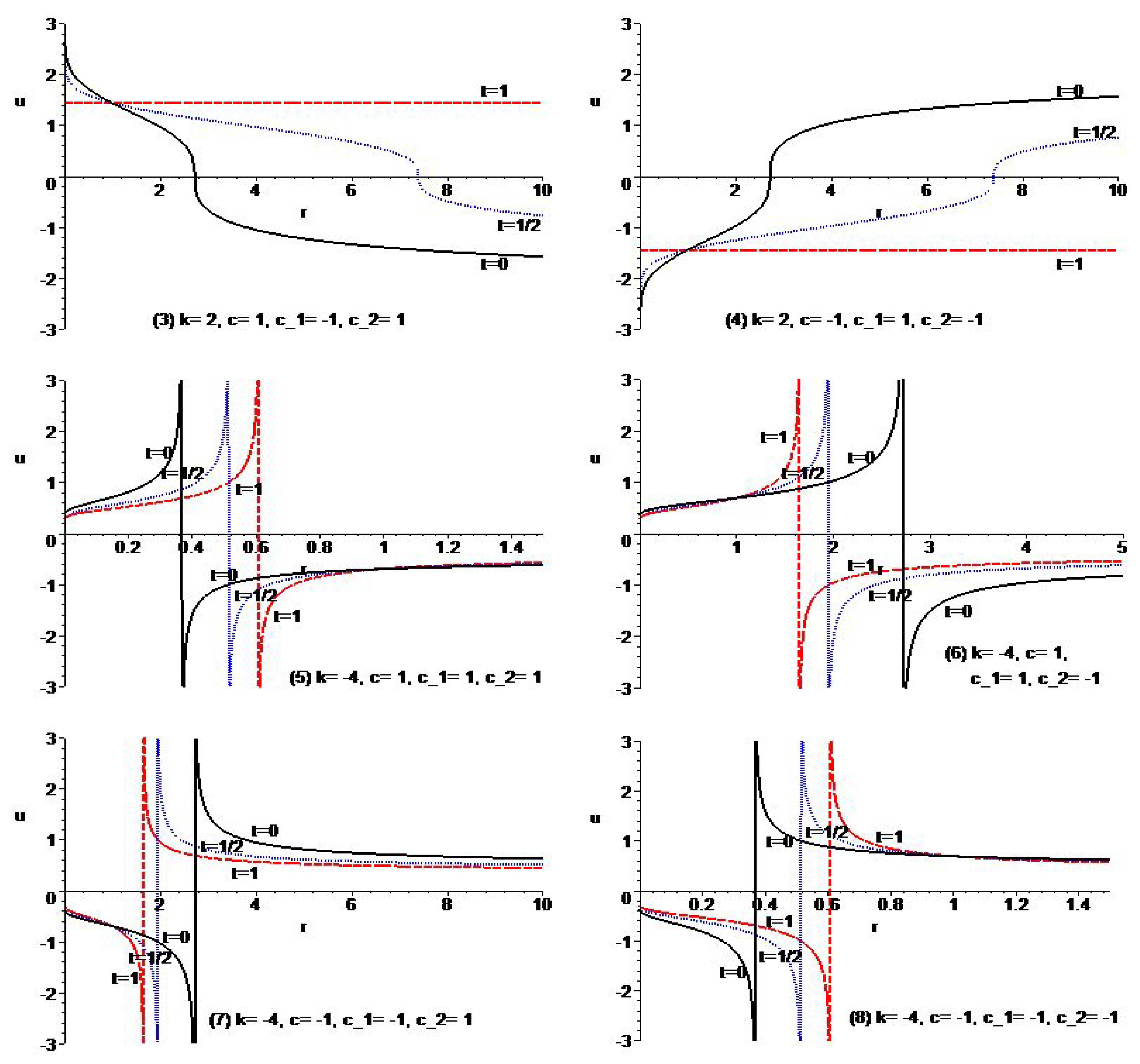
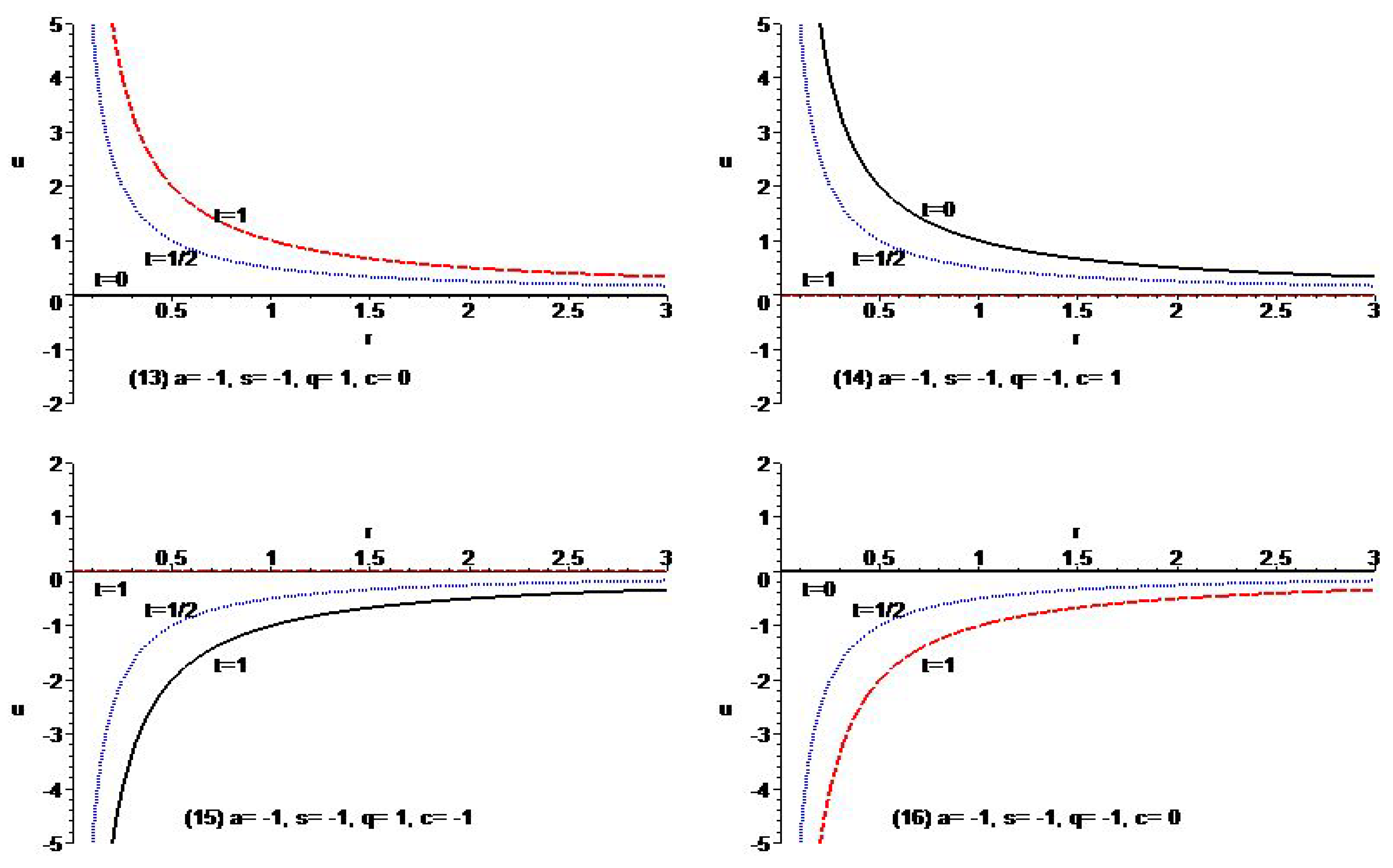
4. Exact Solutions of Nonlinear Diffusion Equation
- (i)
- For ,
- (ii)
- For ,
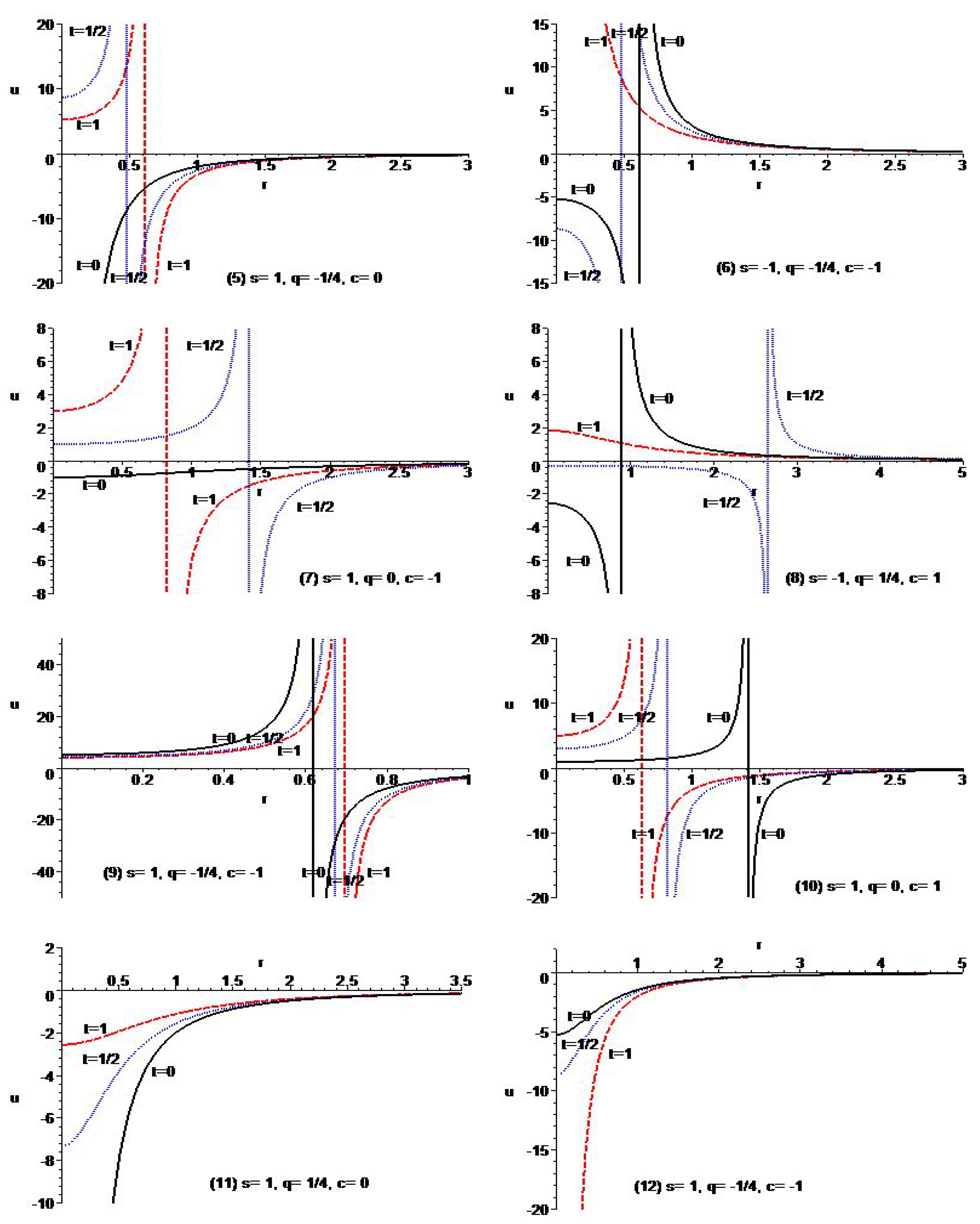
- (i)
- For ,
- (ii)
- For ,
- (i)
- For ,
- (ii)
- For ,
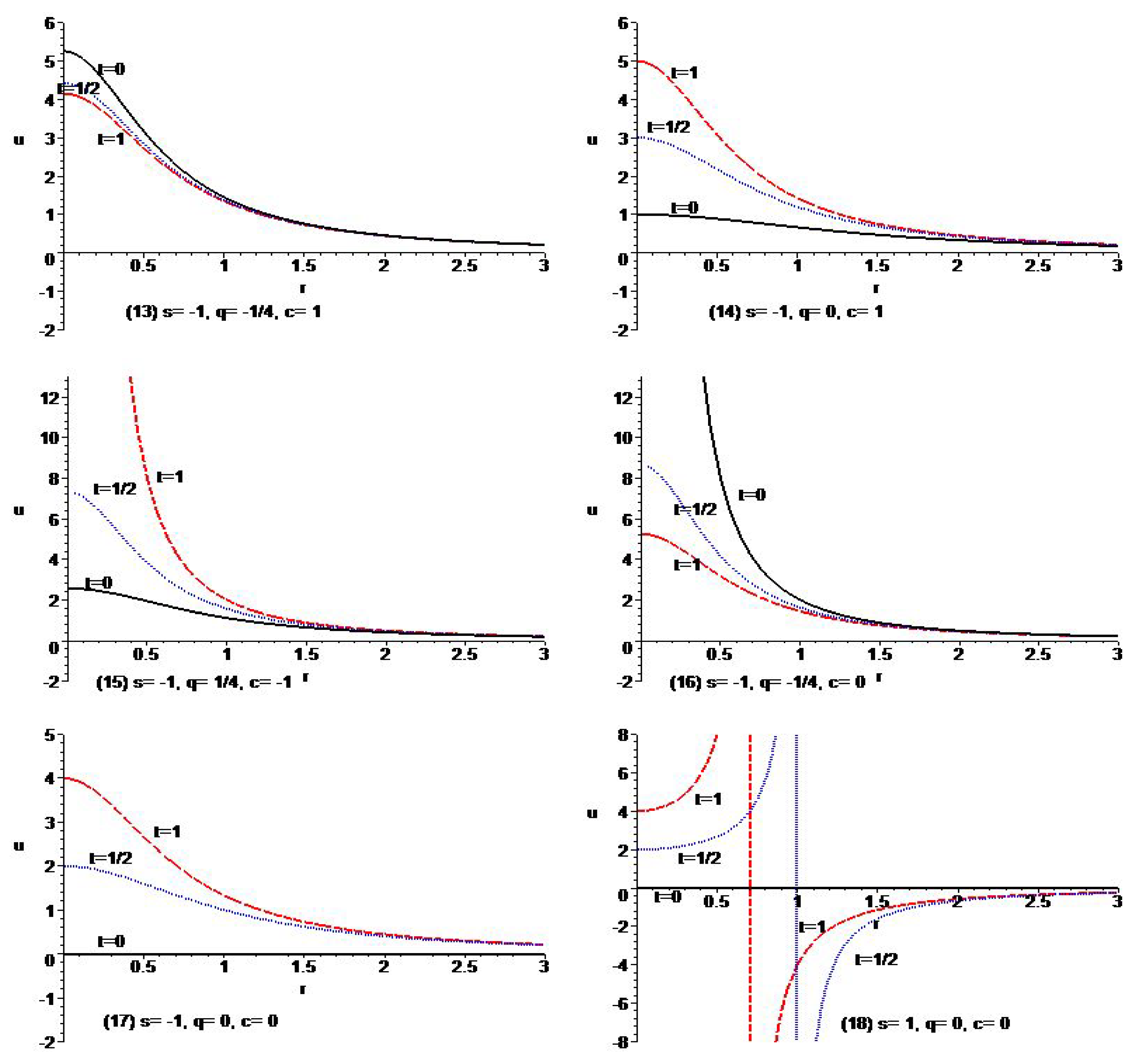
- (i)
- For ,
- (ii)
- For ,
- (iii)
- For ,
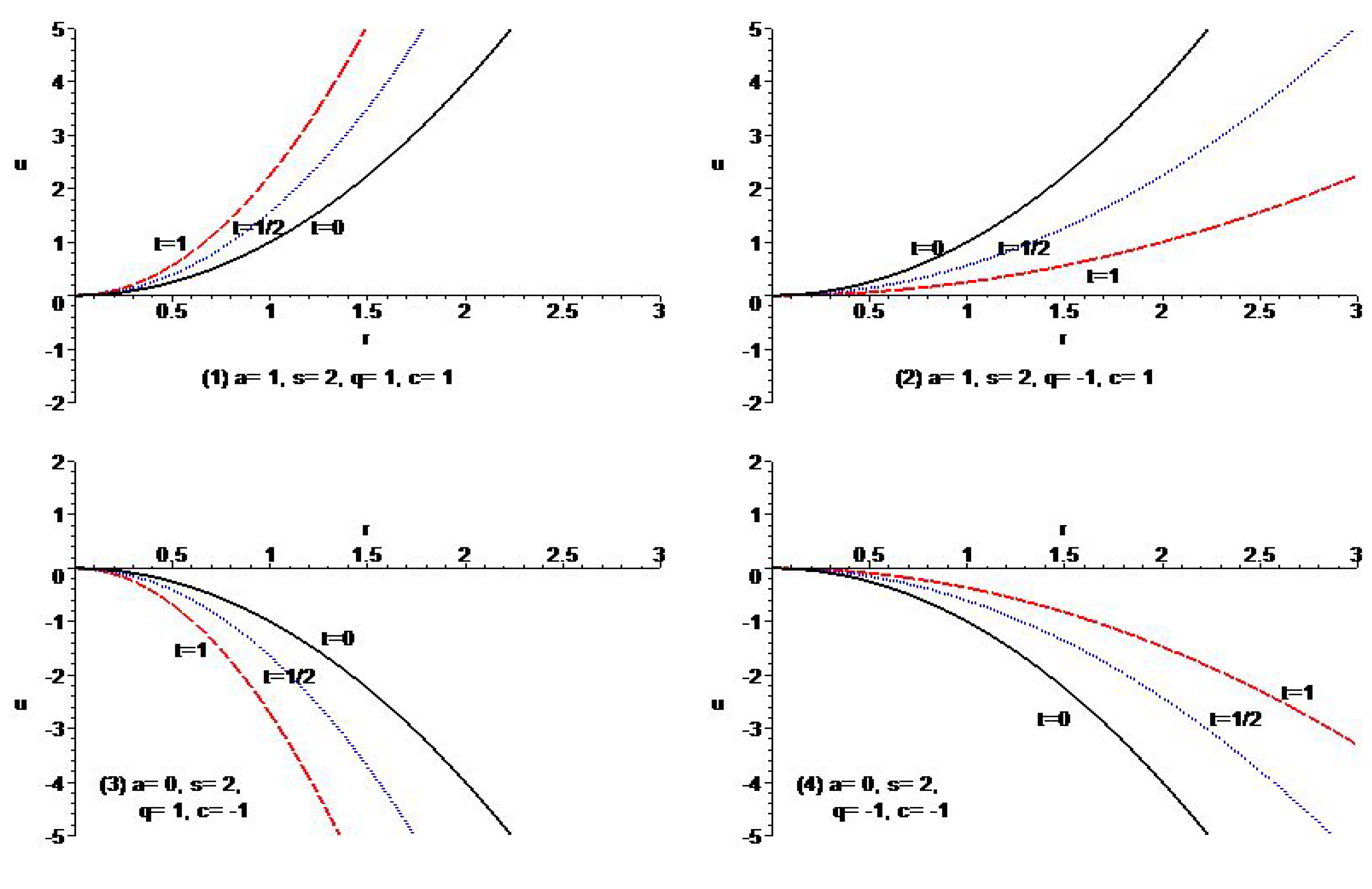
- (i)
- For ,
- (ii)
- For ,
- (i)
- For ,
- (ii)
- For ,
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qu, C.Z.; Estévez, P.G. On nonlinear diffusion equations with x-dependent convection and absorption. Nonlinear Anal. TMA 2004, 57, 549–557. [Google Scholar] [CrossRef]
- Qu, C.; Ji, L.; Wang, L. Conditional Lie Bäcklund Symmetries and Sign-Invariants to Quasi-Linear Diffusion Equations. Stud. Appl. Math. 2007, 119, 355–391. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, X.; Yan, R. Conditional Lie–Bäcklund symmetries and sign-invariants to second-order evolution equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3476–3482. [Google Scholar] [CrossRef]
- Galaktionov, V.A. Quasilinear heat equations with first-order sign-invariants and new explicit solutions. Nonlinear Anal. Theory Methods Appl. 1994, 23, 1595–1621. [Google Scholar] [CrossRef]
- Galaktionov, V.A.; Posashkov, S.A. New explicit solutions of quasilinear heat equations with general first-order sign-invariants. Phys. D Nonlinear Phenom. 1996, 99, 217–236. [Google Scholar] [CrossRef]
- Galaktionov, V.A.; Svirshchevskii, S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Galaktionov, V.A.; Posashkov, S.A. Maximal sign-invariants of quasilinear heat equations with gradient diffusivity. J. Math. Phys. 1998, 39, 4948–4964. [Google Scholar] [CrossRef]
- Olver, P.J. Direct reduction and differential constraints. Proc. R. Soc. Lond. A 1994, 444, 509–523. [Google Scholar] [CrossRef]
- Galaktionov, V.A. Two methods of comparison of solutions of parabolic equations. Sov. Phys. Dok. 1980, 25, 250–252. [Google Scholar]
- Ji, L.; Feng, W. Second-Order Conditional Lie–Bäcklund Symmetries and Differential Constraints of Nonlinear Reaction–Diffusion Equations with Gradient-Dependent Diffusivity. Symmetry 2018, 10, 267. [Google Scholar] [CrossRef] [Green Version]
- Grarilov, V.P.; Klepikova, N.V.; Rodean, H.C. Trials of nonlinear diffusion equation as a model of turbulent diffusion. Atmo. Env. 1995, 29, 2317–2322. [Google Scholar]
- Pascal, J.; Pascal, H. On some non-linear shear flows of non-Newtonian fluids. Int. J. Nonlinear Mech. 1995, 30, 487–500. [Google Scholar] [CrossRef]
- Assis, P.C., Jr.; Da Silva, L.R.; Lenzi, E.K.; Malacarne, L.C.; Mendes, R.S. Nonlinear diffusion equation, Tsallis formalism and exact solutions. J. Math. Phys. 2005, 46, 123303. [Google Scholar] [CrossRef]
- Bokhari, H.; AI Deweik, A.Y.; Kara, A.H.; Zaman, F.D. A symmetry analysis of some classes of evolutionary nonlinear (2+1)-diffusion equations with variable diffusivity. Nonlinear Dyn. 2010, 62, 127–138. [Google Scholar] [CrossRef]
- Opanasenko, S.; Boyko, V.; Popovych, R.O. Enhanced group classification of nonlinear diffusion–reaction equations with gradient-dependent diffusivity. J. Math. Anal. Appl. 2020, 484, 123739. [Google Scholar] [CrossRef] [Green Version]
- Cherniha, R.; Kovalenko, S. Lie symmetries and reductions of multi-dimensional boundary value problems of the Stefan type. J. Phys. A Math. Theor. 2011, 44, 485202. [Google Scholar] [CrossRef]
- Cherniha, R.; Serov, M.; Prystavka, Y. A complete Lie symmetry classification of a class of (1+2)-dimensional reaction-diffusion-convection equations. Commun. Nonlinear Sci. Numer. Simul. 2020, 92, 105466. [Google Scholar] [CrossRef]
- Cherniha, R.; King, J.R.; Kovalenko, S. Lie symmetry properties of nonlinear reaction-diffusion equations with gradient-dependent diffusivity. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 98–108. [Google Scholar] [CrossRef] [Green Version]
- Cherniha, R.; King, J.R. Lie and Conditional Symmetries of a Class of Nonlinear (1 + 2)-Dimensional Boundary Value Problems. Symmetry 2015, 7, 1410–1435. [Google Scholar] [CrossRef] [Green Version]
- Broadbridge, P.; Bradshaw-Hajek, B.H.; Triadis, D. Exact non-classical symmetry solutions of Arrhenius reaction–diffusion. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150580. [Google Scholar] [CrossRef] [Green Version]
- Broadbridge, P.; Daly, E.; Goard, J.M. Exact solutions of the Richards equation with nonlinear pant-root extraction. Water Resour. Res. 2017, 53, 9679–9691. [Google Scholar] [CrossRef]
- Goard, J.; Broadbridge, P. Nonclassical symmetry analysis of nonlinear reaction-diffusion equations in two spatial dimensions. Nonlinear Anal. Theory Methods Appl. 1996, 26, 735–754. [Google Scholar] [CrossRef]
- Ji, L.; Wang, R. Conditional Lie-Bäcklund Symmetries and Differential Constraints of Radially Symmetric Nonlinear Convection-Diffusion Equations with Source. Entropy 2020, 22, 873. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.Y.; Yin, H. Separation of variables solutions of nonlinear reaction-diffusion system. J. Phys. A Math. Theor. 2007, 40, 3389–3398. [Google Scholar]
- Zhu, X.N.; Zhang, S.L. Sign-invariant and explicit solutions of nonlinear reaction-diffusion systems. Comm. Theor. Phys. 2008, 49, 1361–1364. [Google Scholar]
- Friedman, A.; McLeod, B. Blow-up of positive solutions of semilinear heat equation. Ind. Univ. Math. J. 1985, 34, 425–447. [Google Scholar] [CrossRef]
- Galaktionov, V.A.; Posashkov, S.A. Single point blow-up for N-dimensional quasi-linear equations with gradient diffusion and source. Ind. Univ. Math. J. 1991, 40, 1041–1060. [Google Scholar] [CrossRef]
- Galaktionov, V.A. Groups of scalings and invariant sets for higher-order nonlinear evolution equations. Diff. Int. Equ. 2001, 14, 913–924. [Google Scholar]
- Qu, C.; Estévez, P. Extended rotation and scaling groups for nonlinear evolution equations. Nonlinear Anal. Theory, Methods Appl. 2003, 52, 1655–1673. [Google Scholar] [CrossRef]
- Qu, C. Symmetries and solutions to the thin film equations. J. Math. Anal. Appl. 2006, 317, 381–397. [Google Scholar] [CrossRef] [Green Version]
- Britton, N.F. Essential Mathematical Biology; Springer: Singapore, 2003. [Google Scholar]
- Benia, Y.; Scapellato, A. Existence of solution to Korteweg-de Vries equation in a non-parabolic domain. Nonlinear Anal. Theory Methods Appl. 2020, 195, 111758. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, L.; Luo, X.; Zeng, J.; Xiao, M.; Meng, Y. First-Order Sign-Invariants and Exact Solutions of the Radially Symmetric Nonlinear Diffusion Equations with Gradient-Dependent Diffusivities. Symmetry 2022, 14, 386. https://doi.org/10.3390/sym14020386
Ji L, Luo X, Zeng J, Xiao M, Meng Y. First-Order Sign-Invariants and Exact Solutions of the Radially Symmetric Nonlinear Diffusion Equations with Gradient-Dependent Diffusivities. Symmetry. 2022; 14(2):386. https://doi.org/10.3390/sym14020386
Chicago/Turabian StyleJi, Lina, Xiankang Luo, Jiao Zeng, Min Xiao, and Yuanhua Meng. 2022. "First-Order Sign-Invariants and Exact Solutions of the Radially Symmetric Nonlinear Diffusion Equations with Gradient-Dependent Diffusivities" Symmetry 14, no. 2: 386. https://doi.org/10.3390/sym14020386
APA StyleJi, L., Luo, X., Zeng, J., Xiao, M., & Meng, Y. (2022). First-Order Sign-Invariants and Exact Solutions of the Radially Symmetric Nonlinear Diffusion Equations with Gradient-Dependent Diffusivities. Symmetry, 14(2), 386. https://doi.org/10.3390/sym14020386





