Semi-Analytical Method for Unsymmetrical Doublet Flow Using Sink- and Source-Dominant Formulation
Abstract
1. Introduction
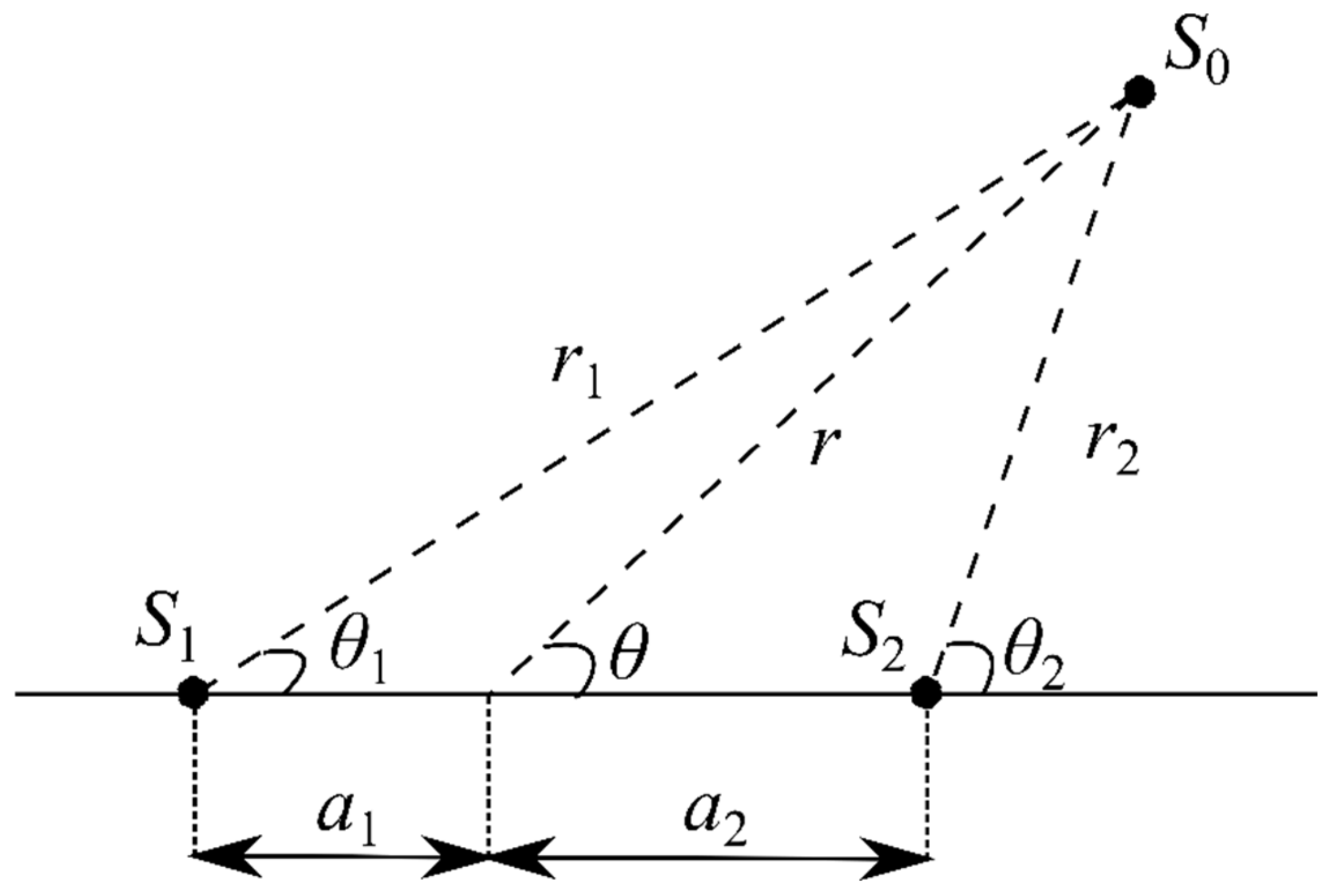
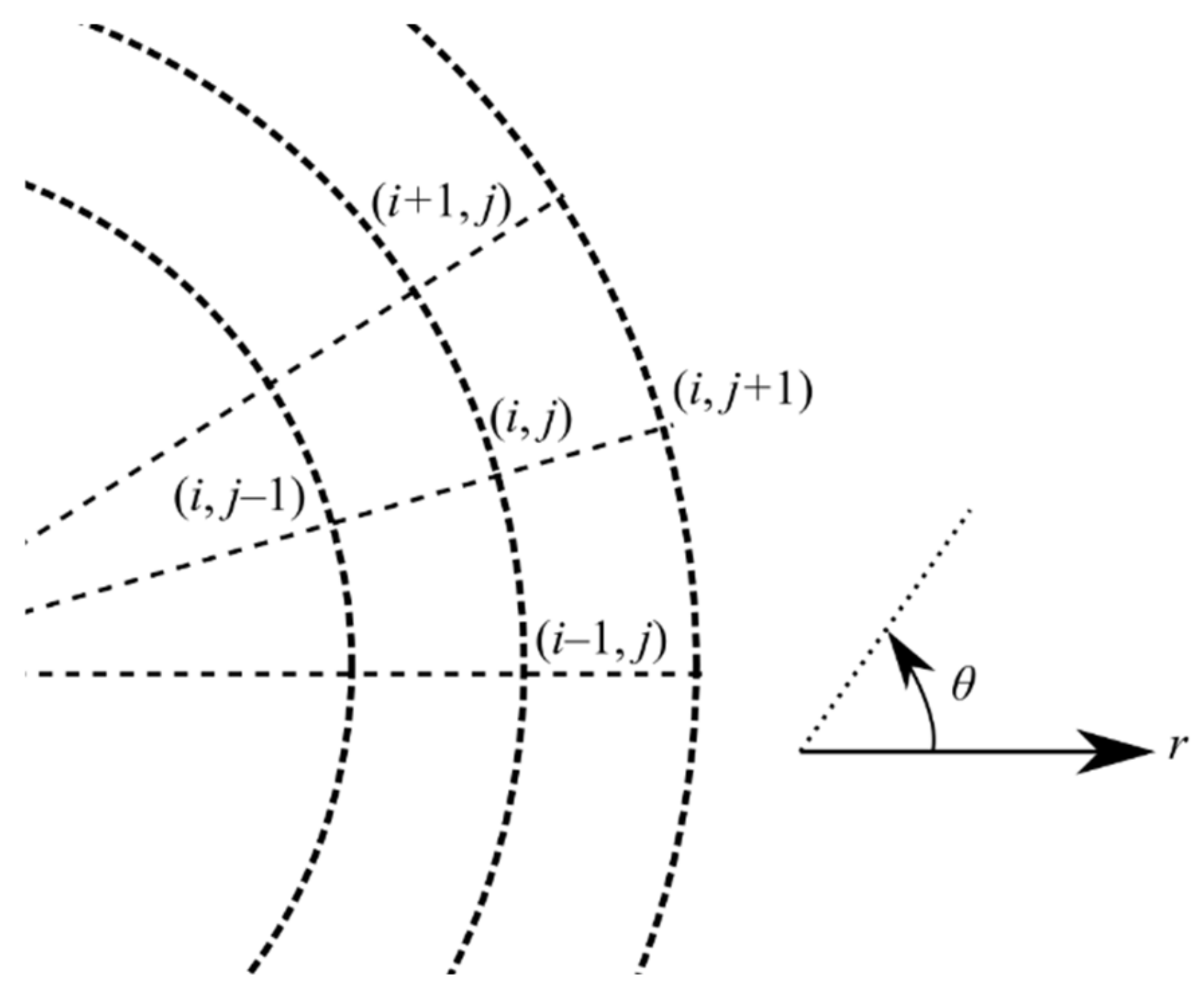
2. Mathematical Formulation of Unsymmetrical Doublet Flow
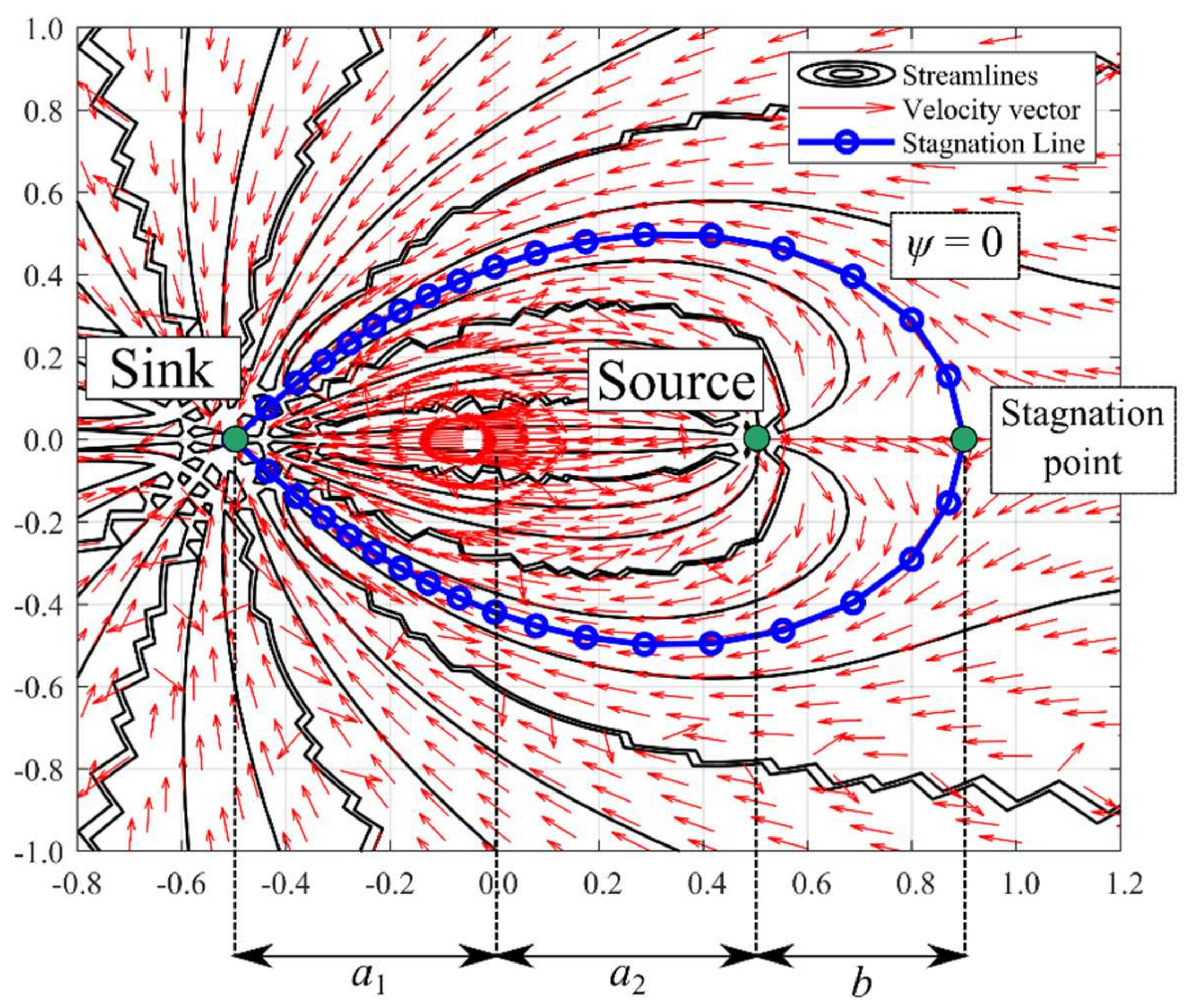
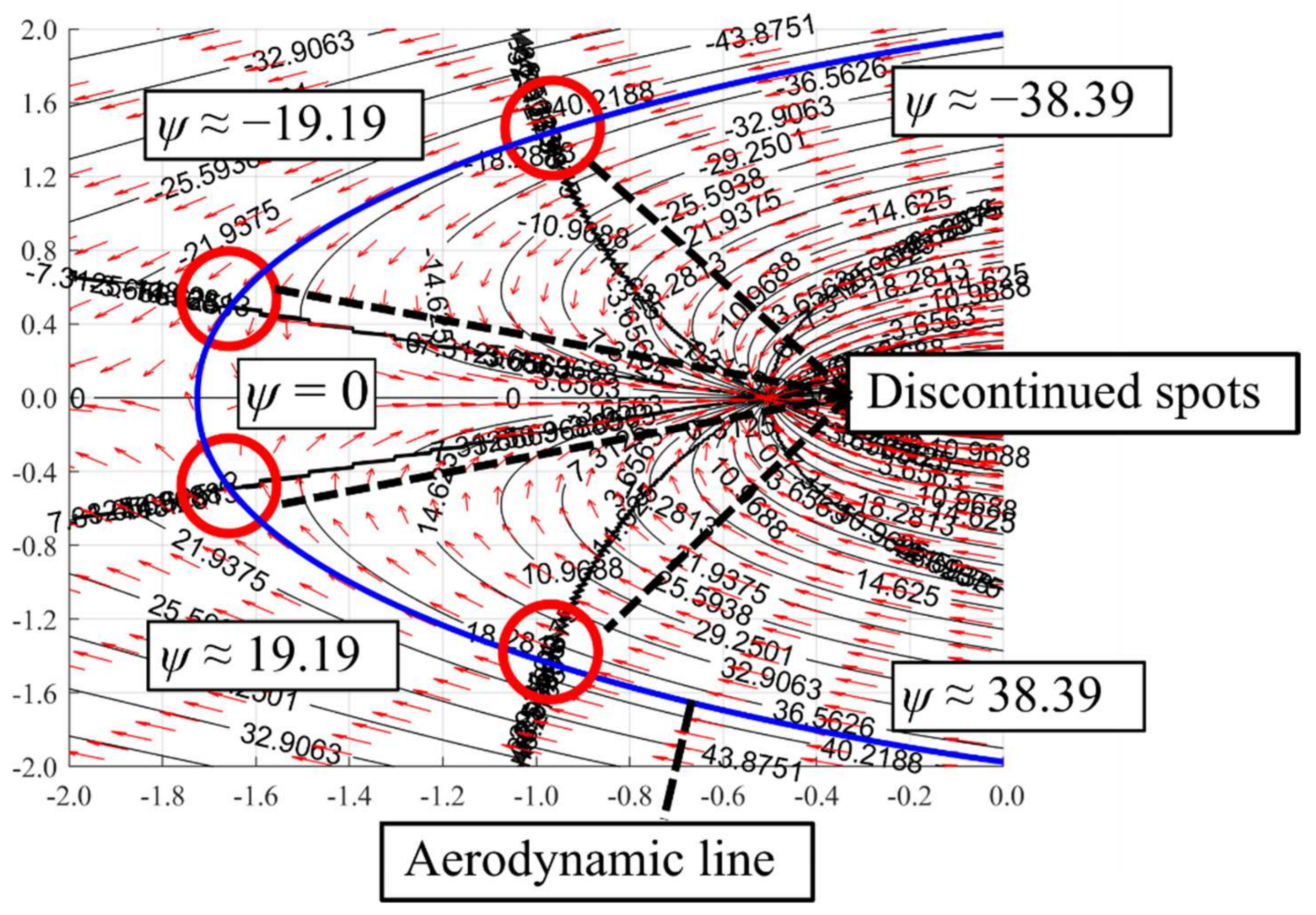
3. Flow Structure of Unsymmetrical Doublet Flows
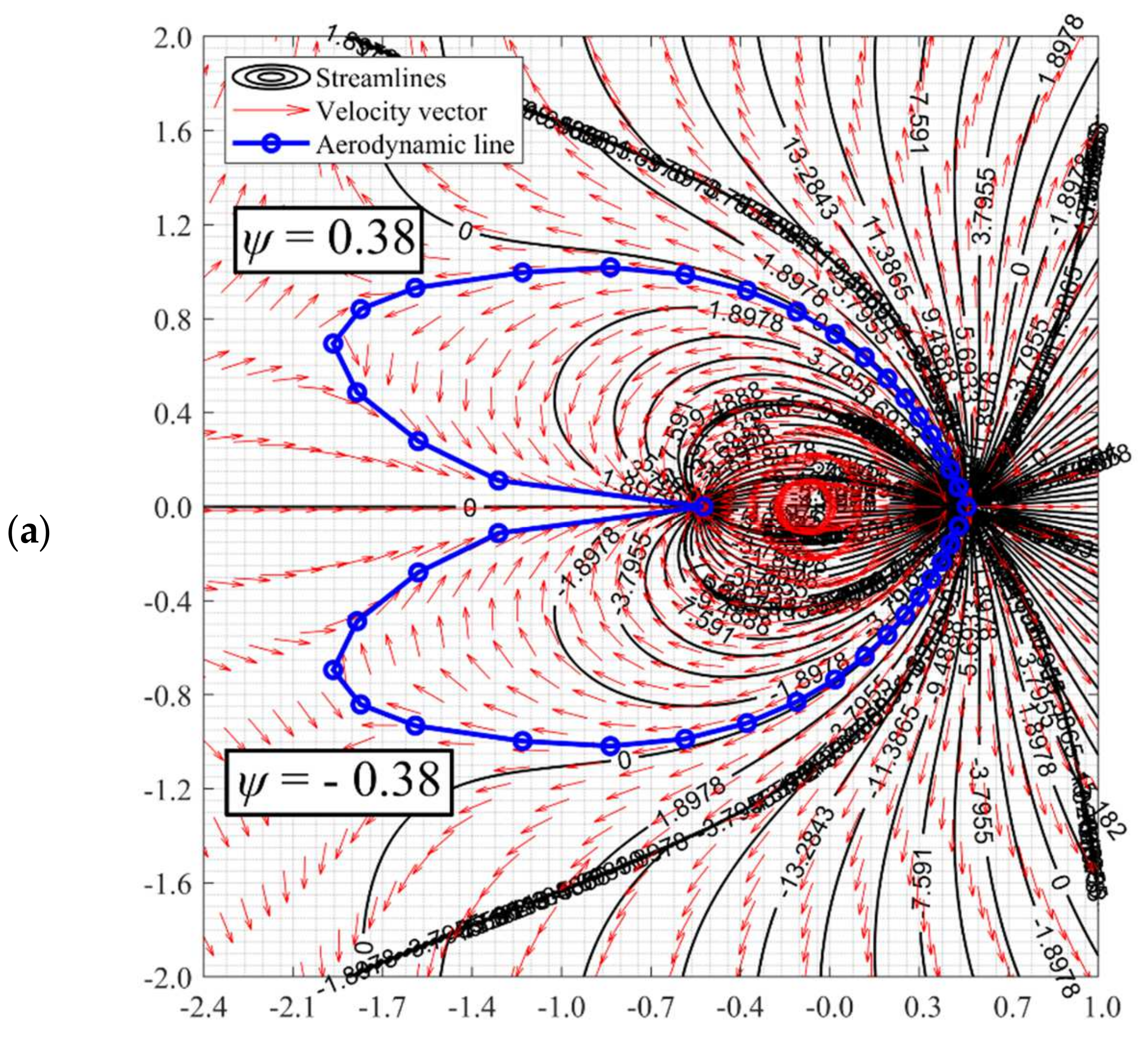
3.1. Pure Unsymmetrical Doublet Flow
3.2. Superposition of Unsymmetrical Doublet Flow with Far-Field Flow
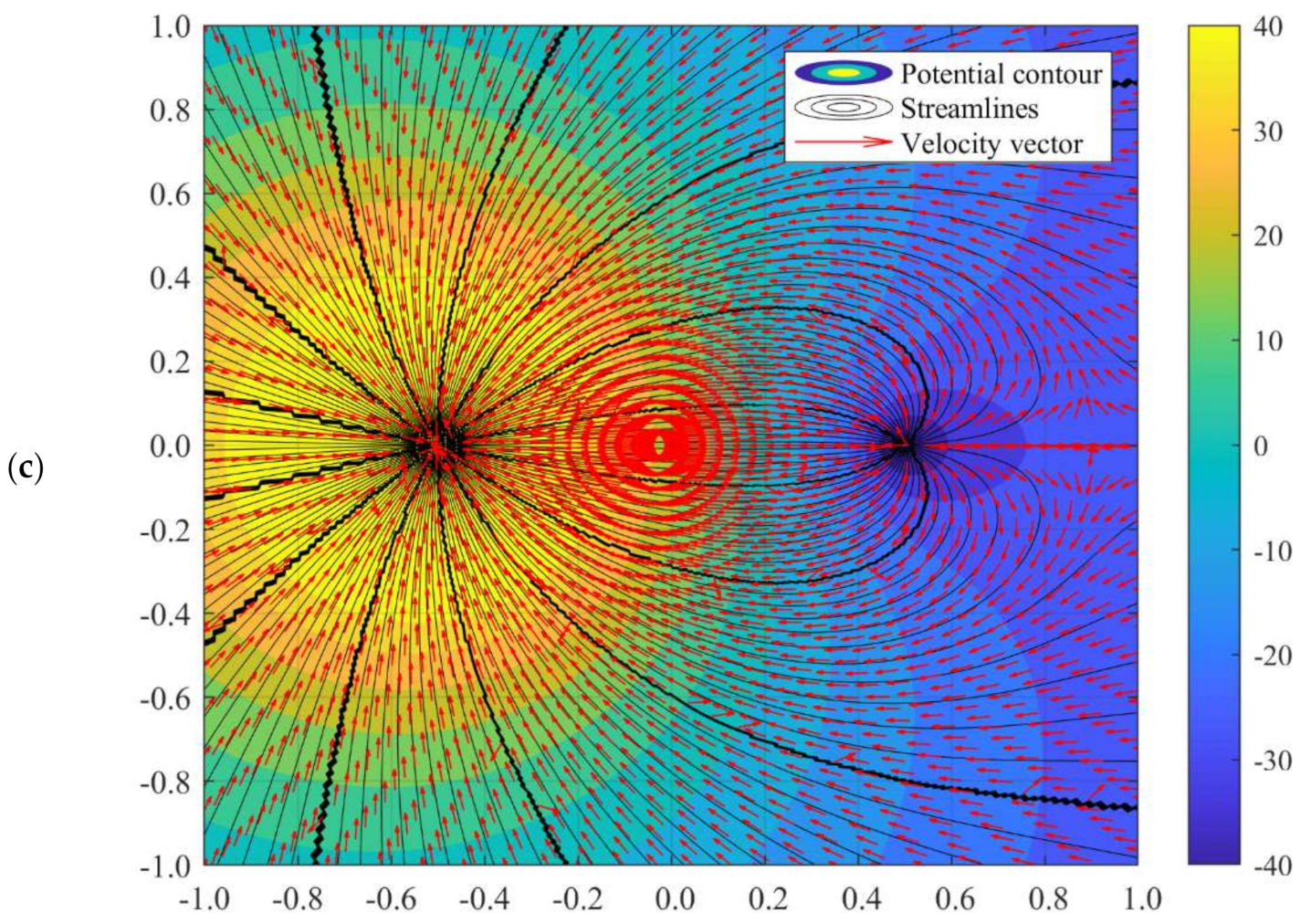
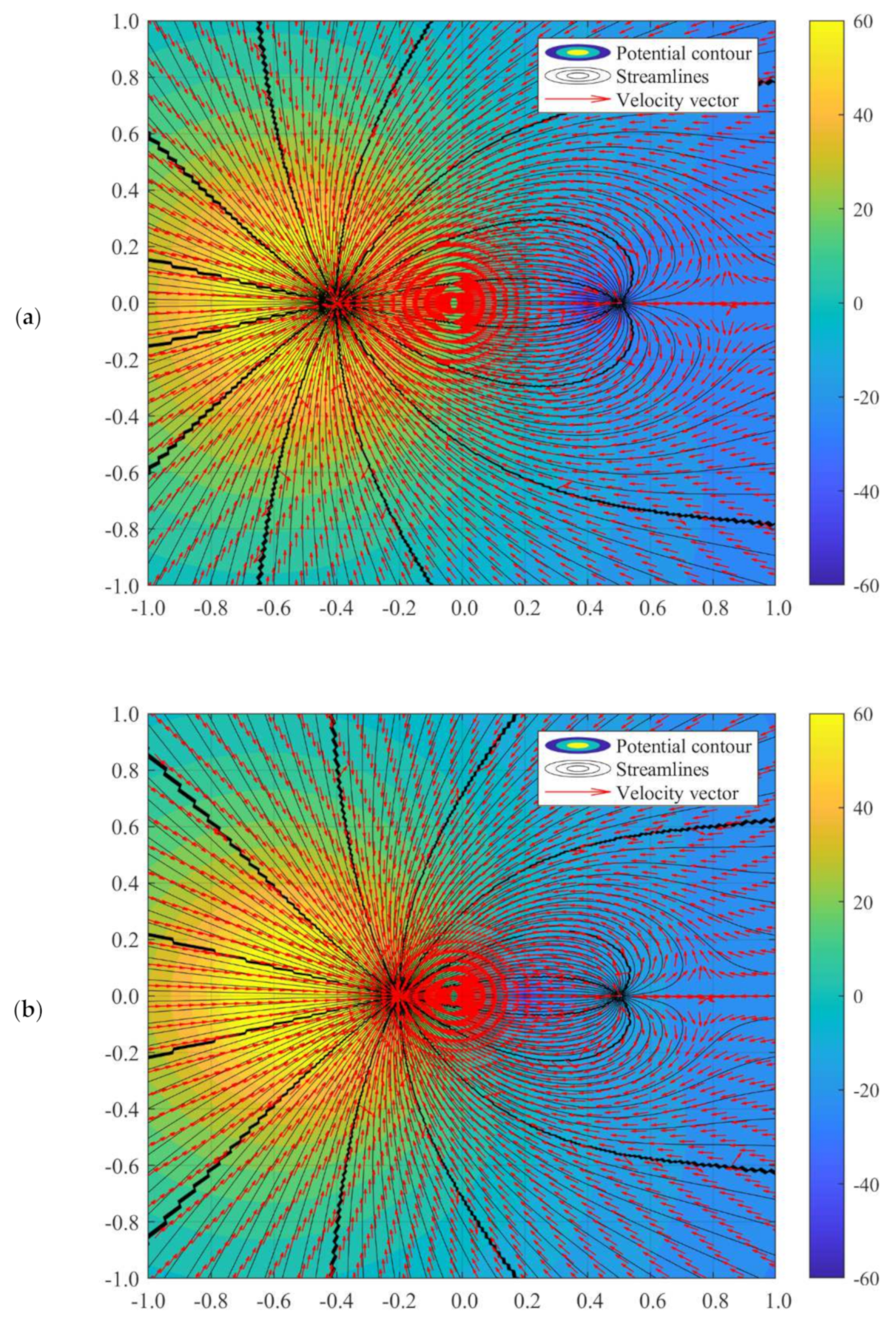
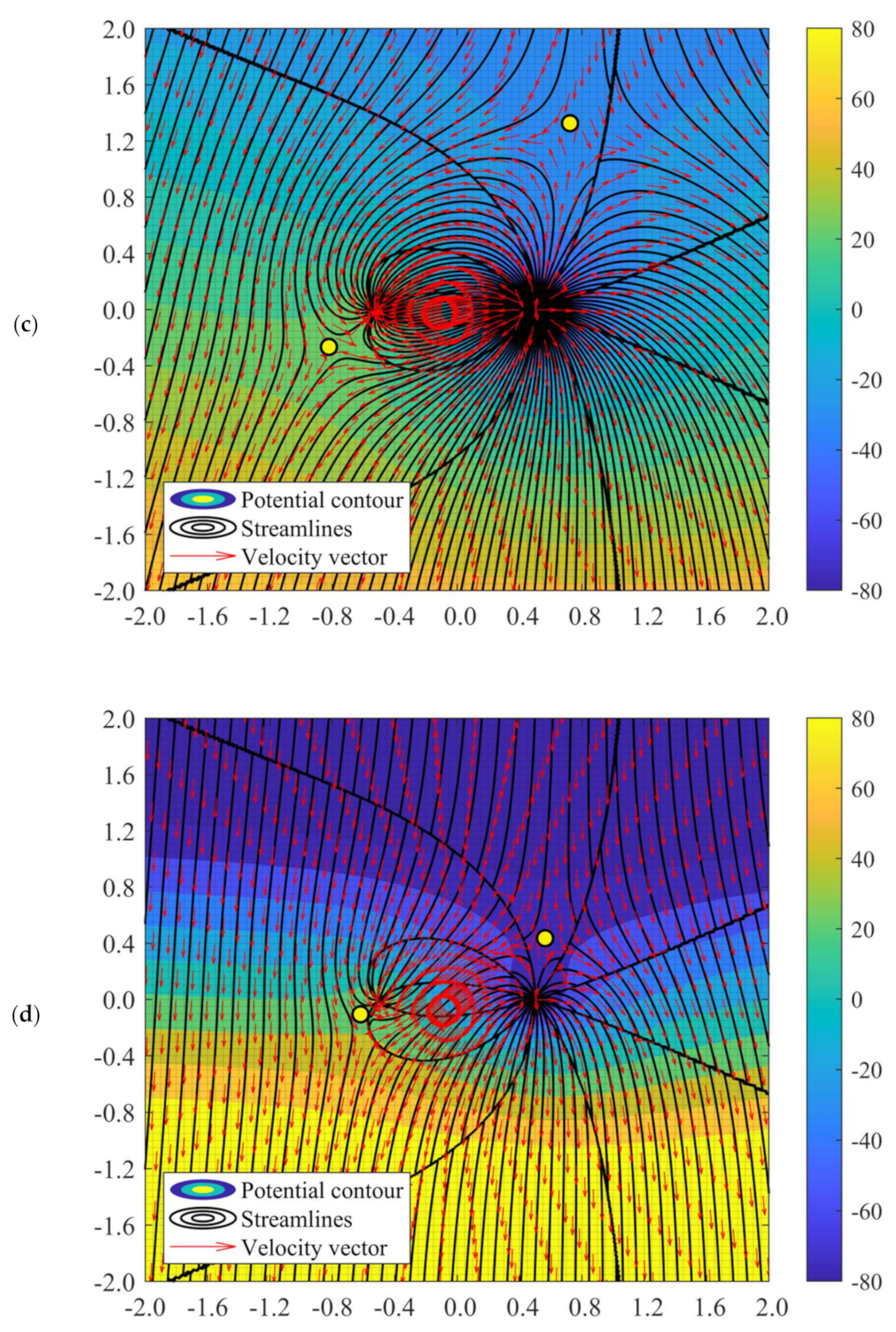
3.2.1. Sink-Dominant Superposed Flow
3.2.2. Source-Dominant Superposed Flow
3.3. Effects of Far-Field Flow Orientation on Unsymmetrical Doublet Flow
4. Potential Aerodynamic Applications of Unsymmetrical Doublet Flows
5. Conclusions and Recommendation
- Doublet boundary would be distorted to form convex (due to low far-field velocity), concave (due to high far-field velocity), and other interesting shapes (in what condition).
- The conceptual study provides deeper insight into the flow structure of the effect of unbalanced sink-source strength.
- The research output potentially to apply in innovative environmental flow design and renders an alternative to formulate an aerodynamic curve for the design of bio-inspired structures in the near future.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| ϕ | Velocity potential |
| ψ | Stream function |
| m | Strength of source/sink |
| r | Distance from source/sink to arbitrary point within the problem domain |
| u | Velocity |
References
- Bruce, R.M.; Donald, F.Y.; Theodore, H.O. Fundamentals of Fluid Mechanics, 5th ed.; John Wiley & Sons (Asia) Pte Ltd.: Singapore, 2006. [Google Scholar]
- Holzbecher, E. Potential Flow. In Encyclopedia of Water; Wiley: Hoboken, NJ, USA, 2019; pp. 1–10. [Google Scholar]
- Katopodes, N.D. Ideal Fluid Flow. In Free-Surface Flow; Elsevier: Amsterdam, The Netherlands, 2019; pp. 428–515. [Google Scholar]
- Jiang, T.; Zhang, J.; Wan, W.; Cui, S.; Deng, D. 3D transient numerical flow simulation of groundwater bypass seepage at the dam site of Dongzhuang hydro-junction. Eng. Geol. 2017, 231, 176–189. [Google Scholar] [CrossRef]
- Mategaonkar, M. Simulation of groundwater flow using meshfree collocation method with Cubic Spline function. Groundw. Sustain. Dev. 2021, 13, 100579. [Google Scholar] [CrossRef]
- Seyedpour, S.; Kirmizakis, P.; Brennan, P.; Doherty, R.; Ricken, T. Optimal remediation design and simulation of groundwater flow coupled to contaminant transport using genetic algorithm and radial point collocation method (RPCM). Sci. Total Environ. 2019, 669, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.-J.; Hwang, H.-T.; Suzuki, S.; Saegusa, H.; Nojiri, K.; Tanaka, T.; Bruines, P.; Abumi, K.; Morita, Y.; Illman, W. Improving precision in regional scale numerical simulations of groundwater flow into underground openings. Eng. Geol. 2020, 274, 105727. [Google Scholar] [CrossRef]
- Xie, Y.; Wu, J.; Nan, T.; Xue, Y.; Xie, C.; Ji, H. Efficient triple-grid multiscale finite element method for 3D groundwater flow simulation in heterogeneous porous media. J. Hydrol. 2017, 546, 503–514. [Google Scholar] [CrossRef]
- Xia, C.-A.; Pasetto, D.; Hu, B.X.; Putti, M.; Guadagnini, A. Integration of moment equations in a reduced-order modeling strategy for Monte Carlo simulations of groundwater flow. J. Hydrol. 2020, 590, 125257. [Google Scholar] [CrossRef]
- Pathania, T.; Eldho, T.; Bottacin-Busolin, A. Coupled simulation of groundwater flow and multispecies reactive transport in an unconfined aquifer using the element-free Galerkin method. Eng. Anal. Bound. Elem. 2020, 121, 31–49. [Google Scholar] [CrossRef]
- Swathi, B.; Eldho, T. Groundwater flow simulation in unconfined aquifers using meshless local Petrov–Galerkin method. Eng. Anal. Bound. Elem. 2014, 48, 43–52. [Google Scholar] [CrossRef]
- Hanssen, F.-C.W.; Greco, M. A potential flow method combining immersed boundaries and overlapping grids: Formulation, validation and verification. Ocean Eng. 2021, 227, 108841. [Google Scholar] [CrossRef]
- Anderson, E.I. An analytical solution representing groundwater-surface water interaction. Water Resour. Res. 2003, 39, 1071. [Google Scholar] [CrossRef]
- Wang, C.; Mu, X.; He, Y.; Li, D.; Shi, Y. A novel potential flow model for granular flow in two-dimensional flat-bottomed packed bed with centric discharge. Powder Technol. 2019, 342, 545–554. [Google Scholar] [CrossRef]
- Bakker, M.; Miller, A.D.; Morgan, L.; Werner, A. Evaluation of analytic solutions for steady interface flow where the aquifer extends below the sea. J. Hydrol. 2017, 551, 660–664. [Google Scholar] [CrossRef]
- Liu, W.-Q.; Xiong, L.-N.; Zhang, G.-W.; Yang, M.; Wu, W.-G.; Song, X.-M. Research on Hydroelastic Response of an FMRC Hexagon Enclosed Platform. Symmetry 2021, 13, 1110. [Google Scholar] [CrossRef]
- Magdalena, I.; Firdaus, K. Numerical Study for Unsteady Waves Generated by Flow over a Permeable Wavy Bed. Fluids 2021, 7, 9. [Google Scholar] [CrossRef]
- Chen, Z.-M.; Price, W.G. Dissipative free-surface solver for potential flow around hydrofoil distributed with doublets. Appl. Math. Mech. 2012, 33, 1467–1480. [Google Scholar] [CrossRef]
- Frayssinhes, R.; Girardon, S.; Denaud, L.; Collet, R. Modeling the Influence of Knots on Douglas-Fir Veneer Fiber Orientation. Fibers 2020, 8, 54. [Google Scholar] [CrossRef]
- Sahin, I.; Hyman, M. Numerical calculation for the flow of submerged bodies under a free surface. Ocean Eng. 1993, 20, 339–347. [Google Scholar] [CrossRef]
- Huggins, A.; Packwood, A. The optimum dimensions for a long-range, autonomous, deep-diving, underwater vehicle for oceanographic research. Ocean Eng. 1994, 21, 45–56. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Q.; Gorodtsov, V. Wave drag of rapidly and horizontally moving Rankine ovoid in uniformly stratified fluid. Prog. Nat. Sci. 2008, 18, 723–727. [Google Scholar] [CrossRef]
- Suner, M.; Salci, S.A.; Yigit, K.S.; Kandemir, I. Analytical analysis of hydrodynamics of the perforated Rankine oval. Ocean Eng. 2015, 108, 227–240. [Google Scholar] [CrossRef]
- Raven, H.C. A method to correct shallow-water model tests for tank wall effects. J. Mar. Sci. Technol. 2018, 24, 437–453. [Google Scholar] [CrossRef]
- Roisman, I.; Yarin, A.; Rubin, M. Normal penetration of an eroding projectile into an elastic–plastic target. Int. J. Impact Eng. 2001, 25, 573–597. [Google Scholar] [CrossRef]
- Rubin, M.; Kositski, R.; Rosenberg, Z. Essential physics of target inertia in penetration problems missed by cavity expansion models. Int. J. Impact Eng. 2016, 98, 97–104. [Google Scholar] [CrossRef]
- Rubin, M. A simplified and modified model for long rod penetration based on ovoids of Rankine. Int. J. Impact Eng. 2021, 156, 103927. [Google Scholar] [CrossRef]
- Trivedi, C. A review on fluid structure interaction in hydraulic turbines: A focus on hydrodynamic damping. Eng. Fail. Anal. 2017, 77, 1–22. [Google Scholar] [CrossRef]
- Cola, B.A.; Schaffer, D.; Fisher, T.S.; Stremler, M. A Pulsed Source-Sink Fluid Mixing Device. J. Microelectromech. Syst. 2006, 15, 259–266. [Google Scholar] [CrossRef]
- Basu, A.S.; Gianchandani, Y.B. Microfluidic doublets in aqueous samples generated by microfabricated thermal probes. Sens. Actuators A Phys. 2010, 158, 116–120. [Google Scholar] [CrossRef]
- Benouaguef, I.; Musunuri, N.; Amah, E.C.; Blackmore, D.; Fischer, I.S.; Singh, P. Solutocapillary Marangoni flow induced in a waterbody by a solute source. J. Fluid Mech. 2021, 922. [Google Scholar] [CrossRef]
- Pinsker, F.; Berloff, N.G. Transitions and excitations in a superfluid stream passing small impurities. Phys. Rev. A 2014, 89, 053605. [Google Scholar] [CrossRef]
- Luo, F.; Xu, R.-N.; Jiang, P.-X. Numerical investigation of fluid flow and heat transfer in a doublet enhanced geothermal system with CO2 as the working fluid (CO2–EGS). Energy 2014, 64, 307–322. [Google Scholar] [CrossRef]
- Willems, C.; Nick, H.M.; Weltje, G.J.; Bruhn, D.F. An evaluation of interferences in heat production from low enthalpy geothermal doublets systems. Energy 2017, 135, 500–512. [Google Scholar] [CrossRef]
- Zhao, Z.; Dou, Z.; Liu, G.; Chen, S.; Tan, X. Equivalent flow channel model for doublets in heterogeneous porous geothermal reservoirs. Renew. Energy 2021, 172, 100–111. [Google Scholar] [CrossRef]
- Mahbaz, S.B.; Yaghoubi, A.; Dehghani-Sanij, A.; Sarvaramini, E.; Leonenko, Y.; Dusseault, M.B. Well-Doublets: A First-Order Assessment of Geothermal SedHeat Systems. Appl. Sci. 2021, 11, 697. [Google Scholar] [CrossRef]
- Kong, Y.; Pang, Z.; Shao, H.; Kolditz, O. Optimization of well-doublet placement in geothermal reservoirs using numerical simulation and economic analysis. Environ. Earth Sci. 2017, 76, 118. [Google Scholar] [CrossRef]
- Romanov, D.; Leiss, B. Analysis of Enhanced Geothermal System Development Scenarios for District Heating and Cooling of the Göttingen University Campus. Geosciences 2021, 11, 349. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Mohammadzadeh-Habili, J.; Parsaie, A. Development of an evaluation method for velocity distribution over cylindrical weirs using doublet concept. Flow Meas. Instrum. 2018, 61, 79–83. [Google Scholar] [CrossRef]
- Severino, G. Dispersion in doublet-type flows through highly anisotropic porous formations. J. Fluid Mech. 2021, 931. [Google Scholar] [CrossRef]
- Weijermars, R.; Van Harmelen, A. Breakdown of doublet recirculation and direct line drives by far-field flow in reservoirs: Implications for geothermal and hydrocarbon well placement. Geophys. J. Int. 2016, 206, 19–47. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamentals and Applications; McGraw Hill: New York, NY, USA, 2014; ISBN 9780073380322. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Differentiation and Integration. In Numerical Methods for Engineers; McGraw Hill: New York, NY, USA, 2010; pp. 585–698. [Google Scholar]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Cheah, C.K.; Tey, W.Y. Construction on Morphology of Aquatic Animals via Moving Least Squares Method. J. Phys. Conf. Ser. 2020, 1489, 012014. [Google Scholar] [CrossRef]
- Tey, W.Y.; Sidik, N.A.C.; Asako, Y.; Muhieldeen, M.W.; Afshar, O. Moving Least Squares Method and its Improvement: A Concise Review. J. Appl. Comput. Mech. 2021, 7, 883–889. [Google Scholar]
- Durst, F. Potential Flow. In Fluid Mechanics: An Introduction to the Theory of Fluids; Springer: Berlin/Heidelberg, Germany, 2008; pp. 275–288. [Google Scholar]
- Wright, J.R.; Cooper, J.E. Potential Flow Aerodynamics. In Introduction to Aircraft Aeroelasticity and Loads; John Wiley & Sons Ltd.: Chichester, UK, 2015; pp. 415–436. [Google Scholar]
- Lippert, T.; Bandelin, J.; Schlederer, F.; Drewes, J.E.; Koch, K. Impact of ultrasound-induced cavitation on the fluid dynamics of water and sewage sludge in ultrasonic flatbed reactors. Ultrason. Sonochem. 2019, 55, 217–222. [Google Scholar] [CrossRef] [PubMed]
- Aono, H.; Liu, H. Flapping wing aerodynamics of a numerical biological flyer model in hovering flight. Comput. Fluids 2013, 85, 85–92. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Sun, M. Aerodynamics of Ascending Flight in Fruit Flies. J. Bionic Eng. 2017, 14, 75–87. [Google Scholar] [CrossRef]
- Liu, H. Integrated modeling of insect flight: From morphology, kinematics to aerodynamics. J. Comput. Phys. 2009, 228, 439–459. [Google Scholar] [CrossRef]
- Zimmerman, S.; Abdelkefi, A. Review of marine animals and bioinspired robotic vehicles: Classifications and characteristics. Prog. Aerosp. Sci. 2017, 93, 95–119. [Google Scholar] [CrossRef]
- Scaradozzi, D.; Palmieri, G.; Costa, D.; Pinelli, A. BCF swimming locomotion for autonomous underwater robots: A review and a novel solution to improve control and efficiency. Ocean Eng. 2017, 130, 437–453. [Google Scholar] [CrossRef]
- Bian, J.; Xiang, J. QUUV: A quadrotor-like unmanned underwater vehicle with thrusts configured as X shape. Appl. Ocean Res. 2018, 78, 201–211. [Google Scholar] [CrossRef]
- Salazar, R.; Fuentes, V.; Abdelkefi, A. Classification of biological and bioinspired aquatic systems: A review. Ocean Eng. 2018, 148, 75–114. [Google Scholar] [CrossRef]
- Hudson, O.A.; Fanni, M.; Ahmed, S.M.; Sameh, A. Autonomous Flight Take-off in Flapping Wing Aerial Vehicles. J. Intell. Robot. Syst. 2019, 98, 135–152. [Google Scholar] [CrossRef]
- Hilfinger, A.; Chattopadhyay, A.K.; Jülicher, F. Nonlinear dynamics of cilia and flagella. Phys. Rev. E 2009, 79, 051918. [Google Scholar] [CrossRef] [PubMed]
- Frumkin, V.; Gommed, K.; Bercovici, M. Dipolar thermocapillary motor and swimmer. Phys. Rev. Fluids 2019, 4, 074002. [Google Scholar] [CrossRef]
- Klindt, G.S.; Friedrich, B.M. Flagellar swimmers oscillate between pusher- and puller-type swimming. Phys. Rev. E 2015, 92, 063019. [Google Scholar] [CrossRef]
- Junqiang, L.; Yiling, Y.; Chuanyu, W.; Guoping, L.; Tehuan, C.; Jianqiang, M. Underwater oscillation performance and 3D vortex distribution generated by miniature caudal fin-like propulsion with macro fiber composite actuation. Sens. Actuators A Phys. 2020, 303, 111587. [Google Scholar] [CrossRef]
- Moore, P. Examining dolphin hydrodynamics provides clues to calf-loss during tuna fishing. J. Biol. 2004, 3, 6. [Google Scholar] [CrossRef][Green Version]
- Herrel, A.; Choi, H.-F.; De Schepper, N.; Aerts, P.; Adriaens, D. Kinematics of swimming in two burrowing anguilliform fishes. Zoology 2011, 114, 78–84. [Google Scholar] [CrossRef]
- Xiang, J.; Liu, K.; Li, D.; Du, J. Effects of micro-structure on aerodynamics of Coccinella septempunctata elytra (ladybird) in forward flight as assessed via electron microscopy. Micron 2017, 102, 21–34. [Google Scholar] [CrossRef]
- Lehmann, F.-O.; Wehmann, H.-N. Aerodynamic interference depends on stroke plane spacing and wing aspect ratio in damselfly model wings. Int. J. Odonatol. 2020, 23, 51–61. [Google Scholar] [CrossRef]




| αg | tan (αgθg) |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tey, W.Y.; Lam, W.H.; Teng, K.H.; Wong, K.Y. Semi-Analytical Method for Unsymmetrical Doublet Flow Using Sink- and Source-Dominant Formulation. Symmetry 2022, 14, 391. https://doi.org/10.3390/sym14020391
Tey WY, Lam WH, Teng KH, Wong KY. Semi-Analytical Method for Unsymmetrical Doublet Flow Using Sink- and Source-Dominant Formulation. Symmetry. 2022; 14(2):391. https://doi.org/10.3390/sym14020391
Chicago/Turabian StyleTey, Wah Yen, Wei Haur Lam, Kah Hou Teng, and Keng Yinn Wong. 2022. "Semi-Analytical Method for Unsymmetrical Doublet Flow Using Sink- and Source-Dominant Formulation" Symmetry 14, no. 2: 391. https://doi.org/10.3390/sym14020391
APA StyleTey, W. Y., Lam, W. H., Teng, K. H., & Wong, K. Y. (2022). Semi-Analytical Method for Unsymmetrical Doublet Flow Using Sink- and Source-Dominant Formulation. Symmetry, 14(2), 391. https://doi.org/10.3390/sym14020391







