PSO, a Swarm Intelligence-Based Evolutionary Algorithm as a Decision-Making Strategy: A Review

Abstract

Companies are constantly changing in their organization and the way they treat information. In this sense, relevant data analysis processes arise for decision makers. Similarly, to perform decision-making analyses, multi-criteria and metaheuristic methods represent a key tool for such analyses. These analysis methods solve symmetric and asymmetric problems with multiple criteria. In such a way, the symmetry transforms the decision space and reduces the search time. Therefore, the objective of this research is to provide a classification of the applications of multi-criteria and metaheuristic methods. Furthermore, due to the large number of existing methods, the article focuses on the particle swarm algorithm (PSO) and its different extensions. This work is novel since the review of the literature incorporates scientific articles, patents, and copyright registrations with applications of the PSO method. To mention some examples of the most relevant applications of the PSO method; route planning for autonomous vehicles, the optimal application of insulin for a type 1 diabetic patient, robotic harvesting of agricultural products, hybridization with multi-criteria methods, among others. Finally, the contribution of this article is to propose that the PSO method involves the following steps: (a) initialization, (b) update of the local optimal position, and (c) obtaining the best global optimal position. Therefore, this work contributes to researchers not only becoming familiar with the steps, but also being able to implement it quickly. These improvements open new horizons for future lines of research.

1. Introduction

For all companies, decision making implies a risk that for some is minor and for others is so high that it can lead to large economic losses. Decision making implies a process of generating, searching, analyzing, and interpreting information to choose a solution among several possibilities [1,2]. In this way, it establishes priorities according to the information available, to make the best decision [3,4].

In addition, the rapid changes in technology applied to the industry must be considered, where companies must quickly learn and adapt strategies to make decisions, and thus be prepared for market demands [1,2]. This has led to the creation of a range of strategies, methodologies, and techniques for analysis and decision making. These methods are used in the fields of Social Sciences and Psychology, as well as in Natural Sciences and Artificial Intelligence, to study decision making through optimization methods [2].

Without a doubt, this variety of optimization methods has proven its efficiency in analyzing and simplifying problems. Even so, the number of methods to improve the efficiency and robustness of the results continue to increase [5,6]. Taking into account that the improvements of optimization methods are related to the symmetric and asymmetric problems with multiple criteria that the decision maker faces [7], where symmetry not only transforms the decision space, but also reduces search time by visiting symmetric solutions. In addition to unstructured, messy environments, with uncertainty and dynamic data, as well as the interpretation of the information [7,8], these conditions are changing the behavior of the industry, driving it towards better competitiveness and economic growth [9,10].

The interest in studying this topic arises from the need to analyze the information and provide the best results for the people who make decisions. Therefore, the application of optimization and multi-criteria methods is a reference for data analysis and treatment. There is a wide range within these methods, but we will focus on the particle swarm algorithm (PSO).

The organization of this article includes four main sections, beginning with the introduction. Section 2 describes the methodology used for the literature review, which includes (1) the research of scientific articles on decision making, optimization methods, metaheuristics, multi-criteria, and the particle swarm optimization (PSO) algorithm using the ScienceDirect, IEEExplore, ProQuest, JSTOR, and SAGE databases and Google Scholar; (2) patent location, on the USPTO platform, that use PSO; (3) search for registrations with the US Copyright Office where they implement PSO. Section 3 presents the results, providing the importance of analysis and decision making. Continuing with the multi-criteria strategies, we can prioritize the criteria and, thus, choose the best solution alternative. This is followed by optimization methods and metaheuristics as strategies for data analysis. To finish, we explore the PSO evolutionary algorithm, contributing its concept, applications, and structure with the mathematical formulation for its implementation. Finally, Section 4 presents the conclusions and the future work that the authors intend to carry out.

In relation to the findings found in the literature review of scientific articles, the period from 2017 to 2021 shows a significant increase in publications of the topics sought. Regarding the location of patents, of the 135 registries that use the PSO method, only 29 applied it within software. Similarly, from the copyright records, the 25 located works that implement the PSO method belong to texts on this topic. Now, among the applications shown in this article, they include improvements in robot welding processes [11], improvements in the speed and control of robots [12], and in the collection of products with a robot [13]. In addition, the PSO method helps in trajectories [14] with unmanned vehicles [15] and autonomous cars [16].

2. Methodology of the Literature Review

This section presents three parts, showing the resources and statistics of the findings for the literature review. The first part uses the databases: ScienceDirect (database website: https://www.sciencedirect.com), IEEExplore (database website: https://ieeexplore.ieee.org), ProQuest (database website: https://www.proquest.com/), JSTOR (database website: https://www.jstor.org/), SAGE (database website: https://journals.sagepub.com/), and Google Scholar (search engine website: https://scholar.google.com/) to locate articles not only on PSO, but also on topics related to it. The topics to look for are: decision making, multi-criteria, optimization methods, and metaheuristics, having as objectives the search of concepts, classifications, and methods used, as well as the steps of the algorithms, applications, results of the cases that are presented and problems raised for future work. In the following, we focus on the PSO algorithm. In the second part, we use the USPTO (website for patent search: https://www.uspto.gov/) platform to locate patents, and in the third part, the US Copyright Office (website for copyright search: https://www.copyright.gov/) to find the records of works that implement PSO.

2.1. Scientific Articles

This section begins with the search for scientific articles in the aforementioned databases with the words “decision-making” and “multi-criteria”. Later, we continue the search with “optimization methods” and “metaheuristics”, and finish with “particle swarm optimization”. The authors consider this search order, to go from the general to the particular, as shown in Figure 1.

To begin the search for articles, the topics to be investigated were identified, beginning with the words: decision making and multi-criteria, in the aforementioned databases. In Figure 2, it can be seen that JSTOR was an important promoter of these topics, but in the last decade, ScienceDirect and Google Scholar better support the location of this type of article. Similarly, Figure 3 shows an increase in the period 1997–2001 in scientific research with multi-criteria methods for decision making.

In

Table 1. Decision making and multi-criteria publications.

Period	IEEExplore	ProQuest	SAGE	JSTOR	ScienceDirect	Google Scholar
1997–2001	1	88	2240	9446	3427	1455
2002–2006	2	235	3324	11,499	6962	3575
2007–2011	57	665	4645	13,831	13,077	9720
2012–2016	43	2066	5955	14,946	24,062	19,700
2017–2021	53	3366	7935	6126	37,977	30,360

, the periods 2007–2011 and 2017–2021 show an increase in publications. JSTOR was constant in its publications, but they decreased from 2017–2021. Meanwhile, ScienceDirect increased its content on the topics of decision making and multi-criteria.

Subsequently, the topics of optimization methods and metaheuristics are sought, considering articles published in journals and book chapters between 1997 and 2021, in which it is once again verified that they are becoming increasingly important in the scientific community, due to the increase in publications (see Figure 4).

Within

Table 2. Optimization methods and metaheuristics publications.

Period	ScienceDirect	IEEExplore	ProQuest	JSTOR	SAGE	Google Scholar
2001–1997	177	14	0	244	55	7
2006–2002	533	64	0	891	165	15
2011–2007	1689	333	0	2283	269	78
2016–2012	4548	614	6	4768	251	181
2021–2017	9212	889	0	6361	46	322

, we see again that ScienceDirect maintains a higher number of publications with optimization methods and metaheuristics. In the same way, JSTOR takes importance to these topics for its publications.

The next topic to look for is the particle swarm optimization (PSO) algorithm.

Table 3. Scientific literature of the PSO algorithm.

Database/Period	1995–2001	2002–2011	2012–2021
ScienceDirect	130	3617	33,520
IEEE	64	9296	18,232
SAGE	1	510	3701
ProQuest	0	12	117
JSTOR	0	3	5
TOTALS	195	13,438	55,578

shows the use of PSO, where in the first six years there was little scientific literature found; this increased by 19.4% in the period 2002 to 2011, and an increase of 80.3% from 2012 to 2021. Therefore, it can be concluded that the PSO algorithm is a solution for the scientific community, solving real problems.

2.2. Patents Employing the PSO Algorithm

After reviewing the scientific articles, the search continues on the USPTO platform. The next section focuses on the topic of “particle swarm optimization”, with the purpose of locating the patents that apply PSO to solve a problem in the best way.

First, 135 patents that use PSO were located. The first patent using PSO was registered 13 years after it was proposed by Russell Eberhart and James Kennedy in 1995 [14]. While the most recent patent, registered at the end of October 2021, belongs to the Shandong University of the People’s Republic of China (PRC) [17].

In Figure 5, there are 135 patents in the United States of America (USA) at the top of the list with the highest number of registered patents, followed by the PRC. Likewise, of the 135 patents, only 29 implemented the algorithm in an SW, see Figure 6.

Among the 135 patents that used PSO, 29 implemented the algorithm in an SW (it is important to point out that for this work the programs, systems, or software will be named SW, taking into account that the concepts are different, but they will serve to be able to group all these elements in a single word), see Figure 7.

In these 29 patents, the US emerged as the topic leader until 2017 (

Table 4. Patents registered in USPTO that implement PSO in an SW.

Country	2009–2012	2013–2017	2019–2021
Saudi Arabia	1	0	0
Germany	0	1	0
France	0	3	0
United States of America	4	8	0
Taiwan	0	0	1
Ireland	0	0	1
People’s Republic of China	0	0	10

). However, in the 2019–2020 period, the PRC has made significant progress, becoming the leader, although the US still has the highest number of patents. Thus, it can be concluded that, in recent years, the PRC has made great scientific advances with PSO, with the largest number of patents, and being the first to patent in 2021 (Figure 8).

The importance that researchers are giving to PSO can be seen in the increase in patents. In 2021 alone, 21 patents with PSO were located, and within this group are the first patents from the countries of India, Ireland, and Germany (Figure 9).

PSO is also used within research laboratories, such as the US-based Malibu HRL, which generated ten patents between 2009 and 2014 using classic PSO or combining it with another method (

Table 5. USPTO registered patents assigned to HRL lab.

Patent	Inventors	Year of Assignment	Reference
8793200	Chen Yang et al.	2014	[20]
7558762	Owechko Yuri et al.	2009	[21]
7599894	Owechko Yuri, Medasani Swarup	2009	[22]
7636700	Owechko Yuri, Medasani Swarup	2009	[23]
7672911	Owechko Yuri, Medasani Swarup	2010	[24]
8645294	Owechko Yuri et al.	2014	[25]
8213709	Medasani Swarup et al.	2012	[26]
8370114	Saisan Payam	2013	[27]
8589315	Medasani Swarup, Owechko Yuri	2013	[28]
8437558	Medasani Swarup, Owechko Yuri	2013	[29]

). Likewise, multinational companies use the PSO algorithm in their patents, as is the case of Huawei Technologies [18] and the company Trilithic [19].

2.3. Copyright with the PSO Algorithm

In this third part, the keywords used were: “PSO”, “particle swarm optimization algorithm”, and “particle swarm optimization”, to locate the records on the platform of the US Copyright Office.

The first two proposed words did not yield records of the entire PSO theme. The first returned information that was not related to the algorithm, and the second word removed some records that had a method and no algorithm.

The information provided by the records contains: name of the author(s), title of the work, registration number, date of registration, type of registered service, among other data. Because the records do not contain complete information or a copy of the work, the information to request it is also given.

The first record from 2002 corresponds to computer text data on multiphase particle swarm optimization [30]. Meanwhile, the most recent record is from 2019, which corresponds to an electronic file, on the subject of optimization assisted by machine learning with applications in the diesel engine with PSO [31].

In Figure 10, there are two parameters: texts and strings. These are part of the registered literary works. The years with the most records were 2009 and 2017, but the number of copyrighted works was minimal compared to the number of scientific papers or patents using PSO.

Twenty-five literary works intended to explain a document containing PSO (

Table 6. US Copyright Office records employing PSO.

Year	Text	Serials	Computer Files
2002	1	0	0
2004	2	0	0
2009	4	0	0
2010	1	0	0
2011	3	0	0
2012	1	1	0
2013	1	0	0
2014	3	0	0
2015	0	1	0
2016	1	0	0
2017	3	1	0
2018	1	0	0
2019	1	0	0

) were registered. However, no records of websites, blogs, or other web content related to PSO were located. Nor were SWs located that directly or indirectly applied PSO to solve a problem.

In conclusion, when using six databases for scientific articles and two platforms for patents and copyright, it can be seen that 2017 was a benchmark for PSO due to the increases that were observed.

3. Results of the Literature Review

This section contains the results of the literature review, starting with the optimization methods for analysis and decision making and continuing with the multi-criteria methods—those that precede the metaheuristics. The section ends with the particle swarm optimization algorithm (PSO), addressing its concept, uses, and implementations, and the structure of the algorithm for its implementation.

3.1. Analysis and Decision-Making

Businesses have been transformed over the years since their first revolution in the mid-17th century; going through mechanization, electricity, automation, and the use of information technologies until we reach what we know as industry 4.0—where innovation is the main promoter for technological development and knowledge management [1].

In this sense, technological development requires data analysis processes. Due to the amount of data that is being generated, a range of technologies, tools, strategies, and techniques have been created. These are not only affecting the organization and conduct of the industry, but also the data collection, digitization, and analysis for decision making [2,10].

In this way, it can be pointed out that technologies are making data analysis more efficient, for which they used strategies and techniques that integrate the collection, processing, modeling, and visualization of said data [32], converting information into results that help identify problems, risks, or competitive advantages, contributing to more efficient and faster decision making [33,34]. Efficiency in data analysis has led decision makers to face increasingly complex situations [3], and with dynamic data [35].

However, the decision maker not only faces the aforementioned situations, but also the need to obtain increasingly precise and reliable results [36,37], in addition to handling data with uncertainty [4,8]. This is why the strategies created for data analysis help decision makers obtain the best solution. Among these strategies are the multi-criteria methods and the optimization methods, which are detailed in the following sections.

3.2. Multi-Criteria Methods

Decision makers have a great responsibility that comes from analyzing the data to arrive at the best solution [32]. The decision maker’s success increases when he considers multiple criteria or outcomes [8]. This leads to advantages and disadvantages of each alternative that reduce costs and increase benefits [8]. Multi-criteria decision-making (MCDM) problems are part of the most used strategies for decision making [38,39]. With these methods, a set of finite alternatives is compared, evaluated, and classified with respect to a set of attributes that are also finite [8].

In other words, the MCDM are designed to help the decision maker choose the best option among a group of possibilities [38]. These possibilities are called alternatives, and form the choice set [40]. To choose from this choice set, the decision maker must consider a variety of conflicting points of view, called criteria [8,39]. The MCDM is used in problems that have several solutions and the answer is not determined with a true or false [41]. Otherwise, with a variety of answers that evaluate multiple conditions with algorithms and mathematical tools to obtain the best solution [42,43].

Therefore, the main objective of the MCDM is to provide, to the decision maker, solutions to a problem with multiple criteria, which are often contradictory [43,44]. This makes MCDM efficient strategies to obtain the best solution, using strategies to evaluate multiple criteria [6,42].

Below are two tables with MCDM methods.

Table 7. Some of the best known MCDMs.

MCDM	Proposed by:	Year	References
ELECTRE	Bernard Roy	1968	[45]
TOPSIS	Hwang Yoon	1981	[46,47]
AHP	Saaty	1981	[36,48]
VIKOR	Opricovic	1988	[48,49]
PROMETHEE	Brans and Mareschar	2005	[50,51]
MOORA	Brauers and Zavadskas	2006	[52,53]
CODAS	Ghorabee	2016	[54,55]

contains some of the more popular methods, while

Table 8. Some of the MCDMs with fuzzy logic.

MCDM-Fuzzy	Proposed by:	Year	References
FS	Lotfi A. Zaden and Dieter Klaua	1965	[45,53]
IFS	Krassimir Atanassov	1986	[56]
BFS	Zhang Wen-Ran	1994	[56,57]
Fuzzy PSO	Bo Wang, GuoQiang Liang and ChaLin, Wang	2006	[58]
Fuzzy TOPSIS	Chen and Tsao	2008	[59]
PFS	Zadeh and Yanger	2013	[41,60]
q-ROF	Yager	2017	[51,52]
TSFS	Smarandache, Florentin	2019	[61,62]

shows MCDM methods with fuzzy logic. The tables contain the abbreviation MCDM, the author(s), and the year it was first published. Subsequently, the strategies contained in these tables are detailed.

The first method corresponds to elimination and choice translating reality (ELECTRE), and comprises a family of classification methods. The similarities of this family of methods lie in the pairwise comparison of the alternatives, based on the primary notions of agreement and disagreement sets. In addition, they use ranking charts to point out the best alternative. Bernard Roy is credited as the creator of ELECTRE [45].

For 1981, two methods appear. The technique for order preference by similarity to an ideal solution (TOPSIS), compares the distance of all alternatives with the best and worst solutions [46,47]. The analytical hierarchy process (AHP) decomposes the elements in all hierarchies and determines the priority of the elements through quantitative judgment for integration and evaluation [36,48].

In 1988, the multiple criteria compromise and optimization solution (VIKOR) method appears, seeking multi-criteria optimization by classifying a set of alternatives against several conflicts [48,49]. Later, in 2005, the preference ranking organization method for evaluation enrichment (PROMETHEE) appeared, which calculates the dominant flows of alternatives [50,51]. Meanwhile, in 2006, the multi-objective optimization method based on ratio analysis (MOORA) appeared, which evaluates the ranking of each alternative based on ratio analysis [52,53]. The most recent of this group are the combinatorial distance-based evaluation (CODAS) models that use the alternative Euclidean distance of the negative ideal and the Taxicab distance [54,55].

A disadvantage of the MCDM lies in the subjective determination of the weights by the decision makers, presenting complexity and uncertainty when evaluating the information [40,63]. Due to this complexity, in 1965, Lotfi Zadeh introduced fuzzy sets (FS), allowing the analysis of a wide variety of situations that resemble decision making in situations of uncertainty or inaccuracy [45,53]. Since that year, there has been an increase in the development of new methods or improvements, among which is the intuitionist fuzzy set (IFS), developed in 1986, which considers the function of the degree of membership and that of non-members [56]. Meanwhile, in 1994, it evolved, becoming the bipolar fuzzy set (BFS) with positive and negative membership function degree [56,57].

Later, in 2006, the Fuzzy PSO method appeared, solving the convergence conflict of group particles, in addition to maintaining a faster speed and convergence precision [58]. Meanwhile, in 2008, the Fuzzy TOPSIS method found positive and negative ideal solutions as a comparison criterion for each choice. Later, it compares the Euclidean distance between the alternatives and the ideal solution to obtain the proximity of the alternatives and perform the classification of the pros and cons of the alternatives [59].

After some time, by 2013, the IFS evolved, modeling uncertainty and vagueness through linguistic terms, called Pythagorean fuzzy sets (PFS) [41,60].

Among the most recent methods of 2017, is the q-rung orthopair (q-ROF) fuzzy set, which is based on IFS and PFN, which presents, in parallel, the degrees of membership, non-membership, and indeterminacy of decision makers [51,52]. Meanwhile, the T-spherical fuzzy set, from 2019, has the flexibility to unite the sum of the q-th power of membership, abstinence, and non-membership between one and zero [61,62].

Although the use of optimization methods as a decision making strategy has shown efficiency, many of them require a lot of time to perform the calculations [2,37]. Just as the application of a single algorithm does not guarantee having the best solution, comparing several algorithms or a hybrid increases the efficiency and effectiveness of the result [36,64]. An example of this is the combination of interval analytical hierarchy process (IAHP) and combinative distance-based assessment (CODAS) to prioritize alternative energy storage technologies [65].

3.3. Metaheuristics

The objective of this section is to make a classification of metaheuristic algorithms. Therefore, the origin of the metaheuristics within the optimization methods must first be identified.

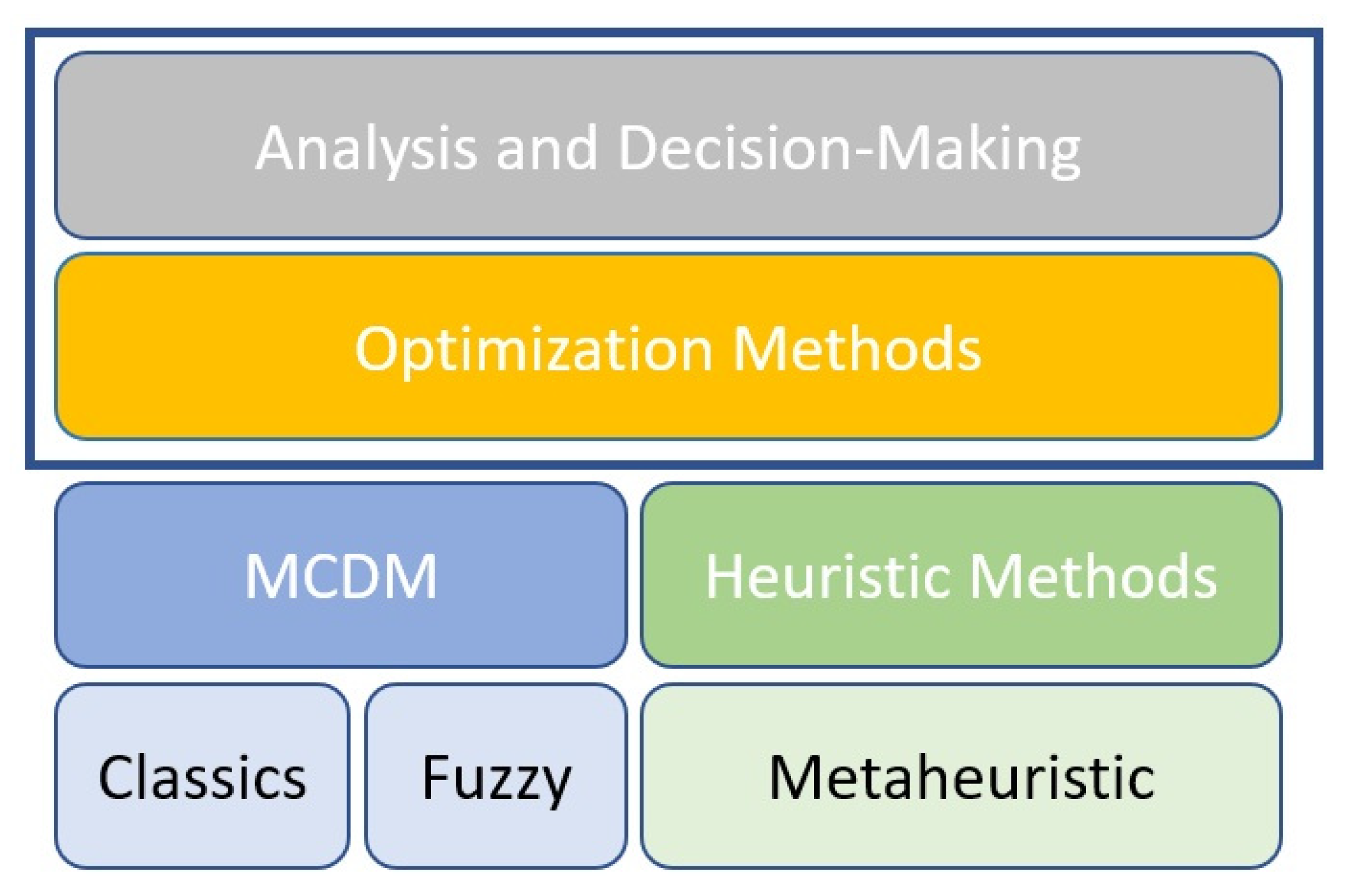
Optimization methods (OM) are one of the strategies for data analysis. OM involves a series of mathematical steps to visualize wins, gains, losses, risks, or errors [66,67], where the location of the decision variables is by maximizing or minimizing their objective function [68].

Figure 11 shows a classification that the authors visualize between exact and heuristic methods, where the exact methods give an optimal solution, while the heuristics compute the fastest result, getting closer to the optimal solution [67,69]. Among the heuristic methods are the approximation and metaheuristic algorithms, where their main difference lies in the number of iterations used in their process [49,66].

The metaheuristic algorithms apply rules with a sequential ordering in the processes in a simpler, more precise, and faster way [38,63]. These algorithms improve the solutions because they are based on the intelligence of the population [66,67]. The use of these algorithms has been found to reduce costs, assign tasks, distribute times, and find the best path or location [37,70]. Currently, metaheuristic algorithms have solved problems in the field of engineering, economics, science, and computer security [38].

There is a wide variety of algorithms within metaheuristics, including novel algorithms and hybridization of several algorithms, which makes it difficult to determine which of them provides the most efficient solution [68,71]. That is why the authors have made four categories according to behaviors and characteristics, see Figure 12. These categories correspond to: (1) those based on unique or population solutions, (2) inspired or not by nature, (3) iterative or greedy, and (4) with or without memory.

In the first category are population-based algorithms that provide a set of solutions, improving local search with the ability to explore solutions close to the optimum [6,66]. The vast majority of these algorithms are initialized with random solutions, which improve with each iteration [72]. These algorithms include the arithmetic optimization algorithm (AOA) [68] and the evolutionary algorithms (EA) [73,74], among which are the genetic algorithms (GA) [66], and the swarm optimization of particles (PSO) [73,75]. These methods are based on one path at a time and this solution may not be within the search neighborhood, they are the single solution algorithms, among which are the simulated annealing algorithm (SA) [67] and Taboo (TS) [40].

Then, there is the category of algorithms inspired by nature that establish rules for the behavior of a population in a situation that occurs in nature [33,70]. Some authors, such as Abualigah et al. [68], name these as swarm intelligence algorithms. Tzanetos in 2021, located 256 algorithms in this category, of which 125 have demonstrated their efficiency in solving a real-life problem [70]. Within this category, they are classified into swarm intelligence algorithms and those based on organisms. In the swarm intelligence algorithms are the: PSO [37,40], ant colony algorithm (ACO) [37,76], bat algorithm (BA) [38,70], and among the most recent, the reptile search algorithm (RSA) [77,78]. While in the algorithms based on organisms, one finds the algorithms of coyotes [79,80], dolphins [81,82], penguins [83,84], and moths [85,86].

On the other hand, there are algorithms that do not incorporate the elements of nature, showing two classifications. The first comprises algorithms based on the behavior of physical or chemical laws, such as the SA [70,87], the multiverse optimizer (MVO) [68,73], and the differential evolution algorithm (DE) [66]. The second classification bases its processes on cultural or emotional behavior, including social theory [33,68]. An example is the imperialist competitive algorithm (ICA) based on human sociopolitical growth [88,89] and the optimization algorithm based on teaching learning (MTLBO) [90,91].

Another category of metaheuristic algorithms comprises the iterative and the greedy. Iterative algorithms perform repetitions within their procedure to find the best solution, for example, the PSO [37,72] and AOA [68]. While greedy algorithms start with an empty solution and in their search process, the decision variable finds the result, an example of this type of algorithm is the greedy random adaptive search procedure (GRASP) [70].

Memory algorithms, however, store previous and present information during the search process, these include AOA [68] and PSO [92,93]. On the other hand, there are algorithms without memory, which only use the present data of the search, among the examples of these algorithms this SA [87] and GRASP [70].

In Figure 13, we see the topics addressed so far, showing the vision of the authors and the connection they have between them.

In the next section, we focus on the PSO algorithm, explaining its concept, advantages and disadvantages, applications, and the mathematical structure for its implementation.

3.4. Particle Swarm Algorithm (PSO)

Within the family of metaheuristic algorithms is the mathematical model called particle swarm optimization (PSO) [52]. PSO finds the best spot, based on the group intelligence of flocks of birds and schools of fish, during predation and foraging [15,94].

The PSO works within a set of solutions (swarm) that contain a working sequence with a series of solutions (particles), where each particle updates its speed, considering past and present locations, to compare them with those of the swarm and thus establish the best global position [52,95].

Figure 14 shows the movement of the particle in the swarm, with the solid line, while the dotted line indicates the best position (pbest) and the best global position (gbest) [21,95].

Russell Eberhart and James Kennedy, in 1995, first presented the PSO algorithm, starting with the current position and the change produced by each particle within the swarm [25]. Three years later, Russell Eberhart, together with Yuhui Shi, announced a modification of the PSO, in which they introduced the inertial weight and the best state found at the moment by the particle and the swarm [68].

Among the advantages of PSO is the ease of application to solve problems in different areas of agricultural, engineering, and materials, health, natural, and social sciences [2,5,13]. It is applied in the engineering sciences, which include industrial processes, transportation, electrical, and computer engineering [17,96]. In addition to applications in health sciences, including medical sciences and bioinformatics [29,94]. However, although PSO is effective in complex optimization problems, its disadvantages include premature stalling [97,98], fast convergence [94], and stochastic excess problem [97].

3.4.1. PSO Applications

The PSO algorithm in its classical form has proven to be efficient for solving complex problems [11,99], achieving an approximation of the particles to the optimum of the problem—that is, a fast convergence [52,100]. Even so, PSO has some drawbacks, as mentioned. When combined with other algorithms, it generates hybrid algorithms that increase the validation of the results [11,75].

In 2008, the first patent using PSO was registered, that is, 13 years after PSO was first published. In this patent, the position of the access node between multiple paths, between the main path and the estimation result, is located by means of PSO [14].

In 2009, PSO was applied in recognition of 3D objects seen from multiple points of view [21]. PSO is also incorporated in the classifiers with attention mechanisms [22]. Additionally, an object recognition SW with PSO and the possibilistic particle swarm algorithm (PPSO) is developed. In said SW, PSO performs the search and classification in a multidimensional solution space. While PPSO determines the size and optimizes the parameters of the classifier, with the simultaneous work of the particles [23]. In another implementation that year, PSO trained a neural network to monitor the input to a network, making comparisons of input and known frequency spectra [19].

Around 2010, applications in recognition of structured objects and groups of images were performed by fuzzy attribute relational graphics (FARG) and PSO, where PSO matches the graphics [24]. In 2012, PSO performed the searches and classifications of visual images in a directed area, while cognitive Bayesian reasoning makes the decision with uncertainty in the data [26].

In 2013, a method and apparatus for the optimal placement of responsible actuators, shaping elastically deformable structures, was developed. Making the coincidence and location of the optimal actuator solution with PSO [27] occurred in 2013. In that same year, PSO was implemented in two software, one for the detection and verification of objects in a region and the hierarchical representation scheme for the grouping and indexing of images in the database [29]. Another method for the recognition of behavior between objects in a video sequence uses the fuzzy attribute relational graph (FARG) for the organization of the scene in the organization module and classifies objects in video data with PSO [28].

Meanwhile, in 2014, systems implementing PSO were developed. The first for image registration with a new PSO approach makes a comparison of test image features with references unnecessary. This new approach improves the convergence rate and reduces the cost of calculations in the comparison [25], and the second one achieves a true optimal solution and avoids premature convergence, allowing a random walk process for PSO [20].

Among the applications reported in 2018, PSO, together with ABC (artificial bee colony algorithm), optimizes the calculations of the mechanical performance of wireless sensors of a bicycle disc rotor [93]. In another implementation, PSO is used in a rational function model (RFM) to extract geometric information from images [101]. Likewise, it is implemented to improve a robot welder, reduce costs, and increase productivity, implementing PSO with discrete particles together with the genetic algorithm GA, which they called DPSO [11].

By 2019, MCPSO, a modified centralized algorithm based on PSO, was generated in which the MCPSO assigns tasks to supply medicine and food for the victims in specific places using unmanned aerial vehicles [15]. Another application of that year is the artificial neural network (ANN) training to find the weights of the network, implementing PSO and quasi-Newton (QN) on the CPU-GPU platform with OpenCL [102].

On the other hand, in 2020, PSO performed better than GA by using an integral squared error as an objective function, employing a nano-network that uses three resources: the photovoltaic array, the wind turbine, and the fuel cell [103]. In this same year, the GLPSOK algorithm provided better results than the classical or latest generation of clustering algorithms. GLPSOK implements the Gaussian distribution method and Lévy flight to help search for PSO [104].

In 2021, an improved fractional-order Darwinian particle swarm optimization technique called FODPSO was developed, which improves the fractional-order calculation to identify the electrical parameters of photovoltaic solar cells and modules. FOSPSO allows an additional degree of freedom in the speed change of the position [75]. Furthermore, three systems that implement PSO were generated. One system prints the route planning method for autonomous vehicles, determining the PSO parameters by the complete simplex sequence [16], and another controls the movement of biomimetric robotic fish, improving the speed and stability of swimming forward and backward with PSO [12], and a third party makes online decisions for generator start-up, optimizing the maximum total generation capacity in a power system situation through PSO [17].

Among the most recent applications of PSO in 2022 is the optimization of parameters in the calibration of camera image quality [96], as well as the application to determine the minimum insulin for a type 1 diabetic patient, using the analytical convergence of the fractional calculation particle swarm optimization algorithm (FOPSO), which improves PSO stagnation [94]. In addition to the harvesting of agricultural products by means of a robot, using PSO to segment green images [13].

3.4.2. Structure of the Classic PSO Algorithm

The authors present a vision of three main steps for the process of the classical PSO algorithm: initialization, update of the local optimum-position, and obtaining the best global optimum-position [105,106]. These most important steps can be seen in the flowchart in Figure 15.

The following paragraphs details the classic PSO mathematical model, using the corresponding formulas for its implementation.

Next, some notations that are used both in Figure 15 and in the formulas that will be shown after the table are explained in

Table 9. Notations and definitions used in control parameters. Source based on [92,107].

Notation	Definition
i	Independent unit, called a particle.
N	Number of particles in the swarm, also called search space dimension or population $N=\{i_1,i_2,\cdots ,i_N\}.$
$\omega$	Coefficient of the weight of inertia, increases or decreases the speed, keeping the current speed and moment of the particle.
$t,T$	Current number of iterations (t) and the total number of iterations expected to be performed (T).
$c_1,c_2$	Non-negative acceleration factors, known as learning factors. Driving each particle towards the pbest and gbest positions.
$r_1,r_2$	Numbers between [0, 1], for the circulation of each particle. That is, they simulate the influence of nature on the particle.

.

Steps 1.

Initialization

1. 

Set the control parameters: N, ω, $c_1$, $c_2$, $r_1$, $r_2$, and T (definition in Table 9), the number current number of iterations with a value of 1 ($t=1$) because it is the first iteration, and the fitness function to initialize the swarm.

The variable ω makes convergence happen in fewer iterations and maintains the balance between local and global searches. A smaller value of ω leads to a local search and a larger value than a global search. If ω has a large value, the algorithm starts the search globally and ends with a local search [108,109].

2. 

Determine the first local position of the particles randomly, considering $i=\{1,2,\cdots ,N\}$:

$$C{P}_N^i\left(t\right)=(C{P}_1^i\left(t\right),C{P}_2^i\left(t\right),\cdots ,C{P}_N^i\left(t\right))$$

(1)

3. 

Randomly set the first local velocity of the particles (from 1 to N):

$$V_N^i\left(t\right)=(V_1^i\left(t\right),V_2^i\left(t\right),\cdots ,V_N^i\left(t\right))$$

(2)

4. 

Evaluate the fitness function with the first position (Equation (1)), to obtain the best current optimum:

$$C{F}_N^i\left(t\right)=f\left(x\right)=f\left(C{P}_N^i\left(t\right)\right)$$

(3)

5. 

To establish the best local position (LBP), we use the first local position (Equation (1)). While, for the first best local optimum (LBF), we use the current best optimum (Equation (3)):

$$LB{P}_N^i\left(t\right)=C{P}_N^i\left(t\right)$$

(4)

$$LB{F}_N^i\left(t\right)=C{F}_N^i\left(t\right)$$

(5)

6. 

To obtain the best global optimum with the maximum value of the best local optimum (Equation (5)); that is, the maximum value of the dataset of the best local optimum (LBF):

$$GBF\left(t\right)=max\left(LB{F}_N^i\left(t\right)\right)$$

(6)

7. 

To obtain the best global position, we extract the particle position in i from the best global optimum (Equation (6)). Position (z) provides the value of the best local position and becomes the best global position:

z = particle position in i of GBF(t)

$$GBP\left(t\right)=LBF\left(z\right)$$

(7)

To continue with step 2, we increment the current number of iterations ($t=t+1$).

Steps 2.

Position updating and local optimal

1. 

Update speed and position of the particle.

From this step, ($t-1$) indicates the value of the previous iteration, while (t) is the current iteration.

To update the velocity, we use the inertial weight coefficient (ω), the learning factors ($c_1$ and $c_2$), and the particle circulation values ($r_1$ and $r_2$), as well as the values of the previous iteration of the speed, local position, and best local and global positions.

Meanwhile, for the current position, we add the previous current position and the new speed:

$$V_N^i\left(t\right)=\omega (V_N^i(t-1)+c_1{r}_1(LB{P}_N^i(t-1)-C{P}_N^i(t-1))+c_2{r}_2(GBP(t-1)-C{P}_N^i(t-1))$$

(8)

$$C{P}_N^i\left(t\right)=C{P}_N^i(t-1)+V_N^i\left(t\right)$$

(9)

2. 

To obtain the best current optimum, evaluating the fitness function with the current position (Equation (9)):

$$C{F}_N^i\left(t\right)=f\left(x\right)=f\left(C{P}_N^i\left(t\right)\right)$$

(10)

3. 

Update best local position with current position (Equation (9)):

$$LB{P}_N^i\left(t\right)=CP\left(t\right)$$

(11)

4. 

To obtain the best local position, we select the maximum value between the best current optimum (Equation (10)) and the best local optimum of the previous iteration (Equation (5)):

$$LB{F}_N^i\left(t\right)=max(CF\left(t\right),LBF(t-1))$$

(12)

5. 

Obtain the best global optimum with the maximum value of the best local optimum (Equation (12)). That is, the maximum value of the dataset of the best local optimum (LBF):

$$GBF\left(t\right)=max\left(LB{F}_N^i\left(t\right)\right)$$

(13)

6. 

To obtain the best global position, we extract the particle position in i from the best global optimum (Equation (11)). That position (z) provides the value of the best local position and becomes the best global position:

z = particle position in i of GBF(t)

$$GBP\left(t\right)=LBP\left(z\right)$$

(14)

Steps 3.

Obtaining the best global-optimal position

1. 

If the current iteration is less than the total iterations, it is convergent; therefore, we increment the iteration and continue from step 2:

$$t<T\to (t=t+1)$$

(15)

Continue from step 2 (Equation (8))

2. 

The process ends when the total iteration is equal to or greater than the current iteration. We obtain the best position and the best optimum from the last values of the best global position and the best global optimum:

$$t\ge T=\left\{\begin{array}{c}pbest\left(T\right)=GBP\left(t\right)\hfill \\ gbest\left(T\right)=GBF\left(t\right)\hfill \end{array}\right.$$

(16)

4. Conclusions and Future Work

The study carried out in this article manages to conceptualize and categorize the MCDM and metaheuristic methods. Of the most relevant MCDM methods, they were classified as follows: (a) classical form and (b) with fuzzy extensions. At the same time, it opens the opportunity to more effectively validate the results of the PSO method. Furthermore, another of the results obtained deals with the classification of optimization methods in the following way: heuristic, metaheuristic, and exact (see Figure 11). It can be said, then, that metaheuristic methods categorize by behavior and characteristics into: (1) inspired or not by nature, (2) based on unique solutions or populations, (3) iterative or greedy, and (4) with or without memory (see Figure 12). Data analysis is an important point in any decision making, so researchers have made a great effort to achieve results more efficiently. Due to the large number of algorithms that exist, it is difficult to have an updated ranking or to experiment with all the optimization algorithms. The literature research addresses the PSO method and its extensions with other methods, and the results indicate that there is a significant opportunity to make improvements to the algorithm. The same is confirmed in the literature reviewed on this topic (PSO), given that it has potentially increased in the last 5 years. On the other hand, the articles found on the PSO method in its classical form were very few. However, it has proven to be efficient in decision making both in terms of results and implementation. Likewise, the PSO method shows the ability to solve complex problems, and its application is not limited to a single area. Furthermore, the number of patents found using the PSO method was 135 records, where the countries with the main patent registrations were the United States of America and the People’s Republic of China. Additionally, the most recent patent filings incorporated the countries of India, Ireland, and Germany. It is important to point out that the study of this document addresses the review of patents not only of Universities or research centers, but also of multinational companies. Similarly, the registration of copyright works, from 2002 to date, was 25 registrations, noting that it is an unexploited field and its use is limited to subject text records. Additionally, with this literature, there will be a basis for the implementation of the said algorithm in an intelligent system for data analysis, and it will serve as the basis for the research of other authors with this approach. Among the future works that the authors have planned is to continue the research, focusing on the improvements of the PSO algorithm and not exclusively with the classic PSO. Therefore, we will start with test cases, comparing PSO with other algorithms like ACO, BA, and others that have fuzzy logic. Furthermore, it is planned to use PSO combined with some MCDM, such as TOPSIS, CODAS, and q-ROF, to increase the effectiveness of the results.