Chiral Chemical Potential and Magnetic Effects on QCD Matter in NJL Model with a Self-Consistent Method
Abstract
:1. Introduction
2. The Lagrangian and Gap Equations
2.1. Basic Formulae and the Inconsistency
2.2. The Minimal Consistency Ansatz
3. Solve the Gap Equations
3.1. The Chiral Symmetry Restoring Phase
3.2. The Chiral Symmetry Breaking Phase
3.3. The Modified CME in Chiral Symmetry Breaking Phase—A Rigorous Proof
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QCD | Quantum Chromodynamics |
| QGP | Quark-Gluon Plasma |
| NJL | Nambu-Jona-Lasinio |
| CME | Chiral Magnetic Effect |
Appendix A. The Properties of |ωn; n, a; p3〉
Appendix B. Several Schemes for Deducing the Gap Equations
References
- Svetitsky, B. Symmetry Aspects of finite-temperature confinement transitions. Phys. Rep. 1986, 132, 1–53. [Google Scholar] [CrossRef]
- Meyer-Ortmanns, H. Phase transitions in quantum chromodynamics. Rev. Mod. Phys. 1996, 68, 473–598. [Google Scholar] [CrossRef] [Green Version]
- Cabibbo, N.; Parisi, G. Exponential hadronic spectrum and quark liberation. Phys. Lett. B 1975, 59, 67–69. [Google Scholar] [CrossRef]
- Cleymans, J.; Gavai, R.; Suhonen, E. Quarks and gluons at high temperatures and densities. Phys. Rep. 1986, 130, 217–292. [Google Scholar] [CrossRef]
- Rischke, D. The quark-gluon plasma in equilibrium. Prog. Part. Nucl. Phys. 2004, 52, 197–296. [Google Scholar] [CrossRef]
- Rajagopla, K.; Wilczek, F. The condensed matter physics of QCD. In At the Frontier of Particle Physics/Handbook of QCD; Shifman, M., Ed.; World Science: Singapore, 2001; Volume 3, pp. 2061–2151. [Google Scholar]
- Alford, M. Color-superconducting quark matter. Ann. Rev. Nucl. Part. Sci. 2001, 51, 131–160. [Google Scholar] [CrossRef] [Green Version]
- Vogl, U.; Weise, W. The Nambu and Jona-Lasinio model: Its implications for Hadrons and Nuclei. Prog. Part. Nucl. Phys. 1991, 27, 195–272. [Google Scholar] [CrossRef]
- Klevansky, S. The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rep. 1994, 247, 221–367. [Google Scholar] [CrossRef] [Green Version]
- Ripka, G. Quarks Bound by Chiral Fields; Clarendon Press: Oxford, UK, 1997. [Google Scholar]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, A. Thermal properties of gauge fields and quark liberation. Phys. Lett. B 1978, 72, 477–480. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef] [Green Version]
- Megia, E.; Arriola, E.; Salcedo, L. Polyakov loop in chiral quark models at finite temperature. Phys. Rev. D 2006, 74, 065005. [Google Scholar] [CrossRef] [Green Version]
- Su, L.-Q.; Shi, C.; Xia, Y.-H.; Zong, H.-S. Color superconductivity in a self-consistent NJL-type model. Phys. Rev. D 2020, 102, 054028. [Google Scholar] [CrossRef]
- Kharzeev, D.; McLerran, L.; Warringa, H. The effects of topological charge change in heavy ion collisions: Event by event P and CP violation. Nucl. Phys. A 2008, 803, 227–253. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.; Miransky, V.; Shovkovy, I. Dimensional reduction and dynamical chiral symmetry breaking by a magnetic field in 3 + 1 dimensions. Phys. Lett. B 1995, 349, 477–483. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.; Miransky, V.; Shovkovy, I. Dynamical chiral symmetry breaking by a magnetic field in QED. Phys. Rev. D 1995, 52, 4747–4751. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Klimenko, K.; Vdovichenko, M.; Vshivtsev, A. Magnetic oscillations in dense cold quark matter with four-fermion interactions. Phys. Rev. D 1999, 61, 025005. [Google Scholar] [CrossRef] [Green Version]
- Shovkovy, I. Magnetic Catalysis: A Review. In Strongly Interacting Matter in Magnetic Fields; Kharzeev, D., Landsteiner, K., Schmitt, A., Yee, H.-U., Eds.; Springer: Berlin, Germany, 2013; pp. 13–49. [Google Scholar]
- Chodos, A.; Everding, K.; Owen, D. QED with a chemical potential: The case of a constant magnetic field. Phys. Rev. D 1990, 42, 2881–2892. [Google Scholar] [CrossRef]
- Andersen, J.; Naylor, W.; Tranberg, A. Phase diagram of QCD in a magnetic field. Rev. Mod. Phys. 2016, 88, 025001. [Google Scholar] [CrossRef]
- Endrödi, G. Critical point in the QCD phase diagram for extremely strong background magnetic fields. J. High Energy Phys. 2015, 7, 173. [Google Scholar] [CrossRef]
- Bali, G.; Bruckmann, F.; Endrödi, G.; Fodor, Z.; Katz, S.; Schäfer, A. QCD quark condensate in external magnetic fields. Phys. Rev. D 2012, 86, 071502. [Google Scholar] [CrossRef] [Green Version]
- Alekseev, A.; Cheianov, V.; Frohlich, J. Universality of Transport Properties in Equilibrium, the Goldstone Theorem, and Chiral Anomaly. Phys. Rev. Lett. 1998, 81, 2503–2506. [Google Scholar] [CrossRef] [Green Version]
- Metlitski, M.; Zhitnitsky, A. Anomalous axion interactions and topological currents in dense matter. Phys. Rev. D 2005, 72, 045011. [Google Scholar] [CrossRef] [Green Version]
- Newman, G.; Son, D. Response of strongly interacting matter to a magnetic field: Some exact results. Phys. Rev. D 2006, 73, 045006. [Google Scholar] [CrossRef] [Green Version]
- Fukushima, K.; Kharzeev, D.; Warringa, H. Chiral magnetic effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Gao, J.-H.; Liang, Z.-T.; Pu, S.; Wang, Q.; Wang, X.-N. Chiral Anomaly and Local Polarization Effect from the Quantum Kinetic Approach. Phys. Rev. Lett. 2012, 109, 232301. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.-T.; Wang, X.-N. Globally Polarized Quark-Gluon Plasma in Noncentral A+A Collisions. Phys. Rev. Lett. 2005, 94, 102301. [Google Scholar] [CrossRef] [Green Version]
- Becattini, F.; Piccinini, F.; Rizzo, J. Angular momentum conservation in heavy ion collisions at very high energy. Phys. Rev. C 2008, 77, 024906. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.-H.; Chen, S.-W.; Deng, W.-T.; Liang, Z.-T.; Wang, Q.; Wang, X.-N. Global quark polarization in noncentral A+A collisions. Phys. Rev. C 2008, 77, 044902. [Google Scholar] [CrossRef] [Green Version]
- Kharzeev, D.; Son, D. Testing the Chiral Magnetic and Chiral Vortical Effects in Heavy Ion Collisions. Phys. Rev. Lett. 2011, 106, 062301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Du, Y.-L.; Shi, S. Quark Self-Energy and Condensates in NJL Model with External Magnetic Field. Symmetry 2021, 13, 1410. [Google Scholar] [CrossRef]
- Shi, S.; Yang, Y.-C.; Xia, Y.-H.; Cui, Z.-F.; Liu, X.-J.; Zong, H.-S. Dynamical chiral symmetry breaking in the NJL model with a constant external magnetic field. Phys. Rev. D 2015, 91, 036006. [Google Scholar] [CrossRef] [Green Version]
- Creutz, M. One flavor QCD. Ann. Phys. 2007, 322, 1518. [Google Scholar] [CrossRef] [Green Version]
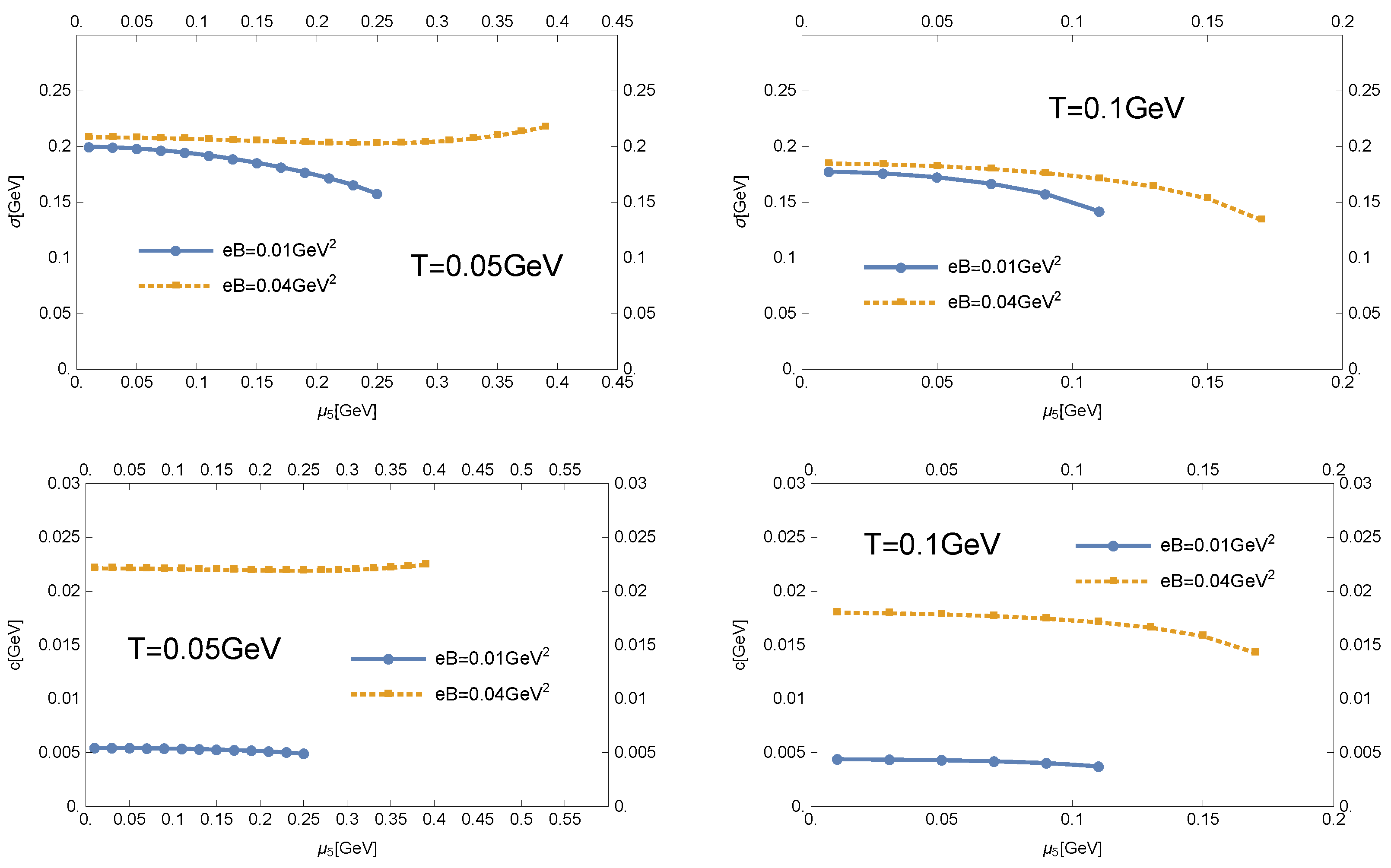

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shi, S. Chiral Chemical Potential and Magnetic Effects on QCD Matter in NJL Model with a Self-Consistent Method. Symmetry 2022, 14, 502. https://doi.org/10.3390/sym14030502
Liu J, Shi S. Chiral Chemical Potential and Magnetic Effects on QCD Matter in NJL Model with a Self-Consistent Method. Symmetry. 2022; 14(3):502. https://doi.org/10.3390/sym14030502
Chicago/Turabian StyleLiu, Juan, and Song Shi. 2022. "Chiral Chemical Potential and Magnetic Effects on QCD Matter in NJL Model with a Self-Consistent Method" Symmetry 14, no. 3: 502. https://doi.org/10.3390/sym14030502
APA StyleLiu, J., & Shi, S. (2022). Chiral Chemical Potential and Magnetic Effects on QCD Matter in NJL Model with a Self-Consistent Method. Symmetry, 14(3), 502. https://doi.org/10.3390/sym14030502





