How Symmetry Influences the Dissociation of Protonated Cyclic Peptides
Abstract
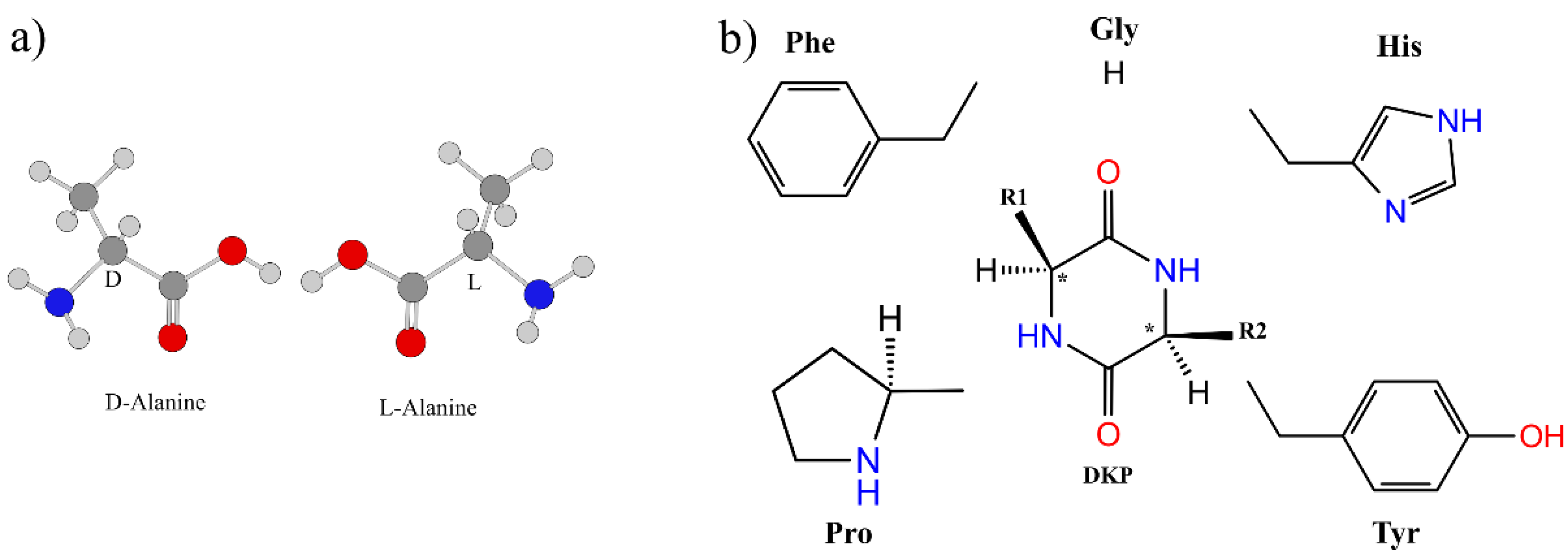
:1. Introduction
2. Experimental and Theoretical Methods
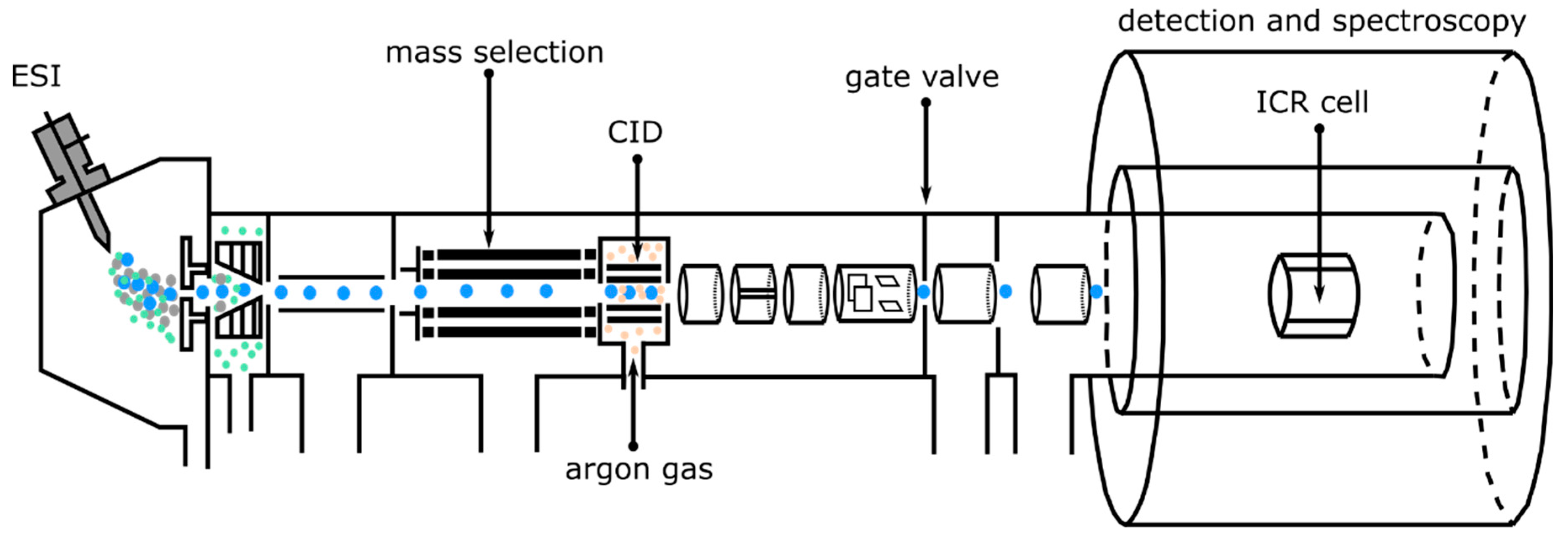
2.1. Experimental Methods: Collision-Induced Dissociation
2.2. Theoretical Methods–Fragmentation Simulations
3. Results and Discussion
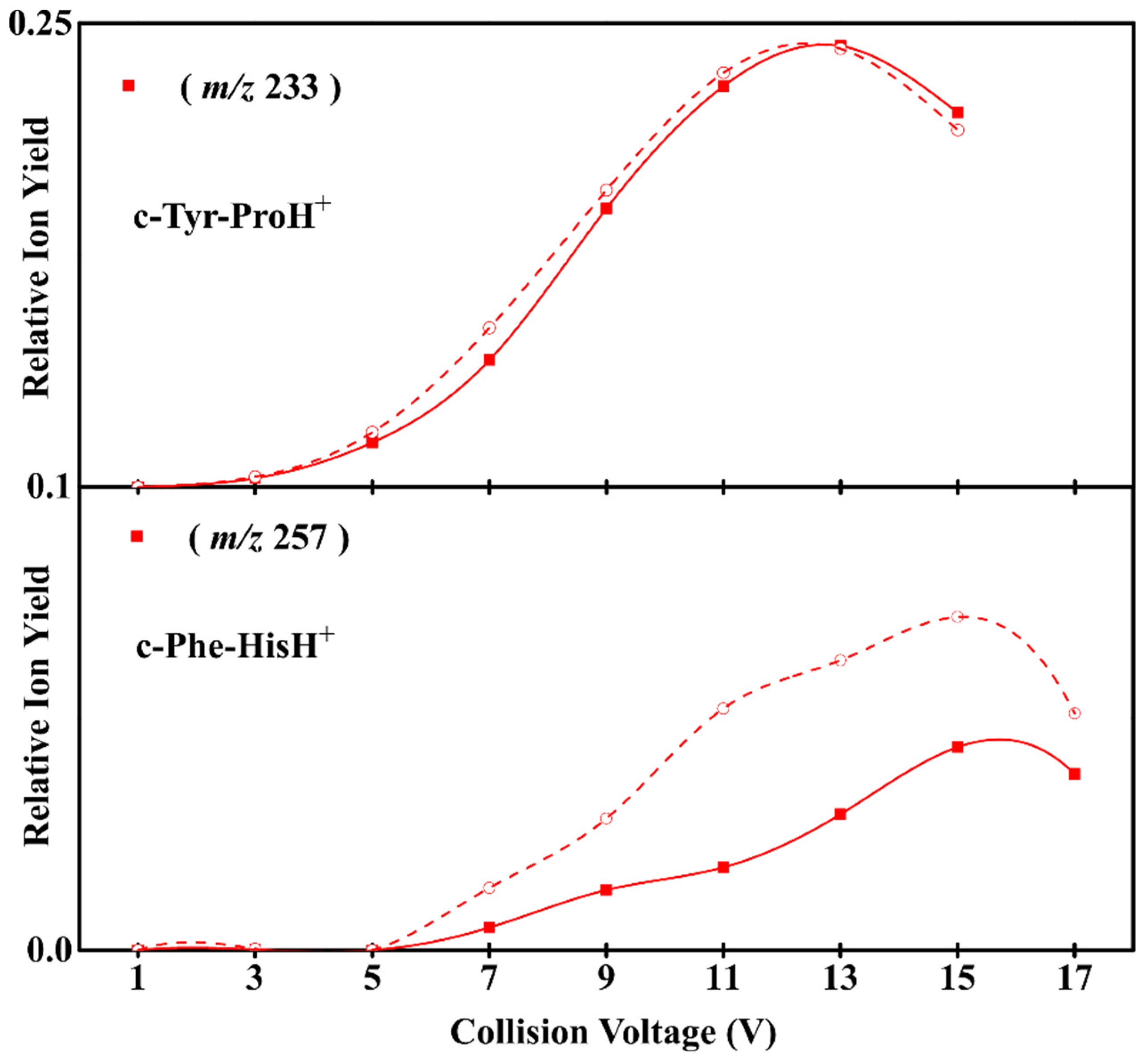
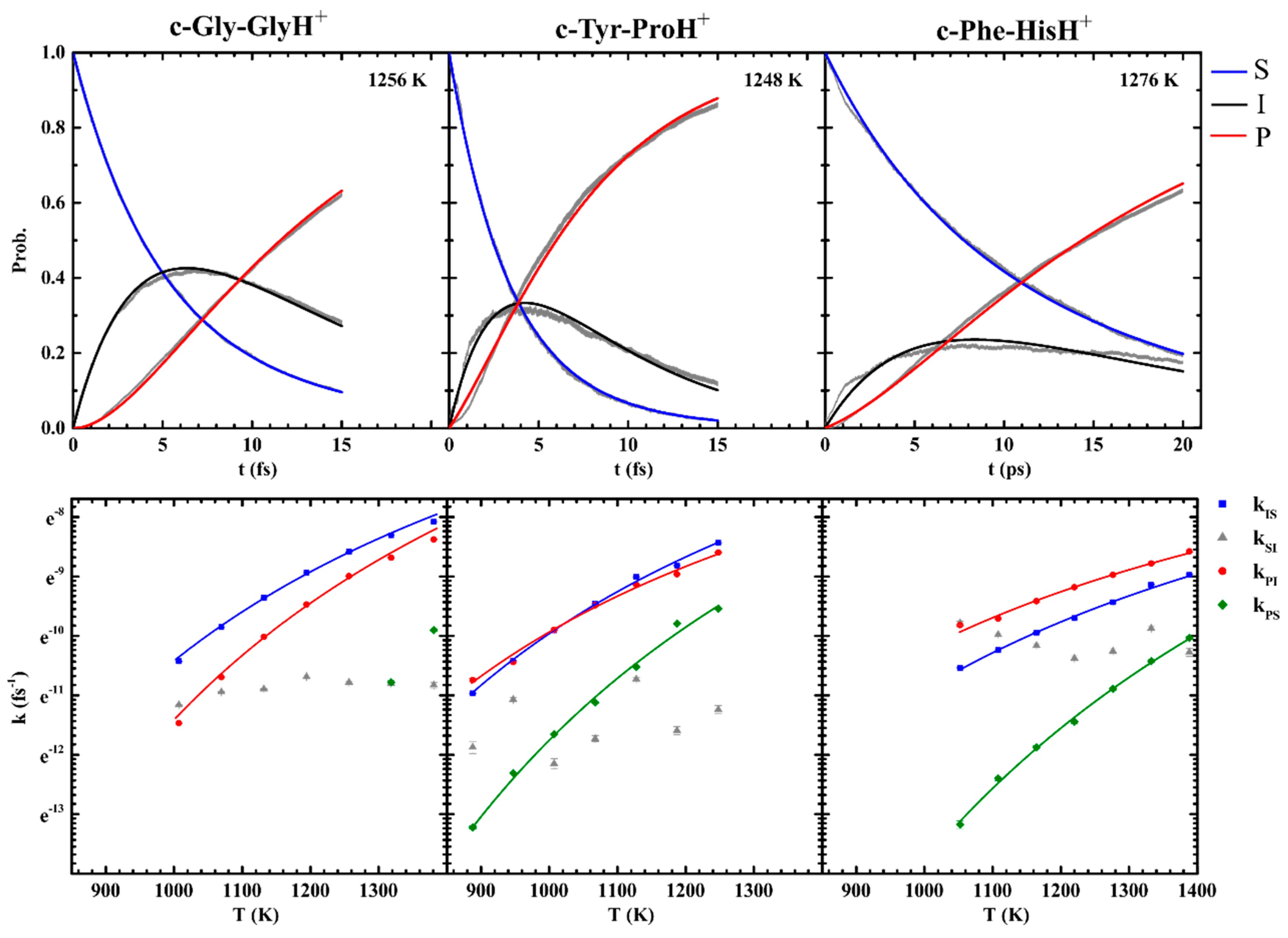
3.1. Experimental Results on the Fragmentation of Diketopiperazine Peptides
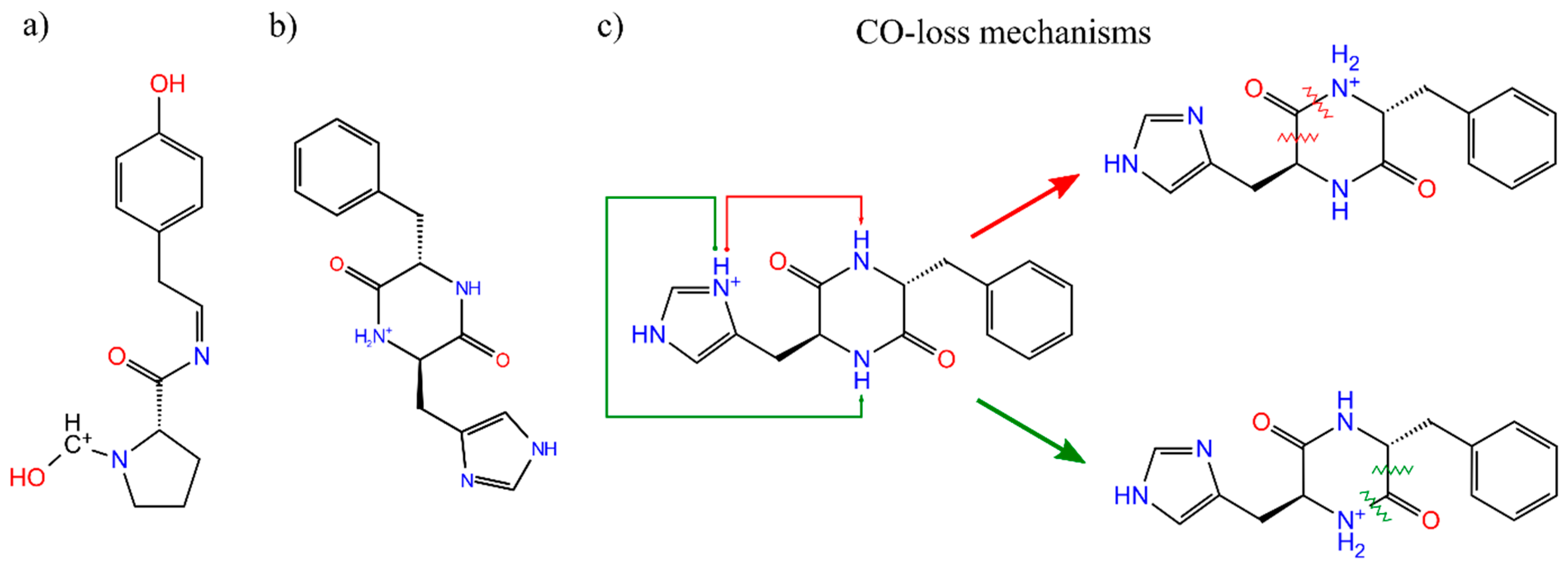
3.2. Sidechain Effect on Primary Fragmentation of Diketopiperazine Peptides
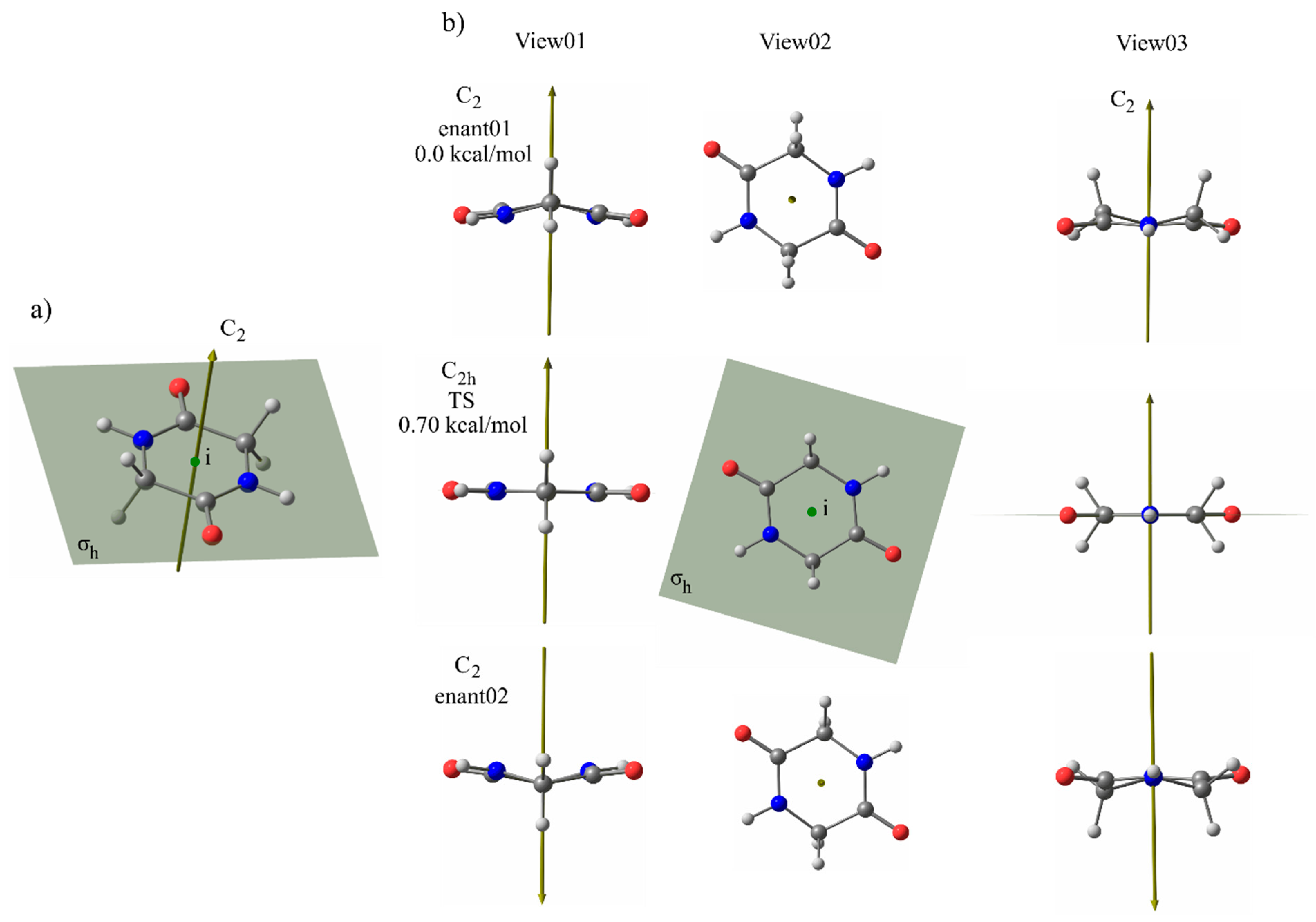
3.3. Effect of Symmetry and Chirality
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bunker, P.R.; Jensen, R. Molecular Symmetry and Spectroscopy, 2nd ed.; NRC Research Press: Ottawa, ON, Canada, 1998. [Google Scholar]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry; Academic Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Gal, J. Pasteur and the art of chirality. Nat. Chem. 2017, 9, 604–605. [Google Scholar] [CrossRef] [PubMed]
- Milne, P.J.; Hunt, A.L.; Rostoll, K.; Van Der Walt, J.J.; Graz, C.J.M. The biological activity of selected cyclic dipeptides. J. Pharm. Pharmacol. 1998, 50, 1331–1337. [Google Scholar] [CrossRef] [PubMed]
- Alata, I.; Perez-Mellor, A.; Ben Nasr, F.; Scuderi, D.; Steinmetz, V.; Gobert, F.; Jaidane, N.E.; Zehnacker-Rentien, A. Does the Residues chirality modify the conformation of a cyclo-dipeptide? Vibrational spectroscopy of protonated cyclo-diphenylalanine in the gas phase. J. Phys. Chem. A 2017, 121, 7130–7138. [Google Scholar] [CrossRef] [PubMed]
- BenNasr, F.; Perez-Mellor, A.; Alata, I.; Lepere, V.; Jaidane, N.E.; Zehnacker, A. Stereochemistry-dependent hydrogen bonds stabilise stacked conformations in jet-cooled cyclic dipeptides: (LD) vs. (LL) cyclo tyrosine-tyrosine. Faraday Discuss. 2018, 212, 399–419. [Google Scholar] [CrossRef]
- Perez-Mellor, A.; Alata, I.; Lepere, V.; Zehnacker, A. Chirality effects in the structures of jet-cooled bichromophoric dipeptides. J. Mol. Spectrosc. 2018, 349, 71–84. [Google Scholar] [CrossRef]
- Pérez Mellor, A.; Zehnacker, A. Chirality effects in jet-cooled cyclic dipeptides. In Physical Chemistry of Cold Gas-Phase Functional Molecules and Clusters; Ebata, T., Fujii, M., Eds.; Springer: Singapore, 2019; pp. 63–87. [Google Scholar]
- Perez-Mellor, A.; Alata, I.; Lepere, V.; Zehnacker, A. Conformational study of the jet-cooled diketopiperazine peptide cyclo tyrosyl-prolyl. J. Phys. Chem. B 2019, 123, 6023–6033. [Google Scholar] [CrossRef]
- Perez-Mellor, A.; Le Barbu-Debus, K.; Lepere, V.; Alata, I.; Spezia, R.; Zehnacker, A. Structure and collision-induced dissociation of the protonated cyclo his-phe dipeptide: Mechanistic studies and stereochemical effects. Eur. Phys. J. D 2021, 75, 165. [Google Scholar] [CrossRef]
- Perez-Mellor, A.; Le Barbu-Debus, K.; Zehnacker, A. Solid-state synthesis of cyclo LD-diphenylalanine: A chiral phase built from achiral subunits. Chirality 2020, 32, 693–703. [Google Scholar] [CrossRef]
- Perez-Mellor, A.; Zehnacker, A. Vibrational circular dichroism of a 2,5-diketopiperazine (DKP) peptide: Evidence for dimer formation in cyclo LL or LD diphenylalanine in the solid state. Chirality 2017, 29, 89–96. [Google Scholar] [CrossRef]
- Pérez Mellor, A.; Spezia, R. Determination of kinetic properties in unimolecular dissociation of complex systems from graph theory based analysis of an ensemble of reactive trajectories. J. Chem. Phys. 2021, 155, 124103. [Google Scholar] [CrossRef]
- Nonappa; Ahonen, K.; Lahtinen, M.; Kolehmainen, E. Cyclic dipeptides: Catalyst/promoter-free, rapid and environmentally benign cyclization of free amino acids. Green Chem. 2011, 13, 1203–1209. [Google Scholar] [CrossRef]
- Hirst, J.D.; Joakim Persson, D. Ab initio calculations of the vibrational and electronic spectra of diketopiperazine. J. Phys. Chem. A 1998, 102, 7519–7524. [Google Scholar] [CrossRef]
- Bettens, F.L.; Bettens, R.P.A.; Brown, R.D.; Godfrey, P.D. The microwave spectrum, structure, and ring-puckering of the cyclic dipeptide diketopiperazine. J. Am. Chem. Soc. 2000, 122, 5856–5860. [Google Scholar] [CrossRef]
- Wang, D.; Gulyuz, K.; Stedwell, C.N.; Polfer, N.C. Diagnostic NH and OH Vibrations for oxazolone and diketopiperazine structures: B(2) from protonated triglycine. J. Am. Soc. Mass Spectrom. 2011, 22, 1197–1203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sletten, E. Conformation of cyclic dipeptides. The crystal and molecular structures of cyclo-D-alanyl-L-alanyl and cyclo-L-alanyl-L-alanyl (3,6-dimethylpiperazine-2,5-dione). J. Am. Chem. Soc. 1970, 92, 172–177. [Google Scholar] [CrossRef]
- Strickland, E.H.; Wilchek, M.; Horwitz, J.; Billups, C. Low temperature circular dichorism of tyrosyl and tryptophanyl diketopiperazines. J. Biol. Chem. 1970, 245, 4168–4177. [Google Scholar] [CrossRef]
- Yamazaki, T.; Nunami, K.I.; Goodman, M. Cyclic retro–inverso dipeptides with two aromatic side chains. II. Conformational analysis. Biopolymers 1991, 31, 1513–1528. [Google Scholar] [CrossRef]
- Maitre, P.; Le Caer, S.; Simon, A.; Jones, W.; Lemaire, J.; Mestdagh, H.; Heninger, M.; Mauclaire, G.; Boissel, P.; Prazeres, R.; et al. Ultrasensitive first coupling of FTICR and FEL. Nucl. Instrum. Methods Sect. A 2003, 507, 541–546. [Google Scholar]
- Bakker, J.M.; Besson, T.; Lemaire, J.; Scuderi, D.; Maitre, P. Gas-phase structure of a pi-allyl-palladium complex: Efficient infrared spectroscopy in a 7 T fourier transform mass spectrometer. J. Phys. Chem. A 2007, 111, 13415–13424. [Google Scholar] [CrossRef]
- Wysocki, V.H.; Tsaprailis, G.; Smith, L.L.; Breci, L.A. Special feature: Commentary—Mobile and localized protons: A framework for understanding peptide dissociation. J. Mass Spectrom. 2000, 35, 1399–1406. [Google Scholar] [CrossRef]
- Frison, G.; van der Rest, G.; Turecek, F.; Besson, T.; Lemaire, J.; Maitre, P.; Chamot-Rooke, J. Structure of electron-capture dissociation fragments from charge-tagged peptides probed by tunable infrared multiple photon dissociation. J. Am. Chem. Soc. 2008, 130, 14916–14917. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Spezia, R. Theoretical Mass Spectrometry: Tracing Ions with Classical Trajectories; De Gruyter: Boston, MA, USA, 2018. [Google Scholar]
- Meroueh, S.O.; Wang, Y.F.; Hase, W.L. Direct dynamics Simulations of collision- and surface-induced dissociation of N-protonated glycine. Shattering fragmentation. J. Phys. Chem. A 2002, 106, 9983–9992. [Google Scholar] [CrossRef]
- Bleiholder, C.; Osburn, S.; Williams, T.D.; Suhai, S.; Van Stipdonk, M.; Harrison, A.G.; Paizs, B. Sequence-scrambling fragmentation pathways of protonated peptides. J. Am. Chem. Soc. 2008, 130, 17774–17789. [Google Scholar] [CrossRef] [PubMed]
- Brodbelt, J.S. Ion activation methods for peptides and proteins. Anal. Chem. 2016, 88, 30–51. [Google Scholar] [CrossRef] [Green Version]
- Bythell, B.J.; Suhai, S.; Somogyi, A.; Paizs, B. Proton-driven amide bond-cleavage pathways of gas-phase peptide ions lacking mobile protons. J. Am. Chem. Soc. 2009, 131, 14057–14065. [Google Scholar] [CrossRef]
- Harrison, A.G.; Young, A.B.; Bleiholder, C.; Suhai, S.; Paizs, B. Scrambling of sequence information in collision-induced dissociation of peptides. J. Am. Chem. Soc. 2006, 128, 10364–10365. [Google Scholar] [CrossRef]
- Tsaprailis, G.; Nair, H.; Somogyi, A.; Wysocki, V.H.; Zhong, W.Q.; Futrell, J.H.; Summerfield, S.G.; Gaskell, S.J. Influence of secondary structure on the fragmentation of protonated peptides. J. Am. Chem. Soc. 1999, 121, 5142–5154. [Google Scholar] [CrossRef]
- Wells, J.M.; McLuckey, S.A. Collision-induced dissociation (CID) of peptides and proteins. In Biological Mass Spectrometry; Burlingame, A.L., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 402, pp. 148–185. [Google Scholar]
- Carra, A.; Spezia, R. In silico tandem mass spectrometer: An analytical and fundamental tool. Chem.-Methods 2021, 1, 123–130. [Google Scholar] [CrossRef]
- Martin-Somer, A.; Martens, J.; Grzetic, J.; Hase, W.L.; Oomens, J.; Spezia, R. Unimolecular fragmentation of deprotonated diproline pro(2)-H (-) studied by chemical dynamics simulations and IRMPD spectroscopy. J. Phys. Chem. A 2018, 122, 2612–2625. [Google Scholar] [CrossRef]
- Perez-Mellor, A.; Alata, I.; Lepere, V.; Spezia, R.; Zehnacker-Rentien, A. Stereospecific collision-induced dissociation and vibrational spectroscopy of protonated cyclo (Tyr-Pro). Int. J. Mass Spectrom. 2021, 465, 116590. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef] [PubMed]
- Halls, M.D.; Velkovski, J.; Schlegel, H.B. Harmonic frequency scaling factors for hartree-fock, S-VWN, B-LYP, B3-LYP, B3-PW91 and MP2 with the sadlej pVTZ electric property basis set. Theor. Chem. Acc. 2001, 105, 413. [Google Scholar] [CrossRef]
- Rocha, G.B.; Freire, R.O.; Simas, A.M.; Stewart, J.J.P. RM1: A reparameterization of AM1 for H, C, N, O, P, S, F, Cl, Br, and I. J. Comput. Chem. 2006, 27, 1101–1111. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Hase, W.L.; Buckowski, D.G. Monte-carlo sampling of a micro-canonical ensemble of classical harmonic-oscillators. Chem. Phys. Lett. 1980, 74, 284–287. [Google Scholar] [CrossRef]
- Verlet, L. Computer experiments on classical fluids.i. thermodynamical properties of lennard-jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Forst, W. Theory of Unimolecular Reactions; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Hase, W.L.; Duchovic, R.J.; Hu, X.; Komornicki, A.; Lim, K.F.; Lu, D.-H.; Peslherbe, G.H.; Swamy, K.N.; Vande Linde, S.R.; Zhu, L.; et al. VENUS96: A general chemical dynamics computer program. QCPE Bull. 1996, 16, 43. [Google Scholar]
- Stewart, J.J.P.; Fiedler, L.J.; Zhang, P.; Zheng, J.; Rossi, I.; Hu, W.-P.; Lynch, G.C.; Liu, Y.-P.; Chuang, Y.Y.; Pu, J.; et al. MOPAC 5.022mn; Department of Chemistry and Supercomputing Institute, University of Minnesota: Minneapolis, MN, USA, 2015. [Google Scholar]
- Oomens, J.; Young, S.; Molesworth, S.; van Stipdonk, M. Spectroscopic evidence for an oxazolone structure of the b(2) fragment ion from protonated tri-alanine. J. Am. Soc. Mass Spectrom. 2009, 20, 334–339. [Google Scholar] [CrossRef] [Green Version]
- Perkins, B.R.; Chamot-Rooke, J.; Yoon, S.H.; Gucinski, A.C.; Somogyi, A.; Wysocki, V.H. Evidence of diketopiperazine and oxazolone structures for HA b(2)(+) ion. J. Am. Chem. Soc. 2009, 131, 17528–17529. [Google Scholar] [CrossRef] [Green Version]
- Shek, P.Y.I.; Lau, J.K.-C.; Zhao, J.; Grzetic, J.; Verkerk, U.H.; Oomens, J.; Hopkinson, A.C.; Siu, K.W.M. Fragmentations of protonated cyclic-glycylglycine and cyclic-alanylalanine. Int. J. Mass Spectrom. 2012, 316, 199–205. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Mellor, A.F.; Spezia, R.; Zehnacker, A. How Symmetry Influences the Dissociation of Protonated Cyclic Peptides. Symmetry 2022, 14, 679. https://doi.org/10.3390/sym14040679
Pérez-Mellor AF, Spezia R, Zehnacker A. How Symmetry Influences the Dissociation of Protonated Cyclic Peptides. Symmetry. 2022; 14(4):679. https://doi.org/10.3390/sym14040679
Chicago/Turabian StylePérez-Mellor, Ariel F., Riccardo Spezia, and Anne Zehnacker. 2022. "How Symmetry Influences the Dissociation of Protonated Cyclic Peptides" Symmetry 14, no. 4: 679. https://doi.org/10.3390/sym14040679
APA StylePérez-Mellor, A. F., Spezia, R., & Zehnacker, A. (2022). How Symmetry Influences the Dissociation of Protonated Cyclic Peptides. Symmetry, 14(4), 679. https://doi.org/10.3390/sym14040679





