Abstract
An adaptive moving mesh method for optimal control problems in viscous incompressible fluid is proposed with the incompressible Navier–Stokes system used to describe the motion of the fluid. The moving distance of nodes in the adopted mesh moving strategy is found by solving a diffusion equation with source terms, and an algorithm that fully considers the characteristics of the control problem is given with symmetry reduction to the incompressible Navier–Stokes equations. Numerical examples are provided to show that the proposed algorithm can solve the optimal control problem stably and efficiently on the premise of ensuring high precision.
1. Introduction
The optimal control problems constrained by PDEs play an increasingly important role in engineering and have attracted widespread attention from many scholars. These problems cover various fields, such as feedback control, the control of fluid flow and optimal shape design [1,2,3]. The research on numerical methods for these problems has been an active area in recent decades. To approximate the solutions of control problems, the FEM (finite element method) proves to be a powerful method and has been used as the main method in dealing with numerical analysis for optimal control problems [4,5,6,7].
Efficient numerical solutions to optimal control problems constrained by PDEs involve many fields, and this is particularly true for fluid dynamics problems. Within the context of optimal control problems, the flow control is crucial for various engineering applications [8,9,10]. Therefore, flow control has become an increasingly active field and has undergone much progress in its theoretical aspects [11,12,13,14,15,16,17].
From the perspective of numerical solutions only, effective discretization schemes for the non-linear state equations are quite challenging, especially when considering practical industrial application problems. The finite element method is undoubtedly the most appropriate tool to compute the flow control problems. Recently, there has been extensive research in theoretical analysis and numerical approximation of the fluid dynamics equations in the scientific literature [18,19].
Researchers have developed some results of the FEM for flow control problems [16,20]. There is also some research on state-constrained control problems constrained by fluid dynamics equations [13,14]. In [11], Abergel and Temam studied first order optimality conditions and gave a gradient algorithm. Wang obtained some theoretical results of state-constrained optimal control problems for 3-D instantaneous fluid flow [21]. Gunzburger, Hou and Svobodny first studied the FEM for optimal control problems about steady-state fluid flow in [15]. Similar problems were discussed in [16]. However, most of those works were based on a uniform mesh, which leads to a time-consuming procedure.
Hydrodynamic problems generally involve interface tracking, shock waves, singularities of solutions, phase changes, and high vorticity or complex areas. When numerically solving these problems, there is usually some form of spatial mesh, and mesh-dependent methods were adopted. However, these methods are not so efficient when the solution involves a large change in the local area [21,22]. It should be noted that there are usually regularities in optimal control problems, and the singularities likely distribute to different positions, which means that the uniform triangulation strategy may be inefficient. The adaptive mesh method is more efficient to deal with in that case. This enables us to use as few meshes as possible to solve the state equations using the adaptive mesh method [23,24,25].
Adaptive FEM, which was proposed by the pioneering work in [26], is becoming an active field in scientific and engineer computations for its high efficiency among various kinds of finite element methods.To achieve a higher accuracy and minimize the computational work as much as possible, adaptive FEM is undoubtedly a particularly appropriate finite element tool in solving PDEs [27,28,29,30,31,32].
The adaptive mesh method usually divides the working domain uniformly first, and then adds or deletes mesh nodes to locally refine or coarsen according to a posteriori error estimation. This is the basic idea of the h-method, and many commercial software programs are also based on this strategy. Another method is the p-method, which increases the number of interpolation polynomials to improve the accuracy of the solution, most commonly in the FEM.
The p-method can be combined with the h-method, and the -method [33,34] is obtained through a posteriori error estimation. The -method has been developed to relative maturity; however, the implementation of this method is quite complicated, because a posteriori error estimation depends heavily on certain assumptions of the solution, and these assumptions may be difficult to obtain for many nonlinear problems. This work considers another adaptive mesh method—namely, the r-method (moving mesh method).
Although the r-method is not as widely used as the h- or p-methods, it has also been used in many fields and has achieved good results [35,36,37,38,39,40]. Although the r-method has many promising features in solving complex problems, there are more problems that need to be solved compared to the h-method and the p-method. The idea of the r-method is to start with a given initial mesh, then move the nodes according to the characteristics of the solution or region and keep the mesh topology and the number of nodes unchanged during the solution process.
In the end, the nodes are concentrated in local areas, which usually have more drastic solution changes or more complex geometric shapes. Therefore, the moving mesh method could save computational effort while the same accuracy is achieved. These techniques can be widely used in physics, mechanics, engineering and other fields and are applied to various problems and algorithm selection, including solving various dynamic equations, detonation simulation and other problems.
In order to solve the optimal control problems constrained by PDEs, we integrate the sensitivity analysis results with the moving mesh strategy and take the incompressible viscous fluid as an example. The structure of this study is the following: In Section 2, the optimal control problem with a Navier–Stokes equation as the state constraint is given, and sensitivity analysis results are obtained by the adjoint method. Section 3 presents an improved moving mesh method. Section 4 presents an adaptive moving mesh method to solve the optimal control problem, and a verification example is provided. A brief summary is given in the last section.
2. Optimal Control Problem and Sensitivity Analysis
We assume that and are two Hilbert spaces, and our goal is to find the minimum value of the functional
constrained by
where and represent the state variable and the control variable, respectively. depends on u—that is, . Usually, there is , . and are admissible spaces. For steady problems, constraints (2) are PDEs with corresponding boundary conditions. For the Navier–Stokes equations, the constraints (2) are:
where is the working area. The constraint variable and the speed and pressure p are unknown. f is the volume force. is the viscosity coefficient. g is a known function. The functions and are control variables. and are both Dirichlet boundary conditions for speed, which can be homogeneous or non-homogeneous; however, the meaning is different at the boundary. Non-homogeneous on generally means inflow or outflow, and homogeneous means that there is no slip condition on the solid wall, while on the boundary , non-homogeneous means the value of the control variable. n represents the unit normal vector. The boundary of the region is .
The typical objective functional in the optimal control problem is:
Equation (4) means the distance between the state Equation (2) to a given goal or expectation of the state . In order for the problem to be well posed, we also include the control in the cost functional, together with a Tikhonov regularization parameter , which is usually chosen a priori, and the control volume is . Equation (4) means the distance between the state Equation (2) to a given goal or expectation of the state . Similarly, we can define this distance as the target functional only on the boundary or part of it.
Let , which means that the function itself and its first derivative belong to the Sobolev space formed by the vector value function of . Let
and
Then, the weak form of the Navier–Stokes problem (3) is:
where represents the inner product of .
Let the area be a triangulation with h as the parameter , and are two finite element spaces. Then, the finite element solution of problem (5) is:
Find , such that
Let the Lagrange multiplier . Using integration by parts, we have
Deriving the above equation in the direction , we can obtain the weak form of the adjoint problem:
As , then using integration by parts, we have
Let , the adjoint problem can be written as follows:
Combining the adjoint problem (10), the sensitivity analysis result of the objective function about the control variable can be obtained from (11).
3. Moving Mesh Strategy
In our previous work, the moving mesh strategy was as follows [41]. Assume that the finite element triangulation at time is , and the coordinate of the k-th node is , then the coordinate of the k-th node at the moment of can be obtained by the following relationship:
where is an adjustable parameter, and is the amount of node movement, which is obtained by solving the following diffusion problem that takes the solution of the Navier–Stokes problem (3) as the source term:
where is the monitor function and v is the solution of Equation (3).
In the first equation of question (13), the right-hand term v reflects the effect of the fluid required by the Navier–Stokes problem (3) on the movement of the mesh. Although it is usually apt to appear with discontinuities and high vorticity where the flow velocity is large, the change of the solution is not necessarily dramatic. The measure taken in [41] is to introduce the gradient information of the solution in the monitor function. In problem (13), homogeneous Dirichilet boundary conditions forcing nodes could not move on the boundary. In this work, the mesh moving equation is improved as:
In the moving mesh method, the monitor function plays a crucial role. In fact, the selection and construction of the monitor function is critical in the moving mesh method. A good monitor function can improve the accuracy of the solution or reduce the local error. For the Navier–Stokes problem, there are some monitor functions that have been suggested in existing works. For example, the monitor functions adopted in [42] are:
where , are adjustable parameters, and is the error
is the leap along the boundary l.
For the problems studied in this paper, we use the following monitor functions:
where are adjustable parameters—that is, the source term was replaced by the sensitivity analysis result of the objective functional. The numerical example shows that this choice could achieve better results. is the residual-type a posteriori error estimation of the Navier–Stokes problem,
where is the Neumann boundary, ( is the triangle), and denotes the jumps. Assume have a common side, and are unit normal vectors accordingly, then:
For more discussion on the a posteriori error estimation of the Navier–Stokes problem, please refer to [43,44].
4. Numerical Algorithm and Numerical Example
4.1. Numerical Algorithm
Based on the results in the previous sections, we give the moving mesh method to solve the optimal control problem constraints by the Navier–Stokes equation as follows:
- I
- Divide the working domain uniformly to obtain the initial triangulation and the corresponding coordinates of the node is . Then, solve the Navier–Stokes problem (3) to obtain the solution and the solution of the adjoint problem (10) . Obtain the value . Select the appropriate parameters , , ; given the termination criteria ;.
- II
- If , then iterate as follows. Step includes the following items:
- From , we find the new triangulation .
- Solve the Navier–Stokes problem (3) to obtain the solution and the solution of the adjoint problem (10) . Find the values of . Calculate .
4.2. Numerical Example
We consider the classical backstep flow with (i.e., ). Assume that on the inflow boundary, , on the outflow boundary, and on the rest of the boundaries. The computational domain of the backstep problem is depicted in Figure 1. The target flow field with is shown in Figure 2.
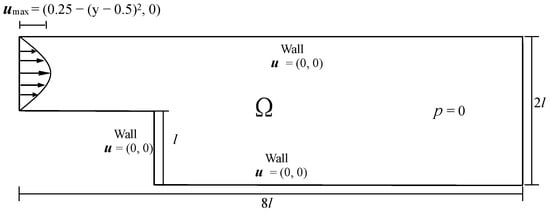
Figure 1.
The computational domain of the back-step problem.
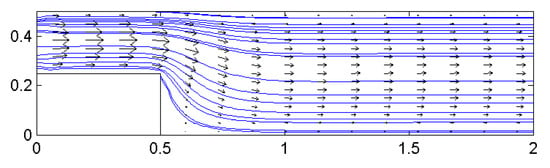
Figure 2.
The target flow field.
Figure 3 gives the initial triangulation, and Figure 4 shows the moving mesh produced by the strategy we proposed.
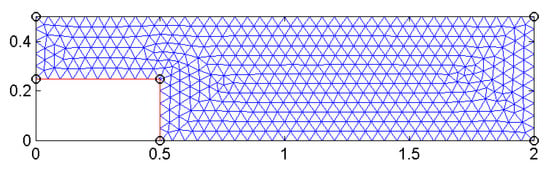
Figure 3.
The initial mesh.

Figure 4.
The mesh after moving.
The numerical solution without control is shown in Figure 5, and Figure 6 is the controlled fluid flow.
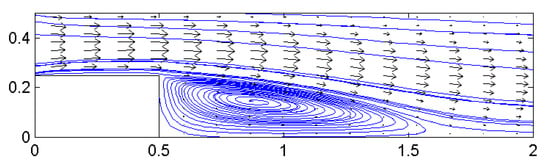
Figure 5.
The uncontrolled fluid flow.
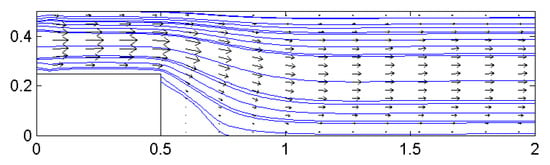
Figure 6.
The controlled fluid flow.
The value of the objective function without control is 1.05, while the valued of the objective function after control is . This means that the value of the objective function has been reduced to about .
It can be seen from the results that the mesh will be automatically focused on the place where the solution change is relatively large. We also solved the problem with uniform triangulation. To achieve the same numerical accuracy, the nodes need to be doubled and the time-consumption increased by more than 1.5 times. This shows that the proposed algorithm is efficient.
5. Conclusions
An adaptive moving mesh method for optimal control problems in viscous incompressible fluid is proposed in this paper, and this is an effective method to solve classical optimal control problems that are constrained by PDEs. The moving distance of the nodes in the proposed strategy is achieved by solving the diffusion equation. An algorithm fully considering the characteristics of the control problem is given.
The fluid states is dominated by the incompressible Navier–Stokes equation in this paper, and thus the proposed method and algorithm can easily generalize to other optimal control problems that are constrained by PDEs. Finally, the numerical examples provided show that the mesh can be concentrated in areas where the solution changes drastically, and the points on the boundary are not forced to remain unchanged.
Author Contributions
Conceptualization, J.L. and H.X.; methodology, X.D.; software, X.D.; validation, J.L., H.X. and X.D.; formal analysis, J.L.; investigation, J.L.; resources, J.L.; data curation, X.D.; writing—original draft preparation, J.L.; writing—review and editing, J.L.; visualization, J.L.; supervision, J.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the the Natural Science Foundations of Shaanxi Province of China (2020JM-571, 2021JM1002) and the Science Foundation of the Education Department of Shaanxi Province of China (17JK0344).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the referees and the editors for their valuable comments that led to improvements of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bonnans, J.F.; Shapiro, A. Perturbation Analysis of Optimization Problem; Springer: New York, NY, USA, 2000. [Google Scholar]
- Clarke, F.H. Optimization and Nonsmooth Analysis; John Wiley Sons: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Lions, J.L. Optinal Control of System Governed by Partial Differential Equations; Springer: Berlin, Germany, 1971. [Google Scholar]
- Hinze, M.; Pinnau, R.; Ulbrich, M.; Ulbrich, S. Optimization with PDE Constraints; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Liu, W.B.; Yan, N.N. Adaptive Finite Elements Methods for Optimal Control Problem Governed by PDEs; Sciences Press: Beijing, China, 2008. [Google Scholar]
- Neittaanmaki, P.; Sprekels, J.; Tiba, D. Optimization of Elliptic Systems: Theory and Applications; Springer Science Business Media Inc.: New York, NY, USA, 2006. [Google Scholar]
- Tiba, D. Optimal Control of Nonsmooth Distributed Parameter Systems; Lecture Notes in Math. 459; Springer: Berlin, Germany, 1990. [Google Scholar]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1998, 3, 233–260. [Google Scholar] [CrossRef]
- Jameson, A.; Martinelli, L.; Pierce, N.A. Optimum aerodynamic design using the Navier–Stokes equations. Theor. Comput. Fluid Dyn. 1998, 10, 213–237. [Google Scholar] [CrossRef]
- Mackenzie, J.A.; Nolan, M.; Rowlatt, C.F.; Insall, R.H. An adaptive moving mesh method for forced curve shortening flow. SIAM J. Sci. Comput. 2019, 41, A1170–A1200. [Google Scholar] [CrossRef]
- Abergel, F.; Temam, R. On Some Control Problems in Fluid Mechanics. Theor. Comput. Fluid Dyn. 1990, 1, 303–325. [Google Scholar] [CrossRef]
- Barbu, V. Optimal contrtol of Navier–Stokes equations with perioeic inputs. Nonlinear Anal. 1998, 31, 1531. [Google Scholar] [CrossRef]
- De Los Reyes, J.C.; Griesse, R. State-constrained optimal control of the three dimensional stationary Navier–Stokes equations. J. Math. Anal. Appl. 2008, 343, 257–272. [Google Scholar] [CrossRef][Green Version]
- De los Reyes, J.C.; Troltzsch, F. Optimal control of the stationary Navier–Stokes equations with mixed control-state constraints. SIAM J. Control Optim. 2007, 46, 604–629. [Google Scholar] [CrossRef]
- Gunzburger, M.D. Flow Control; Springer: New York, NY, USA, 1995. [Google Scholar]
- Casas, E. Error estimates for the numerical approximation of a distributed control prob lem for the steady-state Navier-stokes equations. SIAM J. Control Optim. 2007, 46, 952–982. [Google Scholar] [CrossRef]
- Roul, P. A robust adaptive moving mesh technique for a time-fractional reaction–diffusion model. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106290. [Google Scholar] [CrossRef]
- Girault, V.; Raviart, P. Finite Element Method for Navier–Stokes Equations: Theory and Algorithms; Springer: Heidelberg, Germany, 1996. [Google Scholar]
- Temam, R. Navier–Stokes Equations and Nonlinear Functional Analysis; SIAM: Philadelphia, PA, USA, 1983. [Google Scholar]
- Liu, W.B.; Yan, N.N. A posteriori error estimates for control problems governed by Stokes equations. SIAM J. Numer. Anal. 2003, 40, 1850–1869. [Google Scholar] [CrossRef]
- Wang, G. Optimal control of 3-dimensional Navier–Stokes equations with state constraints. SIAM J. Control Optim. 2002, 41, 583–606. [Google Scholar] [CrossRef]
- Li, R.; Liu, W.B.; Ma, H.; Tang, T. Adaptive finite element approximation of elliptic optimal control. SIAM J. Control Optim. 2002, 41, 1321–1349. [Google Scholar] [CrossRef]
- Kurganov, A.; Qu, Z.; Rozanova, O.S.; Wu, T. Adaptive Moving Mesh Central-Upwind Schemes for Hyperbolic System of PDEs: Applications to Compressible Euler Equations and Granular Hydrodynamics. Commun. Appl. Math. Comput. 2021, 3, 445–480. [Google Scholar] [CrossRef]
- Duan, J.M.; Tang, H.Z. High-order accurate entropy stable adaptive moving mesh finite difference schemes for special relativistic (magneto)hydrodynamics. J. Comput. Phys. 2022, 456, 111038. [Google Scholar] [CrossRef]
- Almatrafi, M.B.; Alharbi, A.; Lotfy, K.; El-Bary, A.A. Exact and numerical solutions for the GBBM equation using an adaptive moving mesh method. Alex. Eng. J. 2021, 60, 4441–4450. [Google Scholar] [CrossRef]
- Babuska, I.; Rheinboldt, W.C. Error estimates for adaptive finite element computations. SIAM J. Numer. Anal. 1978, 15, 736–754. [Google Scholar] [CrossRef]
- Oden, J.T.; Wu, W.; Ainsworth, M. An a posteriori error estimate for finite element approximations of the Navier-stokes equations. Comput. Methods Appl. Mech. Eng. 1993, 111, 185–202. [Google Scholar] [CrossRef]
- Verfurth, R. A Review of a Posteriori Error Estimation and Adaptive Mesh-Refinement Techniques; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Verfurth, R. A posteriori error estimators for the Stokes equations. Numer. Math. 1989, 55, 309–325. [Google Scholar] [CrossRef]
- Luo, D.; Huang, W.; Qiu, J. A quasi-lagrangian moving mesh discontinuous galerkin method for hyperbolic conservation laws. J. Comput. Phys. 2019, 396, 544–578. [Google Scholar] [CrossRef]
- Hubbard, M.E.; Ricchiuto, M.; Sarmany, D. Space-time residual distribution on moving meshes. Comput. Math. Appl. 2020, 79, 1561–1589. [Google Scholar] [CrossRef]
- Bagherpoorfard, M.; Soheili, A.R. Moving mesh version of wave propagation algorithm based on augmented riemann solver. Appl. Math. Comput. 2020, 375, 125087–125103. [Google Scholar] [CrossRef]
- Ainsworth, M.; Oden, J.T. A Posteriori Error Estimation in Finite Element Analysis; Pure and Applied Mathematics; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Koncz, V.; Izsák, F.; Noszticzius, Z.; Kály-Kullai, K. Adaptive moving mesh algorithm based on local reaction rate. Heliyon 2021, 7, e05842. [Google Scholar] [CrossRef] [PubMed]
- Tang, T. Moving mesh methods for computational fluid dynamics. Contemp. Math. 2004, 383, 141–173. [Google Scholar]
- Mackenzie, J.A.; Mekwi, W.R. On the Use of Moving Mesh Methods to Solve PDEs. In Adaptive Computations: Theory and Algorithms; Tang, T., Xu, J., Eds.; Science Press: Beijing, China, 2007. [Google Scholar]
- Ceniceros, H.D.; Hou, T.Y. An efficient dynamically adaptive mesh for potentially singular solutions. J. Comput. Phys. 2001, 172, 609–639. [Google Scholar] [CrossRef]
- Huang, W.; Zhan, X. Adaptive moving mesh modeling for two dimensional groundwater flow and transport. In Recent Advances in Adaptive Computation, Contemporary Mathematics; AMS: Providence, RI, USA, 2004; Volume 383, pp. 283–296. [Google Scholar]
- Budd, C.J.; Williams, J.F. Parabolic Monge-Ampere methods for blow-up problems in several spatial dimensions. J. Phys. A 2006, 39, 5425–5444. [Google Scholar] [CrossRef]
- Zegeling, P.A.; Kok, H.P. Adaptive moving mesh computations for reaction-diffusion systems. J. Comput. Appl. Math. 2004, 168, 519–528. [Google Scholar] [CrossRef]
- Duan, X.; Cao, Q.; Tan, H. A new moving mesh method for solving the two-dimensional Navier–Stokes equation. Chin. J. Eng. Math. 2019, 36, 431–438. [Google Scholar]
- Di, Y.; Li, R.; Tang, T.; Zhang, P. Moving Mesh Finite Element Methods for the Incompressible Navier–Stokes Equations. SIAM J. Sci. Comput. 2016, 26, 1036–1056. [Google Scholar] [CrossRef]
- Song, L.; Su, H.; Feng, X. Recovery-based error estimatorfor stabilized finite element method for the stationary Navier–Stokes problem. SIAM J. Sci. Comput. 2016, 38, A3758–A3772. [Google Scholar] [CrossRef]
- Zhang, T.; Li, S. A posteriori error estimates of finite element method for the time-dependent navier-stokes equations. Appl. Math. Comput. 2017, 315, 13–26. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).






