Robust Finite-Time Control of Discrete-Time Switched Positive Time-Varying Delay Systems with Exogenous Disturbance and Their Application
Abstract
:1. Introduction
2. System Descriptions and Preliminaries
3. Main Results
- (a)
- If , then ;
- (b)
- If , then .
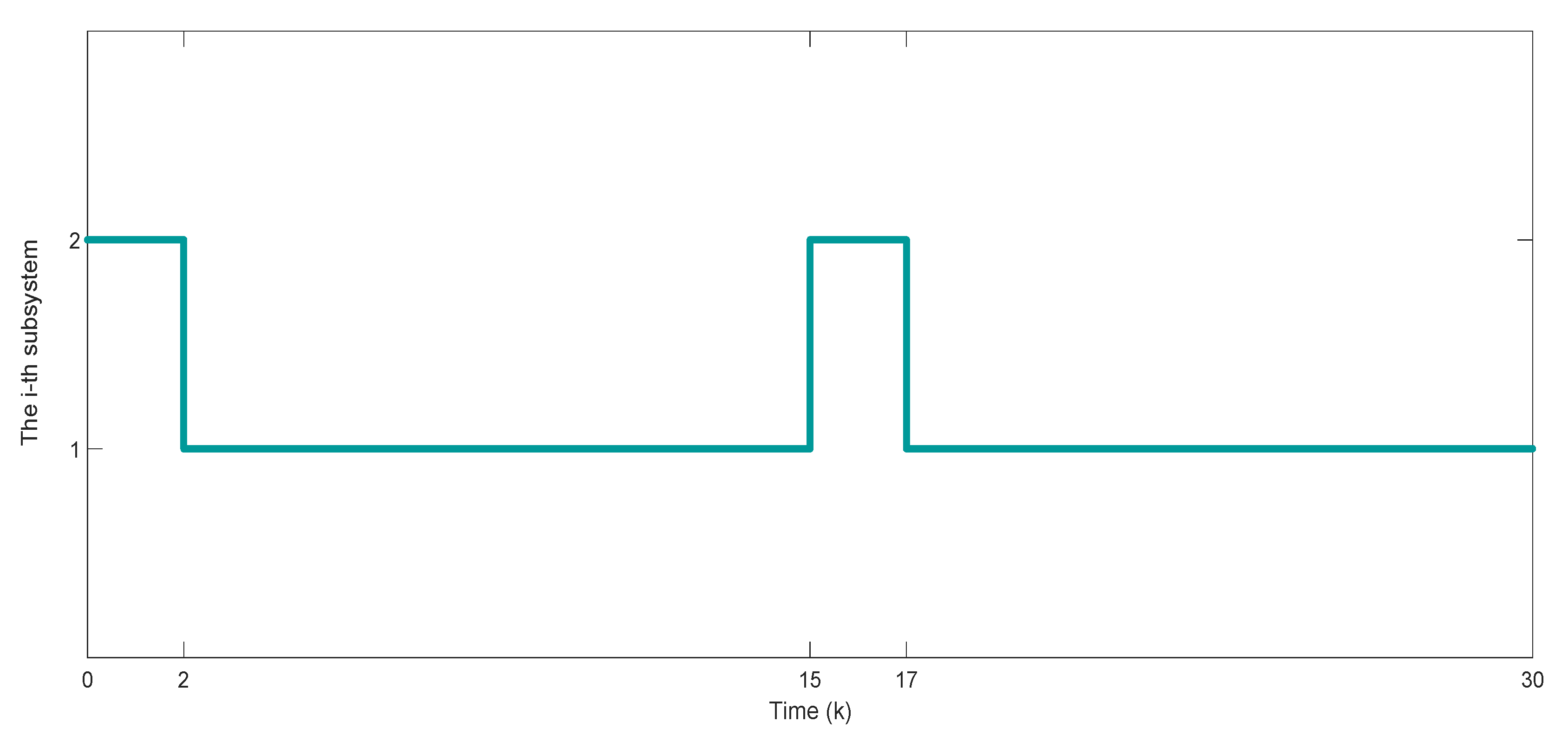
4. Numerical Simulations
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liberzon, D. Switching in Systems and Control; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Mahmoud, M.S. Switched Time-Delay Systems: Stability and Control; Springer: New York, NY, USA, 2010. [Google Scholar]
- Wang, D.; Shi, P.; Wang, W. Robust Filtering and Fault Detection of Switched Delay Systems; Springer: Berlin, Germany, 2013. [Google Scholar]
- Zhang, J.; Sun, Y. Practical exponential stability of discrete-time switched linear positive systems with impulse and all modes unstable. Appl. Math. Comput. 2021, 409, 126408. [Google Scholar] [CrossRef]
- Feng, S.; Wang, J.; Zhao, J. Stability and robust stability of switched positive linear systems with all modes unstable. IEEE/CAA J. Autom. Sin. 2019, 6, 167–176. [Google Scholar] [CrossRef]
- Mason, O.; Shorten, R. On linear copositive Lyapunov functions and the stability of switched positive linear systems. IEEE Trans. Autom. Control 2007, 52, 1346–1349. [Google Scholar] [CrossRef] [Green Version]
- Bolajraf, M.; Tadeo, F.; Alvarez, T.; Rami, M.A. State-feedback with memory for controlled positivity with application to congestion control. IET Control Theory Appl. 2010, 4, 2041–2048. [Google Scholar] [CrossRef]
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Mahmoud, M.S. Switched delay-dependent control policy for water-quality systems. IET Control Theory Appl. 2009, 3, 1599–1610. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, J. Almost output regulation for switched positive systems with different coordinates transformations and its application to a positive circuit model. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3968–3977. [Google Scholar] [CrossRef]
- Kharitonov, V. Time-Delay Systems: Lyapunov Functionals and Matrices; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wu, M.; He, Y.; She, J.-H. Stability Analysis and Robust Control of Time-Delay Systems; Springer: Berlin, Germany, 2010. [Google Scholar]
- Botmart, T.; Noun, S.; Mukdasai, K.; Weera, W.; Yotha, N. Robust passivity analysis of mixed delayed neural networks with interval nondifferentiable time-varying delay based on multiple integral approach. AIMS Math. 2021, 6, 2778–2795. [Google Scholar] [CrossRef]
- Luemsai, S.; Botmart, T.; Weera, W.; Charoensin, S. Improved results on mixed passive and H∞ performance for uncertain neural networks with mixed interval time-varying delays via feedback control. AIMS Math. 2021, 6, 2653–2679. [Google Scholar] [CrossRef]
- Xiao, H.; Zhu, Q. Stability analysis of switched stochastic delay system with unstable subsystems. Nonlinear Anal. Hybrid Syst. 2021, 42, 101075. [Google Scholar] [CrossRef]
- Ratchagit, K.; Phat, V.N. Stability criterion for discrete-time systems. J. Inequal. Appl. 2010, 2010, 201459. [Google Scholar] [CrossRef] [Green Version]
- Wangrat, S.; Yotha, N. Practical exponential stability of discrete time impulsive system with delay. Thai J. Math. 2020, 18, 1639–1648. [Google Scholar]
- Fan, L.; Zhu, Q. Mean square exponential stability of discrete-time Markov switched stochastic neural networks with partially unstable subsystems and mixed delays. Inf. Sci. 2021, 580, 243–259. [Google Scholar] [CrossRef]
- Rodriguse-Licea, M.-A.; Perez-Pinal, F.-J.; Olivares, J.P. Robust stabilization of linear switched systems with unstable subsystems. Appl. Sci. 2018, 8, 2620. [Google Scholar] [CrossRef] [Green Version]
- Rajchakit, G.; Rojsiraphisal, T.; Rajchakit, M. Robust stability and stabilization of uncertain switched discrete-time systems. Adv. Differ. Equ. 2012, 2012, 134. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H. Dwell time stability and stabilization of interval discrete-time switched positive linear systems. Nonlinear Anal. Hybrid Syst. 2019, 33, 116–129. [Google Scholar] [CrossRef]
- Rajchakit, G. Switching design for the robust stability of nonlinear uncertain stochastic switched discrete-time systems with interval time-varying delay. J. Comput. Anal. Appl. 2014, 16, 10–19. [Google Scholar]
- Zhang, J.; Han, Z. Robust stabilization of switched positive linear systems with uncertainties. Int. J. Control Autom. Syst. 2013, 11, 41–47. [Google Scholar] [CrossRef]
- Ma, R.; Wang, X.; Liu, Y. Robust stability of switched positive linear systems with interval uncertainties via multiple time-varying linear copositive Lyapunov functions. Nonlinear Anal. Hybrid Syst. 2018, 30, 285–292. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Niamsup, P.; Yimnet, S. Global uniform asymptotic stability criteria for linear uncertain switched positive time-varying delay systems with all unstable subsystems. Mathematics 2020, 8, 2118. [Google Scholar] [CrossRef]
- Chousurin, R.; Mouktonglang, T.; Wongsaijai, B.; Poochinapan, K. Performance of compact and non-compact structure preserving algorithms to traveling wave solutions modeled by the Kawahara equation. Numer. Algorithms 2020, 85, 523–541. [Google Scholar] [CrossRef]
- Tamang, N.; Wongsaijai, B.; Mouktonglang, T.; Poochinapan, K. Novel algorithm based on modification of Galerkin finite element method to general Rosenau-RLW equation in (2+1)-dimensions. Appl. Numer. Math. 2020, 148, 109–130. [Google Scholar] [CrossRef]
- Wongsaijai, B.; Poochinapan, K. Optimal decay rates of the dissipative shallow water waves modeled by coupling the Rosenau-RLW equation and the Rosenau-Burgers equation with power of nonlinearity. Appl. Math. Comput. 2021, 405, 126202. [Google Scholar] [CrossRef]
- Wongsaijai, B.; Charoensawan, P.; Chaobankoh, T.; Poochinapan, K. Advance in compact structure-preserving manner to the Rosenau-Kawahara model of shallow-water wave. Math. Methods Appl. Sci. 2021, 44, 7048–7064. [Google Scholar] [CrossRef]
- Faybusovich, L.; Mouktonglang, T.; Tsuchiya, T. Numerical experiments with universal barrier functions for cones of Chebyshev systems. Comput. Optim. Appl. 2008, 41, 205–223. [Google Scholar] [CrossRef]
- Faybusovich, L.; Mouktonglang, T. Multi-target linear-quadratic control problem and second-order cone programming. Syst. Control Lett. 2004, 52, 17–23. [Google Scholar] [CrossRef]
- Faybusovich, L.; Mouktonglang, T.; Tsuchiya, T. Implementation of infinite-dimensional interior-point method for solving multi-criteria linear-quadratic control problem. Optim. Methods Softw. 2006, 21, 315–341. [Google Scholar] [CrossRef]
- Amato, F.; Ariola, M.; Cosentino, C. Finite-time control of discrete-time linear systems: Analysis and design conditions. Automatica 2010, 46, 919–924. [Google Scholar] [CrossRef]
- Puangmalai, W.; Puangmalai, J.; Rojsiraphisal, T. Robust finite-time control of linear system with non-differentiable time-varying delay. Symmetry 2020, 12, 680. [Google Scholar] [CrossRef]
- Puangmalai, J.; Tongkum, J.; Rojsiraphisal, T. Finite-time stability criteria of linear system with non-differentiable time-varying delay via new integral inequality. Math. Comput. Simul. 2020, 171, 170–186. [Google Scholar] [CrossRef]
- Liu, L.; Xing, H.; Cao, X.; Fu, Z.; Song, S. Guaranteed cost finite-time control of discrete-time positive impulsive switched systems. Complexity 2018, 2018, 5790681. [Google Scholar] [CrossRef] [Green Version]
- Weiss, L.; Infante, E.F. Finite time stability under perturbing forces and on product spaces. IEEE Trans. Autom. Control 1967, 12, 54–59. [Google Scholar] [CrossRef]
- Hou, L.-L.; Zong, G.-D.; Wu, Y.-Q. Finite-time control for discrete-time switched systems with time delay. Int. J. Control Autom. Syst. 2012, 10, 855–860. [Google Scholar] [CrossRef]
- Moradi, E.; Jahed-Motlagh, M.R.; Yazdi, M.B. Delay-dependent finite-time stabilization of uncertain switched time-delay systems with norm-bounded disturbance. IETE J. Res. 2018, 64, 195–208. [Google Scholar] [CrossRef]
- Yimnet, S.; Niamsup, P. Finite-time stability and boundedness for linear switched singular positive time-delay systems with finite-time unstable subsystems. Syst. Sci. Control Eng. 2020, 8, 541–568. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, W.; Yang, Z.; Zou, Y. Finite-time boundedness of switched systems with time-varying delays via sampled-data control. Int. J. Robust Nonlinear Control 2020, 30, 2953–2976. [Google Scholar] [CrossRef]
- Feng, L.; Zhao, P. Finite-time stability and stabilization of switched linear time-varying systems with time-varying delay. Math. Probl. Eng. 2021, 2021, 8880744. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, L.; Shi, P. Stability of a class of switched positive linear time-delay systems. Int. J. Robust Nonlinear Control 2013, 23, 578–589. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z. Finite-time L1 control for positive switched linear systems with time-varying delay. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3158–3166. [Google Scholar] [CrossRef]
- Yu, T.; Zhong, Y.; Chen, T.; Chen, C. Finite-time stabilization of uncertain switched positive linear systems with time-varying delays. Discrete Dynamics in Nature and Society 2015, 2015, 954782. [Google Scholar] [CrossRef]
- Liu, Y.; Tao, W.; Lee, L.; Lu, J. Finite-time boundedness and L2-gain analysis for switched positive linear systems with multiple time delays. Int. J. Robust Nonlinear Control 2017, 27, 3508–3523. [Google Scholar]
- Liu, J.; Lian, J.; Zhuang, Y. Output feedback L1 finite-time control of switched positive delayed systems with MDADT. Nonlinear Anal. Hybrid Syst. 2015, 15, 11–22. [Google Scholar] [CrossRef]
- Liu, L.-J.; Zhao, X.; Wu, D. Stability of switched positive linear time-delay systems. IET Control Theory Appl. 2019, 13, 912–919. [Google Scholar] [CrossRef]
- Hernandez-Vargas, E.; Colaneri, P.; Middleton, R.; Blanchini, F. Discrete-time control for switched positive systems with application to mitigating viral escape. Int. J. Robust Nonlinear Control 2011, 21, 1093–1111. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Z.; Wu, H. Robust finite-time stability and stabilisation of switched positive systems. IET Control Theory Appl. 2014, 8, 67–75. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z. Exponential stability of discrete-time switched linear positive systems with time-delay. Appl. Math. Comput. 2014, 230, 193–199. [Google Scholar] [CrossRef]
- Li, X.; Lin, X.; Li, S.; Zuo, Y. Finite-time stability of switched nonlinear systems with finite-time unstable subsystems. J. Franklin Inst. 2015, 352, 1192–1214. [Google Scholar] [CrossRef]
- Tan, J.; Wang, W.; Yao, J. Finite-time stability and boundedness of switched systems with finite-time unstable subsystems. Circuits Syst. Signal Process. 2019, 38, 2931–2950. [Google Scholar] [CrossRef]
- Garg, K.; Panagou, D. Finite-time stability of hybrid systems with unstable modes. Front. Control Eng. 2021, 2, 707729. [Google Scholar] [CrossRef]
- Tian, Y.; Cai, Y.; Sun, Y. Stability of switched nonlinear time-delay systems with stable and unstable subsystems. Nonlinear Anal. Hybrid Syst. 2017, 24, 58–68. [Google Scholar] [CrossRef]
- Pashaei, S.; Hashemzadeh, F. New finite-time stability and boundedness conditions for time-delay switched linear systems with finite-time unstable and unbounded subsystems. In Proceedings of the 27th Iranian Conference on Electrical Engineering (ICEE2019), Yazd, Iran, 30 April–2 May 2019. [Google Scholar]
- Gao, Z.; Wang, Z.; Wu, X.; Wang, W.; Liu, Y. Finite-time stability analysis of a class of discrete-time switched nonlinear systems with partial finite-time unstable modes. Asian J. Control 2022, 24, 309–319. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, Y.; Yu, P. Stability analysis of discrete-time switched positive nonlinear systems with unstable subsystems under different switching strategies. IEEE Trans. Circuits Syst. II Exp. Briefs 2021, 68, 1957–1961. [Google Scholar] [CrossRef]
- Mouktonglang, T.; Yimnet, S. Finite-time boundedness of linear uncertain switched positive time-Varying delay systems with finite-time unbounded subsystems and exogenous disturbance. Mathematics 2022, 10, 65. [Google Scholar] [CrossRef]
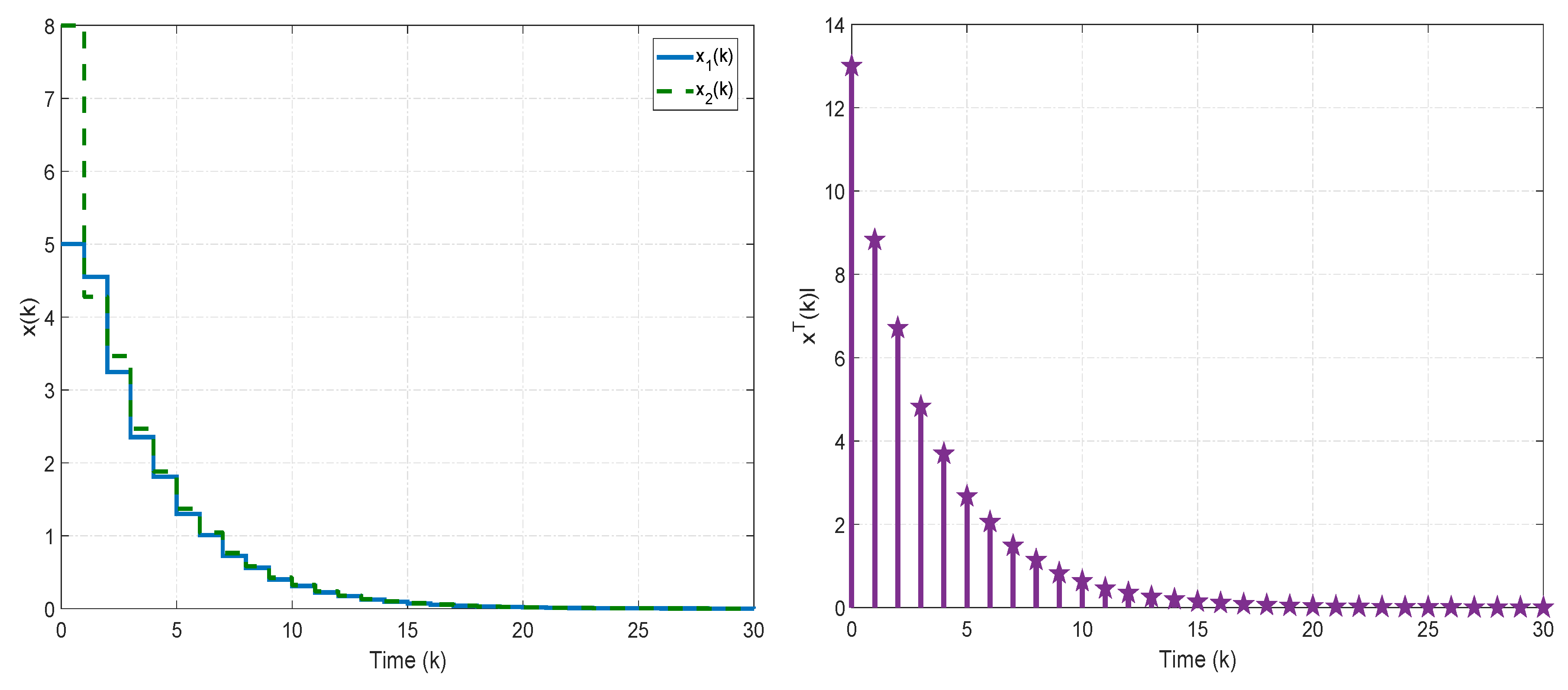

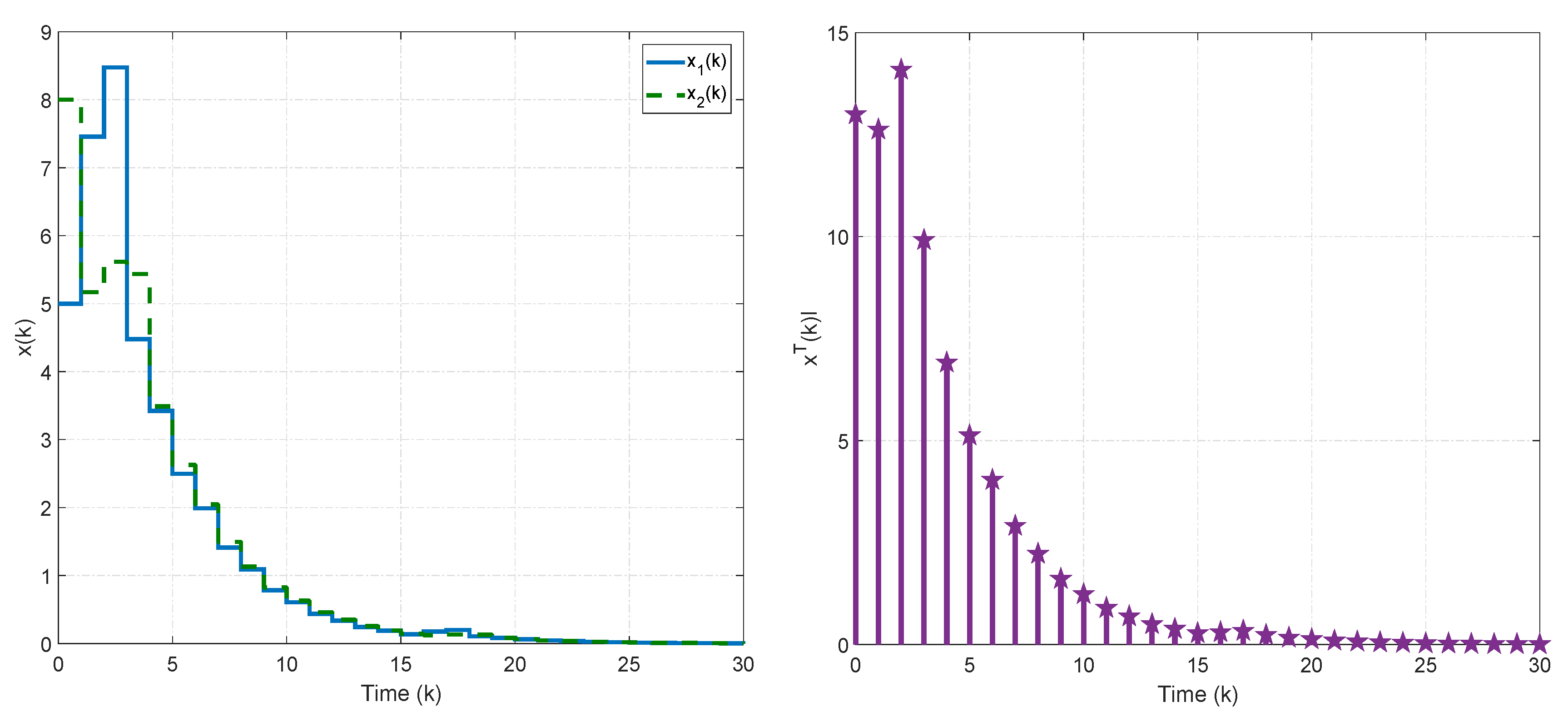
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouktonglang, T.; Poochinapan, K.; Yimnet, S. Robust Finite-Time Control of Discrete-Time Switched Positive Time-Varying Delay Systems with Exogenous Disturbance and Their Application. Symmetry 2022, 14, 735. https://doi.org/10.3390/sym14040735
Mouktonglang T, Poochinapan K, Yimnet S. Robust Finite-Time Control of Discrete-Time Switched Positive Time-Varying Delay Systems with Exogenous Disturbance and Their Application. Symmetry. 2022; 14(4):735. https://doi.org/10.3390/sym14040735
Chicago/Turabian StyleMouktonglang, Thanasak, Kanyuta Poochinapan, and Suriyon Yimnet. 2022. "Robust Finite-Time Control of Discrete-Time Switched Positive Time-Varying Delay Systems with Exogenous Disturbance and Their Application" Symmetry 14, no. 4: 735. https://doi.org/10.3390/sym14040735
APA StyleMouktonglang, T., Poochinapan, K., & Yimnet, S. (2022). Robust Finite-Time Control of Discrete-Time Switched Positive Time-Varying Delay Systems with Exogenous Disturbance and Their Application. Symmetry, 14(4), 735. https://doi.org/10.3390/sym14040735




