Overview: State-of-the-Art in the Energy Harvesting Based on Piezoelectric Devices for Last Decade
Abstract
1. Introduction
2. Piezoelectric Materials and Energy-Harvesting Systems
2.1. Common Background
2.2. Material Performance
2.3. High-Temperature Application
2.4. Polymer Piezoelectrics
2.5. Optimization of Piezoelectric Materials and Energy Harvesters
- (i)
- The dynamic response of the harvesting construction;
- (ii)
- Electrical circuit providing generated voltage and charge;
- (iii)
- The related electromechanics of the system, which represents a key step in energy harvesting and presents a complex multiphysical problem.
3. Piezoelectric Rotary Harvesters
3.1. State-of-the-Art in Piezoelectric Harvesters
3.2. Some Solutions for Rotary Harvesters
3.2.1. Rotary Harvester with Parallel Coaxial Plates
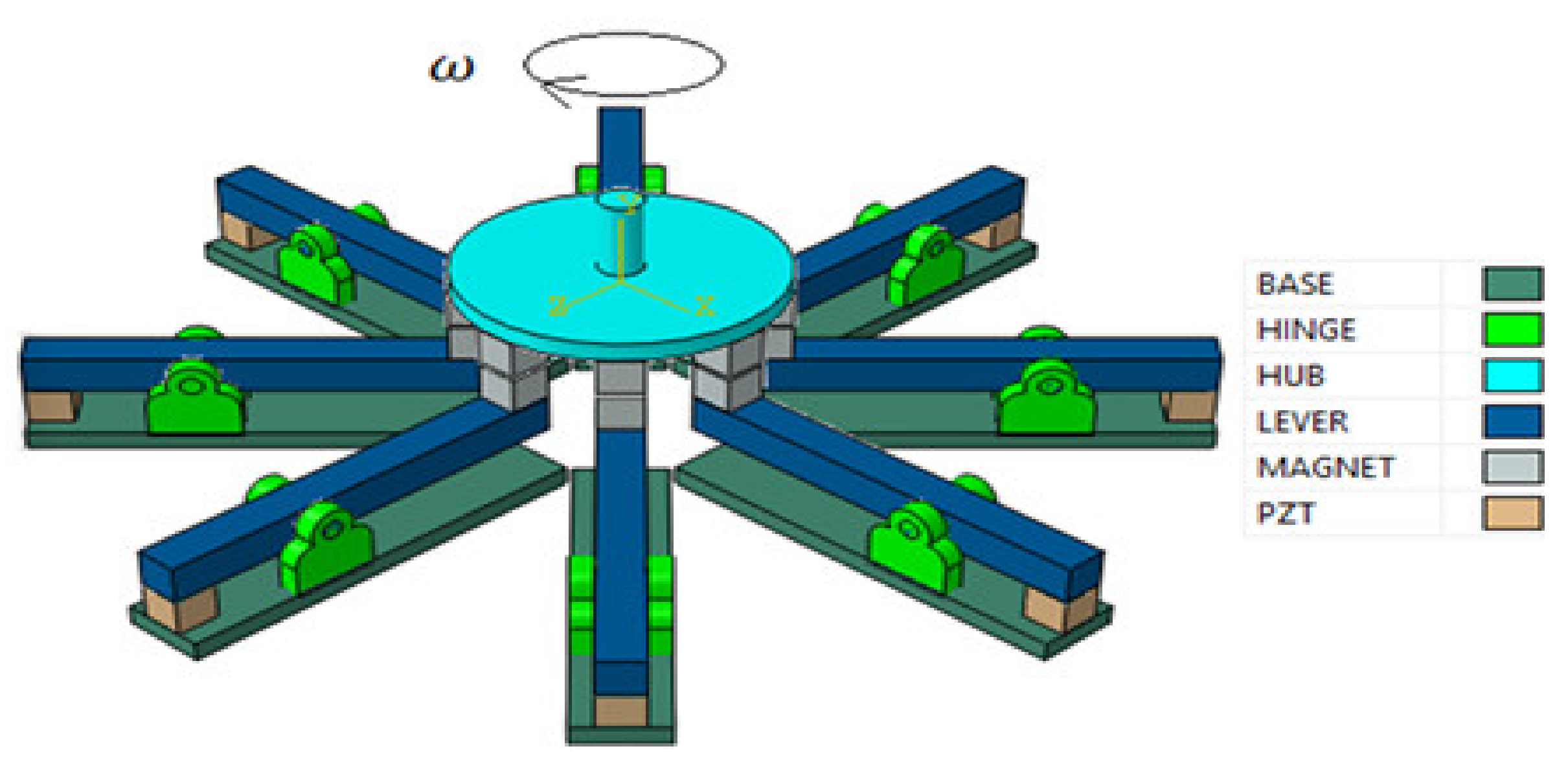
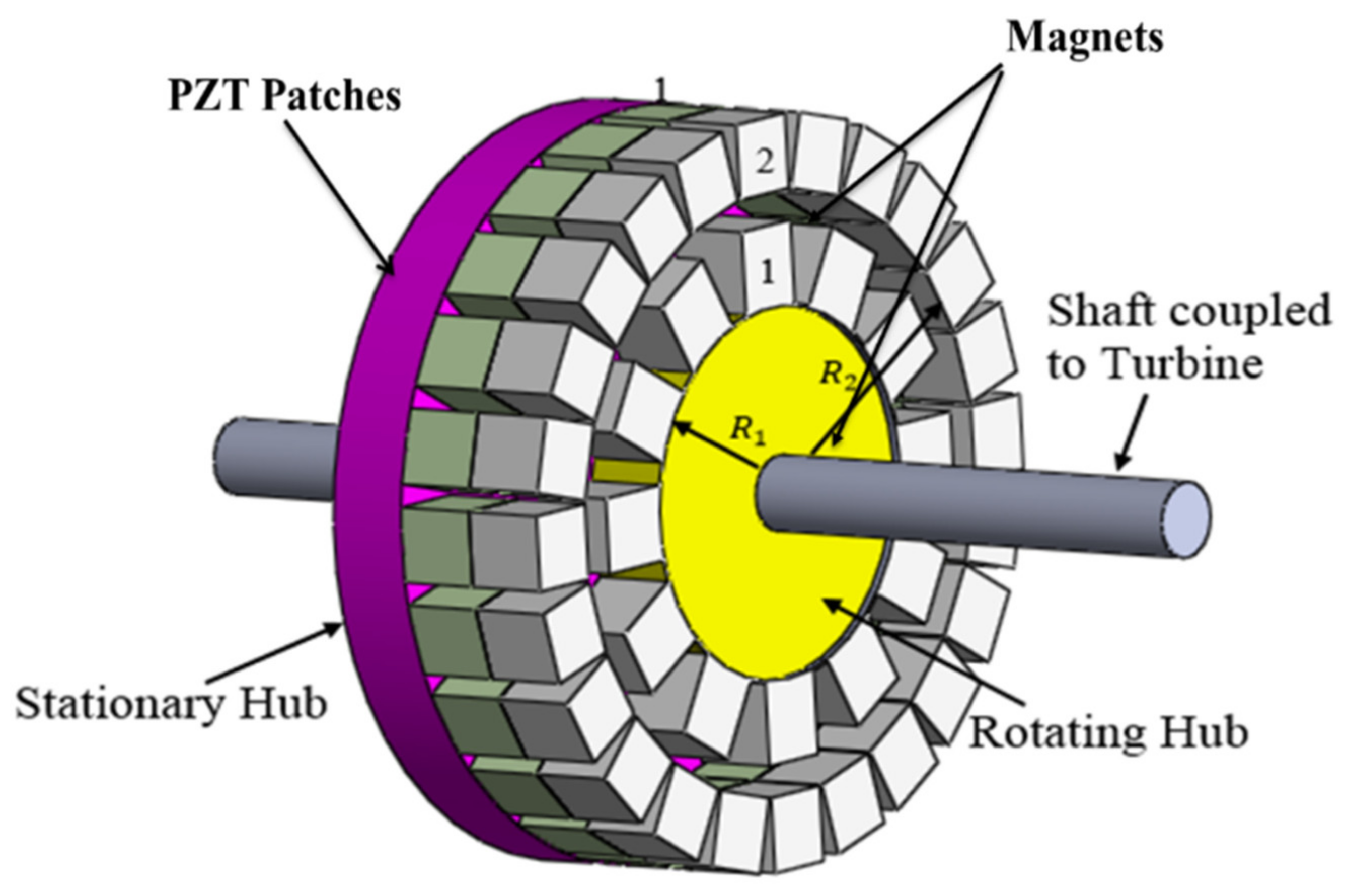
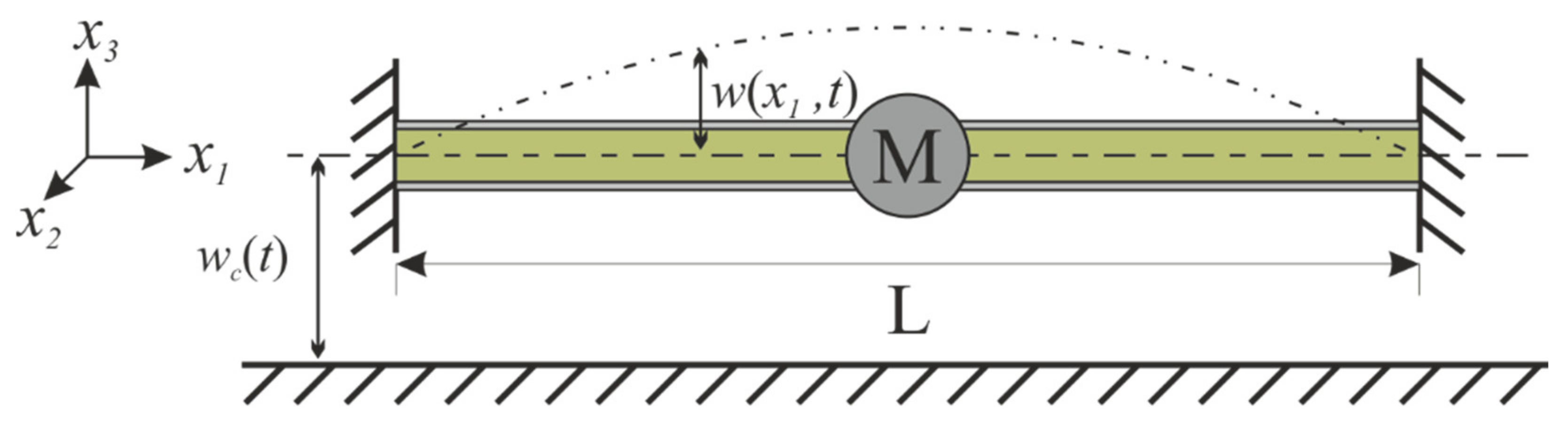
3.2.2. Rotary Hub Energy Harvester
3.2.3. Shear-Mode Piezoelectric Energy Harvester with Scissor Mechanism
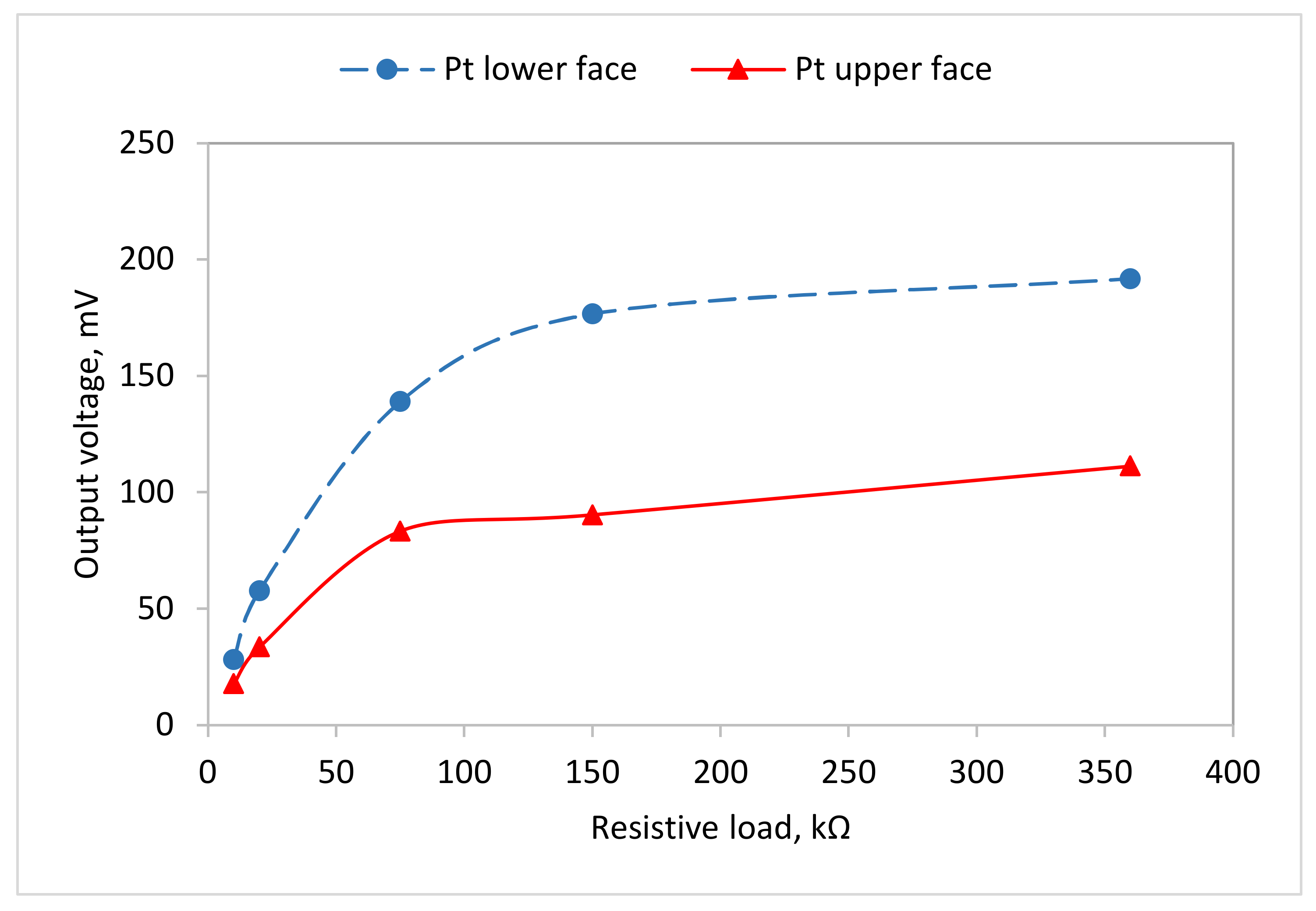
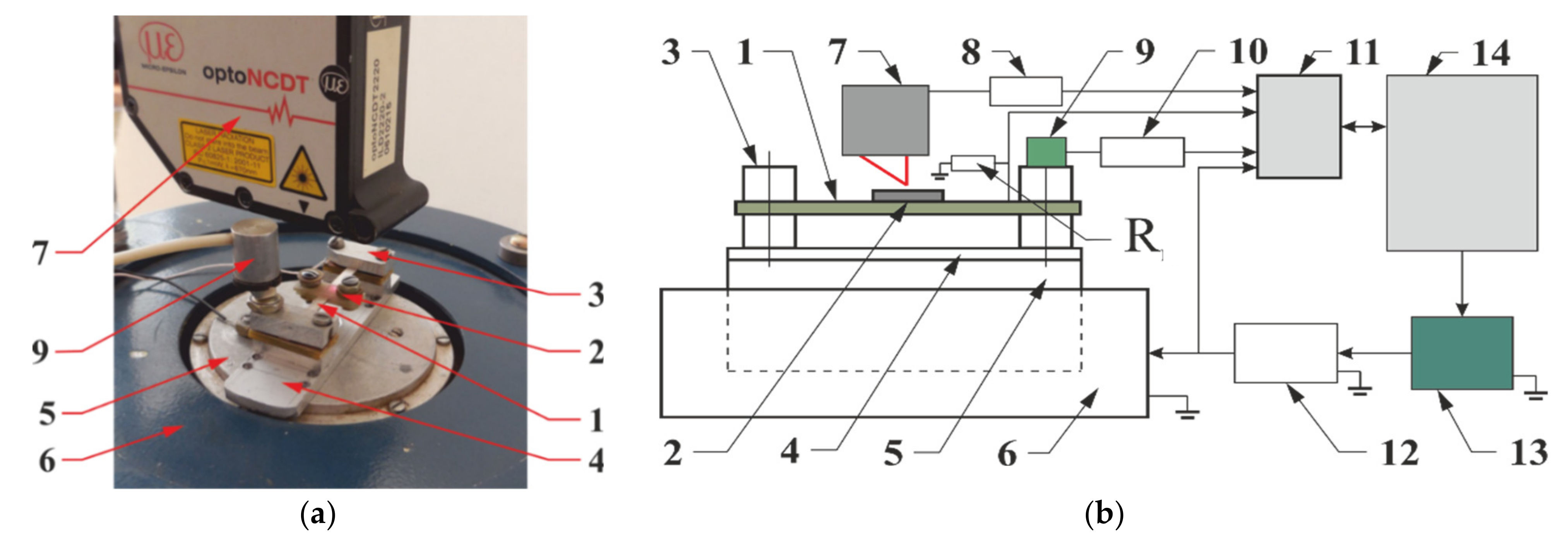
3.2.4. Shear-Mode Piezoelectric Energy Harvester for Rotational Motion
4. Flexoelectric Effect
5. Piezoelectric Generators
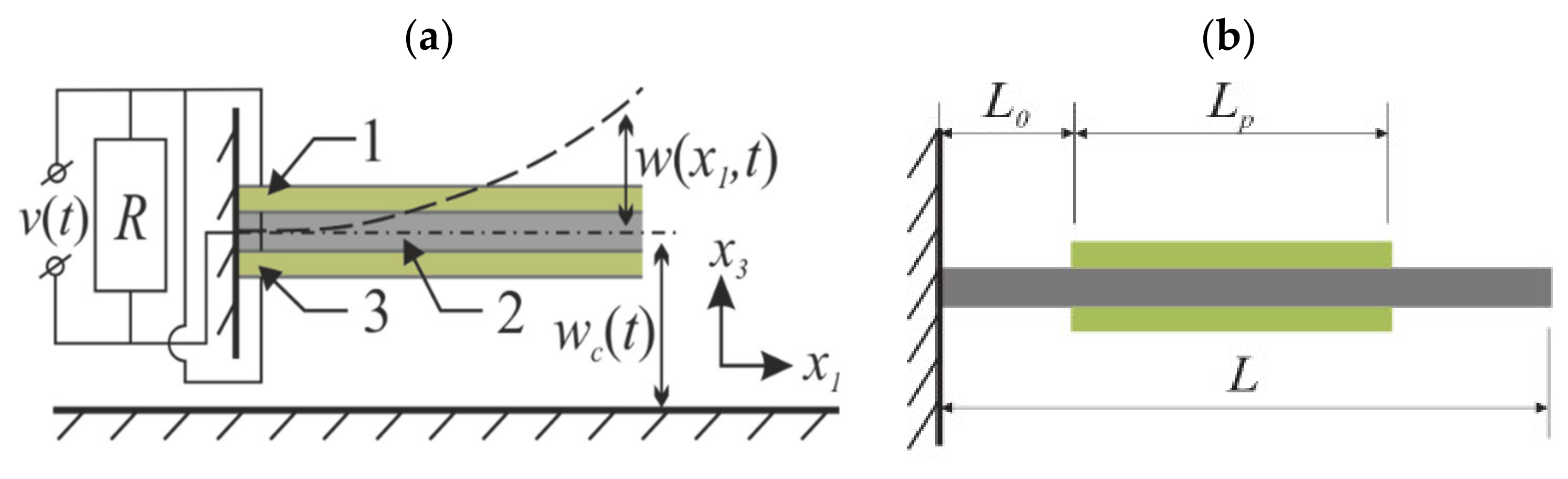
5.1. Cantilever-Type PEG: Experiment
5.2. Some Solutions for Test Study of Cantilever-Type PEG with Proof Mass
5.3. Cantilever-Type PEG: Modeling
5.3.1. Cantilever-Type PEG with Symmetrical and Asymmetrical Location of Proof Mass
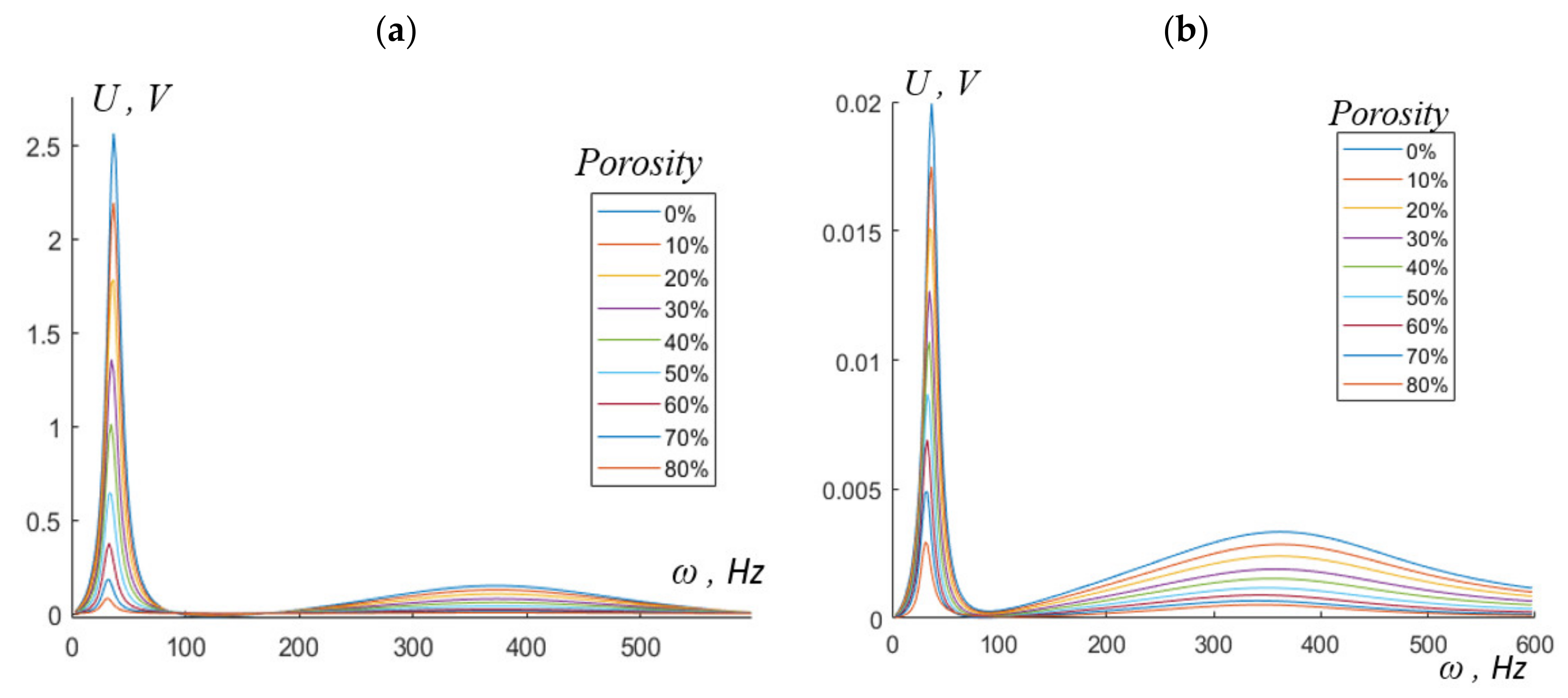
5.3.2. Cantilever-Type PEG, Based on Porous Piezoceramic, with Proof Mass
5.3.3. Numerical Optimization of Cantilever-Type PEG with Incomplete Covering Substrate by Piezoelectric Elements
5.3.4. Modeling Double-Console PEG
5.3.5. Bistable and Tristable Energy Harvesting in Cardiology
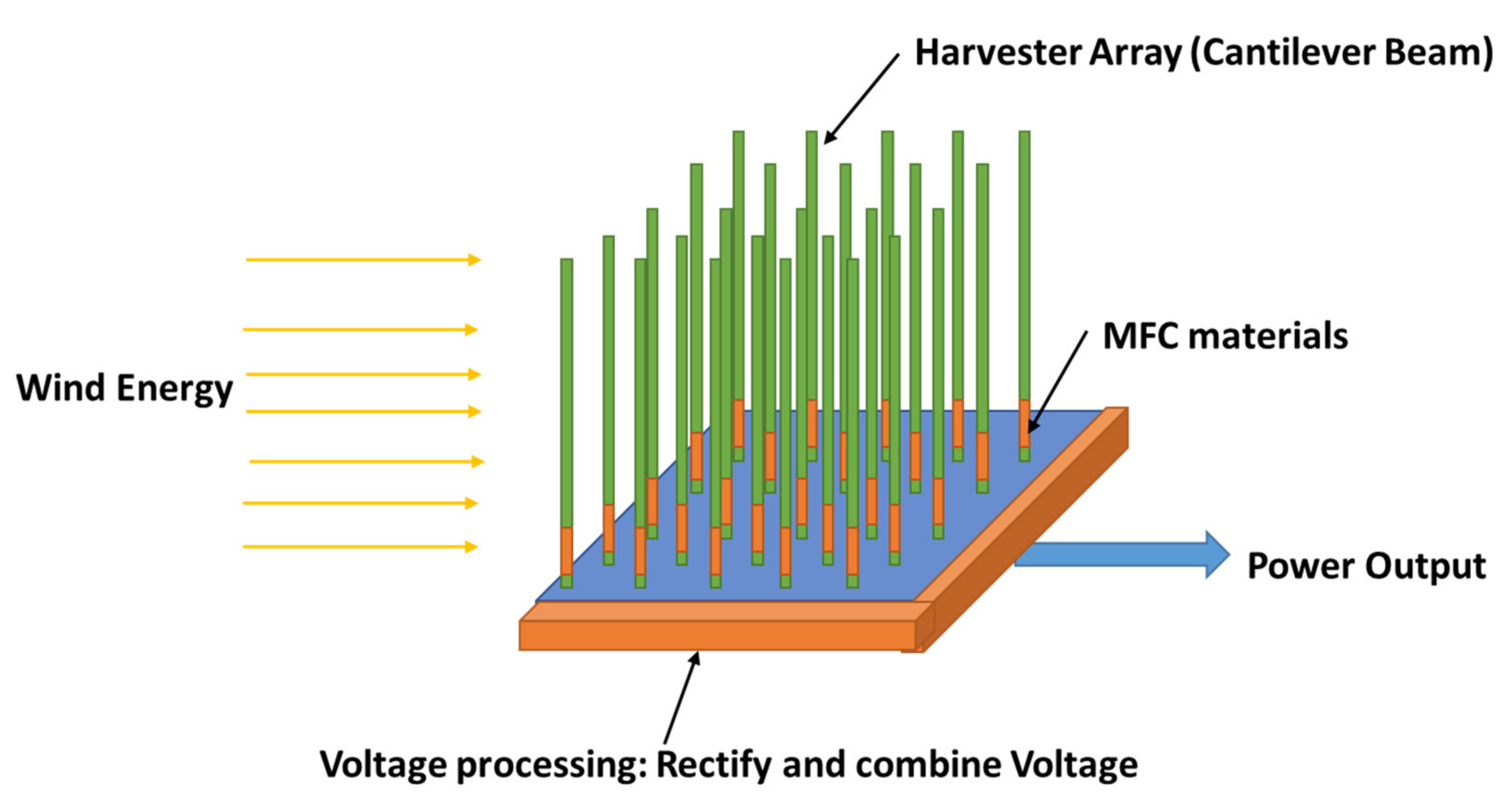
5.3.6. Wind Energy Harvesting from Artificial Grass
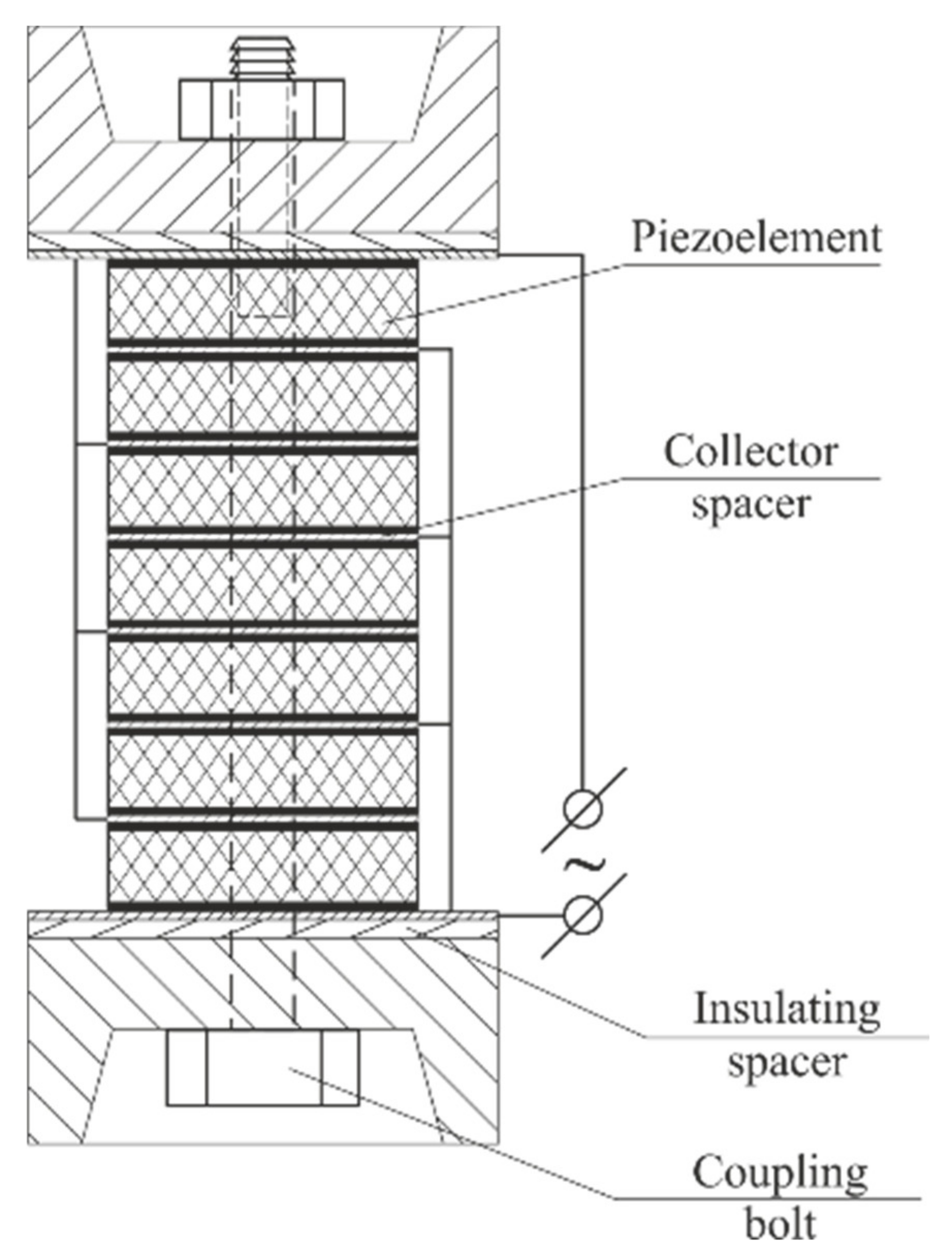
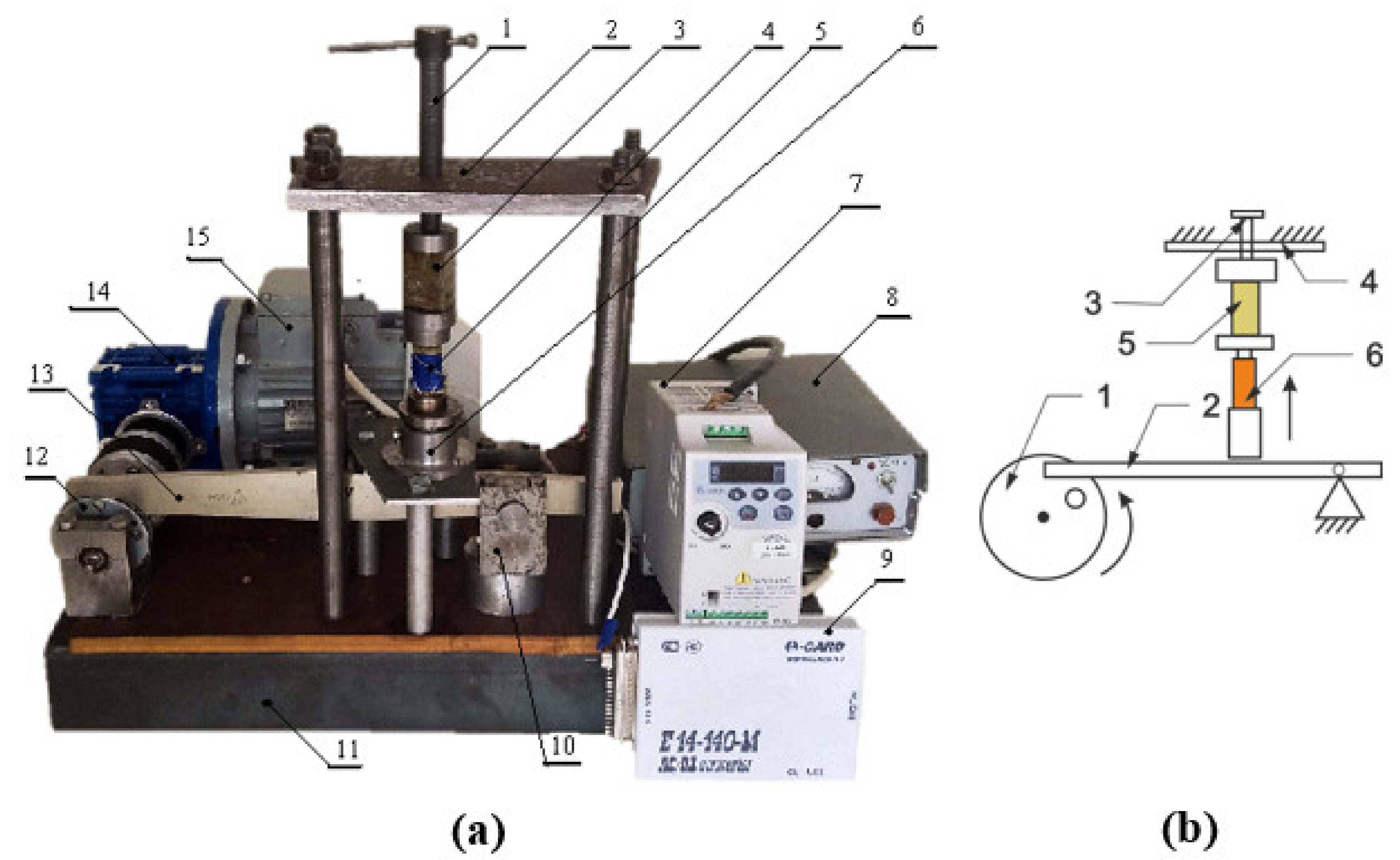
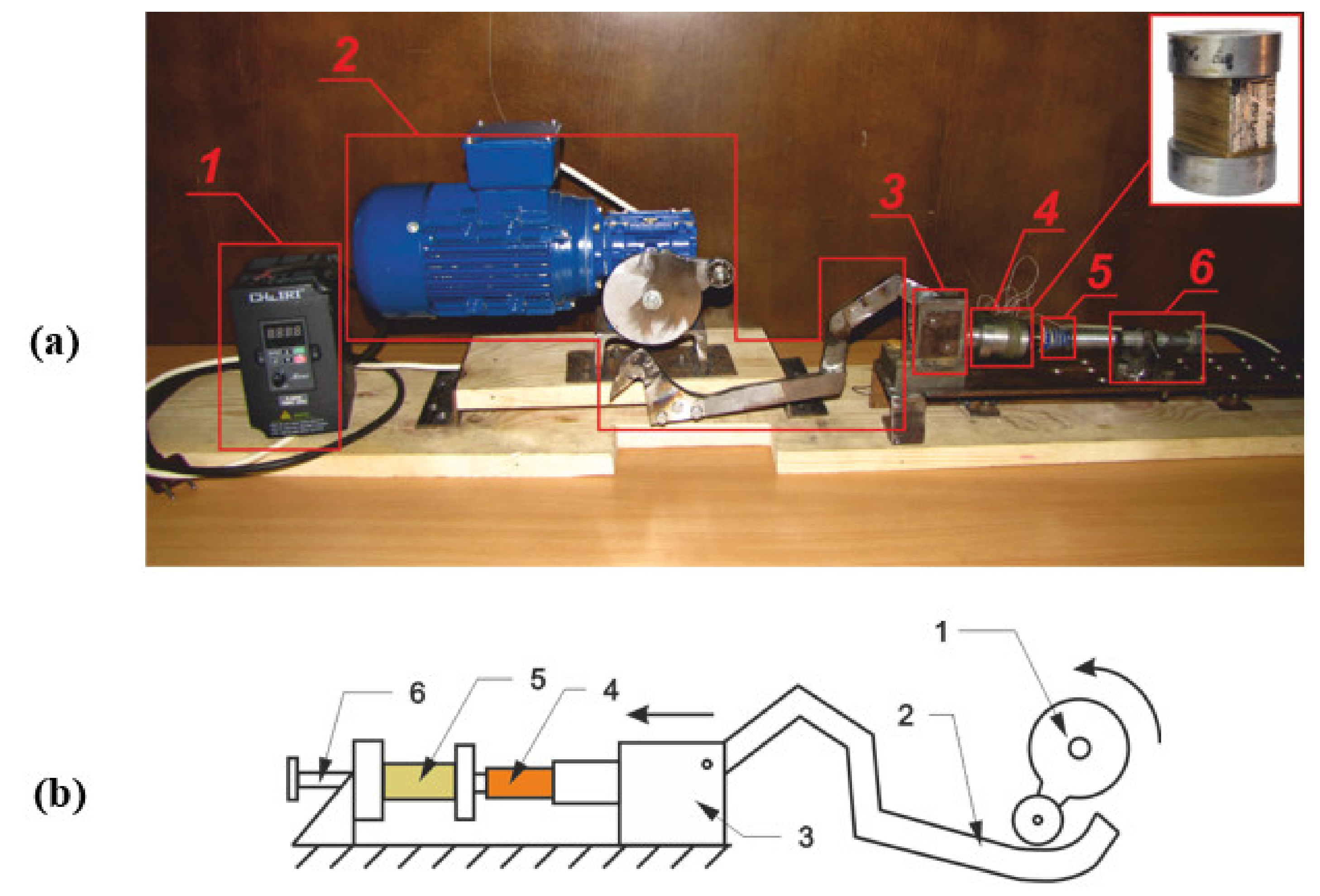
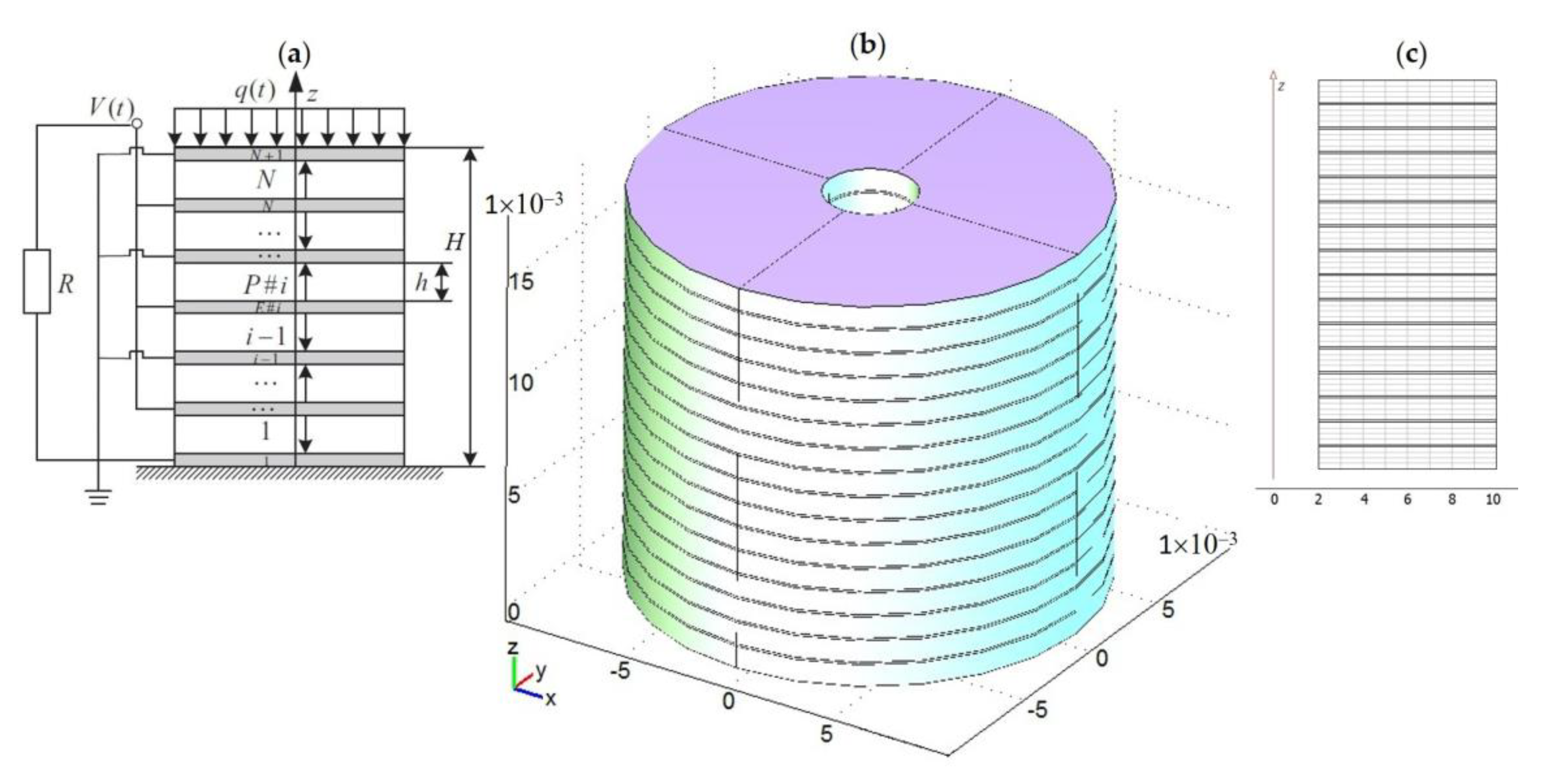
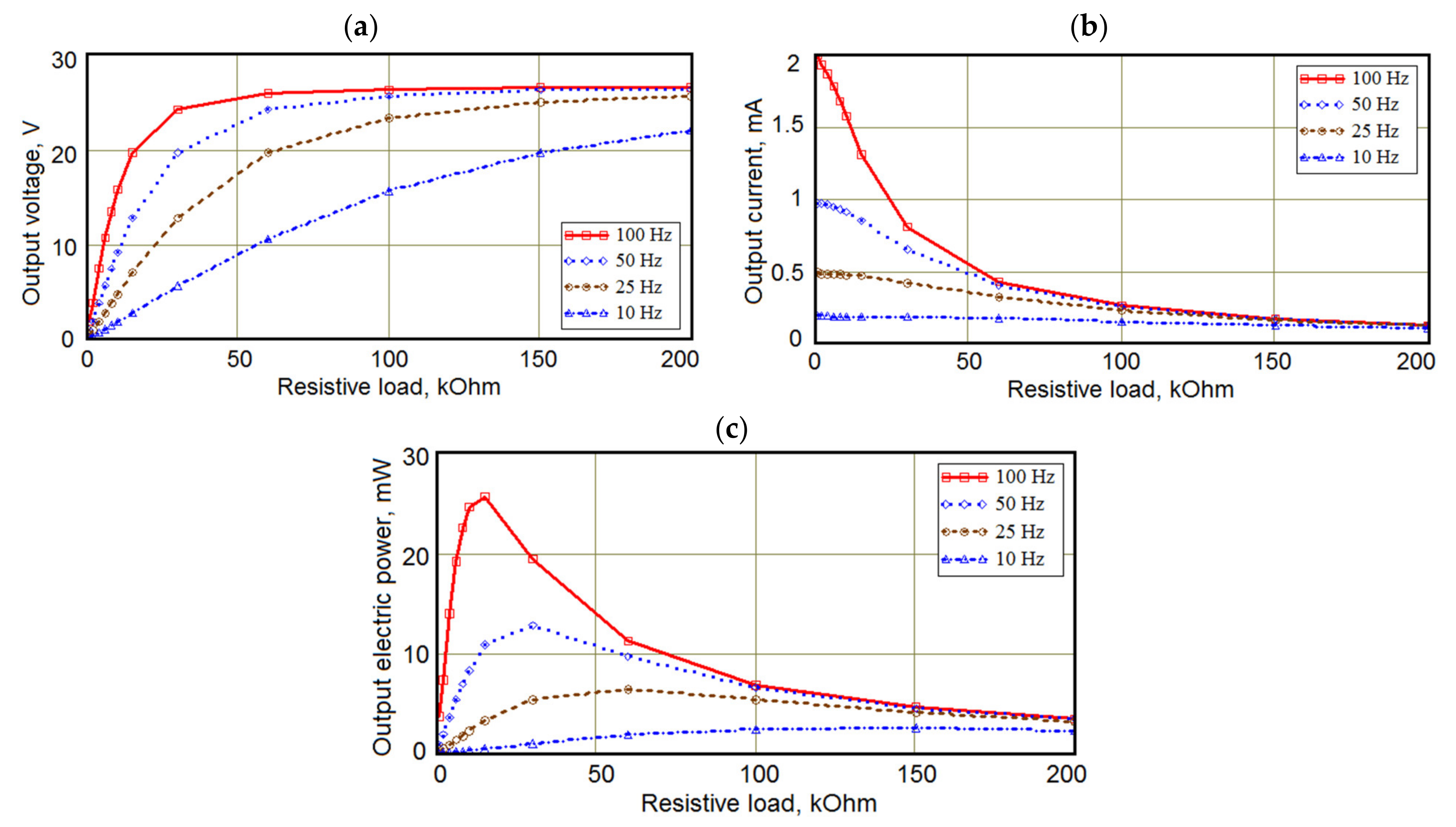
5.4. Stack-Type PEG: Experiment
5.5. Stack-Type PEG: Modeling
5.6. Comparative Optimization of Cantilever-Type and Stack-Type PEGs
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Malakooti, M.H.; Sodano, H.A. Piezoelectric energy harvesting through shear mode operation. Smart Mater. Struct. 2015, 24, 055005. [Google Scholar] [CrossRef]
- Paulo, J.; Gaspar, P. Review and future trend of energy harvesting methods for portable medical devices. In Proceedings of the World Congress on Engineering 2010 (WCE 2010), London, UK, 30 June–2 July 2010; 2010; Volume II. Available online: http://www.iaeng.org/publication/WCE2010/WCE2010_pp909-914.pdf (accessed on 2 December 2021).
- Pellegrini, S.P.; Tolou, N.; Schenk, M.; Herder, J.L. Bistable vibration energy harvesters: A review. J. Intell. Mater. Syst. Struct. 2013, 24, 1303–1312. [Google Scholar] [CrossRef]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renew. Sustain. Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Wang, Z.L.; Zhu, G.; Yang, Y.; Wang, S.; Pan, C. Progress in nanogenerators for portable electronics. Mater. Today 2012, 15, 532–543. [Google Scholar] [CrossRef]
- Guo, X.; Liu, L.; Zhang, Z.; Gao, S.; He, T.; Shi, Q.; Lee, C. Technology evolution from micro-scale energy harvesters to nanogenerators. J. Micromechanics Microengineering 2021, 31, 093002. [Google Scholar] [CrossRef]
- Nechibvute, A.; Chawanda, A.; Luhanga, P. Piezoelectric energy harvesting devices: An alternative energy. Smart Mater. Res. 2012, 2012, 853481. [Google Scholar] [CrossRef]
- Soloviev, A.N.; Parinov, I.A.; Cherpakov, A.V.; Chebanenko, V.A.; Rozhkov, E.V. Analysing the Output Characteristics of a Double-console PEG Based on Numerical Simulation. Mater. Phys. Mech. 2018, 37, 168–175. [Google Scholar] [CrossRef]
- Qi, Y.; McAlpine, M.C. Nanotechnology-enabled flexible and biocompatible energy harvesting. Energy Environ. Sci. 2010, 3, 1275–1285. [Google Scholar] [CrossRef]
- Radousky, H.B.; Liang, H. Energy harvesting: An integrated view of materials, devices and applications. Nanotechnology 2012, 23, 502001. [Google Scholar] [CrossRef]
- Wang, H.; Jasim, A.; Chen, X. Energy harvesting technologies in roadway and bridge for different applications–A comprehensive review. Appl. Energy 2018, 212, 1083–1094. [Google Scholar] [CrossRef]
- Wang, X. Piezoelectric nanogenerators−Harvesting ambient mechanical energy at the nanometer scale. Nano Energy 2012, 1, 13–24. [Google Scholar] [CrossRef]
- Wang, Z.L. From nanogenerators to piezotronics—A decade long study of ZnO nanostrucutres. MRS Bull. 2012, 37, 814–827. [Google Scholar] [CrossRef]
- Wang, Z.L. Progress in piezotronics and piezo-phototronics. Adv. Mater. 2012, 24, 4632–4646. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Wu, W. Nanotechnology enabled energy harvesting for self-powered micro/nanosystems. Angew. Chem. 2012, 51, 11700–11721. [Google Scholar] [CrossRef] [PubMed]
- Bowen, C.R.; Topolov, V.Y.; Kim, H.A. (Eds.) Modern Piezoelectric Energy-Harvesting Materials. Springer Series in Materials Science; Springer: Cham, Switzerland, 2016; Volume 238. [Google Scholar] [CrossRef]
- Li, L.; Xu, J.; Liu, J.; Gao, F. Recent progress on piezoelectric energy harvesting: Structures and materials. Adv. Compos. Hybrid Mater. 2018, 1, 478–505. [Google Scholar] [CrossRef]
- Maurya, D.; Yan, Y.; Priy, S. Piezoelectric Materials for Energy Harvesting. In Advanced Materials for Clean Energy; Xu, Q., Jo, K., Kobayashi, T., Eds.; CRC Press: Boca Raton, FA, USA, 2015; pp. 143–178. [Google Scholar] [CrossRef]
- Husain, A.A.F.; Hasan, W.Z.W.; Shafie, S.; Hamidon, M.N.; Pandey, S.S. A review of transparent solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2018, 94, 779–791. [Google Scholar] [CrossRef]
- Ng, C.H.; Lim, H.N.; Hayase, S.; Zainal, Z.; Huang, N.M. Photovoltaic performances of mono-and mixed-halide structures for perovskite solar cell: A review. Renew. Sustain. Energy Rev. 2018, 90, 248–274. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Mishra, R.K.; Solanki, S.C. Photovoltaic modules and their applications: A review on thermal modelling. Appl. Energy 2011, 88, 2287–2304. [Google Scholar] [CrossRef]
- Wang, Z.L.; Yang, R.; Zhou, J.; Qin, Y.; Xu, C.; Hu, Y.; Xu, S. Lateral nanowire/nanobelt based nanogenerators, piezotronics and piezo-phototronics. Mater. Sci. Eng. R. Rep. 2010, 70, 320–329. [Google Scholar] [CrossRef]
- Hunter, S.R.; Lavrik, N.V.; Mostafa, S.; Rajic, S.; Datskos, P.G. Review of pyroelectric thermal energy harvesting and new MEMs-based resonant energy conversion techniques. SPIE Def. Secur. Sens. 2012, 8377, 83770D. [Google Scholar] [CrossRef]
- Junior, O.H.A.; Maran, A.L.O.; Henao, N.C. A review of the development and applications of thermoelectric microgenerators for energy harvesting. Renew. Sustain. Energy Rev. 2018, 91, 376–393. [Google Scholar] [CrossRef]
- Khan, F.U.; Qadir, M.U. State-of-the-art in vibration-based electrostatic energy harvesting. J. Micromechanics Microengineering 2016, 26, 103001. [Google Scholar] [CrossRef]
- Narita, F.; Fox, M. A review on piezoelectric, magnetostrictive, and magnetoelectric materials and device technologies for energy harvesting applications. Adv. Eng. Mater. 2018, 20, 1700743. [Google Scholar] [CrossRef]
- Saadon, S.; Sidek, O. A review of vibration-based MEMS piezoelectric energy harvesters. Energy Convers. Manag. 2011, 52, 500–504. [Google Scholar] [CrossRef]
- Ahmed, R.; Mir, F.; Banerjee, S. A review on energy harvesting approaches for renewable energies from ambient vibrations and acoustic waves using piezoelectricity. Smart Mater. Struct. 2017, 26, 085031. Available online: https://iopscience.iop.org/article/10.1088/1361-665X/aa7bfb (accessed on 2 April 2022). [CrossRef]
- Kim, H.S.; Kim, J.H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Parinov., I.; Chang, S.H.; Topolov, V. (Eds.) Advanced Materials. Manufacturing, Physics, Mechanics and Applications. Springer Proceedings in Physics; Springer: Cham, Switzerland, 2016; Volume 175, p. 707. [Google Scholar] [CrossRef]
- Advanced Materials. PHENMA 2017. Springer Proceedings in Physics; Parinov, I., Chang, S.H., Gupta, V., Eds.; Springer: Cham, Switzerland, 2018; Volume 207, p. 640. [Google Scholar] [CrossRef]
- Parinov, I.; Chang, S.H.; Gupta, V. (Eds.) Advanced Materials. PHENMA 2018. Springer Proceedings in Physics; Springer: Cham, Switzerland, 2019; Volume 224, p. 666. [Google Scholar] [CrossRef]
- Parinov, I.; Chang, S.H.; Gupta, V. (Eds.) Advanced Materials. PHENMA 2019. Springer Proceedings in Materials; Springer: Cham, Switzerland, 2020; Volume 6, p. 621. [Google Scholar] [CrossRef]
- Chang, S.-H.; Parinov, I.A.; Topolov, V.Y. (Eds.) Advanced Materials. Physics, Mechanics and Applications. Springer Proceedings in Physics; Springer: Cham, Switzerland, 2014; Volume 152, p. 380. [Google Scholar] [CrossRef]
- Parinov, I.A.; Chang, S.H.; Theerakulpisut, S. (Eds.) Advanced Materials. Studies and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2015; p. 527. Available online: https://novapublishers.com/shop/advanced-materials-studies-and-applications (accessed on 2 April 2022).
- Parinov, I.A.; Chang, S.H.; Jani, M. (Eds.) Advanced Materials. Techniques, Physics, Mechanics and Applications. Springer Proceedings in Physics; Springer: Cham, Switzerland, 2017; Volume 193, p. 637. [Google Scholar] [CrossRef]
- Parinov, I.A. (Ed.) Advanced Nano- and Piezoelectric Materials and Their Applications; Nova Science Publishers: Hauppauge, NY, USA, 2014; p. 250. Available online: https://novapublishers.com/shop/advanced-nano-and-piezoelectric-materials-and-their-applications/ (accessed on 2 April 2022).
- Akopyan, V.A.; Soloviev, A.N.; Parinov, I.A.; Shevtsov, S.N. Definition of Constants for Piezoceramic Materials; Nova Science Publishers: Hauppauge, NY, USA, 2010; Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=11404 (accessed on 2 April 2022).
- Parinov, I.A. (Ed.) Ferroelectrics and Superconductors: Properties and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2012; 287p, Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=24233 (accessed on 2 April 2022).
- Khanbareh, H.; Topolov, V.Y.; Bowen, C.R. Piezo-Particulate Composites. Manufacturing, Properties, Applications, Springer Series in Materials Science; Springer: Cham, Switzerland, 2019; Volume 283. [Google Scholar] [CrossRef]
- Parinov, I.A. (Ed.) Nano- and Piezoelectric Technologies, Materials and Devices; Nova Science Publishers: Hauppauge, NY, USA, 2013; p. 261. Available online: https://novapublishers.com/shop/nano-and-piezoelectric-technologies-materials-and-devices/ (accessed on 2 April 2022).
- Parinov, I.A. Microstructure and Properties of High-Temperature Superconductors, 2nd ed.; Springer: Heidelberg, Germany, 2013; 779p. [Google Scholar] [CrossRef]
- Parinov, I.; Chang, S.H. (Eds.) Physics and Mechanics of New Materials and Their Applications; Nova Science Publishers: Hauppauge, NY, USA, 2013; 444p, Available online: https://novapublishers.com/shop/physics-and-mechanics-of-new-materials-and-their-applications/ (accessed on 2 April 2022).
- Parinov, I.A.; Chang, S.H.; Kim, Y.H.; Noda, N.A. (Eds.) Physics and Mechanics of New Materials and Their Applications. PHENMA 2020. Springer Proceedings in Materials. Springer: Cham, Switzerland, 2021; Volume 10, 601p. [Google Scholar] [CrossRef]
- Parinov, I.A. (Ed.) Piezoceramic Materials and Devices; Nova Science Publishers: Hauppauge, NY, USA, 2010; p. 335. Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=11605 (accessed on 2 April 2022).
- Parinov, I.A. (Ed.) Piezoelectric Materials and Devices; Nova Science Publishers: Hauppauge, NY, USA, 2012; p. 328. Available online: www.novapublishers.org/catalog/product_info.php?products_id=20009 (accessed on 2 April 2022).
- Parinov, I.A. (Ed.) Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2015; p. 283. Available online: https://novapublishers.com/shop/piezoelectrics-and-nanomaterials-fundamentals-developments-and-applications/ (accessed on 2 April 2022).
- Parinov, I.A. (Ed.) Piezoelectrics and Related Materials: Investigations and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2012; p. 306. Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=30669 (accessed on 2 April 2022).
- Rybyanets, A.N. Microstructural Features, Electrophysical Properties and Wave Processes in Spatially Inhomogeneous Ferroactive and Dissipative Media. Ph.D. Thesis, Southern Federal University, Rostov-on-Don, Russia, 2018. (In Russian). [Google Scholar]
- Topolov, V.Y. Heterogeneous Ferroelectric Solid Solutions. Phases and Domain States. Springer Series in Materials Science, 2nd ed.; Springer: Cham, Switzerland, 2018; Volume 151. [Google Scholar] [CrossRef]
- Topolov, V.Y.; Bisegna, P.; Bowen, C.R. Piezoactive Composites. Orientation Effects and Anisotropy Factors. Springer Series in Materials Science; Springer: Cham, Switzerland, 2014; Volume 185. [Google Scholar] [CrossRef]
- Topolov, V.Y.; Bowen, C.R.; Bisegna, P. Piezo-Active Composites. Microgeometry–Sensitivity Relations. Springer: Cham, Switzerland, 2018; Volume 271. [Google Scholar] [CrossRef]
- Uchino, K. Piezoelectric energy harvesting systems—Essentials to successful developments. Energy Technol. 2018, 6, 829–848. [Google Scholar] [CrossRef]
- Erturk, A. Piezoelectric energy harvesting for civil infrastructure system applications: Moving loads and surface strain fluctuations. J. Intell. Mater. Syst. Struct. 2011, 22, 1959–1973. [Google Scholar] [CrossRef]
- Le, M.Q.; Capsal, J.-F.; Lallart, M.; Hebrard, Y.; Van Der Ham, A.; Reffe, N.; Geynet, L.; Cottinet, P.-J. Review on energy harvesting for structural health monitoring in aeronautical applications Prog. Aerosp. Sci. 2015, 79, 147–157. [Google Scholar] [CrossRef]
- Shevtsov, S.N.; Soloviev, A.N.; Parinov, I.A.; Cherpakov, A.V.; Chebanenko, V.A. Piezoelectric Actuators and Generators for Energy Harvesting. Innovation and Discovery in Russian Science and Engineering; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Luo, A.; Hu, Y.; Li, X.; Wang, F. Micro electrostatic energy harvester with both broad bandwidth and high normalized power density. Appl. Energy 2018, 212, 362–371. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Zhang, A.; Peng, Z.; Luo, D.; Chen, R.; Wang, F. Electrostatic energy harvesting device with dual resonant structure for wideband random vibration sources at low frequency. Rev. Sci. Instrum. 2016, 87, 125001. [Google Scholar] [CrossRef] [PubMed]
- Banerji, S.; Bagchi, A.; Khazaeli, S. Energy harvesting methods for structural health monitoring using wireless sensors: A review. Resilient Infrastruct. Lond. 2016, 2016, 1–10. [Google Scholar]
- Tan, Y.; Dong, Y.; Wang, X. Review of MEMS electromagnetic vibration energy harvester. J. Microelectromechanical Syst. 2017, 26, 1–16. [Google Scholar] [CrossRef]
- Saxena, P.; Shukla, P. A comprehensive review on fundamental properties and applications of poly(vinylidene fluoride) (PVDF). Adv. Compos. Hybrid Mater. 2021, 4, 8–26. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric nanogenerators as new energy technology and self-powered sensors—Principles, problems and perspectives. Faraday Discuss. 2015, 176, 447–458. [Google Scholar] [CrossRef]
- Xu, L.; Jiang, T.; Lin, P.; Shao, J.J.; He, C.; Zhong, W.; Chen, X.Y.; Wang, Z.L. Coupled triboelectric nanogenerator networks for efficient water wave energy harvesting. ACS Nano 2018, 12, 1849–1858. [Google Scholar] [CrossRef]
- Anton, S.R. Multifunctional Piezoelectric Energy Harvesting Concepts. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blackburn, VA, USA, 2011. [Google Scholar]
- Chebanenko, V.A.; Akopyan, V.A.; Parinov, I.A. Piezoelectric Generators and Energy Harvesters: Modern State of the Art. In Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications; Parinov, I.A., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2015; pp. 243–277. Available online: https://novapublishers.com/shop/piezoelectrics-and-nanomaterials-fundamentals-developments-and-applications/ (accessed on 2 April 2022).
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Guyomar, D.; Lallart, M. Recent Progress in Piezoelectric Conversion and Energy Harvesting Using Nonlinear Electronic Interfaces and Issues in Small Scale Implementation. Micromachines 2011, 2, 274–294. [Google Scholar] [CrossRef]
- Grudén, M.; Hinnemo, M.; Dancila, D.; Zherdev, F.; Edvinsson, N.; Brunberg, K.; Andersson, L.; Byström, R.; Rydberg, A. Field operational testing for safety improvement of freight trains using wireless monitoring by sensor network. IET Wirel. Sens. Syst. 2014, 4, 54–60. [Google Scholar] [CrossRef]
- Tianchen, Y.; Jian, Y.; Ruigang, S.; Xiaowei, L. Vibration energy harvesting system for railroad safety based on running vehicles. Smart Mater. Struct. 2014, 23, 125046. [Google Scholar] [CrossRef]
- Zhu, M.; Edkins, S. Analytical modelling results of piezoelectric energy harvesting devices for self-power sensors/sensor networks in structural health monitoring. Procedia Eng. 2011, 25, 195–198. [Google Scholar] [CrossRef][Green Version]
- Abdelkefi, A.; Ghommem, M. Piezoelectric energy harvesting from morphing wing motions for micro air vehicles. Theor. Appl. Mech. Lett. 2013, 3, 052004. [Google Scholar] [CrossRef]
- Fu, X.; Hosta-Rigau, L.; Chandrawati, R.; Cui, J. Multi-Stimuli-Responsive Polymer Particles, Films, and Hydrogels for Drug Delivery. Chem 2018, 4, 2084–2107. [Google Scholar] [CrossRef]
- Hatai, J.; Hirschhäuser, C.; Niemeyer, J.; Schmuck, C. Multi-Stimuli-Responsive Supramolecular Polymers Based on Noncovalent and Dynamic Covalent Bonds. ACS Appl. Mater. Interfaces 2020, 12, 2107–2115. [Google Scholar] [CrossRef]
- Schattling, P.; Jochum, F.D.; Theato, P. Multi-stimuli responsive polymers—the all-in-one talents. Polym. Chem. 2014, 5, 25–36. [Google Scholar] [CrossRef]
- Shevtsov, S.; Akopyan, V.; Rozhkov, E.; Chebanenko, V.; Yang, C.-C.; Lee, C.-Y.J.; Kuo, C.-X. Optimization of the Electric Power Harvesting System Based on the Piezoelectric Stack Transducer. In Advanced Materials. Springer Proceedings in Physics; Parinov., I., Chang, S.H., Topolov, V., Eds.; Springer: Cham, Switzerland, 2016; Volume 175, pp. 639–650. [Google Scholar] [CrossRef]
- Soloviev, A.N.; Chebanenko, V.A.; Parinov, I.A. Mathematical Modelling of Piezoelectric Generators on the Base of the Kantorovich Method. In Analysis and Modelling of Advanced Structures and Smart Systems. Advanced Structured Materials; Altenbach, H., Carrera, E., Kulikov., G., Eds.; Springer: Singapore, 2018; Volume 81, pp. 227–258. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Z.; Han, Z. Analytical solution of piezoelectric. composite stack transducers. J. Intell. Mater. Syst. Struct. 2013, 24, 1626–1636. [Google Scholar] [CrossRef]
- Zhao, S.; Erturk, A. Deterministic and band-limited stochastic energy harvesting from uniaxial excitation of a multilayer piezoelectric stack. Sens. Actuators A: Phys. 2014, 214, 58–65. [Google Scholar] [CrossRef]
- Akopyan, V.A.; Parinov, I.A.; Zakharov, Y.N.; Chebanenko, V.A.; Rozhkov, E.V. Advanced Investigations of Energy Efficiency of Piezoelectric Generators. In Advanced Materials. Studies and Applications; Parinov, I.A., Chang, S.H., Theerakulpisut, S., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2015; pp. 417–436. Available online: https://novapublishers.com/shop/advanced-materials-studies-and-applications/ (accessed on 2 April 2022).
- Akopyan, V.A.; Zakharov, Y.N.; Parinov, I.A.; Rozhkov, E.V.; Shevtsov, S.N.; Chebanenko, V.A. Optimization of output characteristics of the bimorph power harvesters. In Nano- and Piezoelectric Technologies, Materials and Devices; Parinov, I.A., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2013; pp. 111–131. Available online: https://novapublishers.com/shop/nano-and-piezoelectric-technologies-materials-and-devices/ (accessed on 2 April 2022).
- Soloviev, A.N.; Parinov, I.A.; Cherpakov, A.V.; Chebanenko, V.A.; Rozhkov, E.V.; Duong, L.V. Analysis of the performance of the cantilever type piezoelectric generator based on finite element modeling. In Advances in Structural Integrity; Prakash, R., Jayaram, V., Saxena, A., Eds.; Springer: Singapore, 2018; pp. 291–301. [Google Scholar] [CrossRef]
- Gusev, A.A.; Avvakumov, E.G.; Isupov, V.P.; Reznichenko, L.A.; Verbenko, I.A.; Miller, A.I.; Cherpakov, A.V. Mechanochemical Synthesis of Piezoelectrics on the Base of Lead Zirconate Titanate. In Piezoelectric Materials and Devices; Parinov, I.A., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 189–234. Available online: www.novapublishers.org/catalog/product_info.php?products_id=20009 (accessed on 2 April 2022).
- Khasbulatov, S.; Cherpakov, A.; Parinov, I.; Andryushin, K.; Shlkina, L.; Aleshin, V.; Andryushina, I.; Mardaliev, B.; Gordienko, D.; Verbenko, I.; et al. Destruction phenomena in ferroactive materials. J. Adv. Dielectr. 2020, 10, 2050012. [Google Scholar] [CrossRef]
- Bowen, C.R.; Kim, H.A.; Weaver, P.M.; Dunn, S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 2014, 7, 25–44. [Google Scholar] [CrossRef]
- Eliseev, E.A.; Morozovska, A.N.; Svechnikov, G.S.; Gopalan, V.; Shur, V.Y. Static conductivity of charged domain walls in uniaxial ferroelectric semiconductors. Phys. Rev. B 2011, 83, 235313. [Google Scholar] [CrossRef]
- Ghara, S.; Geirhos, K.; Kuerten, L.; Lunkenheimer, P.; Tsurkan, V.; Fiebig, M.; Kézsmárki, I. Giant conductivity of mobile non-oxide domain walls, Nat. Commun. 2021, 12, 3975. [Google Scholar] [CrossRef]
- Werner, C.S.; Herr, S.J.; Buse, K.; Sturman, B.; Soergel, E.; Razzaghi, C.; Breunig, I. Large and accessible conductivity of charged domain walls in lithium niobate. Sci. Rep. 2017, 7, 9862. [Google Scholar] [CrossRef] [PubMed]
- Betts, D.N.; Kim, H.A.; Bowen, C.R.; Inman, D.J. Optimal configurations of bistable piezo-composites for energy harvesting. Appl. Phys. Lett. 2012, 100, 114104. [Google Scholar] [CrossRef]
- Kim, S.; Priya, S.; Kanno, I. Piezoelectric MEMS for energy harvesting. MRS Bull. 2012, 37, 1039–1050. [Google Scholar] [CrossRef]
- Andosca, R.; McDonald, T.G.; Genova, V.; Rosenberg, S.; Keating, J.; Benedixen, C.; Wu, J. Experimental and theoretical studies on MEMS piezoelectric vibrational energy harvesters with mass loading. Sens. Actuators A Phys. 2012, 178, 76–87. [Google Scholar] [CrossRef]
- Briscoe, J.; Bilotti, E.; Dunn, S. Measured efficiency of a ZnO nanostructured diode piezoelectric energy harvesting device. Appl. Phys. Lett. 2012, 101, 093902. [Google Scholar] [CrossRef]
- Zhilin, D.A.; Karapetyan, G.Y.; Kutepov, M.E.; Minasyan, T.A.; Yatsenko, V.I.; Kaidashev, E.M. Growth and Study of Zinc Oxide Nanorods Arrays on Piezoelectric Substrates. In Advanced Materials. PHENMA 2017. Springer Proceedings in Physics; Parinov, I., Chang, S.H., Gupta, V., Eds.; Springer: Cham, Switzerland, 2018; Volume 207, pp. 25–31. [Google Scholar] [CrossRef]
- Hu, Y.; Lin, L.; Zhang, Y.; Wang, Z. Replacing a battery by a nanogenerator with 20 V output. Adv. Mater. 2012, 24, 110–114. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Bernal, R.A.; Minary-Jolandan, M. A review of mechanical and electromechanical properties of piezoelectric nanowires. Adv. Mater. 2012, 24, 4656–4675. [Google Scholar] [CrossRef]
- Varghese, J.; Whatmore, R.W.; Holmes, J.D. Ferroelectric nanoparticles, wires and tubes: Synthesis, characterisation and applications. J. Mater. Chem. C 2013, 1, 2618–2638. [Google Scholar] [CrossRef]
- Briscoe, J.; Jalali, N.; Woolliams, P.; Stewart, M.; Weaver, P.M.; Cain, M.; Dunn, S. Measurement techniques for piezoelectric nanogenerators. Energy Environ. Sci. 2013, 6, 3035–3045. [Google Scholar] [CrossRef]
- Kim, S.; Park, J.; Ahn, H.; Liu, D.; Kim, D. Temperature effects on output power of piezoelectric vibration energy harvesters. Microelectron. J. 2011, 42, 988–991. [Google Scholar] [CrossRef]
- Minary-Jolandan, M.; Bernal, R.A.; Kuljanishvili, I.; Parpoil, V.; Espinosa, H.D. Individual GaN nanowires exhibit strong piezoelectricity in 3D. Nano Lett. 2012, 12, 970–976. [Google Scholar] [CrossRef]
- Le Boulbar, E.D.; Edwards, M.J.; Vittoz, S.; Vanko, G.; Brinkfeldt, K.; Rufer, L.; Johander, P.; Lalinský, T.; Bowen, C.R.; Allsopp, D.W.E. Effect of bias conditions on pressure sensors based on AlGaN/GaN high electron mobility transistor. Sens. Actuators A Phys. 2013, 194, 247–251. [Google Scholar] [CrossRef]
- Kudimi, J.M.R.; Mohd-Yasin, F.; Dimitrijev, S. SiC-based piezoelectric energy harvester for extreme environment. Procedia Eng. 2012, 47, 1165–1172. [Google Scholar] [CrossRef]
- Hou, R.; Hutson, D.; Kirk, K.J.; Fu, Y.Q. AlN thin film transducers for high temperature non-destructive testing. J. Appl. Phys. 2012, 111, 074510. [Google Scholar] [CrossRef]
- Bao, X.; Bar-Cohen, Y.; Scott, J.; Sherrit, S.; Widholm, S.; Badescu, M.; Shrout, T.; Jones, B. Ultrasonic/sonic drill for high temperature application. Proc. SPIE Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2010, 7647, 764739. [Google Scholar] [CrossRef]
- Baba, A.; Searfass, C.T.; Tittmann, B.R. High temperature ultrasonic transducer up to 1000 °C using lithium niobate single crystal. Appl. Phys. Lett. 2010, 97, 232901. [Google Scholar] [CrossRef]
- Lewis, R.W.C.; Allsopp, D.W.F.; Shields, P.; Šatka, A.; Yu, S.; Topolov, V.Y.; Bowen, C.R. Nano-imprinting of highly ordered mano-pillars of lithium niobate (LiNbO3). Ferroelectrics 2012, 429, 62–68. [Google Scholar] [CrossRef][Green Version]
- Zhang, S.; Yu, F. Piezoelectric materials for high temperature sensors. J. Am. Ceram. Soc. 2011, 94, 3153–3170. [Google Scholar] [CrossRef]
- Fang, J.; Niu, H.; Wang, H.; Wang, X.; Lin, T. Enhanced mechanical energy harvesting using needleless electrospun poly(vinylidene fluoride) nanofibre webs. Energy Environ. Sci. 2013, 6, 2196–2202. [Google Scholar] [CrossRef]
- Chang, J.; Dommer, M.; Chang, C.; Lin, L. Piezoelectric nanofibres for energy scavenging applications. Nano Energy 2012, 1, 356–371. [Google Scholar] [CrossRef]
- Lugovaya, M.A.; Naumenko, A.A.; Rybyanets, A.N.; Shcherbinin, S.A. Complex material properties of porous piezoelectric ceramics. Ferroelectrics 2015, 484, 87–94. [Google Scholar] [CrossRef]
- Sun, C.; Shi, J.; Bayerl, D.J.; Wang, X. PVDF microbelts for harvesting energy from respiration. Energy Environ. Sci. 2011, 4, 4508–4512. [Google Scholar] [CrossRef]
- Vatansever, D.; Hadimani, R.L.; Shah, T.; Siores, E. An investigation of energy harvesting from renewable source with PVDF and PZT. Smart Mater. Struct. 2011, 20, 055019. [Google Scholar] [CrossRef]
- Patel, I.; Siores, E.; Shah, T. Utilisation of smart polymers and ceramic based piezoelectric materials for scavenging waste energy. Sens. Actuators A: Phys. 2010, 159, 213–218. [Google Scholar] [CrossRef]
- Anton, S.R.; Farinholt, K.M. An evaluation on low-level vibration energy harvesting using piezoelectret foam. Proc. SPIE. Act. Passiv. Smart Struct. Integr. Syst. 2012, 8341, 83410G. [Google Scholar] [CrossRef]
- Qi, Y.; Jafferis, N.T.; Lyons, K., Jr.; Lee, C.M.; Ahmad, H.; McAlpine, M.C. Piezoelectric ribbons printed onto rubber for flexible energy conversion. Nano Lett. 2010, 10, 524–525. [Google Scholar] [CrossRef]
- Qi, Y.; Nguyen, T.D.; Lisko, B.; Purohit, P.K.; McAlpine, C.M. Enhanced piezoelectricity and stretchability in energy harvesting devices fabricated from buckled PZT ribbons. Nano Lett. 2011, 11, 1331–1336. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Deshmukh, N.; Nagarah, J.M.; Kramer, T.; Purohit, P.K.; Berry, M.J.; McAlpine, M.C. Piezoelectric nanoribbons for monitoring cellular deformations. Nat. Nanotechnol. 2012, 7, 587–593. [Google Scholar] [CrossRef]
- Lee, B.Y.; Zhang, J.; Zueger, C.; Chung, W.-J.; Yoo, S.Y.; Wang, E.; Meyer, J.; Ramesh, R.; Lee, S.-W. Virus-based piezoelectric energy generation. Nat. Nanotechnol. 2012, 7, 351–356. [Google Scholar] [CrossRef] [PubMed]
- Rybyanets, A.N. Advanced functional materials: Modeling, technology, characterization, and applications. In Advanced Materials. Manufacturing, Physics, Mechanics and Applications. Springer Proceedings in Physics; Parinov, I., Chang, S.H., Topolov, V., Eds.; Springer: Cham, Switzerland, 2016; Volume 175, pp. 211–228. [Google Scholar] [CrossRef]
- Shvetsova, N.A.; Lugovaya, M.A.; Shvetsov, I.A.; Makariev, D.I.; Rybyanets, A.N. Dielectric, piezoelectric and elastic properties of PZT/PZT ceramic piezocomposites. In Physics, Mechanics of New Materials and Their Applications; Parinov, I.A., Chang, S.H., Topolov, V.Y., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2016; pp. 407–414. Available online: https://novapublishers.com/shop/proceedings-of-the-2015-international-conference-on-physics-mechanics-of-new-materials-and-their-applications-devoted-to-the-100th-anniversary-of-the-southern-federal-university/ (accessed on 2 April 2022).
- Newnham, R.E. Fifty years of ferroelectrics. In Proceedings of the 14th IEEE International Symposium on Applications of Ferroelectrics (ISAF-04), Montréal, QC, Canada, 23–27 August 2004; pp. 1–6. [Google Scholar]
- Rybyanets, A.N. Ceramic piezocomposites: Modeling, technology, and characterization. In Piezoceramic Materials and Devices; Parinov, I.A., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2010; pp. 113–174. Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=11605 (accessed on 2 April 2022).
- Nasedkin, A.V. Computer design of porous active materials at different dimensional scales. AIP Conf. Proc. 2017, 1909, 020145. [Google Scholar] [CrossRef]
- Nasedkin, A.V.; Shevtsova, M.S. Improved finite element approaches for modeling of porous piezocomposite materials with different connectivity. In Ferroelectrics and Superconductors: Properties and Applications; Parinov, I.A., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 231–254. Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=24233 (accessed on 2 April 2022).
- Nasedkin, A.V.; Shevtsova, M.S. Multiscale computer simulation of piezoelectric devices with elements from porous piezoceramics. In Physics and Mechanics of New Materials and Their Applications; Parinov, I., Chang, S.H., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2013; pp. 185–202. Available online: https://novapublishers.com/shop/physics-and-mechanics-of-new-materials-and-their-applications/.
- Naumenko, A.A.; Lugovaya, M.A.; Shcherbinin, S.A.; Rybyanets, A.N. Elastic losses and dispersion in ceramic matrix composites. Ferroelectrics 2015, 484, 69–77. [Google Scholar] [CrossRef]
- Rybyanets, A.N. Porous piezoelectric ceramics?A historical overview. Ferroelectrics 2011, 419, 90–96. [Google Scholar] [CrossRef]
- Rybyanets, A.N. Porous piezoceramics: Theory, technology, and properties. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1492–1507. [Google Scholar] [CrossRef]
- Rybyanets, A.; Naumenko, A. Nanoparticles transport in ceramic matrixes: A novel approach for ceramic matrix composites fabrication. J. Mod. Phys. 2013, 4, 1041–1049. [Google Scholar] [CrossRef]
- Rybyanets, A.N.; Naumenko, A.A. Elastic losses and spatial dispersion in porous piezoceramics and ceramic matrix composites. In Advanced Materials—Studies and Applications; Parinov, I.A., Chang, S.H., Theerakulpisut, S., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2015; pp. 125–146. Available online: https://novapublishers.com/shop/advanced-materials-studies-and-applications/ (accessed on 2 December 2021).
- Rybyanets, A.; Rybyanets, A. Ceramic piezocomposites: Modeling, technology, and characterization. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1757–1773. [Google Scholar] [CrossRef]
- Rybyanets, A.N.; Naumenko, A.A.; Lugovaya, M.A.; Shvetsova, N.A. Electric power generations from PZT composite and porous ceramics for energy harvesting devices. Ferroelectrics 2015, 484, 95–100. [Google Scholar] [CrossRef]
- Rybyanets, A.N.; Zaharov, Y.N.; Raevskii, I.P.; Akopjan, V.A.; Rozhkov, E.V.; Parinov, I.A. Development of new piezoelectric materials and transducer designs for energy harvesting devices. In Physics and Mechanics of New Materials and Their Applications; Parinov, I., Chang, S.H., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2013; pp. 275–308. Available online: https://novapublishers.com/shop/physics-and-mechanics-of-new-materials-and-their-applications/ (accessed on 2 April 2022).
- Andryushin, K.P.; Andryushina, I.N.; Cherpakov, A.V.; Popov, A.V.; Verbenko, I.A.; Reznichenko, L.A. Features of the electrophysical and mechanical properties of n-component ferroactive solid solutions of composition PZT–PZN–PMN. J. Adv. Dielectr. 2021, 11, 2160001. [Google Scholar] [CrossRef]
- Nasedkin, A.; Nasedkina, A.; Rybyanets, A. Finite element simulation of effective properties of microporous piezoceramic material with metallized pore surfaces. Ferroelectrics 2017, 508, 100–107. [Google Scholar] [CrossRef]
- Nasedkin, A.; Nassar, M.E. Effective properties of a porous inhomogeneously polarized by direction piezoceramic material with full metalized pore boundaries: Finite element analysis. J. Adv. Dielectr. 2020, 10, 2050018. [Google Scholar] [CrossRef]
- Nasedkin, A.; Nassar, M.E. Numerical investigation of the effects of partial metallization at the pore surface on the effective properties of a porous piezoceramic composite. J. Adv. Dielectr. 2021, 11, 2160009. [Google Scholar] [CrossRef]
- Benasciutti, D.; Moro, L.; Zelenika, S.; Brusa, E. Vibration energy scavenging via piezoelectric bimorphs of optimized shapes, Microsyst. Technol. 2010, 16, 657–668. [Google Scholar] [CrossRef]
- Dietl, J.M.; Garcia, E. Beam shape optimization for power harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 633–646. [Google Scholar] [CrossRef]
- Friswell, M.I.; Adhikari, S. Sensor shape design for piezoelectric cantilever beams to harvest vibration energy. J. Appl. Phys. 2010, 108, 014901. [Google Scholar] [CrossRef]
- Paquin, S.; St-Amant, Y. Improving the performance of a piezoelectric energy harvester using a variable thickness beam. Smart Mater. Struct. 2010, 19, 105020. [Google Scholar] [CrossRef]
- Wang, L. Design, Fabrication and Experimental Analysis of Piezoelectric Energy Harvesters with Non-Traditional Geometries. Ph.D. Thesis, Rutgers University, New Brunswick, NJ, USA, 2011. [Google Scholar]
- Park, J.; Lee, S.; Kwak, B.M. Design optimization of piezoelectric energy harvester subject to tip excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Gonsalez, C.G.; Shiki, S.B.; Brennan, M.J.; Da Silva, D.; Juni, V.L. Piezoelectric energy harvesting system optimization. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Portugal, 6–9 September 2010; pp. 1–8. [Google Scholar]
- Benkhelifa, E.; Moniri, M.; Tiwari, A.; De Rueda, A.G. Evolutionary multi-objective design optimisation of energy harvesting MEMS: The case of a piezoelectric. In Proceedings of the 2011 IEEE Congress of evolutionary computation (CEC 2011), New Orleans, LA, USA, 5–8 June 2011; pp. 1856–1863. [Google Scholar] [CrossRef]
- Bourisli, R.I.; Al-Ajmi, M.A. Optimization of smart beams for maximum modal electromechanical coupling using genetic algorithms. J. Intell. Mater. Syst. Struct. 2010, 21, 907–914. [Google Scholar] [CrossRef]
- Hadas, Z.; Kurfurst, J.; Ondrusek, C.; Singule, V. Artificial intelligence based optimization for vibration energy harvesting applications. Microsyst. Technol. 2012, 18, 1003–1014. [Google Scholar] [CrossRef]
- Dunning, P.D.; Kim, H.A. A new method for creating holes in level-set function based topology optimisation. Int. J. Numer. Methods Eng. 2013, 93, 118–134. [Google Scholar] [CrossRef]
- Chen, S.; Gonella, S.; Chen, W.; Liu, W.K. A level set approach for optimal design of smart energy harvesters. Comput. Methods Appl. Mech. Eng. 2010, 199, 2532–2543. [Google Scholar] [CrossRef]
- Sun, K.H.; Kim, Y.Y. Layout design optimization for magneto-electro-elastic laminate composites for maximized energy conversion under mechanical loading. Smart Mater. Struct. 2010, 19, 055008. [Google Scholar] [CrossRef]
- Kim, J.E.; Kim, D.S.; Kim, Y.Y. Multi-physics interpolation for the topology optimization of piezoelectric systems. Computer Methods in Appl. Mech. Eng. 2010, 199, 3153–3168. [Google Scholar] [CrossRef]
- Noh, J.Y.; Yoon, G.H. Topology optimization of piezoelectric energy harvesting devices considering static and harmonic dynamic loads. Adv. Eng. Softw. 2012, 53, 45–60. [Google Scholar] [CrossRef]
- Vatanabe, S.L.; Paulino, G.H.; Silva, E.C.N. Influence of pattern gradation on the design of piezocomposite energy harvesting devices using topology optimization. Compos. Pt B 2012, 43, 2646–2654. [Google Scholar] [CrossRef]
- Lin, Z.Q.; Gea, H.C.; Liu, S.T. Design of piezoelectric energy harvesting devices subjected to broadband random vibrations by applying topology optimization. Acta Mech. Sin. 2011, 27, 730–737. [Google Scholar] [CrossRef]
- Wein, F.; Kaltenbacher, M.; Stingl, M. Topology optimization of a cantilevered piezoelectric energy harvester using stress norm constraints. Struct. Multidiscip. Optim. 2013, 48, 173–185. [Google Scholar] [CrossRef]
- Hehn, T.; Manoli, Y. Efficient Power Extraction, Interface Modeling and Loss Analysis, Springer Series in Advanced Microelectronics; Springer: Cham, Switzerland, 2015; Volume 38. [Google Scholar] [CrossRef]
- Wang, D.-A.; Liu, N.-Z. A shear mode piezoelectric energy harvester based on a pressurized water flow. Sens. Actuators A Phys. 2011, 2011 167, 449–458. [Google Scholar] [CrossRef]
- Nechibvute, A.; Akande, A.R.; Luhanga, P.V.C. Modelling of a PZT Beam for Voltage Generation. Pertanika J. Sci. Technol. 2011, 19, 259–271. Available online: http://www.pertanika.upm.edu.my/pjst/browse/regular-issue?article=JST-0163-2009.
- Lin, J.-T.; Lee, B.; Alphenaar, B. The magnetic coupling of a piezoelectric cantilever for enhanced energy harvesting efficiency. Smart Mater. Struct. 2010, 19, 045012. [Google Scholar] [CrossRef]
- Rezaei-Hosseinabadi, N.; Tabesh, A.; Dehghani, R.; Aghili, A. An efficient piezoelectric windmill topology for energy harvesting from low-speed air flows. IEEE Trans. Ind. Electron. 2015, 62, 3576–3583. [Google Scholar] [CrossRef]
- Kishore, R.A.; Vučković, D.; Priya, S. Ultra-low wind speed piezoelectric windmill. Ferroelectrics 2014, 460, 98–107. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, Z.; Shu, C.; Zhang, J.; Zhang, Q.; Li, C. A rotational piezoelectric energy harvester for efficient wind energy harvesting. Sens. Actuators A: Phys. 2017, 262, 123–129. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Harvesting Wind Energy Using a Galloping Piezoelectric Beam. J. Vib. Acoust. 2012, 134, 011009. [Google Scholar] [CrossRef]
- Mineto, A.T.; Souza Braun, M.P.; Navarro, H.A.; Varoto, P.S. Modeling and simulation of a piezoelectric cantilever beam for power harvesting generation. In Proceedings of the 9th Brazilian Conference on Dynamics Control and their Applications (Dincon’10), São Paulo, Brazil, 7–11 June 2010; pp. 599–605. Available online: http://arquivo.sbmac.org.br/dincon/trabalhos/PDF/acoustics/67775.pdf (accessed on 2 December 2021).
- Wu, N.; Wang, Q.; Xie, X. Wind energy harvesting with a piezoelectric harvester. Smart Mater. Struct. 2013, 22, 095023. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Erturk, A.; Lin, J.; Zhou, S.; Cao, J.; Erturk, A.; Lin, J. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 2013, 102, 173901. [Google Scholar] [CrossRef]
- Yang, J.; Wen, Y.; Li, P.; Bai, X.; Li, M. Improved piezoelectric multifrequency energy harvesting by magnetic coupling. Proc. IEEE Sens. 2011, 2011, 28–31. [Google Scholar] [CrossRef]
- Manla, G.; White, N.M.; Tudor, M.J. Numerical Model of a Non-Contact Piezoelectric Energy Harvester for Rotating Objects, IEEE Sens. J. 2012, 12, 1785–1793. [Google Scholar] [CrossRef]
- Sang, Y.; Huang, X.; Liu, H.; Jin, P. A vibration-based hybrid energy harvester for wireless sensor systems. IEEE Trans. Magn. 2012, 48, 4495–4498. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, J.; Zheng, X.J.; Deng, S.F.; Zhao, J.H.; Peng, S.T.; Zhang, Y.; Wang, X.Y.; Cheng, H.B. A model for the energy harvesting performance of shear mode piezoelectric cantilever. Sens. Actuators A Phys. 2012, 179, 185–192. [Google Scholar] [CrossRef]
- Khameneifar, F.; Arzanpour, S.; Moallem, M. A piezoelectric energy harvester for rotary motion applications: Design and experiments. J. Mechatron. IEEE/ASME Trans. 2013, 18, 1527–1534. [Google Scholar] [CrossRef]
- Weinstein, L.A.; Cacan, M.R.; So, P.M.; Wright, P.K. Vortex shedding induced energy harvesting from piezoelectric materials in heating, ventilation and air conditioning flows. Smart Mater. Struct. 2012, 21, 045003. [Google Scholar] [CrossRef]
- Tao, J.X.; Viet, N.V.; Carpinteri, A.; Wang, Q. Energy harvesting from wind by a piezoelectric harvester. Eng. Struct. 2017, 133, 74–80. [Google Scholar] [CrossRef]
- Viet, N.V.; Al-Qutayri, M.; Liew, K.M.; Wang, Q. An octo-generator for energy harvesting based on the piezoelectric effect. Appl. Ocean Res. 2017, 64, 128–134. [Google Scholar] [CrossRef]
- Xie, X.D.; Wang, Q.; Wu, N. A ring piezoelectric energy harvester excited by magnetic forces. Int. J. Eng. Sci. 2014, 77, 71–78. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, Z.; Zhu, Y.; Mei, J.; Peng, S.; Li, L.; Yu, Y. Analysis of Energy Harvesting Performance for Mode Piezoelectric Bimorph in Series Connection Based on Timoshenko Beam Model. IEEE/ASME Trans. Mechatron. 2015, 20, 728–739. [Google Scholar] [CrossRef]
- Rödig, T.; Schönecker, A.; Gerlach, G. A Survey on Piezoelectric Ceramics for Generator Application. J. Am. Ceram. Soc. 2010, 93, 901–912. [Google Scholar] [CrossRef]
- Narolia, T.; Gupta, V.K.; Parinov, I.A. On Extraction of Energy from Rotating Objects. In Advanced Materials. Springer Proceedings in Materials; Parinov, I., Chang, S.H., Long, B., Eds.; Springer: Cham, Switzerland, 2020; Volume 6, pp. 503–511. [Google Scholar] [CrossRef]
- Narolia, T.; Gupta, V.K.; Parinov, I.A. A. A Novel Design for Piezoelectric Based Harvester for Rotating Objects. In Advanced Materials. Springer Proceedings in Physics; Parinov, I., Chang, S.H., Kim, Y.H., Eds.; Springer: Cham, Switzerland, 2019; Volume 224, pp. 603–614. [Google Scholar] [CrossRef]
- Narolia, T.; Gupta, V.K.; Parinov, I.A. A. A Scissor Mechanism Shear Mode Piezoelectric Energy Harvester for Windmill. In Physics and Mechanics of New Materials and Their Applications. PHENMA 2021. Springer Proceedings in Materials; Parinov, I.A., Chang, S.H., Kim, Y.H., Noda, N.A., Eds.; Springer: Cham, Switzerland, 2021; Volume 10, pp. 495–509. [Google Scholar] [CrossRef]
- Narolia, T.; Gupta, V.K.; Parinov, I.A. Design and analysis of a shear mode piezoelectric energy harvester for rotational motion system. J. Adv. Dielectr. 2020, 10, 2050008. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef]
- Li, A.; Zhao, W.; Zhou, S.; Wang, L.; Zhang, L. Enhanced energy harvesting of cantilevered flexoelectric micro-beam by proof mass. AIP Adv. 2019, 9, 115305. [Google Scholar] [CrossRef]
- Li, Z.; Deng, Q.; Shen, S. Flexoelectric Energy Harvesting Using Circular Thin Membranes. J. Appl. Mech. 2020, 87, 091004. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, R.; Hu, S.; Shen, S. Flexoelectric energy harvesters based on Timoshenko laminated beam theory. J. Intell. Mater. Syst. Struct. 2017, 28, 2064–2073. [Google Scholar] [CrossRef]
- Lutokhin, A.G.; Bikyashev, E.A.; Zakharov, Y.N.; Reshetnikova, E.A.; Raevskii, I.P.; Korchagin, N.A. A comprehensive investigation of phase transformations in the Pb0.9975[Zr0.495Sn0.4Ti0.1Nb0.005]O3 ceramics. Phys. Solid State 2012, 54, 1021–1025. [Google Scholar] [CrossRef]
- Sakhnenko, V.P.; Zakharov, Y.N.; Lutokhin, A.G.; Parinov, I.; Filatova, N.S.; Raevski, I.; Chebanenko, V.A.; Rozhkov, E.; Pavlenko, A.V.; Bunin, M.A.; et al. Studies of the unipolarity arising in the non-poled ferroelectric ceramics with electrodes from different metals on the opposite sides. Ferroelectrics 2018, 525, 187–191. [Google Scholar] [CrossRef]
- Sakhnenko, V.P.; Zakharov, Y.N.; Parinov, I.A.; Lutokhin, A.G.; Rozhkov, E.V.; Filatova, N.S.; Raevski, I.P.; Chebanenko, V.A.; Pavlenko, A.V.; Kiseleva, L.I.; et al. Electric response to bending vibrations and pyroelectric effect in unpolarized ferroelectric ceramic plates with electrodes, differing in the magnitude of the coefficient of thermal expansion on opposite surfaces. In Advanced Materials. PHENMA 2017. Springer Proceedings in Physics; Parinov, I., Chang, S.H., Gupta, V., Eds.; Springer: Cham, Switzerland, 2018; Volume 207, pp. 161–169. [Google Scholar] [CrossRef]
- Zakharov, Y.N.; Sakhnenko, V.P.; Parinov, I.A.; Raevsky, I.P.; Bunin, M.A.; Chebanenko, V.A.; Zaerko, M.A.; Sitalo, E.I.; Pavelko, A.A.; Kiseleva, L.I. Possibilities of the practical use of a stationary strain gradient in the interelectrode volume of unpolarized ferroceramic plates. J. Adv. Dielectr. 2020, 10, 2060010. [Google Scholar] [CrossRef]
- Zakharov, Y.N.; Sakhnenko, V.P.; Raevsky, I.P.; Parinov, I.A.; Bunin, M.A.; Raevskaya, S.I.; Chebanenko, V.A.; Filatova, N.S.; Aleshin., V.A.; Sitalo, E.I. Method for Polarization of Ferroelectric Ceramic. Russian Patent for Invention RU 2717164 C1, 18 March 2020. Application No. 2019132704 dated 16.10.2019. Available online: https://elibrary.ru/item.asp?id=42588001 (accessed on 2 December 2021). (In Russian).
- Abdollahi, A.; Peco, C.; Millán, D.; Arroyo, M.; Arias, I. Computational evaluation of the flexoelectric effect in dielectric solids. J. Appl. Phys. 2014, 116, 093502. [Google Scholar] [CrossRef]
- Hu, S.L.; Shen, S.P. Variational principles and governing equations in nano-dielectrics with the flexoelectric effect. Sci. China Phys. Mech. Astron. 2010, 53, 1497–1504. [Google Scholar] [CrossRef]
- Mindlin, R.D. On the Equations of Motion of Piezoelectric Crystals. In Problems of Continuum Mechanics; Muskilishivili, N.I., Ed.; 70th Birthday Volume; SIAM: Philadelphia, PA, USA, 1961; pp. 282–290. [Google Scholar]
- Chebanenko, V.A. Investigation of Oscillations of Piezoelectric Structures in the Composition of Energy Harvesting Devices. Ph.D. Thesis, Southern Federal University, Rostov-on-Don, Russia, 2018. (In Russian). [Google Scholar]
- Soloviev, A.N.; Chebanenko, V.A.; Zakharov, Y.N.; Rozhkov, E.V.; Parinov, I.A.; Gupta, V.K. Study of the Output Characteristics of Ferroelectric Ceramic Beam Made from Non-polarized Ceramics PZT-19: Experiment and Modeling. In Advanced Materials. Springer Proceedings in Physics; Parinov, I.A., Chang, S.H., Jani, M., Eds.; Springer: Cham, Switzerland, 2017; Volume 193, pp. 485–499. [Google Scholar] [CrossRef]
- Soloviev, A.N.; Vernigora, G.D. Identification of effective properties of the piezocomposites on the base of FEM modeling with ACELAN. In Piezoceramic Materials and Devices; Parinov, I., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2010; pp. 219–242. Available online: http://www.novapublishers.org/catalog/product_info.php?products_id=11605 (accessed on 2 April 2022).
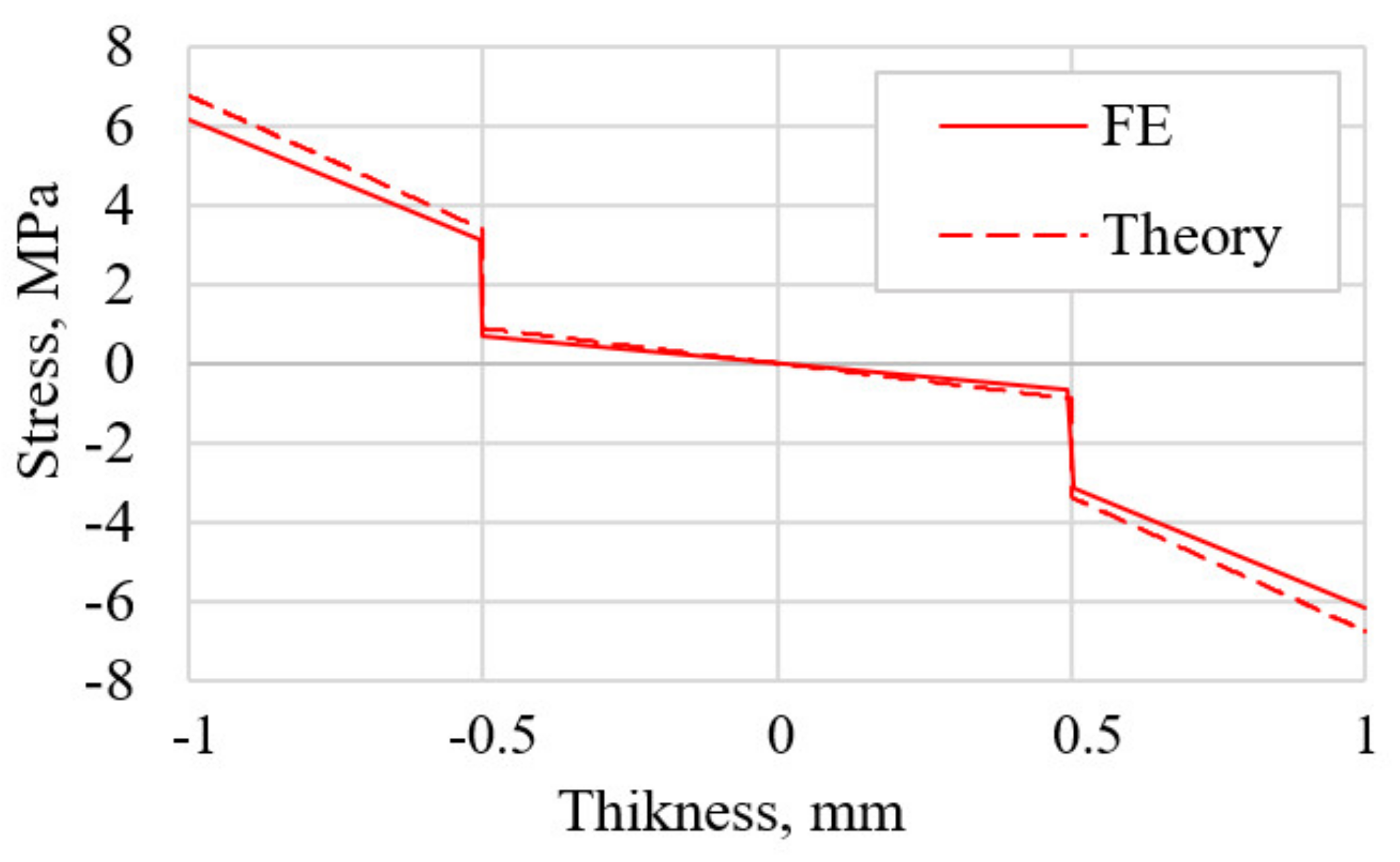
- Soloviev, A.N.; Chebanenko, V.A.; Parinov, I.A.; Oganesyan, P.A. Applied theory of bending vibrations of a piezoelectric bimorph with a quadratic electric potential distribution. Mater. Phys. Mech. 2019, 42, 65–73. [Google Scholar] [CrossRef]
- Liu, H.; Huang, Z.; Xu, T.; Chen, D. Enhancing output power of a piezoelectric cantilever energy harvester using an oscillator. Smart Mater. Struct. 2012, 21, 065004. [Google Scholar] [CrossRef]
- Hao, W.; Lihua, T.; Yaowen, Y.; Chee, K.S. Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2014, 25, 1875–1889. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A novel two-degrees-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2013, 24, 357–368. [Google Scholar] [CrossRef]
- Rguiti, M.; Hajjaji, A.; D’Astorg, S.; Courtois, C.; Leriche, A. Elaboration and characterization of a low frequency and wideband piezoceramic generator for energy harvesting. Opt. Mater. 2013, 36, 8. [Google Scholar] [CrossRef]
- Lim, J.-H.; Jeong, S.-S.; Kim, N.-R.; Cheon, S.-K.; Kim, M.-H.; Park, T.-G. Design and fabrication of a cross-shaped piezoelectric generator for energy harvesting. Ceram. Int. 2013, 39, S641–S645. [Google Scholar] [CrossRef]
- Lim, J.-H.; Park, C.-H.; Kim, J.-W.; Jeong, S.-S.; Kim, M.-H.; Park, T.-G. Generating characteristics of a cross-shaped piezoelectric generator depending on elastic body material and leg length. J. Electroceramics 2013, 30, 108–112. [Google Scholar] [CrossRef]
- Park, J.C.; Park, J.Y. Asymmetric PZT bimorph cantilever for multi-dimensional ambient vibration harvesting. Ceram. Int. 2013, 39, S653–S657. [Google Scholar] [CrossRef]
- Bibo, A.; Li, G.; Daqaq, M.F. Electromechanical modeling and normal form analysis of an aeroelastic micro-power generator. J. Intell. Mater. Syst. Struct. 2011, 22, 577–592. [Google Scholar] [CrossRef]
- Michelin, S.; Doaré, D. Energy harvesting efficiency of piezoelectric flags in axial flows. J. Fluid Mech. 2013, 714, 489–504. [Google Scholar] [CrossRef]
- Bibo, A.; Daqaq, M.F. Investigation of concurrent energy harvesting from ambient vibrations and wind using a single piezoelectric generator. Applied Physics Letters 2013, 102, 243904. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Design of piezoaeroelastic energy harvesters. Nonlinear Dyn. 2012, 68, 519–530. [Google Scholar] [CrossRef]
- Nechibvute, A.; Chawanda, A.; Luhanga, P.; Akande, A. Piezoelectric Energy Harvesting Using Synchronized Switching Techniques. Int. J. Eng. Technol. 2012, 2, 936–945. [Google Scholar]
- Reilly, E.K.; Burghardt, F.; Fain, R.; Wright, P. Powering a wireless sensor node with a vibration-driven piezoelectric energy harvester. Smart Mater. Struct. 2011, 20, 125006. [Google Scholar] [CrossRef]
- Akopyan, V.A.; Zakharov, Y.N.; Parinov, I.A.; Rozhkov, E.V.; Shevtsov, S.N.; Wu, P.C.; Wu, J.K. Theoretical and Experimental Investigations of Piezoelectric Generators of Various Types. In Physics and Mechanics of New Materials and Their Applications; Parinov, I., Chang, S.H., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2013; pp. 309–334. Available online: https://novapublishers.com/shop/physics-and-mechanics-of-new-materials-and-their-applications/ (accessed on 2 April 2022).
- Parinov, I.A.; Cherpakov, A.V.; Rozhkov, E.V.; Soloviev, A.N.; Chebanenko, V.A. Program-signal generator “Sgenerator” RU 2018610408, 10 January 2018. Application No. 2017661586 dated 11/13/2017. Available online: https://elibrary.ru/item.asp?id=39279218 (accessed on 2 December 2021). (In Russian).
- Parinov, I.A.; Soloviev, A.N.; Cherpakov, A.V. The program “Vibrograf” for registration, visualization and processing of vibrations of structures RU 2016612309, 24 February 2016. Application No. 2015663157 dated 12/30/2015. Available online: https://elibrary.ru/item.asp?id=39344305 (accessed on 2 December 2021). (In Russian).
- Chebanenko, V.A.; Zhilyaev, I.V.; Soloviev, A.N.; Cherpakov, A.V.; Parinov, I.A. Numerical optimization of the piezoelectric generators. J. Adv. Dielectr. 2020, 10, 2060016. [Google Scholar] [CrossRef]
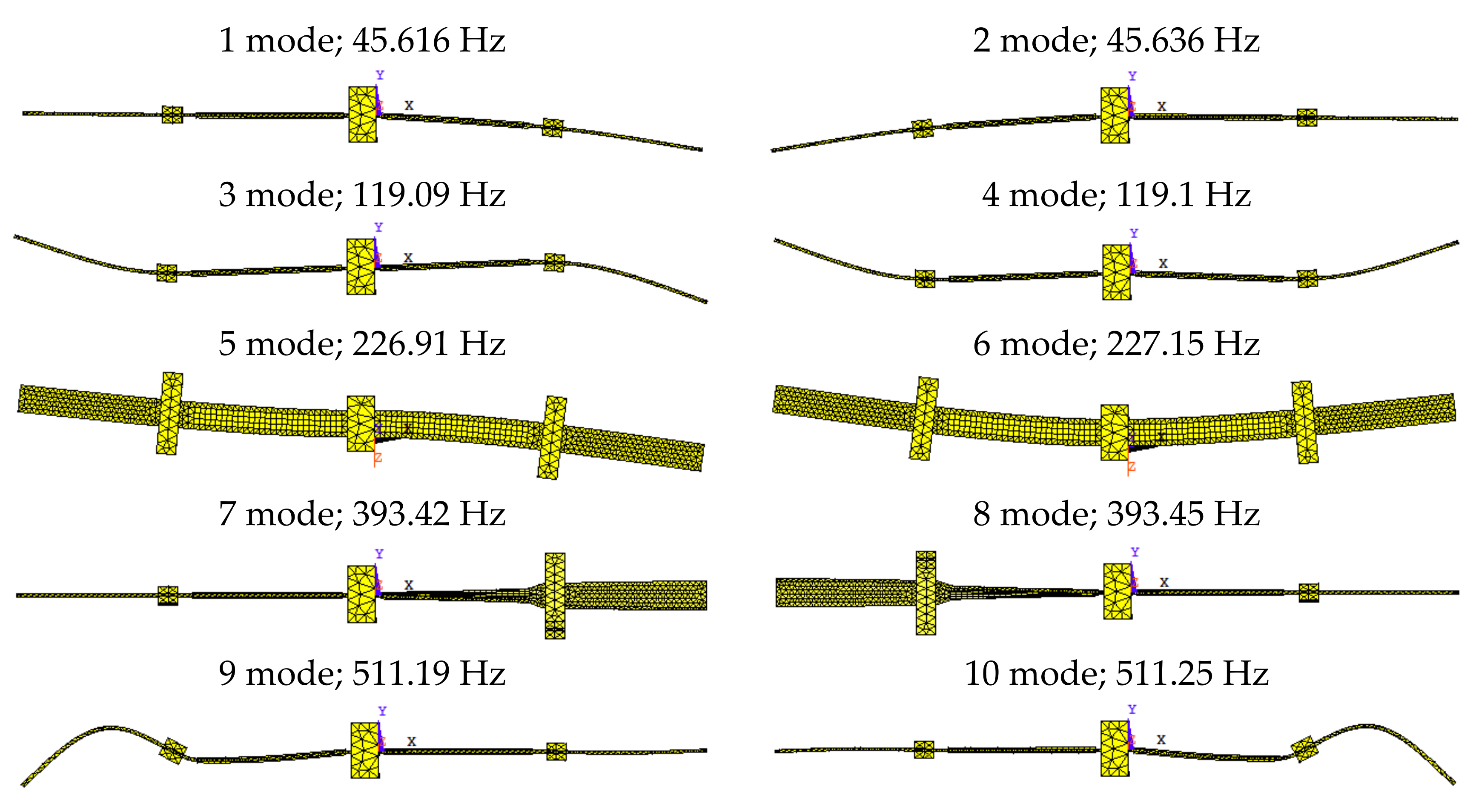
- Cherpakov, A.V.; Kokareva, Y.A. Modal analysis of the cantilever type piezo-electric generator characteristics with active based on numerical simulation. IOP Conf. Ser. Mater. Sci. Eng. 2019, 698, 066020. [Google Scholar] [CrossRef]
- Cherpakov, A.V.; Parinov, I.A.; Soloviev, A.N.; Rozhkov, E.V. Experimental Studies of Cantilever Type PEG with Proof Mass and Active Clamping. In Advanced Materials. Springer Proceedings in Physics; Parinov, I., Chang, S.H., Kim, Y.H., Eds.; Springer: Cham, Switzerland, 2019; Volume 224, pp. 593–601. [Google Scholar] [CrossRef]
- Polyakova, T.V.; Cherpakov, A.V.; Parinov, I.A.; Grigoryan, M.N. Estimation of the output parameters of a numerical model of a cantilever-type piezoelectric generator with attached mass and active termination upon pulsed excitation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 913, 022014. [Google Scholar] [CrossRef]
- Soloviev, A.N.; Chebanenko, V.A.; Zhilyaev, I.V.; Cherpakov, A.V.; Parinov, I.A. Numerical optimization of the cantilever piezoelectric generator. Mater. Phys. Mech. 2020, 44, 94–102. [Google Scholar] [CrossRef]
- Soloviev, A.N.; Parinov, I.A.; Cherpakov, A.V.; Chayka, Y.A.; Rozhkov, E.V. Analysis of Oscillation Forms at Defect Identification in Node of Truss Based on Finite Element Modeling. Mater. Phys. Mech. 2018, 37, 192–197. [Google Scholar] [CrossRef]
- Iovane, G.; Nasedkin, A.V. Finite element modelling of ceramomatrix piezocomposites by using effective moduli method with different variants of boundary conditions. Materials. Physics. Mech. 2019, 42, 1–13. [Google Scholar]
- Iyer, S.; Venkatesh, T.A. Electromechanical response of (3-0, 3-1) particulate, fibrous, and porous piezoelectric composites with anisotropic constituents: A model based on the homogenization method. Int. J. Solids Struct. 2014, 51, 1221–1234. [Google Scholar] [CrossRef]
- Soloviev, A.N.; Parinov, I.A.; Cherpakov, A.V. Modeling the Cantilever Type PEG with Proof Mass and Active Pinching by Using the Porous Piezoceramics with Effective Properties. In Physics and Mechanics of New Materials and Their Applications. PHENMA 2020. Springer Proceedings in Materials; Parinov, I.A., Chang, S.H., Kim, Y.H., Noda, N.A., Eds.; Springer: Cham, Switzerland, 2021; Volume 10, pp. 481–493. [Google Scholar] [CrossRef]
- Nasedkin, A.V. Finite-Element Modeling of Piezoelectric Generators from Highly Porous Piezoceramics; Institute of Hydromechanics, National Academy of Science: Kiev, Ukraine, 2011. [Google Scholar]
- Nasedkin, A.V. Finite Element Design of Piezoelectric and Magnetoelectric Composites with Use of Symmetric Quasidefinite Matrices. In Advanced Materials—Studies and Applications; Parinov, I.A., Chang, S.H., Theerakulpisut, S., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2015; pp. 109–124. Available online: https://novapublishers.com/shop/advanced-materials-studies-and-applications/ (accessed on 2 April 2022).
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Physica D: Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Nechibvute, A.; Chawanda, A.; Luhanga, P. Finite Element Modeling of a Piezoelectric Composite Beam and Comparative Performance Study of Piezoelectric Materials for Voltage Generation. ISRN Mater. Sci. 2012, 921361. [Google Scholar] [CrossRef]
- Solovyev, A.N.; Duong, L.V. Optimization for the Harvesting Structure of the Piezoelectric Bimorph Energy Harvesters Circular Plate by Reduced Order Finite Element Analysis. Int. J. Appl. Mech. 2016, 8, 1650029. [Google Scholar] [CrossRef]
- Stewart, M.; Weaver, P.M.; Cain, M. Charge redistribution in piezoelectric energy harvesters. Appl. Phys. Lett. 2012, 100, 073901. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Broadband vibration energy harvesting techniques. In Advances in Energy Harvesting Methods; Elvin, N., Erturk, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 17–61. [Google Scholar] [CrossRef]
- Zhu, D.; Tudor, M.J.; Beeby, S.P. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2010, 21, 022001. [Google Scholar] [CrossRef]
- Karami, M.A.; Inman, D.J. Powering pacemakers from heartbeat vibrations using linear and nonlinear energy harvesters. Appl. Phys. Lett. 2012, 100, 042901. [Google Scholar] [CrossRef]
- Arrieta, A.F.; Hagedorn, P.; Erturk, A.; Inman, D.J. A piezoelectric bistable plate for nonlinear broadband energy harvesting. Appl. Phys. Lett. 2010, 97, 104102. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Zhao, L. Magnetic Coupled Cantilever Piezoelectric Energy Harvester. Smart Mater. Adapt. Struct. Intell. Syst. 2012, 2, 811–818. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Haldkar, R.K.; Parinov, I.A. Wind Energy Harvesting from Artificial Grass by using Micro Fibre Composite. In Physics and Mechanics of New Materials and Their Applications PHENMA 2021. Springer Proceedings in Materials; Parinov, I.A., Chang, S.H., Kim, Y.H., Noda, N.A., Eds.; Springer: Cham, Switzerland, 2021; Volume 10, pp. 511–518. [Google Scholar] [CrossRef]
- Gao, F.; Liu, G.; Chung, B.L.H.; Chan, H.H.T.; Liao, W.H. Macro fiber composite-based energy harvester for human knee. Appl. Phys. Lett. 2019, 115, 033901. [Google Scholar] [CrossRef]
- Ju, S.; Chae, S.H.; Choi, Y.; Ji, C. Macro fiber composite-based low frequency vibration. energy harvester. Sens. Actuators A Phys. 2015, 226, 126–136. [Google Scholar] [CrossRef]
- Khalatkar, A.; Gupta, V.K.; Haldkar, R. Modeling and simulation of cantilever beam for optimal placement of piezoelectric actuators for maximum energy harvesting. Proc. SPIE 8204 Smart Nano-Micro Mater. Devices 2011, 8204, 82042G. [Google Scholar] [CrossRef]
- Khalatkar, A.M.; Haldkar, R.H.; Gupta, V.K. Finite Element Analysis of Cantilever Beam for Optimal Placement of Piezoelectric Actuator. In Proceedings of the 2nd International Conference on Mechanical, Material Engineering (ICMME 2014), Shiyan, China, 22–23 November 2014; Volume 110–116, pp. 4212–4220. [Google Scholar] [CrossRef]
- Khalatkar, A.M.; Kumar, R.; Haldkar, R.; Jhodkar, D. Arduino-Based Tuned Electromagnetic Shaker Using Relay for MEMS Cantilever Beam; Springer: Singapore, 2019. [Google Scholar]
- Orrego, S.; Shoele, K.; Ruas, A.; Doran, K.; Caggiano, B.; Mittal, R.; Kang, S.H. Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 2017, 194, 212–222. [Google Scholar] [CrossRef]
- Lai, Z.; Wang, S.; Zhu, L.; Zhang, G.; Wang, J.; Yang, K.; Yurchenko, D. A hybrid piezo-dielectric wind energy harvester for high-performance vortex-induced vibration energy. Mech. Syst. Signal Processing 2021, 150, 107212. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Chen, Y.; Zuo, H.; Li, Q. Experimental Research on Wind-Induced Flag-Swing Piezoelectric Energy Harvesters. Shock Vib. 2021, 2021, 8496441. [Google Scholar] [CrossRef]
- Muñoz, C.Q.G.; Alcalde, G.Z.; Márquez, F.P.G. Analysis and Comparison of Macro Fiber Composites and Lead Zirconate Titanate (PZT) Discs for an Energy Harvesting Floor. Appl. Sci. 2020, 10, 5951. [Google Scholar] [CrossRef]
- Wang, J.D.; Yurchenko, D.; Hu, G.; Zhao, L.; Tang, L.; Yang, Y. Perspectives in flow-induced vibration energy harvesting. Appl. Phys. Lett. 2021, 119, 100502. [Google Scholar] [CrossRef]
- Li, X.; Guo, M.; Dong, S.A. flex-compressive-mode piezoelectric transducer for mechanical vibration/strain energy harvesting. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 698–703. [Google Scholar] [CrossRef]
- Zhao, S.; Erturk, A. Energy harvesting from harmonic and noise excitation of multilayer piezoelectric stacks: Modeling and experiment. Act. Passiv. Smart Struct. Integr. Syst. 2013, 8688, 86881Q. [Google Scholar] [CrossRef]
- Rupp, C.J.; Dunn, M.L.; Maute, K. Analysis of piezoelectric energy harvesting systems with non-linear circuits using the harmonic balance method. J. Intell. Mater. Syst. Struct. 2010, 21, 1383–1396. [Google Scholar] [CrossRef]
- Shevtsov, S.; Flek, M.; Acopyan, V.; Samochenko, I.; Axenov, V. On the active vibration control and stability of the tubular structures by piezoelectric patch-like actuators. Math. Eng. Sci. Aerosp. 2011, 2, 145–157. Available online: https://www.researchgate.net/publication/267666291_On_the_active_vibration_control_and_stability_of_the_tubular_structures_by_piezoelectric_patch-like_actuators (accessed on 2 April 2022).
- Wang, Y.; Inman, D.J. A survey of control strategies for simultaneous vibration suppression and energy harvesting via piezoceramics, J. Intell. Mater. Syst. Struct. 2012, 23, 2021–2037. [Google Scholar] [CrossRef]
- Wickenheiser, A.M.; Garcia, E. Power optimization of vibration energy harvesters utilizing passive and active circuits, J. Intell. Mater. Syst. Struct. 2010, 21, 1343–1361. [Google Scholar] [CrossRef]


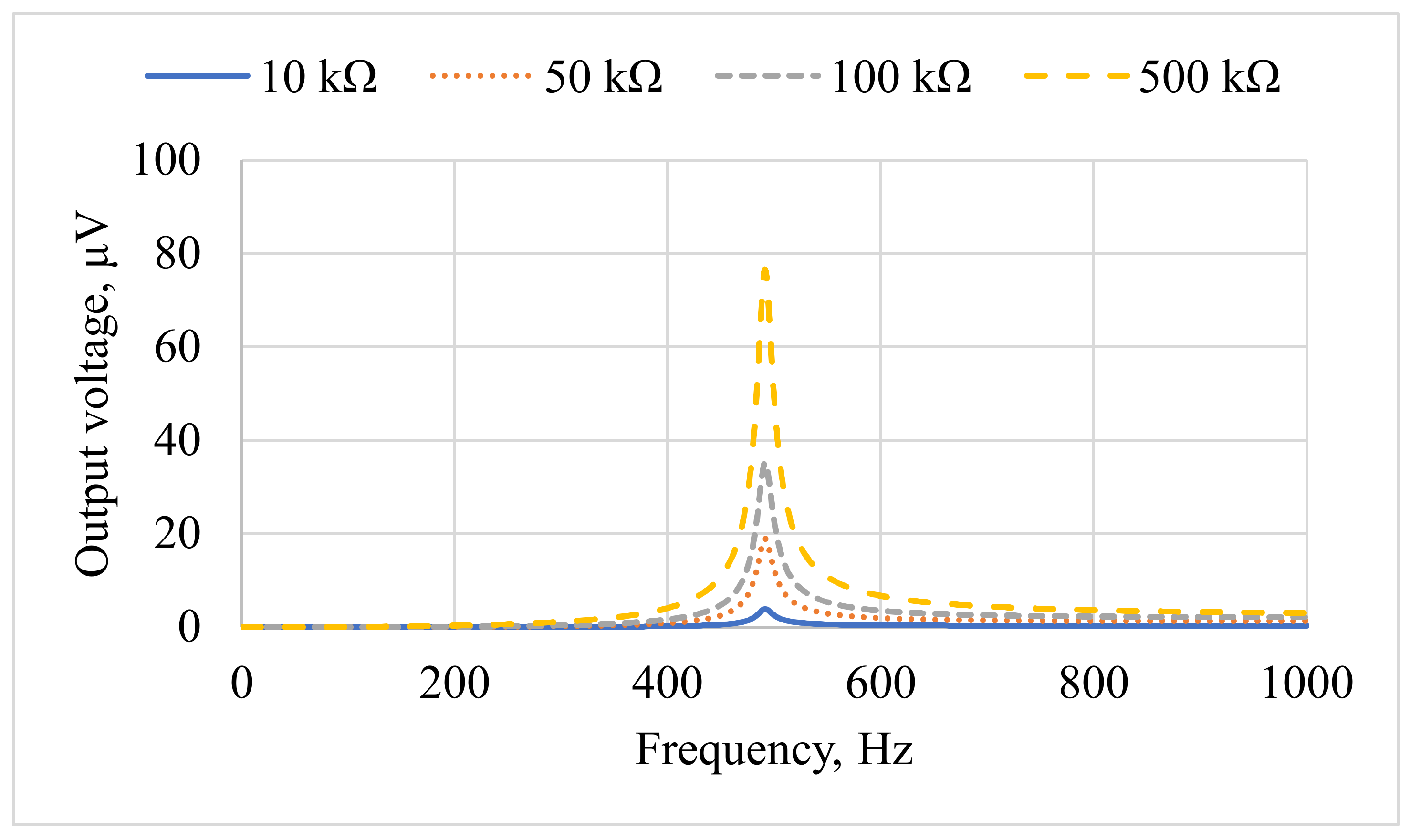


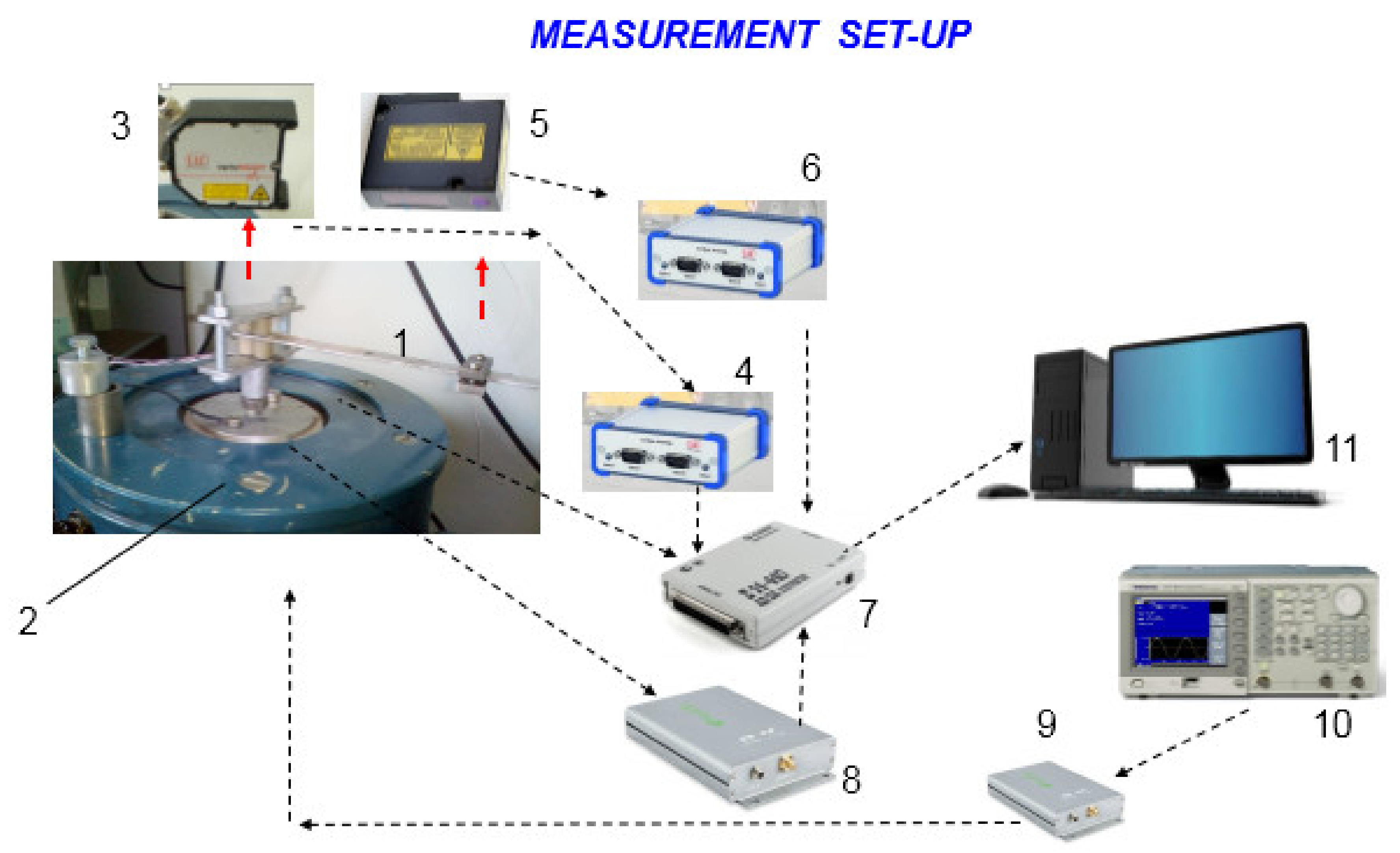


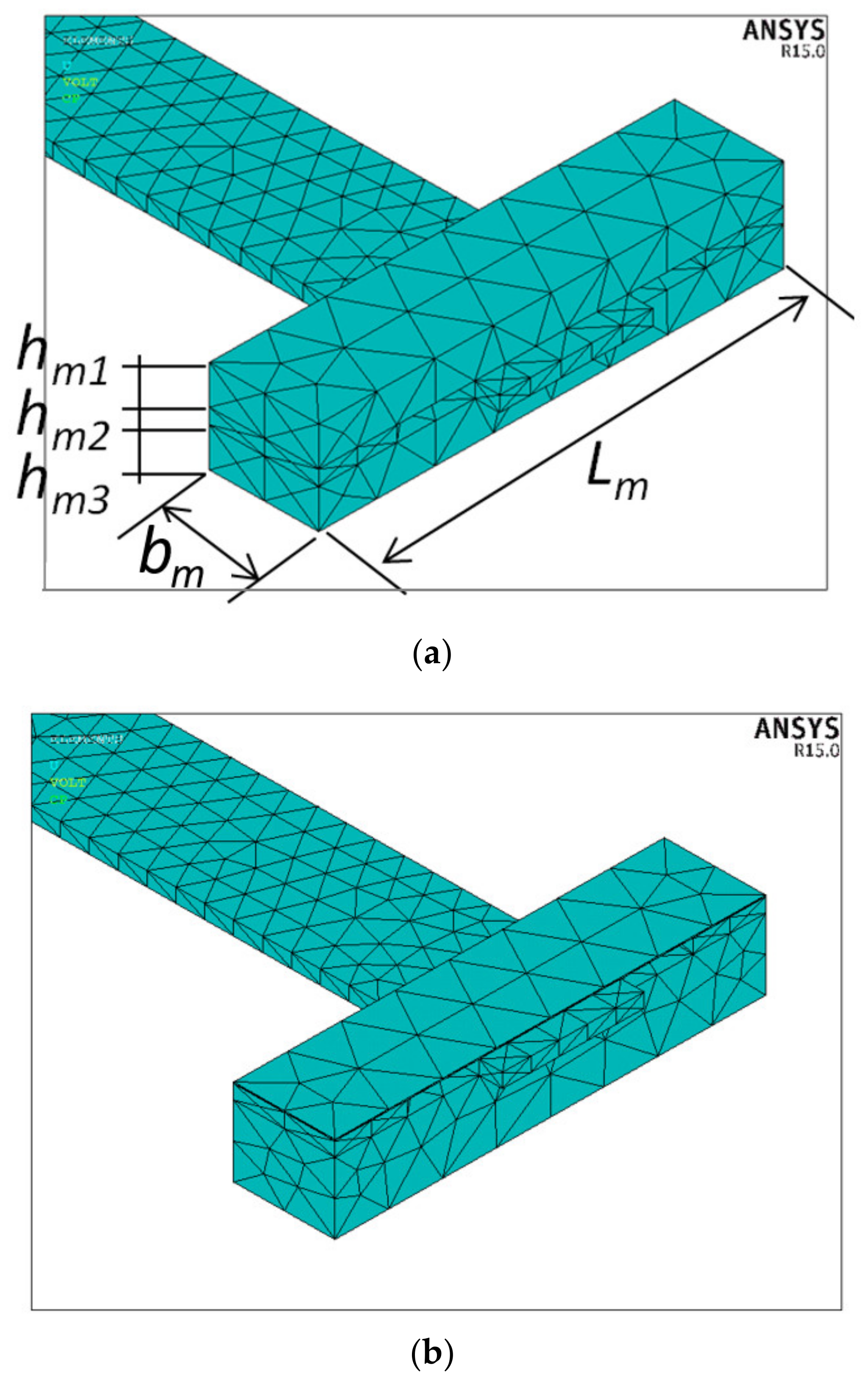
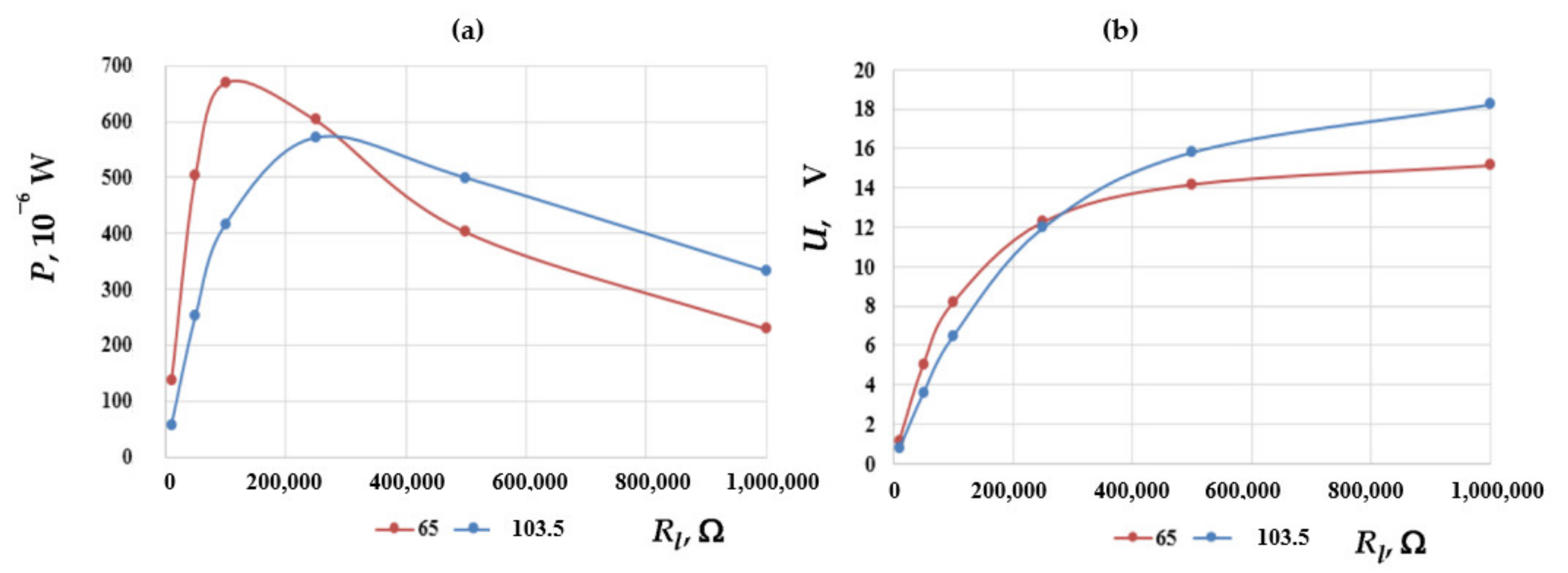
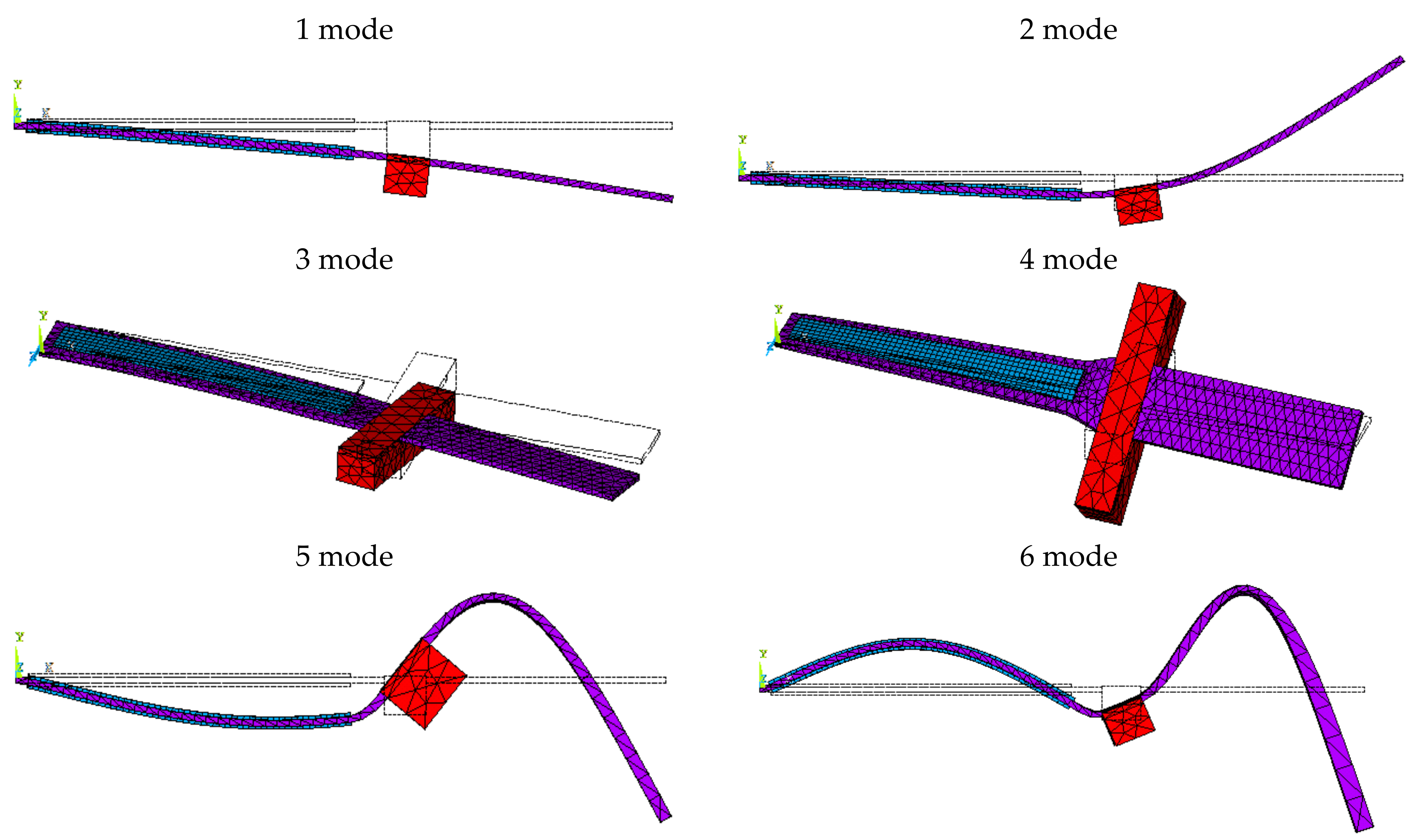
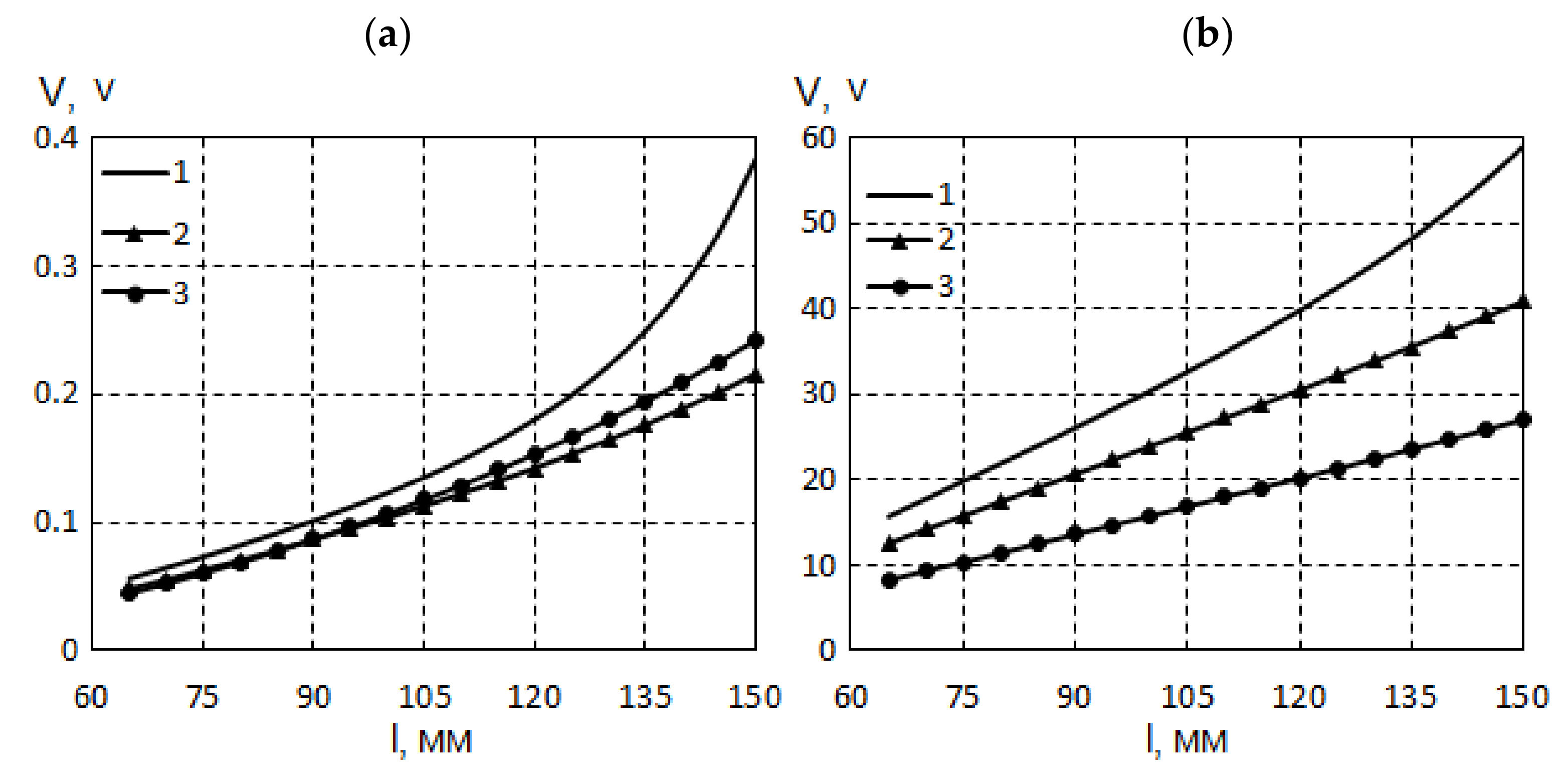
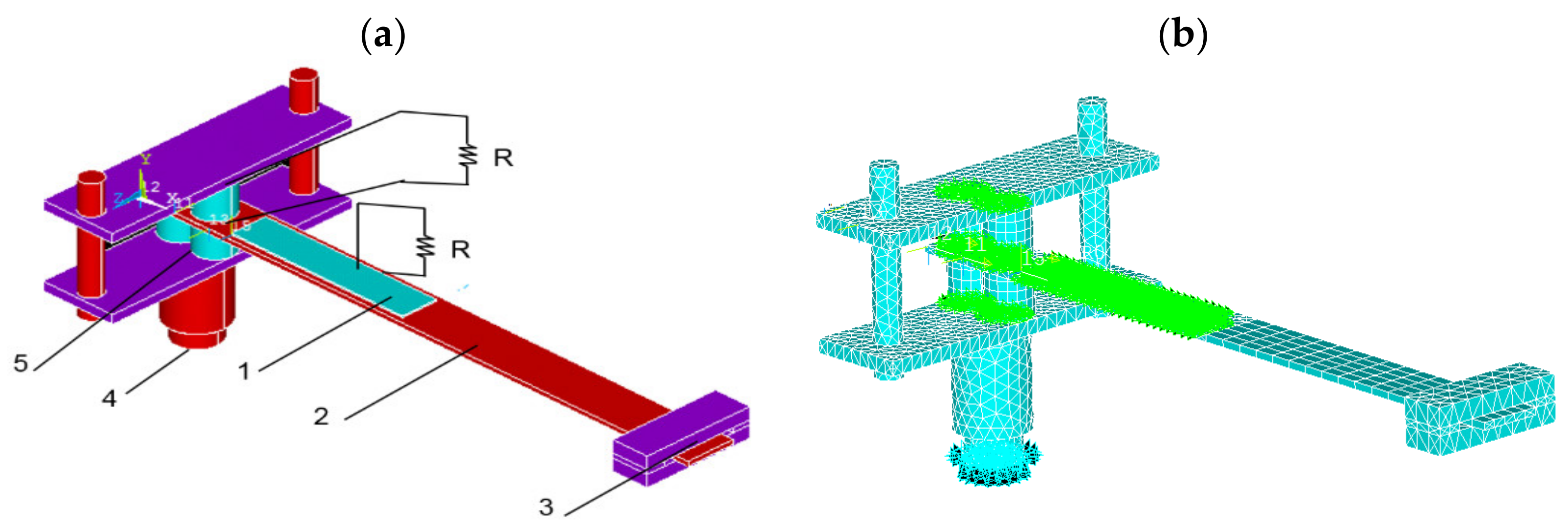


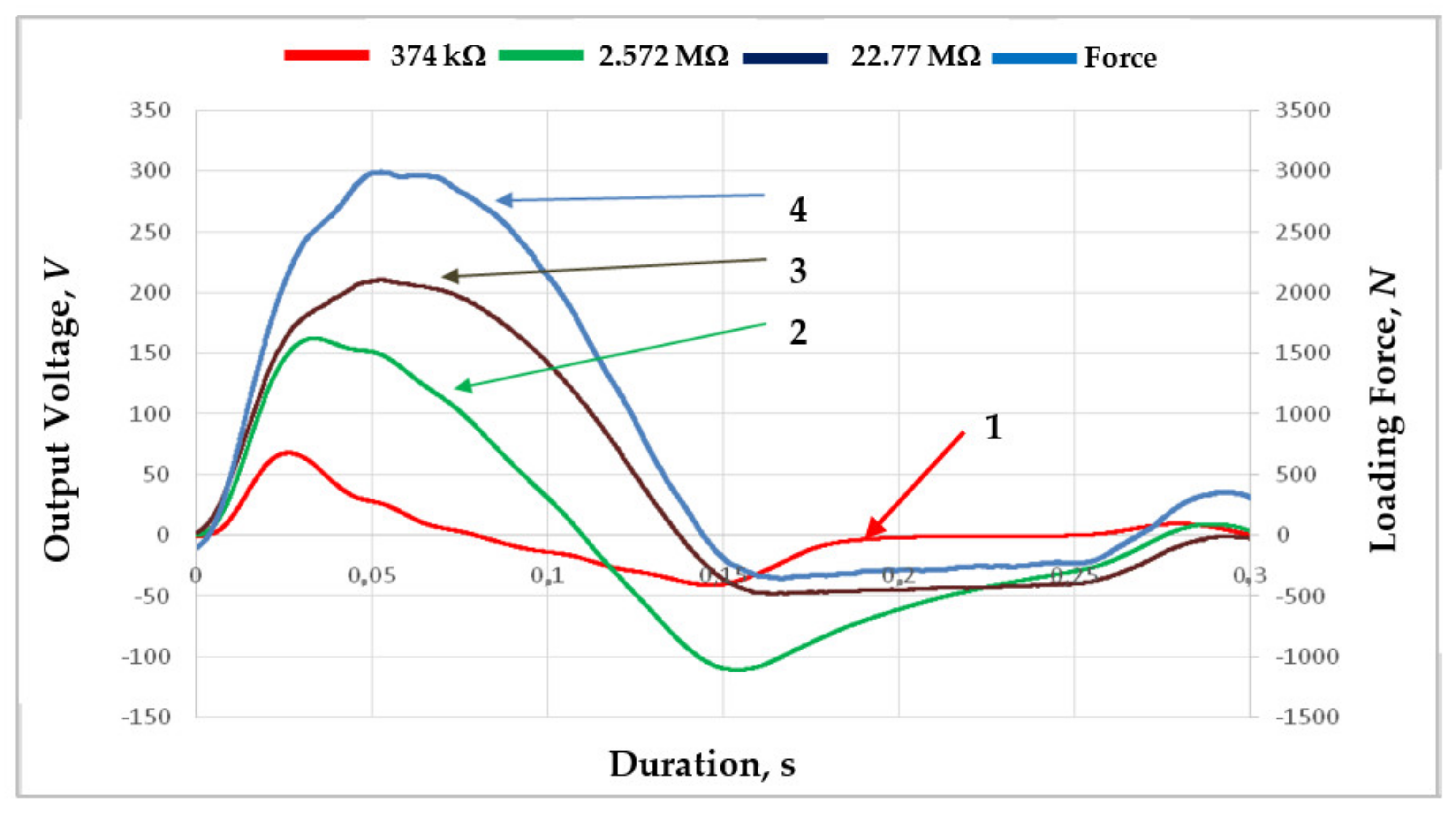

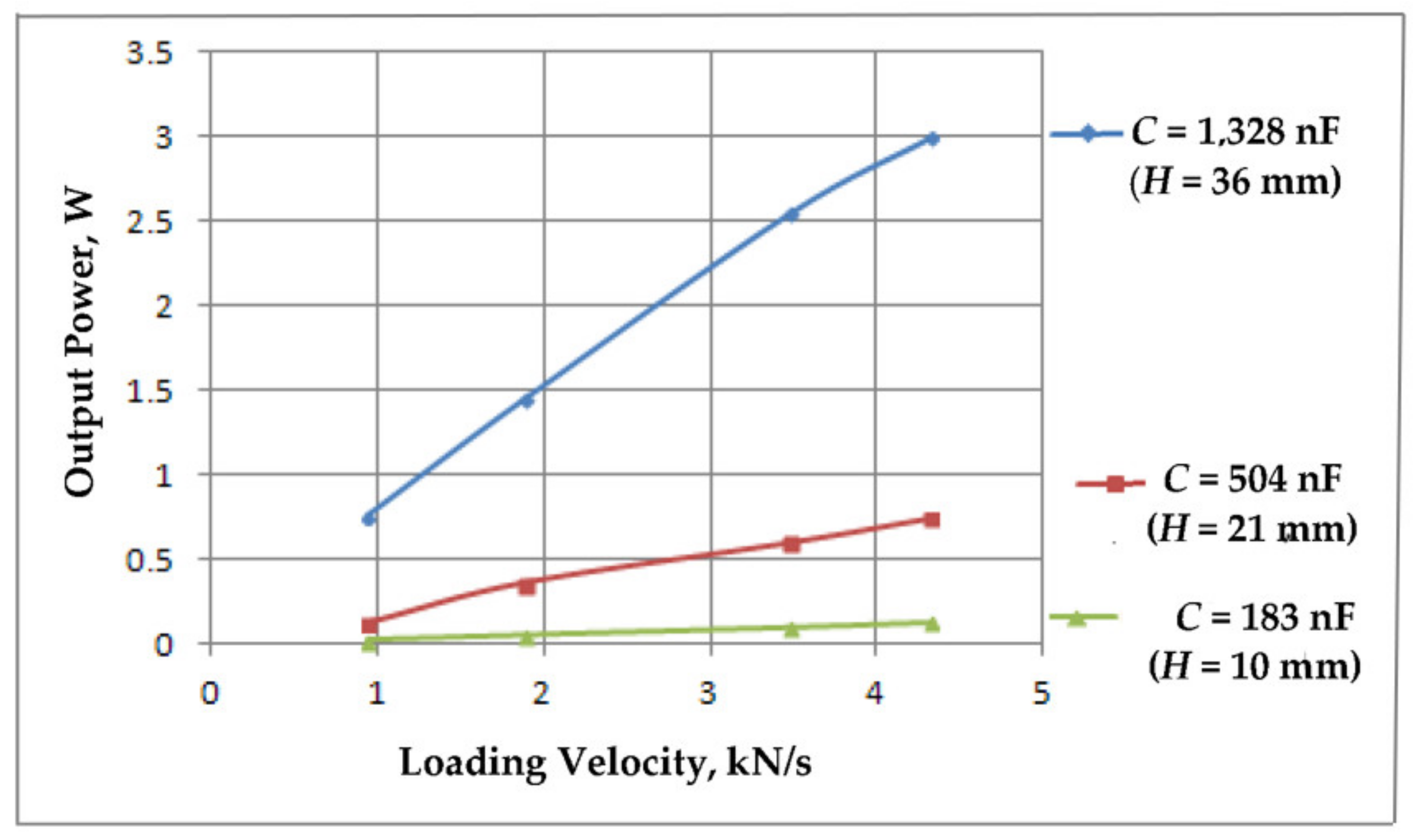
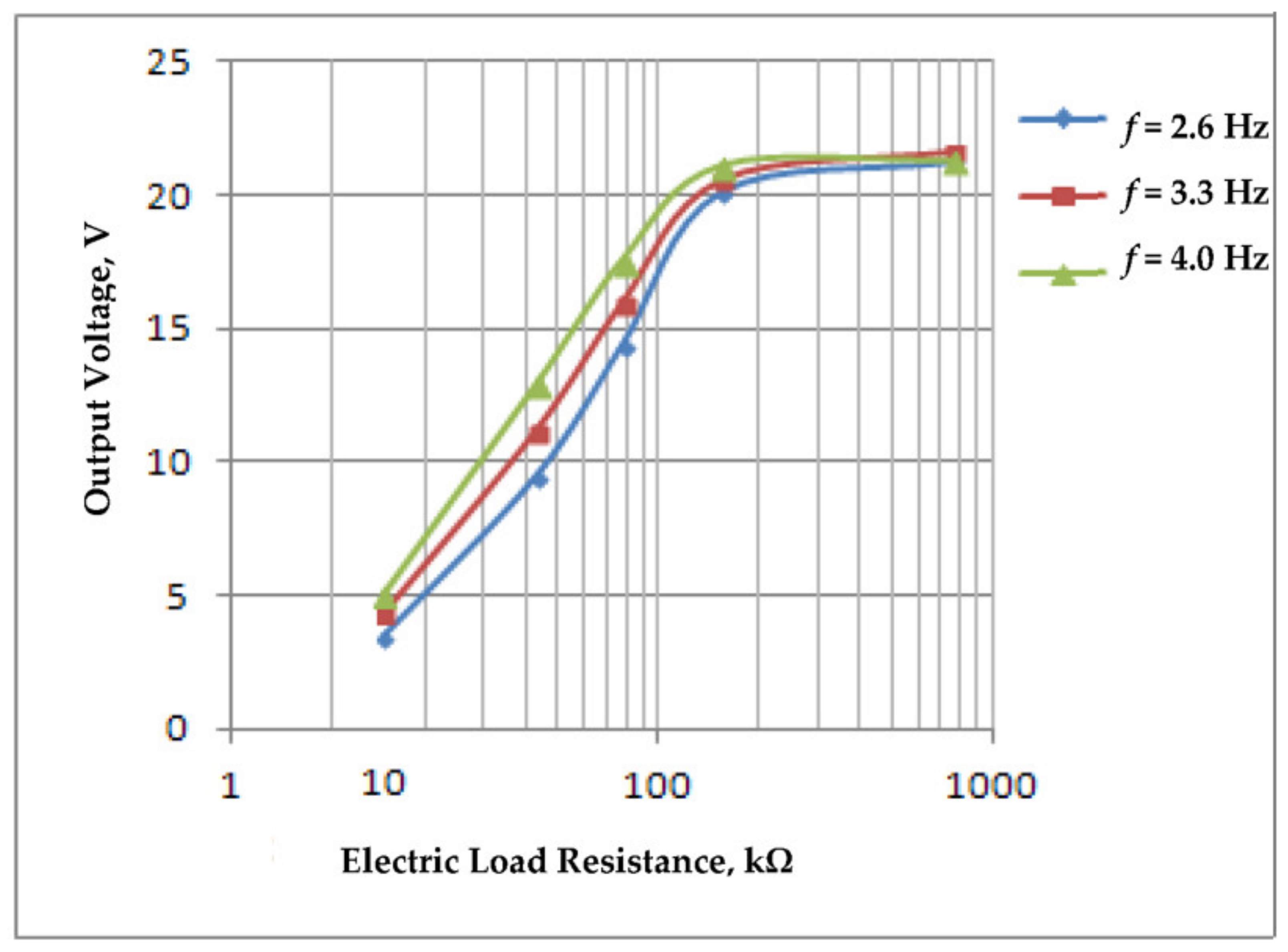
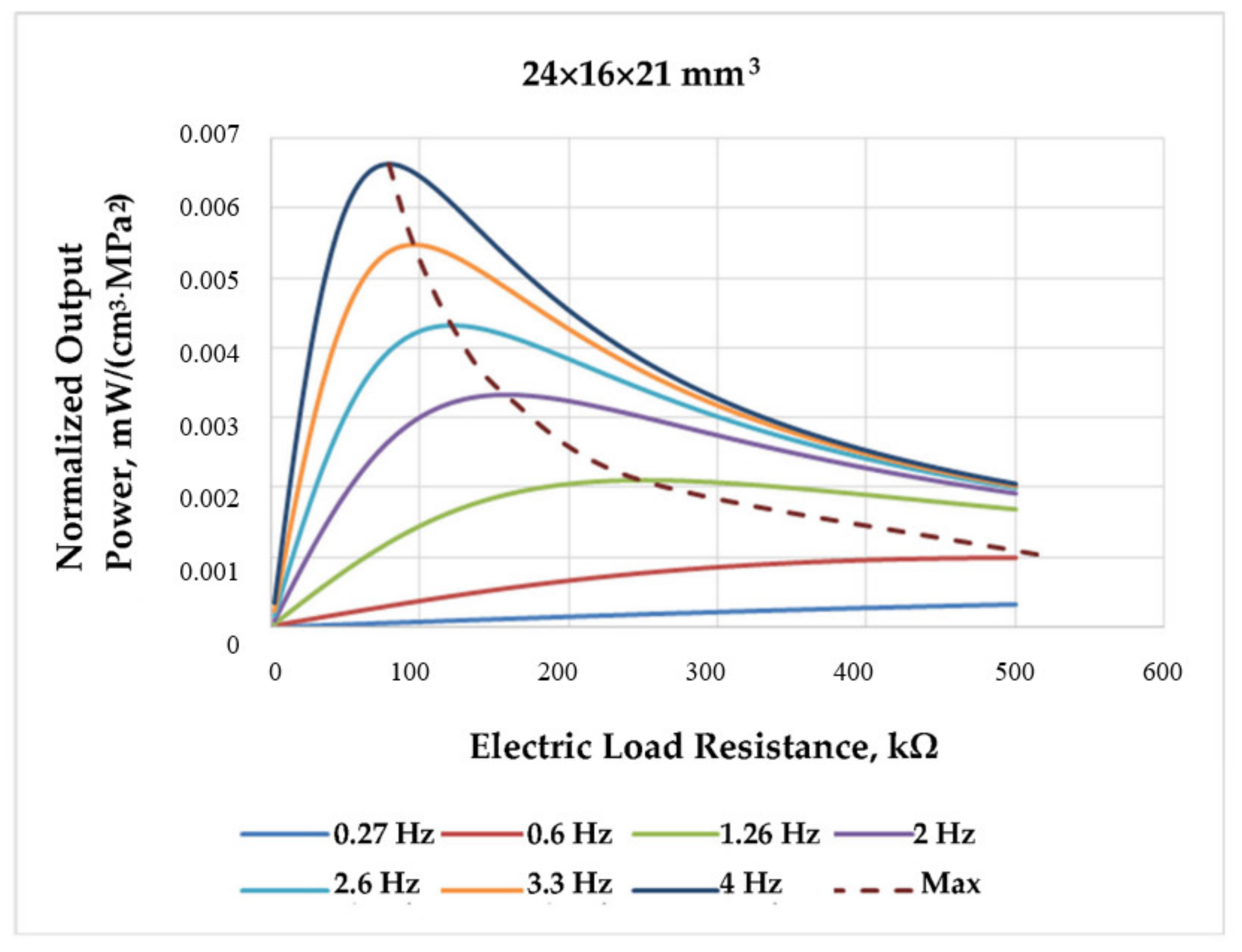
| d33, pC/N | d31, pC/N | d15, pC/N | k33 | |
|---|---|---|---|---|
| GaN | 3.7; 13.2 (NW) | −1.9; −9.4 (NW) | 3.1 | – |
| AlN | 5.0 | −2.0 | 3.6 | 0.23 |
| ZnO | 12.4; 14.3–26.7 (nanobelt) | −5.0 | −8.3 | 0.48 |
| BaTiO3, FC | 149 | −58 | 242 | 0.49 |
| PZT-4 (hard FC) | 289 | −123 | 495 | 0.70 |
| PZT-5H (soft FC) | 593 | −274 | 741 | 0.75 |
| PMN–0.33PT, SC | 2820 | −1330 | 146 | 0.94 |
| LiNbO3, SC | 6 | −1.0 | 69 | 0.23 |
| Poled PVDF | −33 | 21 | −27 | 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parinov, I.A.; Cherpakov, A.V. Overview: State-of-the-Art in the Energy Harvesting Based on Piezoelectric Devices for Last Decade. Symmetry 2022, 14, 765. https://doi.org/10.3390/sym14040765
Parinov IA, Cherpakov AV. Overview: State-of-the-Art in the Energy Harvesting Based on Piezoelectric Devices for Last Decade. Symmetry. 2022; 14(4):765. https://doi.org/10.3390/sym14040765
Chicago/Turabian StyleParinov, Ivan A., and Alexander V. Cherpakov. 2022. "Overview: State-of-the-Art in the Energy Harvesting Based on Piezoelectric Devices for Last Decade" Symmetry 14, no. 4: 765. https://doi.org/10.3390/sym14040765
APA StyleParinov, I. A., & Cherpakov, A. V. (2022). Overview: State-of-the-Art in the Energy Harvesting Based on Piezoelectric Devices for Last Decade. Symmetry, 14(4), 765. https://doi.org/10.3390/sym14040765







