Stochastic Finite-Time Stability for Stochastic Nonlinear Systems with Stochastic Impulses
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
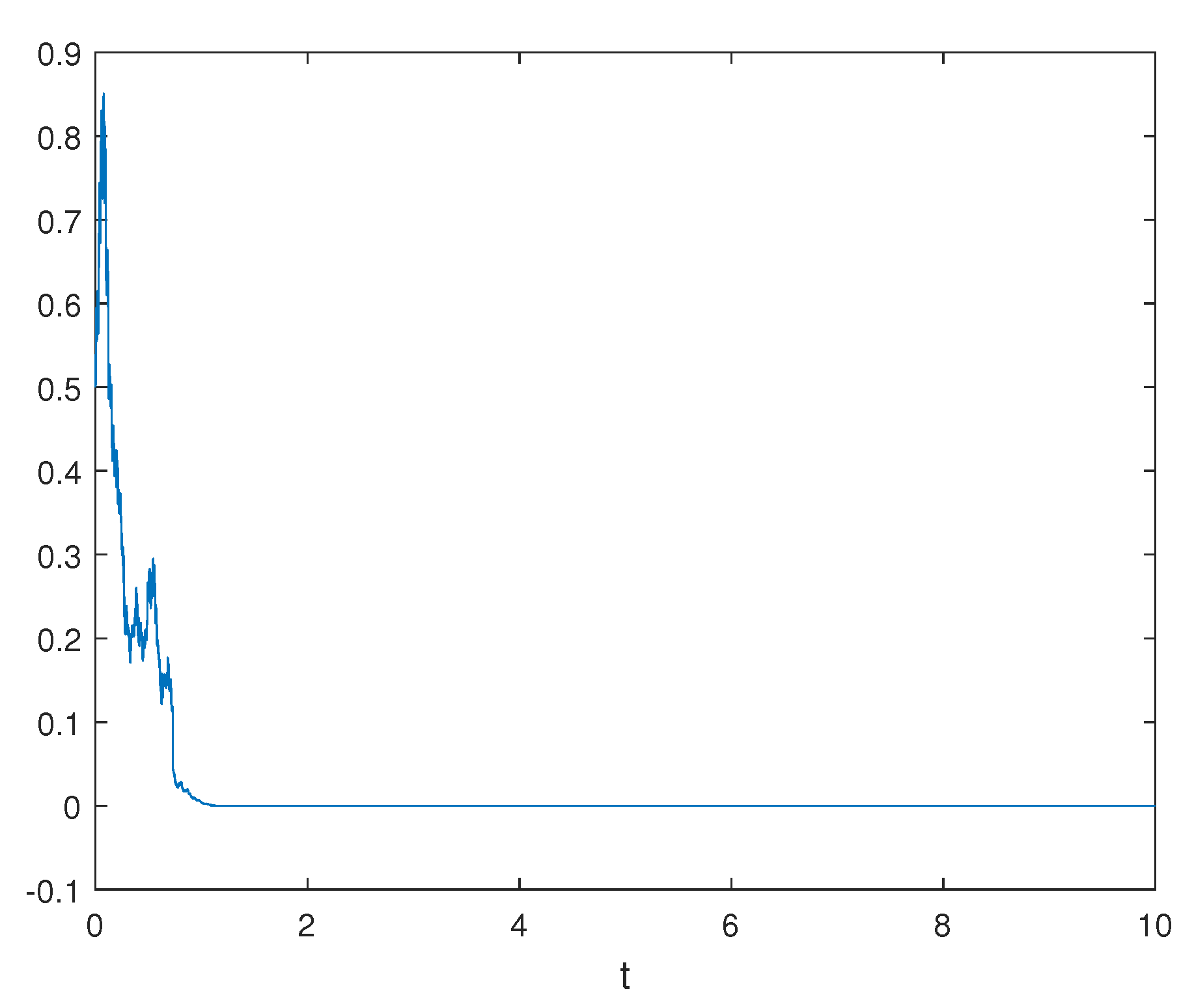
4. Apply to a Stochastic Nonlinear Systems with Stochastic Impulses
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ren, H.; Deng, F.; Peng, Y.; Zhang, B.; Zhang, C. Exponential consensus of nonlinear stochastic multi-agent systems with ROUs and RONs via impulsive pinning control. IET Control Theory Appl. 2017, 11, 225–236. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, Y.; Miao, Q.; Fang, J. Synchronization of Stochastic Dynamical Networks Under Impulsive Control With Time Delays. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1758–1768. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Gao, H.; Zhang, W.; Kurths, J. Leader-following consensus of a class of stochastic delayed multi-agent systems with partial mixed impulses. Automatica 2015, 53, 346–354. [Google Scholar] [CrossRef]
- Cheng, P.; Deng, F.; Yao, F. Exponential stability analysis of impulsive stochastic functional differential systems with delayed impulses. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2104–2114. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q.; Karimi, H. Some improved Razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans. Autom. Control 2019, 64, 5207–5213. [Google Scholar] [CrossRef]
- Peng, S.; Deng, F. New critieria on pth moment input-to-state stability of impulsive stochastic delayed differential systems. IEEE Trans. Autom. Control 2017, 62, 3573–3579. [Google Scholar] [CrossRef]
- Vinodkumar, A.; Senthilkumar, T.; Hariharan, S.; Alzabut, J. Exponential stabilization of fixed and random time impulsive delay differential system with applications. Math. Biosci. Eng. 2012, 16, 2476–2490. [Google Scholar] [CrossRef]
- Rengamannar, K.; Balakrishnan, G.; Palanisamy, M.; Niezabitowski, M. Exponential stability of non-linear stochastic delay differential system with generalized delay-dependent impulsive points. Appl. Math. Comput. 2012, 13, 2476–2490. [Google Scholar] [CrossRef]
- Rengamannar, K.; Palanisamy, M. Exponential stability of non-linear neutral stochastic delay differential system with generalized delay-dependent impulsive points. J. Franklin Inst. 2021, 358, 5014–5038. [Google Scholar]
- Chandrasekar, A.; Rakkiyappan, R. Impulsive controller design for exponential synchronization of delayed stochastic memristor-based recurrent neural networks. Neurocomputing 2016, 173, 1348–1355. [Google Scholar] [CrossRef]
- Hu, L.; Ren, Y.; Sakthivel, R. Stability of square-mean almost automorphic mild solutions to impulsive stochastic differential equations driven by G-Brownian motion. Int. J. Control 2020, 93, 3016–3025. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q. Moment exponential stability of stochastic nonlinear delay systems with impulse effects at random times. Int. J. Robust Nonlinear Control 2019, 29, 3809–3820. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q. Exponential stability of stochastic differential equations with impulse effects at random times. Asian J. Control 2019, 29, 3809–3820. [Google Scholar] [CrossRef]
- Baskonus, H.; Kayan, M. Regarding new wave distributions of the non-linear integro-partial Ito differential and fifth-order integrable equations. Appl. Math. Nonlinear Sci. 2019, 29, 3809–3820. [Google Scholar] [CrossRef]
- Chen, H.; Fakieh, B.; Muwafak, B. Differential equation model of financial market stability based on Internet big data. Appl. Math. Nonlinear Sci. 2021. [Google Scholar] [CrossRef]
- Shengnan, L.; Alassafi, M.; Omar, K. Nonlinear differential equations in the teaching model of educational informatisation. Appl. Math. Nonlinear Sci. 2021. Available online: https://sciendo.com/es/article/10.2478/amns.2021.2.00100 (accessed on 6 April 2022). [CrossRef]
- Wang, P.; Alassafi, M.; Keir, M. Nonlinear dissipative system mathematical equations in the multi-regression Model of information-based teaching. Appl. Math. Nonlinear Sci. 2021. Available online: https://sciendo.com/es/article/10.2478/amns.2021.2.00098 (accessed on 6 April 2022). [CrossRef]
- Li, X.; Yang, X.; Alyoubi, K.; Mahgoub, M. Educational research on mathematics differential equation to simulate the model of children’s mental health prevention and control system. Appl. Math. Nonlinear Sci. 2021. Available online: https://sciendo.com/es/article/10.2478/amns.2021.2.00068 (accessed on 6 April 2022). [CrossRef]
- Tan, Z.; Albarakati, A. Application of Sobolev-Volterra projection and finite element numerical analysis of integral differential equations in modern art design. Appl. Math. Nonlinear Sci. 2021. Available online: https://sciendo.com/es/article/10.2478/amns.2021.2.00054 (accessed on 6 April 2022). [CrossRef]
- Ciancio, A.; Yel, G.; Kumar, A.; Baskonus, H.; Ilhan, E. On the complex mixed dark-bright wave distributions to some conformable nonlinear integrable models. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2022, 30, 2240018. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, X.; Shi, P.; Qian, F. Input-to-state stability for nonlinear systems with stochastic impulses. Automatica 2020, 113, 108766. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Moulay, E.; Perruquetti, W. Finite time stability conditions for nonautonomous continuous systems. Int. J. Control 2008, 81, 797–803. [Google Scholar] [CrossRef]
- Moulay, E.; Dambrine, M.; Yeganefar, N.; Perruquetti, W. Finite-time stability and stabilization of time-delay systems. Syst. Control Lett. 2008, 571, 561–566. [Google Scholar] [CrossRef]
- Chen, W.; Jiao, L. Finite-time stability theorem of stchastic nonlinear systems. Automatica 2010, 46, 2105–2108. [Google Scholar] [CrossRef]
- Yin, J.; Khoo, S.; Man, Z.; Yu, X. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar] [CrossRef]
- Yin, J.; Ding, D.; Liu, Z.; Khoo, S. Some properties of finite-time stable stochastic nonlinear systems. Appl. Math. Comput. 2015, 259, 686–697. [Google Scholar] [CrossRef]
- Jiang, M.; Xie, X. Finite-time stabilization of stochastic low-order nonlinear systems with FT-SISS inverse dynamics. Int. J. Robust Nonlinear Control 2018, 28, 1960–1972. [Google Scholar] [CrossRef]
- Jiang, M.; Xie, X.; Zhang, K. Finite-time stabilization of stochastic high-order nonlinear systems with FT-SISS inverse dynamics. IEEE Trans. Autom. Control 2019, 64, 313–320. [Google Scholar] [CrossRef]
- Khoo, S.; Yin, J.; Man, Z.; Yu, X. Finite-time stabilization of stochastic nonlinear systems in strict-feedback form. Automatica 2013, 49, 1403–1410. [Google Scholar] [CrossRef]
- Lan, Q.; Li, S.; Khoo, S.; Shi, P. Global finite-time stabilization of stochastic nonlinear systems by output feedback. Int. J. Control 2015, 88, 494–506. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Q. Finite-time stabilization of high-order stochastic nonlinear systems in strict-feedback form. Automatica 2015, 54, 284–291. [Google Scholar] [CrossRef]
- Yin, J.; Khoo, S. Continuous finite-time state feedback stabulizers for some nonlinear stochastic systems. Int. J. Robust Nonlinear Control 2015, 25, 1581–1600. [Google Scholar] [CrossRef]
- Zha, W.; Zhai, J.; Ai, W.; Fei, S. Finite-time state-feedback control for a class of stochastic high-order nonlinear systems. Int. J. Comp. Meth. 2018, 98, 285–295. [Google Scholar] [CrossRef]
- Yu, X.; Yin, J.; Khoo, S. New Lyapunov conditions of stochastic finite-time stability and instability of nonlinear time-varying SDEs. Int. J. Control 2021, 94, 1674–1681. [Google Scholar] [CrossRef]
- Yu, X.; Yin, J.; Khoo, S. Generalized Lyapunov criteria on finite-time stability of stochastic nonlinear systems. Automatica 2019, 107, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Li, J.; Liu, S. Finite-time stabilization of weak solutions for a class of non-local Lipschitzian stochastic nonlinear systems with inverse dynamics. Automatica 2018, 98, 285–295. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Wiley/Chapman & Hall: Chichester, UK, 1997. [Google Scholar]
- Li, F.; Liu, Y. Global stability and stabilization of more general stochastic nonlinear systems. J. Math. Anal. Appl. 2014, 413, 841–855. [Google Scholar] [CrossRef]
- Li, P.; Li, X.; Lu, J. Input-to-state stability of impulsive delay systems with multiple impulses. IEEE Trans. Autom. Control 2021, 66, 362–368. [Google Scholar] [CrossRef]
- Mao, X.; Yuan, C. Stochastic Differential Equations with Markovian Switching; Imperial College Press: London, UK, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W. Stochastic Finite-Time Stability for Stochastic Nonlinear Systems with Stochastic Impulses. Symmetry 2022, 14, 817. https://doi.org/10.3390/sym14040817
Hu W. Stochastic Finite-Time Stability for Stochastic Nonlinear Systems with Stochastic Impulses. Symmetry. 2022; 14(4):817. https://doi.org/10.3390/sym14040817
Chicago/Turabian StyleHu, Wei. 2022. "Stochastic Finite-Time Stability for Stochastic Nonlinear Systems with Stochastic Impulses" Symmetry 14, no. 4: 817. https://doi.org/10.3390/sym14040817
APA StyleHu, W. (2022). Stochastic Finite-Time Stability for Stochastic Nonlinear Systems with Stochastic Impulses. Symmetry, 14(4), 817. https://doi.org/10.3390/sym14040817




