Vibration Force Suppression of Magnetically Suspended Flywheel Based on Compound Repetitive Control
Abstract
:1. Introduction
2. Modeling of Magnetically Suspended Flywheel System
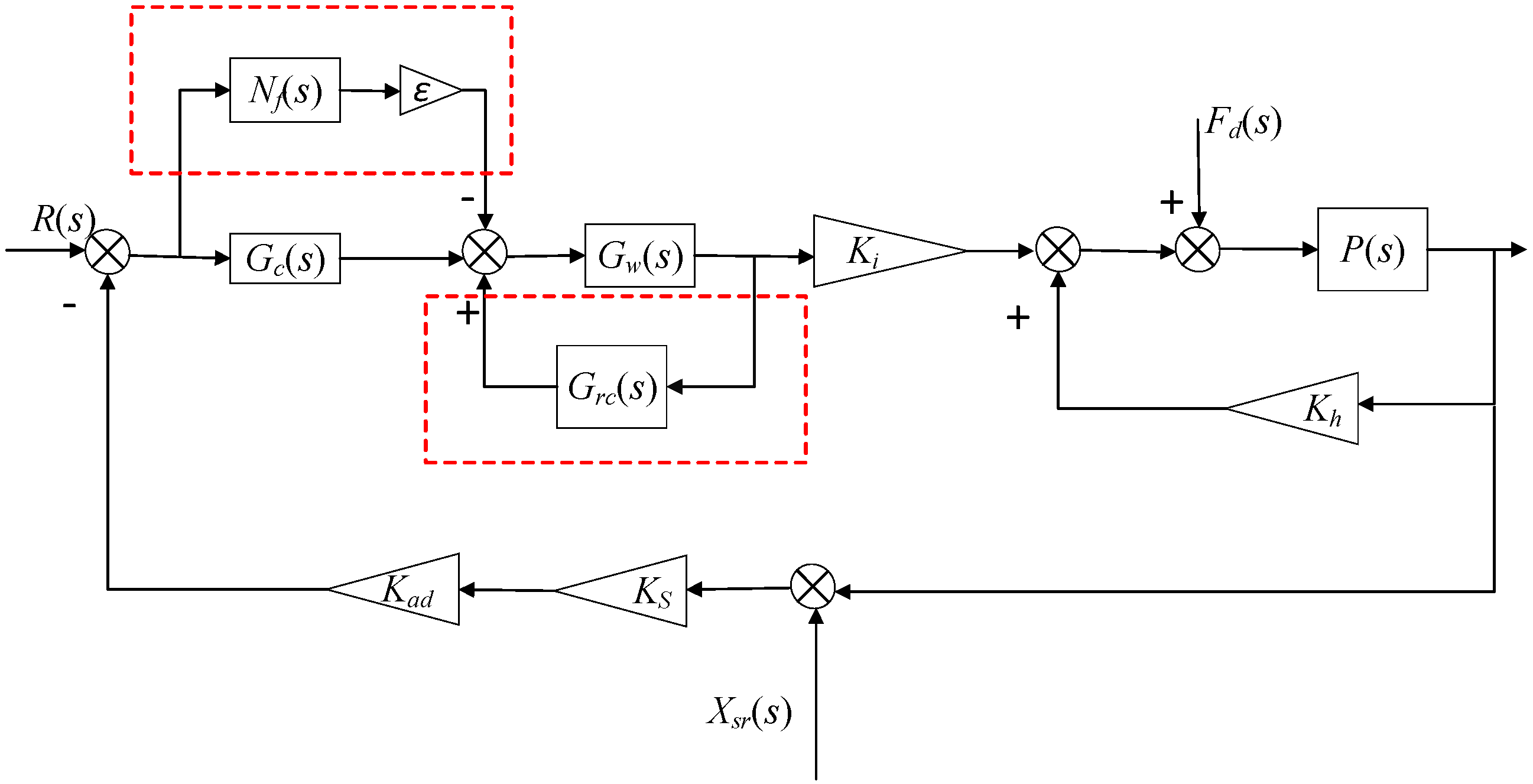
3. Compound Repetitive Control Method for Vibration Force Suppression
3.1. Overview of the Compound Repetitive Control Method
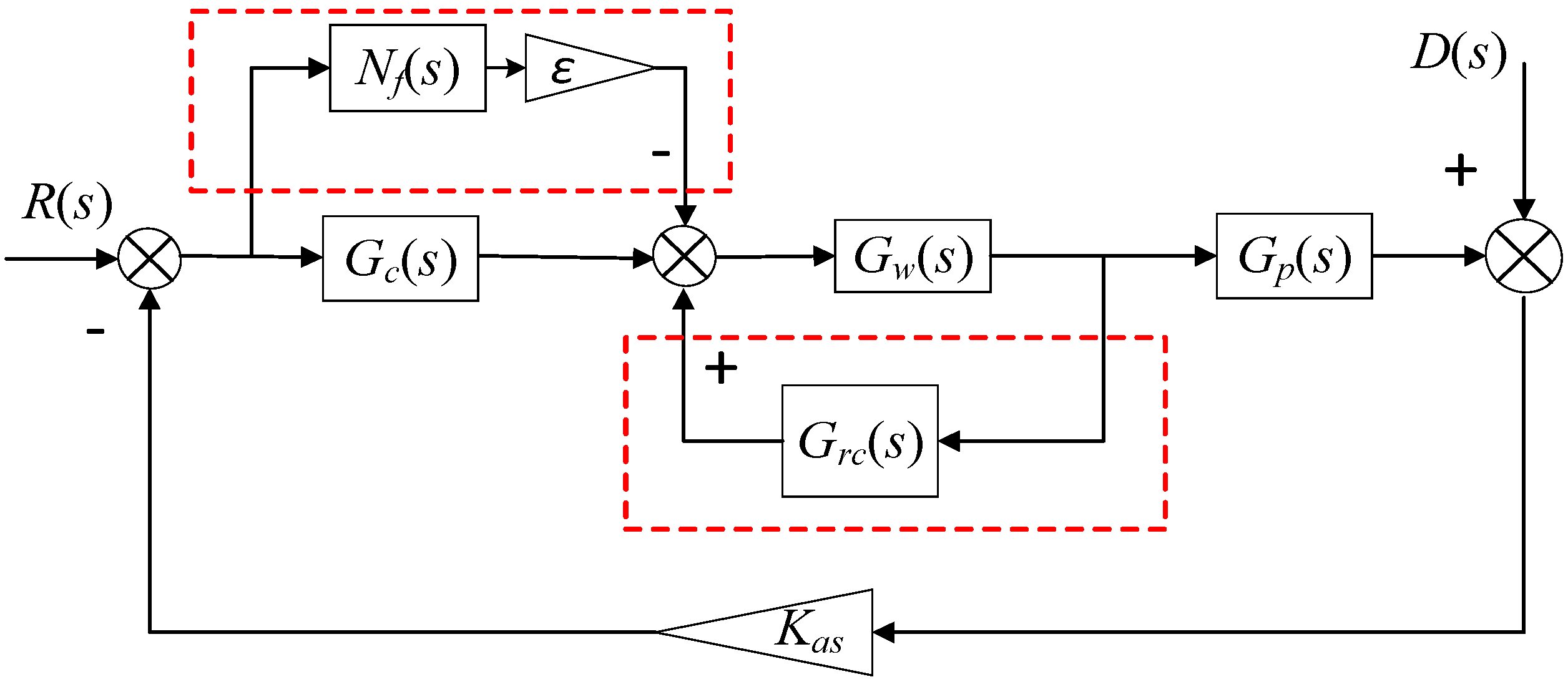
3.2. Suppression Principle of the Compound Control Method
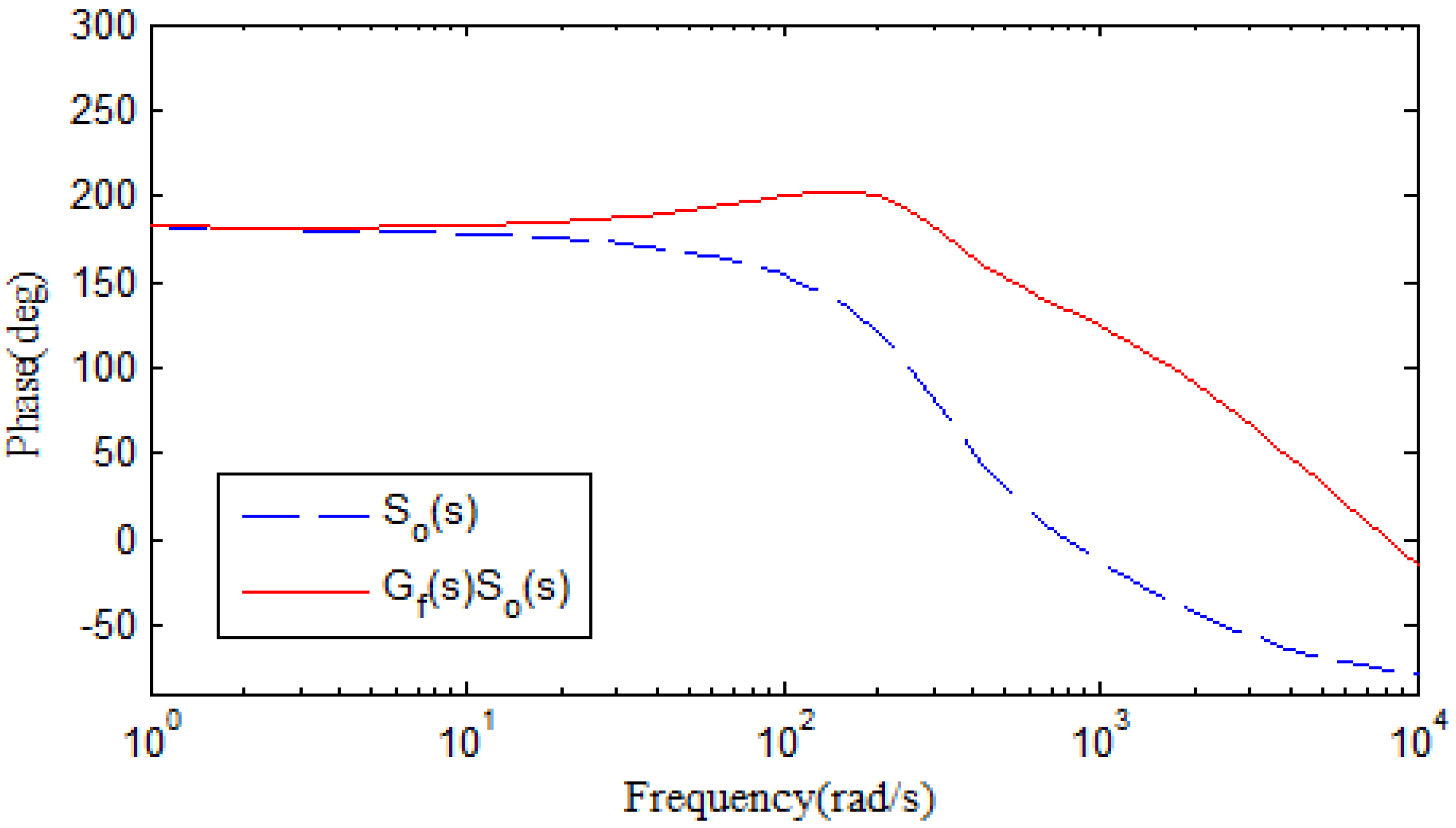
3.3. Stability Analysis of the Compound Control Method
4. Parameter Design and Simulation Analysis
4.1. Parameter Design and Setting
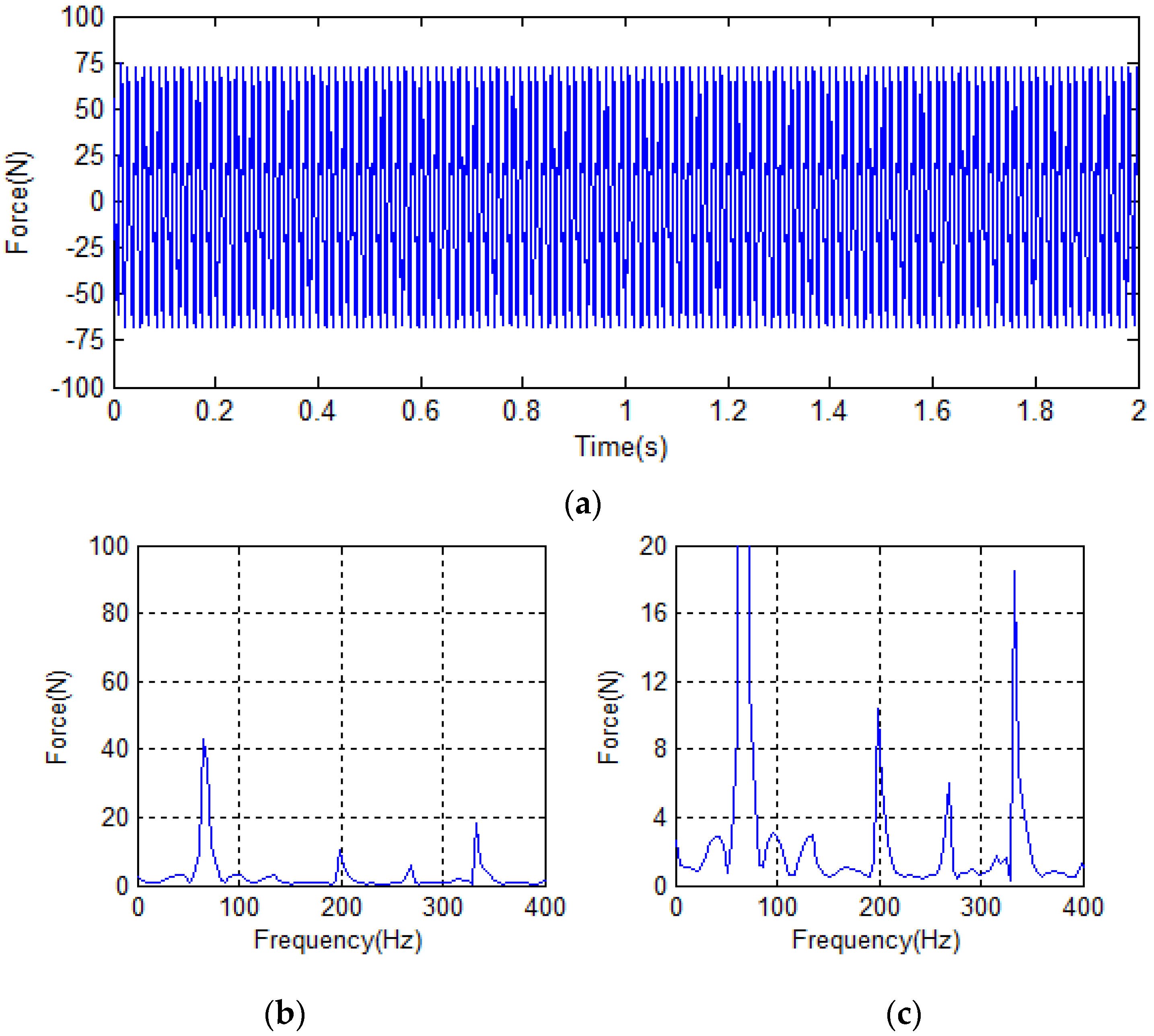
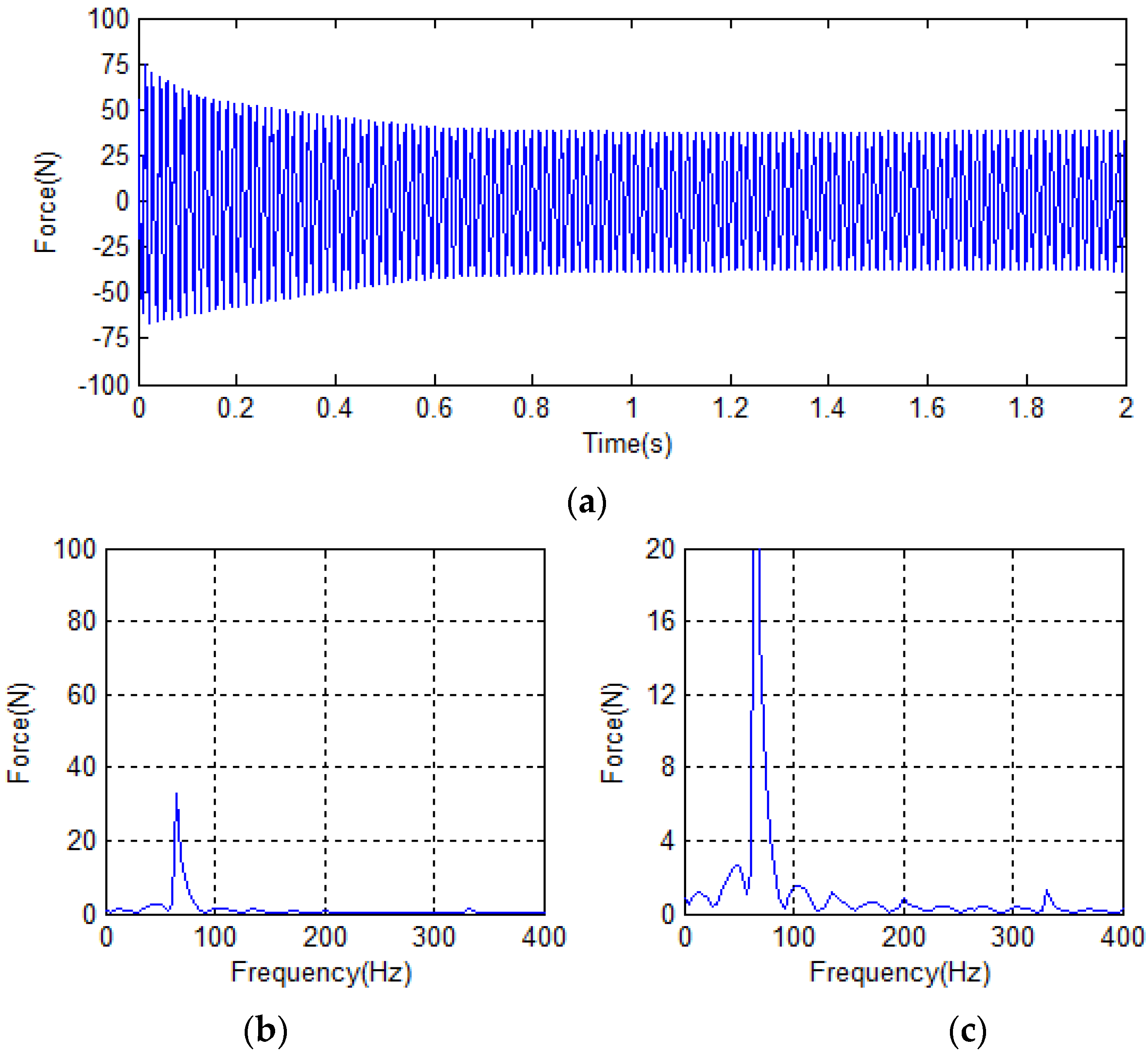
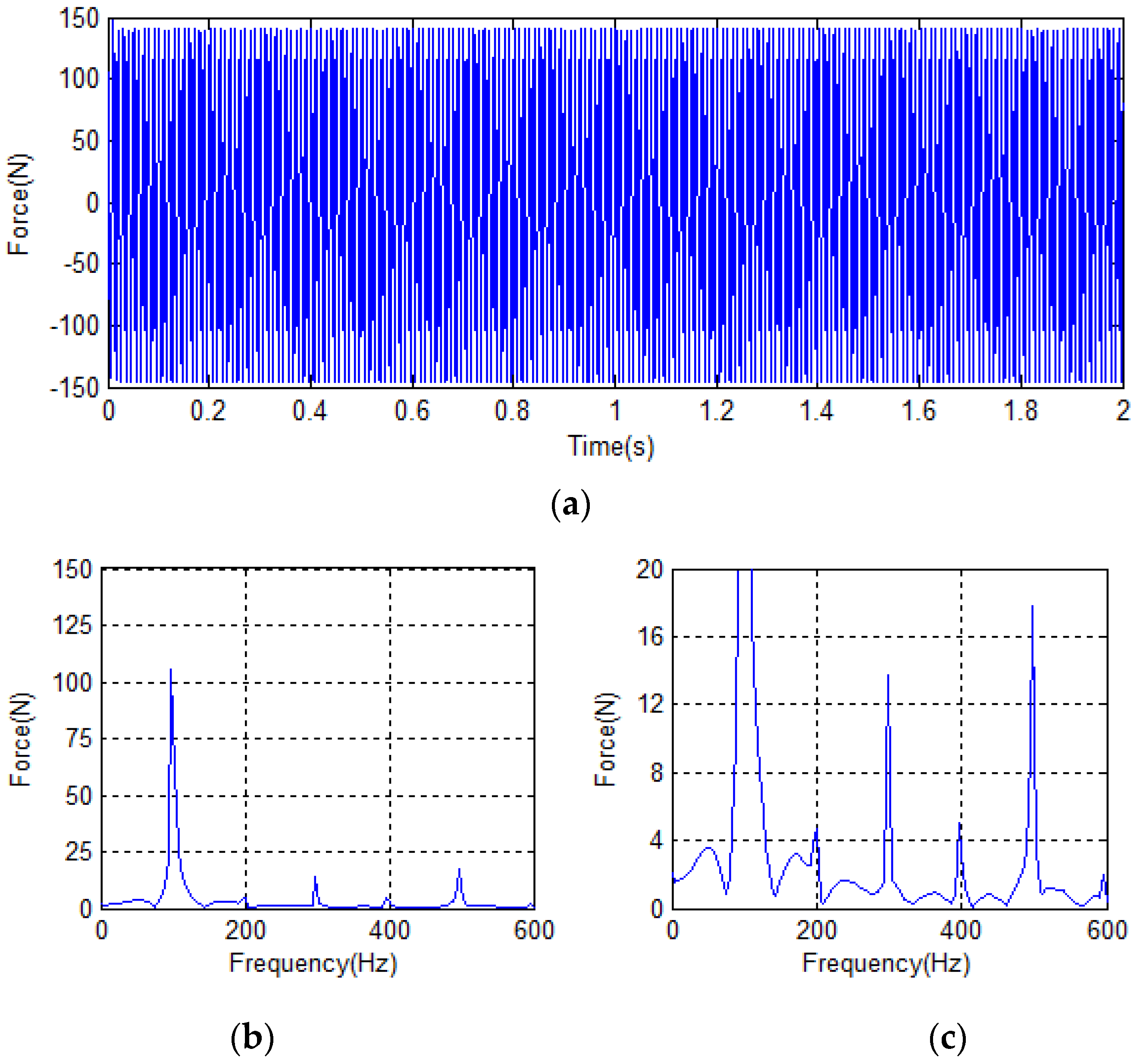
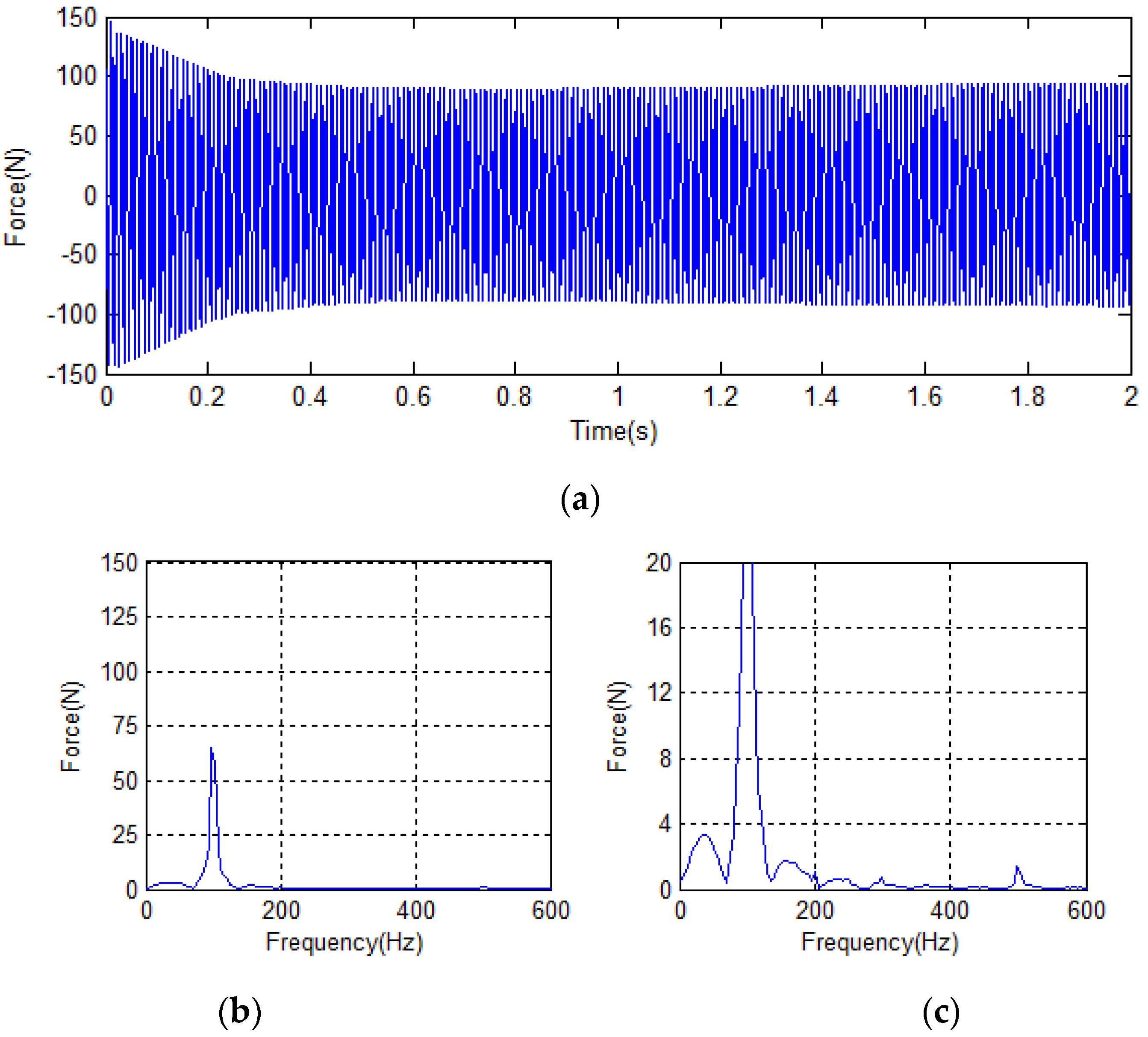
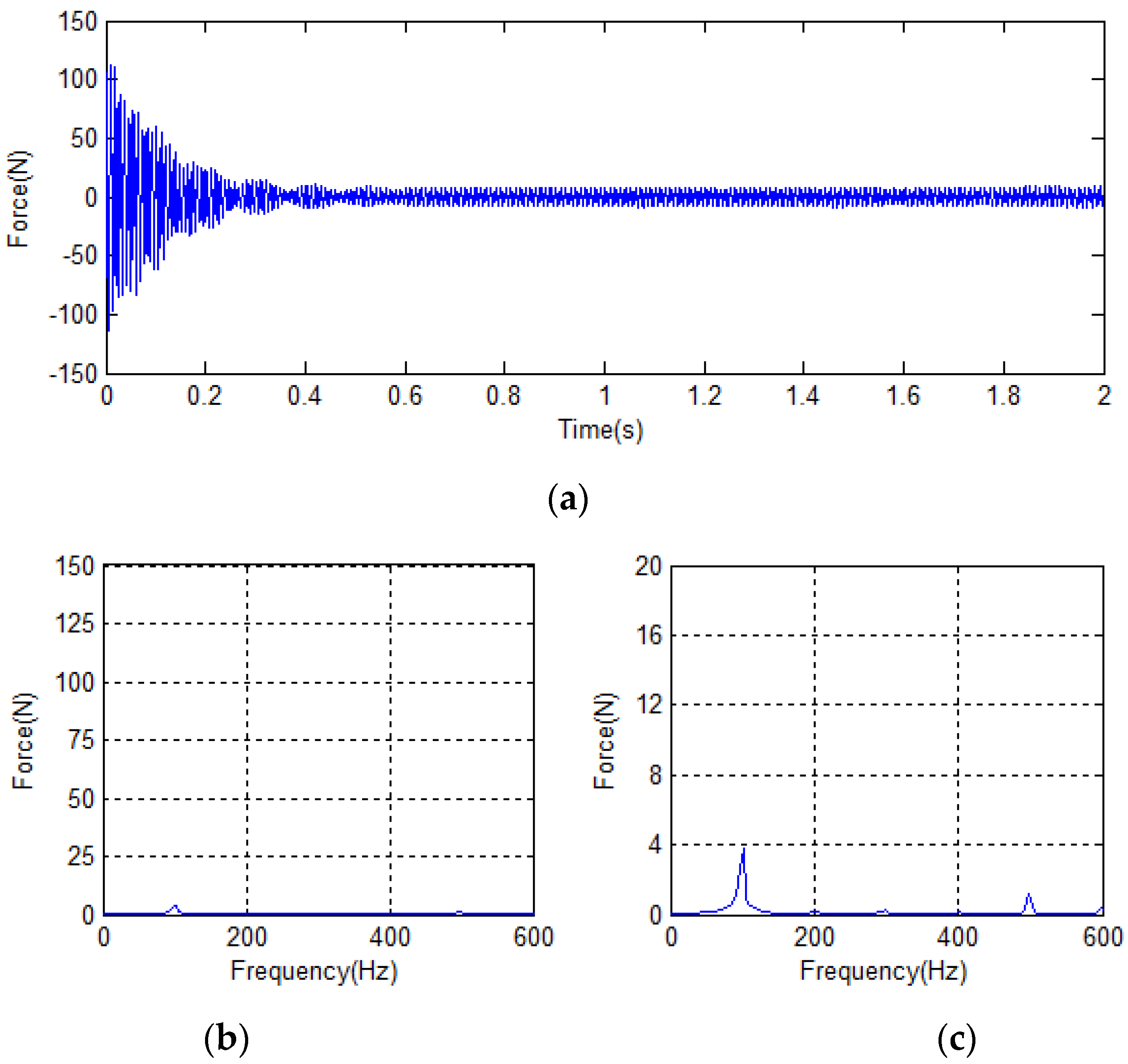
4.2. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schweitzer, G.; Bleuler, H.; Maslen, E.H.; Cole, M.; Keogh, P.; Larsonneur, R.; Maslen, E.; Nordmann, R.; Okada, Y.; Schweitzer, G. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Fang, J.C.; Xu, X.B.; Xie, J.J. Active vibration control of rotor imbalance in active magnetic bearing systems. J. Vib. Control. 2015, 21, 684–700. [Google Scholar] [CrossRef]
- Tang, J.; Xiang, B.; Zhang, Y. Dynamic characteristics of the rotor in a magnetically suspended control moment gyroscope with active magnetic bearing and passive magnetic bearing. ISA Trans. 2014, 53, 1357–1365. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Zheng, S.; Han, B. Attitude Sensing and Dynamic Decoupling Based on Active Magnetic Bearing of MSDGCMG. IEEE Trans. Instrum. Meas. 2012, 61, 338–348. [Google Scholar] [CrossRef]
- Wang, H.; Liu, K.; Ao, P. Magnetic Field and Specific Axial Load Capacity of Hybrid Magnetic Bearing. IEEE T Magn. 2013, 49, 4911–4917. [Google Scholar] [CrossRef]
- Peng, C.; Fang, J.C.; Cui, P.L. Dynamics Modeling and Measurement of the Microvibrations for a Magnetically Suspended Flywheel. IEEE Trans. Instrum. Meas. 2015, 64, 3239–3252. [Google Scholar] [CrossRef]
- Setiawan, J.D.; Mukherjee, R.; Maslen, E.H. Adaptive compensation of sensor runout for magnetic bearings with uncertain parameters: Theory and experiments. J. Dyn. Syst.-T Asme. 2001, 123, 211–218. [Google Scholar] [CrossRef]
- Jiang, K.J.; Zhu, C.S.; Chen, L.L. Unbalance Compensation by Recursive Seeking Unbalance Mass Position in Active Magnetic Bearing-Rotor System. IEEE Trans. Ind. Electron. 2015, 62, 5655–5664. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Zhang, Z. Harmonic vibration suppression for magnetically suspended flywheel with rotor unbalance and sensor runout. AIP Adv. 2018, 8, 105207. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Mo, N.; Zhou, Y.; Shi, Z. Unbalance Compensation and Automatic Balance of Active Magnetic Bearing Rotor System by Using Iterative Learning Control. IEEE Access 2019, 7, 122613–122625. [Google Scholar] [CrossRef]
- Qiao, X.L.; Hu, G.J. Active Control for Multinode Unbalanced Vibration of Flexible Spindle Rotor System with Active Magnetic Bearing. Shock. Vib. 2017, 2017, 9706493. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Xu, L.X. Real-time vibration compensation for active magnetic bearing systems based on LMS algorithm. J. Vib. Eng. 2009, 22, 583–588. [Google Scholar]
- Herzog, R.; Buhler, P.; Gahler, C.; Larsonneur, R. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings. IEEE T Contr. Syst. T 1996, 4, 580–586. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, Q.; Ren, H. Active Balancing Control of AMB-Rotor Systems Using a Phase-Shift Notch Filter Connected in Parallel Mode. IEEE Trans. Ind. Electron. 2016, 63, 3777–3785. [Google Scholar] [CrossRef]
- Peng, C.; Fan, Y.; Huang, Z.; Han, B.; Fang, J. Frequency-varying synchronous micro-vibration suppression for a MSFW with application of small-gain theorem. Mech. Syst. Signal. Pr. 2017, 82, 432–447. [Google Scholar] [CrossRef]
- Xu, X.; Fang, J.; Li, H.; Cui, P. Active suppression of imbalance vibration in the magnetically suspended control moment gyro. J. Vib. Control 2013, 21, 989–1003. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Zheng, S. Suppression of imbalance vibration for AMBs controlled driveline system using double-loop structure. J. Sound Vib. 2015, 337, 1–13. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Han, B. Unbalance vibration suppression for AMBs system using adaptive notch filter. Mech. Syst. Signal. Pr. 2017, 93, 136–150. [Google Scholar] [CrossRef]
- Peng, C.; Zhu, M.; Wang, K.; Ren, Y.; Deng, Z. A Two-Stage Synchronous Vibration Control for Magnetically Suspended Rotor System in the Full Speed Range. IEEE Trans. Ind. Electron. 2020, 67, 480–489. [Google Scholar] [CrossRef]
- Setiawan, J.D.; Mukherjee, R.; Maslen, E.H. Synchronous Sensor Runout and Unbalance Compensation in Active Magnetic Bearings Using Bias Current Excitation. J. Dyn. Syst. Meas. Control 2002, 124, 14–24. [Google Scholar] [CrossRef]
- Cui, P.L.; Li, S.; Wang, Q.R.; Gao, Q.; Cui, J.; Zhang, H.J. Harmonic Current Suppression of an AMB Rotor System at Variable Rotation Speed Based on Multiple Phase-Shift Notch Filters. IEEE Trans. Ind. Electron. 2016, 63, 6962–6969. [Google Scholar] [CrossRef]
- Zhou, K.L.; Wang, D.W.; Zhang, B.; Wang, Y.G. Plug-In Dual-Mode-Structure Repetitive Controller for CVCF PWM Inverters. IEEE Trans. Ind. Electron. 2009, 56, 784–791. [Google Scholar] [CrossRef]
- Han, B.; Lee, J.S.; Kim, M. Repetitive Controller With Phase-Lead Compensation for Cuk CCM Inverter. IEEE Trans. Ind. Electron. 2018, 65, 2356–2367. [Google Scholar] [CrossRef]
- Xu, X.B.; Fang, J.C.; Liu, G.; Zhang, H.J. Model development and harmonic current reduction in active magnetic bearing systems with rotor imbalance and sensor runout. J. Vib. Control 2015, 21, 2520–2535. [Google Scholar] [CrossRef]
- Cui, P.; Li, S.; Zhao, G.; Peng, C. Suppression of Harmonic Current in Active–Passive Magnetically Suspended CMG Using Improved Repetitive Controller. IEEE/ASME Trans. Mechatron. 2016, 21, 2132–2141. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, G. Modified Repetitive Control for Odd Harmonic Current Suppression in Magnetically Suspended Rotor Systems. IEEE Trans. Ind. Electron. 2018, 66, 8008–8018. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, G.; Liu, Z.; Xu, H. Quasi-Resonant Control for Harmonic Current Suppression of a Magnetically Suspended Rotor. IEEE T Power Electr. 2019, 34, 4937–4950. [Google Scholar] [CrossRef]
- Cui, P.L.; Wang, Q.R.; Zhang, G.X.; Gao, Q. Hybrid Fractional Repetitive Control for Magnetically Suspended Rotor Systems. IEEE Trans. Ind. Electron. 2018, 65, 3491–3498. [Google Scholar] [CrossRef]
- Li, J.; Liu, G.; Cui, P.; Zheng, S.; Chen, X. 3/2-Order Dual-Mode Fractional Repetitive Control for Harmonic Vibration Suppression in Magnetically Suspended Rotor. IEEE Sens. J. 2020, 20, 14713–14721. [Google Scholar] [CrossRef]
- Srinivasan, K.; Shaw, F.R. Analysis and Design of Repetitive Control Systems using the Regeneration Spectrum. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990. [Google Scholar]







| Symbol | Parameters | Value | Symbol | Parameters | Value |
|---|---|---|---|---|---|
| m | Rotor mass | 4.8 kg | Low pass coefficient | 0.0001 | |
| Ki | Current stiffness coefficient | 125 N/A | Kh | Displacement stiffness coefficient | 50,000 N/m |
| Kw | Amplifier gain | 0.00004 A/V | N | Differentiator depth coefficient | 10,000 |
| Amplifier time coefficient | 0.0005 | Kp | Proportional coefficient | 3 | |
| Ks | Sensor coefficient | 8000 V/m | Ki | Integration coefficient | 0.1 |
| Kad | Sample gain | 3276.8 V − 1 | Kd | Differential coefficient | 0.012 |
| Symbol | Parameters | Value | Initial Angle |
|---|---|---|---|
| e | Unbalance coefficient | 50 | /6 |
| First sensor runout coefficient | 2 | /5 | |
| Second sensor runout coefficient | 2.2 | /3 | |
| Third sensor runout coefficient | 5 | /8 | |
| Forth sensor runout coefficient | 2 | /4 | |
| Fifth sensor runout coefficient | 8 | /7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Liu, K.; Wei, J.; Zhang, Z. Vibration Force Suppression of Magnetically Suspended Flywheel Based on Compound Repetitive Control. Symmetry 2022, 14, 949. https://doi.org/10.3390/sym14050949
Zeng Y, Liu K, Wei J, Zhang Z. Vibration Force Suppression of Magnetically Suspended Flywheel Based on Compound Repetitive Control. Symmetry. 2022; 14(5):949. https://doi.org/10.3390/sym14050949
Chicago/Turabian StyleZeng, Yuan, Kun Liu, Jingbo Wei, and Zhizhou Zhang. 2022. "Vibration Force Suppression of Magnetically Suspended Flywheel Based on Compound Repetitive Control" Symmetry 14, no. 5: 949. https://doi.org/10.3390/sym14050949
APA StyleZeng, Y., Liu, K., Wei, J., & Zhang, Z. (2022). Vibration Force Suppression of Magnetically Suspended Flywheel Based on Compound Repetitive Control. Symmetry, 14(5), 949. https://doi.org/10.3390/sym14050949






