Analysis of Position, Pose and Force Decoupling Characteristics of a 4-UPS/1-RPS Parallel Grinding Robot
Abstract
:1. Introduction
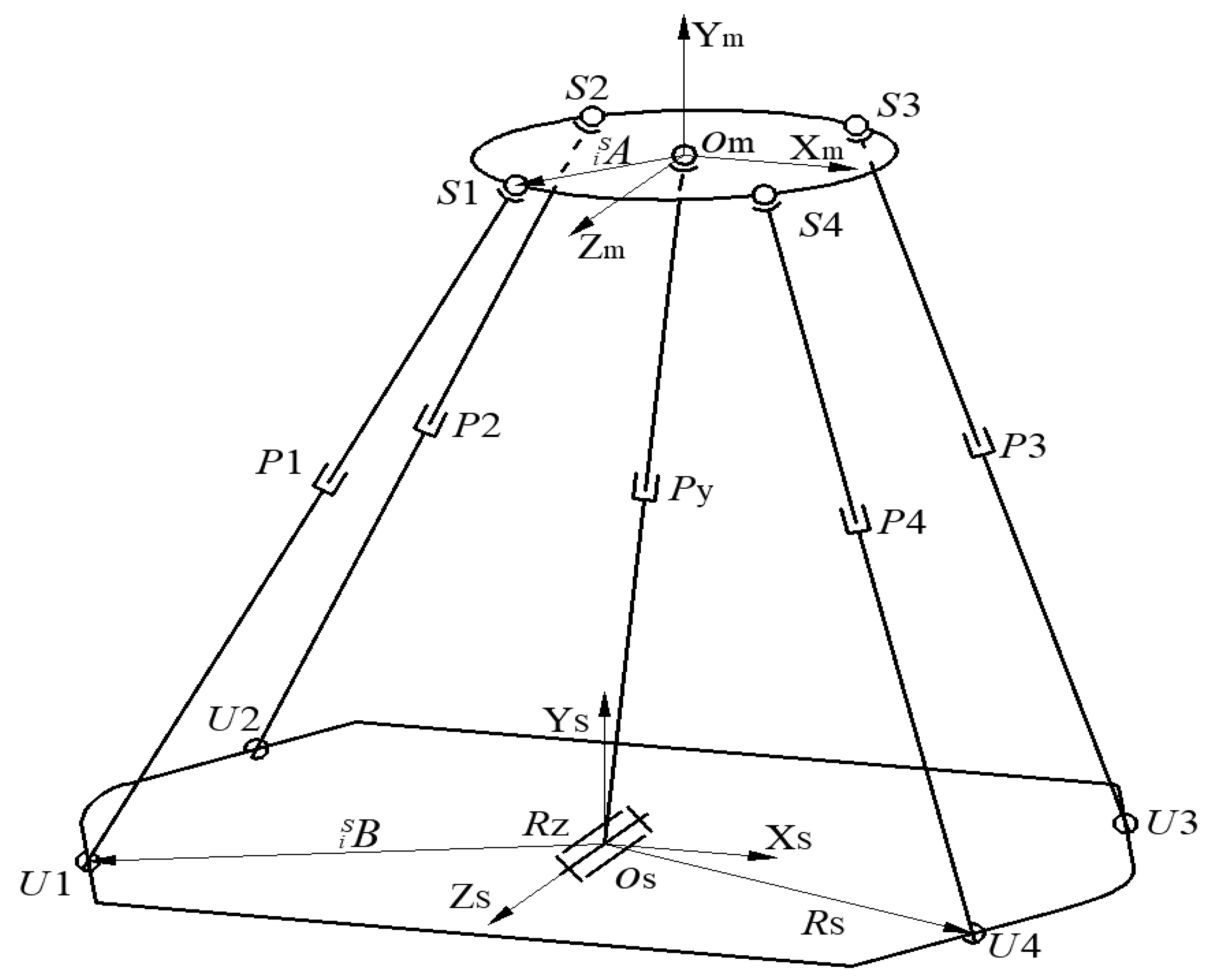
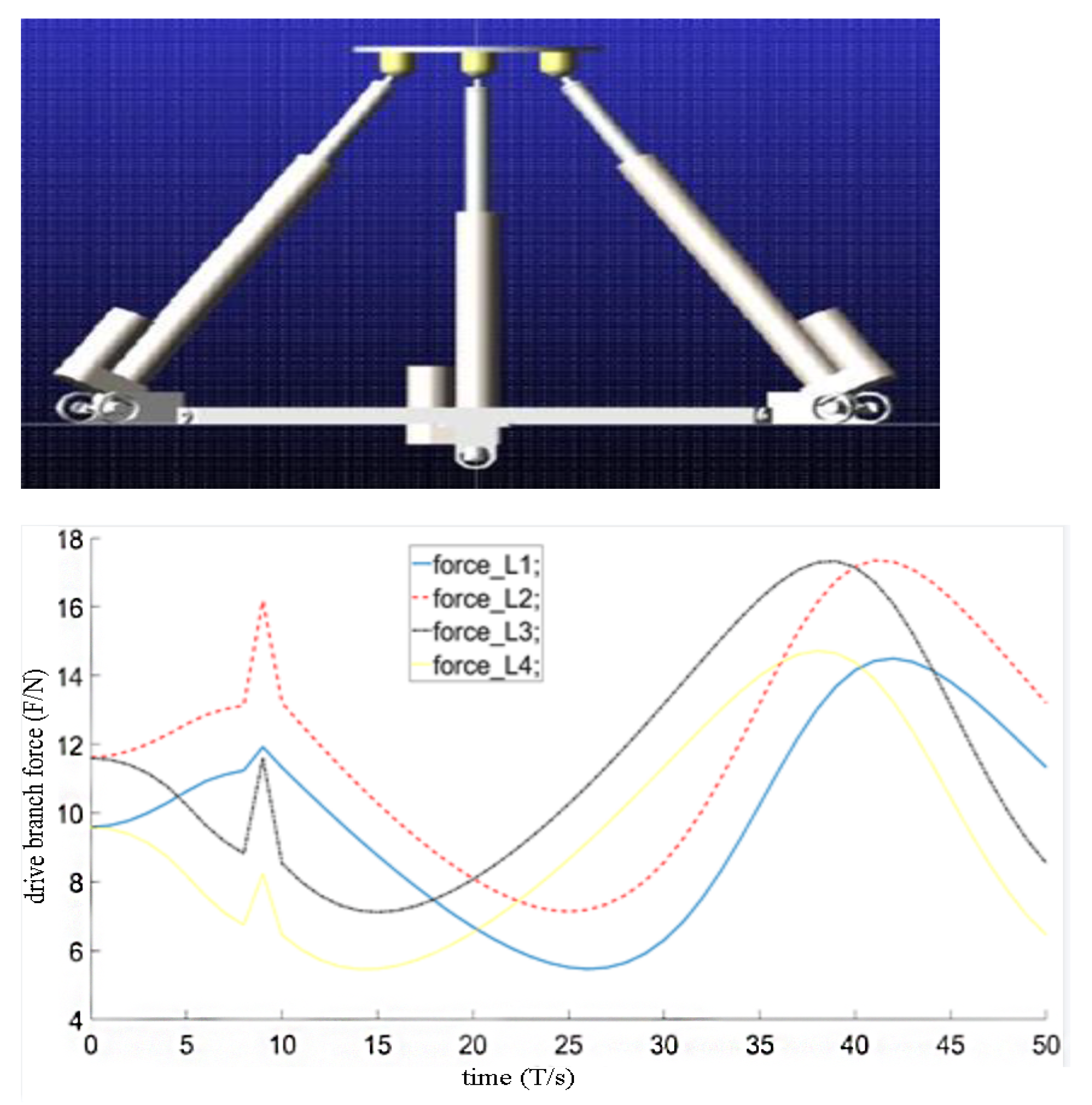
2. Introduction of the Parallel Grinding Robot
3. Analysis of the Characteristics of the Parallel Grinding Robot’s Spatial Poses and Positions
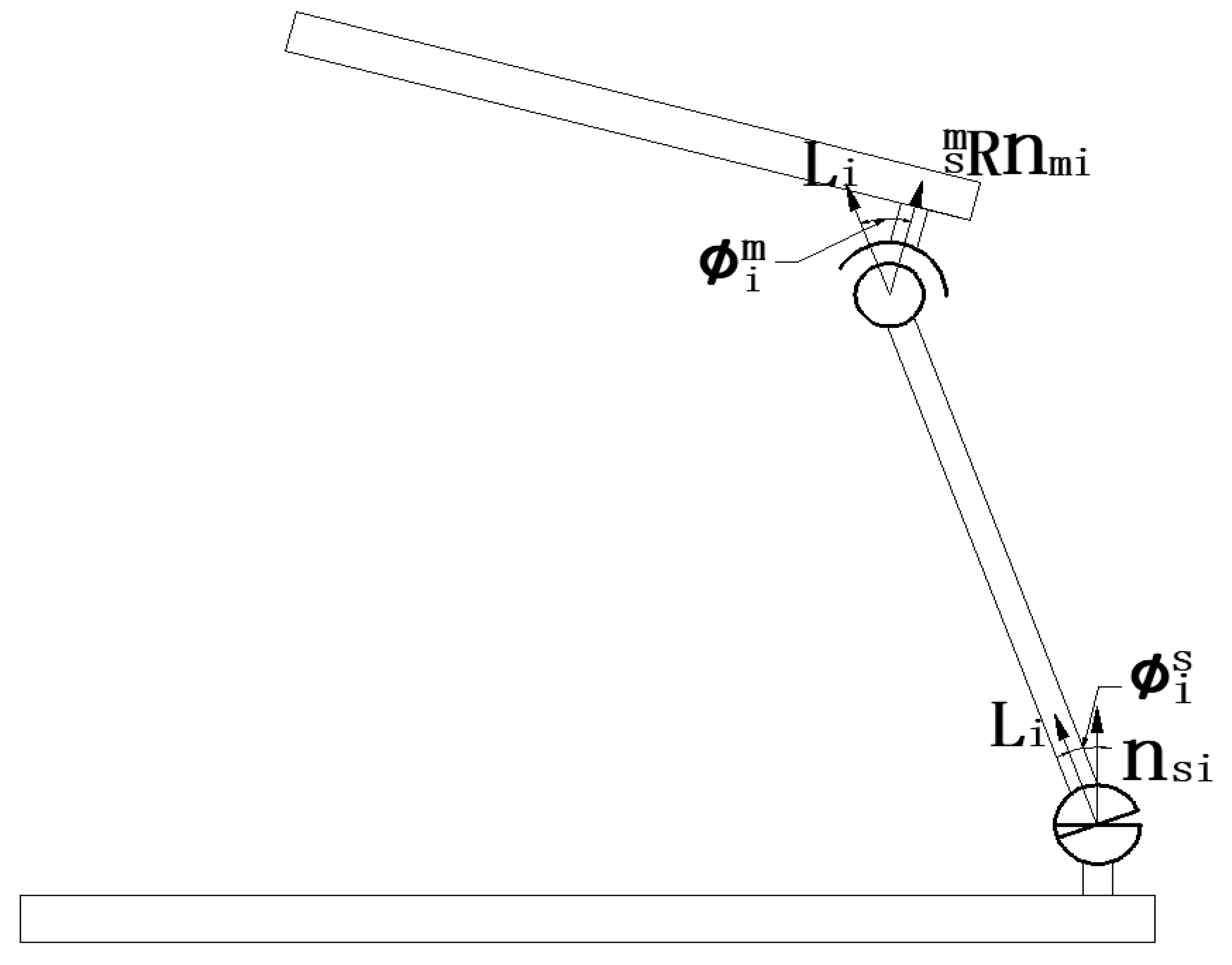
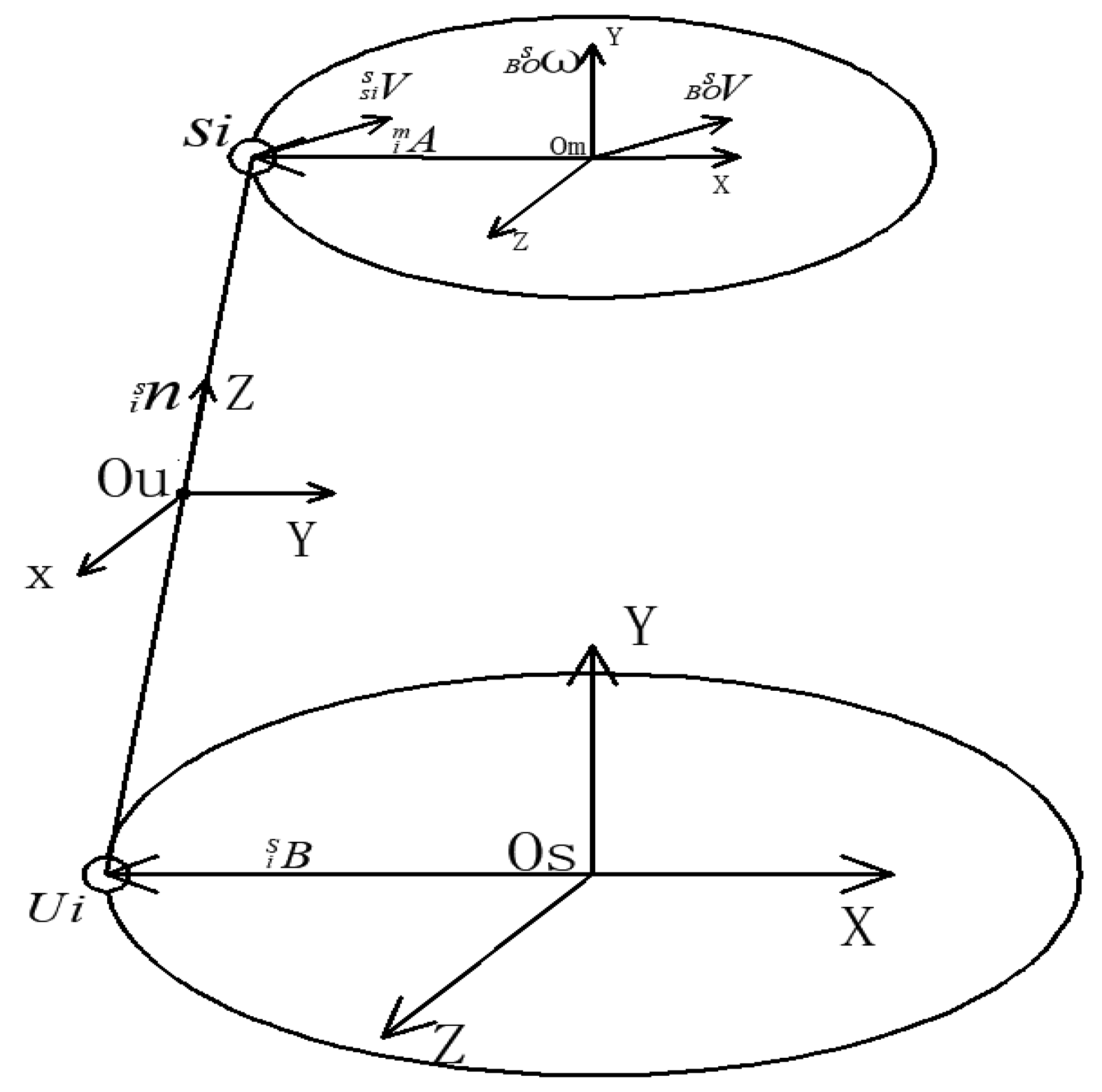
3.1. Constrained Branch DH Analysis
3.2. Inverse Solution Analysis of the Driving Branch (UPS)
3.3. The Analysis of the Workspace of the Parallel Grinding Robot Where Grinding Takes Place
3.3.1. Influencing Factors of Workspace
3.3.2. Analysis of the Spatial Characteristics of the Places Where Grinding Takes Place
3.3.3. Example Calculation
4. Dynamic Modeling and Force Decoupling Analysis
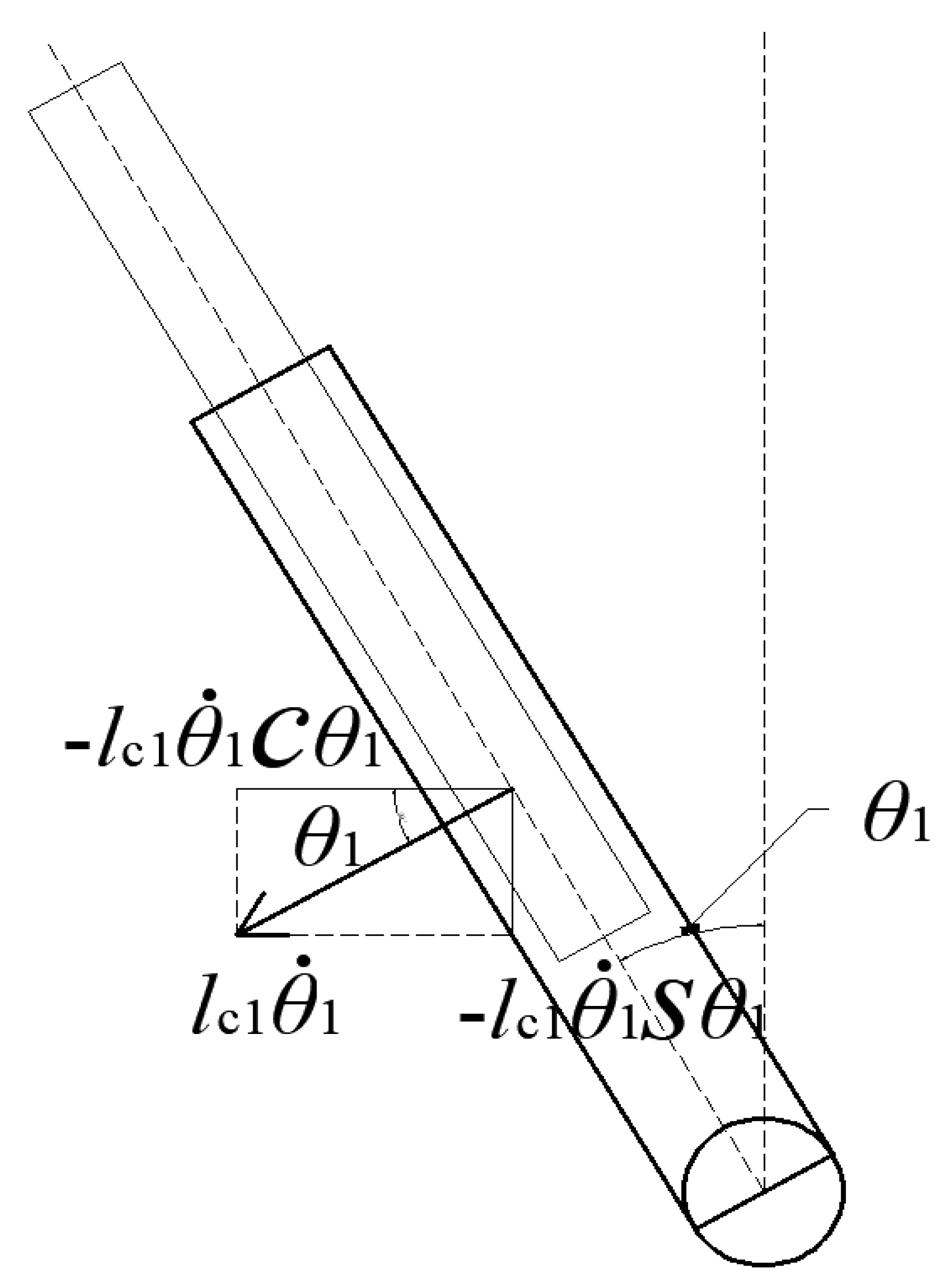
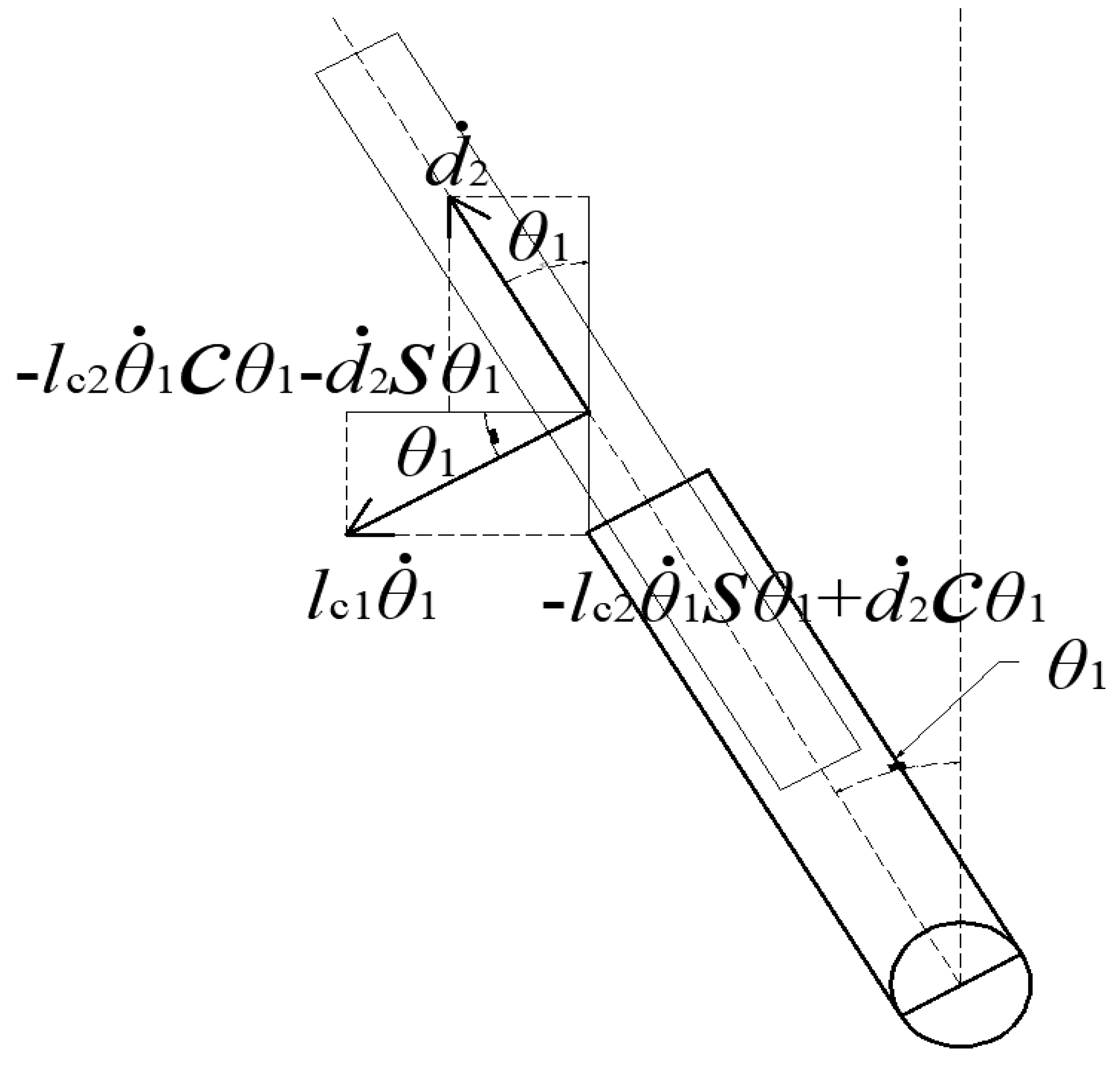
4.1. Kinematic Analysis of the Constraining Branch
4.2. Motion Analysis of the Driving Branch Components
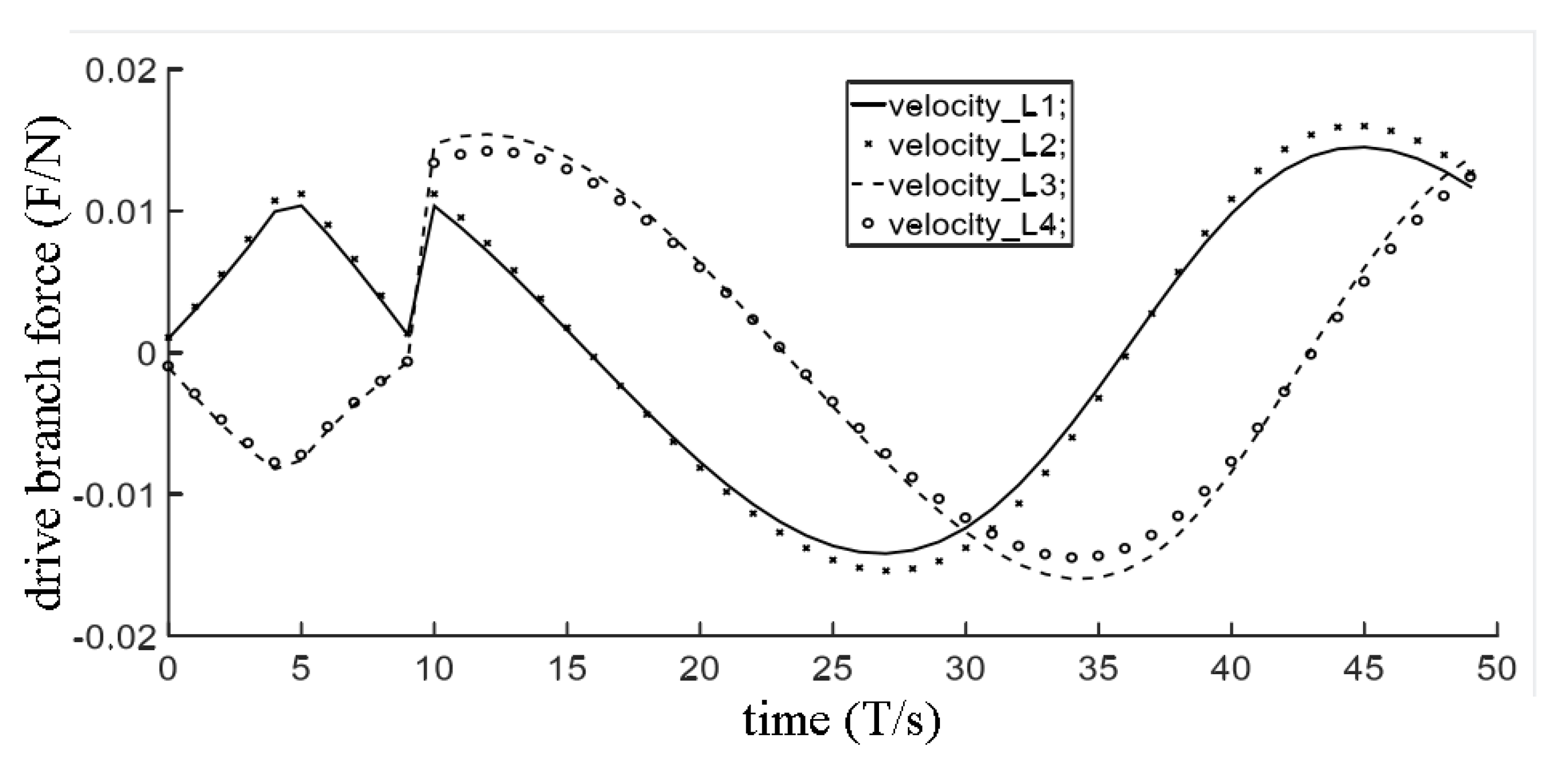
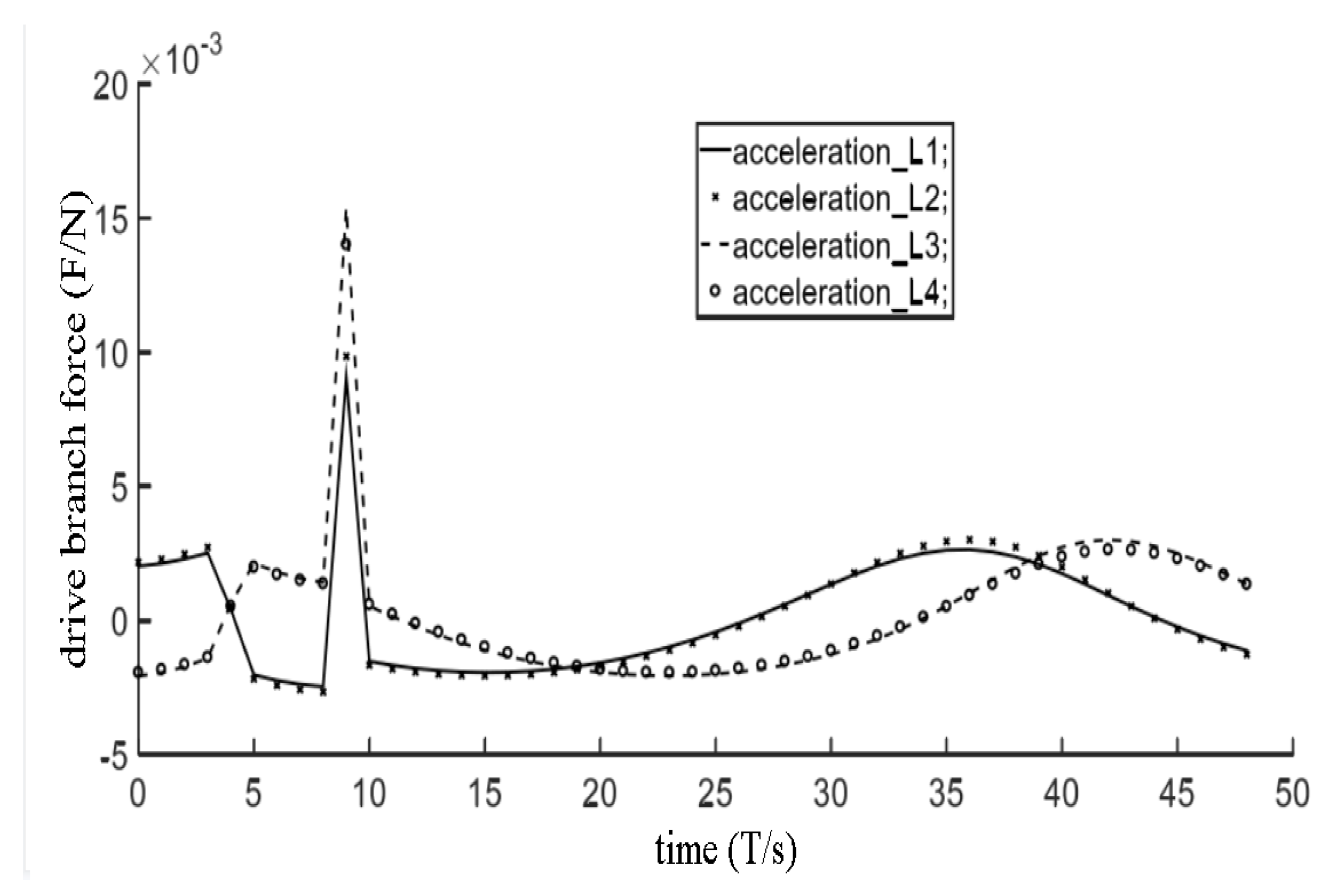
4.3. Analysis of the Mapping Relationship between the Input Velocity of the Stressed Component and the Driving Branch
4.4. Stress Analysis and Model Establishment
4.4.1. Force Analysis
4.4.2. Dynamics Model of the Parallel Grinding Robot
4.5. Decoupling Analysis of Human Types of Parallel Machines
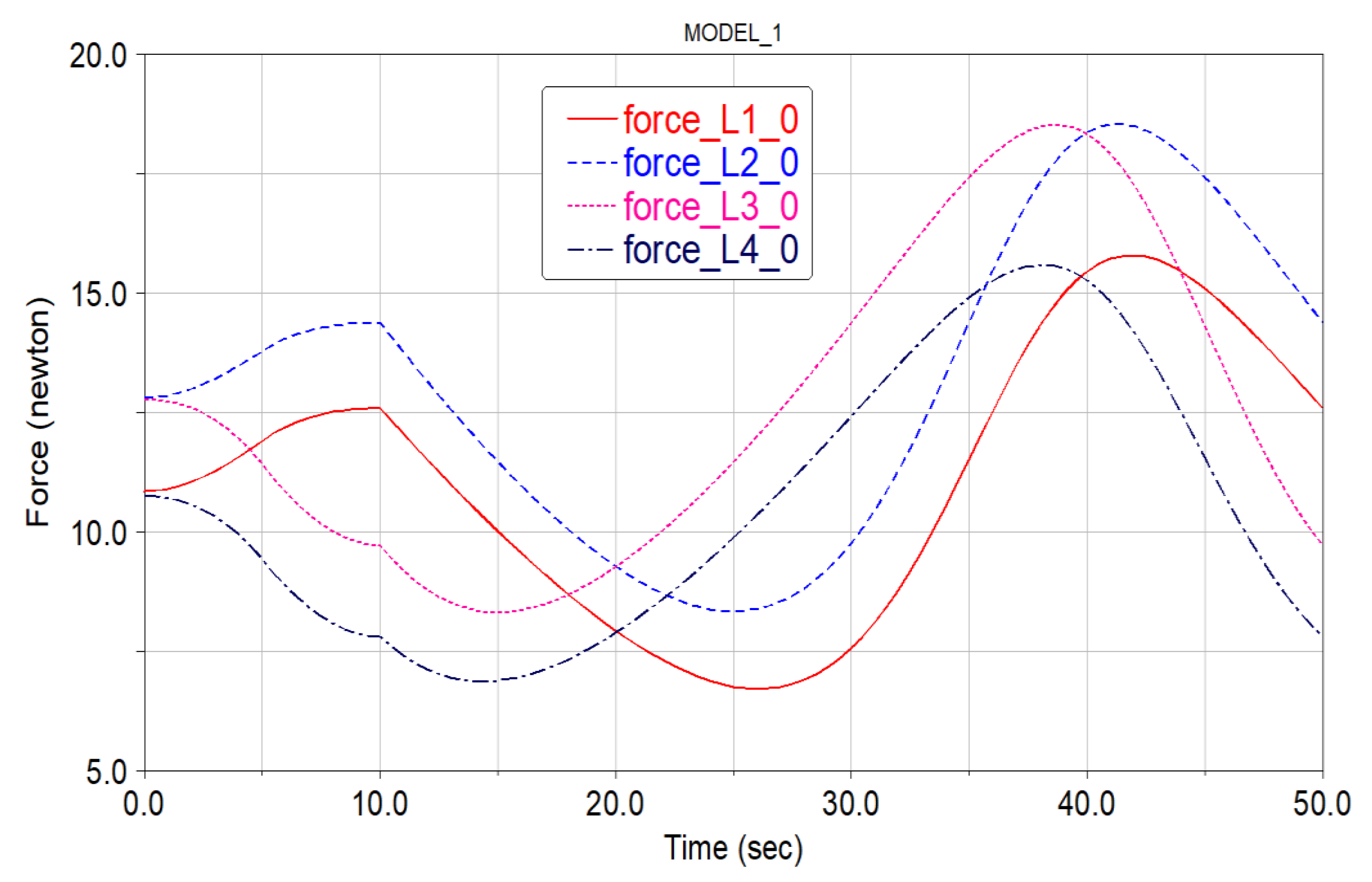
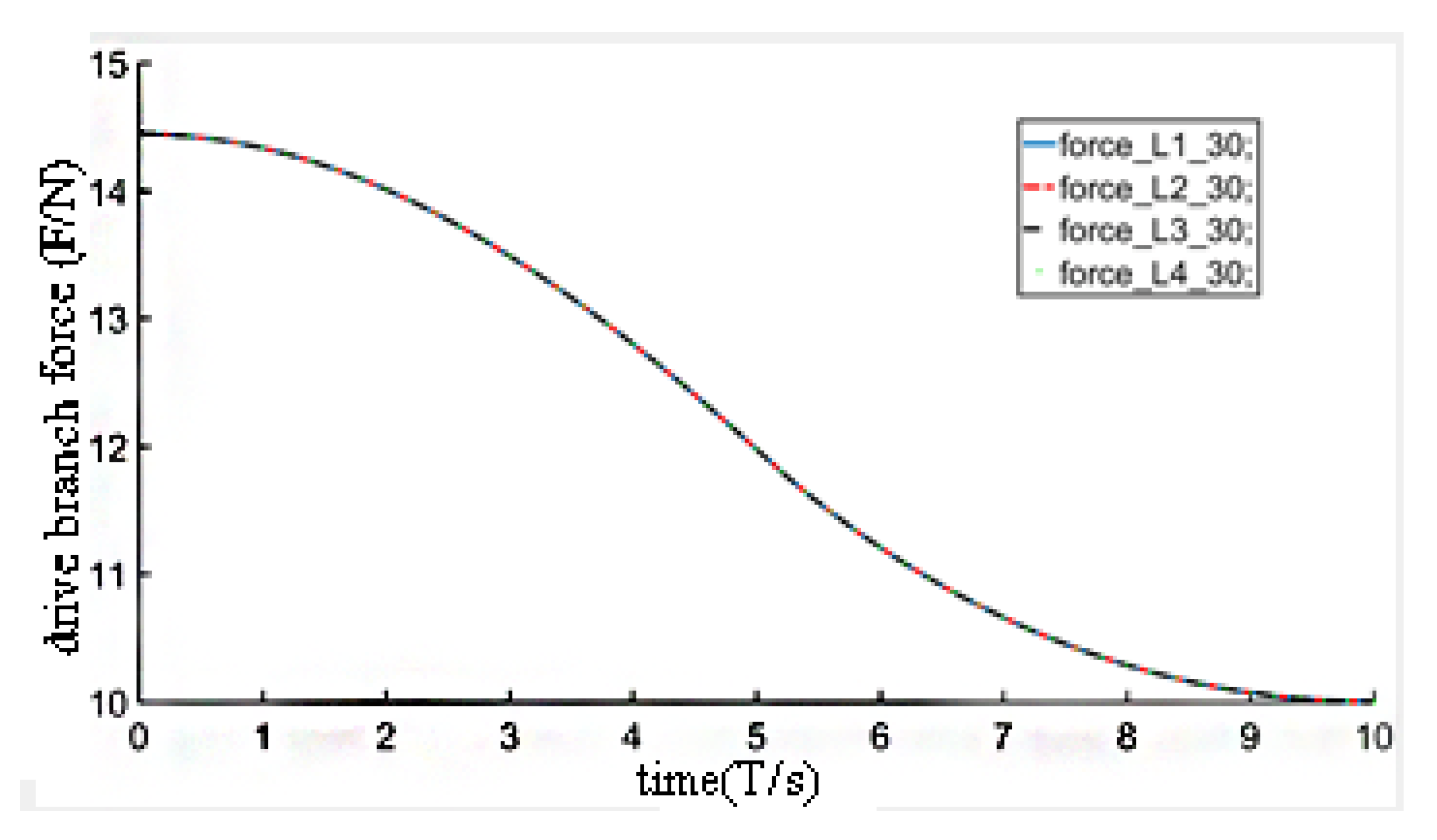
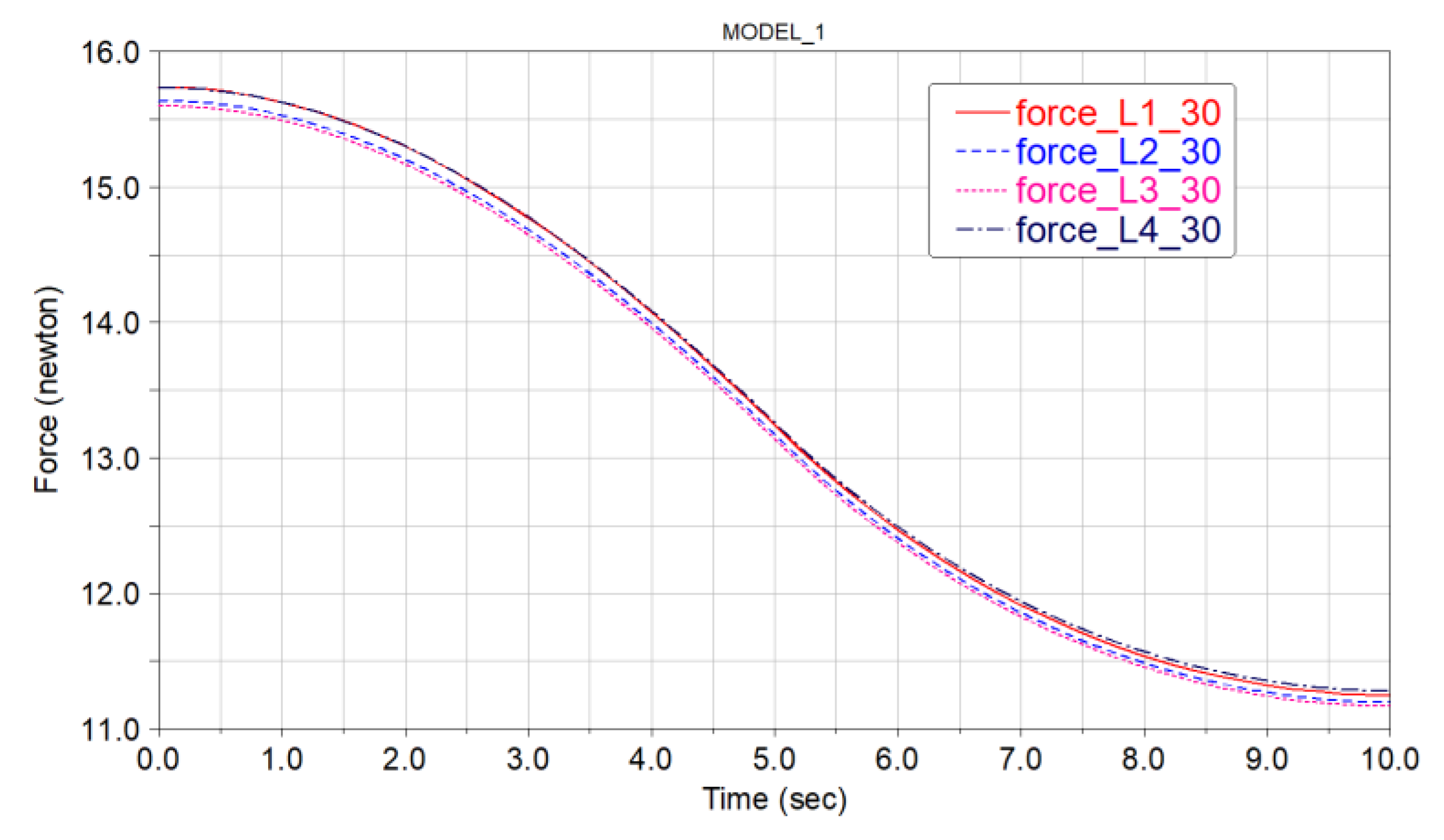
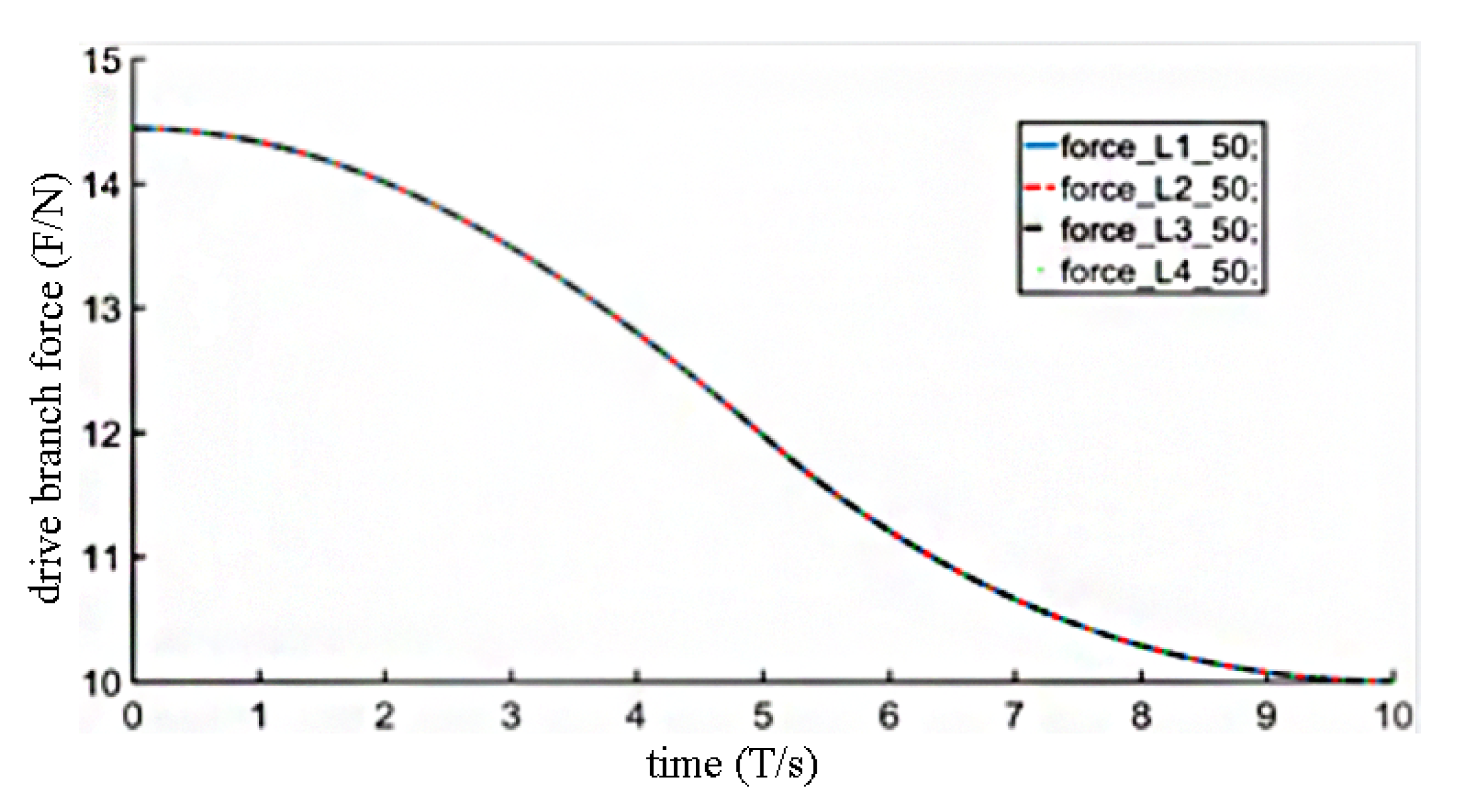
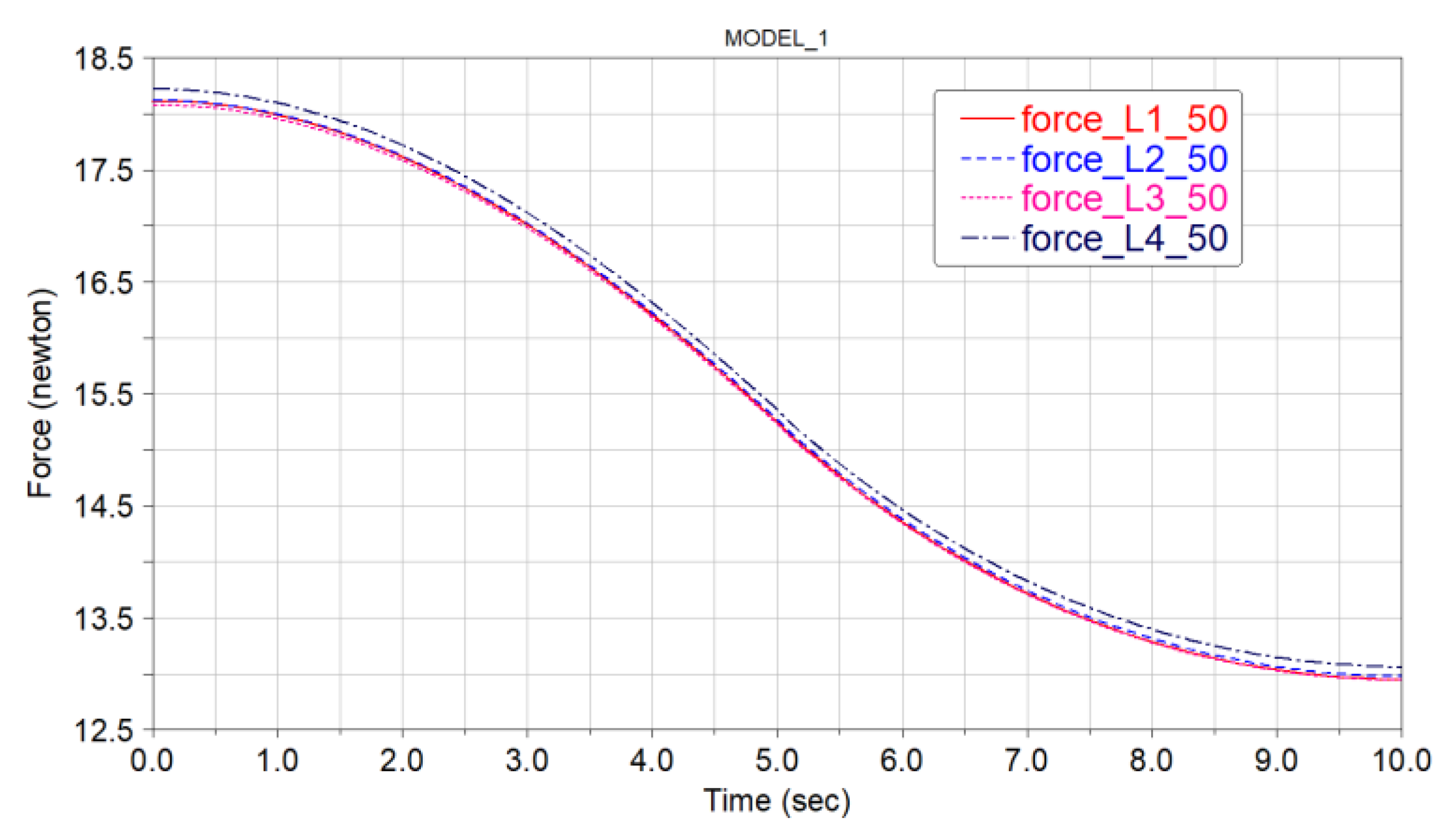
5. Experiments and Results
Experiments and Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gosselin, C.; Schreiber, L.-T. Kinematically Redundant Spatial Parallel Mechanisms for Singularity Avoidance and Large Orientational Workspace. IEEE Trans. Robot. 2016, 32, 286–300. [Google Scholar] [CrossRef]
- Cui, Z.; Tang, X.; Hou, S.; Sun, H.; Wang, D. Calculation and Analysis of Constant Stiffness Space for Redundant Cable-Driven Parallel Robots. IEEE Access 2019, 7, 75407–75419. [Google Scholar] [CrossRef]
- Nabavi, S.N.; Akbarzadeh, A.; Enferadi, J. A Study on Kinematics and Workspace Determination of a General 6- P US Robot. J. Intell. Robot. Syst. 2018, 91, 351–362. [Google Scholar] [CrossRef]
- Qinchuan, Z.Y.Z.K.L.; Xiaojing, T. Kinematics analysis of 5-UPS/PRPU 5-DOF parallel machine tool. Chin. J. Mech. Eng. 2004, 40, 12–16. [Google Scholar]
- Wu, G. Optimal structural design of a Biglide parallel drill grinder. Int. J. Adv. Manuf. Technol. 2017, 90, 2979–2990. [Google Scholar] [CrossRef]
- Xu, P.; Cheung, C.F.; Li, B.; Ho, L.-T.; Zhang, J.-F. Kinematics analysis of a hybrid manipulator for computer controlled ultra-precision freeform polishing. Robot. Comput. Integr. Manuf. 2017, 44, 44–56. [Google Scholar] [CrossRef]
- Tian, H.; Wang, C.; Dang, X.; Sun, L. A 6-DOF parallel bone-grinding robot for cervical disc replacement surgery. Med. Biol. Eng. Comput. 2017, 55, 2107–2121. [Google Scholar] [CrossRef] [PubMed]
- Mei, B.; Xie, F.; Liu, X.J.; Yang, C. Elasto-geometrical error modeling and compensation of a five-axis parallel machining robot. Precis. Eng. 2021, 69, 48–61. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, Y.; Zhao, T. Higher Space Institutional Science; Higher Education Press: Beijing, China, 2006; pp. 89–166. [Google Scholar]
- Zhang, W.; Bai, X.; Xu, Z. Study on experimental method of end effector pose setting for indexing mechanism of space station. Mach. Des. 2018, 35, 89–94. [Google Scholar]
- Dou, Y.; Yao, J.; Gao, S.; Han, X.; Liu, X.; Zhao, Y. Dynamic modeling and driving force coordinated distribution of redundant drive parallel robots. Trans. Chin. Soc. Agric. Mach. 2014, 45, 293–300. [Google Scholar]
- Lin, W.; Li, B.; Yang, X.; Zhang, D. Modelling and Control of inverse Dynamics for a 5-DOF Parallel Kinematic Polishing Machine. Int. J. Adv. Robot. Syst. 2013, 10, 314. [Google Scholar] [CrossRef]
- Kanaan, D.; Wenger, P.; Chablat, D. Kinematic Analysis of a Serial-Parallel Machine Tool: The Verne Machine. Mech. Mach. Theory 2009, 44, 487–498. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhao, Y.; Jin, Y. Kinetostatic-Model-Based Stiffness Analysis of Exechon PKM. Robot. Comput. Integr. Manuf. 2016, 37, 208–220. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Xu, P.; Yang, D.; Liu, H. Stiffness Analysis of a 3CPS Parallel Manipulator for Mirror Active Adjusting Platform in Segmented Telescope. Robot. Comput. Integr. Manuf. 2013, 29, 302–311. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y.; Meng, Q. Mobility Analysis of a 3-PUU Flexure-Based Manipulator Based on Screw Theory and Compliance Matrix Method. Int. J. Precis. Eng. Manuf. 2013, 14, 1345–1353. [Google Scholar] [CrossRef]










| The Serial Number of Each Kinematic Pair i | The Length of Each Link ai | The Torsion Angle αi | The Offset Distance of Each Link di | The Angle of Rotation of Each Link θi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | ||
| 3 | 0 | 0 | ||
| 4 | 0 | 0 | ||
| 5 | 0 | 0 |
| Parameter | Numerical Value |
|---|---|
| Moving platform radius R/m | 0.1 |
| Universal joint position circle radius Rs/m | 0.335 |
| The angle between the center of the fixed platform and U1 and U2 is | 53° |
| The angle between the center of the fixed platform and U2 and U3 is | 127° |
| Distance from fixed platform center to the axis of the revolute pair /m | 0.05 |
| Distance between the grinding point and the moving platform center /m | 0.075 |
| Limit positions of each driving branch , /m | (0.43, 0.68) |
| Limit positions of the constraining branch | (0.32, 0.55) |
| Limit rotation angles of each revolute pair /rad | (−π/3, π/3) |
| Limit rotation angles of each spherical pair , /rad | (−π/4, π/4) |
| Limit rotation angles of each universal joint /rad | (−π/4, π/4) |
| Cylinder diameter D/m | 0.035 |
| Structural Parameters or Characteristics | Value/Unit |
|---|---|
| The mass of the moving platform, | 3.593 kg |
| The mass of the cylinder block of the constraining branch (RPS), | 1.311 kg |
| The mass of. The mass of the cylinder block of each driving branch (UPS), | 1.458 kg |
| The mass of linear moving link of the driving branch (UPS) is | 0.255 kg |
| The rotational inertia of the moving platform around X-axis | 3.30 × 10 −3 kg∙ |
| The rotational inertia of the moving platform around Y-axis | 17.79 × 10 −3 kg∙ |
| The rotational inertiaof the moving platform around Z-axis | 16.28 × 10 −3 kg∙ |
| The rotational inertia of the cylinder block of the constraining branch (RPS) around X-axis | 8.94 × 10 −3 kg∙ |
| The rotational inertia of the cylinder block of the constraining branch (RPS) around Y-axis | 0.67 × 10 −3 kg∙ |
| The rotational inertia of the cylinder block of the constraining branch (RPS) | 9.34 × 10 −3 kg∙ |
| The rotational inertia of the linear moving link of the constraining branch (RPS) around the X-axis | 1.14 × 10 −3 kg∙ |
| The rotational inertia of the linear moving link of the constraining branch (RPS) around Y-axis | 1.14 × 10 −3 kg∙ |
| The rotational inertia of the linear moving link of the constraining branch (RPS) around Z-axis | 0.011 × 10 −3 kg∙ |
| The rotational inertia of the cylinder block of the driving branch (UPS) around X-axis | 15.34 × 10 −3 kg∙ |
| The rotational inertia of the cylinder block of the driving branch (UPS) around Y-axis | 14.92 × 10 −3 kg∙ |
| The rotational inertia of the cylinder block of the driving branch (UPS) around Z-axis | 0.72 × 10 −3 kg∙ |
| The rotational inertia of the linear moving link of the driving branch (UPS) around X-axis | 1.95 × 10 −3 kg∙ |
| The rotational inertia of the linear moving link of the driving branch (UPS) around Y-axi | 1.95 × 10 −3 kg∙ |
| The rotational inertia of the linear moving link of the driving branch (UPS) around Z-axis | 0.013 × 10 −3 kg∙ |
| Centroid distance of the cylinder block of the constraining branch (RPS) | 0.133 m |
| Centroid distance of the linear moving link of the (RPS) | 0.198 m |
| Centroid distance of the cylinder block of the driving branch (UPS) | 0.063 m |
| Centroid distance of the linear moving link of the driving branch (UPS) | 0.155 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liang, F.; Zhou, H.; Yang, M.; Wang, Q. Analysis of Position, Pose and Force Decoupling Characteristics of a 4-UPS/1-RPS Parallel Grinding Robot. Symmetry 2022, 14, 825. https://doi.org/10.3390/sym14040825
Wang J, Liang F, Zhou H, Yang M, Wang Q. Analysis of Position, Pose and Force Decoupling Characteristics of a 4-UPS/1-RPS Parallel Grinding Robot. Symmetry. 2022; 14(4):825. https://doi.org/10.3390/sym14040825
Chicago/Turabian StyleWang, Jun, Fei Liang, Hongjun Zhou, Mingquan Yang, and Quan Wang. 2022. "Analysis of Position, Pose and Force Decoupling Characteristics of a 4-UPS/1-RPS Parallel Grinding Robot" Symmetry 14, no. 4: 825. https://doi.org/10.3390/sym14040825
APA StyleWang, J., Liang, F., Zhou, H., Yang, M., & Wang, Q. (2022). Analysis of Position, Pose and Force Decoupling Characteristics of a 4-UPS/1-RPS Parallel Grinding Robot. Symmetry, 14(4), 825. https://doi.org/10.3390/sym14040825






