Longitudinal Wave Locally Resonant Band Gaps in Metamaterial-Based Elastic Rods Comprising Multi-Degree-of-Freedom DAVI Resonators
Abstract
:1. Introduction
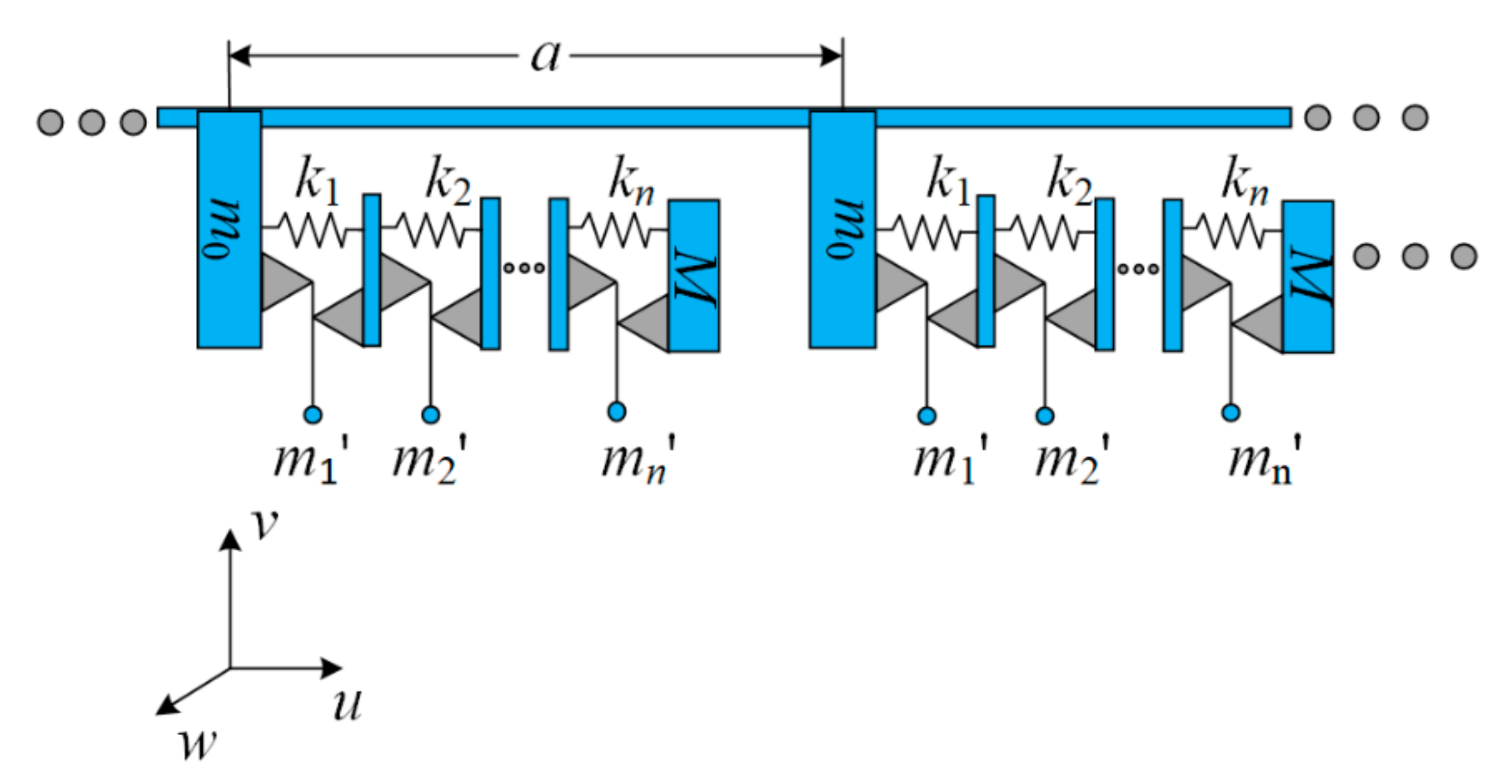
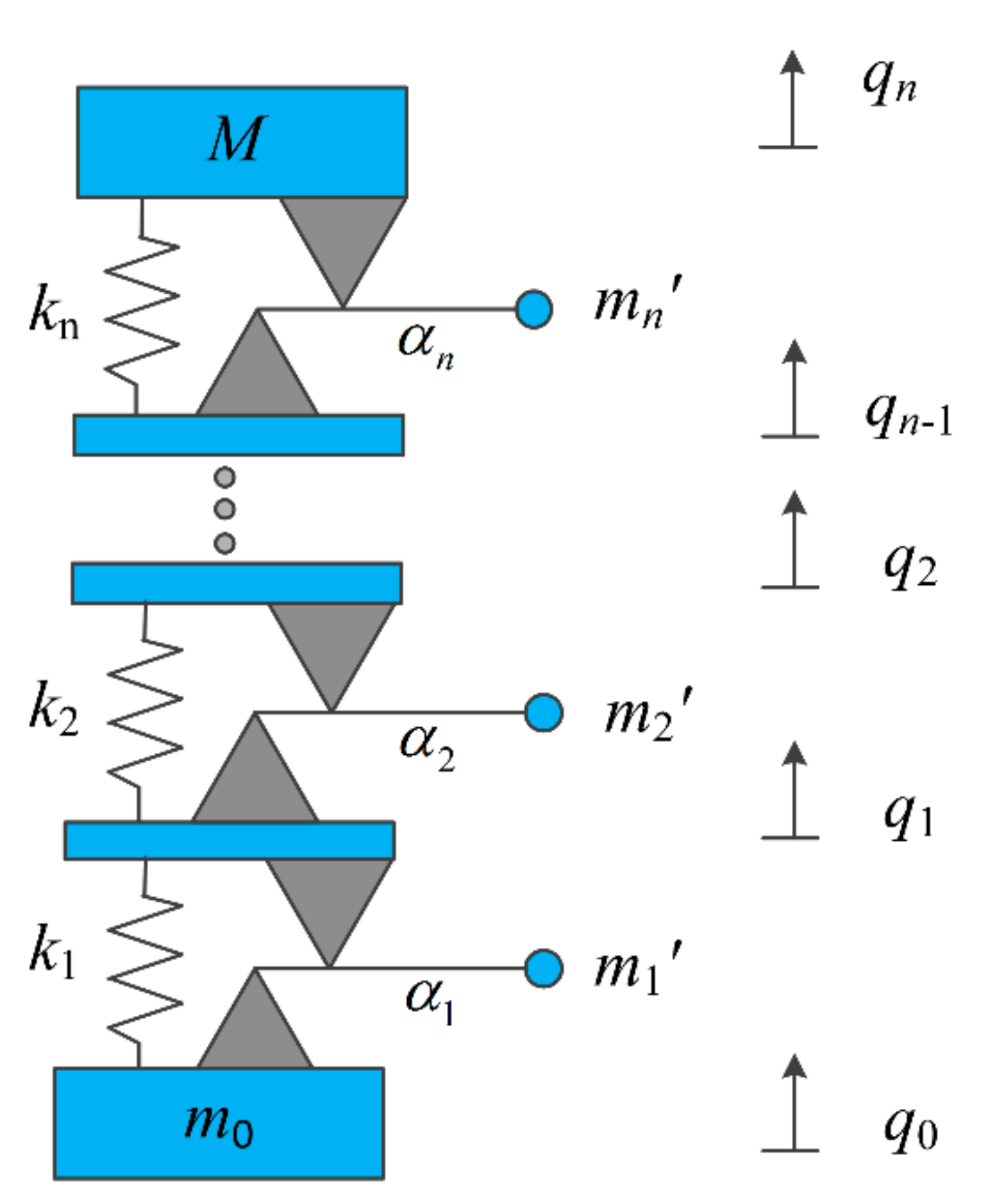
2. The Model and Bandwidth Formulations
2.1. Wave Propagation in an Infinite Periodic System
- i.
- The connection between the resonator and the rod is rigid and massless, and the lever is massless and rigid;
- ii.
- The damping and the friction in the hinge are negligible and the spring is massless, linear, and undamped;
- iii.
- The mass of the stage is negligible and the load mass is rigid;
- iv.
- The amplitude of the vibration is small.
- i.
- un (x, t) represents the longitudinal displacement at the position x and time t;
- ii.
- E and ρ are the Young’s modulus and the density of the rod;
- iii.
- A is the cross-section area of the rod.
- i.
- is the wave number in the rod;
- ii.
- and are constants determined by the boundary conditions.
- (a)
- When and , the corresponding frequency range are band gaps or stop bands, and the phase change of the wave is between 0 and π;
- (b)
- When and , the corresponding frequency range are pass bands, and the phase change range of the wave is between 0 and π.
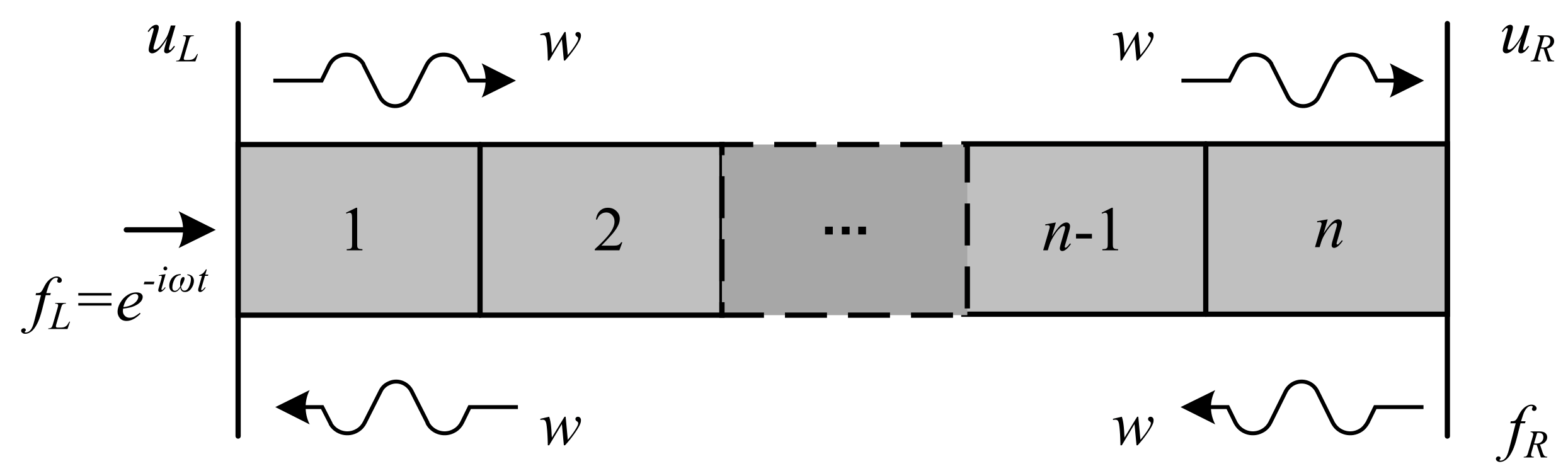
2.2. Vibration Transmission in a Finite Periodic Structure
3. Results and Discussions
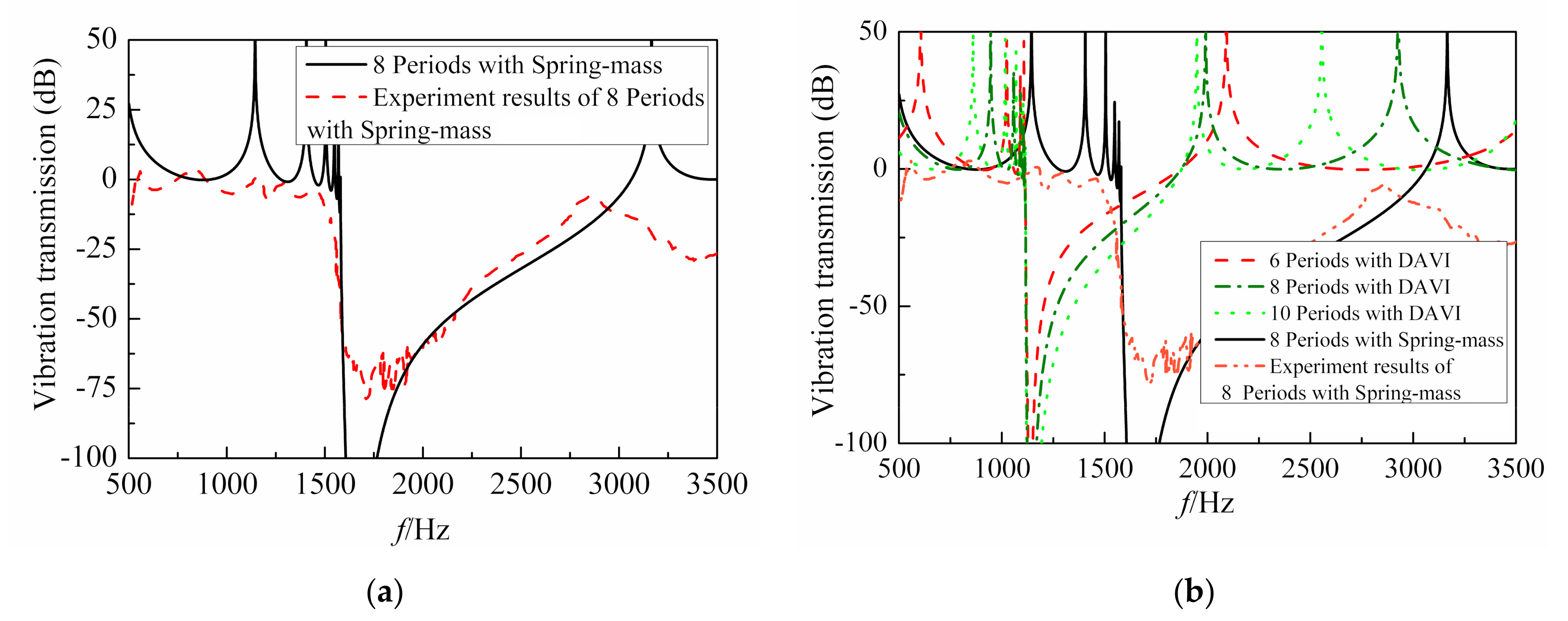
3.1. Illustrative Examples
3.2. Band Gap Formation Mechanisms
3.3. The Optimization Problem
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Spacing of resonators |
| A | Cross-section area of the rod |
| c | Speed of the elastic wave in the matrix material |
| E | Young’s modulus of the rod |
| F0 | Reaction force at attachment point between resonator and periodic structure |
| Fi | External force acting on the i-th stage |
| F | Force vector |
| i | Index |
| I | Imaginary unit |
| k | Stiffness of a single degree-of-freedom dynamic anti-resonant vibration isolator |
| ki | Stiffness of i-th spring of the i-th isolator |
| K | Stiffness matrix |
| l1 | Lever length of the lever in the case of a single-degree-of-freedom lever type anti-resonant vibration isolator |
| l2 | Distance between two pivot points in the case of a single-degree-of-freedom lever type anti-resonant vibration isolator |
| m0 | Lumped mass at attachment point between resonator and periodic structure |
| mis | Isolator mass |
| ith isolator mass of the multi-degree-of-freedom resonator | |
| M | Load mass |
| M | Mass matrix |
| Integral constant of the i-th rod | |
| Integral constant of the i-th rod | |
| q0 | Displacement at the attachment point |
| q | Wave vector |
| q | Displacement vector |
| qi | Displacement of the i-th isolator stage |
| S0 | Dynamic stiffness of resonator at the attachment point between the resonator and the rod |
| t | Time |
| T | Displacement transmissibility |
| u(x,t) | Longitudinal displacement at position x and time t |
| x | Global coordinate |
| α | Lever ratio of a single-degree-of freedom lever-type anti-resonant vibration isolator |
| αi | Lever ratio of the i-th isolator stage in a multi-degree-of-freedom lever type anti-resonant vibration isolator |
| β | Wave number |
| ρ | Density of the rod |
| ω | Circular frequency |
References
- Sigalas, M.; Kushwaha, M.S.; Economou, E.N.; Kafesaki, M.; Psarobas, I.E.; Steurer, W. Classical vibrational modes in phononic lattices: Theory and experiment. Zeitschrift für Kristallographie-Cryst. Mater. 2005, 220, 765–809. [Google Scholar] [CrossRef]
- Xiao, Y.; Mace, B.R.; Wen, J.; Wen, X. Formation and coupling of band gaps in a locally resonant elastic system comprising a string with attached resonators. Phys. Lett. A 2011, 375, 1485–1491. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Yadav, A.; Gerislioglu, B.; Ahmadivand, A.; Kaushik, A.; Cheng, G.J.; Ouyang, Z.; Wang, Q.; Yadav, V.S.; Mishra, Y.K.; Wu, Y.; et al. Controlled self-assembly of plasmon-based photonic nanocrystals for high performance photonic technologies. Nano Today 2021, 37, 101072. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Wang, G.; Cai, L.; Qiu, J. Low frequency torsional vibration gaps in the shaft with locally resonant structures. Phys. Lett. A 2006, 348, 410–415. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, B.M.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 083049. [Google Scholar] [CrossRef]
- Goffaux, C.; Sánchez-Dehesa, J.; Yeyati, A.L.; Lambin, P.; Khelif, A.; Vasseur, J.O.; Djafari-Rouhani, B. Evidence of fano-like interference phenomena in locally resonant materials. Phys. Rev. Lett. 2002, 88, 225502. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Chan, C.T.; Sheng, P. Three-component elastic wave band-gap material. Phys. Rev. B 2002, 65, 165116. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Wen, X.; Wen, J.; Shao, L.; Liu, Y. Two-dimensional locally resonant phononic crystals with binary structures. Phys. Rev. Lett. 2004, 93, 154302. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.; Wen, X. Quasi-one-dimensional phononic crystals studied using the improved lumped-mass method: Application to locally resonant beams with flexural wave band gap. Phys. Rev. B 2005, 71, 104302. [Google Scholar] [CrossRef]
- Hsu, J.C.; Wu, T.T. Lamb waves in binary locally resonant phononic plates with two-dimensional lattices. Appl. Phys. Lett. 2007, 90, 201904. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Dai, H.M.; Chan, N.H.; Ma, G.C.; Sheng, P. Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl. Phys. Lett. 2010, 96, 041906. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Modeling acoustic metamaterials based on reused buttons using data fitting with neural network. J. Acoust. Soc. Am. 2021, 150, 51–63. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Membrane-type acoustic metamaterial using cork sheets and attached masses based on reused materials. Appl. Acoust. 2022, 189, 108605. [Google Scholar] [CrossRef]
- Milton, G.W.; Briane, M.; Willis, J.R. On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 2006, 8, 248. [Google Scholar] [CrossRef]
- Sukhovich, A.; Jing, L.; Page, J.H. Negative refraction and focusing of ultrasound in two-dimensional phononic crystals. Phys. Rev. B 2008, 77, 014301. [Google Scholar] [CrossRef]
- Norris, A.N. Acoustic cloaking theory. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2008, 464, 2411–2434. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez-Dehesa, J. Acoustic cloaking in two dimensions: A feasible approach. New J. Phys. 2008, 10, 063015. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Xia, C.; Fang, N. Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 2011, 106, 024301. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Wen, X.; Wen, J.; Liu, Y. Quasi-one-dimensional periodic structure with locally resonant band gap. J. Appl. Mech. 2006, 73, 167–170. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.; Wen, X. Longitudinal wave band gaps in metamaterial-based elastic rods containing multi-degree-of-freedom resonators. New J. Phys. 2012, 14, 033042. [Google Scholar] [CrossRef]
- Song, Y.; Wen, J.; Yu, D.; Liu, Y.; Wen, X. Reduction of vibration and noise radiation of an underwater vehicle due to propeller forces using periodically layered isolators. J. Sound Vib. 2014, 333, 3031–3043. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, K.; Xu, D.; Ouyang, H. Multi-low-frequency flexural wave attenuation in Euler–Bernoulli beams using local resonators containing negative-stiffness mechanisms. Phys. Lett. A 2017, 381, 3141–3148. [Google Scholar] [CrossRef]
- Zhou, J.; Dou, L.; Wang, K.; Xu, D.; Ouyang, H. A nonlinear resonator with inertial amplification for very low-frequency flexural wave attenuations in beams. Nonlinear Dyn. 2019, 96, 647–665. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Xu, D.; Ouyang, H. Lower band gaps of longitudinal wave in a one-dimensional periodic rod by exploiting geometrical nonlinearity. Mech. Syst. Signal Process. 2019, 124, 664–678. [Google Scholar] [CrossRef]
- Cai, C.; Zhou, J.; Wu, L.; Wang, K.; Xu, D.; Ouyang, H. Design and numerical validation of quasi-zero-stiffness metamaterials for very low-frequency band gaps. Compos. Struct. 2020, 236, 111862. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Ouyang, H.; Cheng, L.; Xu, D. A semi-active metamaterial beam with electromagnetic quasi-zero-stiffness resonators for ultralow-frequency band gap tuning. Int. J. Mech. Sci. 2020, 176, 105548. [Google Scholar] [CrossRef]
- Flannelly, W.G. Dynamic Antiresonant Vibration Isolator. U.S. Patent 3,322,379, 30 May 1967. [Google Scholar]
- Liu, N.; Li, C.; Yin, C.; Dong, X.; Hua, H. Application of a dynamic antiresonant vibration isolator to minimize the vibration transmission in underwater vehicles. J. Vib. Control 2018, 24, 3819–3829. [Google Scholar] [CrossRef]
- Wells, D.A. Theory and Problems of Lagrangian Dynamics; Schaum-Publishing: Mequon, WI, USA, 1967. [Google Scholar]
- Rao, S.S. Vibration of Continuous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Mead, D.J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling. J. Sound Vib. 1973, 27, 235–260. [Google Scholar] [CrossRef]
- Downing, C.A.; Saroka, V.A. Exceptional points in oligomer chains. Commun. Phys. 2021, 4, 254. [Google Scholar] [CrossRef]


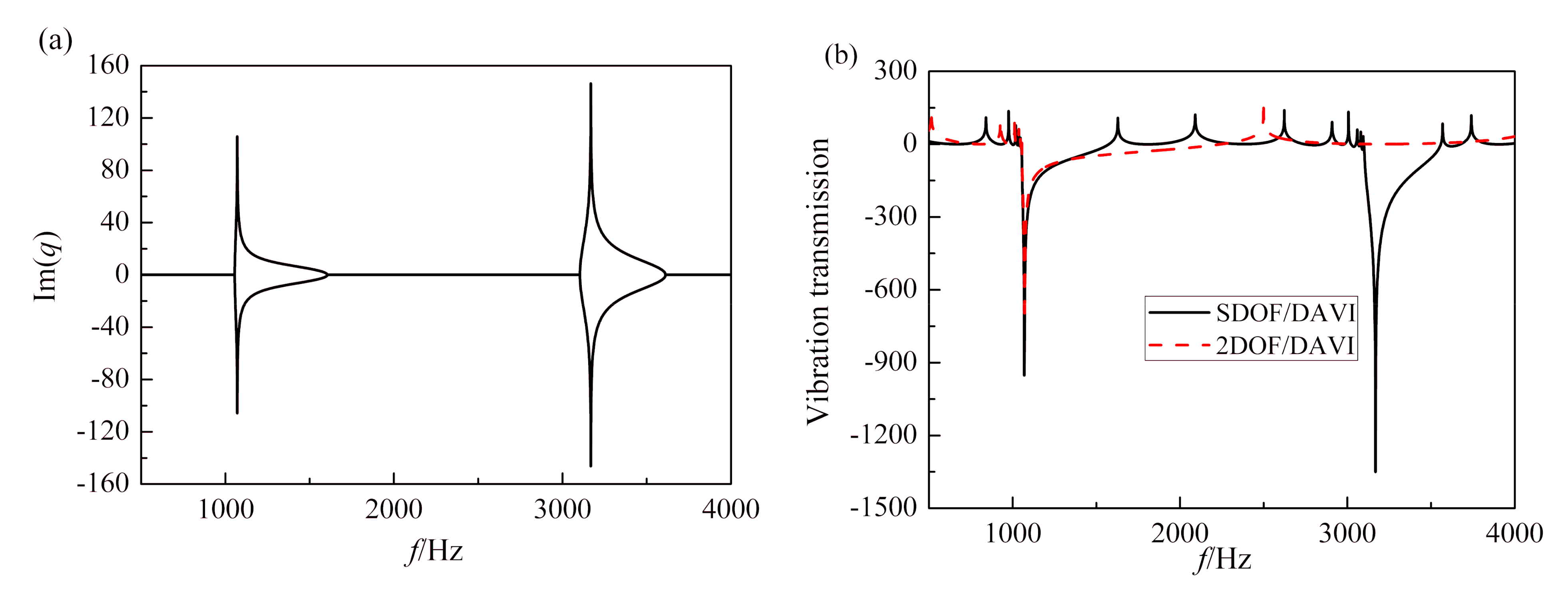

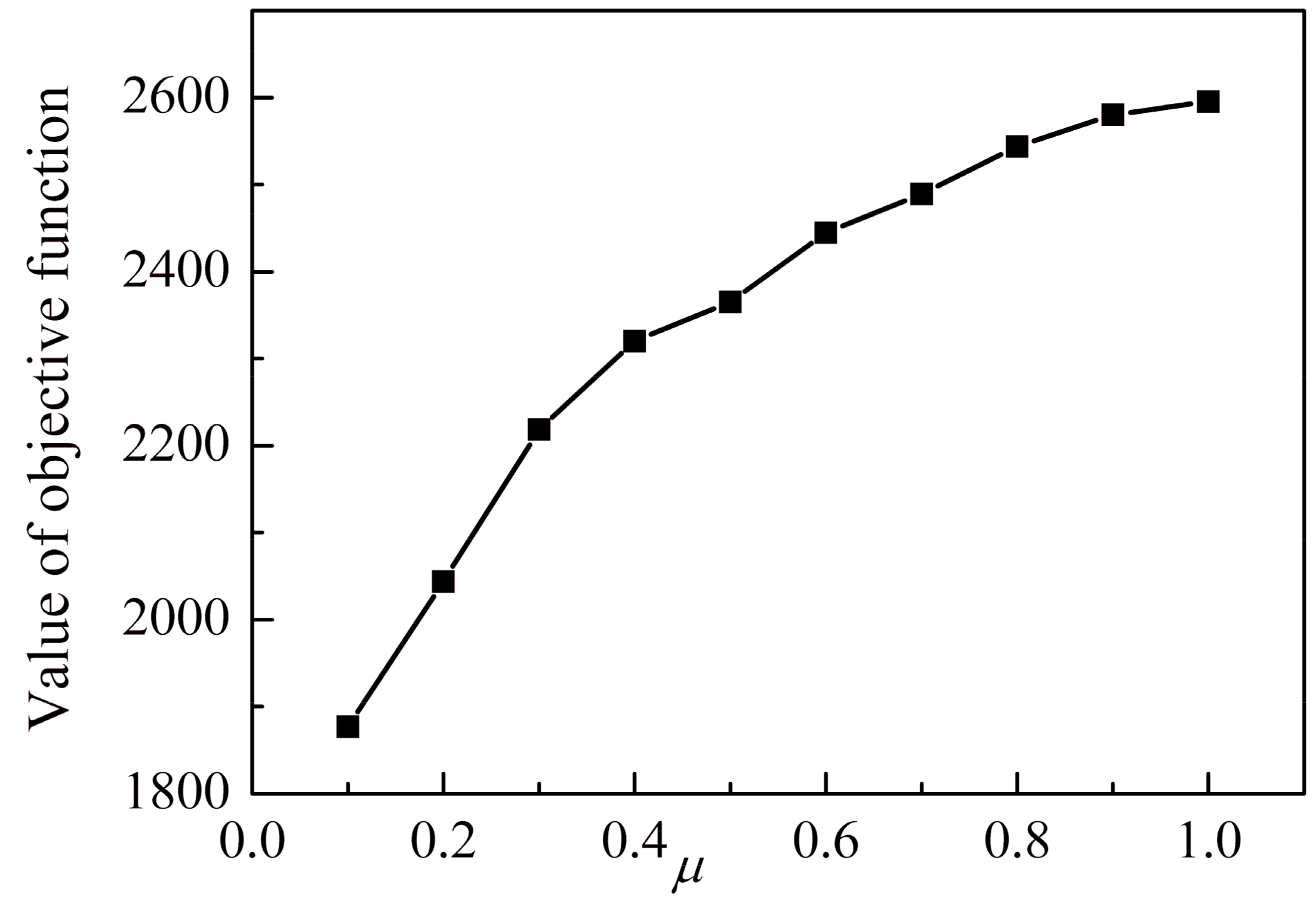

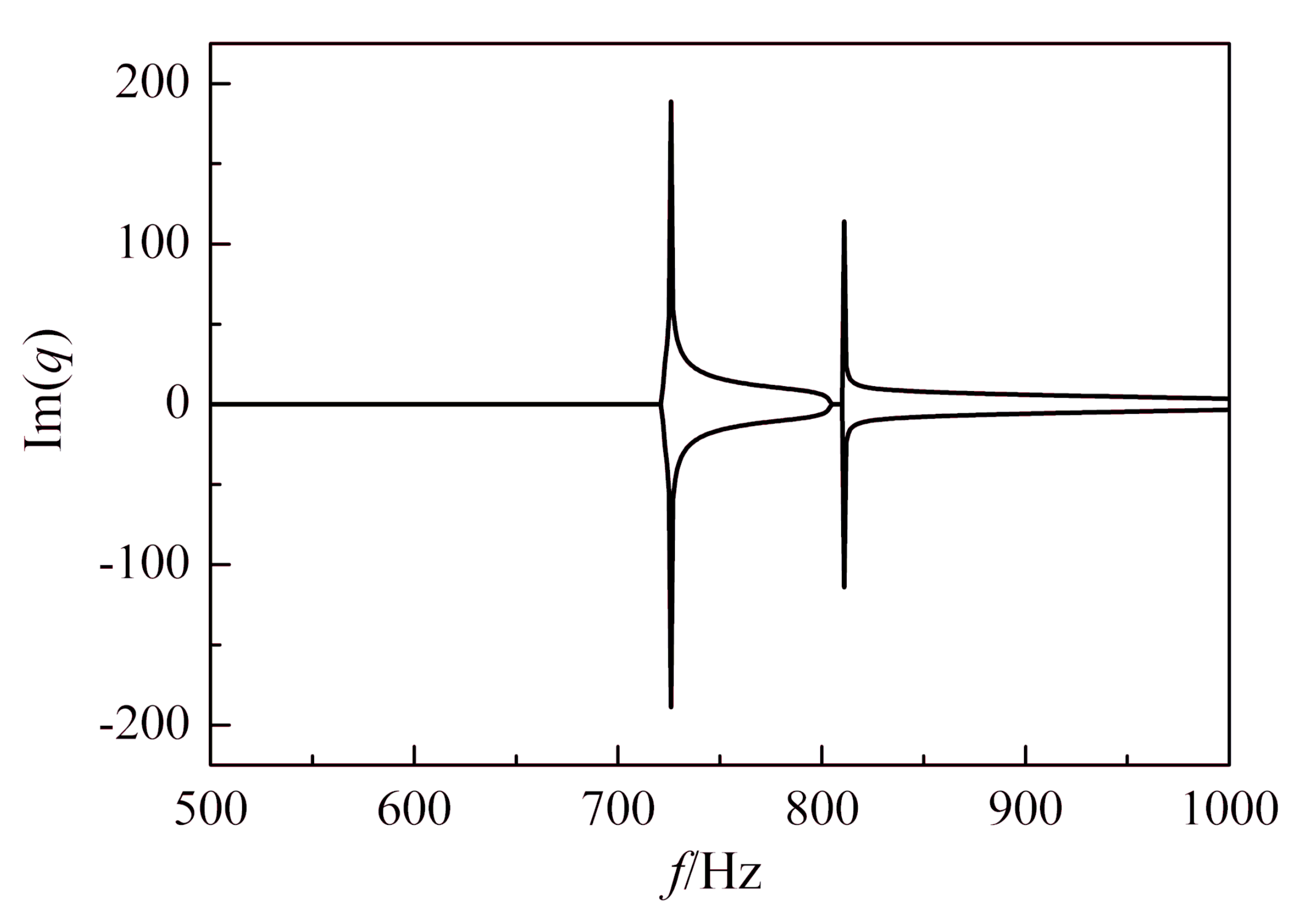
| Parameter Symbol | Value | |
|---|---|---|
| Parameters of the rod | A (m2) | |
| E (Pa) | ||
| ρ (kg/m3) | ||
| The spacing of the resonators | a (m) | 0.05 |
| Parameters of the spring-mass resonator | k (N/m) | |
| m (kg) | 0.0476 | |
| m0 (kg) | 0.016 |
| Object Function | f = ∑ lm (q) | Maximize |
|---|---|---|
| Subject to | for i = 1,2, | |
| DAVI Parameter | Lower Limit | Upper Limit |
|---|---|---|
| 2 | 40 | |
| 2 | 40 | |
| k1 (N/m) | 5.12 × 106 | 5 × 107 |
| m1 (kg) | 0.001 | 0.0238 |
| DAVI Parameter | Optimized |
|---|---|
| 5.2 | |
| 11.4 | |
| k1 (N/m) | 3.4 × 107 |
| k2 (N/m) | 6.1 × 106 |
| m1 (kg) | 0.00719 |
| m2 (kg) | 0.0166 |
| Resonance Gap | First Locally Resonant Band Gap | Second Locally Resonant Band Gap |
|---|---|---|
| Optimization | 1063~1603 Hz | 3103~3611 Hz |
| Optimal | 720~804 Hz | 809~1000 Hz |
| Percentages of decline | 32% | 74% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N.; Lei, X.; Lai, F.; Xue, X. Longitudinal Wave Locally Resonant Band Gaps in Metamaterial-Based Elastic Rods Comprising Multi-Degree-of-Freedom DAVI Resonators. Symmetry 2022, 14, 1030. https://doi.org/10.3390/sym14051030
Liu N, Lei X, Lai F, Xue X. Longitudinal Wave Locally Resonant Band Gaps in Metamaterial-Based Elastic Rods Comprising Multi-Degree-of-Freedom DAVI Resonators. Symmetry. 2022; 14(5):1030. https://doi.org/10.3390/sym14051030
Chicago/Turabian StyleLiu, Niuniu, Xianliang Lei, Fuqiang Lai, and Xin Xue. 2022. "Longitudinal Wave Locally Resonant Band Gaps in Metamaterial-Based Elastic Rods Comprising Multi-Degree-of-Freedom DAVI Resonators" Symmetry 14, no. 5: 1030. https://doi.org/10.3390/sym14051030
APA StyleLiu, N., Lei, X., Lai, F., & Xue, X. (2022). Longitudinal Wave Locally Resonant Band Gaps in Metamaterial-Based Elastic Rods Comprising Multi-Degree-of-Freedom DAVI Resonators. Symmetry, 14(5), 1030. https://doi.org/10.3390/sym14051030






