Experimental and Numerical Simulation of a Symmetrical Three-Cylinder Buoy
Abstract
:1. Introduction
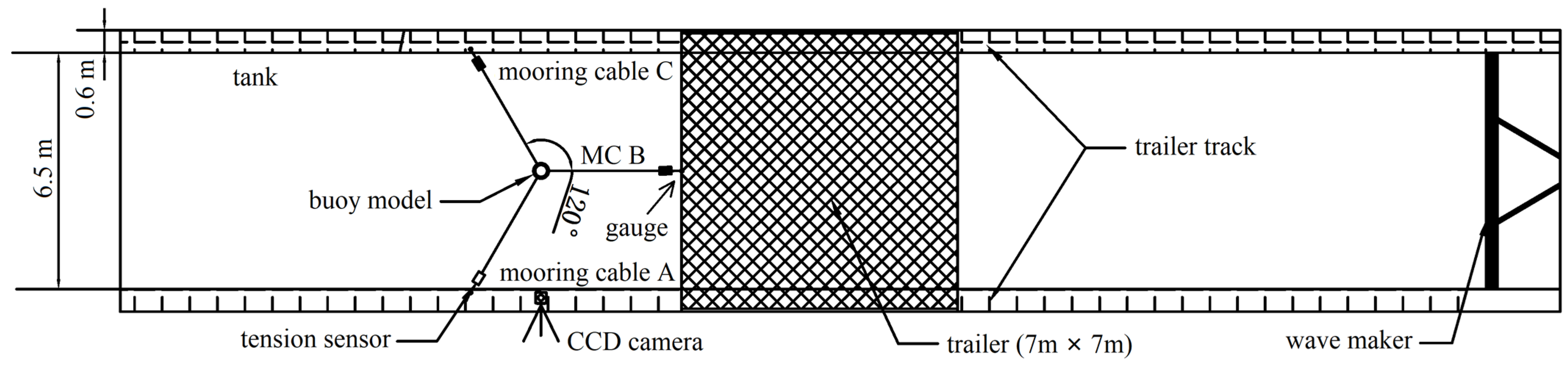
2. Experiment Materials and Methods
2.1. Experiment Model
2.2. Experiment Conditions
2.3. Data Collection and Processing
2.3.1. CCD Image Collection
2.3.2. The Tension Collection of the Mooring Cables
3. Experiment Results and Analysis
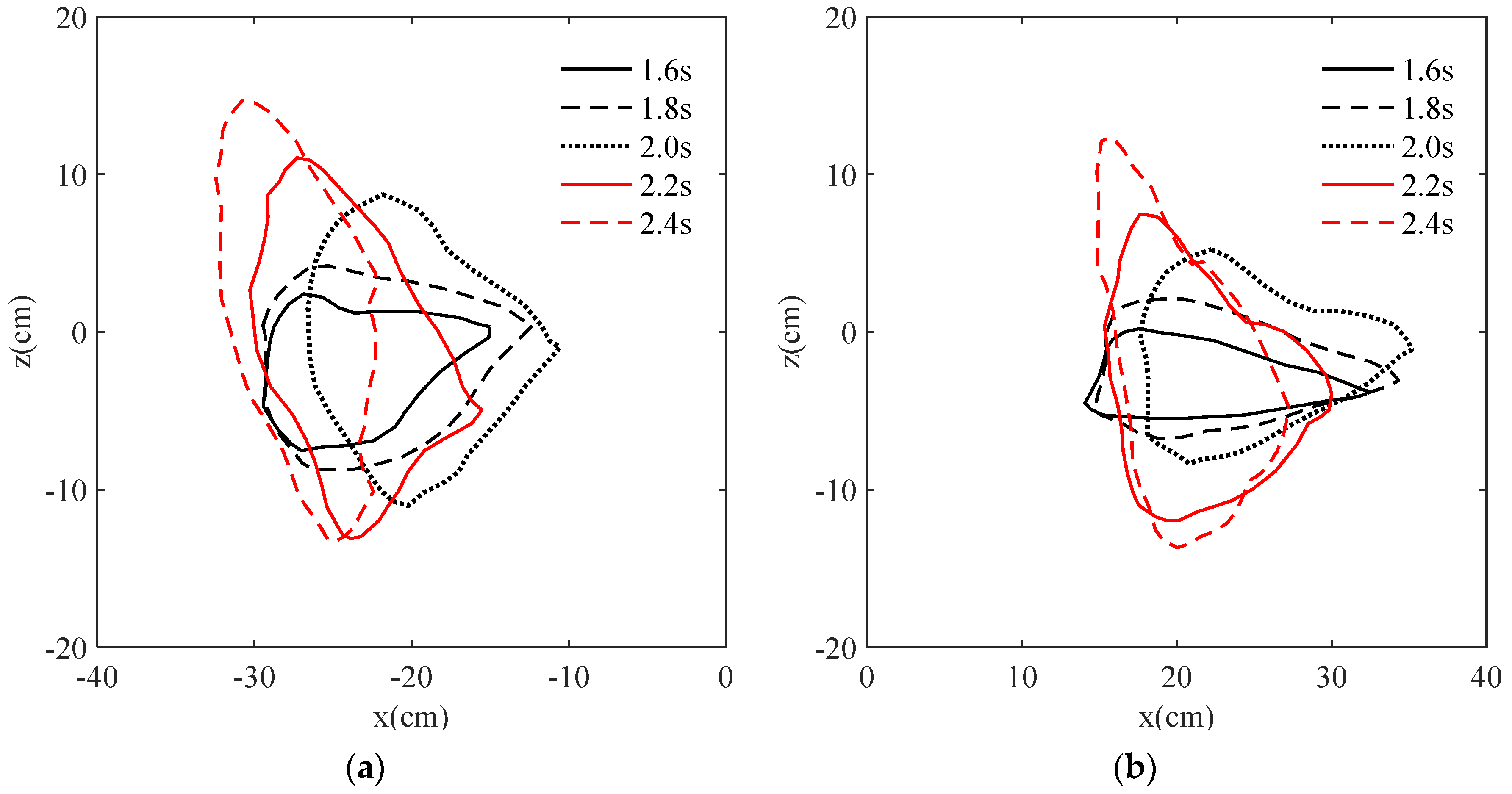
3.1. Analysis of Buoy Trajectory
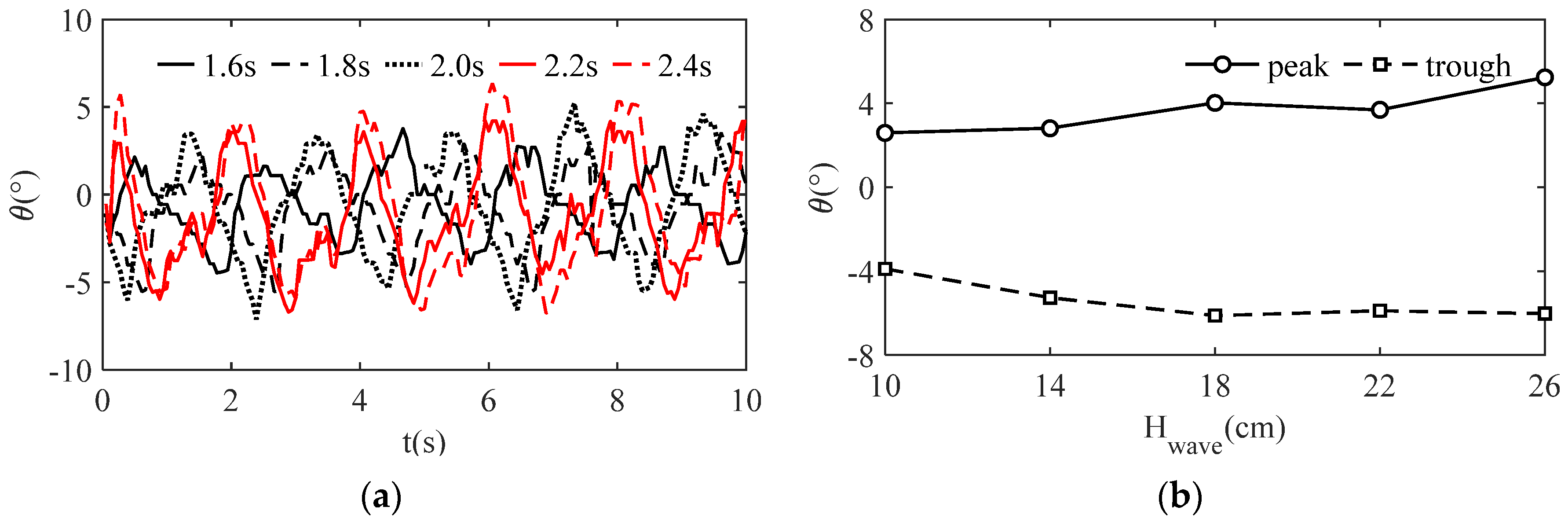
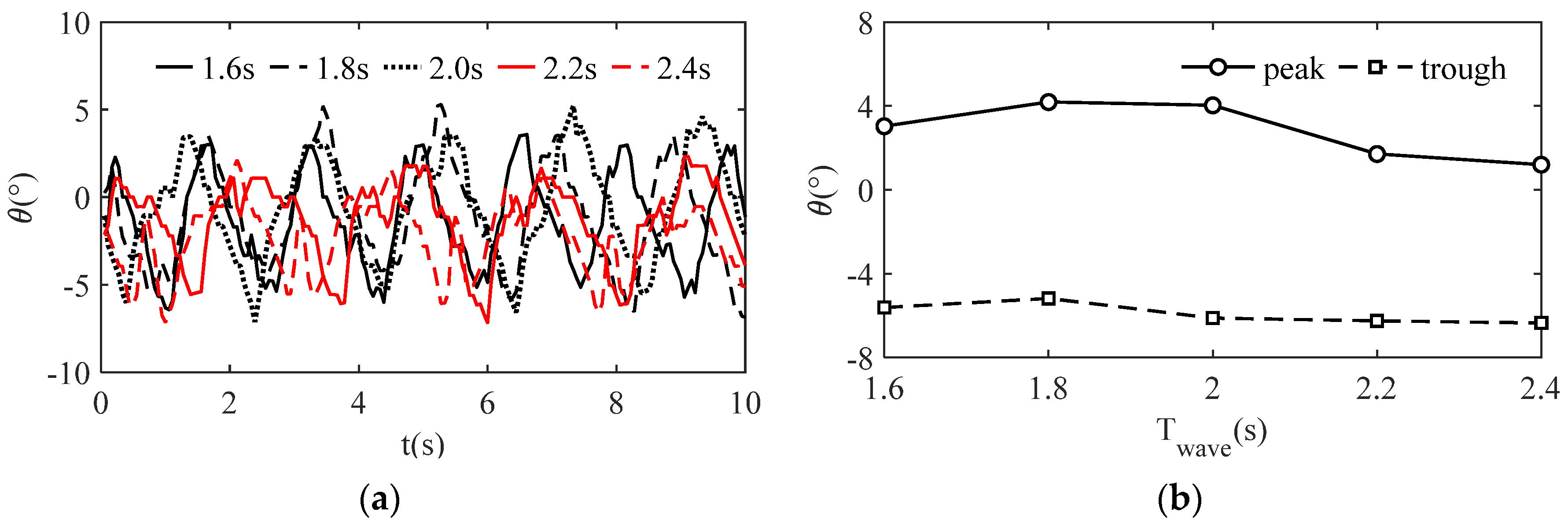
3.2. Rolling Analysis of the Three-Cylinder Buoy
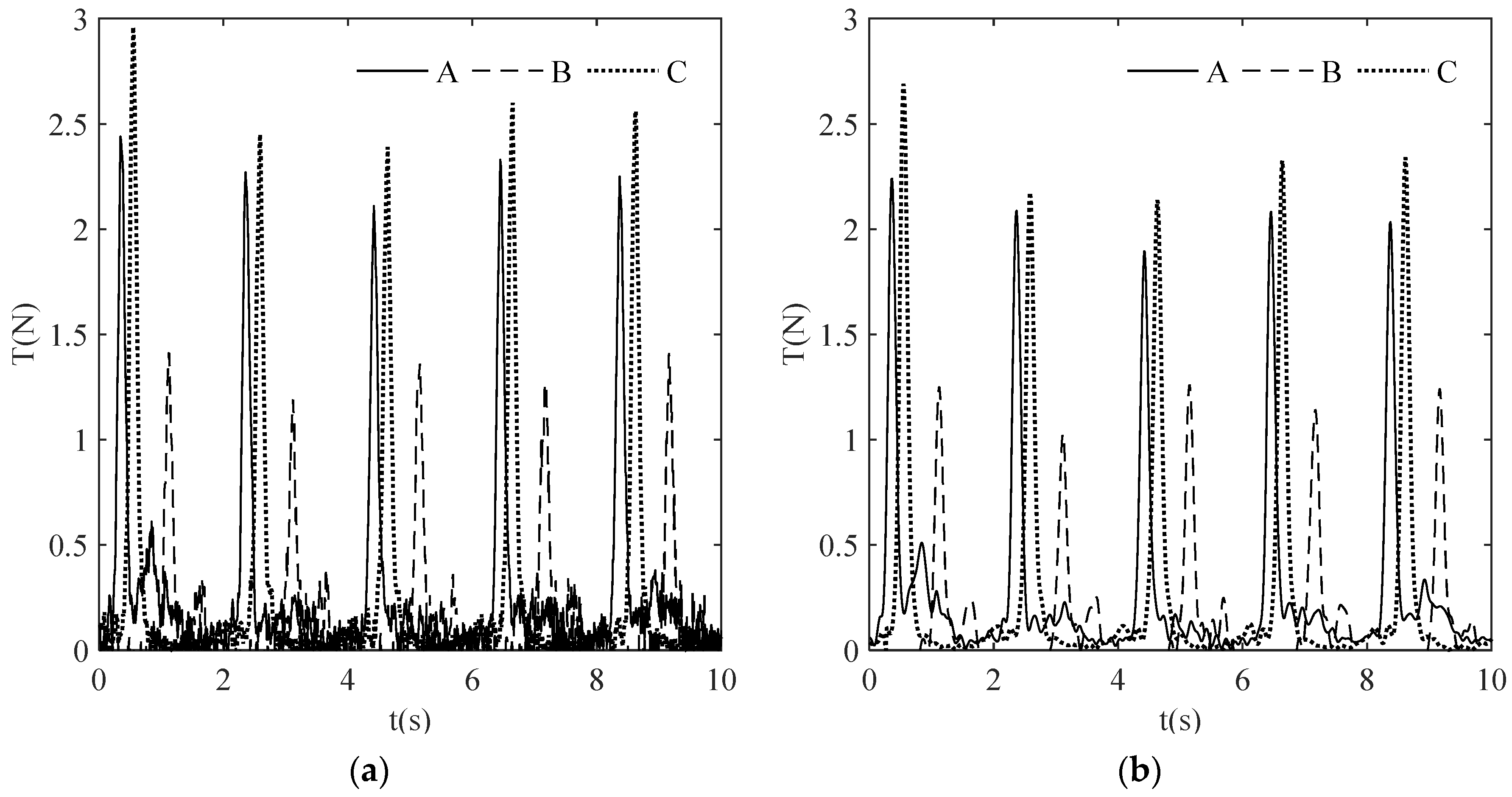
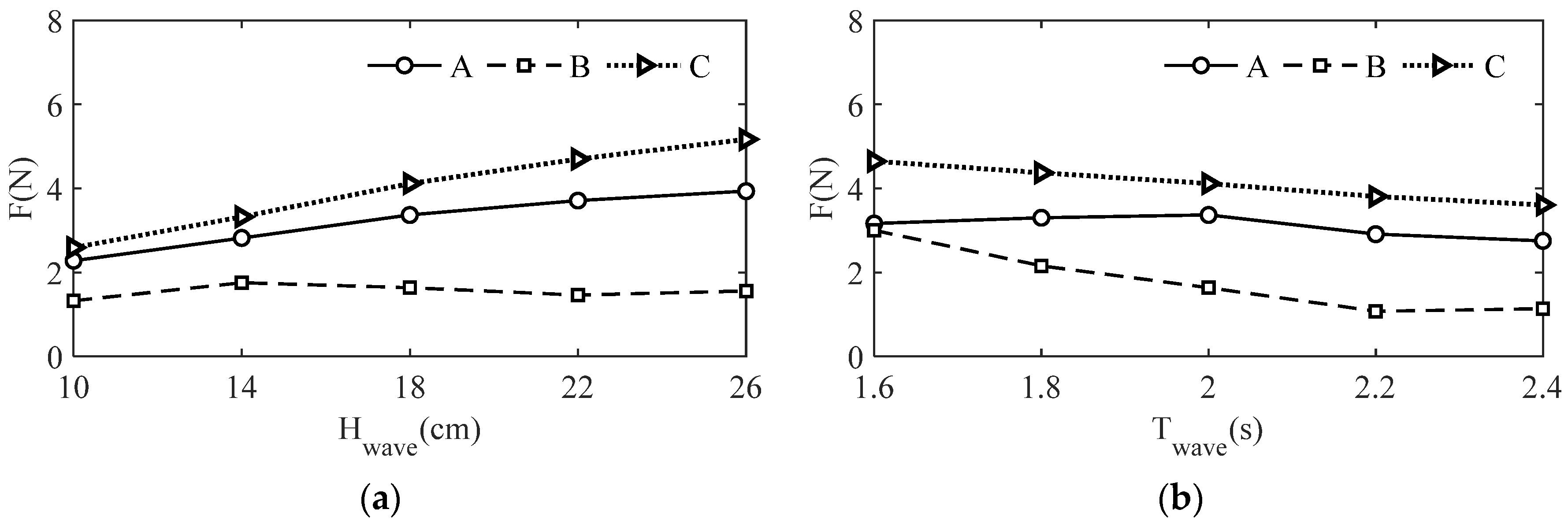
3.3. Tension Analysis of the Mooring Cables
4. Numerical Model
4.1. Establishment Method
4.1.1. Simulation Method of the Three-Cylinder Buoy
- Wave force
- 2.
- Translation and rotation of the floating three-cylinder frame
4.1.2. Simulation Method of the Mooring Cable
4.2. Establishment Method
4.2.1. Motion Status of the Three-Cylinder Buoy at Different Times
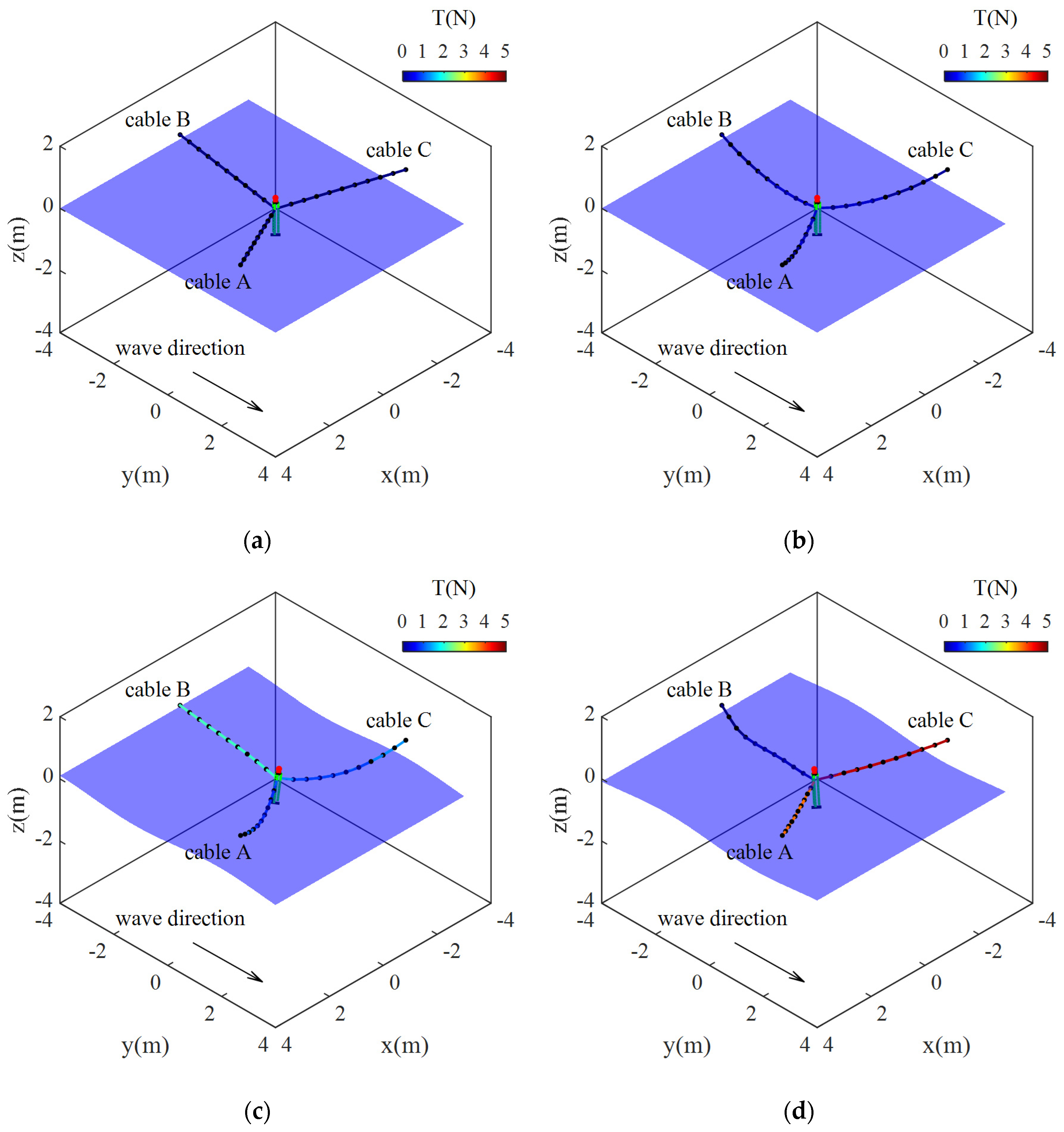
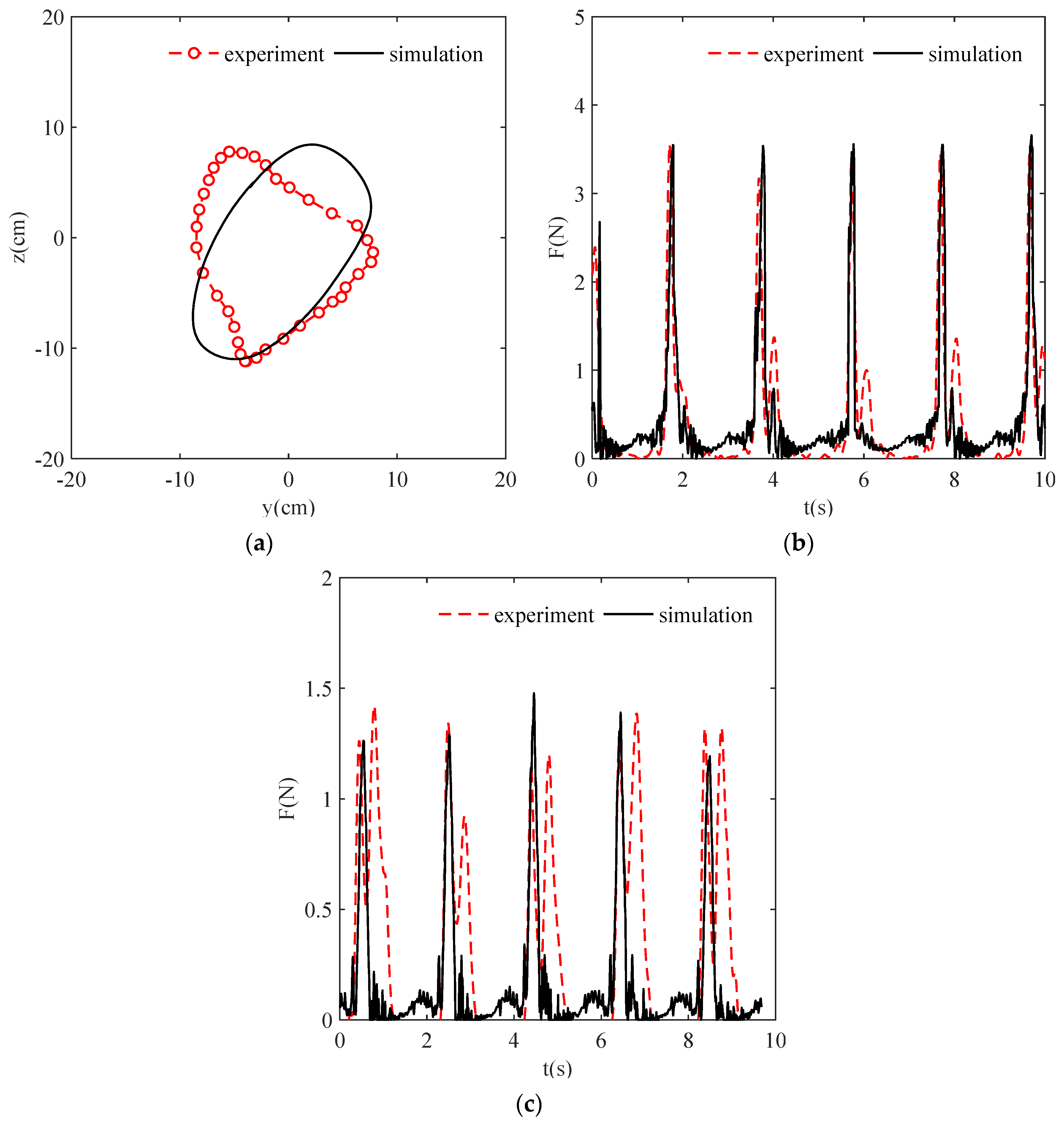
4.2.2. Comparison between the Trajectory of Tracing Points and the Tension of Mooring Cables
5. Discussion
5.1. Physical Experiment
5.2. Numerical Simulation
- In the model experiment, it was difficult to unify the relaxation degree of the three mooring cables, which was avoided by setting parameters in the numerical simulation.
- In the numerical simulation, the static state of the three-cylinder buoy (water entry depth) was taken as the premise. The three-cylinder buoy was regarded as a homogeneous medium to calculate the theoretical density. However, to ensure the water resistance of the buoy, the foam glue, which is not a homogeneous medium, was filled in the cylinder in the physical experiment.
- Due to the complexity of the structure, the three-way connection structure of the floating three-cylinder frame was not considered in the numerical simulation, which resulted in some differences in the movement of the system. On the basis of the analysis of the above reasons and the verification of the results, it could be concluded that the simulation method proposed in this paper was feasible.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Wang, Z.; Wang, Y.; Liu, S.; Li, Y. Current situation and trend of marine data buoy and monitoring network technology of China. Acta Oceanol. Sin. 2016, 35, 1–10. [Google Scholar] [CrossRef]
- Qian, C.; Huang, B.; Yang, X.; Chen, G. Data science for oceanography: From small data to big data. Big Earth Data 2021, 1–15. [Google Scholar] [CrossRef]
- Schmidt, W.; Raymond, D.; Parish, D.; Ashton, I.G.; Miller, P.I.; Campos, C.J.; Shutler, J.D. Design and operation of a low-cost and compact autonomous buoy system for use in coastal aquaculture and water quality monitoring. Aquac. Eng. 2018, 80, 28–36. [Google Scholar] [CrossRef]
- Loverich, G.; Forster, J. Advances in offshore cage design using spar buoys. Mar. Technol. Soc. J. 2000, 34, 18–28. [Google Scholar] [CrossRef]
- Gui, F.; Wang, P.; Pan, Y.; Feng, D.; Zuo, X. Cylindrical Anti Wind and Wave Marine Stratified Sampling Water Quality Monitoring Buoy. Chinese Patent CN108168957B, 16 June 2020. [Google Scholar]
- Shi, Q.; Wang, H.; Wu, H.; Lee, C. Self-powered triboelectric nanogenerator buoy ball for applications ranging from environment monitoring to water wave energy farm. Nano Energy 2017, 40, 203–213. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Wang, F.; Ye, J. Numerical studies on CALM buoy motion responses and the effect of buoy geometry cum skirt dimensions with its hydrodynamic waves-current interactions. Ocean Eng. 2022, 244, 110378. [Google Scholar] [CrossRef]
- Ryu, S.; Duggal, A.S.; Heyl, C.N.; Liu, Y. Coupled analysis of deepwater oil offloading buoy and experimental verification. In Proceedings of the Fifteenth International Offshore and Polar Engineering Conference, Seoul, Korea, 19–24 June 2005. [Google Scholar]
- Ryu, S.; Duggak, A.S.; Heyl, C.N. Prediction of deep water oil offloading buoy response and experimental validation. Int. J. Offshore Polar Eng. 2006, 16, 290–296. [Google Scholar]
- Touzon, I.; Nava, V.; Gao, Z.; Petuya, V. Frequency domain modelling of a coupled system of floating structure and mooring Lines: An application to a wave energy converter. Ocean Eng. 2021, 220, 108498. [Google Scholar] [CrossRef]
- Jin, C.; Kang, H.; Kim, M.; Cho, I. Performance estimation of resonance-enhanced dual-buoy wave energy converter using coupled time-domain simulation. Renew. Energy 2020, 160, 1445–1457. [Google Scholar] [CrossRef]
- Salem, A.G.; Ryu, S.; Duggal, A.S.; Datla, R.V. Linearization of quadratic drag to estimate calm buoy pitch motion in frequency-domain and experimental validation. J. Offshore Mech. Arct. Eng. 2012, 134, 011305. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Wang, F.; Ye, J. Investigation on Hydrodynamic Characteristics, Wave–Current Interaction and Sensitivity Analysis of Submarine Hoses Attached to a CALM Buoy. J. Mar. Sci. Eng. 2022, 10, 120. [Google Scholar] [CrossRef]
- Yang, K.; Abdelkefi, A.; Li, X.; Mao, Y.; Dai, L.; Wang, J. Stochastic analysis of a galloping-random wind energy harvesting performance on a buoy platform. Energy Convers. Manag. 2021, 238, 114174. [Google Scholar] [CrossRef]
- Le Cunff, C.; Ryu, S.; Duggal, A.; Ricbourg, C.; Heurtier, J.M.; Heyl, C.; Beauclair, O. Derivation of calm buoy coupled motion raos in frequency domain and experimental Validation. In Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Zhu, X.; Yoo, W.S. Dynamic analysis of a floating spherical buoy fastened by mooring cables. Ocean Eng. 2016, 121, 462–471. [Google Scholar] [CrossRef]
- Chen, F.; Duan, D.; Han, Q.; Yang, X.; Zhao, F. Study on force and wave energy conversion efficiency of buoys in low wave energy density seas. Energy Convers. Manag. 2019, 182, 191–200. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Wang, F.; Hou, X.; Ye, J. Strength of submarine hoses in Chinese-lantern configuration from hydrodynamic loads on CALM buoy. Ocean Eng. 2019, 171, 429–442. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.W.; Gui, F.K.; Li, Y.C.; Fang, W.H. Hydrodynamic coefficients of a simplified floating system of gravity cage in waves. J. Zhejiang Univ.-Sci. A 2008, 9, 654–663. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.; Pan, Y.; Bai, X.; Wei, D. Distribution characteristics of waves in Sanmen Bay based on field observation. Ocean Eng. 2021, 229, 108999. [Google Scholar] [CrossRef]
- Feng, D.; Meng, A.; Wang, P.; Yao, Y.; Gui, F. Effect of design configuration on structural response of longline aquaculture in waves. Appl. Ocean Res. 2021, 107, 102489. [Google Scholar] [CrossRef]
- Greengard, L.; Lee, J.Y. Accelerating the nonuniform fast Fourier transform. SIAM Rev. 2004, 46, 443–454. [Google Scholar] [CrossRef] [Green Version]
- Geng, B.L.; Teng, B.; Ning, D.Z. A time-domain analysis of wave force on small-scale cylinders of offshore structures. J. Mar. Sci. Technol. 2010, 18, 12. [Google Scholar] [CrossRef]
- Pan, Y.; Tong, H.; Zhou, Y.; Liu, C.; Xue, D. Numerical Simulation Study on Environment-Friendly Floating Reef in Offshore Ecological Belt under Wave Action. Water 2021, 13, 2257. [Google Scholar] [CrossRef]
- Liu, Y.; Dou, C.; Sun, Q.; Xu, Q. Optimal control of path tracking for vehicle-handling dynamics. SAE Int. J. Passeng. Cars-Mech. Syst. 2020, 13, 225–243. [Google Scholar] [CrossRef]
- Zhu, X.; Yoo, W.S. Flexible dynamic analysis of an offshore wind turbine installed on a floating spar platform. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Wang, Y.; Yu, K.; Pei, Y.; Wei, Z.; Zong, L. Dynamic analysis of deep-towed seismic array based on relative-velocity-element-frame. Ocean Eng. 2020, 218, 108243. [Google Scholar] [CrossRef]
- Zhu, X.; Yoo, W.S. Numerical modeling of a spherical buoy moored by a cable in three dimensions. Chin. J. Mech. Eng. 2016, 29, 588–597. [Google Scholar] [CrossRef]




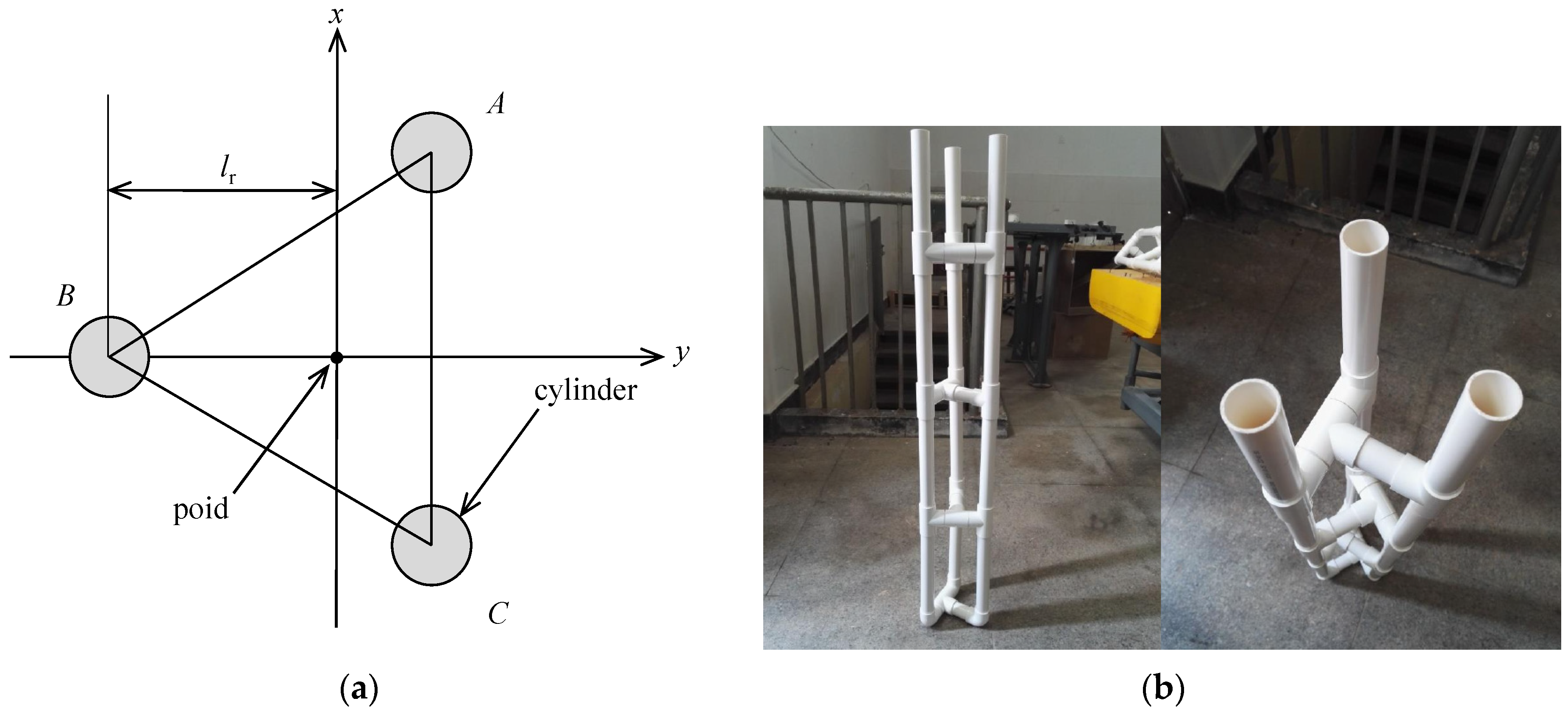
| Parameters | Prototype | Model |
|---|---|---|
| Length of the buoy/m | 8.47 | 1.08 |
| Length of the three-way connection structure/m | 1.25 | 0.166 |
| Mass of the three-cylinder frame/kg | 363.5 | 1.215 |
| Buoyancy of the three-cylinder frame/kg | 1297.4 | 2.749 |
| Mass of the cabin/kg | 260 | 0.374 |
| Mass of the counterweight/kg | 914.8 | 1.315 |
| Wave Height/cm | Area Lp/cm2 | Area Rp/cm2 | Surging Lp/cm * | Heaving Lp/cm | Surging Rp/cm * | Heaving Rp/cm |
|---|---|---|---|---|---|---|
| 10 | 105.986 | 86.712 | 10.723 | 15.474 | 12.515 | 11.834 |
| 14 | 131.083 | 111.778 | 12.045 | 17.229 | 13.965 | 12.816 |
| 18 | 191.362 | 141.817 | 16.029 | 19.754 | 17.511 | 13.582 |
| 22 | 181.677 | 163.482 | 16.265 | 18.974 | 18.165 | 14.113 |
| 26 | 204.631 | 165.236 | 17.755 | 19.879 | 18.559 | 14.804 |
| Period/s | Area Lp/cm2 | Area Rp/cm2 | Surging Lp/cm | Heaving Lp/cm * | Surging Rp/cm * | Heaving Rp/cm |
|---|---|---|---|---|---|---|
| 1.6 | 90.9113 | 65.0382 | 14.428 | 9.961 | 18.217 | 5.691 |
| 1.8 | 152.8007 | 110.1839 | 17.157 | 12.925 | 19.635 | 8.871 |
| 2.0 | 191.3615 | 141.817 | 16.029 | 19.754 | 17.511 | 13.582 |
| 2.2 | 192.5868 | 171.9369 | 14.753 | 24.168 | 14.667 | 19.415 |
| 2.4 | 182.4064 | 174.2035 | 10.186 | 27.949 | 12.396 | 25.942 |
| Mooring Cables | n1/N | n2/N | n3/N | n4/N | n5/N | Average/N |
|---|---|---|---|---|---|---|
| Mooring cable A | 2.44 | 2.27 | 2.11 | 2.23 | 2.35 | 2.28 |
| Mooring cable B | 1.41 | 1.19 | 1.36 | 1.27 | 1.41 | 1.328 |
| Mooring cable C | 2.96 | 2.45 | 2.39 | 2.6 | 2.56 | 2.592 |
| Wave Height/cm | 10 | 14 | 18 | 22 | 26 |
| Wave force/N | 2.915 | 2.999 | 2.925 | 2.999 | 2.929 |
| Period/s | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 |
| Wave force/N | 4.536 | 4.088 | 3.516 | 3.005 | 2.959 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Yang, F.; Tong, H.; Zuo, X.; Shen, L.; Xue, D.; Liu, C. Experimental and Numerical Simulation of a Symmetrical Three-Cylinder Buoy. Symmetry 2022, 14, 1057. https://doi.org/10.3390/sym14051057
Pan Y, Yang F, Tong H, Zuo X, Shen L, Xue D, Liu C. Experimental and Numerical Simulation of a Symmetrical Three-Cylinder Buoy. Symmetry. 2022; 14(5):1057. https://doi.org/10.3390/sym14051057
Chicago/Turabian StylePan, Yun, Fengting Yang, Huanhuan Tong, Xiao Zuo, Liangduo Shen, Dawen Xue, and Can Liu. 2022. "Experimental and Numerical Simulation of a Symmetrical Three-Cylinder Buoy" Symmetry 14, no. 5: 1057. https://doi.org/10.3390/sym14051057
APA StylePan, Y., Yang, F., Tong, H., Zuo, X., Shen, L., Xue, D., & Liu, C. (2022). Experimental and Numerical Simulation of a Symmetrical Three-Cylinder Buoy. Symmetry, 14(5), 1057. https://doi.org/10.3390/sym14051057






