Study of the Influence of Aspect Ratios on Hydrodynamic Performance of a Symmetrical Elliptic Otter Board
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model of the Symmetrical Elliptic Otter Board
2.2. The Flume Test
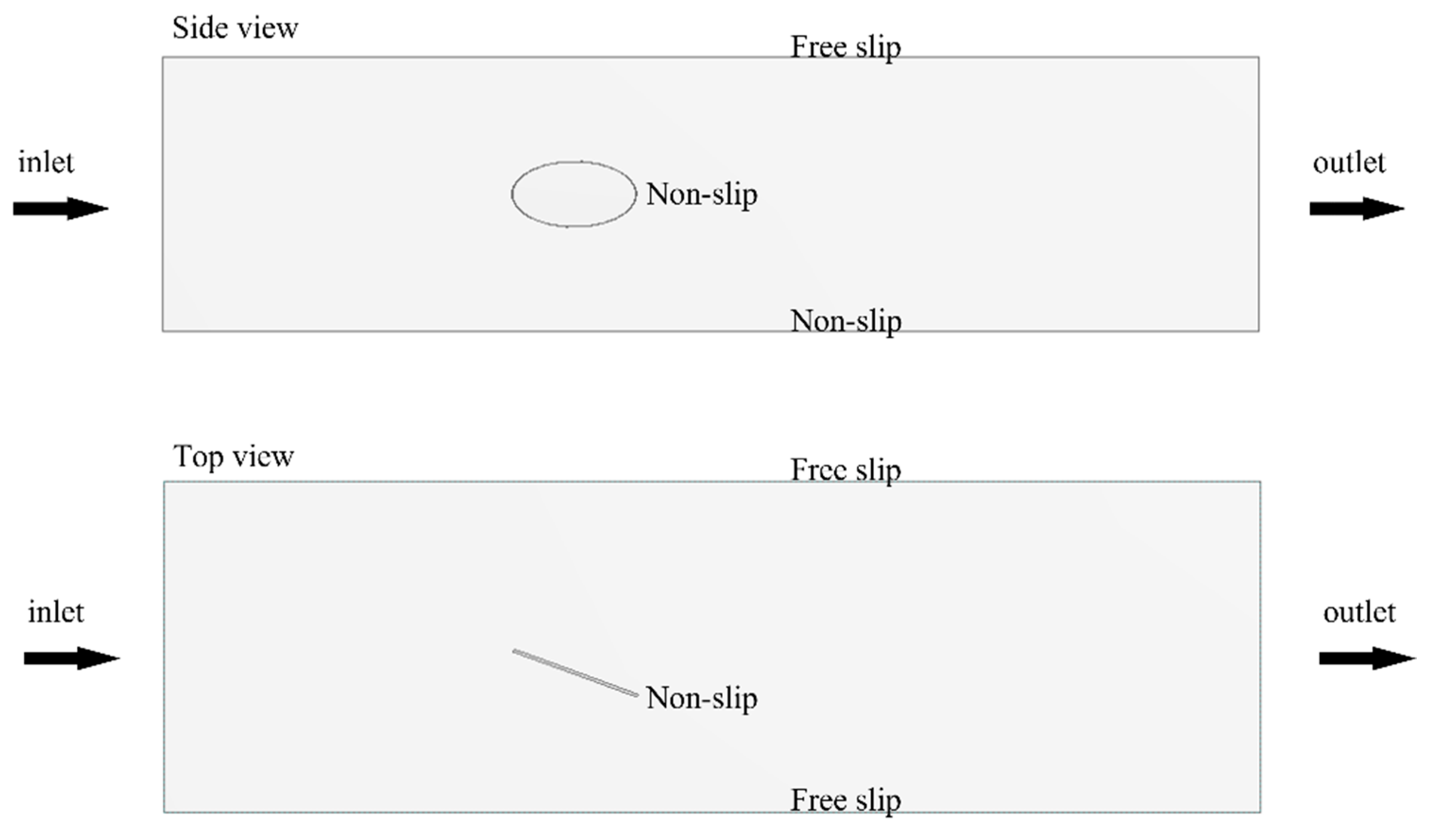
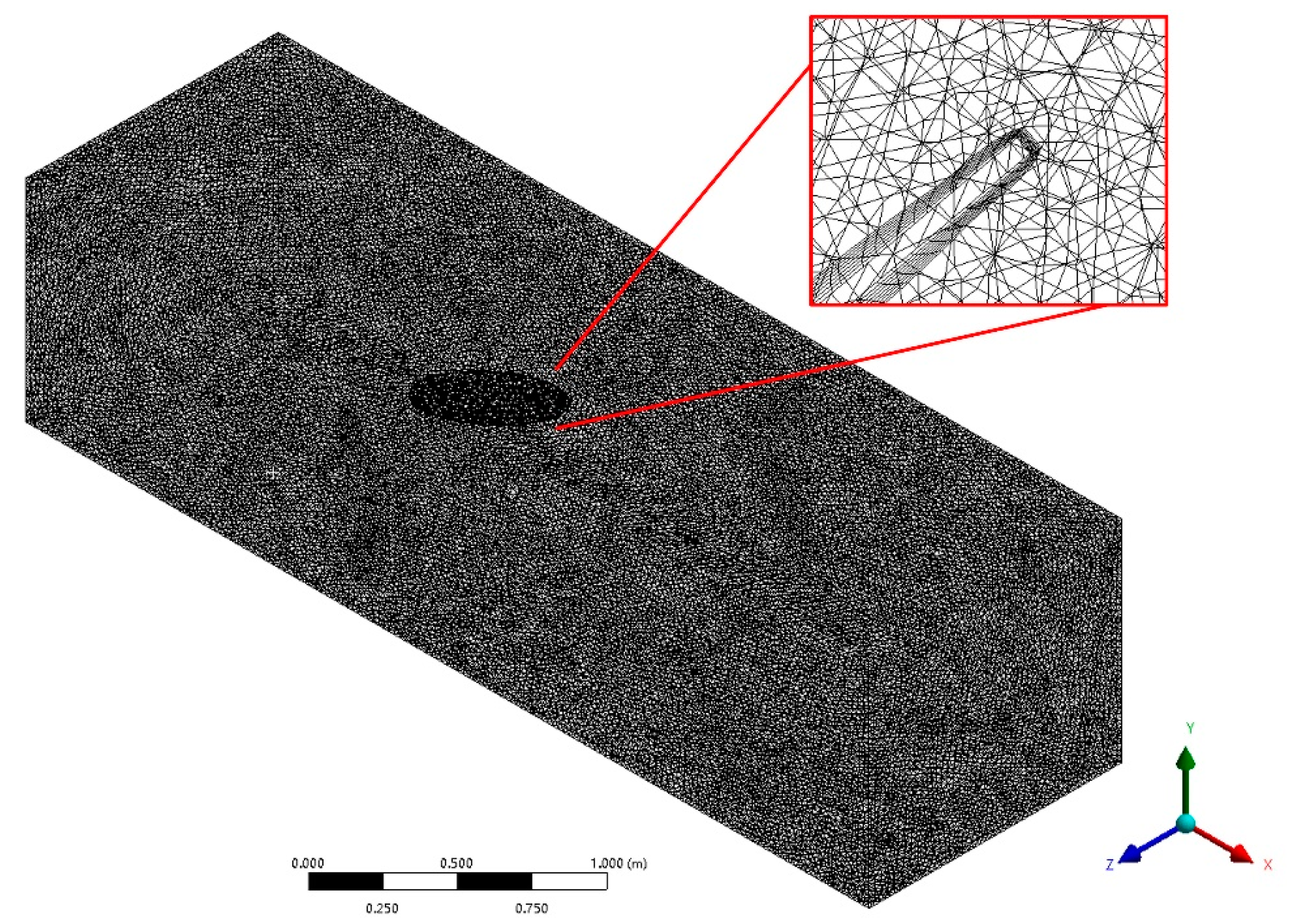
2.3. Numerical Simulation
2.4. Data Process
3. Results
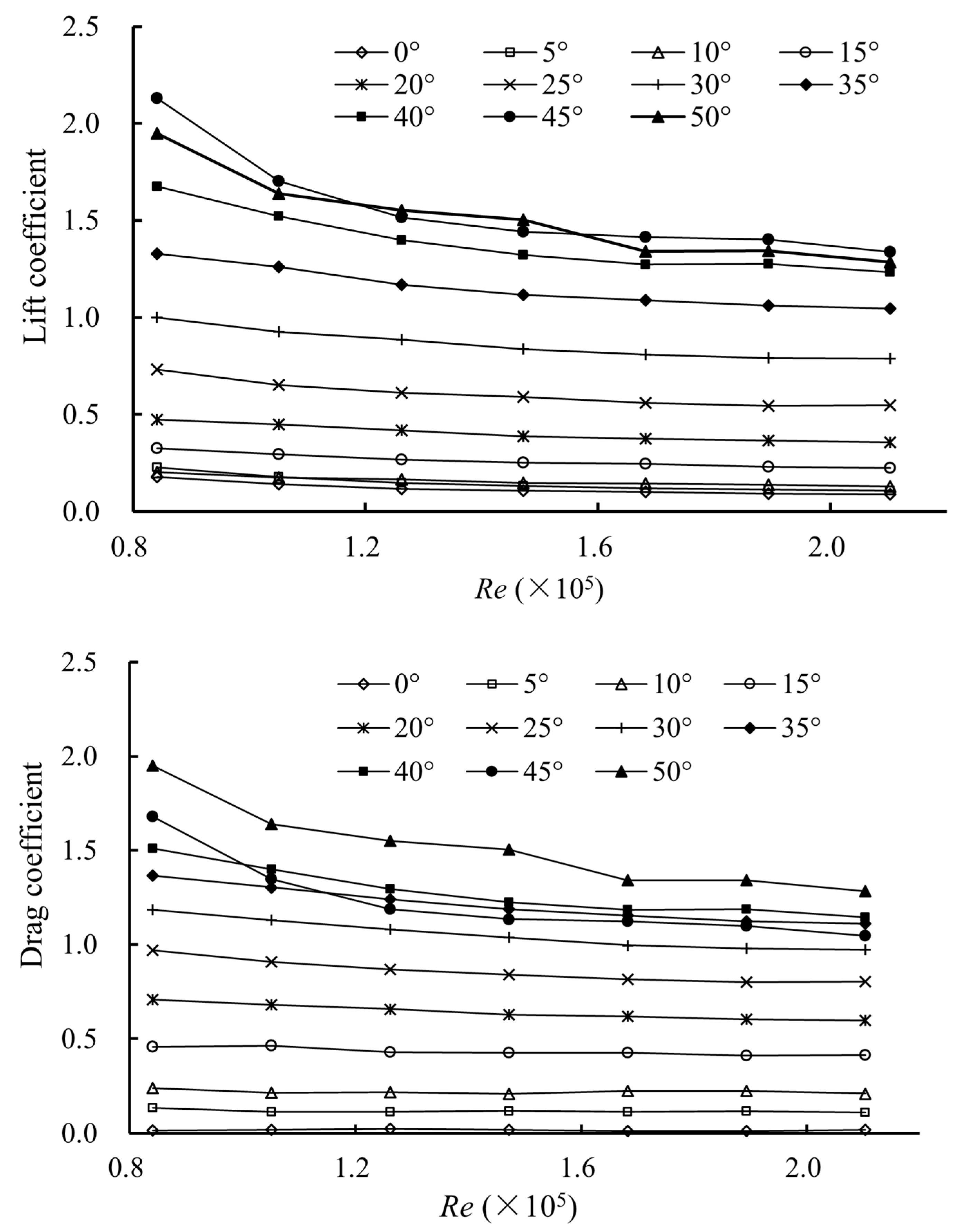
3.1. Relationship between Lift, the Drag Coefficient and the Reynolds Number
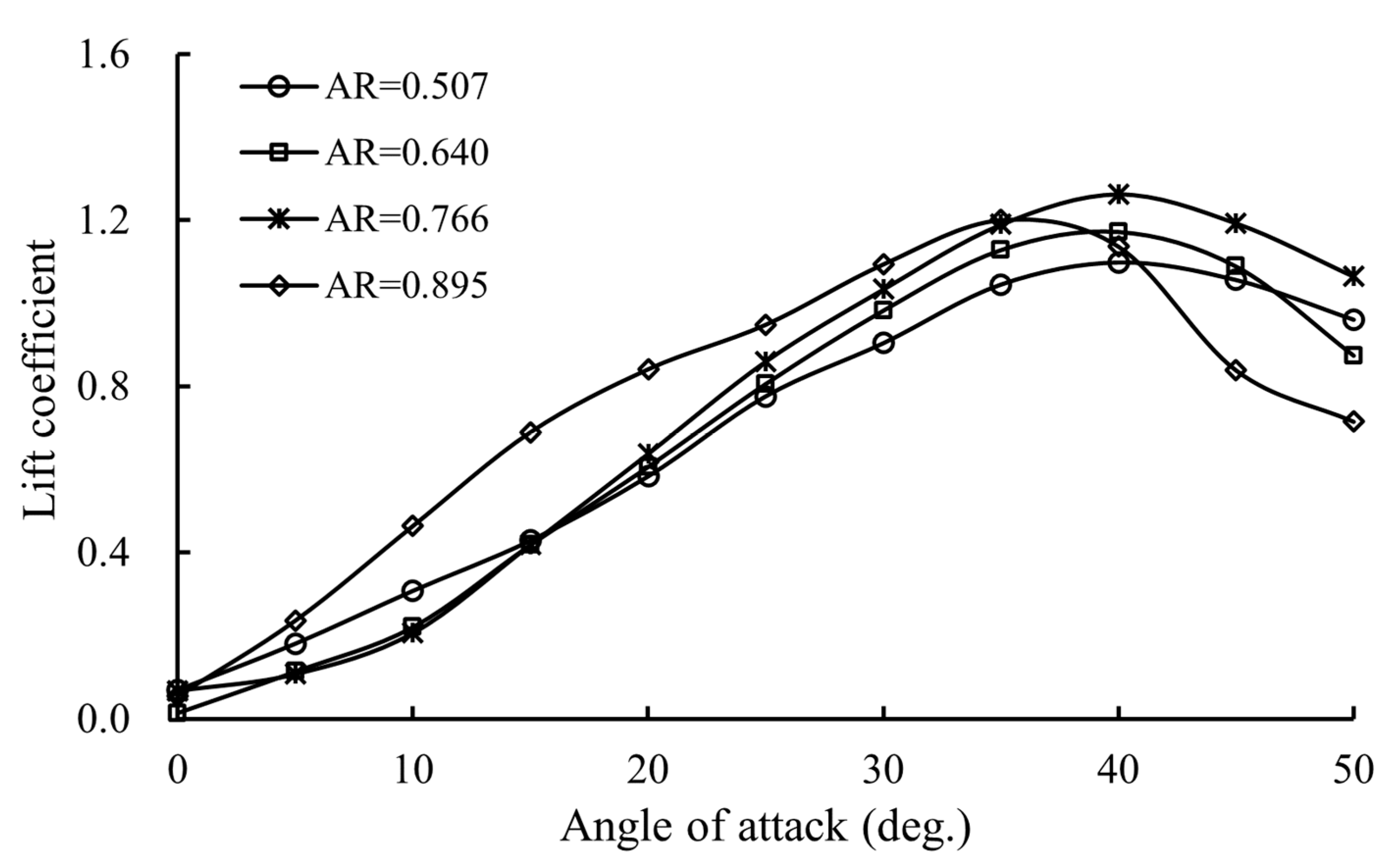
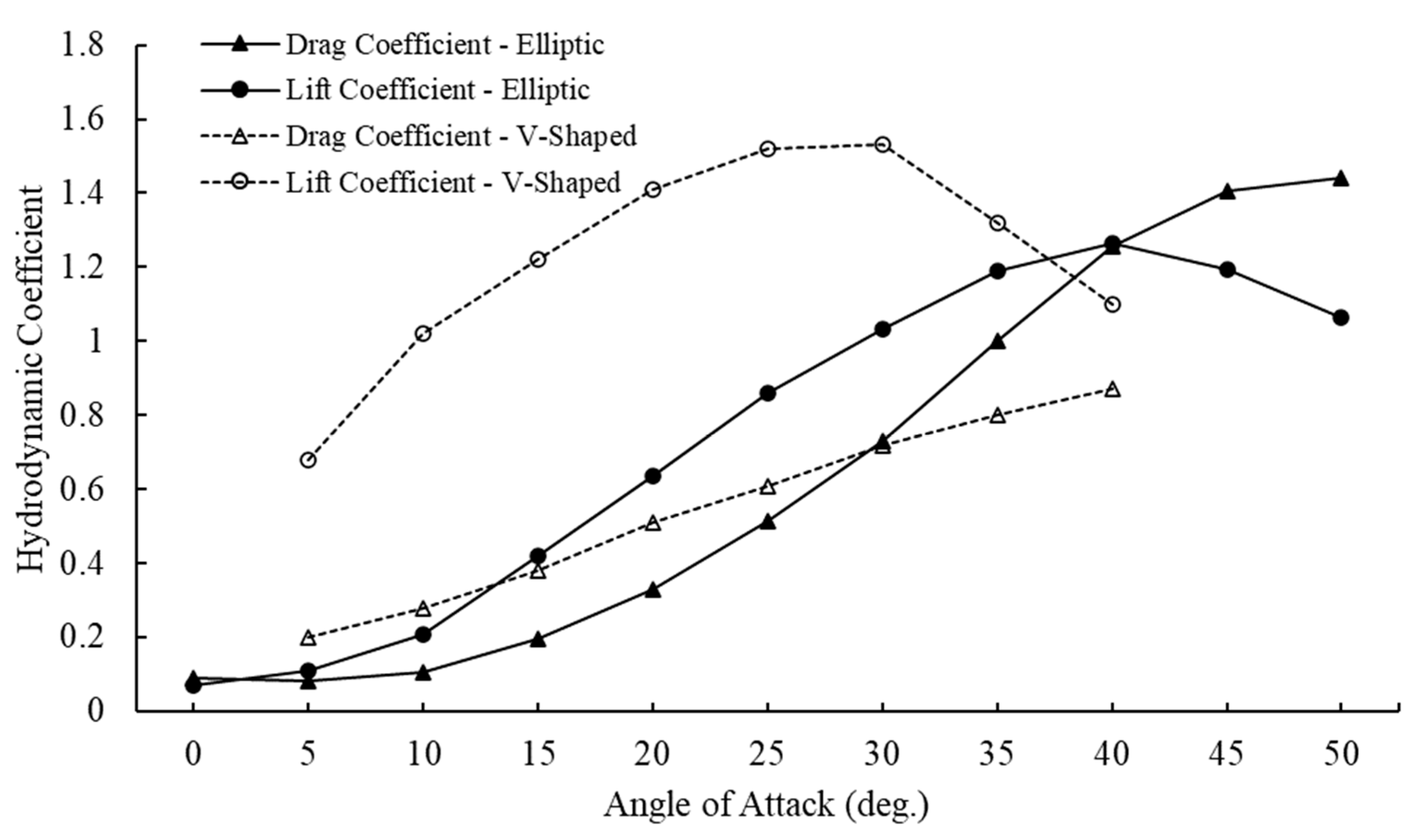
3.2. The Lift Coefficient of the Otter Board
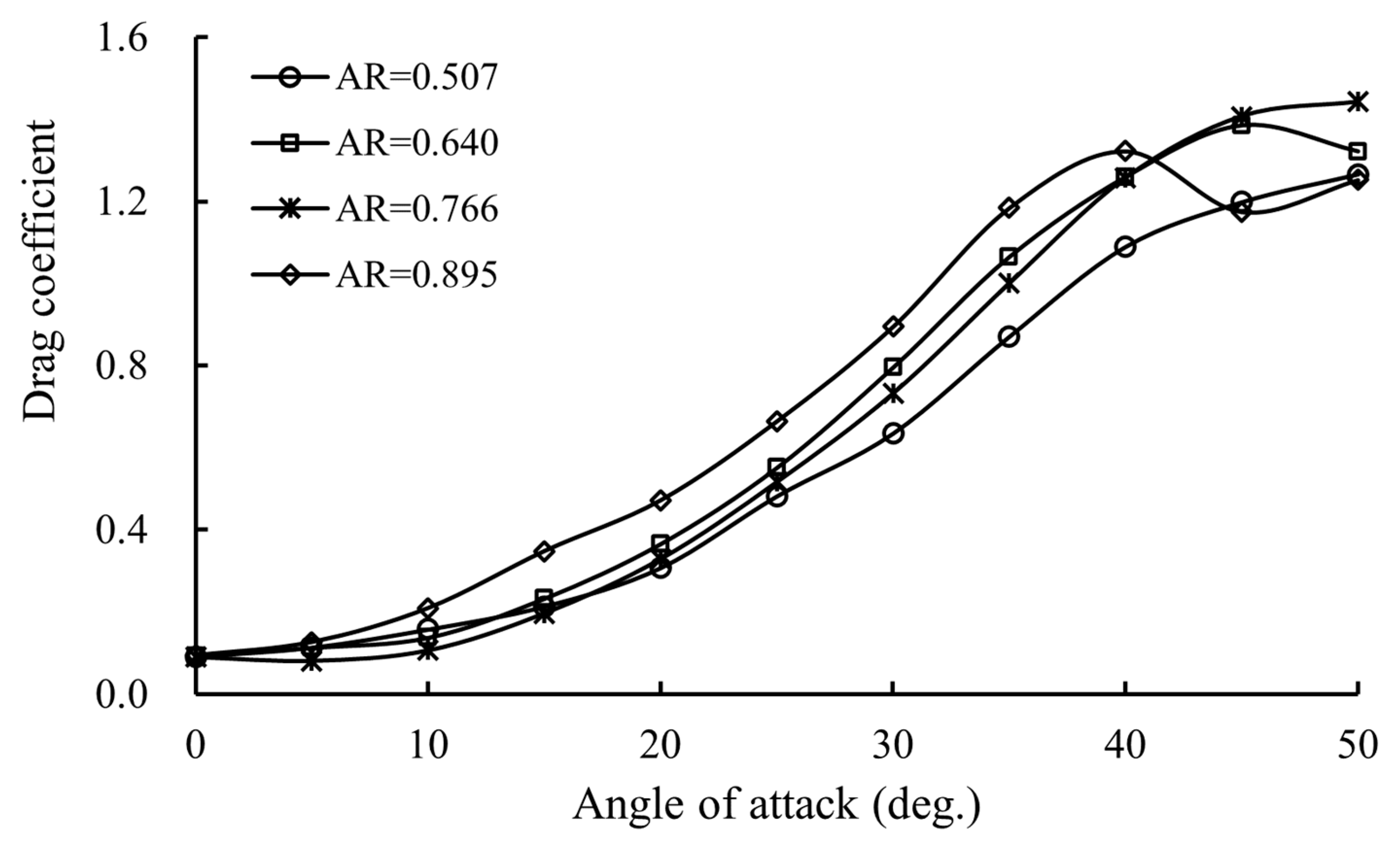
3.3. The Drag Coefficient of the Otter Board
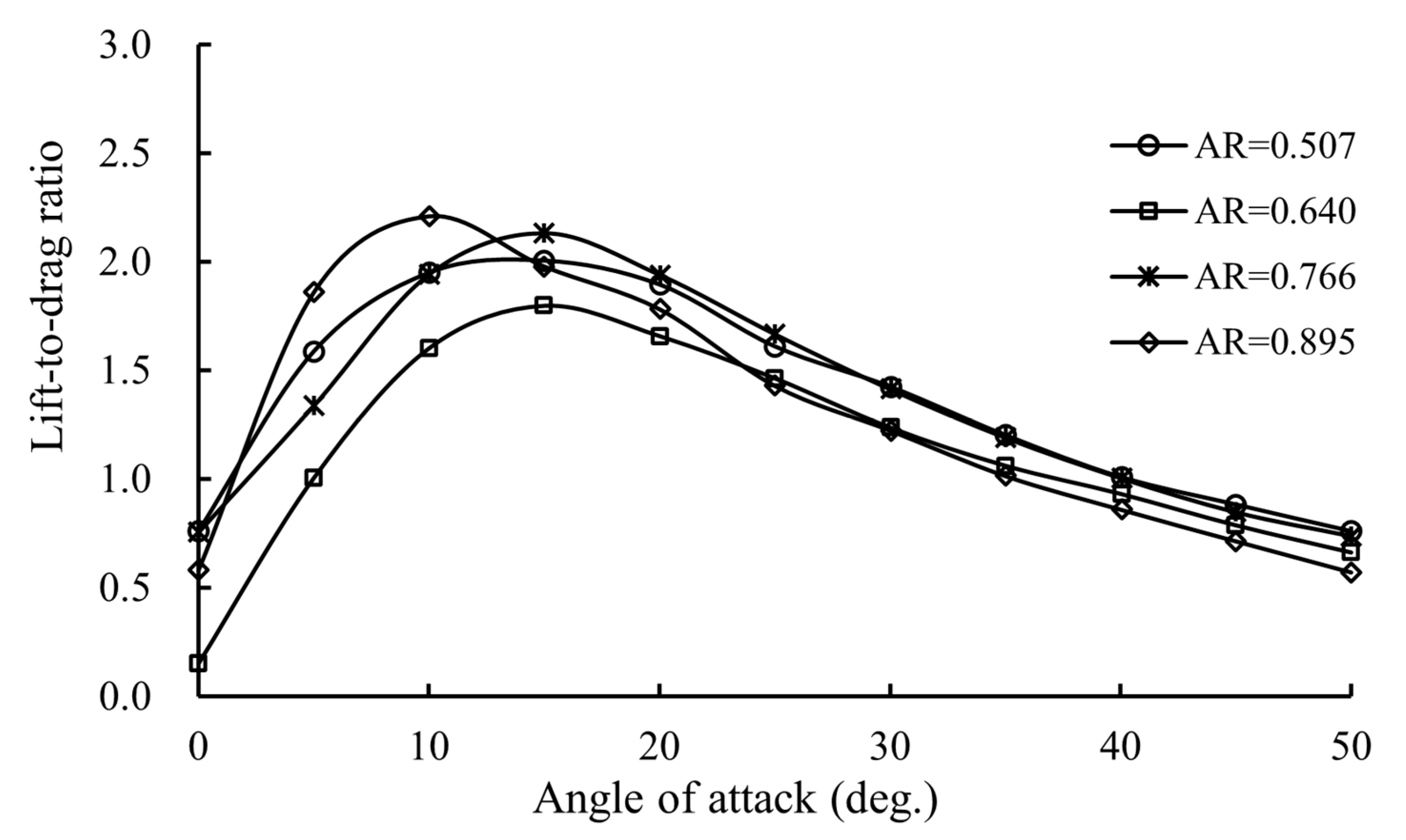
3.4. The Lift-to-Drag Ratio of the Otter Board
3.5. Validation
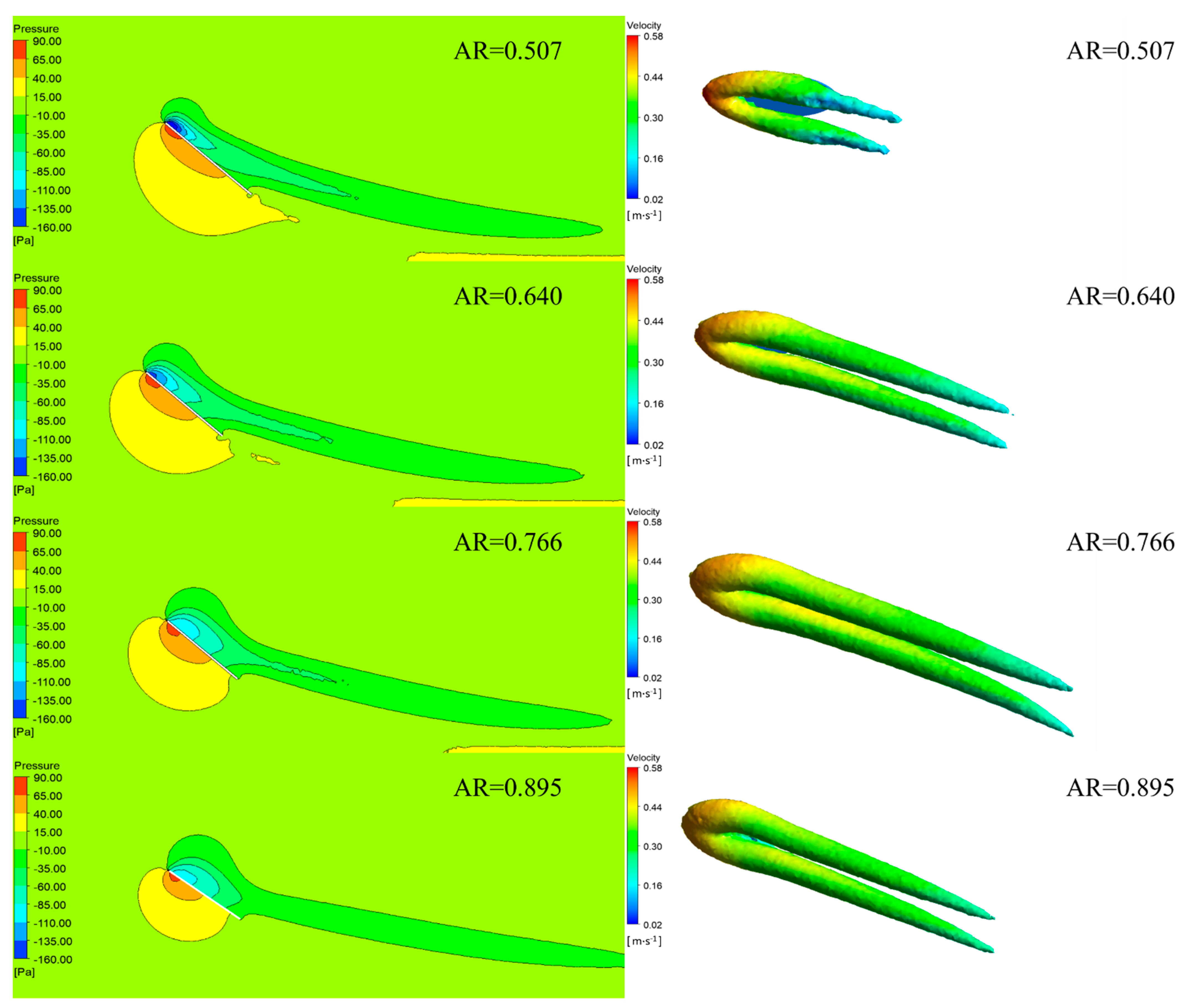
3.6. Flow Distribution around the Otter Board
3.7. Optimal Aspect Ratio of the Otter Board
4. Discussion
5. Conclusions
- When the Reynolds number is larger than 1.682 × 105, the symmetrical elliptic otter board model is within the critical Reynolds number region, and its hydrodynamic coefficient is consistent with the real otter board.
- The maximum lift coefficient firstly increases and then decreases with the increasing aspect ratio, while the drag coefficient and the lift-to-drag ratio fluctuate.
- The volume of the wing-tip vortex reaches the maximum when the aspect ratio is 0.766, and then it begins to decrease and the lift coefficient decreases when the aspect ratio is larger than 0.766.
- When the aspect ratio is 0.766, the symmetrical elliptic otter board has the best hydrodynamic performance, and its maximum lift coefficient and lift-to-drag ratio are 1.05 and 1.14 fold that of the prototype otter board, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, J.Z. Fishing Gears and Fishing Mythology; China Agriculture Press: Beijing, China, 1996; pp. 116–125. [Google Scholar]
- Niedzwiedz, G.; Hopp, M. Rope and net calculations applied to problems in marine engineering and fisheries research. Arch. Fish. Mar. Res. 1998, 46, 125–138. [Google Scholar]
- Yang, L. Energy saving of trawl gears. J. Zhanjiang Ocean Univ. 2000, 20, 76–78. [Google Scholar]
- Sterling, D. The Physical Performance of Prawn Trawling Otter Boards and Low Opening Systems. In AME CRC Report, Project 1.4.4; Sterling Trawl Gear Service: Brisbane, Australia, 2000; p. 204. [Google Scholar]
- Wang, M.Y.; Wang, J.H.; Zhang, X.; Yu, Y.F.; Xu, B.S. Hydrodynamic characteristics of vertical V type otter board. J. Fish. China 2004, 28, 311–315. [Google Scholar]
- Liu, J.; Huang, H.L.; Chen, S.; Li, L.Z.; Wu, Y.; Xu, G.D.; Rao, X. Hydrodynamic characteristics of low aspect ratio vertical cambered otter board. J. Fish. China 2013, 37, 1742–1749. [Google Scholar] [CrossRef]
- Xu, Q.C.; Huang, L.Y.; Zhao, F.F.; Wang, X.X.; Tang, Y.L.; Liang, Z.L.; Wan, R.; Sun, P.; Liu, C.D. Study on the hydrodynamic characteristics of the rectangular V-type otter board using computational fluid dynamics. Fish. Sci. 2017, 83, 181–190. [Google Scholar] [CrossRef]
- Sala, A.; Farran, J.; Antonijuan, J.; Lucchetti, A. Performance and impact on the seabed of an existing- and an experimental-otter board: Comparison between model testing and full-scale sea trials. Fish. Res. 2009, 100, 156–166. [Google Scholar] [CrossRef]
- Sterling, D. An Investigation of Two Methods to Reduce the Benthic Impact of Prawn Trawling. In FRDC Report, Project No. 2004/060; Fisheries Research and Development Corporation: Deakin West, Australia, 2008; p. 96. [Google Scholar]
- Sterling, D. Design, Build and Test Model Batwing Board CP2. In FRDC Report, Project No. 2008/07; Fisheries Research and Development Corporation: Deakin West, Australia, 2010. [Google Scholar]
- Hu, F.; Tokai, T.; Kinoshita, H.; Kumazawa, T. High-Lift Otter Board. U.S. Patent US8943736, 3 February 2015. [Google Scholar]
- Takahashi, Y.; Fujimori, Y.; Hu, F.X.; Shen, X.L.; Kimura, N. Design of trawl otter boards using computational fluid dynamics. Fish. Res. 2015, 161, 400–407. [Google Scholar] [CrossRef]
- Xu, Q.C.; Huang, L.Y.; Zhao, F.F.; Wang, X.X.; Tang, Y.L.; Liang, Z.L.; Wan, R.; Sun, P.; Liu, C.D.; Cheng, H.; et al. Effects of aspect ratio on the hydrodynamic performance of full-scale rectangular otter board: Numerical simulation study. Ocean Eng. 2017, 142, 338–347. [Google Scholar] [CrossRef]
- Xu, Q.C.; Feng, C.L.; Huang, L.Y.; Xu, J.Q.; Wang, L.; Zhang, X.; Liang, Z.L.; Tang, Y.L.; Zhao, F.F.; Wang, X.X.; et al. Parameter optimization of a double-deflector rectangular cambered otter board: Numerical simulation study. Ocean Eng. 2018, 162, 108–116. [Google Scholar] [CrossRef]
- Xu, Q.C.; Huang, L.Y.; Li, X.S.; Li, Y.Y.; Zhao, X.Y. Parameter optimization of a rectangular cambered otter board using response surface method. Ocean Eng. 2020, 220, 108475. [Google Scholar] [CrossRef]
- Huang, L.Y.; Li, Y.Y.; Xu, J.Q.; Xu, Q.C.; Zhao, F.F.; Wang, X.X.; Tang, Y.L.; Jia, M.X.; Liang, Z.L. Effect of Aspect Ratio on the Hydrodynamic Performance of Circular Cambered Otter Board. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Huang, L.Y.; Li, Y.Y.; Jia, M.X.; Wang, G.; Feng, C.L.; Zhao, F.F.; Xu, Q.C.; Cheng, H. Analysis and Optimization on the Hydrodynamic Performance of Hollow Otter Board in Antarctic Krill Trawl. In Proceedings of the Thirtieth International Ocean and Polar Engineering Conference, Shanghai, China, 11–16 October 2020; pp. 1786–1793. [Google Scholar]
- You, X.X.; Hu, F.X.; Kumazawa, T.; Shiode, D.; Tokai, T. Performance of new hyper-lift trawl door for both mid-water and bottom trawling. Ocean Eng. 2020, 199, 106989. [Google Scholar] [CrossRef]
- Wang, G.; Huang, L.Y.; Wang, L.; Zhao, F.F.; Li, Y.Y.; Wan, R. A metamodeling with CFD method for hydrodynamic optimisations of deflectors on a multi-wing trawl door. Ocean Eng. 2021, 232, 109045. [Google Scholar] [CrossRef]
- Xu, B.S.; Zhang, X.; Wang, M.Y. A review on the trawl otter board evolution. J. Fujian Fish. 2010, 1, 86–90. [Google Scholar]
- Filippini, G.; Maliska, C.R.; Vaz, M. A physical perspective of the element-based finite volume method and FEM-Galerkin methods within the framework of the space of finite elements. Int. J. Numer. Methods Eng. 2014, 98, 24–43. [Google Scholar] [CrossRef]
- Balash, C.; Sterling, D.; Broadhurst, M.; Dubois, A.; Behrel, M. Hydrodynamic Evaluation of a Generic Sail Used in an Innovative Prawn-Trawl Otter Board. In Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering OMAE2015, St. John’s, NL, Canada, 31 May–5 June 2015; p. 6. [Google Scholar]
- Xu, Q.C.; Huang, L.Y.; Liang, Z.L.; Zhao, F.F.; Wang, X.X.; Wan, R.; Tang, Y.L.; Dong, T.W.; Cheng, H.; Xu, J.Q. Experimental and Simulative Study on the Hydrodynamics of the Rectangular Otter Board. In Proceedings of the 2nd Annual International Conference on Advanced Material Engineering, Wuhan, China, 15–17 April 2016; pp. 431–437. [Google Scholar]
- Yamasaki, S.; Matsushita, Y.; Kawashima, T.; Tomiyama, M.; Kumazawa, T.; Hirayama, M. Evaluation of a conventional otter board used in trawl fishery in Ise-wan Bay and proposal of a new design. Nippon Suisan Gakkaishi 2007, 73, 220–225. [Google Scholar] [CrossRef]
- Sun, C.L.; Yu, B.L.; Jiang, S.C.; Zhou, G.J.; Liu, D.Y.; Wang, Z.T. A study on otter board with two gaps for small single trawlers. Shandong Fish. 1998, 15, 13–15. [Google Scholar]






| Model | Wing Span/mm | Chord/mm | Aspect Ratio | Plane Area/m2 |
|---|---|---|---|---|
| Prototype | 1200 | 2400 | 0.637 | 2.261 |
| 1 | 216 | 540 | 0.507 | 0.092 |
| 2 | 240 | 480 | 0.640 | 0.090 |
| 3 | 264 | 440 | 0.766 | 0.091 |
| 4 | 287 | 410 | 0.895 | 0.092 |
| Hydrodynamic Characteristics | Aspect Ratio | |||
|---|---|---|---|---|
| 0.507 | 0.640 | 0.766 | 0.895 | |
| Critical AOA | 40° | 40° | 40° | 35° |
| CL at critical AOA | 1.098 | 1.172 | 1.263 | 1.200 |
| CD at critical AOA | 1.090 | 1.260 | 1.257 | 1.322 |
| K at critical AOA | 1.008 | 0.931 | 1.005 | 0.859 |
| KMAX | 2.005 | 1.797 | 2.132 | 2.210 |
| AOA at KMAX | 10°~15° | 15° | 15° | 10° |
| CL at 30° AOA | 0.904 | 0.983 | 1.033 | 1.094 |
| CD at 30° AOA | 0.635 | 0.795 | 0.731 | 0.895 |
| K at 30° AOA | 1.424 | 1.236 | 1.413 | 1.223 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, G.; Xu, Q.; Wang, X.; Zhang, R.; Huang, L. Study of the Influence of Aspect Ratios on Hydrodynamic Performance of a Symmetrical Elliptic Otter Board. Symmetry 2022, 14, 1566. https://doi.org/10.3390/sym14081566
Li Y, Wang G, Xu Q, Wang X, Zhang R, Huang L. Study of the Influence of Aspect Ratios on Hydrodynamic Performance of a Symmetrical Elliptic Otter Board. Symmetry. 2022; 14(8):1566. https://doi.org/10.3390/sym14081566
Chicago/Turabian StyleLi, Yuyan, Gang Wang, Qingchang Xu, Xinxin Wang, Rongjun Zhang, and Liuyi Huang. 2022. "Study of the Influence of Aspect Ratios on Hydrodynamic Performance of a Symmetrical Elliptic Otter Board" Symmetry 14, no. 8: 1566. https://doi.org/10.3390/sym14081566
APA StyleLi, Y., Wang, G., Xu, Q., Wang, X., Zhang, R., & Huang, L. (2022). Study of the Influence of Aspect Ratios on Hydrodynamic Performance of a Symmetrical Elliptic Otter Board. Symmetry, 14(8), 1566. https://doi.org/10.3390/sym14081566






