1. Introduction
Novel coronavirus pneumonia was first discovered in China in December 2019, and until now the number of confirmed cases has reached hundreds of millions worldwide. COVID-19 is highly life threatening to living organisms, and severe disease can present with dyspnea, shock and even multiple organ failure. Since 2021, there have been many cases of local infection in small areas in China. Unlike the initial period of the sudden outbreak of the epidemic in Wuhan, China now has adequate and complete prevention and control measures. First, cases are quarantined and treated immediately, then all possible dense contacts are traced back to the source, isolated and nucleic acid tested. Finally, the risk level of cases and areas where dense contacts have occurred is raised and local areas are blocked. Aggregation is strictly prohibited and nucleic acid tests are conducted on all personnel in the region. Minimize the spread of the epidemic as quickly as possible. The results of prevention and control are impressive. Cases in cities can be quickly cleared and kept under control without affecting the normal life of the people as much as possible.
It can be seen that case activity tracking is similar to building a graph, where each case’s activity route and regions are related to each other, forming a graph network, and regions are nodes. This spatial association has a significant role in predicting the spread trend of infectious diseases. Therefore, for predicting the epidemic transmission trend in the future, scientific prevention and control of the epidemic, and precise implementation of policies, monitoring the spatial and temporal data characteristics of infectious cases is very important and effective.
Currently, there are two data-driven methods to predict the spread trend of epidemic: methods based on time series and methods based on spatial–temporal sequence.
As predicting the infectiousness of COVID-19 is relevant to time series, methods based on time series have mostly been applied. In terms of time series data, the commonly used method is autoregressive integrated moving average (ARIMA). For example, Pan et al. [
1] proposed an ARIMA-based infectious disease prediction model, Mekparyup et al. [
2] established an unconstrained seasonal ARIMA infectious disease prediction model, Anwar et al. [
3] introduced environmental and climate data into ARIMA-built prediction models, and Roy et al. predicted the trend of epidemic in India based on ARIMA [
4]. However, these models require stable time series data and cannot predict the spread trend with nonlinearity.
In response to this, machine learning methods such as Support Vector Regression (SVR) method [
5,
6,
7] and Extreme Gradient Boosting (XGBoost) method [
8,
9] can effectively process non-linear data and obtain higher prediction accuracy. Using general prediction methods based on deep learning, such as Gate recurrent unit (GRU) [
10], Multi-channel LSTM [
11,
12], and LSTM-RNN [
13], which are based on attention mechanisms, can extract more complex and high-dimensional data to predict trends.
Theoretically, measuring the spread trend of epidemics should take into account not only the time dimension (i.e., the number of new infections per day), but also the spatial dimension (i.e., the number of new infections in different cities or regions). Models based on time series data do not take into account the spatial dimension between different nodes, so it is difficult to capture spatial correlation [
14]. Therefore, a spatial–temporal series data-driven approach is proposed. Graph Convolutional Network (GCN) can efficient capture location information and process high-dimensional data, which makes it useful for capturing spatially related features, such as intelligent transportation [
15,
16], behavior recognition [
17,
18], and epidemic trend prediction [
19,
20]. In predicting epidemic trend of infectious diseases, Derr et al. [
19] proposed Epidemic Graph Convolutional Network (EGCN) to capture the spatial characteristics of disease transmission by analyzing the characteristics of an infectious disease transmission network. Heo et al. [
20] used GCN models in the analysis of epidemic space–time data. Graphic convolution networks capture geospatial characteristics, and gated loop units capture temporal dynamics.
However, these methods also have two shortcomings:
The distribution of weights is inaccurate due to the lack of consideration for the importance ranking of features and the lack of attention to important features. For example, a period of time with a larger migration index should have a greater impact on outcomes, and the epidemic transmission of infectious diseases in a region is more affected by its neighboring regions, which cannot be generalized.
Lack of explanation for the results. End-to-end model processing and output results belong to black-box processing, which cannot be traced back to the source and lacks some confidence.
In view of the above problems, this paper mainly makes the following work:
The spatial map information is innovatively introduced into the data, that is, the intensity of association adjacency matrix between risk areas is constructed to represent the relationship between regions and neighborhood characteristics, and to improve the sensitivity of the model to the spatial information of the data.
A prediction model STAGCN based on a space–time series is proposed. The model introduces the attention mechanism to adaptively assign the feature weights of epidemic data in different time periods, and adaptively extracts the spatial information of epidemic data using the attention network. We use the time series model LSTM to compare the effect with the model, and take STACN as the benchmark model to evaluate the generalization ability of the time series and time series models.
The migration index in explainable data is analyzed and interpreted using explanatory methods, taking cities as units.
The structure of this paper is arranged as follows: First, we introduce the data source and composition, then we explain the structure of the benchmark model STGCN and how we can improve on the basis of STGCN to get our proposed model STAGCN, and then introduce the structure of STAGCN in detail. In the next step, we introduce the experiment and result analysis, and finally analyze the interpretability of migration index.
2. Materials and Methods
2.1. Data Description
The experimental data used in this paper are from a desensitized infectious disease dataset provided by a platform from Xi’an, Shaanxi province [
21]. There are 5 cities and 392 regions in the infectious disease data set, with a total of 2,154,184 data records. This data set describes the specific information of infectious diseases in all cities and regions in detail, and provides enough data support for the following model experiments. The goal of our experiment is to predict the number of new infections in the next few days. The data set counts the daily number of new infections of infectious diseases for 60 days from 1 May 2020 to 29 June 2020. The original data set mainly includes the following files:
Migration Data: Indicates the migration of people between different cities. The geographic units are cities.
Grid Density Data: Indicates the current population density of a grid. The geographic units are grids.
Transfer Data: Indicates the intensity of population migration between different grids in a city. The intensity of migration of human traffic is used to indicate the degree of association. The geographic unit is the grid, and the time unit is the hour.
Grid Attribution Area Data: Indicates that a grid belongs to an area. Indicates ownership: The grid belongs to an area.
Infection Data: Indicates the number of new infections per day added to each region of a city, and also indicates the attribution: the area belongs to the city.
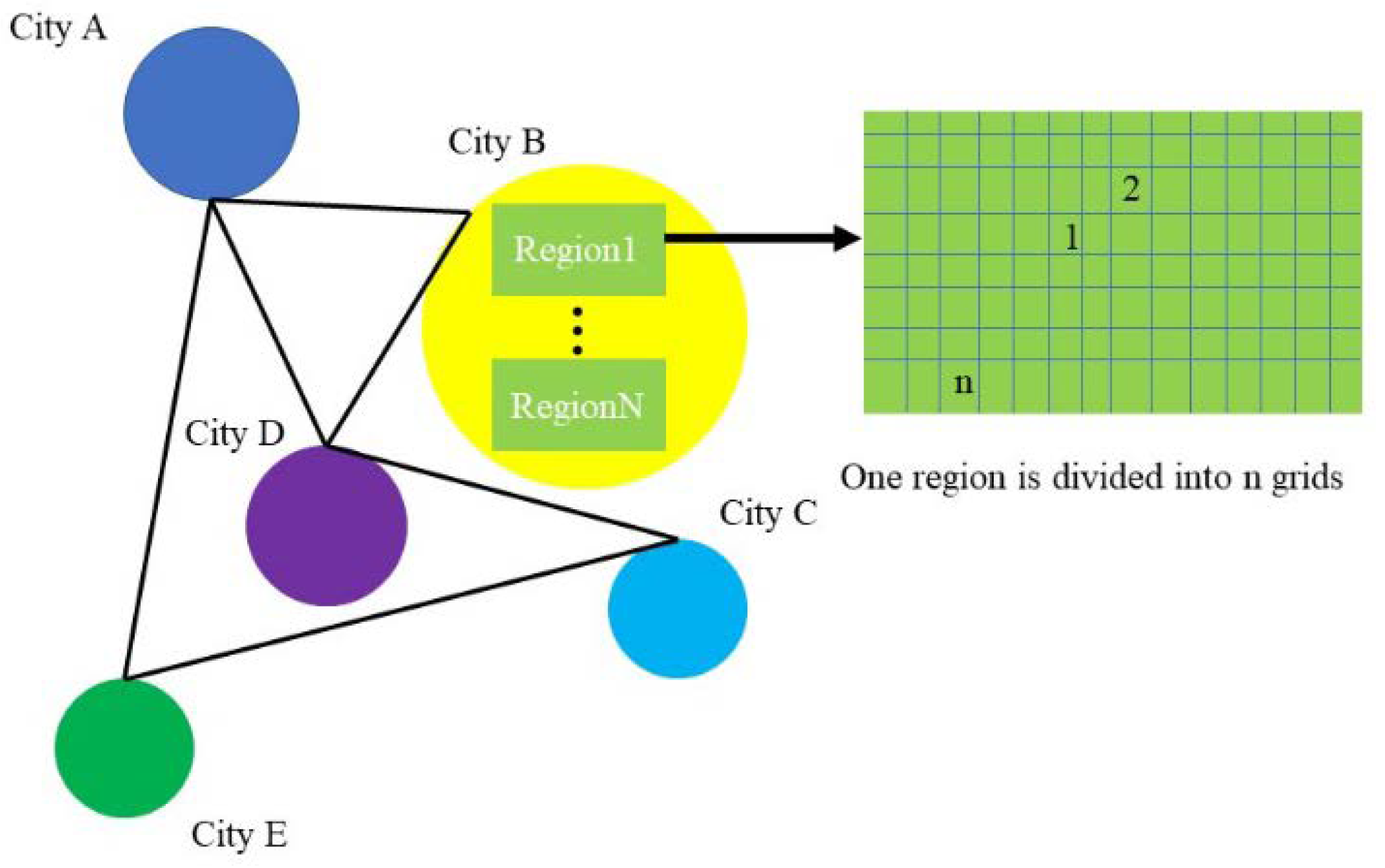
The original data divides a city into areas with their own ID, each of which is densely divided into rectangular grids (in grids), each of which uses four latitude and longitude coordinate points to determine the extent of the area and the grid’s center coordinate to uniquely identify the grid (
Figure 1).
The daily characteristics of each area in each city are shown in the following table (
Table 1). Among them, cities are named with “capital letters”, such as city “A”, and regions are named with “capital letters Arabic numerals”, which is the administrative region of the city, such as region “A_0”. According to the statistics of the distribution of the data set, city C has the largest number of regions, totaling 135, and city B has the smallest number of regions, totaling 30.
Each region contains a period of time series features, so it is necessary to aggregate different features of infectious disease data into one feature, and use this feature to represent the attributes of a regional node, so as to ensure that the time information and spatial information of infectious disease data can be simultaneously input into the model for training and learning (
Figure 2). For all the existing features, the corresponding feature aggregation is required, and the calculation process is shown in Formula (1).
represents the characteristic value of infectious diseases,
represents the corresponding weight of features,
represents the number of features, and
represents the new feature vector set generated by aggregation.
After unifying the time and geographical units, the data features are aggregated to get a region feature file (Region Features), using represents all the regional features of the days, represents the features of the day.
In the process of epidemic prevention and control, each person’s range of activities will associate regions, and each area will become nodes. The degree of association between different regions is the aggregation of people’s activities. Thus, an appropriate graph network can be constructed to represent the spatial characteristics of data. The adjacency matrix is a good data structure to store the network information of a graph. Therefore, we aggregate the region-based intensity data based on the grid’s intensity data, and construct an adjacency matrix from it.
2.2. Construction of Adjacency Matrix
The correlation degree of regions can better reflect the connectivity between different regions. For example, there are different degrees of correlation between the 10 regions of city a and the 8, 9, 11 and 12 regions of city A, which means that they are connected with each other, but the strength of connection is different. The correlation strength between the 10 regions of city a and the regions of other cities such as city B and C is zero, that is, there is no connectivity. The association strength of the region is constructed as an adjacency matrix, which is used as the information supplement when the graph attention network is used to adaptively aggregate the characteristics of the nodes in the neighborhood region, which is helpful to improve the prediction accuracy of the model.
The corresponding adjacency matrix
is constructed based on the data of regional correlation degree, and each element
in the adjacency matrix is calculated as shown in the Equation (2).
The in equation (2) represents the degree of correlation between region and region . and is the threshold that controls the distribution and sparsity of the adjacency matrix. Depending on the actual situation, the and are specified as 10 and 0.5, respectively.
Connectivity between 392 regions in 5 cities in infectious disease data was calculated and an adjacency matrix e was obtained. To visualize the input and output forms of the data during the construction process, the results are shown in
Figure 3.
The data format of the correlation matrix
e is shown in
Table 2.
Finally, we use the and adjacency matrix as the input data.
2.3. STAGCN
2.3.1. STGCN
Traditional convolution neural networks have limited ability to process graph data, because the local structure of each node in the graph data is different, which results in the loss of translation invariance. Due to the ubiquitous existence of graph data, the deep learning model constructed on the graph is gradually active, and the Graph Convolutional Network (GCN) has become an extremely important one [
22]. There are two main methods to build graph convolution neural networks: spectral method and spatial method. The spectral method is mainly based on the convolution operator in the frequency or spectral domain of the Fourier transform. The spatial method is based on the spectral method to parameterize the convolution kernel and use the attention mechanism, serialization model and other means to model the weights between nodes [
18]. The process of defining the graph convolution operator is shown in the Equation (3).
represents the feature information of node on layer , represents the normalization factor, represents the weight matrix of the nodes, represents the feature information of target node on layer . The convolution process can be summarized as transferring the feature information of a node to a neighborhood node, which aggregates its own feature information with the feature information transmitted from the neighborhood. At the same time, an activation function is introduced to transform the nodes to enhance the expressive ability of the model.
The STGCN network reconstructs the predicted space-time convolution modules, each consisting of two time-gated convolutions, one space map convolution, and one time-gated convolution consisting of a 1D convolution and a GLU unit, where the kernel width of the 1D convolution is , the spatial map convolution is the Graph Convolution Neural Network Layer (GCN). This configuration not only greatly reduces the consumption of time-dependent feature capture, but also captures global information through convolution layer.
However, it still has the problem of inaccurate weight distribution. Graphic convolution network (GCN) aggregates neighborhood node information to extract spatial information of data. It is only a simple standardization for the aggregation and calculation of neighborhood node characteristics, and the weights of different neighborhood nodes are the same. Therefore, based on this improvement, we propose our own network framework STAGCN.
2.3.2. STAGCN
The model mainly includes two ST-Blocks and one Output layer. ST-Block inherits the sandwich structure of STGCN network and makes its own improvements. The model first receives the pre-processed data and the adjacency matrix
. After ST-Block processing, the model outputs the daily number of new infections in all areas of the city from the Output layer, which is shown in
Figure 4.
The ST-Block network structure is shown in
Figure 5. The upper and lower layers are time-gated attention convolution network layers (TGACN), and the middle layer is a spatial graphical attention network layer (SGAT). In order to effectively solve the problem of model prediction weight misalignment, we introduced the Attention mechanism into time-gated convolution (TGCN) to become a new time-gated attention convolution (TAGCN), which adaptively assigns weights to infectious disease data at different time steps, thus improving the model’s ability to focus on time information of infectious disease data. The spatial map convolution (GCN) is improved. Graphic Attention Network (GAT) is used to extract the spatial features of infectious disease data, improve the representation of node features, and introduce adjacency matrix to supplement the spatial information of infectious disease data.
Enter
in module. After learning from the multilayer network in the module, the final output is
, as shown in Equation (4).
is the spectral core of the convolution. represents a graph convolution operator used to extract the spatial characteristics of infectious diseases. Define the Fourier transform on the graph, convolute the spatial structure information of the nodes in the GCN, and then use the convolution operator find the basis vectors of the Fourier transform to describe the local structure of the region nodes. and is the time kernel of time-gated attention convolution network layers in the space–time map convolution module to extract the time characteristics of infectious diseases. is an activation function and refers to the graph information.
2.3.3. The TAGCN Layer of ST-Block
The STGCN model [
22] mainly captures the temporal characteristics of infectious diseases in the time dimension through the time-gated convolution network. The time gated convolution layer is composed of one-dimensional convolution and nonlinear gated linear units, in which the kernel width of one-dimensional convolution is
. For each regional node of infectious disease epidemic network, make the channel
, where
represents the number of channels, the input is an infectious disease sequence
with length
. Convolution kernel
is used to map the input infectious disease sequence
to a single output element [
P,
Q] (
P and
Q are divided by the same channel size). Therefore, the time-gated convolution network is defined as Equation (5).
P and Q in Equation (5) are the inputs of gated linear unit, represents Hadamard product, and is the set of real number, is used to control the correlation between the current state P and the composition structure and dynamic change of time series. Based on the network layer, we introduce the attention mechanism so as to improve the attention ability of the model to the time information of infectious disease data.
As shown in
Figure 6, in the attention layer, the network layer inputs the infectious disease data
of
steps, there is a dependency between the infectious disease data of each time step and the data of the next time step, and each time step will generate an implicit state value
. The attention layer obtains the correlation coefficient
by calculating the implicit value
of each time step and the implicit value
generated in the t time step. Finally, the attention coefficient conforming to the probability
is obtained by normalizing the softmax layer. Multiply the infectious disease data of each time step to obtain the infectious disease data of
time steps
(i.e., the next day).
2.3.4. The SGAT Layer of ST-Block
The Graphic Attention Network Layer is composed of two Graphic Attention Network (GAT) [
20] overlays, as shown in
Figure 7.
The input
is the region information of a set of epidemic epidemic networks processed by the time-gated attention convolution network, where
is the historical number of days of infectious disease,
is the kernel width of one-dimensional convolution, and
is the characteristic dimension of the area nodes, that is, each input is the infectious disease area node, and each area node has
feature information. Producing predicted regional node feature information
from the attention layer, which represents the regional node characteristics of the output prediction, with
feature information for each regional node. For better expressive ability, the layer of attention needs several linear transformations based on the input infectious disease characteristics to obtain higher-level features. First, we consider the influence of edge weights between neighbor nodes on the relationship between two nodes. We introduce the adjacency matrix
of epidemic disease network as information complement between nodes, and
transformation for node
. Then, a weight matrix
is trained for all the region nodes, and a shared attention mechanism, self-attention, is applied to each region node of the epidemic network to calculate the attention factor
. The formulas for calculating them are as follows (6).
where
is a function of calculating the correlation degree of two regional nodes (eigenvectors), it is implemented by a single-layer feed-forward neural network parameterized by the weight vector
. The masked attention is also introduced into the epidemic network structure. The function of masked attention is to compute only the first-order neighbor region node
, the region node
, and the interval area node is not obscured as a neighbor area node of area node
. Considering the convenience and comparability of correlation coefficient calculation, the first-order neighbor region node
regularization of all region nodes
is performed using the softmax function, for example, Equation (7).
After adding leaky relu nonlinear activation function, the attention coefficient is calculated as Equation (8).
The attention coefficient calculated by Equation (5) is used to calculate the linear combination of corresponding features. After aggregating the features of all neighbor regional nodes, the output feature
of each regional node is predicted, calculated as Equation (9).
Compared with graph convolution neural network (GCN), the node characteristics of neighbor regions are standardized and summed in a graph convolution operation, as shown in Equation (10).
Graph attention network (GAT) replaces the standardized operation in graph convolution neural network with attention mechanism, adapts and learns the weight coefficient, and finally aggregates the node characteristics of neighbor regions. Through the superposition of the attention layer of the graph, the structure of the epidemic network of infectious diseases is gradually topological, and the migration index of infectious disease data is introduced as the adjacency matrix to supplement the importance between neighborhood nodes, which improves the ability to capture the spatial characteristics of the epidemic network of infectious diseases.
2.3.5. The Output Layer of STAGCN
After two ST-Block processing, the output layer of the model is composed of time gated attention convolution network layer (TGACN) and fully connected networks layer (FCN), as shown in
Figure 8.
After the second ST-Block, the output is
, after gating, pay attention to convolution network layer output to obtain
, and then the one-step prediction value
is obtained by linear change mapping on channel
by the fully connected network layer. The loss function predicted by the infectious disease model uses L2, so its calculation formula is shown in Equation (11).
where
is the prediction result of infectious disease model,
is the true value,
is the relevant training parameter.
3. Experiments and Results
The experimental data comes from the data set of the transmission trend prediction competition of highly pathogenic infectious diseases [
23]. The data of the first 45 days are divided into model training set and verification set, and the remaining 15 days are used as the test set of the model.
The model is run on a Linux server (CPU: 4 cores, GPU: Tesla V100, video memory: 16GB, RAM: 32GB). We will train 60 epochs for the model, set the learning rate to 0.005, and the optimizer defaults to Adam to predict the number of new infections in each region in the next 15 days. In order to test and evaluate the performance of the model, we will use RMSE and RMSLE as error evaluation indexes. The benchmark model selects the common prediction model of infectious disease transmission trend: (1) ARIMA [
24]; (2) LSTM [
25]; and (3) STGCN [
26].
Calculate the error evaluation indexes RMSE and RMSLE of different prediction models under 5 days, 10 days and 15 days. The results are shown in
Table 3.
The error evaluation indexes of STAGCN model based on spatial–temporal sequence data are basically smaller than other benchmark models, which shows that the improved STAGCN model can effectively capture the spatial–temporal characteristics of infectious disease data, and the prediction error results are better than other methods. As can be seen from
Figure 9, the RMSLE value of STAGCN model is 8.59%, 7.76% and 12.30% lower than that of STAGCN model, respectively.
In order to verify the improvement effect of our model, we conducted model ablation experiment, controlled other network layers to remain unchanged, and deleted a specific network layer to observe the prediction accuracy of the model. The results are shown in
Table 4 and
Figure 10.
It is obvious from the chart that the prediction effect will decline in varying degrees after removing the Attention layer or GAT layer in the model. The model error of STAGCN proposed by us is the smallest. Therefore, the attention mechanism and GAT introduced can better improve the prediction accuracy of the model.
Finally, our STAGCN model is used to fit the infectious disease data set. From
Figure 11, it can be seen that the fitting effect of the model is obviously better than that of other models.
In addition to the above analysis of the experimental results, this paper starts with several problems that can best reflect the scenario of infectious disease prediction task, and gets the benchmark list for analysis and display.
The points listed in the table are the most relevant to the method of this paper, and they are the key points that need to be faced and dealt with in the task of infectious disease prediction. The first is the time evolution characteristics. In recent years, most of the research on the prediction of infectious diseases has focused on this point. ARIMA and LSTM have better time series performance. Papers [
24,
25,
27,
28] all use time series data to improve or compare ARIMA and LSTM to predict the growth trend and mortality of infectious diseases in the future, without paying attention to the spatial factors of infectious disease transmission. The second is the spatial characteristics. The spatial transmission characteristics of infectious diseases have great research value and practical significance. Therefore, as shown in article [
29], the author improved the spatial generalized linear mixed model, and got the spatial-temporal prediction model, simulating the predicted quantity, and getting the influence of spatial diffusion. In article [
30], the author constructed the model according to the spatial-temporal characteristics of the number of infected people, which was used to predict and allocate emergency medical resources. On the basis of temporal and spatial characteristics, we should further consider the importance and influence of different spatial characteristics. For example, in the paper [
31], the author constructed and trained the spatial-temporal model based on Bayesian hierarchical spatial-temporal SEIR model, which predicted the spread of illness and death and the spatial-temporal variability in small areas of Britain, pointed out the key factors, and put forward valuable suggestions for regional prevention and control.
As shown in
Table 5, the content of comparison is based on whether the compared works cover the questions raised, with 25 score for each point, totaling four points. Compared with ours, Benchmark#1 [
27] only covers one point, and Benchmark#2 [
28] and Benchmark#3 [
30] cover only two points, while our work covers all.
5. Conclusions
Our data set is very comprehensive, covering almost a series of characteristics that lead to the spread of the virus. Based on this, our model takes into account the temporal and spatial characteristics, and uses attention mechanism to enhance the model’s attention to important characteristics, thus improving the prediction level of the number of infected people from all aspects of data and methods, according to the results of the experiments, we can see the best accuracy and the smallest error compared with other time or spatial-temporal series models.
Through our research, it is proved that spatial characteristics have an important influence on epidemic prevention and control, and how to effectively reduce spatial mobility is the key to reduce the number of infected people. Therefore, through interpretable analysis of migration index, we pointed out the direction and suggestions for spatial prevention and control from the perspective of scientific analysis, and provided scientific guarantee for perfecting the epidemic prevention and control management mechanism.
However, our method still has some shortcomings. From the data point of view, we do not take into account the incubation period of the virus and the special migration situation in various holidays. Methodologically, we only applied the attention mechanism to the characteristics of time dimension, but the more important migration matrix did not do this, and could not get the arrangement of urban areas with serious epidemic situation. In the future, we will improve from these two directions to further optimize the forecasting ability.