New Results and Open Questions for SIR-PH Epidemic Models with Linear Birth Rate, Loss of Immunity, Vaccination, and Disease and Vaccination Fatalities
Abstract
:1. Introduction
2. The SAIRS Model with Linear Birth Rate
- 1.
- and denote the average birth and death rates in the population (in the absence of the disease), respectively.
- 2.
- The parameters and denote the infection rates for infective and exposed individuals, respectively;
- 3.
- is the vaccination rate, is the rate at which the exposed individuals become infected or recovered, denotes the rate at which immune individuals lose immunity (this is the reciprocal of the expected duration of immunity), is the rate at which infected individuals recover from the disease.
- 4.
- , , are rates of transfer from E to I and R, respectively.
- 5.
- is the extra death rate in the infected compartment due to the disease.
- 1.
- 2.
2.1. Some History of the SEIRS and SAIRS Varying Population Models
- 1.
- ([17], Thm 2.1) proves the global stability of the DFE when(by using the Lyapunov function , which is different from the Lyapunov function used in [33], . This leaves open the case , when the DFE is locally, but perhaps not globally stable, and also the question of choosing the “most performant” Lyapunov function.
- 2.
- ([17], Thm 2.1) establishes global stability of a unique endemic point in certain cases and suggests that outside those cases, “there may exist stable periodic solutions”.
2.2. Warm-Up: The Weak Alternative for the DFE Equilibrium
- 1.
- If then the disease-free equilibrium is locally asymptotically stable.
- 2.
- If , the disease-free equilibrium is unstable.
2.3. The Endemic Point for the FA Approximation, and the Determinant Formula
3. A Review of Arino and Rank-One SIR-PH Models
3.1. SIR-PH Models with Demography, Loss of Immunity, Vaccination and One Susceptible and One Removed Classes
- 1.
- is a row vector whose components model a set of disease states (or classes).
- 2.
- accounts for individuals who recovered from the infection.
- 3.
- B is a matrix, where each entry represents the force of infection of the disease class i onto class j. We will denote by the vector containing the sum of the entries in each row of B, namely, .
- 4.
- A is a Markovian sub-generator matrix (i.e., a Markovian generator matrix for which the sum of at least one row is strictly negative), where each off-diagonal entry , , satisfies and describes the rate of transition from disease class i to disease class j; while each diagonal entry satisfies and describes the rate at which individuals in the disease class i leave towards non-infectious compartments. Alternatively, is a non-singular M-matrix [8,49]. (Recall that an M-matrix is a real matrix V with and having eigenvalues whose real parts are nonnegative [50].)
- 5.
- is a row vector describing the death rates in the disease compartments, which are caused by the epidemic.
- 6.
- is the rate at which individuals lose immunity (i.e., transition from recovered states to the susceptible state).
- 7.
- is the rate at which individuals are vaccinated (immunized).
- 1.
- Note that is a vector with a well-known probabilistic interpretation in the theory of phase-type distributions: it is the column vector that completes a matrix with negative row sums to a matrix with zero row sums.
- 2.
- A particular but revealing case is that when the matrix B has rank 1 and is necessarily hence of the form , where is aprobability column vectorwhose components represent the fractions of susceptibles entering into the diseased compartment j when infection occurs. We call this case “rank one SIR-PH”, following Riano [49], who emphasized its probabilistic interpretation—see also [51], and see [52] for an early appearance of such models.
3.2. The Eigenstructure of the Jacobian for the SIR-PH Scaled Model
3.3. The Basic Reproduction Number for SIR-PH, via the Next Generation Matrix Method
- 1.
- The unique disease-free equilibrium is
- 2.
- The DFE is locally asymptotically stable if and is unstable if , wherewhere , (see 26), and denotes the (dominant) Perron Frobenius eigenvalue.
- 3.
- For of rank one, we further have
- (a)
- (b)
- The critical vaccination defined by solving with respect to is given by
3.4. The Endemic Point of the SIR-PH-FA Model
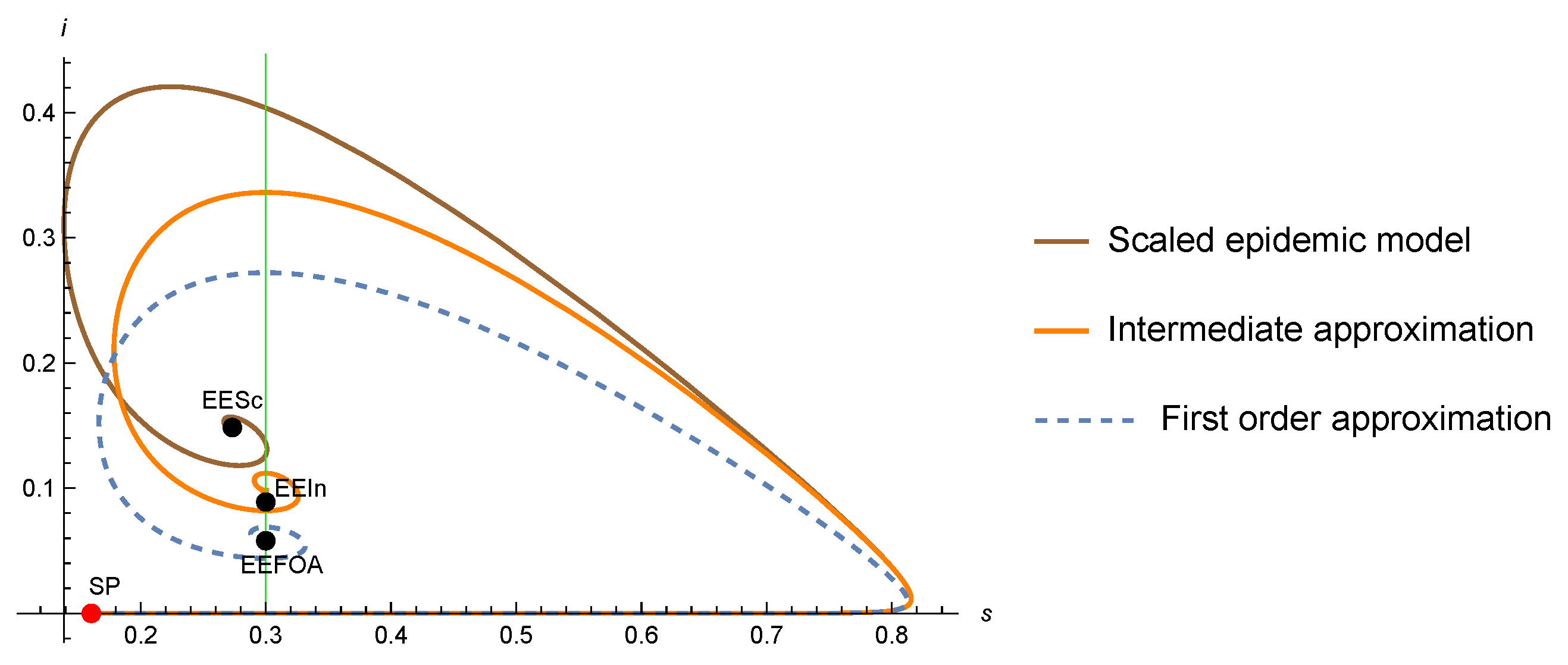
4. A Glimpse of the Intermediate Approximation for the SIR-PH Model
- 1.
- The DFE points of the scaled, the intermediate approximation, and the FA are equal, given by .
- 2.
- An endemic point must satisfy that is a positive eigenvector of the matrix for the eigenvalue 0 (same as for theFA), thatand thatSince this equation is quadratic (see (41)), we may have a priori two, one, or zero endemic points.
5. The Scaled SAIRS Model: Existence, Uniqueness, and Local Stability of the Endemic Point
5.1. Reduction to One Dimension and the Problem of Existence of Endemic Equilibrium
5.2. Conjecture for the SEIRS Model
6. Conclusions and Further Work
- 1.
- 2.
- 3.
- Study the scaled model as a perturbation of the FA model.
- 4.
- Study stability via the geometric approach of Li, Graef, Wang, Karsai, Muldoney, and Lu [15].
- 5.
- We hope that the use of more sophisticated and fast software will allow researchers in the future to progress with the interesting questions raised by models with higher dimensions. Here, exploiting symmetries may turn out helpful.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, W.m.; Levin, S.A.; Iwasa, Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 1986, 23, 187–204. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.m.; Hethcote, H.W.; Levin, S.A. Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 1987, 25, 359–380. [Google Scholar] [CrossRef] [PubMed]
- Vyska, M.; Gilligan, C. Complex dynamical behaviour in an epidemic model with control. Bull. Math. Biol. 2016, 78, 2212–2227. [Google Scholar] [CrossRef] [Green Version]
- Roostaei, A.; Barzegar, H.; Ghanbarnejad, F. Emergence of Hopf bifurcation in an extended SIR dynamic. arXiv 2021, arXiv:2107.10583. [Google Scholar]
- Gupta, R.; Kumar, A. Endemic bubble and multiple cusps generated by saturated treatment of an SIR model through Hopf and Bogdanov–Takens bifurcations. Math. Comput. Simul. 2022, 197, 1–21. [Google Scholar] [CrossRef]
- De la Sen, M.; Nistal, R.; Alonso-Quesada, S.; Ibeas, A. Some formal results on positivity, stability, and endemic steady-state attainability based on linear algebraic tools for a class of epidemic models with eventual incommensurate delays. Discret. Dyn. Nat. Soc. 2019, 2019, 8959681. [Google Scholar] [CrossRef] [Green Version]
- De la Sen, M.; Ibeas, A.; Alonso-Quesada, S.; Nistal, R. On the Carrying and Evolution Matrices in Epidemic Models. J. Phys. Conf. Ser. 2021, 1746, 012015. [Google Scholar] [CrossRef]
- Arino, J.; Brauer, F.; van den Driessche, P.; Watmough, J.; Wu, J. A final size relation for epidemic models. Math. Biosci. Eng. 2007, 4, 159. [Google Scholar]
- Avram, F.; Adenane, R.; Ketcheson, D.I. A review of matrix SIR Arino epidemic models. Mathematics 2021, 9, 1513. [Google Scholar] [CrossRef]
- Avram, F.; Adenane, R.; Basnarkov, L.; Bianchin, G.; Goreac, D.; Halanay, A. On matrix-SIR Arino models with linear birth rate, loss of immunity, disease and vaccination fatalities, and their approximations. arXiv 2021, arXiv:2112.03436. [Google Scholar]
- Robinson, M.; Stilianakis, N.I. A model for the emergence of drug resistance in the presence of asymptomatic infections. Math. Biosci. 2013, 243, 163–177. [Google Scholar] [CrossRef] [PubMed]
- Ottaviano, S.; Sensi, M.; Sottile, S. Global stability of SAIRS epidemic models. Nonlinear Anal. Real World Appl. 2022, 65, 103501. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Further notes on the basic reproduction number. In Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 159–178. [Google Scholar]
- Greenhalgh, D. Hopf bifurcation in epidemic models with a latent period and nonpermanent immunity. Math. Comput. Model. 1997, 25, 85–107. [Google Scholar] [CrossRef]
- Li, M.Y.; Graef, J.R.; Wang, L.; Karsai, J. Global dynamics of a SEIR model with varying total population size. Math. Biosci. 1999, 160, 191–213. [Google Scholar] [CrossRef] [Green Version]
- Li, M.Y.; Muldowney, J.S. Dynamics of differential equations on invariant manifolds. J. Differ. Equ. 2000, 168, 295–320. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Hsieh, Y.H. Global analysis of an SEIR model with varying population size and vaccination. Appl. Math. Model. 2010, 34, 2685–2697. [Google Scholar] [CrossRef]
- Britton, T.; Ouédraogo, D. SEIRS epidemics with disease fatalities in growing populations. Math. Biosci. 2018, 296, 45–59. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.; Lu, Z. Global asymptotic stability for the SEIRS models with varying total population size. Math. Biosci. 2018, 296, 17–25. [Google Scholar] [CrossRef]
- Douris, P.; Markakis, M. Global Connecting Orbits of a SEIRS Epidemic Model with Nonlinear Incidence Rate and Nonpermanent Immunity. Eng. Lett. 2019, 27, 1–10. [Google Scholar]
- Ansumali, S.; Kaushal, S.; Kumar, A.; Prakash, M.K.; Vidyasagar, M. Modelling a pandemic with asymptomatic patients, impact of lockdown and herd immunity, with applications to SARS-CoV-2. Annu. Rev. Control 2020, 50, 432–447. [Google Scholar] [CrossRef]
- Graef, J.R.; Li, M.Y.; Wang, L. A Study on the Effects of Disease Caused Death in a Simple Epidemic Model; American Institute of Mathematical Sciences: Springfield, MI, USA, 1998; Volume 1998, p. 288. [Google Scholar]
- Ferreira, R.A.; Silva, C.M. A nonautonomous epidemic model on time scales. J. Differ. Equ. Appl. 2018, 24, 1295–1317. [Google Scholar] [CrossRef]
- Russo, G.; Wirth, F. Matrix measures, stability and contraction theory for dynamical systems on time scales. arXiv 2020, arXiv:2007.08879. [Google Scholar] [CrossRef]
- Avram, F.; Adenane, R.; Bianchin, G.; Halanay, A. Stability Analysis of an Eight Parameter SIR-Type Model Including Loss of Immunity, and Disease and Vaccination Fatalities. Mathematics 2022, 10, 402. [Google Scholar] [CrossRef]
- Goh, B.S. Global stability in many-species systems. Am. Nat. 1977, 111, 135–143. [Google Scholar] [CrossRef]
- Bacaër, N. Mathématiques et Épidémies. 2021. Available online: https://hal.archives-ouvertes.fr/hal-03331469 (accessed on 20 March 2022).
- Ballyk, M.M.; McCluskey, C.C.; Wolkowicz, G.S. Global analysis of competition for perfectly substitutable resources with linear response. J. Math. Biol. 2005, 51, 458–490. [Google Scholar] [CrossRef]
- Fall, A.; Iggidr, A.; Sallet, G.; Tewa, J.J. Epidemiological models and Lyapunov functions. Math. Model. Nat. Phenom. 2007, 2, 62–83. [Google Scholar] [CrossRef]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef]
- Busenberg, S.; Van den Driessche, P. Analysis of a disease transmission model in a population with varying size. J. Math. Biol. 1990, 28, 257–270. [Google Scholar] [CrossRef] [Green Version]
- Li, M.Y.; Muldowney, J.S. A geometric approach to global-stability problems. SIAM J. Math. Anal. 1996, 27, 1070–1083. [Google Scholar] [CrossRef]
- Shuai, Z.; van den Driessche, P. Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef] [Green Version]
- LeVeque, R.J.; Mitchell, I.M.; Stodden, V. Reproducible research for scientific computing: Tools and strategies for changing the culture. Comput. Sci. Eng. 2012, 14, 13–17. [Google Scholar] [CrossRef]
- Wang, W. Backward bifurcation of an epidemic model with treatment. Math. Biosci. 2006, 201, 58–71. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Huang, D.; Ruan, S.; Zhang, W. Coexistence of limit cycles and homoclinic loops in a SIRS model with a nonlinear incidence rate. SIAM J. Appl. Math. 2008, 69, 621–639. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Fan, M. Dynamics of an SIR epidemic model with limited medical resources revisited. Nonlinear Anal. Real World Appl. 2012, 13, 312–324. [Google Scholar] [CrossRef]
- Sun, S. Global dynamics of a SEIR model with a varying total population size and vaccination. Int. J. Math. Anal. 2012, 6, 1985–1995. [Google Scholar]
- Wiggers, S.L.; Pedersen, P. Routh–hurwitz-liénard–chipart criteria. In Structural Stability and Vibration; Springer: Berlin/Heidelberg, Germany, 2018; pp. 133–140. [Google Scholar]
- Anderson, B.; Jury, E. A simplified Schur-Cohn test. IEEE Trans. Autom. Control 1973, 18, 157–163. [Google Scholar] [CrossRef]
- Daud, A.A.M. A Note on Lienard-Chipart Criteria and its Application to Epidemic Models. Math. Stat. 2021, 9, 41–45. [Google Scholar] [CrossRef]
- Ma, J.; Earn, D.J. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol. 2006, 68, 679–702. [Google Scholar] [CrossRef]
- Feng, Z. Final and peak epidemic sizes for SEIR models with quarantine and isolation. Math. Biosci. Eng. 2007, 4, 675. [Google Scholar]
- Andreasen, V. The final size of an epidemic and its relation to the basic reproduction number. Bull. Math. Biol. 2011, 73, 2305–2321. [Google Scholar] [CrossRef]
- Georgescu, P.; Hsieh, Y.H. Global stability for a virus dynamics model with nonlinear incidence of infection and removal. SIAM J. Appl. Math. 2007, 67, 337–353. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Ma, W.; Ruan, S. Analysis of SIR epidemic models with nonlinear incidence rate and treatment. Math. Biosci. 2012, 238, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Razvan, M. Multiple equilibria for an SIRS epidemiological system. arXiv 2001, arXiv:math/0101051. [Google Scholar]
- Yang, W.; Sun, C.; Arino, J. Global analysis for a general epidemiological model with vaccination and varying population. J. Math. Anal. Appl. 2010, 372, 208–223. [Google Scholar] [CrossRef] [Green Version]
- Riaño, G. Epidemic Models with Random Infectious Period. medRxiv 2020. [Google Scholar] [CrossRef]
- Plemmons, R.J. M-matrix characterizations. I—Nonsingular M-matrices. Linear Algebra Its Appl. 1977, 18, 175–188. [Google Scholar] [CrossRef] [Green Version]
- Hurtado, P.J.; Kirosingh, A.S. Generalizations of the ‘Linear Chain Trick’: Incorporating more flexible dwell time distributions into mean field ODE models. J. Math. Biol. 2019, 79, 1831–1883. [Google Scholar] [CrossRef] [Green Version]
- Hyman, J.M.; Li, J.; Stanley, E.A. The differential infectivity and staged progression models for the transmission of HIV. Math. Biosci. 1999, 155, 77–109. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [Green Version]
- Gasca, M.; Pena, J.M. Total positivity and Neville elimination. Linear Algebra Its Appl. 1992, 165, 25–44. [Google Scholar] [CrossRef] [Green Version]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2015; Volume 61. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avram, F.; Adenane, R.; Halanay, A. New Results and Open Questions for SIR-PH Epidemic Models with Linear Birth Rate, Loss of Immunity, Vaccination, and Disease and Vaccination Fatalities. Symmetry 2022, 14, 995. https://doi.org/10.3390/sym14050995
Avram F, Adenane R, Halanay A. New Results and Open Questions for SIR-PH Epidemic Models with Linear Birth Rate, Loss of Immunity, Vaccination, and Disease and Vaccination Fatalities. Symmetry. 2022; 14(5):995. https://doi.org/10.3390/sym14050995
Chicago/Turabian StyleAvram, Florin, Rim Adenane, and Andrei Halanay. 2022. "New Results and Open Questions for SIR-PH Epidemic Models with Linear Birth Rate, Loss of Immunity, Vaccination, and Disease and Vaccination Fatalities" Symmetry 14, no. 5: 995. https://doi.org/10.3390/sym14050995
APA StyleAvram, F., Adenane, R., & Halanay, A. (2022). New Results and Open Questions for SIR-PH Epidemic Models with Linear Birth Rate, Loss of Immunity, Vaccination, and Disease and Vaccination Fatalities. Symmetry, 14(5), 995. https://doi.org/10.3390/sym14050995





