New Results and Open Questions for SIR-PH Epidemic Models with Linear Birth Rate, Loss of Immunity, Vaccination, and Disease and Vaccination Fatalities

Abstract

Our paper presents three new classes of models: SIR-PH, SIR-PH-FA, and SIR-PH-IA, and states two problems we would like to solve about them. Recall that deterministic mathematical epidemiology has one basic general law, the “${\mathcal{R}}_0$ alternative” of Van den Driessche and Watmough, which states that the local stability condition of the disease-free equilibrium may be expressed as ${\mathcal{R}}_0<1$, where ${\mathcal{R}}_0$ is the famous basic reproduction number, which also plays a major role in the theory of branching processes. The literature suggests that it is impossible to find general laws concerning the endemic points. However, it is quite common that 1. When ${\mathcal{R}}_0>1$, there exists a unique fixed endemic point, and 2. the endemic point is locally stable when ${\mathcal{R}}_0>1$. One would like to establish these properties for a large class of realistic epidemic models (and we do not include here epidemics without casualties). We have introduced recently a “simple” but broad class of “SIR-PH models” with varying populations, with the express purpose of establishing for these processes the two properties above. Since that seemed still hard, we have introduced a further class of “SIR-PH-FA” models, which may be interpreted as approximations for the SIR-PH models, and which include simpler models typically studied in the literature (with constant population, without loss of immunity, etc.). For this class, the first “endemic law” above is “almost established”, as explicit formulas for a unique endemic point are available, independently of the number of infectious compartments, and it only remains to check its belonging to the invariant domain. This may yet turn out to be always verified, but we have not been able to establish that. However, the second property, the sufficiency of ${\mathcal{R}}_0>1$ for the local stability of an endemic point, remains open even for SIR-PH-FA models, despite the numerous particular cases in which it was checked to hold (via Routh–Hurwitz time-onerous computations, or Lyapunov functions). The goal of our paper is to draw attention to the two open problems above, for the SIR-PH and SIR-PH-FA, and also for a second, more refined “intermediate approximation” SIR-PH-IA. We illustrate the current status-quo by presenting new results on a generalization of the SAIRS epidemic model.

1. Introduction

Motivation. One of the hardest challenges facing epidemic models is dealing with models within which death is possible, in which the total population N varies, and in which the infection rates depend on N (as is the case in reality, except for a short period of time at the start of an epidemic). As these features confront the researcher with challenging behaviors (the first being that the uniqueness of the fixed endemic point may stop holding), sometimes hard to explain epidemiologically, it seems natural to attempt to identify the simplest class of realistic models for which a theory may be developed. The natural choice is “standard incidence rates”—see (1), since models with nonlinear infection rates are quite complex—see for example [1,2,3,4,5] for the very complex dynamical behaviors which may arise otherwise.

The next issue is choosing the type of birth function $b\left(N\right)$ to work with. The easiest case is when $b\left(N\right)$ is constant, but this corresponds to immigration rather than birth, and so our favorite are linear birth rates $b\left(N\right)=\mathsf{\Lambda }N$. A bonus for this choice, as well known, is that normalization by the total population leads to a model with constant parameters, which looks similar to classic constant population models, but involves some extra nonlinear terms—see (2). The well-studied classic models may then be recovered via a heuristic “first approximation” (FA) of ignoring the extra terms. This approximation, which deserves to be investigated rigorously via slow-fast/singular perturbation/homogenization techniques, has the merit of putting under one umbrella constant and varying population models with linear birth rates.

At this point, let us mention that we believe that epidemic models should be ideally parameterized by the two matrices $F,V$, which intervene in the next generation matrix approach, which has been called disease-carrying and state evolution matrices [6,7]. A foundational paper in this direction is [8], Arino shows that further simplifications arise for models having only one susceptible class and disease-carrying matrix of rank one. The first fundamental question, the uniqueness of the endemic point when ${\mathcal{R}}_0>1$, may be resolved explicitly for the “FA approximation” (and hence also for “small perturbations”, numerically). This has motivated us to propose [9,10] to develop the theory of this class of models, which we call “Arino” or “SIR–PH” models.

Contributions and contents. The goal of our paper is to draw attention to two interesting open problems, for the SIR-PH, SIR-PH-FA, and also for a second, more refined “intermediate approximation” SIR-PH-IA. We illustrate the current status-quo by presenting new results on a generalization of the SAIRS epidemic model of [11,12].

The SAIRS model (2) is presented in Section 2. The history of the problem and some oversights and errors in the literature are recalled in Section 2.1. The basic reproduction number ${\mathcal{R}}_0$ and the weak ${\mathcal{R}}_0$ alternative for the DFE equilibrium are established via the next generation matrix approach in Section 2.2. The local stability of the endemic point when the basic reproduction number satisfies ${\mathcal{R}}_0>1$ for the FA model is established in Section 2.3.

A review of the theory of SIR-PH models is provided in Section 3, and some new results in Section 4.

The scaled SAIRS model is revisited in the Section 5, where some previous results in the literature are corrected and completed.

2. The SAIRS Model with Linear Birth Rate

In this paper, we consider a ten parameters SAIR (also called SEIR in the classic literature [13]) epidemic model inspired by [12,14,15,16,17,18,19,20], which we call SAIR/V+S (or SAIR for short) as it groups together immunized people in an R/V compartment. The letter A (from asymptomatic) stands for the fact that the individuals in this compartment may infect the susceptibles. This important feature, already present in [13], was further studied in [11,12,21]. The model studied in [12] is the most complete in the sense that it misses only one of the parameters of interest, namely the important extra death rate due to the disease—see for example [22]. The explanation for this omission in [12] lies probably in the fact that this paper follows the tradition of the “short term constant population epidemics”, in which the total population N is assumed constant, and the endemic point is unique and easy to find explicitly. Our paper investigates, for the model of [12], the topic of the first six papers cited, i.e., we attempt to deal with the variation of $N\left(t\right)$ during epidemics that may last for a long time and which may never be totally eradicated. We generalize the uniqueness of the endemic point and the local stability results of these six papers and, at the same time, draw attention to certain unnecessary assumptions and mistakes. The hardest issue of global stability is only illustrated via some numerical simulations.

SAIR Model. Letting $S\left(t\right)$, $E\left(t\right)$, $I\left(t\right)$, $R\left(t\right)$, $D\left(t\right)$ and $D_e\left(t\right)$ represent Susceptible individuals, Exposed individuals, Infective individuals, Recovered individuals, naturally Dead individuals and Dead individuals due to the disease, respectively, the model we consider is:

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =\mathsf{\Lambda }N\left(t\right)-S\left(t\right)\left(\frac{{\beta }_i}{N\left(t\right)}I\left(t\right)+\frac{{\beta }_e}{N\left(t\right)}E\left(t\right)+{\gamma }_s+\mu \right)+{\gamma }_{r}R\left(t\right),\hfill \\ \hfill E^{\prime }\left(t\right)& =S\left(t\right)\left(\frac{{\beta }_i}{N\left(t\right)}I\left(t\right)+\frac{{\beta }_e}{N\left(t\right)}E\left(t\right)\right)-({\gamma }_e+\mu )E\left(t\right),{\gamma }_e=e_i+e_r\hfill \\ \hfill I^{\prime }\left(t\right)& =e_{i}E\left(t\right)-I\left(t\right)\left(\gamma +\mu +\delta \right),\hfill \\ \hfill R^{\prime }\left(t\right)& ={\gamma }_{s}S\left(t\right)+e_{r}E\left(t\right)+\gamma I\left(t\right)-({\gamma }_r+\mu )R\left(t\right),\hfill \\ \hfill D^{\prime }\left(t\right)& =\mu \left(S\right(t)+E(t)+I(t)+R(t\left)\right):=\mu N\left(t\right),\hfill \\ \hfill D_e^{\prime }\left(t\right)& =\delta I\left(t\right),\hfill \\ \hfill N\left(t\right)& =S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)⟹N^{\prime }\left(t\right)=(\mathsf{\Lambda }-\mu )N\left(t\right)-\delta I\left(t\right).\hfill \end{array}$$

(1)

Epidemiologic meaning of the parameters:

1.

$\mathsf{\Lambda }\in {\mathbb{R}}_{\ge 0}$ and $\mu \in {\mathbb{R}}_{\ge 0}$ denote the average birth and death rates in the population (in the absence of the disease), respectively.

2.

The parameters ${\beta }_i\in {\mathbb{R}}_{\ge 0}$ and ${\beta }_e\in {\mathbb{R}}_{\ge 0}$ denote the infection rates for infective and exposed individuals, respectively;

3.

${\gamma }_s\in {\mathbb{R}}_{\ge 0}$ is the vaccination rate, ${\gamma }_e\in {\mathbb{R}}_{\ge 0}$ is the rate at which the exposed individuals become infected or recovered, ${\gamma }_r\in {\mathbb{R}}_{\ge 0}$ denotes the rate at which immune individuals lose immunity (this is the reciprocal of the expected duration of immunity), $\gamma \in {\mathbb{R}}_{>0}$ is the rate at which infected individuals recover from the disease.

4.

$e_i\in {\mathbb{R}}_{\ge 0}$, $e_r\in {\mathbb{R}}_{\ge 0}$, are rates of transfer from E to I and R, respectively.

5.

$\delta \in {\mathbb{R}}_{\ge 0}$ is the extra death rate in the infected compartment due to the disease.

Some particular cases.

1.

If ${\beta }_e=e_r=0$, we obtain a SEIRS type model. If furthermore ${\gamma }_r={\gamma }_s=0$, we arrive to the model masterly studied in [15]; if only one of these parameters is zero, we arrive to the models studied in [16,17,18,19].

2.

If ${\beta }_i={\gamma }_r={\gamma }_s=0=\delta$, we obtain the SIQR model [23,24].

Remark 1.

Note the notation scheme employed above, which could be applied to any compartmental model. A linear rate of transfer from compartment m to compartment c is denoted by $m_c$, and the total linear rate out of m is denoted by ${\gamma }_m$, which implies ${\sum }_c{m}_c={\gamma }_m$, for example ${\gamma }_e=e_i+e_r$. Extra death rates due to the epidemics in a department c are denoted by ${\delta }_c$. An exception is made though for the infectious compartment $\mathsf{i}$, where we simply use the classic notations $\gamma ,\delta$, instead of ${\gamma }_i,{\delta }_i$. Our scheme would simplify a lot, if adopted, perusing the rather random notations used in the literature.

The scaled model. It is convenient to reformulate (1) in terms of the normalized fractions $\mathsf{s}=\frac{S}{N},\mathsf{e}=\frac{E}{N},\mathsf{i}=\frac{I}{N},\mathsf{r}=\frac{R}{N}.$ Using $N^{\prime }\left(t\right)=(\mathsf{\Lambda }-\mu )N\left(t\right)-\delta I\left(t\right),$ this yields the following nine parameters SEIRS epidemic model (the common death rate $\mu$ simplifies, and an extra $\delta \mathsf{i}c$ appears in the equation of each compartment c–see for example [25] for similar computations).

$$\left\{\begin{array}{c}{\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-\mathsf{s}\left(t\right)\left({\beta }_i\mathsf{i}\left(t\right)+{\beta }_e\mathsf{e}\left(t\right)+{\gamma }_s+\mathsf{\Lambda }\right)+{\gamma }_r\mathsf{r}\left(t\right)+\delta \mathsf{s}\left(t\right)\mathsf{i}\left(t\right)\hfill \\ \left(\begin{array}{c}{\mathsf{e}}^{\prime }\left(t\right)\\ {\mathsf{i}}^{\prime }\left(t\right)\end{array}\right)=\left[\mathsf{s}\left(t\right)\left(\begin{array}{cc}{\beta }_e& {\beta }_i\\ 0& 0\end{array}\right)+\left(\begin{array}{cc}-({\gamma }_e+\mathsf{\Lambda })& 0\\ e_i& -\left(\mathsf{\Lambda }+\gamma +\delta \right)\end{array}\right)+\delta {\mathsf{i}}_{t}Id\right]\left(\begin{array}{c}\mathsf{e}\left(t\right)\\ \mathsf{i}\left(t\right)\end{array}\right)\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)={\gamma }_s\mathsf{s}\left(t\right)+e_r\mathsf{e}\left(t\right)+\gamma \mathsf{i}\left(t\right)-({\gamma }_r+\mathsf{\Lambda })\mathsf{r}\left(t\right)+\delta \mathsf{i}\left(t\right)\mathsf{r}\left(t\right)\hfill \end{array}\right..$$

(2)

Remark 2.

Note that we have written the “infectious” middle equations to emphasize first the factorized form, similar to that encountered for Lotka-Volterra networks—see for example [26]. Secondly, for the factor appearing in these equations, we have emphasized the form

$$F-V+\delta \mathsf{i}{I}_2:=\mathsf{s}B-V+\delta \mathsf{i}{I}_2.$$

(3)

Note that the matrices $F,V$ are featured in the famous the (Next Generation Matrix) approach [13], that some authors refer to them as “new infections” and “transmission matrices”, that [7] call them the disease-carrying and state evolution matrices, and that ([27], Ch 5) gives a way to define an associated stochastic birth and death model associated to these matrices. The matrix B is further useful in defining and studying more general SIR-PH models—see [9,10] and below, and see also [28], ([29], (2.1)), [6] for related works.

Since the computations will become soon very cumbersome, we will start using from now on the following notations:

$$\left\{\begin{array}{c}{v}_0=\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s,\hfill \\ v_1=\mathsf{\Lambda }+{\gamma }_e,\hfill \\ v_2=\mathsf{\Lambda }+\gamma +\delta .\hfill \end{array}\right.$$

(4)

Note that $v_z,withz=\{1,2\},$ are the diagonal elements of V, and that $v_0$ appears as denominator in the DFE (9).

Figure 1 compares the qualitative behavior and equilibrium points of the $(\mathsf{s},\mathsf{i})$ coordinates of the three variants of a SIR-type example (discussed in detail in [25]).

We restrict our study to the biological feasible region

$${\mathcal{D}}_4=\left\{(\mathsf{s},\mathsf{e},\mathsf{i},\mathsf{r})\in {\mathbb{R}}_{+}^4,\mathsf{s}+\mathsf{e}+\mathsf{i}+\mathsf{r}=1\right\}.$$

Its invariance is ensured by the fact that

$${(\mathsf{s}+\mathsf{e}+\mathsf{i}+\mathsf{r})}^{\prime }=\left(\delta \mathsf{i}-\mathsf{\Lambda }-{\gamma }_r\right)(\mathsf{s}+\mathsf{e}+\mathsf{i}+\mathsf{r}-1),$$

(5)

hence ${\mathsf{s}}_0+{\mathsf{e}}_0+{\mathsf{i}}_0+{\mathsf{r}}_0=1$ implies $\mathsf{s}+\mathsf{e}+\mathsf{i}+\mathsf{r}=1$, for all $t>0$.

We will work in three dimensions by eliminating $\mathsf{r}=1-\mathsf{s}-\mathsf{e}-\mathsf{i}$. The first equation of (2) changes then, and the system becomes

$$\left\{\begin{array}{c}{\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }+{\gamma }_r-{\gamma }_r(\mathsf{e}\left(t\right)+\mathsf{i}\left(t\right))-\mathsf{s}\left(t\right){}_{\stackrel{++}{=}}\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s+({\beta }_i-\delta )\mathsf{i}\left(t\right)+{\beta }_e\mathsf{e}\left(t\right),\hfill \\ \left(\begin{array}{c}{\mathsf{e}}^{\prime }\left(t\right)\\ {\mathsf{i}}^{\prime }\left(t\right)\end{array}\right)=[\left(\begin{array}{cc}{\beta }_e\mathsf{s}\left(t\right)-v_1& {\beta }_i\mathsf{s}\left(t\right)\\ e_i& -v_2\end{array}\right)+\delta \mathsf{i}\left(t\right)I_2]\left(\begin{array}{c}\mathsf{e}\left(t\right)\\ \mathsf{i}\left(t\right)\end{array}\right)\hfill \\ (\mathsf{s},\mathsf{e},\mathsf{i})\in {\mathcal{D}}_3:=\{(\mathsf{s},\mathsf{e},\mathsf{i})\in {\mathbb{R}}_{+}^3,\mathsf{s}+\mathsf{e}+\mathsf{i}\le 1\}\hfill \end{array}\right..$$

(6)

Concerning fixed points, we note first, following ([15], (4.2)), ([17], (13)), the following necessary condition at a fixed endemic point:

$$\begin{array}{cc}& s^{\prime }+e^{\prime }+i^{\prime }=0\iff e({\gamma }_e-e_i)+\gamma i+s{\gamma }_s={\gamma }_{r}r+\mathsf{\Lambda }r-\delta ir\hfill \\ & \iff (1-\left(e+i+s\right))(\mathsf{\Lambda }+{\gamma }_r-\delta i)=e\left({\gamma }_e-e_i\right)+\gamma i+s\gamma s⟹i<i_c:=min[1,(\mathsf{\Lambda }+{\gamma }_r)/\delta ],\hfill \end{array}$$

(7)

where the last implications follows since the right hand side of the last equation in (7) is positive, due to $e_r={\gamma }_e-e_i\ge 0$.

Thus, the search for fixed points may be reduced to the domain

$${\mathcal{D}}_f:={\mathcal{D}}_3\cap \{\mathsf{i}:\mathsf{i}<i_c=min[1,(\mathsf{\Lambda }+{\gamma }_r)/\delta ]\}.$$

(8)

As a quick preview of the next generation matrix “factorization” idea, we note now that the disease free equation ${\mathsf{s}}^{\prime }=\mathsf{\Lambda }-\mathsf{s}(\mathsf{\Lambda }+{\gamma }_s)+{\gamma }_r(1-\mathsf{s})$ (defined by $e=i=0$, $r=1-s$) has fixed point

$${\mathsf{s}}_{dfe}=\frac{\mathsf{\Lambda }+{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s}⟹{\mathsf{r}}_{dfe}=1-{\mathsf{s}}_{dfe}=\frac{{\gamma }_s}{\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s},$$

(9)

whenever $\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s\ne 0$, which will be assumed from now on. Note this formula contains only three of the parameters.

The other 6 parameters $\gamma$, $\delta$, ${\beta }_i$, ${\beta }_e$, $e_i$, ${\gamma }_e$ intervene in the “infection equations” for $\mathsf{e},\mathsf{i}$, and will determine the basic reproduction number (12)

$${\mathcal{R}}_0=\frac{{\mathsf{s}}_{dfe}}{\mathsf{\Lambda }+{\gamma }_e}{}_{\stackrel{++}{=}}{\beta }_e+\frac{{\beta }_i{e}_i}{\mathsf{\Lambda }+\gamma +\delta }:={\mathsf{s}}_{dfe}\mathcal{R},$$

where $\mathcal{R}$ is precisely the ${\mathcal{R}}_0$ which would be obtained in the absence of vaccination.

When $\delta =0$, our model (6) reduces to the eight parameters constant population model studied in [12], which has a unique endemic point, with coordinates expressible in terms of ${\mathcal{R}}_0$; for example ${\mathsf{s}}_{ee}=\frac{{\mathsf{s}}_{dfe}}{{\mathcal{R}}_0}:=\frac{1}{\mathcal{R}}.$ Its global stability is, however, hard to prove ([12], Conjecture 15), and the authors resolve only the case ${\beta }_e<\gamma$.

2.1. Some History of the SEIRS and SAIRS Varying Population Models

A first important paper on the varying population SEIRS model (recall that both notations SEIRS and SAIRS have been used already for the same model) is [14], where ${\beta }_e=e_r=0$ and where a proportion q of vaccines is allocated to the newborn. We took for simplicity $q=0$, as this parameter does not modify in an essential way the mathematics involved. Note that $\delta$, $\mathsf{\Lambda }$, ${\gamma }_e$, ${\gamma }_s$ and ${\gamma }_r$ are denoted in [14] by $\alpha$, r, $\sigma$, p and $ϵ$, respectively.

Besides the typical weak ${\mathcal{R}}_0$ alternative, ([14], Thm 2.3(i)) establishes also global asymptotic stability (GAS) of disease free equilibrium when ${\mathcal{R}}_0<1$ and when either (I) $\frac{{\beta }_i{\gamma }_e}{\mathsf{\Lambda }+{\gamma }_e}\le \delta$, (II) ${\gamma }_s=0$, or a certain non-explicit condition holds. A second result ([14], Thm 2.3(ii)) establishes the uniqueness of the endemic point when ${\mathcal{R}}_0>1,\mathrm{and},{\gamma }_r\le min[{\gamma }_e,\gamma ].$

Stimulated by the many open cases left above, in [15], the authors considered the particular case ${\beta }_e=e_r={\gamma }_r={\gamma }_s=0$.As the authors explain, the difficulties met, especially in the global stability problem, forced them to devise new ingenious methods. (12) becomes now ${\mathcal{R}}_0=\frac{{\beta }_i{\gamma }_e}{\left({\gamma }_e+\mathsf{\Lambda }\right)\left(\mathsf{\Lambda }+\gamma +\delta \right)}$ (note that $\beta$, ${\gamma }_e$, $\mathsf{\Lambda }$, $\delta$ and ${\mathcal{R}}_0$ are denoted in [15] by $\lambda$, $ϵ$, b, $\alpha$ and $\sigma$, respectively, and that ${\mathsf{s}}_{dfe}=1$). Building on previous results in the limiting cases $\delta =0$ for SEIR models with constant population [30] and ${\gamma }_e\to \infty$ for SIR models with varying populations [31], they establish the uniqueness and global stability of the endemic point ([15], Cor. 6.2, Thm6.5) when ${\mathcal{R}}_0>1$.

Note that the Corollary is under the assumption of non-existence of non-constant periodic solutions and the Theorem requires the additional assumption $\delta <{\gamma }_e$; thus, the complementary case was left open.

Next, the reference [16] studied the case of waning immunity, leaving again open many cases. Note that the so-called “geometric approach to stability” method, initiated in [15,16,32], was used many times afterward —see for example [19].

Eleven years later, the authors in [17] re-attacked the [14] problem with ${\beta }_e=e_r={\gamma }_r=0$ and vaccination ${\gamma }_s\ge 0$ (denoted by $a\sigma$). We note, by adding the two infection rates in ([17], Figure 1), which yields $\lambda (1-a\sigma ),$ that the model depends only on $a\sigma$, and so introducing two parameters for ${\gamma }_s$ unnecessarily complicates the mathematics. Furthermore, the infection rate $\lambda (1-a\sigma )$ might as well be denoted by one parameter, and we chose the classical $\beta$. Finally, one can relate their results to ours by substituting $\beta$ with $\gamma$ and setting $\sigma =1$ (i.e., giving up the second source of infections), and $\lambda =\beta /(1-{\gamma }_s)$. Then, ([17], (8))

$${\mathcal{R}}_0={\mathsf{s}}_{dfe}\frac{{\beta }_i{\gamma }_e}{\left(\mathsf{\Lambda }+{\gamma }_e\right)\left(\mathsf{\Lambda }+\gamma +\delta \right)}:=\mathcal{R}{\mathsf{s}}_{dfe},$$

(10)

where

$$\mathcal{R}=\frac{{\beta }_i{\gamma }_e}{\left(\mathsf{\Lambda }+{\gamma }_e\right)\left(\mathsf{\Lambda }+\gamma +\delta \right)}\mathrm{and}{\mathsf{s}}_{dfe}=\frac{\mathsf{\Lambda }}{\mathsf{\Lambda }+{\gamma }_s}.$$

See also (12).

Remark 3.

Let us note two open problems left in [17].

1.

([17], Thm 2.1) proves the global stability of the DFE when

$$\mathcal{R}\le 1$$

(by using the Lyapunov function ${\gamma }_{e}e+({\gamma }_e+\mathsf{\Lambda })i$, which is different from the Lyapunov function used in [33], $e(\gamma +\mathsf{\Lambda }+\delta )+{\gamma }_{e}i$. This leaves open the case ${\mathcal{R}}_0<1<\mathcal{R}$, when the DFE is locally, but perhaps not globally stable, and also the question of choosing the “most performant” Lyapunov function.

2.

([17], Thm 2.1) establishes global stability of a unique endemic point in certain cases and suggests that outside those cases, “there may exist stable periodic solutions”.

Seven years later, the reference [18] revisited the [16] problem with ${\gamma }_s=0$ and waning immunity ${\gamma }_r\ge 0$ (denoted by $\rho$). The authors remark that in this particular case, there are still open questions: “We have not proved, but we strongly believe that if ${\mathcal{R}}_0>1$, then the system (2) has one and only one endemic equilibrium and that this equilibrium is globally asymptotically stable”. The [16] problem was revisited then in [19], who claims to have also removed the restriction $\delta <{\gamma }_e$ of [15]; however, their crucial equation ([19], (3.28)) is wrong, see Section 5. The fact that the papers [17,19] contain unnecessary conditions, mistakes, and wrong conjectures suggests that for complicated epidemic models with infection rates depending on N, ingenuity stops being enough, and it must be accompanied by verifications via symbolic software, rendered public, as is the case with our paper (in line with the so-called “reproducible research” [34]).

Finally, the authors in [12] apply the geometric approach to global stability, taking into account vaccination and loss of immunity, and also the possibility that the exposed, or rather the asymptomatic, are infectious, but for a simplified constant population model with $\delta =0,\mathsf{\Lambda }\ge 0$. The basic reproduction number (12) becomes now ([12], (5))

$${\mathcal{R}}_0=[{\beta }_e+\frac{{\beta }_i{e}_i}{\mathsf{\Lambda }+\gamma }]\frac{{\mathsf{s}}_{dfe}}{{\gamma }_e+\mathsf{\Lambda }}$$

(with the correspondence $\mathsf{\Lambda }\to \mu$, ${\beta }_e\to {\beta }_A$, $e_i\to \alpha$, $e_r\to {\delta }_A$, $\gamma \to {\delta }_I$, ${\gamma }_r\to \gamma$, ${\gamma }_s\to \delta$). The global stability is proven only in the case ${\beta }_e<\gamma$.

These multiple but only partially successful attempts at solving the [14] problem motivated us to revisit it. (Yet another motivation was the literature on bifurcation analysis of SIR and SEIR-type models [1,3,5,35,36,37], and [2,20] which contains yet another plethora of open problems.)

2.2. Warm-Up: The Weak ${\mathcal{R}}_0$ Alternative for the DFE Equilibrium

Note that the DFE (9) is a stable point for the disease-free equation

$${\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }+{\gamma }_r-\mathsf{s}\left(t\right)\left(\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s\right).$$

Then, we may check that the quadratic—linear decomposition of

$$\left(\begin{array}{c}{\mathsf{e}}^{\prime }\left(t\right)\\ {\mathsf{i}}^{\prime }\left(t\right)\end{array}\right)=\left(\begin{array}{cc}{\beta }_e\mathsf{s}\left(t\right)+\delta \mathsf{i}\left(t\right)-({\gamma }_e+\mathsf{\Lambda })& {\beta }_i\mathsf{s}\left(t\right)\\ e_i& \delta \mathsf{i}\left(t\right)-v_2\end{array}\right)\left(\begin{array}{c}\mathsf{e}\left(t\right)\\ \mathsf{i}\left(t\right)\end{array}\right)=\mathcal{F}(\mathsf{e},\mathsf{i})-\mathcal{V}(\mathsf{e},\mathsf{i}),$$

where

$$\begin{array}{c}\hfill \mathcal{F}(\mathsf{e},\mathsf{i})=\left(\begin{array}{c}{\beta }_e\mathsf{s}\mathsf{e}+{\beta }_i\mathsf{s}\mathsf{i}+\delta \mathsf{e}\mathsf{i}\\ \delta {\mathsf{i}}^2\end{array}\right),\mathcal{V}(\mathsf{e},\mathsf{i})=\left(\begin{array}{c}(\mathsf{\Lambda }+{\gamma }_e)\mathsf{e}\\ -e_i\mathsf{e}+\mathsf{i}{v}_2\end{array}\right)\end{array}$$

satisfies the splitting assumptions of the NGM (Next Generation Matrix) method [13].

The partial derivatives at the DFE of $\mathcal{F}(\mathsf{e},\mathsf{i}),\mathcal{V}(\mathsf{e},\mathsf{i})$ are

$$F={\mathsf{s}}_{dfe}\left(\begin{array}{cc}{\beta }_e& {\beta }_i\\ 0& 0\end{array}\right),V=\left(\begin{array}{cc}{v}_1& 0\\ -e_i& v_2\end{array}\right),$$

(11)

and

$$\begin{array}{c}\hfill F{V}^{-1}=\left(\begin{array}{cc}{\beta }_e{\mathsf{s}}_{dfe}& {\beta }_i{\mathsf{s}}_{dfe}\\ 0& 0\end{array}\right)\left(\begin{array}{cc}\frac{1}{v_1}& 0\\ \frac{e_i}{v_1{v}_2}& \frac{1}{v_2}\end{array}\right)=\left(\begin{array}{cc}{\mathsf{s}}_{dfe}[\frac{{\beta }_e}{v_1}+\frac{{\beta }_i{e}_i}{v_1{v}_2}]& \frac{{\mathsf{s}}_{dfe}{\beta }_i}{v_2}\\ 0& 0\end{array}\right).\end{array}$$

We may conclude then by the well-known next generation matrix result of [13] that:

Proposition 1.

The SAIR/V+S basic reproductive number is

$${\mathcal{R}}_0:={\mathsf{s}}_{dfe}\frac{{\beta }_t}{v_1{v}_2},$$

(12)

where $v_i$ were defined in (4) and where

$${\beta }_t:={\beta }_i{e}_i+{\beta }_e{v}_2.$$

(13)

Furthermore, the weak ${\mathcal{R}}_0$ alternative (The strong ${\mathcal{R}}_0$ alternative [33] also covers he case ${\mathcal{R}}_0=1$.) holds, i.e.,

1.

If ${\mathcal{R}}_0<1\iff (\mathsf{\Lambda }+{\gamma }_r){\beta }_t<v_0{v}_1{v}_2$ then the disease-free equilibrium is locally asymptotically stable.

2.

If ${\mathcal{R}}_0>1\iff (\mathsf{\Lambda }+{\gamma }_r){\beta }_t>v_0{v}_1{v}_2$, the disease-free equilibrium is unstable.

Remark 4.

The formula for ${\mathcal{R}}_0$ follows also from the [8] formula for SIR-PH models with new infection matrix of rank one $F=s\mathbf{\alpha }\overrightarrow{\beta }$—see [9,10], and below, for the definition of this class. This formula becomes, after including demography parameters $\mathsf{\Lambda },\overrightarrow{\delta }$,

$${\mathcal{R}}_0=\overrightarrow{\beta }{V}^{-1}\mathbf{\alpha },V=-A+Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1}),$$

In the particular SAIRS case, this formula may be applied with the parameters defining the model, which are

$$\overrightarrow{\beta }=\left(\begin{array}{cc}{\beta }_e,& {\beta }_i\end{array}\right),\mathbf{\alpha }=\left(\begin{array}{c}1\\ 0\end{array}\right),A=\left(\begin{array}{cc}-{\gamma }_e& 0\\ e_i& -\gamma \end{array}\right),\overrightarrow{\delta }=\left(\begin{array}{cc}0,& \delta \end{array}\right).$$

Finally, we will write

$$\overrightarrow{a}:=\overrightarrow{1}(-A)=\left(\begin{array}{cc}{\gamma }_e-e_i,& \gamma \end{array}\right)\mathrm{in}\mathrm{this}\mathrm{example},$$

for a quantity which will appear often below.—See for example (24) where we used the standard notation in the theory of phase-type distributions.

A direct proof of Proposition (1) is also easy here. Indeed, after reducing (2) to a three order system by $r=1-s-e-i$, the Jacobian matrix is

$$\begin{array}{c}\hfill J=\left(\begin{array}{ccc}-\overrightarrow{\beta }\mathsf{i}+\delta i-\mathsf{\Lambda }-{\gamma }_r-{\gamma }_s& -s{\beta }_e-{\gamma }_r& s(\delta -{\beta }_i)-{\gamma }_r\\ \overrightarrow{\beta }\mathsf{i}& s{\beta }_e+i\delta -v_1& e\delta +{\beta }_{i}s\\ 0& e_i& -\gamma +(2i-1)\delta -\mathsf{\Lambda }\end{array}\right),\end{array}$$

(where $\overrightarrow{\beta }\mathsf{i}={\beta }_{e}e+{\beta }_{i}i$), and

$$\begin{array}{c}\hfill J_{DFE}=\left(\begin{array}{ccc}-v_0& -{\beta }_e{\mathsf{s}}_{dfe}-{\gamma }_r& (\delta -{\beta }_i){\mathsf{s}}_{dfe}-{\gamma }_r\\ 0& {\beta }_e{\mathsf{s}}_{dfe}-v_1& {\beta }_i{\mathsf{s}}_{dfe}\\ 0& e_i& -v_2\end{array}\right).\end{array}$$

Note the evident block structure $\left\{s\right\},\{e,i\}$ (which is the driving idea behind the next generation matrix method), with one negative eigenvalue $-v_0$.

Now the “infectious” determinant $v_1{v}_2-{\mathsf{s}}_{dfe}{\beta }_t$ is positive iff

$$v_1{v}_2(1-{\mathsf{s}}_{dfe}\frac{{\beta }_t}{v_1{v}_2})=v_1{v}_2(1-{\mathcal{R}}_0)>0\iff {\mathcal{R}}_0<1.$$

This is also the stability condition, since it may be shown that ${\mathsf{s}}_{dfe}{\beta }_t<v_1{v}_2$ implies also the trace condition ${\beta }_e{\mathsf{s}}_{dfe}-v_1-v_2<0$, and so the ${\mathcal{R}}_0$ alternative holds.

Remark 5.

As usual, it is useful to introduce critical vaccination and critical “total contact” (recall ${\beta }_t={\beta }_i{e}_i+{\beta }_e{v}_2$) parameters, as the unique solutions of ${\mathcal{R}}_0=1$ with respect to ${\gamma }_s$ and ${\beta }_t$. The critical values are

$${\gamma }_s^{*}=(\mathsf{\Lambda }+{\gamma }_r)[\frac{{\beta }_t}{v_1{v}_2}-1]:=(\mathsf{\Lambda }+{\gamma }_r)[\mathcal{R}-1],{\beta }_t^{*}=\frac{v_0{v}_1{v}_2}{\mathsf{\Lambda }+{\gamma }_r}=\frac{v_1{v}_2}{{\mathsf{s}}_{dfe}}.$$

(14)

These are particular cases of the SIR-PH Formulas (29).

2.3. The Endemic Point for the FA Approximation, and the Determinant Formula

We consider now the following “first approximation” (FA) of the SIR-PH-FA varying population dynamics

$$\left\{\begin{array}{c}{\mathit{i}}^{\prime }\left(t\right)=\left[\mathsf{s}\right(t)B-V]\mathit{i}\left(t\right)\hfill \\ {\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-\mathsf{s}\left(t\right)\overrightarrow{\beta }\mathit{i}\left(t\right)-\left(\mathsf{\Lambda }+{\gamma }_s\right)\mathsf{s}\left(t\right)+{\gamma }_r\mathsf{r}\left(t\right)\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)=\overrightarrow{a}\mathit{i}\left(t\right)+\mathsf{s}\left(t\right){\gamma }_s-\mathsf{r}\left(t\right)\left({\gamma }_r+\mathsf{\Lambda }\right)\hfill \\ (\mathsf{s}\left(t\right),\mathit{i}\left(t\right),\mathsf{r}\left(t\right))\in {\mathbb{R}}_{+}^4\hfill \end{array}\right.,$$

(15)

where $\mathit{i}\left(t\right):=\left(\begin{array}{c}\mathsf{e}\left(t\right)\\ \mathsf{i}\left(t\right)\end{array}\right),\overrightarrow{\beta }and\overrightarrow{a}$ are defined in Remarks 4, and V in (11). Here the extra deaths $\delta$ due to the disease in state i are kept, but the quadratic interaction terms involving $\delta i$ were neglected. Under this approximation, the endemic point and the determinant of the Jacobian have elegant formulas in terms of ${\mathcal{R}}_0$, some already discovered and others hidden in the particular cases of [11,12].

Remark 6.

For this approximation, the sum of the variables is constant only if $\delta =0$; therefore, $\mathsf{r}$ may not be eliminated, and we must work in four dimensions.

Lemma 1.

(a) For the SAIR model (15) with extra deaths δ, put ${\mathit{i}}_{ee}=\left(\begin{array}{c}{\mathsf{e}}_{ee}\\ {\mathsf{i}}_{ee}\end{array}\right)$ and

$$\left\{\begin{array}{c}{v}_0:=\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s,\hfill \\ v_1:=\mathsf{\Lambda }+{\gamma }_e,\hfill \\ v_2:=\mathsf{\Lambda }+\gamma +\delta ,\hfill \\ v_3:=(v_1+{\gamma }_r)v_2+{\gamma }_r{e}_i.\hfill \end{array}\right.$$

Then, the following formulas hold at the endemic point:

$$\left\{\begin{array}{cc}{\mathsf{s}}_{ee}=\hfill & {\displaystyle \frac{{\mathsf{s}}_{dfe}}{{\mathcal{R}}_0}}=\frac{1}{\mathcal{R}},\hfill \\ \left(\begin{array}{c}{\mathsf{e}}_{ee}\\ {\mathsf{i}}_{ee}\end{array}\right)=\hfill & \frac{\mathsf{\Lambda }+{\gamma }_r}{\mathsf{\Lambda }{v}_3+{\gamma }_r\delta e_i}(1-\frac{1}{{\mathcal{R}}_0})\left(\begin{array}{c}{v}_2\\ e_i\end{array}\right),\hfill \\ \overrightarrow{\beta }{\mathit{i}}_{ee}=\hfill & {\beta }_t\frac{\mathsf{\Lambda }+{\gamma }_r}{\mathsf{\Lambda }{v}_3+{\gamma }_r\delta e_i}(1-\frac{1}{{\mathcal{R}}_0})=\frac{\mathsf{\Lambda }({\mathcal{R}}_0-1)v_0{v}_1{v}_2}{\mathsf{\Lambda }{v}_3+{\gamma }_r\delta e_i}=:EI,\hfill \\ \overrightarrow{a}{\mathit{i}}_{ee}=\hfill & \frac{\mathsf{\Lambda }+{\gamma }_r}{\mathsf{\Lambda }{v}_3+{\gamma }_r\delta e_i}(1-\frac{1}{{\mathcal{R}}_0}){}_{\stackrel{++}{=}}{\gamma }_e\gamma +(\mathsf{\Lambda }+\delta )e_r,\hfill \\ {\mathsf{r}}_{ee}=\hfill & \left({\gamma }_s\left(\mathsf{\Lambda }+v_2+e_i(\mathsf{\Lambda }+\delta )\right)+\mathsf{\Lambda }(\mathcal{R}-1)\left(v_2{e}_r+\gamma e_i\right)\right)\times \frac{1}{\mathcal{R}\left(\mathsf{\Lambda }{v}_3+{\gamma }_r\delta e_i\right)}.\hfill \end{array}\right.$$

(16)

(b) All the coordinates are positive iff ${\mathcal{R}}_0>1$.

(c) The vector ${\mathsf{i}}_{ee}$ checks the general SIR-PH normalization Formula (36).

Proof. 

(a) One can do a direct computation or apply ([10], Prop. 2), a particular case of which is included for completeness as Proposition 3, Section 3. That result is expressed in terms of the Perron Frobenius eigenvector of the matrix $M=\frac{1}{\mathcal{R}}B-V$ (for the 0 eigenvalue); in our case, this is $\left(\begin{array}{c}{v}_2\\ e_i\end{array}\right)$, see second equation in (16).

(b) Is obvious.

(c) May be easily checked, combining the last two rows in (16). □

Remark 7.

Several particular cases of this problem have been studied in the literature. The case $\delta =0$ is studied in [12], and the reference [38] considered the case ${\beta }_e={\gamma }_r=e_r=0,\delta >0$, where

$$\begin{array}{c}\hfill \mathbf{\alpha }=\left(\begin{array}{c}1\\ 0\end{array}\right),A=\left(\begin{array}{cc}-{\gamma }_e& 0\\ {\gamma }_e& -\gamma \end{array}\right),{\overrightarrow{a}}^t:={(-A)}^{t}1=\left(\begin{array}{c}0\\ \gamma \end{array}\right),\overrightarrow{\beta }=\left(\begin{array}{cc}0& {\beta }_i\end{array}\right),\overrightarrow{\delta }=\left(\begin{array}{cc}0& \delta \end{array}\right).\end{array}$$

The normalization Formula (36) reduces in this case to

$$\overrightarrow{\beta }\mathsf{i}=\mathsf{\Lambda }[\mathcal{R}-\frac{1}{{\mathsf{s}}_{dfe}}]=\mathsf{\Lambda }\left(\frac{{\beta }_i{\gamma }_e}{(\mathsf{\Lambda }+\gamma +\delta )\left({\gamma }_e+\mathsf{\Lambda }\right)}-1\right)-{\gamma }_s.$$

Lemma 2.

The following remarkable identity holds

$$Det\left(J_{ee}\right)=\mathsf{\Lambda }{v}_0{v}_1{v}_2(1-{\mathcal{R}}_0)=-Det\left(J_{dfe}\right),$$

(17)

where $v_i$ are defined in (4).

Proof. 

See the proof of Proposition 3. □

Remark 8.

We conjecture that the endemic point is always locally stable when $1<{\mathcal{R}}_0$. We have attempted to apply the classic Routh–Hurwitz–Lienard–Chipart–Schur–Cohn–Jury (RH) methods [39,40,41], which are formulated in terms of the coefficients of the characteristic polynomial $Det(J-z{I}_n)={(-z)}^n+a_1{z}^{n-1}+...+a_n$, and of certain Hurwitz determinants $H_i$ ([39], (15.22)). At order four, $Det(J-z{I}_3)=z^4-Tr\left(J\right)z^3+z^2{M}_2\left(J\right)-z{M}_3\left(J\right)+Det\left(J\right)$, where $M_2,M_3$ are the sums of the second and third order principal leading minors of J, and one ends up with ([39], pg. 137)

$$\left\{\begin{array}{c}Tr\left(J\right)<0,M_2>0,M_3<0,Det\left(J\right)>0,\hfill \\ 0<Tr\left(J\right)\left(M_2{M}_3-Tr\left(J\right)Det\left(J\right)\right)-M_3^2\hfill \end{array}\right..$$

Now in our example the determinant is positive when ${\mathcal{R}}_0>1$ by Lemma 2, and the trace, given by

$$\begin{array}{c}\hfill -\frac{{\gamma }_r{e}_i({\gamma }_s+\mathsf{\Lambda })(\mathsf{\Lambda }+\delta )+\mathsf{\Lambda }{v}_2\left(v_1(\mathcal{R}(\mathsf{\Lambda }+{\gamma }_r)+\mathsf{\Lambda })+{\gamma }_r(\mathsf{\Lambda }+{\gamma }_s)\right)}{e_i{\gamma }_r(\mathsf{\Lambda }+\delta )+\mathsf{\Lambda }{v}_2({\gamma }_r+v_1)}-v_2-(\mathsf{\Lambda }+{\gamma }_r)-\frac{e_i{\beta }_i}{\mathcal{R}{v}_2}\end{array}$$

is negative. However, the check of the sum of the second and third-order principal leading minors of the Jacobian at EE and the additional Hurwitz criterion seemed to exceed our machine power. (At order three, RH becomes $\left\{\begin{array}{c}Tr\left(J\right)<0,\hfill \\ Tr\left(J\right)M\left(J\right)<Det\left(J\right)<0,\hfill \end{array}\right.$ where M is the sum of the second-order principal leading minors of J, which is considerably simpler.)

3. A Review of Arino and Rank-One SIR-PH Models

3.1. SIR-PH Models with Demography, Loss of Immunity, Vaccination and One Susceptible and One Removed Classes

The fundamental concept of basic reproduction number ${\mathcal{R}}_0$ can be only defined (as the spectral radius of the next generation matrix) for epidemic models to which the next generation matrix assumptions apply. It seems more practical, therefore, to restrict to “Arino models” where ${\mathcal{R}}_0$ may be explicitly expressed in terms of the matrices that define the model [8,42,43,44].

The idea behind these models is to further divide the noninfected compartments into (Susceptible) (or input) classes, defined by producing “new non-linear infections”, and output R classes (like $D,D_e$ in our first example), which are fully determined by the rest and may, therefore, be omitted from the dynamics. Furthermore, it is convenient to restrict to epidemic models with the linear force of infection as it is known that non-linear forces of infection may lead to very complex dynamics [1,2,5,36,45,46], which are not always easy to interpret epidemiologically. This is in contrast with the Arino models, where typically one may establish the absence of periodic solutions (closed orbits, homoclinic loops, and oriented phase polygons) [47,48].

It is convenient to restrict even further to the case of one removed class (w.l.o.g. ) and only one susceptible class (a significant simplification).

Definition 1.

A “SIR-PH epidemic” of type n, with demography parameters $(\mathsf{\Lambda },\mu )$ (scalars), loss of immunity and vaccination parameters ${\gamma }_r,{\gamma }_s$, is characterized by two matrices $A,B$ of dimensions $n\times n$ and a column vector of extra death rates $\overrightarrow{\delta }$. This model contains one susceptible class S, one removed state R (healthy, vaccinated, etc), and a n-dimensional vector of “disease” states I (which may contain latent/exposed, infective, asymptomatic, etc). The dynamics are:

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =\mathsf{\Lambda }N-\frac{S\left(t\right)}{N}\overrightarrow{\beta }I\left(t\right)-({\gamma }_s+\mu )S\left(t\right)+R\left(t\right){\gamma }_r,\overrightarrow{\beta }=\overrightarrow{1}B,\hfill \\ \hfill I^{\prime }\left(t\right)& =[\frac{S\left(t\right)}{N}B+A-Diag(\overrightarrow{\delta }+\mu \overrightarrow{1})]I\left(t\right),\hfill \\ \hfill R^{\prime }\left(t\right)& =\overrightarrow{a}I\left(t\right)+{\gamma }_{s}S\left(t\right)-R\left(t\right)({\gamma }_r+\mu ),\overrightarrow{a}=\overrightarrow{1}(-A)\hfill \\ \hfill N^{\prime }\left(t\right)& =S^{\prime }\left(t\right)+\overrightarrow{1}{I}^{\prime }\left(t\right)+R^{\prime }\left(t\right)=(\mathsf{\Lambda }-\mu )N-I\left(t\right)\overrightarrow{\delta },\hfill \\ \hfill D^{\prime }\left(t\right)& =\mu (S\left(t\right)+\overrightarrow{1}I\left(t\right)+R\left(t\right)),\hfill \\ \hfill D_e^{\prime }\left(t\right)& =I\left(t\right)\overrightarrow{\delta }.\hfill \end{array}$$

(18)

Here,

1.

$I\left(t\right)\in {\mathbb{R}}^n$ is a row vector whose components model a set of disease states (or classes).

2.

$R\left(t\right)$ accounts for individuals who recovered from the infection.

3.

B is a $n\times n$ matrix, where each entry $B_{i,j}$ represents the force of infection of the disease class i onto class j. We will denote by $\overrightarrow{\beta }$ the vector containing the sum of the entries in each row of B, namely, $\overrightarrow{\beta }=\overrightarrow{1}B$.

4.

A is a $n\times n$ Markovian sub-generator matrix (i.e., a Markovian generator matrix for which the sum of at least one row is strictly negative), where each off-diagonal entry $A_{i,j}$, $i\ne j$, satisfies $A_{i,j}\ge 0$ and describes the rate of transition from disease class i to disease class j; while each diagonal entry $A_{i,i}$ satisfies $A_{i,i}\le 0$ and describes the rate at which individuals in the disease class i leave towards non-infectious compartments. Alternatively, $-A$ is a non-singular M-matrix [8,49]. (Recall that an M-matrix is a real matrix V with $v_{ij}\le 0,\forall i\ne j,$ and having eigenvalues whose real parts are nonnegative [50].)

5.

$\overrightarrow{\delta }\in {\mathbb{R}}^n$ is a row vector describing the death rates in the disease compartments, which are caused by the epidemic.

6.

${\gamma }_r$ is the rate at which individuals lose immunity (i.e., transition from recovered states to the susceptible state).

7.

${\gamma }_s$ is the rate at which individuals are vaccinated (immunized).

Remark 9.

1.

Note that ${\overrightarrow{a}}^t:={(-A)}^{t}1$ is a vector with a well-known probabilistic interpretation in the theory of phase-type distributions: it is the column vector that completes a matrix with negative row sums to a matrix with zero row sums.

2.

A particular but revealing case is that when the matrix B has rank 1 and is necessarily hence of the form $B=\mathbf{\alpha }\overrightarrow{\beta }$, where $\mathbf{\alpha }\in {\mathbb{R}}^n$ is aprobability column vectorwhose components ${\alpha }_j$ represent the fractions of susceptibles entering into the diseased compartment j when infection occurs. We call this case “rank one SIR-PH”, following Riano [49], who emphasized its probabilistic interpretation—see also [51], and see [52] for an early appearance of such models.

It is convenient to reformulate (18) in terms of the fractions normalized by the total population

$$\begin{array}{ccccccc}\hfill \mathsf{s}& =\frac{S}{N},\hfill & \hfill \mathit{i}& =\frac{1}{N}I,\hfill & \hfill \mathsf{r}& =\frac{1}{N}R,\hfill & \hfill N=\mathsf{s}+\overrightarrow{1}\mathit{i}+\mathsf{r}.\end{array}$$

(19)

The reader may check that the following equations hold for the scaled variables:

$$\left\{\begin{array}{c}{\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-\left(\mathsf{\Lambda }+{\gamma }_s\right)s\left(t\right)+r\left(t\right){\gamma }_r-s\left(t\right)\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\mathit{i}\left(t\right)\hfill \\ {\mathit{i}}^{\prime }\left(t\right)=[s\left(t\right)B+A-Diag\left(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1}\right)+\overrightarrow{\delta }\mathit{i}\left(t\right)I_n]\mathsf{i}\left(t\right)\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)=s\left(t\right){\gamma }_s+\overrightarrow{a}\mathit{i}\left(t\right)-r\left(t\right)\left({\gamma }_r+\mathsf{\Lambda }\right)+r\left(t\right)\overrightarrow{\delta }\mathit{i}\left(t\right)\hfill \\ s\left(t\right)+\overrightarrow{1}\mathit{i}\left(t\right)+r\left(t\right)=1\hfill \end{array}\right.,$$

(20)

and the Jacobian, using $\nabla \overrightarrow{\delta }\mathsf{i}\left(t\right)\mathit{i}\left(t\right)=\mathit{i}\left(t\right)\overrightarrow{\delta }+\overrightarrow{\delta }\mathsf{i}\left(t\right)I_n$, is

$$J=\left(\begin{array}{ccc}-\overrightarrow{\beta }\mathsf{i}-(\mathsf{\Lambda }+{\gamma }_s)& -\mathsf{s}\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)& {\gamma }_r\\ B\mathsf{i}& \mathsf{s}B-V+\mathsf{i}\overrightarrow{\delta }& 0\\ {\gamma }_s& \overrightarrow{a}+\mathsf{r}\overrightarrow{\delta }& -({\gamma }_r+\mathsf{\Lambda })\end{array}\right)+\overrightarrow{\delta }\mathsf{i}{I}_{n+2}.$$

(21)

By letting $\mathsf{n}:=\mathsf{s}+\overrightarrow{1}\mathsf{i}+\mathsf{r},$ we have

$${\mathsf{n}}^{\prime }\left(t\right)=(\mathsf{\Lambda }-\overrightarrow{\delta }\mathsf{i}\left(t\right))(1-\mathsf{n}\left(t\right))=0;$$

The above equation guarantees that if $\mathsf{s}\left(t_0\right)+\mathsf{i}\left(t_0\right)+\mathsf{r}\left(t_0\right)=1$ for some $t_0\in {\mathbb{R}}_{\ge 0}$, then $s\left(t\right)+i\left(t\right)+r\left(t\right)=1$ for all $t\ge t_0$. Accordingly, in what follows we will always assume that $n\left(t_0\right)=1$, which guarantees that $\mathsf{n}\left(t\right)=1,\forall t$.

The following definition puts in a common framework the dynamics for the scaled process and two interesting approximations.

Definition 2.

Let ${\mathsf{\Phi }}_s,{\mathsf{\Phi }}_i,{\mathsf{\Phi }}_r\in \{0,1\}$ and let

$$\begin{array}{cc}\hfill {\mathsf{s}}^{\prime }\left(t\right)& =\mathsf{\Lambda }-\left(\mathsf{\Lambda }+{\gamma }_s\right)s\left(t\right)+r\left(t\right){\gamma }_r-s\left(t\right)i\left(t\right)\overrightarrow{\beta }+{\mathsf{\Phi }}_{s}s\left(t\right)\overrightarrow{\delta }i\left(t\right),\hfill \\ \hfill i^{\prime }\left(t\right)& =[s\left(t\right)B+A-Diag\left(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1}\right))+{\mathsf{\Phi }}_i\overrightarrow{\delta }i\left(t\right)]i\left(t\right),\hfill \\ \hfill {\mathsf{r}}^{\prime }\left(t\right)& =s\left(t\right){\gamma }_s+\overrightarrow{a}i\left(t\right)-r\left(t\right)Diag\left({\gamma }_r+\mathsf{\Lambda }\overrightarrow{1}\right)+{\mathsf{\Phi }}_{r}r\left(t\right)\overrightarrow{\delta }i\left(t\right),\hfill \\ \hfill s\left(t\right)& +\overrightarrow{1}i\left(t\right)+r\left(t\right)=1.\hfill \end{array}$$

(22)

1.

The model (22) with ${\mathsf{\Phi }}_s={\mathsf{\Phi }}_i={\mathsf{\Phi }}_r=1$ will be called scaled model (SM).

2.

The model (22) with ${\mathsf{\Phi }}_s={\mathsf{\Phi }}_i={\mathsf{\Phi }}_r=0$ will be called first approximation (FA).

3.

The model (22) with ${\mathsf{\Phi }}_s={\mathsf{\Phi }}_r=1$, ${\mathsf{\Phi }}_i=0$ will be called intermediate approximation (IA).

Example 1.

The classic SEIRS model

$$\left\{\begin{array}{c}{\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-s\left(t\right)\left({\beta }_{i}i\left(t\right)+{\gamma }_s+\mathsf{\Lambda }\right)+{\gamma }_{r}r\left(t\right)\hfill \\ \left(\begin{array}{c}{\mathsf{e}}^{\prime }\left(t\right)\\ {\mathsf{i}}^{\prime }\left(t\right)\end{array}\right)=\left(\begin{array}{cc}-({\gamma }_e+\mathsf{\Lambda })& {\beta }_{i}s\left(t\right)\\ {\gamma }_e& -\left(\gamma +\mathsf{\Lambda }+\delta \right)\end{array}\right)\left(\begin{array}{c}\mathsf{e}\left(t\right)\\ \mathsf{i}\left(t\right)\end{array}\right)\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)={\gamma }_{s}s\left(t\right)+\gamma i\left(t\right)-r\left(t\right)({\gamma }_r+\mathsf{\Lambda })\hfill \end{array}\right..$$

(23)

is a particular case of SIR-PH-FA model obtained when

$$\left\{\begin{array}{c}\mathbf{\alpha }=\left(\begin{array}{c}1\\ 0\end{array}\right),A=\left(\begin{array}{cc}-{\gamma }_e& 0\\ {\gamma }_e& -\gamma \end{array}\right),\overrightarrow{a}=\overrightarrow{1}(-A)=\left(\begin{array}{cc}0& \gamma \end{array}\right),\overrightarrow{\beta }=\left(\begin{array}{cc}0& {\beta }_i\end{array}\right),soB=\left(\begin{array}{cc}0& {\beta }_i\\ 0& 0\end{array}\right),\overrightarrow{\delta }=\left(\begin{array}{cc}0& \delta \end{array}\right).\hfill \end{array}\right.$$

The SAIR is obtained by modifying the parameters to

$$\left\{\begin{array}{c}\mathbf{\alpha }=\left(\begin{array}{c}1\\ 0\end{array}\right),A=\left(\begin{array}{cc}-{\gamma }_e& 0\\ e_i& -\gamma \end{array}\right),\overrightarrow{a}=\overrightarrow{1}(-A)=\left(\begin{array}{cc}{e}_r& \gamma \end{array}\right),\overrightarrow{\beta }=\left(\begin{array}{cc}{\beta }_e& {\beta }_i\end{array}\right),soB=\left(\begin{array}{cc}{\beta }_e& {\beta }_i\\ 0& 0\end{array}\right),\overrightarrow{\delta }=\left(\begin{array}{cc}0& \delta \end{array}\right).\hfill \end{array}\right.$$

(24)

3.2. The Eigenstructure of the Jacobian for the SIR-PH Scaled Model

For the scaled model, we can eliminate r. Then, the system becomes then $n+1$ dimensional:

$$\left\{\begin{array}{c}{\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }+{\gamma }_r-\left(\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s\right)s\left(t\right)-{\gamma }_r\overrightarrow{1}i\left(t\right)-s\left(t\right)\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)i\left(t\right)\hfill \\ i^{\prime }\left(t\right)=[s\left(t\right)B+A-Diag\left(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1}\right)+\overrightarrow{\delta }i\left(t\right)I_n]i\left(t\right)\hfill \\ s\left(t\right)+\overrightarrow{1}i\left(t\right)\le 1\hfill \end{array}\right..$$

(25)

The Jacobian matrix of the scaled model is given by

$$\begin{array}{cc}J& =\left(\begin{array}{cc}-(\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s)-\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\mathit{i}& -{\gamma }_r\overrightarrow{1}-\mathsf{s}\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\\ B\mathit{i}& \mathsf{s}B+A-Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})+\overrightarrow{\delta }\mathit{i}+\overrightarrow{\delta }\mathit{i}{I}_n\end{array}\right)\hfill \\ & :=\left(\begin{array}{cc}-(\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s)-\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\mathit{i}& -{\gamma }_r\overrightarrow{1}-\mathsf{s}\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\\ B\mathit{i}& \mathsf{s}B-V+\overrightarrow{\delta }\mathit{i}+\overrightarrow{\delta }\mathit{i}{I}_n\end{array}\right),\hfill \end{array}$$

(26)

and

$$\begin{array}{c}\hfill J_{dfe}=\left(\begin{array}{cc}-v_0& -{\gamma }_r\overrightarrow{1}-\mathsf{s}\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\\ 0& {\mathsf{s}}_{dfe}B-V\end{array}\right),\end{array}$$

where $V:=Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A$.

Remark 10.

Note the block structure (which suggested probably the next generation matrix approach), and that

$$Det\left(J_{dfe}\right)=-v_{0}Det({\mathsf{s}}_{dfe}B-V).$$

We highlight next a simple but important consequence of the fact that $V=Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A$ is an invertible matrix, especially when B is assumed to have rank 1.

Lemma 3.

(a) When $B=\mathbf{\alpha }\overrightarrow{\beta }$ is of rank 1, the matrix $B{V}^{-1}$ has precisely one non-zero eigenvalue.

(b) The remaining eigenvalue equals the trace

$$Tr\left(B{V}^{-1}\right)=\overrightarrow{\beta }{V}^{-1}\mathbf{\alpha }:=\mathcal{R}$$

Hence, the Perron-Frobenius eigenvalue of $B{V}^{-1}$ is

$${\lambda }_{PF}\left(B{V}^{-1}\right)=\mathcal{R}.$$

Proof. 

(a) Since $B=\mathbf{\alpha }\overrightarrow{\beta }$ has rank 1, the same holds for $B{V}^{-1}$, and the ”rank-nullity theorem” $rank\left(B{V}^{-1}\right)+nullity\left(B{V}^{-1}\right)=n$ [53] implies that $(n-1)$ of the eigenvalues of $B{V}^{-1}$ are zero.

(b) Using the invariance of the trace under cyclic permutations, we conclude that the trace of $\mathbf{\alpha }\overrightarrow{\beta }{V}^{-1}$ equals $\overrightarrow{\beta }{V}^{-1}\mathbf{\alpha }$. Since $V^{-1}$ has only nonnegative entries, this value must be positive and hence the Perron-Frobenius eigenvalue. □

3.3. The Basic Reproduction Number for SIR-PH, via the Next Generation Matrix Method

We follow up here on a remark preceding ([8], Thm 2.1), and via the next generation matrix method [54,55], and show in the following proposition that their simplified formula for the basic reproduction number still holds when the loss of immunity and vaccination are allowed, provided that $B=\mathbf{\alpha }\overrightarrow{\beta }$ has rank one.

Proposition 2.

Consider a SIR-PH model (20), with parameters

$$(A,B,\mathsf{\Lambda },\overrightarrow{\delta },{\gamma }_s,{\gamma }_r).$$

1.

The unique disease-free equilibrium is $(s_{dfe},\overrightarrow{0},r_{dfe})=\left(\frac{\mathsf{\Lambda }+{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s},\overrightarrow{0},\frac{{\gamma }_s}{\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s}\right).$

2.

The DFE is locally asymptotically stable if ${\mathcal{R}}_0<1$ and is unstable if ${\mathcal{R}}_0>1$, where

$${\mathcal{R}}_0={\lambda }_{PF}\left(F{V}^{-1}\right),$$

(27)

where $F={\mathsf{s}}_{dfe}B$, $V=Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A$ (see 26), and ${\lambda }_{PF}$ denotes the (dominant) Perron Frobenius eigenvalue.

3.

For $B:=\mathbf{\alpha }\overrightarrow{\beta }$ of rank one, we further have

(a) 

$${\mathcal{R}}_0=s_{dfe}\mathcal{R},\mathrm{where}\mathcal{R}=\mathbf{\alpha }{V}^{-1}\overrightarrow{\beta }.$$

(28)

(b)  

The critical vaccination defined by solving ${\mathcal{R}}_0=1$ with respect to ${\gamma }_s$ is given by

$${\gamma }_s^{*}:=(\mathsf{\Lambda }+{\gamma }_r)\left(\mathbf{\alpha }{V}^{-1}b-1\right)=(\mathsf{\Lambda }+{\gamma }_r)\left(\mathcal{R}-1\right).$$

(29)

Proof. 

1. The disease free system (with $\mathsf{i}=0,\mathsf{r}=1-\mathsf{s}$) reduces to

$${\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-({\gamma }_s+\mathsf{\Lambda })s\left(t\right)+\left({\gamma }_{r}s\left(t\right)\right)(1-s\left(t\right)).$$

(30)

2. It is enough to show that the conditions of ([13], Thm 2) hold.

The DFE and its local stability for the disease-free system have already been checked in the SAIR/V+S example.

We provide now a splitting for the infectious equations:

$$\begin{array}{ccc}\hfill {\mathit{i}}^{\prime }\left(t\right)& =& [s\left(t\right)B+\overrightarrow{\delta }i\left(t\right)I_n]i\left(t\right)-\left[Diag\right(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A]i\left(t\right):=\mathcal{F}(s,i)-\mathcal{V}\left(i\right)\hfill \end{array}$$

(where $\mathsf{r}=1-\mathsf{s}-\mathit{i}1$). The corresponding gradients at the DFE $\mathsf{i}=0$ are

$$\left\{\begin{array}{c}F=\left[\frac{\partial \mathcal{F}\left(X^{\left(DFE\right)}\right)}{\partial \mathit{i}}\right]=\mathsf{s}B\hfill \\ V=\left[\frac{\partial \mathcal{V}\left(X^{\left(DFE\right)}\right)}{\partial \mathit{i}}\right]=Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A.\hfill \end{array}\right.$$

(31)

We note that F has non-negative elements and that V is an M-matrix, and, therefore, $V^{-1}$ exists and has non-negative elements, $\forall \mathsf{\Lambda },\overrightarrow{\delta }$. We may check that the next generation matrix conditions [13] are satisfied.

For example, the last non-negativity condition

$$\mathit{i}\left(t\right)\left[Diag\right(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A]1\ge 0,\forall \mathsf{i}\in \mathcal{D},$$

(32)

is a consequence of $-A$ being a M-matrix, which implies $-A1\ge 0,$ componentwise.

3. (a) Using Lemma 3 and the obvious linearity in $\mathsf{s}$, we may conclude that

$${\mathcal{R}}_0={\lambda }_{PF}\left(F{V}^{-1}\right)={\mathsf{s}}_{dfe}{\lambda }_{PF}\left(B{V}^{-1}\right)={\mathsf{s}}_{dfe}\mathcal{R}.$$

3. (b) May be easily verified □

3.4. The Endemic Point of the SIR-PH-FA Model

In this section, we give more explicit results for the endemic equilibrium of the following approximate model, referred to as SIR-PH-FA

$$\left\{\begin{array}{c}{\mathit{i}}^{\prime }\left(t\right)=\left[\mathsf{s}\right(t)B-V]\mathit{i}\left(t\right)\hfill \\ {\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-\mathsf{s}\left(t\right)\overrightarrow{\beta }\mathit{i}\left(t\right)-\left(\mathsf{\Lambda }+{\gamma }_s\right)\mathsf{s}\left(t\right)+{\gamma }_r\mathsf{r}\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)=\overrightarrow{a}\mathit{i}\left(t\right)+\mathsf{s}\left(t\right){\gamma }_s-\mathsf{r}\left(t\right)\left({\gamma }_r+\mathsf{\Lambda }\right)\hfill \\ (\mathsf{s}\left(t\right),\mathit{i}\left(t\right),\mathsf{r}\left(t\right))\in {\mathbb{R}}_{+}^{n+2}\hfill \end{array}\right..$$

(33)

Remark 11.

For this approximation, the sum of the variables is constant only if $\delta =0$; therefore, $\mathsf{r}$ may not be eliminated.

If ${\mathcal{R}}_0>1$, then (33) may have a second fixed point within its forward-invariant set. This endemic fixed point must be such that the quasi-positive matrix ${\mathsf{s}}_{ee}B-V$ is singular, and that $\mathsf{i}$ is a Perron-Frobenius positive eigenvector.

Let ${\mathsf{i}}_0$ denote an arbitrary positive solution of

$$({\mathsf{s}}_{ee}B-V)i_0:=M{i}_0=0,$$

(34)

and let

$$i=\frac{\mathsf{\Lambda }[\frac{1}{{\mathsf{s}}_{ee}}-\frac{1}{{\mathsf{s}}_{dfe}}]}{\left(\overrightarrow{\beta }-\frac{1}{{\mathsf{s}}_{ee}}\frac{{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}\overrightarrow{a}\right)i_0}{i}_0$$

(35)

denote the unique vector of disease components $i_{ee}$ which satisfies also the normalization:

$$\left(\overrightarrow{\beta }-\frac{1}{{\mathsf{s}}_{ee}}\frac{{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}\overrightarrow{a}\right)\mathsf{i}=\mathsf{\Lambda }[\frac{1}{{\mathsf{s}}_{ee}}-\frac{1}{{\mathsf{s}}_{dfe}}].$$

(36)

Proposition 3.

Consider a SIR-PH-FA model (33) with parameters $(\mathsf{\Lambda },A,B,\overrightarrow{\delta },{\gamma }_s,{\gamma }_r),$ where A is assumed irreducible, with ${\mathcal{R}}_0>1$. Then:

1.  

There exists a unique endemic fixed point within its forward-invariant set ${\mathbb{R}}_{+}^{n+2}$ iff

$$\left(\overrightarrow{\beta }-\mathcal{R}\overrightarrow{a}\frac{{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}\right){\mathit{i}}_0>0.$$

This fixed point satisfies

(a)  

${\mathsf{s}}_{ee}=\frac{1}{\mathcal{R}},$

(b)  

that $\mathsf{i}$ given by (35) is a Perron-Frobenius positive eigenvector of the quasi-positive singular matrix ${\mathsf{s}}_{ee}B-V$,

(c)  

the normalization (36).

2.  

The determinant identity $Det\left(J_{dfe}\right)=-Det\left(J_{ee}\right)$ holds.

Proof. 

Recall the fixed point system

$$\begin{array}{ccc}\hfill & & \left\{\begin{array}{c}0=({\mathsf{s}}_{ee}B-V)\mathit{i}\hfill \\ 0=\mathsf{\Lambda }-\left(\mathsf{\Lambda }+{\gamma }_s\right){\mathsf{s}}_{ee}+{\mathsf{r}}_{ee}{\gamma }_r-{\mathsf{s}}_{ee}\overrightarrow{\beta }\mathsf{i},\hfill \\ 0=\overrightarrow{a}\mathsf{i}+{\mathsf{s}}_{ee}{\gamma }_s-{\mathsf{r}}_{ee}({\gamma }_r+\mathsf{\Lambda })⟹{\mathsf{r}}_{ee}=\frac{1}{{\gamma }_r+\mathsf{\Lambda }}\left(\overrightarrow{a}\mathsf{i}+{\gamma }_s{\mathsf{s}}_{ee}\right)\hfill \end{array}\right.\hfill \end{array}$$

and note that ${\mathsf{r}}_{ee}$ is positive if $\mathsf{i},{\mathsf{s}}_{ee}$ are.

1. Let us examine the two cases which arise from factoring the disease equations. More precisely, we will search separately in the disease free set $\{\mathsf{i}=\overrightarrow{0}\}$ and in its complement. Then: (A) either $\mathsf{i}\in \{\mathsf{i}=\overrightarrow{0}\}$ and solving

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathsf{\Lambda }=\left(\mathsf{\Lambda }+{\gamma }_s\right)\mathsf{s}-\mathsf{r}{\gamma }_r\hfill \\ \overrightarrow{0}=\mathsf{s}{\gamma }_s-\mathsf{r}({\gamma }_r+\mathsf{\Lambda })\hfill \end{array}\right.=\left(\begin{array}{cc}\mathsf{s}& \mathsf{r}\end{array}\right)\left(\begin{array}{cc}\mathsf{\Lambda }+{\gamma }_s& {\gamma }_s\\ -{\gamma }_r& -({\gamma }_r+\mathsf{\Lambda })\end{array}\right)\end{array}$$

for $\mathsf{s},\mathsf{r}$ yields the unique DFE, or

(B) the determinant of the resulting homogeneous linear system for $\mathsf{i}\ne \overrightarrow{0}$ must be 0, which implies that $\mathsf{s}={\mathsf{s}}_{ee}$ satisfies

$$det{}_{\stackrel{++}{=}}{\mathsf{s}}_{ee}B-V=0.$$

(37)

Using that $V=Diag(\overrightarrow{\delta }+\mathsf{\Lambda }\overrightarrow{1})-A$ is an invertible matrix, and $det\left(U{U}^{\prime }\right)=det\left(U\right)det\left(U^{\prime }\right)$, (37) may be written as

$$Det\left[\left({\mathsf{s}}_{ee}B-V\right)V^{-1}\right]=0\iff Det\left[B{V}^{-1}-\frac{1}{{\mathsf{s}}_{ee}}\mathbf{I}\right]=0.$$

(38)

Thus:

(a) $\frac{1}{{\mathsf{s}}_{ee}}$ must equal the Perron Frobenius eigenvalue $\mathcal{R}$ (recall Lemma 3). Note that ${\mathsf{s}}_{ee}<1$ follows from $\mathcal{R}\ge {\mathcal{R}}_0>1$.

(b) $\mathsf{i}$ is a Perron-Frobenius eigenvector of the quasi-positive matrix ${\mathsf{s}}_{ee}B-V$, and hence may be chosen as positive.

(c) To determine the proportionality constant, it remains to solve the second equation:

$$\begin{array}{ccc}& & \left(\overrightarrow{\beta }{\mathsf{s}}_{ee}-\overrightarrow{a}\frac{{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}\right)i=\mathsf{\Lambda }-\left(\mathsf{\Lambda }+{\gamma }_s\right){\mathsf{s}}_{ee}+\frac{{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}{\gamma }_s{\mathsf{s}}_{ee}\iff \left(\overrightarrow{\beta }-\overrightarrow{a}\frac{\mathcal{R}{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}\right)i=\hfill \\ & & \mathsf{\Lambda }\mathcal{R}-\mathsf{\Lambda }+{\gamma }_s\left(\frac{{\gamma }_r}{{\gamma }_r+\mathsf{\Lambda }}-1\right)=\mathsf{\Lambda }\mathcal{R}-\mathsf{\Lambda }-{\gamma }_s\left(\frac{\mathsf{\Lambda }}{{\gamma }_r+\mathsf{\Lambda }}\right)=\mathsf{\Lambda }\left(\mathcal{R}-\frac{{\gamma }_s+{\gamma }_r+\mathsf{\Lambda }}{{\gamma }_r+\mathsf{\Lambda }}\right),\hfill \end{array}$$

yielding (36).

2. At the DFE, the infectious equations decouple, and the triangular block structure implies

$$Det\left(J_{dfe}\right)=\mathsf{\Lambda }{v}_{0}Det({\mathsf{s}}_{dfe}B-V).$$

For the EE, we will compute the determinant of the Jacobian matrix:

$$\begin{array}{c}\hfill J=\left(\begin{array}{ccc}\mathsf{s}B-V& Bi& 0\\ -\mathsf{s}\overrightarrow{\beta }& -\overrightarrow{\beta }i-(\mathsf{\Lambda }+{\gamma }_s)& {\gamma }_r\\ \overrightarrow{a}& {\gamma }_s& -({\gamma }_r+\mathsf{\Lambda })\end{array}\right),\end{array}$$

after applying simplifying row and column operations which preserve the determinant (“Neville eliminations” [56]), to be denoted by ∝.

However, first, we will take a detour through the more explicit SAIRS-FA model (15), where $i=\left(\begin{array}{c}e\\ i\end{array}\right)$,

$$\begin{array}{ccc}\hfill J& & =\left(\begin{array}{cccc}{\beta }_{e}s-v_1& {\beta }_{i}s& {\beta }_{e}e+{\beta }_{i}i& 0\\ e_i& -v_2& 0& 0\\ -{\beta }_{e}s& -{\beta }_{i}s& -(\mathsf{\Lambda }+{\gamma }_s)-{\beta }_{i}i-{\beta }_{e}e& {\gamma }_r\\ e_r& \gamma & {\gamma }_s& -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right)\hfill \\ & & \propto \left(\begin{array}{cccc}s{\beta }_e-v_1& {\beta }_{i}s& {\beta }_{e}e+{\beta }_{i}i& 0\\ e_i& -v_2& 0& 0\\ -v_1& 0& -(\mathsf{\Lambda }+{\gamma }_s)& {\gamma }_r\\ e_r& \gamma & {\gamma }_s& -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right)\hfill \end{array}$$

(here we added row one to row three), and $Det\left(J_{dfe}\right)$ simplifies to

$$Det\left(J_{dfe}\right)=\mathsf{\Lambda }{v}_0(v_1{v}_2-{\mathsf{s}}_{dfe}{\beta }_t)=\mathsf{\Lambda }{v}_0{v}_1{v}_2(1-{\mathcal{R}}_0).$$

The Jacobian at the endemic point is

$$\begin{array}{ccc}& & J_{ee}=\left(\begin{array}{cccc}\frac{{\beta }_e}{\mathcal{R}}-v_1& \frac{{\beta }_i}{\mathcal{R}}& {\beta }_e{e}_{ee}+{\beta }_i{i}_{ee}& 0\\ e_i& -v_2& 0& 0\\ -v_1& 0& -(\mathsf{\Lambda }+{\gamma }_s)& {\gamma }_r\\ e_r& \gamma & {\gamma }_s& -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right)\hfill \end{array}$$

requires more work, and we will start by asking Mathematica for the LUDecomposition $J=PerLU⟹Det\left(J\right)=Det\left(Per\right)Det\left(U\right)$. The first factor $Per$ is a permutation matrix with determinant $-1$ in our case, the second, L, is lower triangular with one on the diagonal, and the second is upper triangular

$$\begin{array}{c}\hfill U=\left(\begin{array}{cccc}{e}_i& -v_2& 0& 0\\ 0& \frac{v_2{\gamma }_e-e_i(\mathsf{\Lambda }+\delta )}{e_i}& {\gamma }_s& {\gamma }_s-v_0\\ 0& 0& \frac{\mathsf{\Lambda }{v}_0{v}_1{v}_2(1-{\mathcal{R}}_0)}{-{\gamma }_r{e}_i(\mathsf{\Lambda }+\delta )+v_2\mathsf{\Lambda }(-{\gamma }_r-v_1)}& 0\\ 0& 0& 0& \frac{-{\gamma }_r{e}_i(\mathsf{\Lambda }+\delta )+v_2\mathsf{\Lambda }(-{\gamma }_r-v_1)}{e_i(\mathsf{\Lambda }+\delta )-{\gamma }_e{v}_2}\end{array}\right),\end{array}$$

with determinant

$$-Det\left(U\right)=\mathsf{\Lambda }{v}_0{v}_1{v}_2({\mathcal{R}}_0-1)=Det\left(J_{ee}\right).$$

We provide now a second derivation based on determinant preserving transformations

$$\begin{array}{ccc}& & J_{ee}\propto \left(\begin{array}{cccc}\frac{{\beta }_e}{\mathcal{R}}-v_1& \frac{{\beta }_i}{\mathcal{R}}& {\beta }_e{e}_{ee}+{\beta }_i{i}_{ee}& 0\\ e_i& -v_2& 0& 0\\ -v_1& 0& -v_0& {\gamma }_r\\ e_r& \gamma & v_0& -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right)\hfill \\ & & \propto \left(\begin{array}{cccc}\frac{{\beta }_e}{\mathcal{R}}-v_1& \frac{{\beta }_i}{\mathcal{R}}& {\beta }_e{e}_{ee}+{\beta }_i{i}_{ee}& 0\\ e_i& -v_2& 0& 0\\ -v_1& 0& -v_0& {\gamma }_r\\ e_r-v_1& \gamma & 0& -\mathsf{\Lambda }\end{array}\right),\hfill \end{array}$$

where we substracted column four from three, and then added row three to row four and where $e_{ee}$ and $i_{ee}$ are defined in (16). We develop now by third column:

$$\begin{array}{ccc}& & Det\left(J_{ee}\right)=EI\left|\begin{array}{ccc}{e}_i& -v_2& 0\\ -v_1& 0& {\gamma }_r\\ e_r-v_1& \gamma & -\mathsf{\Lambda }\end{array}\right|+v_0\left|\begin{array}{ccc}\frac{{\beta }_e}{\mathcal{R}}-v_1& \frac{{\beta }_i}{\mathcal{R}}& 0\\ e_i& -v_2& 0\\ e_r-v_1& \gamma & -\mathsf{\Lambda }\end{array}\right|\hfill \\ & & =EI\left|\begin{array}{ccc}{e}_i& -v_2& 0\\ -v_1& 0& {\gamma }_r\\ e_r-v_1& \gamma & -\mathsf{\Lambda }\end{array}\right|-v_0\mathsf{\Lambda }\left|\begin{array}{cc}\frac{{\beta }_e}{\mathcal{R}}-v_1& \frac{{\beta }_i}{\mathcal{R}}\\ e_i& -v_2\end{array}\right|\hfill \\ & & =EI\left|\begin{array}{ccc}{e}_i& -v_2& 0\\ -v_1-{\gamma }_r& 0& {\gamma }_r\\ 0& -(\mathsf{\Lambda }+\delta )& -\mathsf{\Lambda }\end{array}\right|-v_0\mathsf{\Lambda }\left|\begin{array}{cc}\frac{{\beta }_e}{\mathcal{R}}-v_1& \frac{{\beta }_i}{\mathcal{R}}\\ e_i& -v_2\end{array}\right|\hfill \\ & & =EI\left(e_i{\gamma }_r(\mathsf{\Lambda }+\delta )+v_2\mathsf{\Lambda }(v_1+{\gamma }_r)\right)+\mathsf{\Lambda }{v}_0\left(v_2(\frac{{\beta }_e}{\mathcal{R}}-v_1)-e_i\frac{{\beta }_i}{\mathcal{R}}\right)\hfill \\ & & =EI\left(\mathsf{\Lambda }{v}_3+\delta {\mathsf{e}}_i{\gamma }_r\right)\hfill \end{array}$$

where $EI$ is defined in (16), and the third equality follows by substracting column three from column one and then adding row one to row three. Then using ${\beta }_e=\frac{\mathcal{R}{v}_1{v}_2-e_i{\beta }_i}{v_2}$, the last product in the equality four cancels, and recall $EI={\beta }_e{e}_{ee}+{\beta }_i{i}_{ee}=\frac{\mathsf{\Lambda }({\mathcal{R}}_0-1)v_0{v}_1{v}_2}{\mathsf{\Lambda }{v}_3+{\gamma }_r\delta e_i}$, this yields

$$\begin{array}{c}\hfill Det\left(J_{ee}\right)=\mathsf{\Lambda }{v}_0{v}_1{v}_2({\mathcal{R}}_0-1)=-Det\left(J_{dfe}\right).\end{array}$$

Or, by developing the first row, the determinant reads

$$\begin{array}{cc}& Det\left(J_{ee}\right)=(\frac{{\beta }_e}{\mathcal{R}}-v_1)\left|\begin{array}{ccc}-v_2& 0& 0\\ 0& -(\mathsf{\Lambda }+{\gamma }_s)& {\gamma }_r\\ \gamma & {\gamma }_s& -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right|-\frac{{\beta }_i}{\mathcal{R}}\left|\begin{array}{ccc}{e}_i& 0& 0\\ -v_1& -(\mathsf{\Lambda }+{\gamma }_s)& {\gamma }_r\\ e_r& {\gamma }_s& -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right|\\ & +EI\left|\begin{array}{ccc}{e}_i& -v_2& 0\\ -v_1& 0& {\gamma }_r\\ e_r& \gamma & -(\mathsf{\Lambda }+{\gamma }_r)\end{array}\right|\\ & =-(\frac{{\beta }_e}{\mathcal{R}}-v_1)\mathsf{\Lambda }{v}_0{v}_2-\frac{{\beta }_i}{\mathcal{R}}\mathsf{\Lambda }{e}_i{v}_0+EI\left(-\gamma {\gamma }_r{e}_i+v_2(v_1(\mathsf{\Lambda }+{\gamma }_r)-e_r{\gamma }_r)\right)\\ & =EI\left(-\gamma {\gamma }_r{e}_i+v_2(v_1(\mathsf{\Lambda }+{\gamma }_r)-e_r{\gamma }_r)\right)(byusing{\beta }_e=\frac{\mathcal{R}{v}_1{v}_2-e_i{\beta }_i}{v_2})\\ & =EI\left(-\gamma {\gamma }_r{e}_i-v_2{\gamma }_r(v_1-\mathsf{\Lambda }-e_i)+v_1{v}_2(\mathsf{\Lambda }+{\gamma }_r)\right)\\ & =EI\left(v_1{v}_2\mathsf{\Lambda }+e_i{\gamma }_r(v_2-\gamma )+\mathsf{\Lambda }{\gamma }_r{v}_2\right)\\ & =EI\left(\mathsf{\Lambda }(v_1{v}_2+e_i{\gamma }_r+{\gamma }_r{v}_2)+e_i{\gamma }_r\delta \right)\\ & =EI\left(\mathsf{\Lambda }{v}_3+e_i{\gamma }_r\delta \right),\end{array}$$

thus, $Det\left(J_{ee}\right)=\mathsf{\Lambda }{v}_0{v}_1{v}_2({\mathcal{R}}_0-1)=-Det\left(J_{dfe}\right).$ □

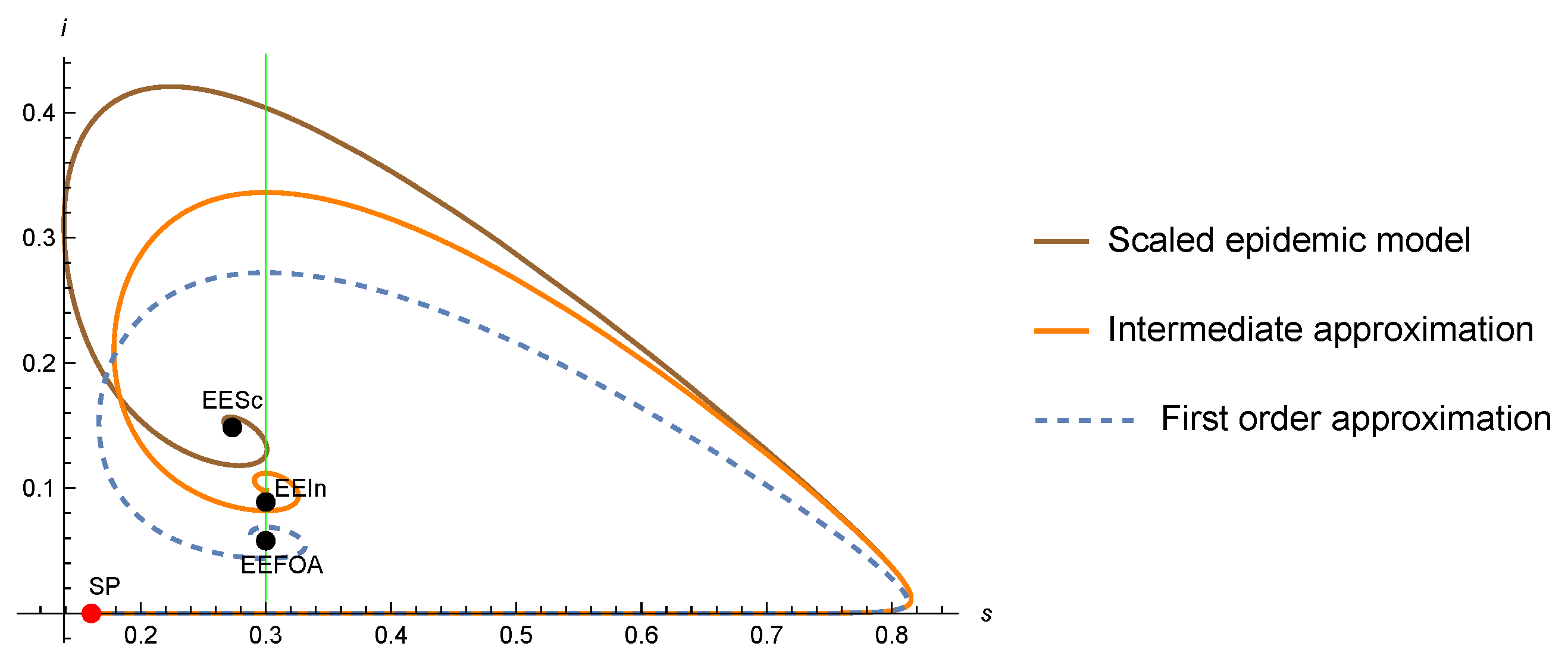
4. A Glimpse of the Intermediate Approximation for the SIR-PH Model

The intermediate approximation associated to (20) is

$$\left\{\begin{array}{c}{\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-\left(\mathsf{\Lambda }+{\gamma }_s\right)\mathsf{s}\left(t\right)+\mathsf{r}\left(t\right){\gamma }_r-\mathsf{s}\left(t\right)\left(\overrightarrow{\beta }-\overrightarrow{\delta }\right)\mathit{i}\left(t\right)\hfill \\ {\mathit{i}}^{\prime }\left(t\right)=\left(\mathsf{s}\left(t\right)B-V\right)\mathit{i}\left(t\right)\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)=\mathsf{s}\left(t\right){\gamma }_s+\overrightarrow{a}\mathit{i}\left(t\right)-\mathsf{r}\left(t\right)\left(\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }\mathit{i}\left(t\right))\right)\hfill \end{array}\right.;$$

(39)

Proposition 4.

1.  

The DFE points of the scaled, the intermediate approximation, and the FA are equal, given by $(\frac{\mathsf{\Lambda }+{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s},\overrightarrow{0},\frac{{\gamma }_s}{\mathsf{\Lambda }+{\gamma }_r+{\gamma }_s})$.

2.  

An endemic point must satisfy that ${\mathit{i}}_{ee}$ is a positive eigenvector of the matrix ${\mathsf{s}}_{ee}B-V$ for the eigenvalue 0 (same as for theFA), that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{s}_{ee}=\frac{1}{\mathcal{R}},\hfill \\ r_{ee}=\frac{\frac{{\gamma }_s}{\mathcal{R}}+\overrightarrow{a}{\mathit{i}}_{ee}}{\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }{\mathit{i}}_{ee}}>0\hfill \end{array}\right.,\end{array}$$

and that

$$\mathsf{\Lambda }(\mathcal{R}-1)-{\gamma }_s+\frac{{\gamma }_s{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }{\mathit{i}}_{ee}}=[(\overrightarrow{\beta }-\overrightarrow{\delta })-\mathcal{R}\frac{{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }{\mathit{i}}_{ee}}\overrightarrow{a}]{\mathit{i}}_{ee}.$$

(40)

Since this equation is quadratic (see (41)), we may have a priori two, one, or zero endemic points.

Proof. 

1.

The equations determining the DFE for the three models coincide.

2.

$s_{ee}=\frac{1}{\mathcal{R}}$ has been established in the proof of Proposition 3, and $r_{ee}=\frac{\frac{{\gamma }_s}{\mathcal{R}}+\overrightarrow{a}{\mathit{i}}_{ee}}{\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }{\mathit{i}}_{ee}}$ follows immediately from the last equation in (39). By susbtitution of $r_{ee}$ and $s_{ee}$ into the first equation in (39), we obtain

$$\begin{array}{cc}& \mathsf{\Lambda }(\mathcal{R}-1)-{\gamma }_s+\frac{{\gamma }_s{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }{\mathit{i}}_{ee}}=[(\overrightarrow{\beta }-\overrightarrow{\delta })-\mathcal{R}\frac{{\gamma }_r}{\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }{\mathsf{i}}_{ee}}\overrightarrow{a}]{\mathsf{i}}_{ee},\end{array}$$

which yields the result.

□

Remark 12.

1.

Under the substitution $\overrightarrow{\delta }{\mathit{i}}_{ee}\to 0$, (40) reduces to Formula (36).

2.

The existence of positive solutions to (40) requires studying a quadratic equation $X{\lambda }^2+Y\lambda +Z$. Indeed, putting ${\mathit{i}}_{ee}=\lambda {\mathit{i}}_0$, (40) may also be written as

$$\begin{array}{c}\iff (\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }\lambda {\mathit{i}}_0)(\mathsf{\Lambda }(\mathcal{R}-1)-{\gamma }_s)+{\gamma }_s{\gamma }_r=(\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }\lambda {\mathit{i}}_0)(\overrightarrow{\beta }-\overrightarrow{\delta })\lambda {\mathit{i}}_0-\mathcal{R}{\gamma }_r\overrightarrow{a}\lambda {\mathit{i}}_0\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\iff {\gamma }_s{\gamma }_r=(\mathsf{\Lambda }+{\gamma }_r-\overrightarrow{\delta }\lambda {\mathit{i}}_0)\left[(\overrightarrow{\beta }-\overrightarrow{\delta })\lambda {\mathit{i}}_0+{\gamma }_s-\mathsf{\Lambda }(\mathcal{R}-1)\right]-\mathcal{R}{\gamma }_r\overrightarrow{a}\lambda {\mathit{i}}_0,\hfill \end{array}$$

(41)

and we find

$$\begin{array}{c}\hfill \left\{\begin{array}{c}X=\overrightarrow{\delta }{\mathit{i}}_0(\overrightarrow{\beta }-\overrightarrow{\delta }){\mathit{i}}_0,\hfill \\ Y=\left(({\gamma }_s-\mathsf{\Lambda }(\mathcal{R}-1))\overrightarrow{\delta }+\mathcal{R}{\gamma }_r\overrightarrow{a}+(\mathsf{\Lambda }+{\gamma }_r)(\overrightarrow{\delta }-\overrightarrow{\beta })\right){\mathit{i}}_0,\hfill \\ Z={\gamma }_s{\gamma }_r+(\mathsf{\Lambda }+{\gamma }_r)(\mathsf{\Lambda }(\mathcal{R}-1)-{\gamma }_s).\hfill \end{array}\right.\end{array}$$

Example 2. The intermediate approximation of the SAIRS modelis

$$\left\{\begin{array}{c}\left(\begin{array}{c}{\mathsf{e}}^{\prime }\left(t\right)\\ i^{\prime }\left(t\right)\end{array}\right)=\left(\begin{array}{cc}-({\gamma }_e+\mathsf{\Lambda })+{\beta }_e\mathsf{s}\left(t\right)& {\beta }_i\mathsf{s}\left(t\right)\\ e_i& -\left(\gamma +\mathsf{\Lambda }+\delta \right)\end{array}\right)\left(\begin{array}{c}\mathsf{e}\left(t\right)\\ {\mathsf{i}}_t\end{array}\right)\hfill \\ {\mathsf{s}}^{\prime }\left(t\right)=\mathsf{\Lambda }-\mathsf{s}\left(t\right)\left({\beta }_i{\mathsf{i}}_t+{\beta }_e\mathsf{e}\left(t\right)+{\gamma }_s+\mathsf{\Lambda }-\delta {\mathsf{i}}_t\right)+{\gamma }_r\mathsf{r}\left(t\right)\hfill \\ {\mathsf{r}}^{\prime }\left(t\right)={\gamma }_s\mathsf{s}\left(t\right)+e_r\mathsf{e}\left(t\right)+\gamma {\mathsf{i}}_t-\mathsf{r}\left(t\right)({\gamma }_r+\mathsf{\Lambda }-\delta {\mathsf{i}}_t)\hfill \end{array}\right..$$

(42)

is a particular case of SIR-PH-IA model ($\mathbf{\alpha },A,\overrightarrow{a},\overrightarrow{\beta }$ and $\overrightarrow{\delta }$ were defined in (24)).

For the SAIRS model (38) with extra deaths δ, putting ${\mathit{i}}_{ee}^{(1,2)}=\left(\begin{array}{c}{\mathsf{e}}_{ee}^{(1,2)}\\ {\mathsf{i}}_{ee}^{(1,2)}\end{array}\right)$, the following formulas hold at the endemic points:

$$\left\{\begin{array}{cc}\hfill & {\mathsf{s}}_{ee}={\displaystyle \frac{{\mathsf{s}}_{dfe}}{{\mathcal{R}}_0}}=\frac{1}{\mathcal{R}}\hfill \\ \hfill & {\mathsf{e}}_{ee}^{(1,2)}=\frac{v_2{e}_i\left(v_0(\delta -\mathcal{R}(\mathsf{\Lambda }+\delta ))+\mathsf{\Lambda }\delta +\mathsf{\Lambda }\mathcal{R}\left(\mathsf{\Lambda }+{\gamma }_s\right)+\delta \mathcal{R}{\gamma }_s\right)+v_2^2\mathsf{\Lambda }\mathcal{R}\left(-v_0-v_1+\mathsf{\Lambda }+{\gamma }_s\right)}{2\delta e_i\left(\delta e_i-v_1{v}_2\mathcal{R}\right)}\hfill \\ & \pm \frac{\sqrt{v_2^2\left(\left(v_0{e}_i(\delta -\mathcal{R}(\mathsf{\Lambda }+\delta ))+\delta e_i\left(\mathsf{\Lambda }+\mathcal{R}{\gamma }_s\right)+\mathsf{\Lambda }\mathcal{R}{e}_i\left(\mathsf{\Lambda }+{\gamma }_s\right)+v_2\mathsf{\Lambda }\mathcal{R}\left(-v_0-v_1+\mathsf{\Lambda }+{\gamma }_s\right)\right){}^2+4\mathsf{\Lambda }\delta e_i\left(\mathcal{R}{\gamma }_s-v_0(\mathcal{R}-1)\right)\left(v_1{v}_2\mathcal{R}-\delta e_i\right)\right)}}{2\delta e_i\left(\delta e_i-v_1{v}_2\mathcal{R}\right)}\hfill \\ \hfill & {\mathsf{i}}_{ee}^{(1,2)}=\frac{v_2{e}_i\left(v_0(\delta -\mathcal{R}(\mathsf{\Lambda }+\delta ))+\mathsf{\Lambda }\delta +\mathsf{\Lambda }\mathcal{R}\left(\mathsf{\Lambda }+{\gamma }_s\right)+\delta \mathcal{R}{\gamma }_s\right)+v_2^2\mathsf{\Lambda }\mathcal{R}\left(-v_0-v_1+\mathsf{\Lambda }+{\gamma }_s\right)}{2v_2\delta \left(\delta e_i-v_1{v}_2\mathcal{R}\right)}\hfill \\ & \pm \frac{\sqrt{v_2^2\left(\left(v_0{e}_i(\delta -\mathcal{R}(\mathsf{\Lambda }+\delta ))+\delta e_i\left(\mathsf{\Lambda }+\mathcal{R}{\gamma }_s\right)+\mathsf{\Lambda }\mathcal{R}{e}_i\left(\mathsf{\Lambda }+{\gamma }_s\right)+v_2\mathsf{\Lambda }\mathcal{R}\left(-v_0-v_1+\mathsf{\Lambda }+{\gamma }_s\right)\right){}^2+4\mathsf{\Lambda }\delta e_i\left(\mathcal{R}{\gamma }_s-v_0(\mathcal{R}-1)\right)\left(v_1{v}_2\mathcal{R}-\delta e_i\right)\right)}}{2v_2\delta \left(\delta e_i-v_1{v}_2\mathcal{R}\right)}\hfill \end{array}\right.$$

(43)

Remark 13.

A yet another open problem is whether the endemic point must always exist for theFAandIAmodels..

5. The Scaled SAIRS Model: Existence, Uniqueness, and Local Stability of the Endemic Point

5.1. Reduction to One Dimension and the Problem of Existence of Endemic Equilibrium

We will follow here the idea of the particular cases ([15], (4.3)), ([17], (14)) and ([19], (3.28)), in which the authors eliminate $e,s$ in the fixed point equations

$$\begin{array}{c}\hfill \left\{\begin{array}{c}0=\mathsf{\Lambda }+{\gamma }_r(1-e-i)-s{}_{\stackrel{++}{=}}{v}_0+({\beta }_i-\delta )i+{\beta }_{e}e,\hfill \\ \left(\begin{array}{c}0\\ 0\end{array}\right)={}_{\stackrel{++}{=}}\left(\begin{array}{cc}{\beta }_{e}s-v_1& {\beta }_{i}s\\ e_i& -v_2\end{array}\right)+\delta i{I}_2\left(\begin{array}{c}e\\ i\end{array}\right)\hfill \end{array}\right.\end{array}$$

and study a resulting polynomial equation in i. An alternative to the successive eliminations suggested in [15,17,19] is to notice that a strictly positive endemic point must satisfy that the determinant

$$\mathsf{\Delta }=\left|\begin{array}{cc}{\beta }_e\mathsf{s}+\delta \mathsf{i}-v_1& {\beta }_i\mathsf{s}\\ e_i& \delta \mathsf{i}-v_2\end{array}\right|=0.$$

After eliminating $\mathsf{s}$ from the first equation, the denominator of the determinant is the denominator of $\mathsf{s}$, and the numerator of the determinant is a fifth-order polynomial in $\mathsf{i}$, with factor $\mathsf{i}$.

$$e=\frac{i(v_2-i\delta )}{e_i},s=\frac{\mathsf{\Lambda }+{\gamma }_r\left(1-e-i\right)}{v_0+i({\beta }_i-\delta )+e{\beta }_e}.$$

(44)

From the equation of s in (44), we note a typo in ([17], (15)), which should be $s=\frac{\mathsf{\Lambda }}{i({\beta }_i-\delta )+\mathsf{\Lambda }+{\gamma }_s}$.

The next result shows that the existence of endemic points may be reduced for SAIRS to a one-dimensional problem.

Lemma 4.

An endemic point $E_{ee}$ satisfying $0<{\mathsf{i}}_{ee}<min[1,(\mathsf{\Lambda }+{\gamma }_r)/\delta ]$ and

$${\gamma }_r({\mathsf{e}}_{ee}+{\mathsf{i}}_{ee}-1)\le \mathsf{\Lambda }$$

(45)

will satisfy $E_{ee}\in {\mathcal{D}}_e$.

Proof. 

By (44), $0<{\mathsf{i}}_{ee}<1⟹{\mathsf{e}}_{ee}>0$. Also, the numerator of ${\mathsf{s}}_{ee}$, given by $\mathsf{\Lambda }+(1-{\mathsf{i}}_{ee}-{\mathsf{e}}_{ee})$${\gamma }_r$, is positive by (45). Furthermore, $0<{\mathsf{i}}_{ee}<i_c$ (recall (7)) implies that the denominator of ${\mathsf{s}}_{ee}$ is positive.

Finally, $0<1-{\mathsf{s}}_{ee}-{\mathsf{e}}_{ee}-{\mathsf{i}}_{ee}$ follows from (7) and ${\mathsf{s}}_{ee}>0$, ${\mathsf{e}}_{ee}>0$, ${\mathsf{i}}_{ee}>0$. □

The next result shows that the endemic point is unique, without the unnecessary extra conditions assumed in [17].

Proposition 5.

${\mathcal{R}}_0>1$ ensures the existence and uniqueness of the endemic point for the [17] SIR-PH-SM problem.

Proof. 

For the [17] problem (45) holds trivially (since ${\gamma }_r=0$, ${\gamma }_s\ge 0$). Thus, it only remains to show that the third order polynomial $p\left(\mathsf{i}\right)$ which results from the elimination has precisely one root in $(0,i_c)$, when ${\mathcal{R}}_0>1$. (The polynomial is of fourth order in general, with a complicated formula, but the leading coefficient is $-{\delta }^3{\beta }_e$, and when ${\beta }_e=0$ and $\delta =0$, the fourth order polynomial becomes of third and first order, respectively. )It turns out that this polynomial satisfies

$$\left\{\begin{array}{c}p\left(0\right)=-({\mathcal{R}}_0-1){\gamma }_e{v}_1{v}_2\left(\mathsf{\Lambda }+{\gamma }_s\right)<0\hfill \\ p\left(i_c\right)=\frac{{\gamma }_e^2\left({\beta }_i\gamma \mathsf{\Lambda }+\delta (\gamma +\delta ){\gamma }_s\right)}{\delta }>0\hfill \end{array}\right..$$

This implies that when ${\mathcal{R}}_0>1$, $p\left(i\right)$ must have either one, two or three roots in $(0,i_c).$

The last case may be ruled out using an interesting algebraic identity ([15], (4.3)), ([17], (14))

$$p\left(i\right)={\mathcal{R}}_0-f_{SH}\left(i\right),f_{SH}\left(i\right)=f_{Li}\left(i\right):=\left(1+\frac{{\beta }_i-\delta }{{\gamma }_s+\mathsf{\Lambda }}i\right)\left(1-\frac{i\delta }{v_2}\right)\left(1-\frac{i\delta }{v_1}\right).$$

(46)

This shows that solving the equation $p\left(i\right)=0$ (which provides the endemic equilibrium values of $\mathsf{i}$) is equivalent to equating to ${\mathcal{R}}_0$ a function with known roots $f_{SH}\left(i\right).$

As a sanity check, note that when $i=0$, this equation reduces to ${\mathcal{R}}_0=1$, which is consistent with the fact that the endemic point only appears at this threshold (equivalently, when ${\mathcal{R}}_0=1$, the polynomial $p\left(i\right)={\mathcal{R}}_0-f_{SH}\left(i\right)$ admits only one root, namely $\mathsf{i}=0$).

Refer now to the Figure 2 which plots the function $f_{SH}\left(i\right)$. It may be easily checked that the roots of $f_{SH}\left(i\right),$ given by $i_1=\frac{v_1}{\delta }$, $i_2=\frac{v_2}{\delta }$, $i_3=\frac{\mathsf{\Lambda }}{{\beta }_i-\delta }$, do not belong to the range $(0,i_c=min[1,\frac{\mathsf{\Lambda }}{\delta }])$ (recall that ${\gamma }_r=0$). Indeed, ${\mathsf{i}}_2>1$, ${\mathsf{i}}_1>\frac{\mathsf{\Lambda }}{\delta }$, and ${\mathcal{R}}_0>1\iff {\beta }_t>{\beta }_t^{*}⟹{\beta }_i>\delta ⟹i_3<0$. It follows that the largest root of $f_{SH}\left(i\right)={\mathcal{R}}_0$ must be outside the interval $(0,\frac{\mathsf{\Lambda }}{\delta })$, ending the proof. In ([17], Thm 3.3), the authors used a slightly different approach which leads to several unnecessary cases, as seen above. □

From the proof above, when ${\mathcal{R}}_0>1$, the line $f={\mathcal{R}}_0$ has exactly one intersection $(i_{ee},f_{SH}\left(i_{ee}\right))$ with the graph of $f_{SH}\left(i\right)$ that satisfies $i_{ee}\in [0,i_c]$,– see Figure 2.

Figure 3a displays the bifurcation diagrams of the equilibrium value(s) of $\mathsf{i}$ for the [17] problem with respect to $\beta$; we note the usual forward bifurcation diagram when ${\mathcal{R}}_0$ reaches its critical value 1. Figure 3b displays the bifurcation diagrams of the equilibrium value(s) of $\mathsf{i}$ with respect to $\delta$; we notice that nothing happens in the critical points identified in ([17], Thm 3.3).

Figure 4 compares the qualitative behavior and equilibrium points of the ( s,e+i)-coordinates of the three variants of the SEIRS scaled model discussed in [17], and note that the endemic coordinates $s_{EEFA}=s_{EEIn}=1/\mathcal{R},$ which is illustrated by a vertical green line.

5.2. Conjecture for the SEIRS Model

The uniqueness of the endemic point and its local stability when ${\mathcal{R}}_0>1$ was also claimed in [19], and we conjecture that these results are true, even for SEIRS, with ${\beta }_e=e_r=0,{\gamma }_s\ge 0,{\gamma }_r\ge 0$.

However, this must be viewed as an open problem even in the case ${\beta }_e=e_r=0={\gamma }_s$, since the crucial analog of (46), the equation ([19], (3.28)) used intensively in their proof is wrong, see Figure 5.

Indeed, recall that the i equation may be written as

$$f_{Lu}\left(i_{ee}\right)={\mathcal{R}}_0+g_{Lu}\left(i_{ee}\right),$$

(47)

where $f_{Lu}\left(i\right)=f_{SH}\left(i\right)$ (with ${\gamma }_s$ replaced by 0). The equation ([19], (3.30)) states that $g_{Lu}\left(i\right)$ is rational, which implies that the polynomial $p\left(i\right)$ is of fourth order, while the correct order of $p\left(i\right)$ is 3. In fact, ([19], (3.30)) should be replaced by the second order polynomial

$$g_{Lu}\left(i\right)={\mathcal{R}}_0\frac{{\gamma }_r-i{\gamma }_r}{\mathsf{\Lambda }}+1-\frac{{\gamma }_r(\gamma -i\delta +\mathsf{\Lambda }+\delta )\left({\gamma }_e+i({\beta }_i-\delta )+\mathsf{\Lambda }\right)}{\mathsf{\Lambda }(\mathsf{\Lambda }+\gamma +\delta )\left(v_1\right)}$$

(48)

We conjecture that their result holds true, since in this case also the third order polynomial resulting from the elimination when ${\mathcal{R}}_0>1$ satisfies

$$\left\{\begin{array}{c}p\left(0\right)=-({\mathcal{R}}_0-1){\gamma }_e\mathsf{\Lambda }(\mathsf{\Lambda }+\gamma +\delta )\left(v_1\right)<0,\hfill \\ p\left(i_c\right)=\frac{{\beta }_i\gamma {\gamma }_e^2\mathsf{\Lambda }}{\delta }>0,\hfill \end{array}\right.$$

and so $p\left(i\right)$ must still have either one, two or three roots in $(0,i_c)$.

6. Conclusions and Further Work

Our paper highlighted several open problems for SIR-PH, SIR-PH-IA, and SIR-PH-FA models. The following general directions seem worthy of further work.

1.

Investigate whether the beautiful determinant Formula (17) hidden in the papers of [11,12] (valid when $\delta =0$) may be extended to SIR-PH models, exploiting the partition (26).

2.

Study the case of two or more compartments susceptible to become infected (for example the SEIT model [13,57]).

3.

Study the scaled model as a perturbation of the FA model.

4.

Study stability via the geometric approach of Li, Graef, Wang, Karsai, Muldoney, and Lu [15].

5.

We hope that the use of more sophisticated and fast software will allow researchers in the future to progress with the interesting questions raised by models with higher dimensions. Here, exploiting symmetries may turn out helpful.