Magneto-Nanofluid Flow via Mixed Convection Inside E-Shaped Square Chamber

Abstract

Nanofluids play a crucial role in the augmentation of heat transfer in several energy systems. They exhibit better thermal conductivity and physical strength compared to normal fluids. Here, we conduct an evaluative investigation of the magnetized flow of water–copper nanofluid and its heat transport inside a symmetrical E-shaped square chamber via mixed convective impact with a heated corner. The chamber was constructed symmetrically with an inclined magnetic field strength, and the upper surface of the chamber was isolated and set to move at a fixed velocity. The heated corner was set at a fixed hot temperature in both the left and lower directions. The right side was maintained at a fixed cold temperature, while the remaining portions of the left and lower parts were isolated. The investigation was implemented computationally, solving each of the energy and Navier–Stokes models via the application of a symmetrical finite volume method. The following topics have been addressed in this study: the consequences of the magnetic field, the volumetric fraction of nanoparticles, the heat generation–absorption parameters, and the effects of heat-source length and Richardson number on the fluid comportment and heat transport. The outputs of this symmetric study enabled us to arrive at the following derivation: the magnetic field reduces the fluid circulation inside the E-shaped square chamber. The augmentation of the Richardson number leads to an increase in the heat transfer. Moreover, the decrease in heat generation coefficient lowers the nanofluid temperature and weakens the flow fields.

1. Introduction

Mixed convection heat transport is the most utilized phenomenon in several industrial and engineering applications, including nuclear power plants, heat exchangers, solar collectors, and electronic cooling systems [1,2,3,4,5]. Thus, it is a topic of interest for those seeking to understand how it can be managed and controlled to serve its desired purpose. Gangawane [6] investigated mixed convection flow in a square lid-driven enclosure that includes a triangular source of heat. The upper wall of the enclosure moved horizontally whereas the other walls remained fixed. Nayak et al. [7] studied combined convection in a lid-driven cavity. The outputs explained that flow, alongside heat and mass transport, are highly affected by the length and position of the heating and cooling sources. These outputs, which regulate the flow and heat transport, were emphasized by Razera et al. [8], who studied a semi-elliptical heat source in a square lid-driven cavity. Gangawane et al. [9] investigated the effect of the position of a triangular source block on mixed convection in a symmetrical square lid-driven chamber. They concluded that the value of the Nuselt number decreases with an increase in the Richardson number (Ri); furthermore, maximum heat transfer can be achieved when the source is positioned at the center of the cavity. Manchanda and Gangawane [10] studied mixed convection in a dual lid-driven square cavity and a triangular source of heat. The upper and bottom surfaces moved various different directions, whereas the vertical walls remained fixed. They found that the impact of Ri is unnoticeable at power law indexes equaling or less than unity due to having great shear stress, and therefore less viscosity impact. Zhou et al. [11] analyzed mixed convection flow in a double lid-driven enclosure filled with nanofluid. The data suggested that the best configuration for improving heat transport was the fourth of the four cases they examined. Gangawane and Oztop [12] explored compound convective flow in a lid-driven semicircular cavity with an isolated block. They concluded that the best heat-transport improvement resulted from the application of a triangular block shape.

Lately, investigators have been working with several novel types of fluids to achieve more efficient results. The host fluid plays a significant role in a nanofluid mix. In the past, researchers only worked with simple base fluids, but in the last few decades, a preference for nanofluids has arisen. Pioneer analysis of the thermophysical properties of nanofluids has been provided by Choi and Eastman [13]. They noticed that the heat transfer and thermal conductivity of nanofluids have improved compared to basic single-phase base-fluid solvents. Nanofluids are liquids comprised of nanosized particles. Generally, metals, carbides, and oxides are used to form nanofluids in a highly volatile liquid, for example, ethylene glycol, water, oil, paraffin, etc. Nanoparticles are made from ingredients that are completely saturated. To obtain effective thermal conductivity, present-day researchers assemble nanoparticles with unique constructions, as variations in size, basic medium, and particle selection influence effective conductivity. Nanoparticles are useful in a wide range of applications such as car engines, generators, cooling systems and more. Their flexibility allows for their application in advanced industries such as electronic cooling, automotive cooling, heating systems, surfactants, lubricants, metal welding, medical production, solar heating, cooling equipment, integrated engines, cooling engines, cooling integrated circuits (ICs), heat transfer to nuclear reactors, etc. Later, various investigators studied these fluids, as Shahi et al. [14] analyzed combined convection in a ventilated square cavity by producing a nanofluid via explosion. They concluded that, as the concentration of solids increases, so does the heat transfer rate. These outputs have developed via [15,16], who examined combined convection in a cavity with an inclined lid, filled with nanofluid. Ismael et al. [17] explored mixed convection in a lid-driven cavity filled with nanofluid and heated from the bottom corner. They found that when the mixed convection parameter is weak, the effect of the nanoparticles on heat improvement is not remarkable, though this impact becomes pronounced with large Richardson number values. Alsabery et al. [18] analyzed mixed convection in a lid-driven cavity filled with nanofluid, containing a square obstacle. They examined various positions for the obstacle. They concluded that adding nanoparticles improves the heat transport as long as the Re is high. However, the effect of adding more nanoparticles to a cavity with low Re can adversely affect heat transfer. Cho et al. [19] and pal et al. [20] studied the impact of a lid-driven cavity with a wavy wall on nanofluids. Karbasifar et al. [21] studied mixed convection in a square, lid-driven, inclined cavity with a hot elliptical centric cylinder. They deduced that Nusselt number trends are inversely affected by cavity angle, volume fraction, and fluid velocity. Ali et al. [22] used a finite volume scheme to investigate the mixed convection flow of hybrid nanofluid in a double lid-driven cavity. Elshehabey and Ahmed [23] analyzed magneto-mixed convection in a lid-driven cavity that was heated from the sides and filled with nanofluid. Mehmood et al. [24] examined magneto-combined convection in a lid-driven cavity filled with nanofluid. Hussain et al. [25] considered the magnetized nanofluid flow via mixed convection in a dual lid-driven cavity. Mondal and Mahapatra [26] studied the magneto-nanofluid flow via a compound convection in a trapezoidal cavity. Many studies by numerous researchers are devoted to nanofluid flow via mixed convection in enclosures [27,28,29,30,31,32,33,34].

In the view of applied study, especially in the field of fluid dynamics, magnetic fields play an essential role. Scientists from past decades conducted a great deal of research on the properties of magnetic fields. Aspects such as heat transfer, fluid characteristics, and other factors influencing fluid transfer have been studied. However, most of the studies had only a numerical and theoretical basis, meaning not much experimental work has been done regarding magnetic exchange and heat transfer. In the present day, we need experimental results, which are advantageous for industrial application. Cooling devices such as air conditioners and refrigerators are essential for industries in which heat transfer is involved. The use of advanced, modern cooling technology is expected in these situations. In most heat-transfer appliances, upgrades require an increase in surface area, which, in turn, require an increase in overall size and volume. Therefore, overcoming these problems requires more efficient cooling methods. The interactions of Nanofluids with magnetic fields offer possible new solutions regarding the transmission of nanofluid heat. There are two ways to approach the problem. Well-regulated magnetic fields can be used effectively for efficient conversion and thermal management of multi-physical transport. The fixed magnet field changes the speed of the fluid. The multiple physical conditions involved, such as the porous surface and the various properties of nanofluid, make the transport process extremely difficult. For this reason, the magnetic field-based control strategy is widely accepted in many modern systems, and its use is rapidly increasing in various fields of engineering and industry, see [35,36,37,38,39,40,41,42,43].

In light of the gaps in the above investigative literature, we realized that no research was done to examine the magnetized convection flow and heat transport characteristics of water–Cu-based nanofluid inside an E-shaped square chamber. Hence, the current study investigates the magnetized mixed convective of (Cu–water) nanofluid flow inside an E-shaped square cavity with heated corners. Impacts of several related parameters, such as volumetric fraction of nanoparticles, Hartmann number, heat generation/absorption parameters, length of heat source, and Reynolds number are reported. However, nano-colloidal dispersion provides a highly encapsulated method to promote heat transfer, suggesting that the study of a magnetic field’s influence on the thermophysical characteristics of such a fluid would be advantageous. We believe that our efforts will prove valuable to forthcoming nanoscience technologies, from both the scientific and applicative angles.

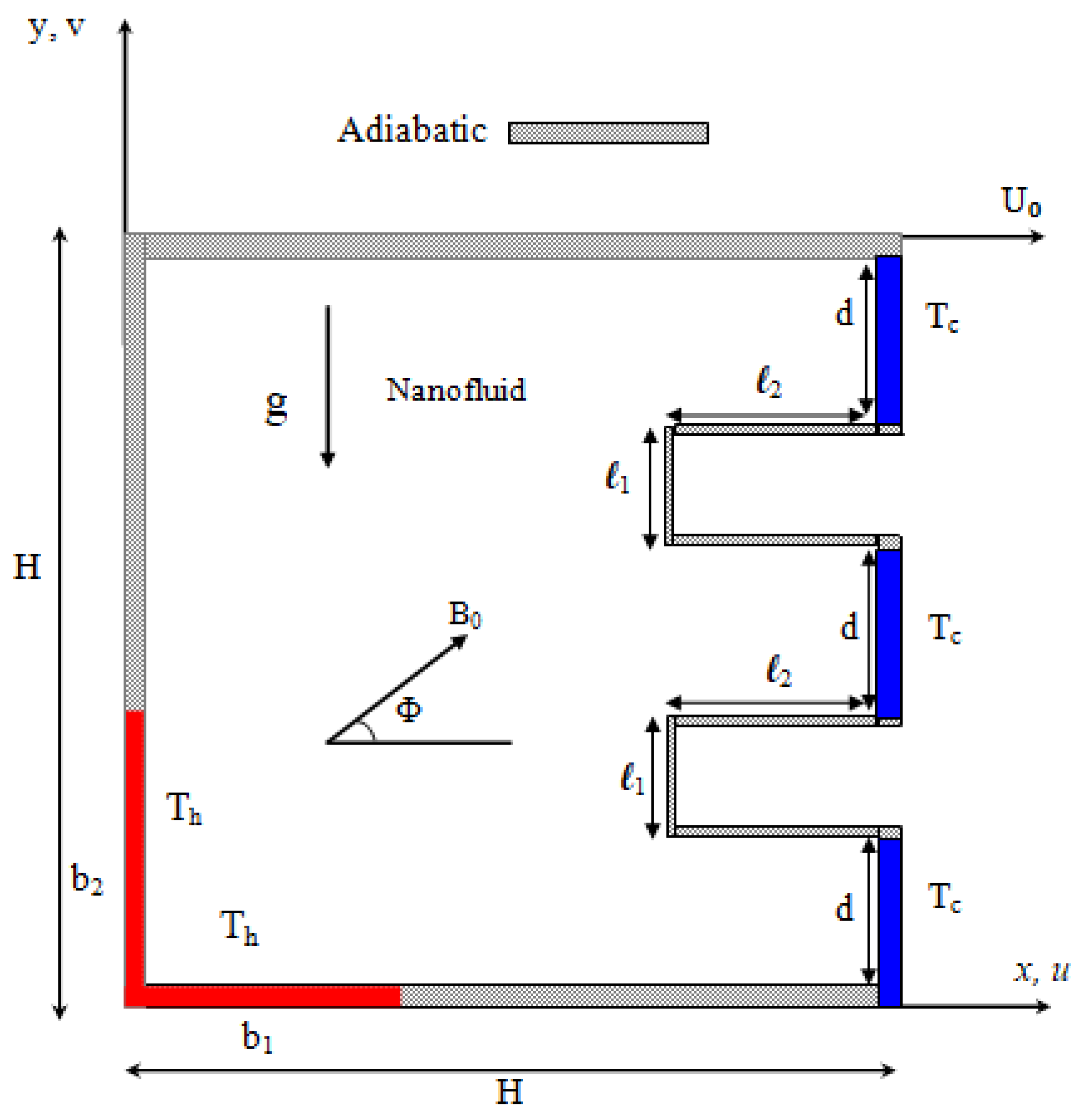
2. Modeling

An examination of magneto-nanofluid mixed convective flow inside an E-shaped square chamber with length H is performed with the heat corners indicated in Figure 1. The following parameters are established for the exploration:

⮚

Steady viscous mixed convection flow.

⮚

The chamber filled with copper-water nanofluid is considered to be steady Newtonian, Laminar, and incompressible.

⮚

The upper surface of the chamber is adiabatic and moves with a fixed velocity U₀.

⮚

The heated corner is submitted to a fixed hot temperature T_h in both left and lower directions with length sb₁ and b₂.

⮚

The right side is maintained at a fixed cold temperature, T_C, while the remaining portions of the left and lower parts are considered adiabatic.

⮚

The height and width of the portions on the right side are measured as l₁ and l₂, respectively.

⮚

The gravity force is directed downward and internal heat generation at a constant rate of Q₀ is included.

⮚

An application of magnetic strength B₀ is utilized on the left side of the cavity, with angle Φ along the positive horizontal direction.

⮚

It is assumed that the fluid flow within the enclosure is in thermal equilibrium and the working fluid is incompressible nanofluid.

⮚

There will be no jump of temperature between base fluid and nanosized particles, and both the viscous dissipation term and Joule heating term due to magnetic field has been waived.

⮚

The magnetic field created by induction is small enough to be negligible compared to the magnetic field which is applied.

⮚

The thermophysical characteristics of the nanoparticles and the base liquid are addressed in

Table 1. Thermophysical properties of water and nanoparticle materials [26].

	$\mathit{\rho }$ (kg m−3)	${\mathit{C}}_{\mathit{p}}$ (Jkg−1K−1)	$\mathit{k}$ (Wm−1K−1)	$\mathit{\beta }$ (K−1)	$\mathit{\sigma }$ (μS/cm)
Pure water	997.1	4179	0.613	21 × 10−5	0.05
Copper (Cu)	8933	385	401	1.67 × 10−5	5.96 × 107

.

By keeping the above-mentioned presumptions in mind and following Refs. [17,18], the flow and energy equations are addressed below:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{{\rho }_{nf}}\frac{\partial p}{\partial x}+{\nu }_{nf}\hspace{0.17em}(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2})+\frac{{\sigma }_n{B}_0^2}{{\rho }_{nf}}(v\hspace{0.17em}\sin \mathsf{\Phi }\hspace{0.17em}\cos \mathsf{\Phi }-u{\sin }^2\mathsf{\Phi })$$

(2)

$$\begin{array}{l}u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{{\rho }_{nf}}\frac{\partial p}{\partial y}+{\nu }_{nf}\hspace{0.17em}(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2})+\frac{{\sigma }_{nf}{B}_0^2}{{\rho }_{nf}}(u\sin \mathsf{\Phi }\cos \mathsf{\Phi }-v{\cos }^2\mathsf{\Phi })\hspace{0.17em}+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{{(\rho \beta )}_{nf}}{{\rho }_{nf}}g(T-T_c)\end{array}$$

(3)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{nf}(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2})+\frac{Q_0}{{(\rho c_p)}_{nf}}(T-T_c)$$

(4)

The boundary conditions are:

$$\begin{array}{l}x=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T=T_h,\hspace{0.17em}\hspace{0.17em}0\le y\le b_2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial T}{\partial x}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{otherwise}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u=0,v=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(5a)

$$\begin{array}{l}y=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T=T_h,\hspace{0.17em}\hspace{0.17em}0\le x\le b_1,\hspace{0.17em}\hspace{0.17em}\frac{\partial T}{\partial y}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{otherwise}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u=0,\hspace{0.17em}v=0\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(5b)

$$\begin{array}{l}x=H,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T=T_c\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le y\le d\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}d+\hspace{0.17em}{l}_1\le y\le H-(d+l_1)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}2d+2l_1\le y\le H\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial T}{\partial x}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{otherwise}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u=0,v=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(5c)

$$\begin{array}{l}y=H,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial T}{\partial y}=0\hspace{0.17em}\hspace{0.17em}v=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u=\hspace{0.17em}\hspace{0.17em}{U}_0\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(5d)

where:

${\rho }_{nf},{(\rho c_p)}_{nf},{(\rho \beta )}_{nf},{\mu }_{nf},{\alpha }_{nf}$ are defined as (see [44,45]);

$${\rho }_{nf}=(1-\varphi ){\rho }_f+\varphi {\rho }_p$$

(6)

$${(\rho c_p)}_{nf}=(1-\varphi ){(\rho c_p)}_f+\varphi {(\rho c_p)}_p$$

(7)

$${(\rho \beta )}_{nf}=(1-\varphi ){(\rho \beta )}_f+\varphi {(\rho \beta )}_p$$

(8)

$${\alpha }_{nf}=\frac{k_{nf}}{{(\rho c_p)}_{nf}}$$

(9)

$$k_{nf}=k_f\frac{(k_p+2k_f)-2\varphi (k_f-k_p)}{(k_p+2k_f)+\varphi (k_f-k_p)}$$

(10)

$${\mu }_{nf}={\mu }_f{(1-\varphi )}^{-2.5}$$

(11)

$${\sigma }_{nf}={\sigma }_f\left(1+\frac{\left(3(\gamma -1)\varphi \right)}{\left((\gamma +2)-(\gamma -1)\varphi \right)}\right), \gamma =\frac{{\sigma }_p}{{\sigma }_f}$$

(12)

Dimensionless parameters:

$$\begin{array}{l}{L}_1=\frac{l_1}{H}\hspace{0.17em},X=\frac{x}{H},\hspace{0.17em}{L}_2=\frac{l_2}{H},\hspace{0.17em}Y=\frac{y}{H}\hspace{0.17em},\hspace{0.17em}{B}_1=\frac{b_1}{H}\hspace{0.17em},\hspace{0.17em}D=\frac{d}{H},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{B}_2=\frac{b_2}{H},V=\frac{v}{U_0},\\ \\ U=\frac{u}{U_0}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\theta =\frac{(T-T_c^{})}{\Delta T},Ri=\frac{Gr}{{\mathrm{Re}}^2},\hspace{0.17em}\hspace{0.17em}\Delta T=(T_h-T_c),P=\frac{p}{{\rho }_{nf}{U}_0^2},\hspace{0.17em}\hspace{0.17em}Q=\frac{H^2}{k_f}{Q}_0\end{array}$$

(13)

in Equations (1)–(4) produces the following non-dimensional equations:

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$

(14)

$$U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-\frac{\partial P}{\partial X}+\frac{1}{\mathrm{Re}}.(\frac{{\nu }_{nf}}{{\nu }_f})\hspace{0.17em}(\frac{{\partial }^{2}U}{\partial X^2}+\frac{{\partial }^{2}U}{\partial Y^2})+(\frac{{\rho }_f}{{\rho }_{nf}})(\frac{{\sigma }_{nf}}{{\sigma }_f}).\frac{H{a}^2}{\mathrm{Re}}(V\sin \mathsf{\Phi }\cos \mathsf{\Phi }-U{\sin }^2\mathsf{\Phi })$$

(15)

$$\begin{array}{l}U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-\frac{\partial P}{\partial Y}+\frac{1}{\mathrm{Re}}.(\frac{{\nu }_{nf}}{{\nu }_f})\hspace{0.17em}\hspace{0.17em}(\frac{{\partial }^{2}V}{\partial X^2}+\frac{{\partial }^{2}V}{\partial Y^2})+Ri.\frac{{(\rho \beta )}_{nf}}{{\rho }_{nf}.{\beta }_f}.\hspace{0.17em}\theta \\ \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+(\frac{{\rho }_f}{{\rho }_{nf}})(\frac{{\sigma }_{nf}}{{\sigma }_f})\frac{H{a}^2}{\mathrm{Re}}(U\sin \mathsf{\Phi }\cos \mathsf{\Phi }-V{\cos }^2\mathsf{\Phi })\end{array}$$

(16)

$$U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=(\frac{1}{\mathrm{Pr}.\mathrm{Re}})\frac{{\alpha }_{nf}}{{\alpha }_f}(\frac{{\partial }^2\theta }{\partial X^2}+\frac{{\partial }^2\theta }{\partial Y^2})\hspace{0.17em}\hspace{0.17em}+\frac{1}{\mathrm{Re}.\mathrm{Pr}}\frac{{(\rho \hspace{0.17em}{c}_p)}_f}{{(\rho \hspace{0.17em}{c}_p)}_{nf}}.Q.\theta$$

(17)

The non-dimensional boundary conditions (14)–(17) are:

$$\begin{array}{l}X=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta =1,\hspace{0.17em}\hspace{0.17em}0\le Y\le B_2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial \theta }{\partial X}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{otherwise}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}U=V=0\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(18a)

$$\begin{array}{l}Y=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta =1,\hspace{0.17em}\hspace{0.17em}0\le X\le B_1,\hspace{0.17em}\hspace{0.17em}\frac{\partial \theta }{\partial Y}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{otherwise}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}U=0,\hspace{0.17em}\hspace{0.17em}V=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(18b)

$$\begin{array}{l}X=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\theta =0\hspace{0.17em}\hspace{0.17em}\mathrm{at}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le Y\le D\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}D+\hspace{0.17em}{L}_1\le Y\le 1-(D+L_1)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2D+2L_1\le Y\le 1\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial \theta }{\partial X}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{otherwise}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}U=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}V=0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(18c)

$$Y=1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}U=\hspace{0.17em}\hspace{0.17em}{U}_0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}V=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial \theta }{\partial Y}=0$$

(18d)

The local Nusselt number is:

$$N{u}_s=-\hspace{0.17em}\frac{k_{nf}}{k_f}\hspace{0.17em}{(\frac{\partial \theta }{\partial Y})}_{Y=0}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}N{u}_s=-\frac{k_{nf}}{k_f}{(\frac{\partial \theta }{\partial X})}_{X=0}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(19)

The average Nusselt number is:

$$N{u}_m=\frac{N{u}_{X=0}+\hspace{0.17em}N{u}_{Y=0}}{2}$$

(20)

where: $N{u}_{Y=0}=\frac{1}{B_2}{\displaystyle \underset{0}{\overset{B_2}{\int }}\hspace{0.17em}N{u}_s\hspace{0.17em}dY},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}N{u}_{X=0}\hspace{0.17em}=\frac{1}{B_1}{\displaystyle \underset{0}{\overset{B_1}{\int }}N{u}_s\hspace{0.17em}\hspace{0.17em}dX}$.

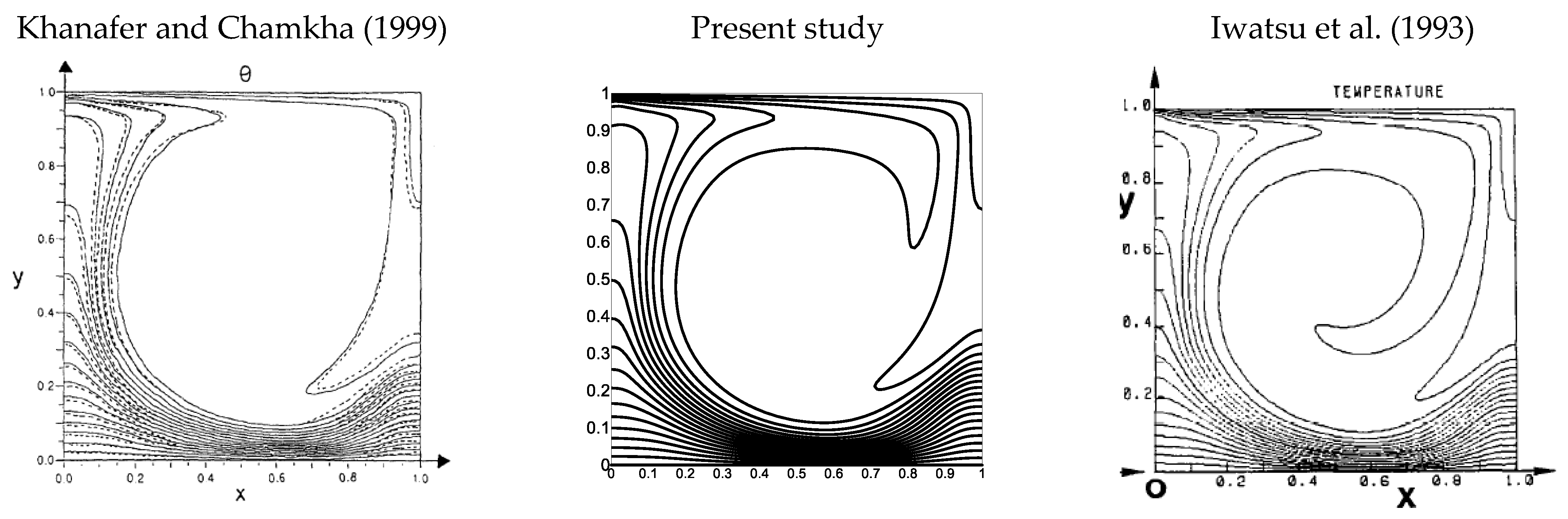
3. Numerical Solution and Validation

In this study, the finite volume method with the SIMPLE algorithm [46] has been used to solve the continuity, momentum, and energy equations. The first step in this method is that Equations (15)–(17) are rewritten in the following general form:

$$\frac{\partial \left(u\varphi \right)}{\partial x}+\frac{\partial \left(v\varphi \right)}{\partial x}=\frac{\partial }{\partial x}\left(\Gamma \frac{\partial \varphi }{\partial x}\right)+\frac{\partial }{\partial y}\left(\Gamma \frac{\partial \varphi }{\partial y}\right)+S_{\varphi }$$

(21)

Integrating the previous system over the control volume gives:

$$\begin{array}{cc}{F}_e{\varphi }_e-F_w{\varphi }_w\hfill & +F_n{\varphi }_n-F_s{\varphi }_s\hfill \\ \hfill & =D_e\left({\varphi }_E-{\varphi }_P\right)-D_w\left({\varphi }_P-{\varphi }_W\right)+D_n\left({\varphi }_N-{\varphi }_P\right)\hfill \\ \hfill & -D_s\left({\varphi }_P-{\varphi }_S\right)+S_{\varphi } Vol\hfill \end{array}$$

(22)

where $e, w, n, s$ refer to the east, west, north, and south locations, respectively. In addition, the discretized form of the continuity equation is expressed as:

$$F_e-F_w+F_n-F_s=0$$

(23)

where:

$$F_e=A_e{u}_e, F_w=A_w{u}_w, F_n=A_n{v}_n, F_s=A_s{v}_s$$

$$D_e=\frac{{\Gamma }_e{A}_e}{\delta x_{PE}}, D_w=\frac{{\Gamma }_w{A}_w}{\delta x_{PW}}, D_n=\frac{{\Gamma }_n{A}_n}{\delta y_{PN}}, D_s=\frac{{\Gamma }_s{A}_s}{\delta y_{PS}}$$

The upwind sachem is used to approximate the cell face values of the convective term as:

$${\varphi }_e=\{\begin{array}{c}{\varphi }_P for F_e>0\\ {\varphi }_E for F_e\le 0\end{array}$$

(24)

Also, it should be noted that the central difference method is used for the diffusive term. The general form of the previous system is given as:

$$a_P{\varphi }_P=a_E{\varphi }_E+a_W{\varphi }_W+a_N{\varphi }_N+a_S{\varphi }_S+Sp$$

(25)

where:

$$a_E=D_e+\max \left(-F_e,0\right)$$

$$a_W=D_w+\max \left(F_w,0\right)$$

$$a_N=D_n+\max \left(-F_n,0\right)$$

$$a_S=D_s+\max \left(F_s,0\right)$$

$$a_P=a_E+a_W+a_N+a_S+F_e-F_w+F_n-F_s$$

$$Sp=S_{\varphi }vol$$

The under-relaxed form is:

$${\varphi }_P=\frac{{\alpha }_{\varphi }}{a_P}\left(a_E{\varphi }_E+a_W{\varphi }_W+a_N{\varphi }_N+a_S{\varphi }_S+Sp \right)+\left(1-{\alpha }_{\varphi }\right){\varphi }_P^0$$

(26)

The alternating direct implicit (ADI) procedure is used to solve the resultant algebraic equations (Equation (25)), while the SIMPLE algorithm is used to correct for the velocities and pressure. The following criteria of convergence was implemented for unknown dependent variables:

$${\displaystyle \sum }_{\mathrm{i},\mathrm{j}}\left|{\mathsf{\chi }}_{\mathrm{i},\mathrm{j}}^{\mathrm{new}}-{\mathsf{\chi }}_{\mathrm{i},\mathrm{j}}^{\mathrm{old}}\right|\le {10}^{-6}$$

(27)

Here, in order to choose the most suitable grid, a grid test is performed and presented in Table 1. It is observed that a grid size of 101 × 101 is most suitable for all calculations.

The obtained outcomes are independent of the grid-size number. The grid independency results are given at Ha = 10, Ri = 1.0, Q = 1.0, Φ = 45, ϕ = 0.05, L₁ = L₂ = 0.5, B₁ = B₂ = 0.5, and presented in

Table 2. Grid-independency study for Cu-water nanofluid.

Grid-Size	41 × 41	61 × 61	81 × 81	91 × 91	101 × 101	121 × 121
$N{u}_m$	1.464692	1.732480	1.904552	1.984808	1.994244	1.9948425

.

Also, Figure 2 exhibits the comparison of the outcomes of this investigation with those of Khanafer and Chamkha [47] and Iwatsu et al. [48]. As observed in this figure, the outcomes are in agreement with these data.

4. Discussions

Numerical simulations are carried out for nanofluid flow via mixed convective (Cu/H₂O) inside an E-shaped square chamber with a heated corner. The effects of Richardson number (0.1 ≤ Ri ≤ 100), Hartmann number (0 ≤ Ha ≤ 100), volumetric fraction of nanoparticles (0 ≤ φ ≤ 0.1), heat generation/absorption parameter (−2 ≤ Q ≤ 2), and length of the heat source (B₁, B₂) on isotherms and streamlines are analyzed. The outputs are obtained for the following fixed parametric values: L₁ = L₂ = 0.5, Φ = π/4, Gr = 10⁴.

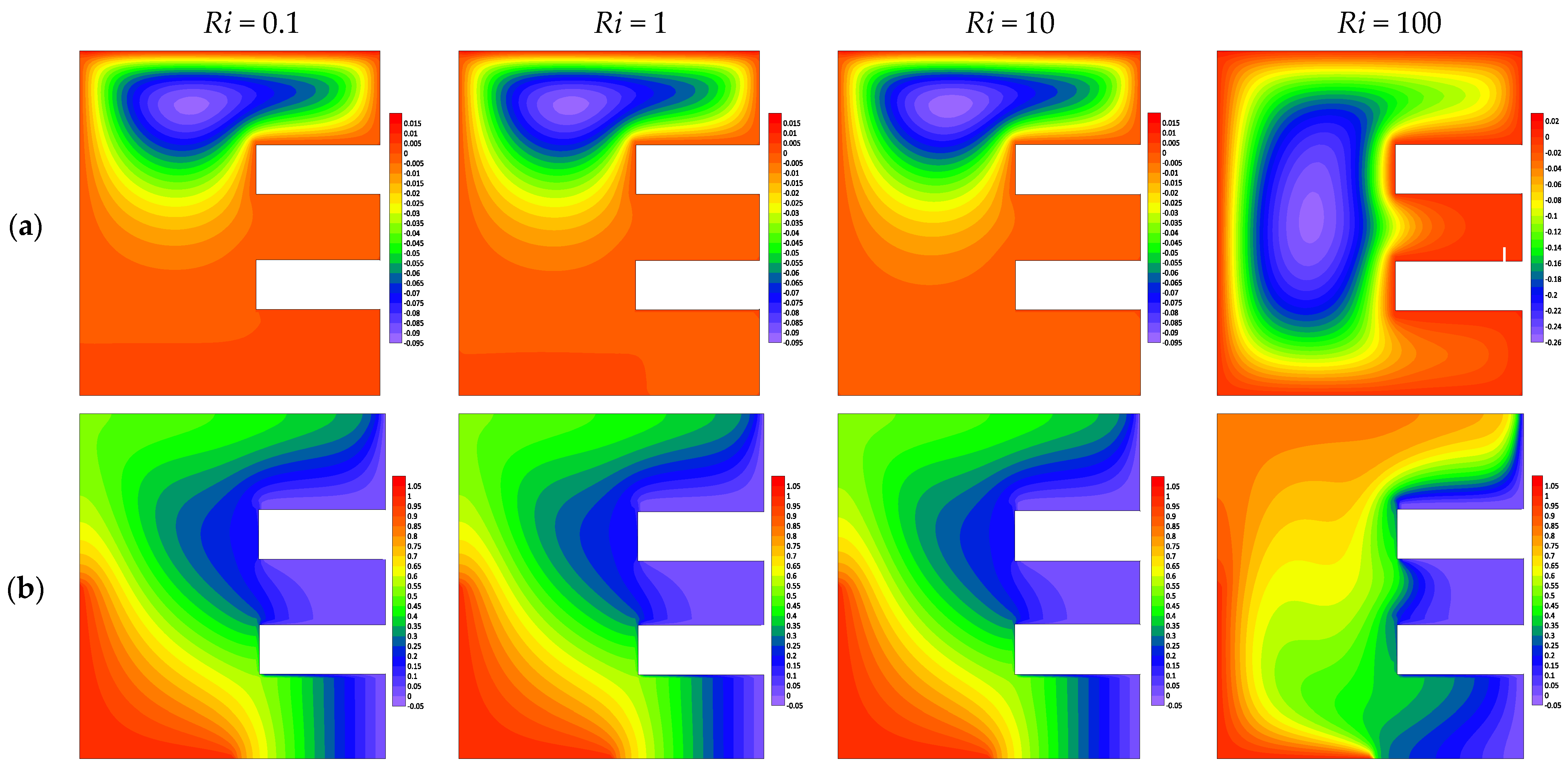
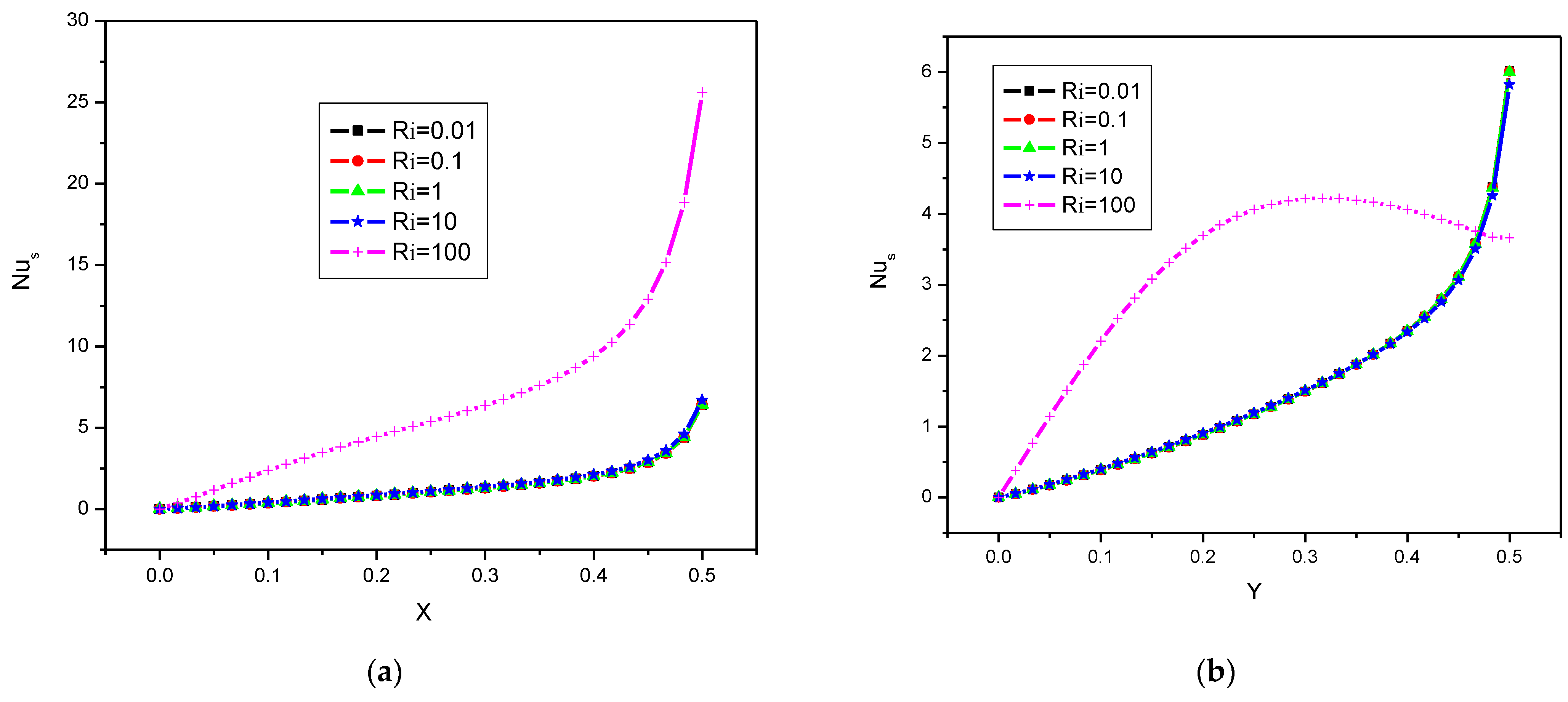
4.1. Effect of Richardson Number Ri

For fixed values of the volumetric fraction of nanoparticles (φ = 0.05) and the (Ha = 10), the isotherms and streamlines at several values of Richardson number (0.1 ≤ Ri ≤ 100) are presented in Figure 3a,b.

The examination of the framework of streamlines exhibited in this figure displays that the circulations inside the chamber are greatly affected by the Richardson number. For low Ri = 0.1, 1, 10 the streamlines are described by the existence of the circulation cell that exists inside the upper surface of the chamber. At the same time, it is clear that the structure of isotherms is equivalent to the symmetrical isothermal surfaces and orthogonal to the adiabatic surface, thus leading to a reduction in temperature gradient. In instances where the Richardson number is weak, the energy-transport impact is governed by the conduction. Moreover, the Richardson number (Ri) is related to Grashof Number per square Reynolds number (Re), and in this section, the Re = 100 and the Richardson number changes via the changing of the Grashof number. However, at Ri = 100, the influence of the Richardson number on the streamlines and isotherms is more remarkable than at Ri = 0.1, where the variation between the compared streamlines and isotherms improves remarkably. By boosting the Richardson number, the impact of the convective heat transport becomes more considerable, and diverse boundary layers form alongside the corner heater parts (B₁ and B₂) of the chamber.

Figure 4a,b explains the local Nusselt number on the heated parts (B₁ and B₂) at varying Richardson number values. It is detected from these figures that the local Nusselt number is boosted with each increment in the Richardson number. This is because as Ri grows, the buoyancy force improves, which impacts their combined convective flow. The most extreme impact of Ri on the local Nusselt number is found in various cases where X = 0.5 and Y = 0.4 at the heated corner side walls (B₁ and B₂). However, to the contrary, alongside the vertical heated wall (B₂), the maximum of the Nusselt number is decreased; Ri value increases from 6.14 to 25.3. It should be noted that the increment of heat transfers outweighs the increment of dynamic viscosity, which causes a decrease in the pressure and force related to Ri = 3.52.

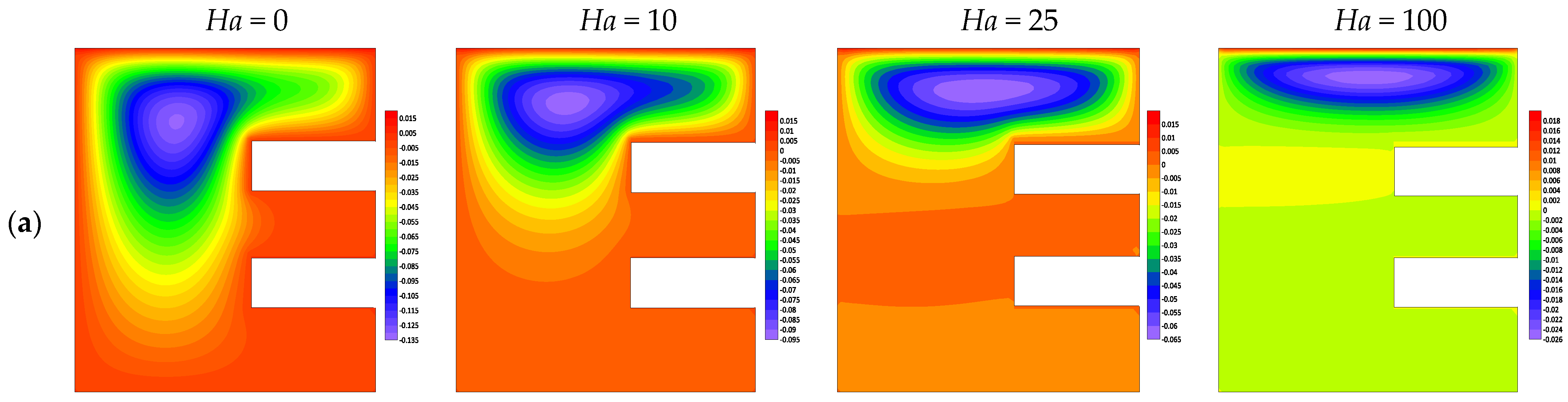
4.2. Effect of the HARTMANN Number Ha

Figure 5a,b demonstrates the influence of the Hartmann number on the isotherms and streamlines with φ = 0.05 and Ri = 1.0 and Q = 1.0. Examining Equation (15), the indication of Ha is reverse to the Reynolds number Re in exporter manifestation. Hence, there is a reverse effectiveness of Ri and Ha on mixed convective flow regime.

The magnetic field reduces the fluid circulation inside the E-shaped square chamber. It is revealed that the temperature gradient on the heated part declines as the Hartmann number boosts. Moreover, the obtained data explain that the strength of the nanofluid temperature in the chamber diminishes as a result of the implementation of the magnetic domain. However, from Ha = 0 to Ha = 25, the increment of Ha causes the diminution in the intensity of the cells and flow, and to some extent, the flow regime rests uncharged. This tendency is also visible for the isothermal lines. That is, the form of these lines does not alert observably up to Ha = 25, while it converts at Ha = 100. The Lorentz force and velocity boundary drive to a different behavior than the Hartmann number.

Figure 6a,b exhibits the local Nusselt number with several Hartmann numbers. The behavior of this figure depicts that the augmentation in the magnetic force effect causes a decrease of the Nusselt number. This can be explained by the existence of magnetic forces in the term of volume forces.

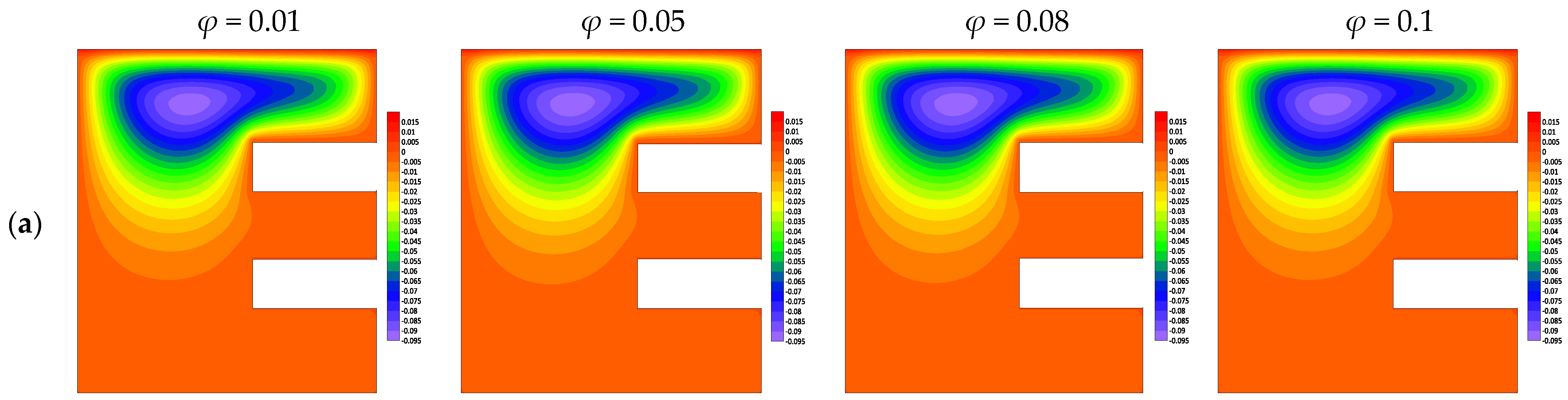
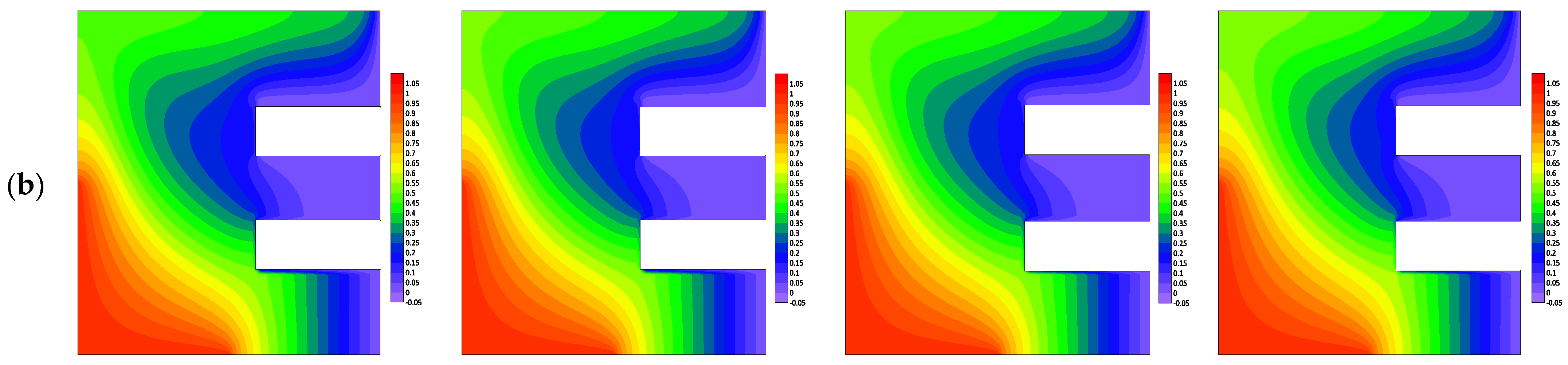
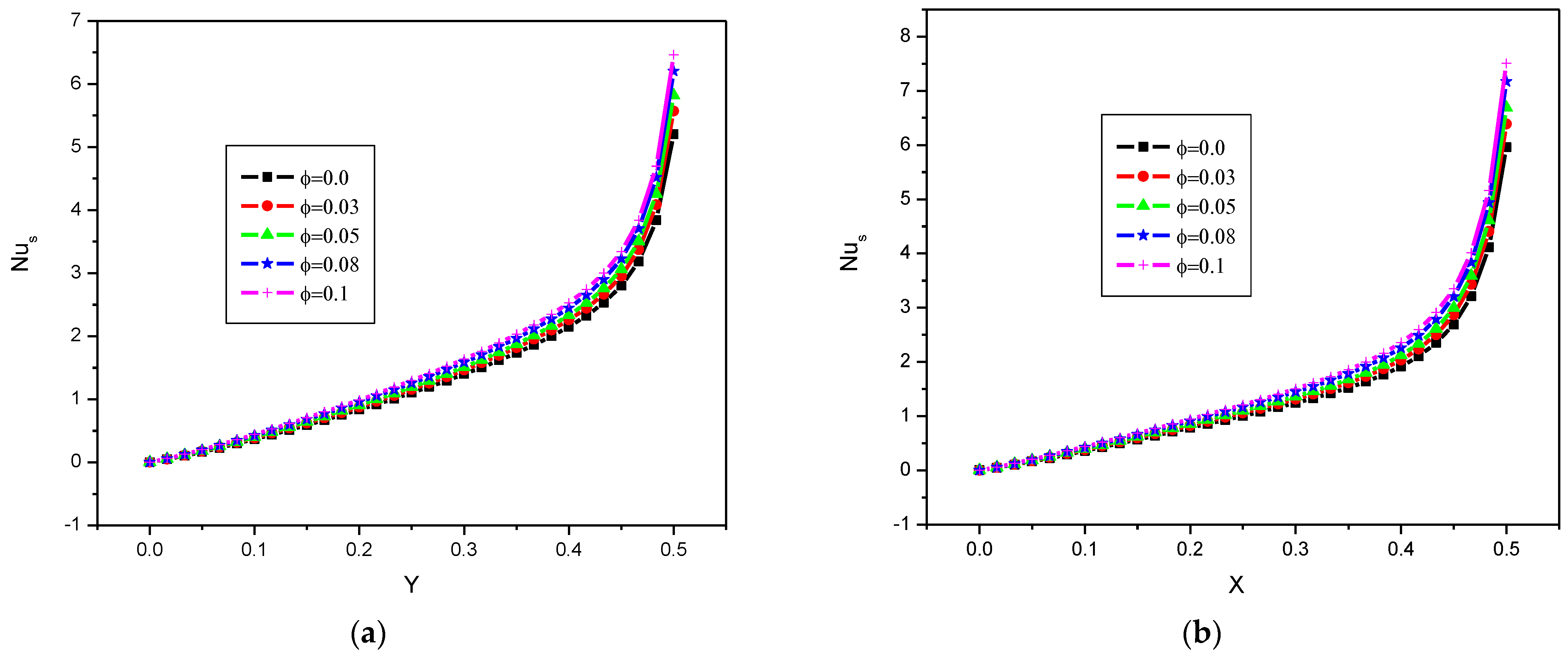
4.3. Effect of Nanoparticle Volume Fraction φ

Figure 7a,b manifests the behavior of volume fraction φ (φ = 0.01, 0.05, 0.08 and 0.1) on the frames of streamlines and temperature contours. It is clear that the circulations inside the chamber and the temperature contours are practically unaffected by the addition of Cu nanoparticles to regular fluid. So the flow direction is not modified.

At the same time, the Nusselt coefficient alongside the heat source grows by boosting the φ, as demonstrated in Figure 8a,b. This is due to the fact that enhancing the thermal conductivity of Cu/H₂O yields an improvement in heat transport. However, it is apparent that the augmentation of the dynamic viscosity due to the existence of the nanoparticles encourages additional resistance, due to shear forces versus the nanofluid motion and decline in fluid velocity. Moreover, any reduction in the fluid velocity would directly minimize the heat transport by diminishing the advection mechanism. The reduction in the advective heat transport mechanism causes a decline in the aggregate heat transport in the chamber. However, the heat transfer rate increases by raising the volume fraction of nanoparticles. Moreover, it is important to point out that the presence of nanoparticles leads to a heightened convective heat transfer coefficient.

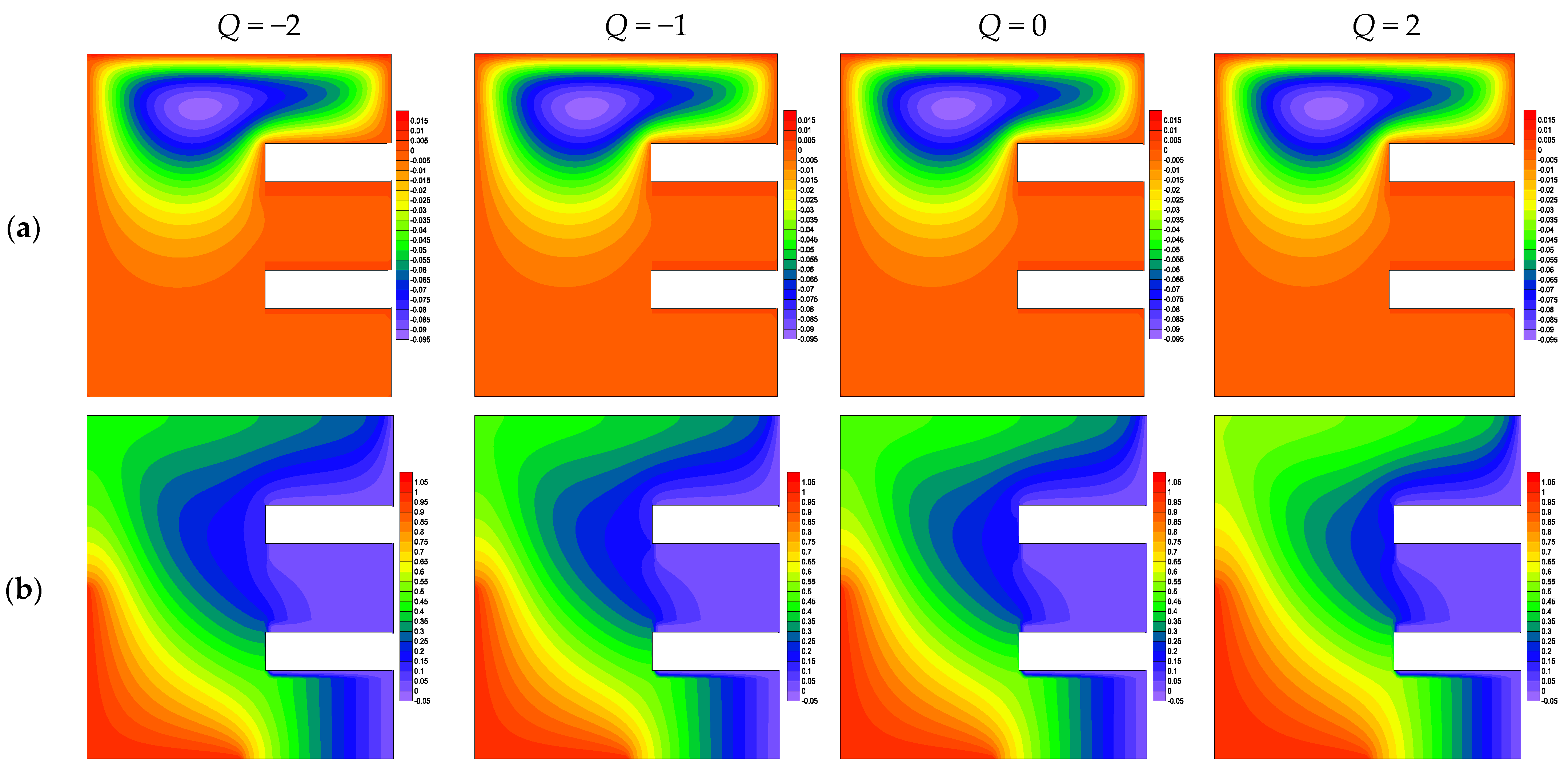
4.4. Effect of Heat Generation Coefficient Q

Figure 9a,b manifests the effect of the heat generation/absorption coefficient on both the flow and temperature contours for Ha = 10, φ = 0.05, B₁ = 0.5, B₂ = 0.5, Q = 1.0 and Ri = 1.0. It can be seen from these plots that the decrease in the heat generation coefficient Q lowers the nanofluid temperature, and that the flow fields for various Q values are almost identical, which results in the presence of nanofluid with reduced heat transport capabilities.

Moreover, in Figure 10a,b, the local Nusselt number with altered Q values are charted. It is visualized here that the Nusselt number decreases with Q; however, heat transport declines with an increase in Q. This is because positive heat generation boosts the temperature scale inside the chamber, hence the temperature gradient around the flux source falls. In contrast, the temperature gradients around the cold parts improve at the same time; that is to say, the Nusselt number at the cold parts slightly enlarges with Q. Alternately, a heat sink (negative Q) enhances the Nusselt number along the bottom and left parts.

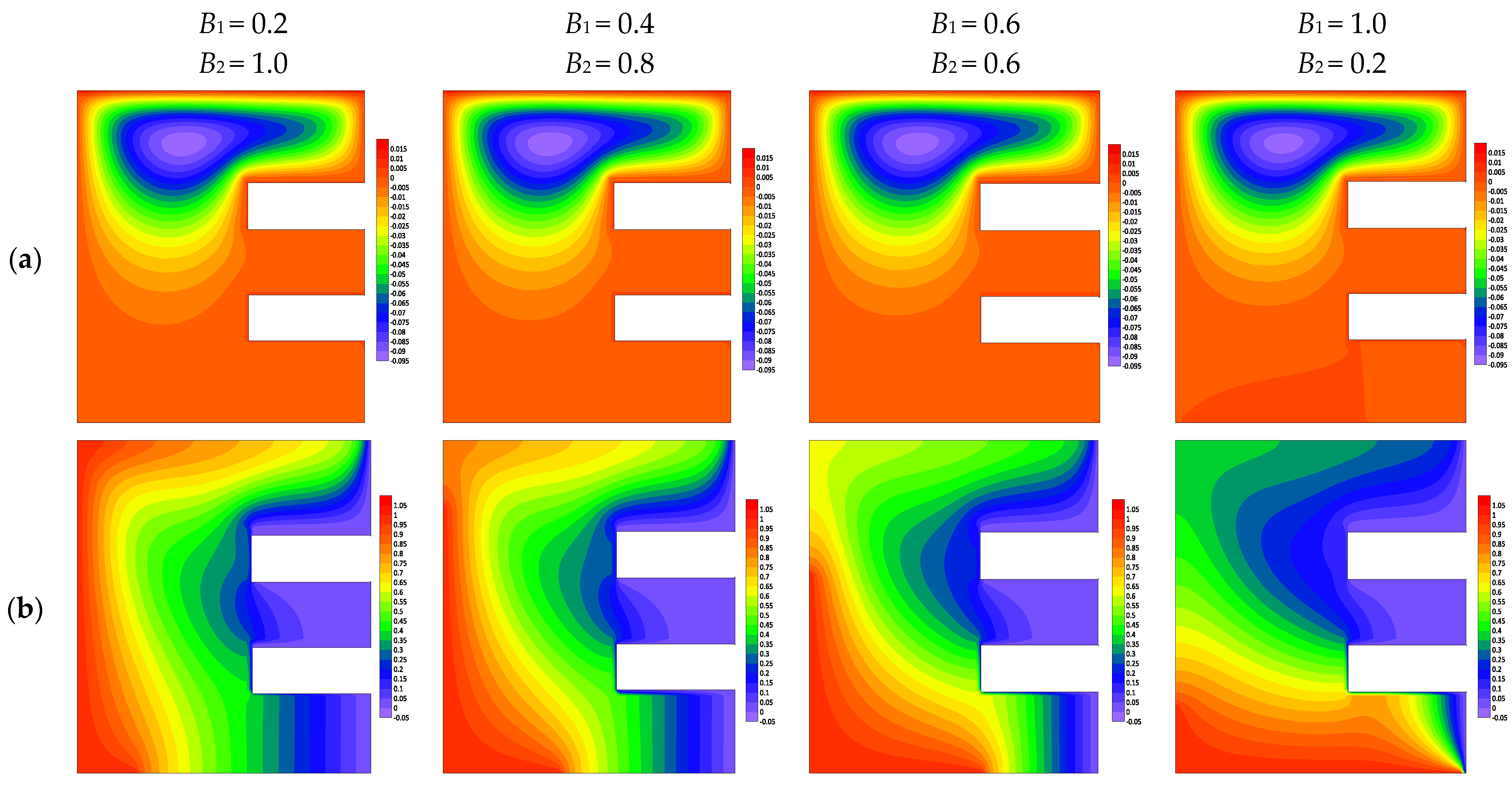
4.5. Effect of Length of the Heat Source B₁ and B₂

Figure 11a,b show the streamlines and isotherms for four different heat source length values (B₁, B₂): case 1 (B₁ = 0.2, B₂ = 1.0), case 2 (B₁ = 0.4, B₂ = 0.8), case 3 (B₁ = 0.6, B₂ = 0.6) and case 4 (B₁ = 1.0, B₂ = 0.5). It is clearly shown that the circulations inside the chamber are practically unaffected by the length of the heat source. Thus, the direction of the flow is not modified. A comparison of the temperature contours obtained for the four heat source lengths mentioned above shows that the most intense fluid temperature is found in case two, and the least significant is observed in case four. For cases one, two, and three, the strength of the nanofluid temperature in the chamber near the vertical left wall is more important, and various boundary layers form along the active walls of the cavity. Conversely, an opposing effect occurs in the intensities of the temperature at the bottom side. For case four, when the length of the heat source (B₁) increases, the intensities of the temperature of nanofluid increase near the bottom side.

5. Conclusions

In this investigation, a symmetric simulation is designed to describe the magnetized flow of a water-copper nanofluid and its heat transport in inside E-shaped square chamber via mixed convective impact with a heated corner. The outcomes of various embedded parameters on various physiological quantities are scrutinized. A few of the challenging significances are as follows:

-

The heat transfer rate increases by raising the volume fraction of nanoparticles. It is important to point out that the presence of nanoparticles leads to height convective heat transfer coefficient.

-

The Nusselt number increases as the thermal conductivity and the size of nanoparticles increase.

-

The increment in heat transfers outweighs the increment in dynamic viscosity, which causes a decrease in pressure and force.

-

The magnetic field reduces the fluid circulation inside the E-shaped square chamber.

-

The augmentation of the Richardson number leads to an increase in the heat transfer.

-

The circulations inside the chamber are practically unaffected by the length of heat source.

-

The circulations and temperature contours are practically unaffected by the addition of nanoparticles to regular fluid.

-

The decrease in heat generation coefficient declines along with the nanofluid temperature and the flow fields.