Spin Interference Effects in a Ring with Rashba Spin-Orbit Interaction Subject to Strong Light–Matter Coupling in Magnetic Field
Abstract
:1. Introduction
2. Model
2.1. The Hamiltonian
2.2. The Eigenvalue Problem
3. Transport Properties
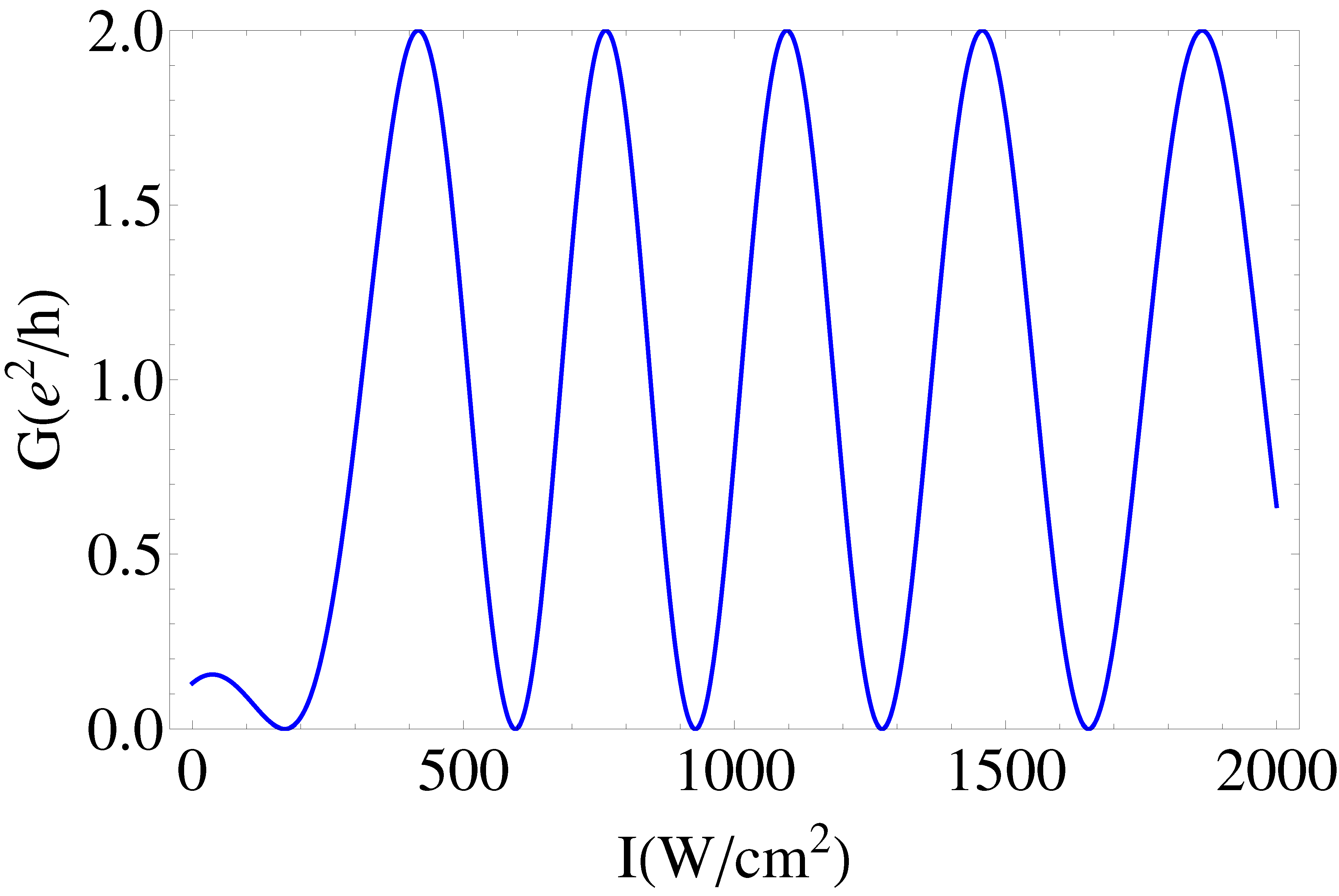
3.1. Conductance
3.2. Spin-Filtering Effect
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
Appendix A. Transmission Probabilities
References
- Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 1955, 100, 580. [Google Scholar] [CrossRef]
- Bychkov, Y.A.; Rashba, E.I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 1984, 39, 78. [Google Scholar]
- Bercioux, D.; Lucignano, P. Quantum transport in Rashba spin-orbit materials: A review. Rep. Prog. Phys. 2015, 78, 106001. [Google Scholar] [CrossRef] [PubMed]
- Pichugin, K.; Puente, A.; Nazmitdinov, R. Kramers degeneracy and spin inversion in a lateral quantum dot. Symmetry 2020, 12, 2043. [Google Scholar] [CrossRef]
- Sheremet, A.S.; Kibis, O.V.; Kavokin, A.V.; Shelykh, I.A. Datta-and-Das spin transistor controlled by a high-frequency electromagnetic field. Phys. Rev. B 2016, 93, 165307. [Google Scholar] [CrossRef] [Green Version]
- Goldman, N.; Dalibard, J. Periodically Driven Quantum Systems: Effective Hamiltonians and Engineered Gauge Fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef] [Green Version]
- Holthaus, M. Floquet engineering with quasienergy bands of periodically driven optical lattices. J. Phys. B 2016, 49, 013001. [Google Scholar] [CrossRef]
- Meinert, F.; Mark, M.J.; Lauber, K.; Daley, A.J.; Nägerl, H.-C. Floquet Engineering of Correlated Tunneling in the Bose-Hubbard Model with Ultracold Atoms. Phys. Rev. Lett. 2016, 116, 205301. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Atom-Photon Interactions: Basic Processes and Applications; Wiley–VCH: Hoboken, NJ, USA, 2004. [Google Scholar]
- Teich, M.; Wagner, M.; Schneider, H.; Helm, M. Semiconductor quantum well excitons in strong, narrowband terahertz fields. New J. Phys. 2013, 15, 065007. [Google Scholar] [CrossRef]
- Joibari, F.K.; Blanter, Y.M.; Bauer, G.E.W. Light-induced spin polarizations in quantum rings. Phys. Rev. B 2014, 90, 155301. [Google Scholar] [CrossRef] [Green Version]
- Koshelev, K.L.; Kachorovskii, V.Y.; Titov, M. Resonant inverse Faraday effect in nanorings. Phys. Rev. B 2015, 92, 235426. [Google Scholar] [CrossRef] [Green Version]
- Foa Torres, L.E.F.; Perez-Piskunow, P.M.; Balseiro, C.A.; Usaj, G. Multiterminal Conductance of a Floquet Topological Insulator. Phys. Rev. Lett. 2014, 113, 266801. [Google Scholar] [CrossRef] [PubMed]
- Mikami, T.; Kitamura, S.; Yasuda, K.; Tsuji, N.; Oka, T.; Aoki, H. Brillouin-Wigner theory for high-frequency expansion in periodically driven systems: Application to Floquet topological insulators. Phys. Rev. B 2016, 93, 144307. [Google Scholar] [CrossRef] [Green Version]
- Nagasawa, F.; Frustaglia, D.; Saarikoski, H.; Richter, K.; Nitta, J. Control of the spin geometric phase in semiconductor quantum rings. Nat. Commun. 2013, 4, 2526. [Google Scholar] [CrossRef]
- Molnár, B.; Peeters, F.M.; Vasilopoulos, P. Spin-dependent magnetotransport through a ring due to spin-orbit interaction. Phys. Rev. B 2004, 69, 155335. [Google Scholar] [CrossRef] [Green Version]
- Frustaglia, D.; Richter, K. Spin interference effects in ring conductors subject to Rashba coupling. Phys. Rev. B 2004, 69, 235310. [Google Scholar] [CrossRef] [Green Version]
- Citro, R.; Romeo, F.; Marinaro, M. Zero-conductance resonances and spin filtering effects in ring conductors subject to Rashba coupling. Phys. Rev. B 2006, 74, 115329. [Google Scholar] [CrossRef] [Green Version]
- Kozin, V.K.; Iorsh, I.V.; Kibis, O.V.; Shelykh, I.A. Quantum ring with the Rashba spin-orbit interaction in the regime of strong light-matter coupling. Phys. Rev. B 2018, 97, 155434. [Google Scholar] [CrossRef] [Green Version]
- Frustaglia, D.; Nitta, J. Geometric spin phases in Aharonov-Casher interference. Sol. State Comm. 2020, 311, 113864. [Google Scholar] [CrossRef]
- Meijer, F.E.; Morpurgo, A.F.; Klapwijk, T.M. One-dimensional ring in the presence of Rashba spin-orbit interaction: Derivation of the correct Hamiltonian. Phys. Rev. B 2002, 66, 033107. [Google Scholar] [CrossRef] [Green Version]
- Eckardt, A.; Anisimovas, E. High-frequency approximation for periodically driven quantum systems from a Floquet-space perspective. New J. Phys. 2015, 17, 093039. [Google Scholar] [CrossRef]
- Heiss, W.D.; Nazmitdinov, R.G. Orbital magnetism in small quantum dots with closed shells. JETP Lett. 1998, 68, 915. [Google Scholar] [CrossRef] [Green Version]
- Ihn, T. Semiconductor Nanostructures; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pudlak, M.; Nazmitdinov, R. Spin Interference Effects in a Ring with Rashba Spin-Orbit Interaction Subject to Strong Light–Matter Coupling in Magnetic Field. Symmetry 2022, 14, 1194. https://doi.org/10.3390/sym14061194
Pudlak M, Nazmitdinov R. Spin Interference Effects in a Ring with Rashba Spin-Orbit Interaction Subject to Strong Light–Matter Coupling in Magnetic Field. Symmetry. 2022; 14(6):1194. https://doi.org/10.3390/sym14061194
Chicago/Turabian StylePudlak, Michal, and R. Nazmitdinov. 2022. "Spin Interference Effects in a Ring with Rashba Spin-Orbit Interaction Subject to Strong Light–Matter Coupling in Magnetic Field" Symmetry 14, no. 6: 1194. https://doi.org/10.3390/sym14061194
APA StylePudlak, M., & Nazmitdinov, R. (2022). Spin Interference Effects in a Ring with Rashba Spin-Orbit Interaction Subject to Strong Light–Matter Coupling in Magnetic Field. Symmetry, 14(6), 1194. https://doi.org/10.3390/sym14061194






