Variable Selection of Heterogeneous Spatial Autoregressive Models via Double-Penalized Likelihood
Abstract
:1. Introduction
2. Variable Selection via Penalized Quasi-Maximum Likelihood
2.1. Heterogeneous SAR Models
2.2. Penalized Quasi-Maximum Likelihood
3. Asymptotic Properties
- (i)
- with probability tending to 1.
- (ii)
4. Computation
4.1. Algorithm
| Algorithm 1 |
Step 1. The ordinary quasi-maximum likelihood estimators (without penalty) of are taken as their initial values. Step 2. are given as current values, then update them by
Step 3. Repeat Step 2 above until , where is a given small number, such as . |
4.2. Choosing the Tuning Parameters
- (i)
- (ii)
5. Simulation Study
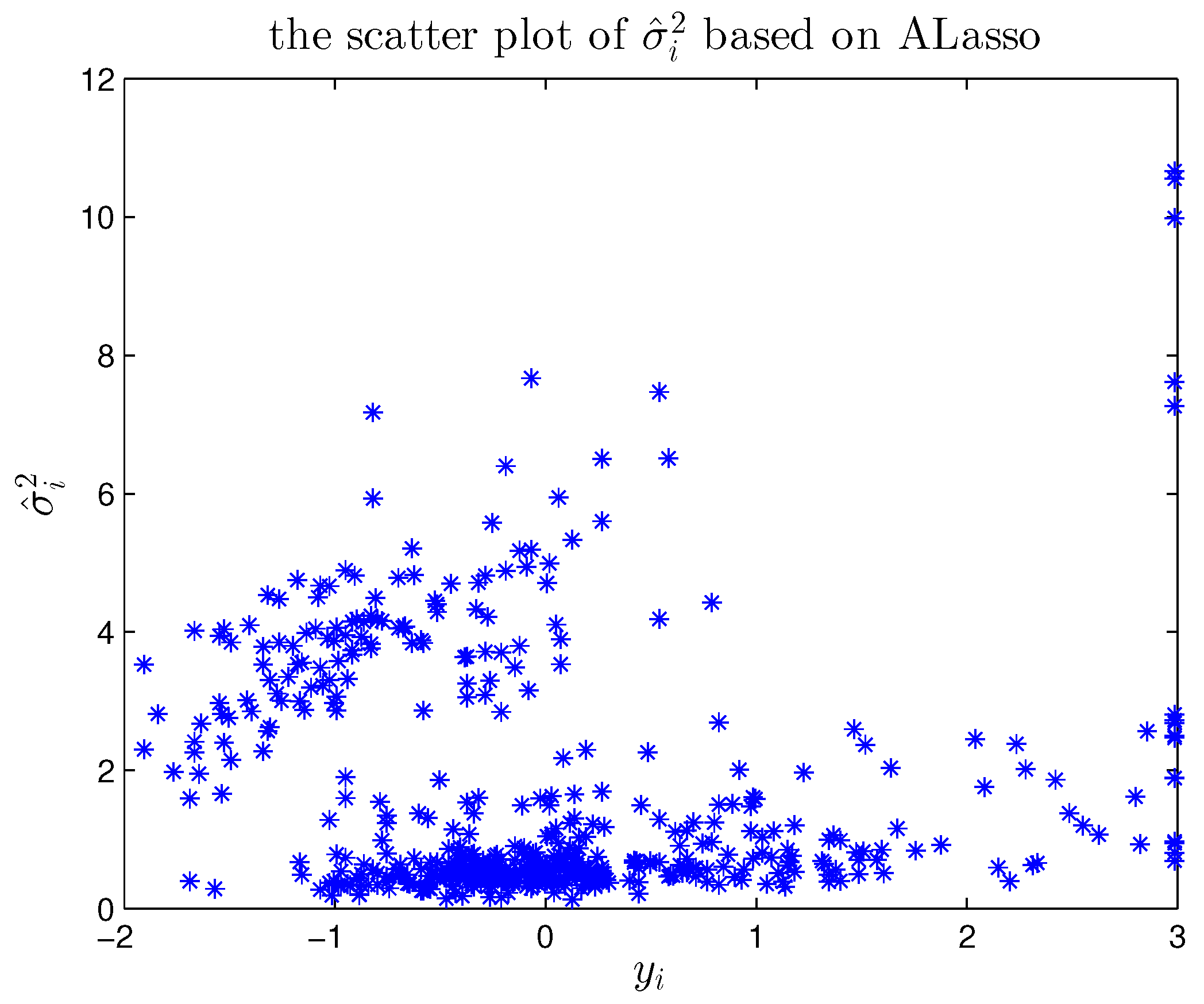
6. Real Data Analysis
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorems
- C1.
- The are independent with and . The moment exists for some .
- C2.
- The elements and are in W, where as .
- C3.
- The matrix S is a nonsingular matrix.
- C4.
- The sequences of matrices and are uniformly bounded in both row and column sums.
- C5.
- The and exist and are nonsingular. The elements of X and Z are uniformly bounded constants for all n.
- C6.
- are uniformly bounded in row or column sums, uniformly in in a closed subset of . The true is an interior point of .
- C7.
- The exists and is a nonsingular matrix.
- C8.
- The exists.
- C9.
- The third derivatives exist for all in an open set that contains the true parameter point . Furthermore, there exist functions such that for all , where for .
- C10.
- The penalty function satisfies
References
- Cliff, A.; Ord, J.K. Spatial Autocorrelation; Pion: London, UK, 1973. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Anselin, L.; Bera, A.K. Spatial Dependence in Linear Regression Models with an Introduction to Spatial Econometrics. In Handbook of Applied Economics Statistics; Ullah, A., Giles, D.E.A., Eds.; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Xu, X.B.; Lee, L.F. A spatial autoregressive model with a nonlinear transformation of the dependent variable. J. Econom. 2015, 186, 1–18. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.B.; Cheng, S.L. A penalized quasi-maximum likelihood method for variable selection in the spatial autoregressive model. Spat. Stat. 2018, 25, 86–104. [Google Scholar] [CrossRef]
- Xie, L.; Wang, X.R.; Cheng, W.H.; Tang, T. Variable selection for spatial autoregressive models. Commun.-Stat. Methods 2021, 50, 1325–1340. [Google Scholar] [CrossRef]
- Xie, T.F.; Cao, R.Y.; Du, J. Variable selection for spatial autoregressive models with a diverging number of parameters. Stat. Pap. 2020, 61, 1125–1145. [Google Scholar] [CrossRef]
- Su, L.J.; Jin, S.N. Profile quasi-maximum likelihood estimation of partially linear spatial autoregressive models. J. Econom. 2010, 157, 18–33. [Google Scholar] [CrossRef]
- Du, J.; Sun, X.Q.; Cao, R.Y.; Zhang, Z.Z. Statistical inference for partially linear additive spatial autoregressive models. Spat. Stat. 2018, 25, 52–67. [Google Scholar] [CrossRef]
- Cheng, S.L.; Chen, J.B. Estimation of partially linear single-index spatial autoregressive model. Stat. Pap. 2021, 62, 485–531. [Google Scholar] [CrossRef]
- Wei, C.H.; Guo, S.; Zhai, S.F. Statistical inference of partially linear varying coefficient spatial autoregressive models. Econ. Model. 2017, 64, 553–559. [Google Scholar] [CrossRef]
- Hu, Y.P.; Wu, S.Y.; Feng, S.Y.; Jin, J.L. Estimation in Partial Functional Linear Spatial Autoregressive Model. Mathematics 2020, 8, 1680. [Google Scholar] [CrossRef]
- Lin, X.; Lee, L.F. GMM estimation of spatial autoregressive models with unknown heteroskedasticity. J. Econom. 2010, 157, 34–52. [Google Scholar] [CrossRef]
- Dai, X.W.; Jin, L.B.; Tian, M.Z.; Shi, L. Bayesian Local Influence for Spatial Autoregressive Models with Heteroscedasticity. Stat. Pap. 2019, 60, 1423–1446. [Google Scholar] [CrossRef]
- Wu, L.C.; Li, H.Q. Variable selection for joint mean and dispersion models of the inverse Gaussian distribution. Metrika 2012, 75, 795–808. [Google Scholar] [CrossRef]
- Xu, D.K.; Zhang, Z.Z. A semiparametric Bayesian approach to joint mean and variance models. Stat. Probab. Lett. 2013, 83, 1624–1631. [Google Scholar] [CrossRef]
- Zhao, W.H.; Zhang, R.Q.; Lv, Y.Z.; Liu, J.C. Variable selection for varying dispersion beta regression model. J. Appl. Stat. 2014, 41, 95–108. [Google Scholar] [CrossRef]
- Li, H.Q.; Wu, L.C.; Ma, T. Variable selection in joint location, scale and skewness models of the skew-normal distribution. J. Syst. Sci. Complex. 2017, 30, 694–709. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, L.C.; Ye, K.Y.; Wang, M. Bayesian quantile semiparametric mixed-effects double regression models. Stat. Theory Relat. Fields 2021, 5, 303–315. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the LASSO. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.Q.; Li, R.Z. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Luo, G.; Wu, M. Variable selection for semiparametric varying-coefficient spatial autoregressive models with a diverging number of parameters. Commun.-Stat. Methods 2021, 50, 2062–2079. [Google Scholar] [CrossRef]
- Li, R.; Liang, H. Variable selection in semiparametric regression modeling. Ann. Stat. 2008, 36, 261–286. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.X.; Xue, L.G. Variable selection for semiparametric varying coefficient partially linear errorsin-variables models. J. Multivar. Anal. 2010, 101, 1872–1883. [Google Scholar] [CrossRef] [Green Version]
- Tian, R.Q.; Xue, L.G.; Liu, C.L. Penalized quadratic inference functions for semiparametric varying coefficient partially linear models with longitudinal data. J. Multivar. Anal. 2014, 132, 94–110. [Google Scholar] [CrossRef]
- Lee, L.F. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 2004, 72, 1899–1925. [Google Scholar] [CrossRef]
- Wang, H.; Li, R.; Tsai, C. Tuning parameter selectors for the smoothly clipped absolute deviation method. Biometrika 2007, 94, 553–568. [Google Scholar] [CrossRef] [PubMed]
- Pace, R.K.; Gilley, O.W. Using the spatial configuration of the data to improve estimation. J. Real Estate Financ. Econ. 1997, 14, 333–340. [Google Scholar] [CrossRef]
- Su, L.; Yang, Z. Instrumental Variable Quantile Estimation of Spatial Autoregressive Models; Working Paper; Singapore Management University: Singapore, 2009. [Google Scholar]
- Kelejian, H.H.; Prucha, I.R. On the asymptotic distribution of the Moran I test statistic with applications. J. Econom. 2001, 104, 219–257. [Google Scholar] [CrossRef] [Green Version]
- Case, A.C. Spatial patterns in household demand. Econometrica 1991, 59, 953–965. [Google Scholar] [CrossRef] [Green Version]


| SCAD | ALASSO | ||||||
|---|---|---|---|---|---|---|---|
| n | MSE | C | IC | MSE | C | IC | |
| 150 | 0.0043 | 4.9360 | 0 | 0.0041 | 4.9760 | 0 | |
| 200 | 0.0029 | 4.9480 | 0 | 0.0027 | 4.9900 | 0 | |
| 300 | 0.0016 | 4.9760 | 0 | 0.0015 | 4.9980 | 0 | |
| n | MSE | C | IC | MSE | C | IC | |
| 150 | 0.0903 | 4.8960 | 0.0040 | 0.0970 | 4.9000 | 0.0040 | |
| 200 | 0.0633 | 4.9040 | 0 | 0.0631 | 4.9400 | 0 | |
| 300 | 0.0342 | 4.9580 | 0 | 0.0352 | 4.9900 | 0 | |
| SCAD | ALASSO | ||||||
|---|---|---|---|---|---|---|---|
| n | MSE | C | IC | MSE | C | IC | |
| 150 | 0.0041 | 4.9180 | 0 | 0.0038 | 4.9700 | 0 | |
| 200 | 0.0027 | 4.9520 | 0 | 0.0026 | 4.9900 | 0 | |
| 300 | 0.0016 | 4.9760 | 0 | 0.0016 | 5.0000 | 0 | |
| n | MSE | C | IC | MSE | C | IC | |
| 150 | 0.0903 | 4.9040 | 0 | 0.0955 | 4.9080 | 0 | |
| 200 | 0.0632 | 4.9200 | 0 | 0.0645 | 4.9460 | 0 | |
| 300 | 0.0387 | 4.9260 | 0 | 0.0383 | 4.9760 | 0 | |
| SCAD | ALASSO | ||||||
|---|---|---|---|---|---|---|---|
| n | MSE | C | IC | MSE | C | IC | |
| 150 | 0.0046 | 4.9080 | 0 | 0.0044 | 4.9560 | 0 | |
| 200 | 0.0032 | 4.9240 | 0 | 0.0030 | 4.9800 | 0 | |
| 300 | 0.0017 | 4.9720 | 0 | 0.0017 | 5.0000 | 0 | |
| n | MSE | C | IC | MSE | C | IC | |
| 150 | 0.0919 | 4.8780 | 0 | 0.1033 | 4.8860 | 0 | |
| 200 | 0.0600 | 4.9220 | 0 | 0.0636 | 4.9500 | 0 | |
| 300 | 0.0363 | 4.9420 | 0 | 0.0372 | 4.9800 | 0 | |
| Variables | Description |
|---|---|
| CRIM | Per capita crime rate by town |
| ZN | Proportion of residential land zoned for lots over 25,000 sq. ft. |
| INDUS | Proportion of non-retail business acres per town |
| CHAS | Charles River dummy variable (=1 if tract bounds river; 0 otherwise) |
| NOX | Nitric-oxides concentration (parts per 10 million) |
| RM | Average number of rooms per dwelling |
| AGE | Proportion of owner-occupied units built prior to 1940 |
| DIS | Weighted distances to five Boston employment centres |
| RAD | Index of accessibility to radial highways |
| TAX | Full-value property-tax rate per USD 10,000 |
| PTRATIO | Pupil–teacher ratio by town |
| B | , where Bk is the proportion of blacks by town |
| LSTAT | % of the population with lower status |
| MEDV | Median value of owner-occupied homes in USD 1000s |
| QMLE | SCAD | ALASSO | |
|---|---|---|---|
| −0.0882 | 0 | 0 | |
| 0.0699 | 0 | 0 | |
| −0.0427 | 0 | 0 | |
| 0.0038 | 0 | 0 | |
| −0.0145 | 0 | 0 | |
| 0.4641 | 0.5709 | 0.6023 | |
| −0.1509 | −0.1788 | −0.1489 | |
| −0.2076 | −0.1287 | −0.1175 | |
| 0.2008 | 0.1440 | 0.0502 | |
| −0.2031 | −0.2049 | −0.1502 | |
| −0.1073 | −0.0750 | −0.0829 | |
| 0.1440 | 0.1638 | 0.1033 | |
| −0.0597 | 0 | 0 | |
| 0.1265 | 0 | 0 | |
| 0.1020 | 0 | 0 | |
| −0.0830 | 0 | 0 | |
| 0.0823 | 0 | 0 | |
| −0.4000 | −0.3673 | 0 | |
| 0.1113 | 0 | 0 | |
| 0.3637 | 0.3461 | 0.2357 | |
| −0.4004 | −0.3877 | −0.2381 | |
| 0.7366 | 0.8952 | 0.9143 | |
| 0.2920 | 0.2105 | 0 | |
| −0.3533 | −0.4085 | −0.2723 | |
| −0.0141 | 0 | 0 | |
| −0.4262 | −0.4586 | −0.3929 | |
| 0.2531 | 0.2881 | 0.2809 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, R.; Xia, M.; Xu, D. Variable Selection of Heterogeneous Spatial Autoregressive Models via Double-Penalized Likelihood. Symmetry 2022, 14, 1200. https://doi.org/10.3390/sym14061200
Tian R, Xia M, Xu D. Variable Selection of Heterogeneous Spatial Autoregressive Models via Double-Penalized Likelihood. Symmetry. 2022; 14(6):1200. https://doi.org/10.3390/sym14061200
Chicago/Turabian StyleTian, Ruiqin, Miaojie Xia, and Dengke Xu. 2022. "Variable Selection of Heterogeneous Spatial Autoregressive Models via Double-Penalized Likelihood" Symmetry 14, no. 6: 1200. https://doi.org/10.3390/sym14061200






