Two-Dimensional Solitons in Nonlocal Media: A Brief Review
Abstract
:1. Introduction
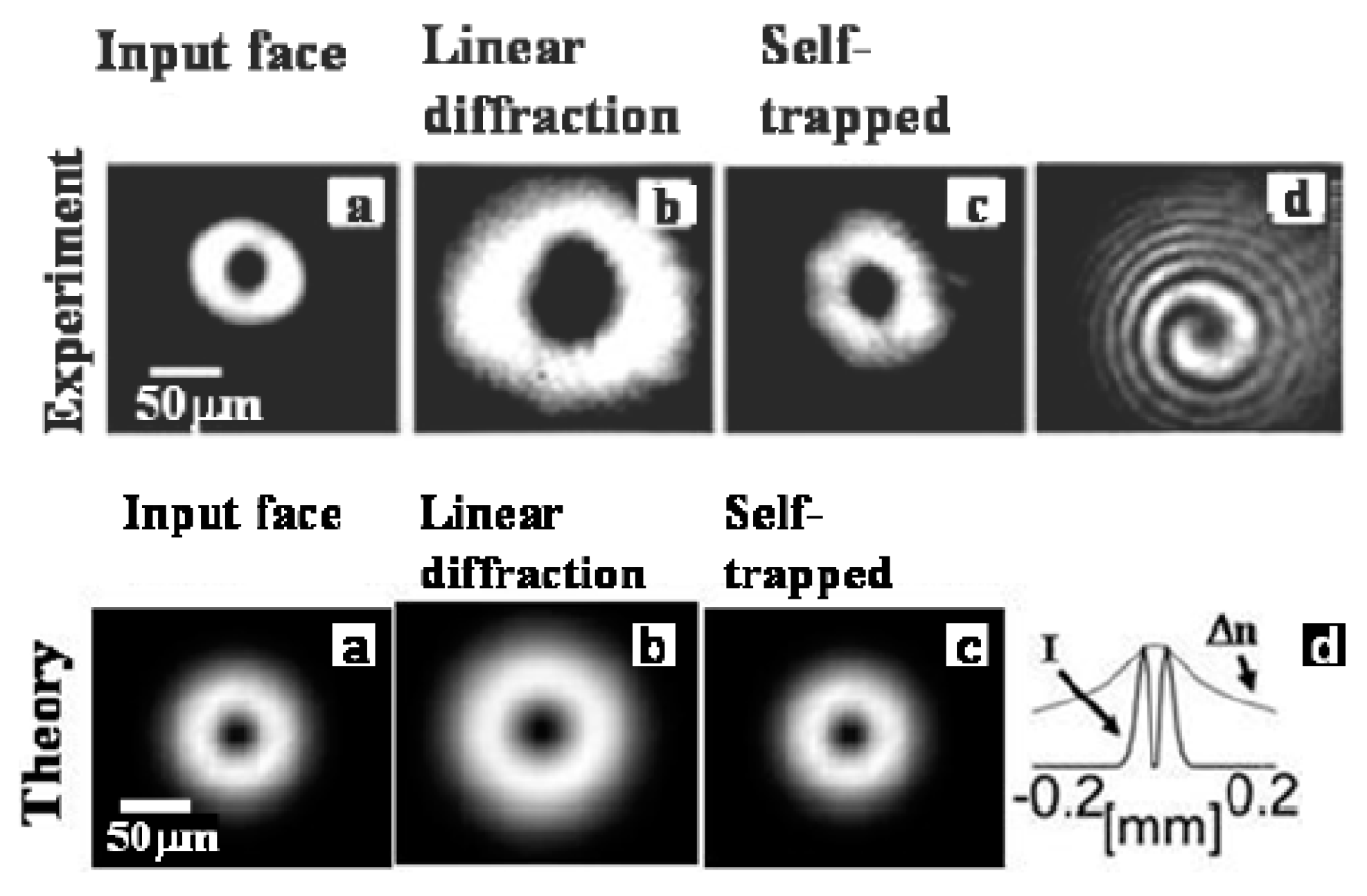
1.1. Established Models: Thermal and Liquid-Crystal (Orientational) Nonlinearities in Optics
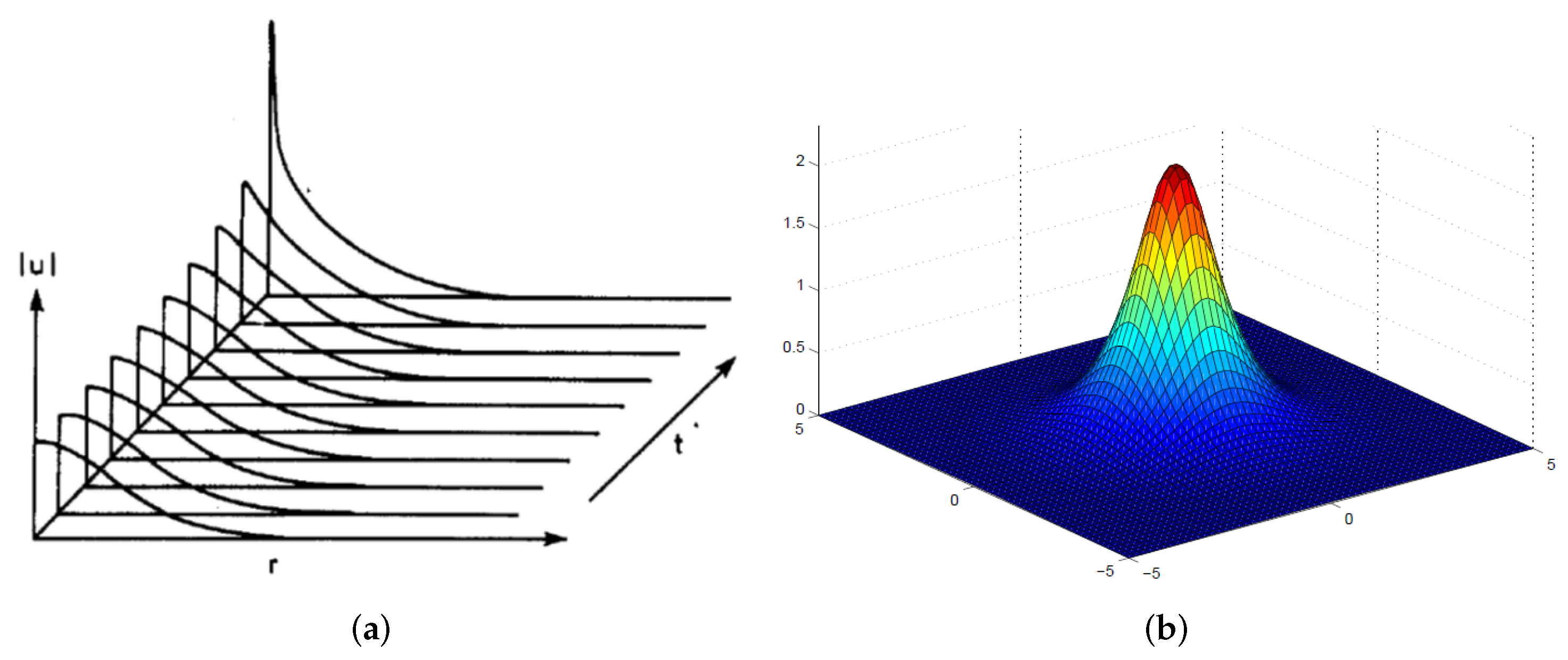
1.2. A New Model with Linear Nonlocality: Fractional Diffraction in 2D
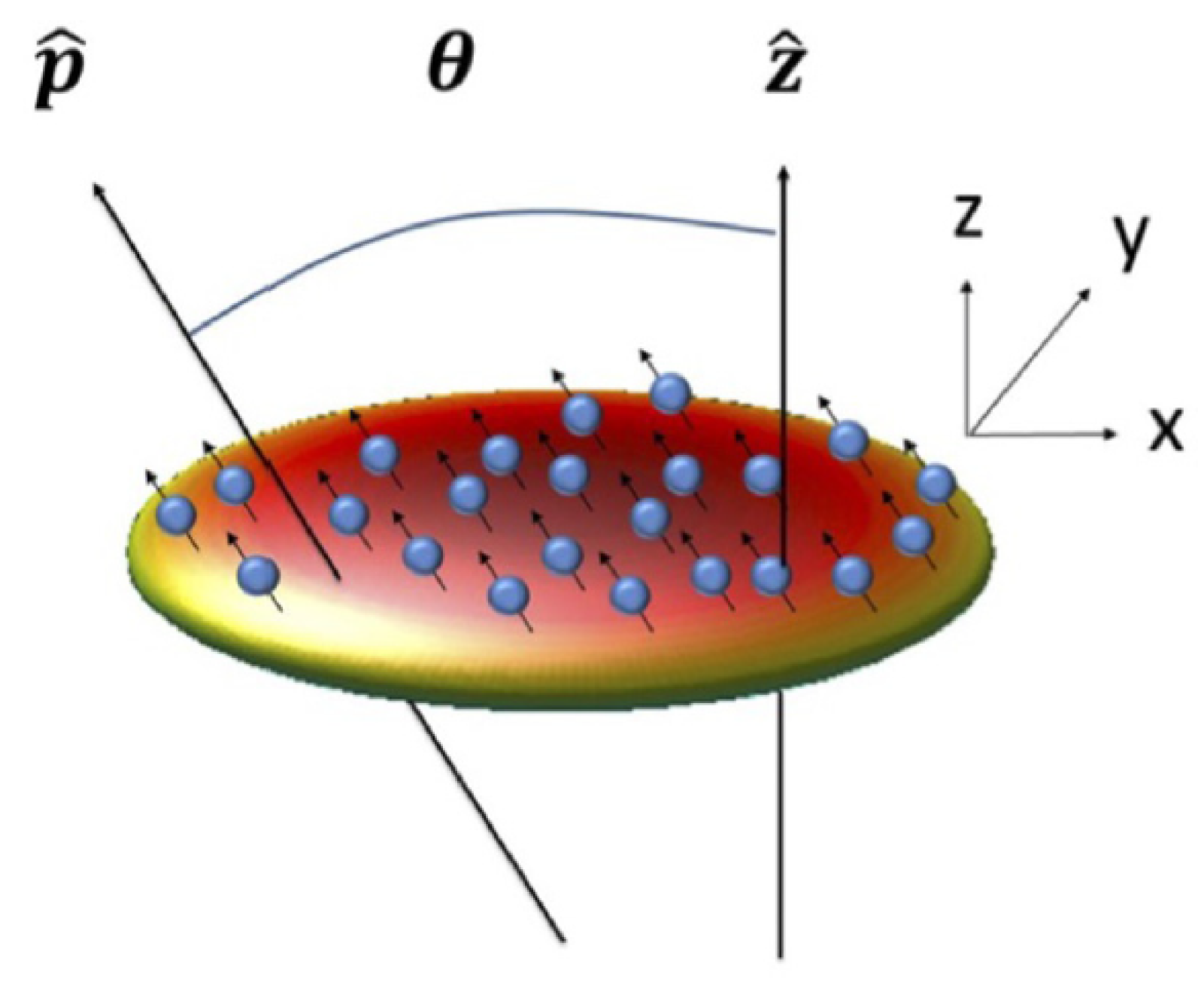
2. Anisotropic Quasi-2D Solitons Built by Dipole-Dipole Interactions (DDIs) in BEC of Magnetic Atoms
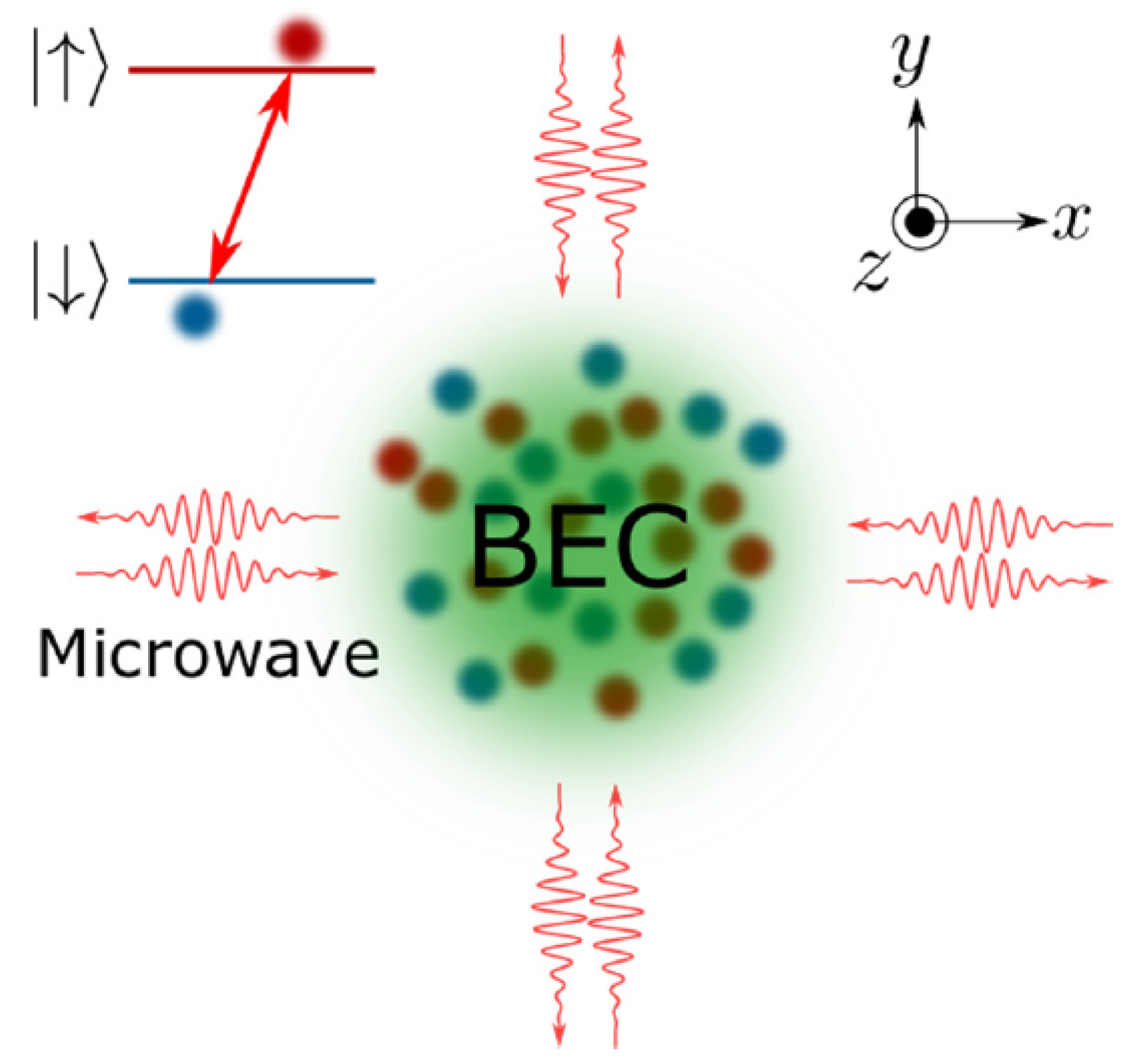
3. Giant Vortex Rings (VRs) in Microwave-Coupled Binary BEC
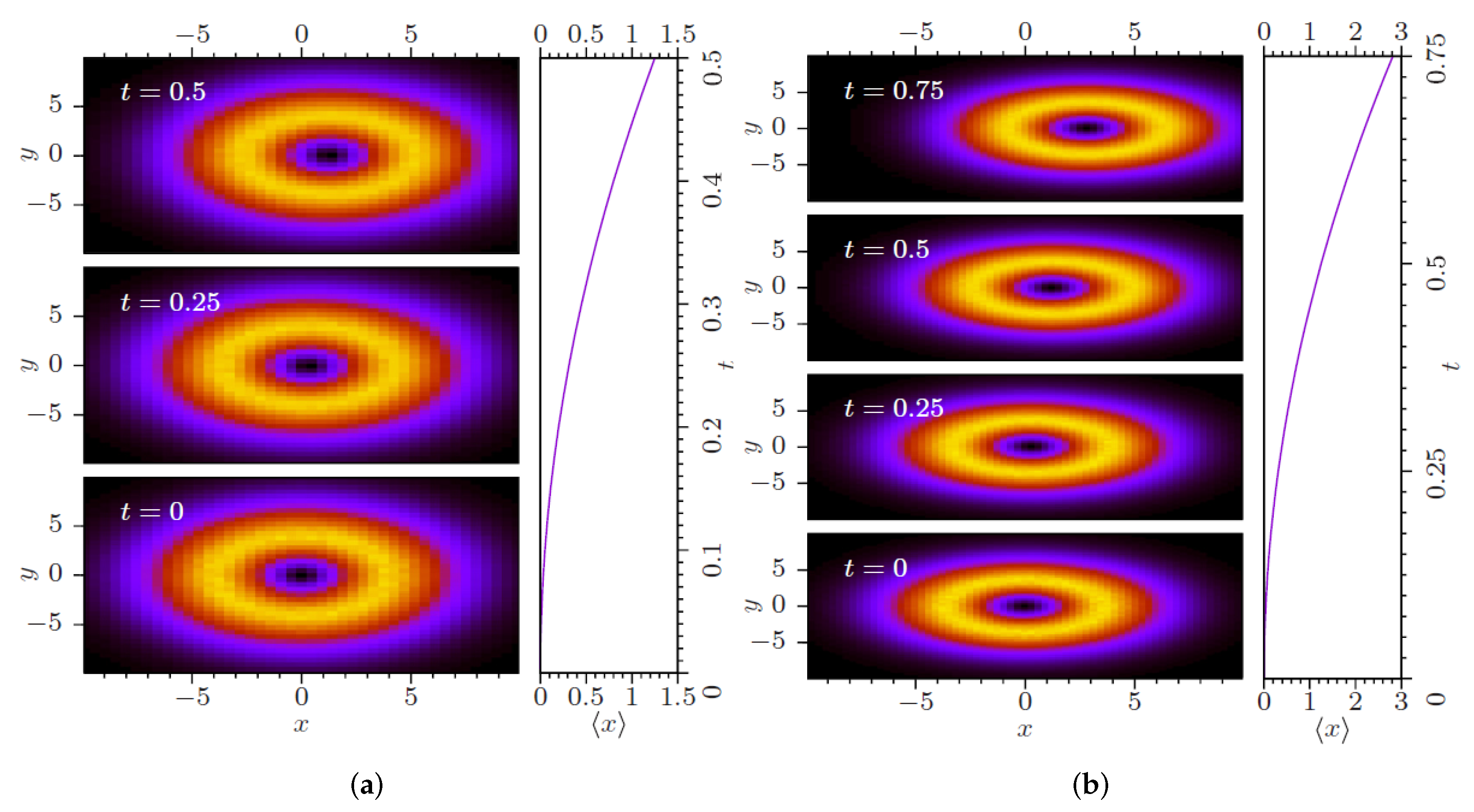
3.1. The Model
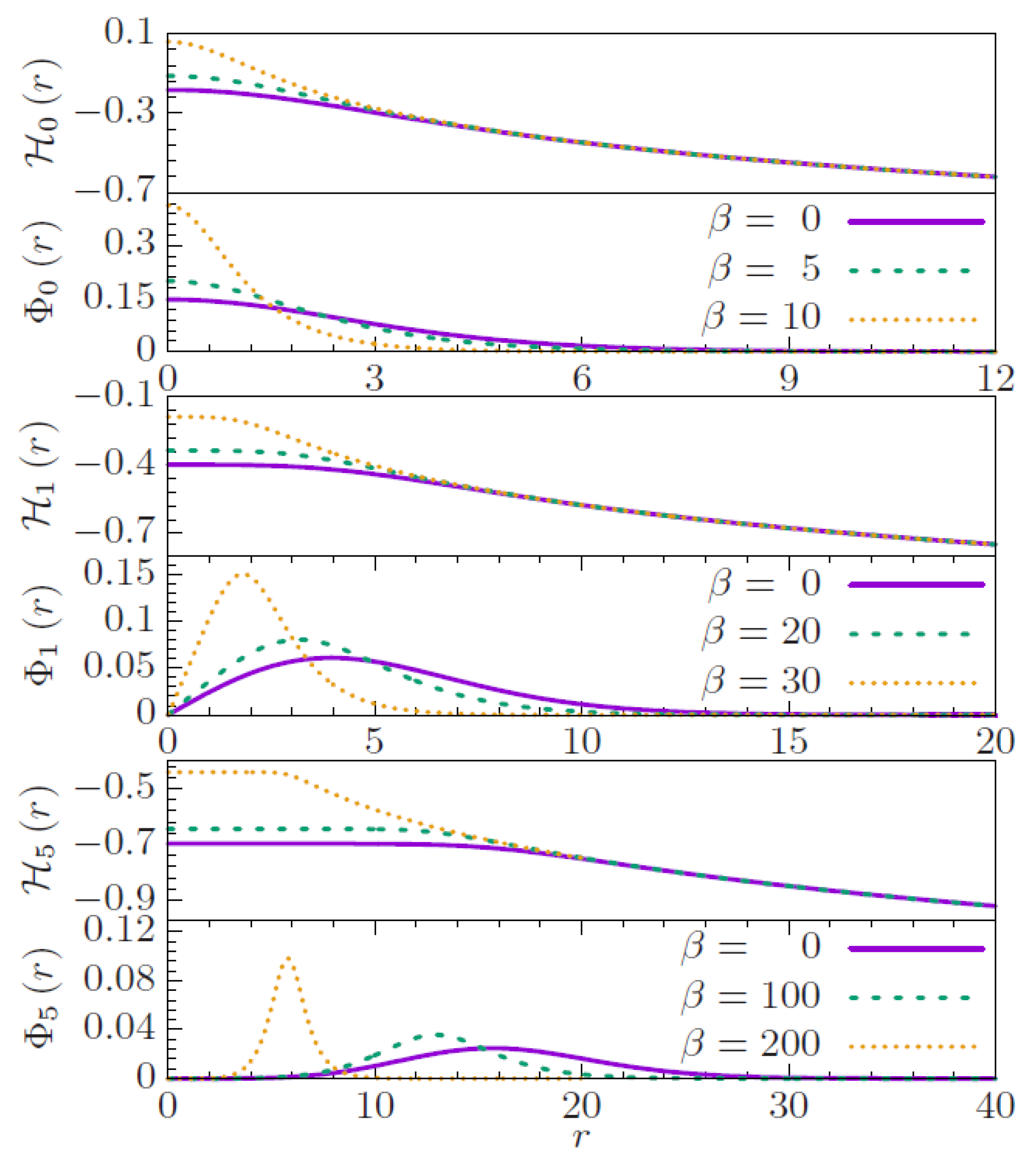
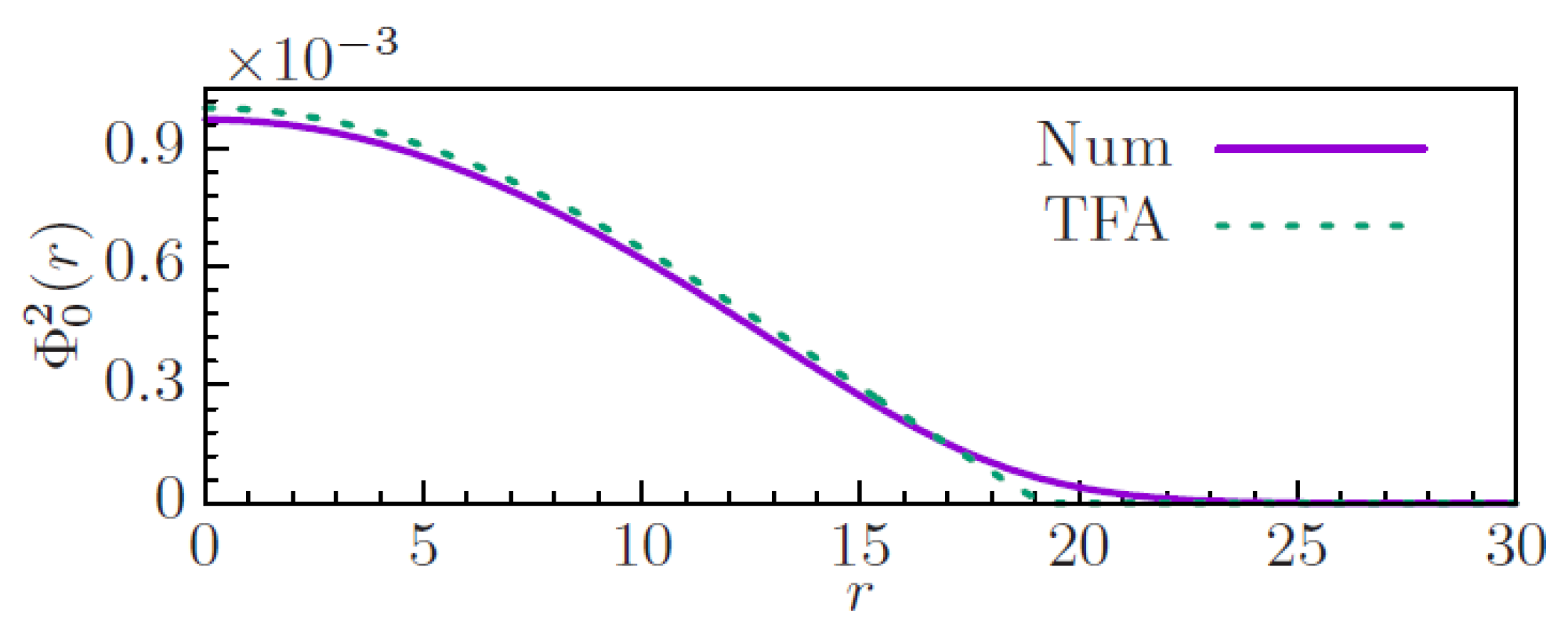
3.2. Results
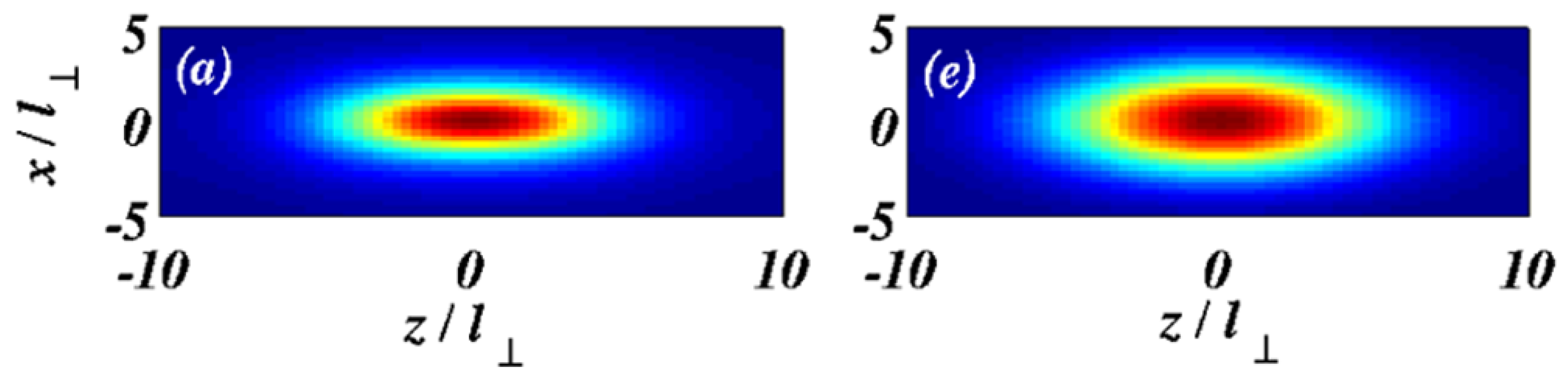
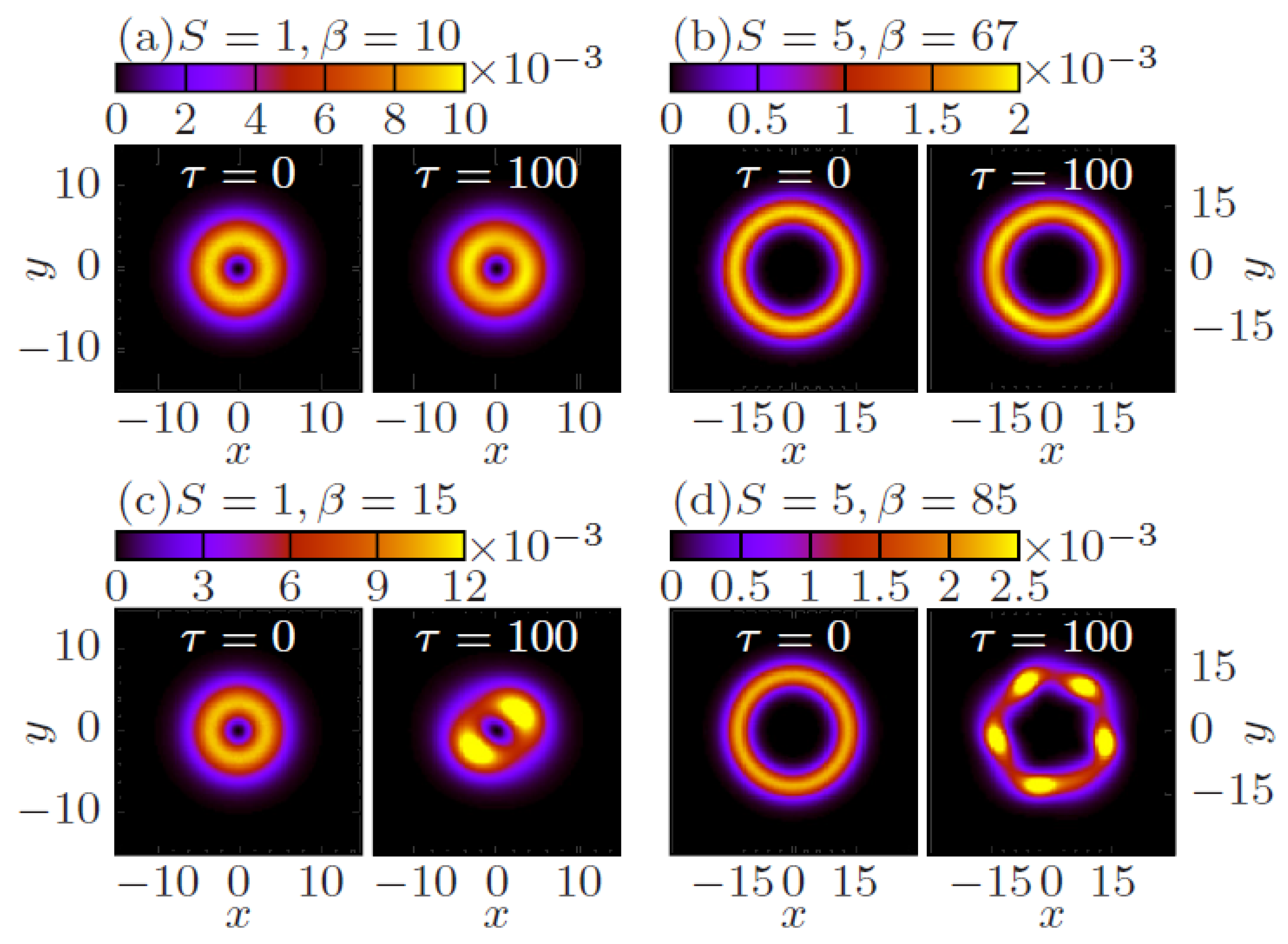
3.3. Self-Accelerating 2D Vortex Rings (VRs)
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manton, N.; Sutcliffe, P. Topological Solitons; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Radu, E.; Volkov, M.S. Stationary ring solitons in field theory: Knots and vortons. Phys. Rep. 2008, 468, 101–151. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Newell, A. Solitons in Mathematics and Physics; SIAM: Philadelphia, PA, USA, 1985. [Google Scholar]
- Zakharov, V.E.; Manakov, S.V.; Novikov, S.P.; Pitaevskii, L. Theory of Solitons: The Inverse Problem Method; Nauka Publishers: Moscow, Russia, 1980; English translation: Consultants Bureau: New York, NY, USA, 1984. [Google Scholar]
- Biondini, G.; Pelinovsky, D. Kadomtsev-Petviashvili equation. Scholarpedia 2008, 3, 6539. [Google Scholar] [CrossRef]
- Manakov, S.V.; Zakharov, V.E.; Bordag, L.A.; Its, A.; Matveev, V.B. Two-dimensional solitons of the Kadomtsev-Petviashvili equation and their interaction. Phys. Lett. A 1977, 63, 205–206. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Desaix, M.; Anderson, D.; Lisak, M. Variational approach to collapse of optical pulses. J. Opt. Soc. Am. B 1991, 8, 2082–2086. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-trapping of optical beams. Phys. Rev. Lett. 1964, 13, 479–482. [Google Scholar] [CrossRef]
- Bradley, C.C.; Sackett, C.A.; Tollett, J.J.; Hulet, R.G. Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions. Phys. Rev. Lett. 1995, 75, 1687–1690, Erratum in: Phys. Rev. Lett. 1997, 79, 1170. [Google Scholar] [CrossRef]
- Bergé, L. Wave collapse in physics: Principles and applications to light and plasma waves. Phys. Rep. 1998, 303, 259–370. [Google Scholar] [CrossRef]
- Fibich, G. The Nonlinear Schrödinger Equation: Singular Solutions and Optical Collapse; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Sulem, C.; Sulem, P.-L. The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse; Springer: New York, NY, USA, 1999. [Google Scholar]
- Zabusky, N.J.; Kruskal, M.D. Interaction of “solitons” in a collisional plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Chen, C.-A.; Hung, C.-L. Observation of universal quench dynamics and Townes soliton formation from modulational instability in two-dimensional Bose gases. Phys. Rev. Lett. 2020, 125, 250401. [Google Scholar] [CrossRef]
- Chen, C.-A.; Hung, C.-L. Observation of scale invariance in two-dimensional matter-wave Townes solitons. Phys. Rev. Lett. 2021, 127, 023604. [Google Scholar]
- Kruglov, V.I.; Logvin, Y.A.; Volkov, V.M. The theory of spiral laser beams in nonlinear media. J. Mod. Phys. 1992, 39, 2277–2291. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Vlasov, R.A. Spiral self-trapping propagation of optical beams. Phys. Lett. A 1985, 111, 401–404. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Volkov, V.M.; Vlasov, R.A.; Drits, V.V. Auto-waveguide propagation and the collapse of spiral light beams in non-linear media. J. Phys. A Math. Gen. 1988, 21, 4381–4395. [Google Scholar] [CrossRef]
- Firth, W.J.; Skryabin, D.V. Optical solitons carrying orbital angular momentum. Phys. Rev. Lett. 1997, 79, 2450–2453. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Schochet, S.H.; Weinstein, M.I. The nonlinear Schrödinger limit of the Zakharov equations governing Langmuir turbulence. Commun. Math. Phys. 1986, 106, 569–580. [Google Scholar] [CrossRef]
- Malomed, B.A. Multidimensional solitons: Well-established results and novel findings. Eur. Phys. J. Spec. Top. 2016, 225, 2507–2532. [Google Scholar] [CrossRef]
- Malomed, B.A. (INVITED) Vortex solitons: Old results and new perspectives. Phys. D 2019, 399, 108–137. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quant. Semicl. Opt. 2005, 7, R53–R72. [Google Scholar]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Viewpoint: On multidimensional solitons and their legacy in contemporary atomic, molecular and optical physics. J. Phys. At. Mol. Opt. Phys. 2016, 49, 170502. [Google Scholar]
- Kartashov, Y.; Astrakharchik, G.; Malomed, B.; Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 2019, 1, 185–197. [Google Scholar] [CrossRef]
- Malomed, B.A. Multidimensional Solitons; American Institute of Physics: University Park, MD, USA, 2022. [Google Scholar]
- Falcão-Filho, L.; de Araújo, C.B.; Boudebs, G.; Leblond, H.; Skarka, V. Robust two-dimensional spatial solitons in liquid carbon disulfide. Phys. Rev. Lett. 2013, 110, 013901. [Google Scholar] [CrossRef] [PubMed]
- Reyna, A.S.; Boudebs, G.; Malomed, B.A.; de Araújo, C.B. Robust self-trapping of vortex beams in a saturable optical medium. Phys. Rev. A 2016, 93, 013840. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low temperature properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef]
- Cabrera, C.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose-Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallem, A.; Recati, A.; Fattori, M. Collisions of self-bound quantum droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets of atomic mixtures in free space? Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Tarruell, L.; Torner, L. Three-dimensional droplets of swirling superfluids. Phys. Rev. A 2018, 98, 013612. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Luo, Z.; Huang, C.; Tan, H.; Pang, W.; Malomed, B.A. Two-dimensional vortex quantum droplets. Phys. Rev. A 2018, 98, 063602. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Li, B.; Malomed, B.A. Creation of two-dimensional composite solitons in spin-orbit-coupled self-attractive Bose-Einstein condensates in free space. Phys. Rev. E 2014, 89, 032920. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Sherman, E.Y.; Malomed, B.A. Vortex solitons in two-dimensional spin-orbit coupled Bose-Einstein condensates: Effects of the Rashba-Dresselhaus coupling and the Zeeman splitting. Phys. Rev. E 2016, 94, 032202. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Belić, M.R.; Zhong, W.; Zhang, Y.; Xiao, M. Propagation dynamics of a light beam in a fractional Schrödinger equation. Phys. Rev. Lett. 2015, 115, 180403. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Torner, L.; Modugno, M.; Sherman, E.Y.; Malomed, B.A.; Konotop, V.V. Multidimensional hybrid Bose-Einstein condensates stabilized by lower-dimensional spin-orbit coupling. Phys. Rev. Res. 2020, 2, 013036. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Sherman, E.Y.; Malomed, B.A.; Konotop, V.V. Stable two-dimensional soliton complexes in Bose–Einstein condensates with helicoidal spin–orbit coupling. New J. Phys. 2020, 22, 103914. [Google Scholar] [CrossRef]
- Benjamin, T. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559–592. [Google Scholar] [CrossRef]
- Ono, H. Algebraic solitary waves in stratified fluids. J. Phys. Soc. Jpn. 1975, 39, 1082–1091. [Google Scholar]
- Fokas, A.S.; Ablowitz, M.J. The inverse scattering transform for the Benjamin-Ono equation, a pivot for multidimensional problems. Stud. Appl. Math. 1983, 68, 1–10. [Google Scholar]
- Kaup, D.; Matsuno, Y. The inverse scattering for the Benjamin-Ono equation. Stud. Appl. Math. 1998, 101, 73–98. [Google Scholar] [CrossRef]
- Turitsyn, S.K. Spatial dispersion of nonlinearity and stability of multidimensional solitons. Theor. Math. Phys. 1985, 64, 797–801. [Google Scholar] [CrossRef]
- Królikowski, W.; Bang, O.; Nikolov, N.I.; Neshev, D.; Wyller, J.; Rasmussen, J.J.; Edmundson, D. Modulational instability, solitons and beam propagation in spatially nonlocal nonlinear media. J. Opt. B Quantum Semiclass. Opt. 2004, 6, S288–S294. [Google Scholar] [CrossRef]
- Snyder, A.W.; Mitchell, D.J. Accessible solitons. Science 1997, 276, 1538–1541. [Google Scholar] [CrossRef]
- Minzoni, A.A.; Smyth, N.F.; Worthy, A.L. Modulation solutions for nematicon propagation in nonlocal liquid crystals. J. Opt. Soc. Am. B 2007, 24, 1549–1556. [Google Scholar] [CrossRef]
- Khoo, I.C. Nonlinear optics of liquid crystalline materials. Phys. Rep. 2009, 471, 221–267. [Google Scholar] [CrossRef]
- Assanto, G.; Karpierz, M.A. Nematicons: Self-localised beams in nematic liquid crystals. Liq. Cryst. 2009, 36, 1161–1172. [Google Scholar] [CrossRef]
- Peccianti, M.; Assanto, G. Nematicons. Phys. Rep. 2012, 516, 147–208. [Google Scholar] [CrossRef]
- Wyller, J.; Królikowski, W.; Bang, O.; Rasmussen, J.J. Generic features of modulational instability in nonlocal Kerr media. Phys. Rev. E 2002, 66, 066615. [Google Scholar] [CrossRef]
- Khalyapin, V.A.; Bugay, A.N. Analytical study of light bullets stabilization in the ionized medium. Chaos Sol. Fract. 2022, 156, 111799. [Google Scholar] [CrossRef]
- Silberberg, Y. Collapse of optical pulses. Opt. Lett. 1990, 15, 1282–1284. [Google Scholar] [CrossRef] [PubMed]
- Briedis, D.; Petersen, D.E.; Edmundson, D.; Krolikowski, W.; Bang, O. Ring vortex solitons in nonlocal nonlinear media. Opt. Exp. 2005, 13, 435–443. [Google Scholar] [CrossRef] [PubMed]
- Skupin, S.; Bang, O.; Edmundson, D.; Krolikowski, W. Stability of two-dimensional spatial solitons in nonlocal nonlinear media. Phys. Rev. E 2006, 73, 066603. [Google Scholar] [CrossRef] [PubMed]
- Yakimenko, A.I.; Zaliznyak, Y.A.; Kivshar, Y. Stable vortex solitons in nonlocal self-focusing nonlinear media. Phys. Rev. E 2005, 71, 065603(R). [Google Scholar] [CrossRef]
- Lopez-Aguayo, S.; Desyatnikov, A.S.; Kivshar, Y.S.; Skupin, S.; Królikowski, W.; Bang, O. Stable rotating dipole solitons in nonlocal optical media. Opt. Lett. 2006, 31, 1100–1102. [Google Scholar] [CrossRef]
- Jung, P.S.; Izdebskaya, Y.V.; Shvedov, V.G.; Christodoulides, D.; Krolikowski, W. Formation and stability of vortex solitons in nematic liquid crystals. Opt. Lett. 2021, 46, 62–65. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Lederer, F.; Malomed, B.A.; Kartashov, Y.V.; Crasovan, L.-C.; Torner, L. Three-dimensional spatiotemporal optical solitons in nonlocal nonlinear media. Phys. Rev. E 2006, 73, 025601(R). [Google Scholar] [CrossRef]
- Walasik, W.; Silahli, S.Z.; Litchinitser, N. Dynamics of necklace beams in nonlinear colloidal suspensions. Sci. Rep. 2017, 7, 11709. [Google Scholar] [CrossRef]
- Suter, D.; Blasberg, T. Stabilization of transverse solitary waves by a nonlocal response of the nonlinear medium. Phys. Rev. A 1993, 48, 4583–4587. [Google Scholar] [CrossRef]
- Peccianti, M.; Assanto, G.; Luca, A.D.; Umeton, C.; Khoo, I.C. Electrically assisted self-confinement and waveguiding in planar nematic liquid crystal cells. Appl. Phys. Lett. 2000, 77, 7–9. [Google Scholar] [CrossRef]
- Rotschild, C.; Cohen, O.; Manela, O.; Segev, M.; Carmon, T. Solitons in nonlinear media with an infinite range of nonlocality: First observation of coherent elliptic solitons and of vortex-ring solitons. Phys. Rev. Lett. 2005, 95, 213904. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, M.; Yang, L.; Tian, B.; Chen, C.; Guo, Q.; Shou, Q.; Hu, W. Higher-charge vortex solitons and vector vortex solitons in strongly nonlocal media. Opt. Lett. 2019, 44, 3098–3101. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, T.; Dai, C. Stabilization of higher-order vortex solitons by means of nonlocal nonlinearity. Phys. Rev. A 2022, 105, 013520. [Google Scholar] [CrossRef]
- Izdebskaya, Y.; Assanto, G.; Krokikovski, W. Observation of stable-vector vortex solitons. Opt. Lett. 2015, 40, 4182–4184. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, T.; Shou, Q.; Guo, Q. Optical elliptic breathers in isotropic nonlocal nonlinear media. Opt. Exp. 2022, 30, 9336–9347. [Google Scholar] [CrossRef]
- Christiansen, P.L.; Grønbech-Jensen, N.; Lomdahl, P.S.; Malomed, B.A. Oscillations of eccentric pulsons. Phys. Scr. 1997, 55, 131–134. [Google Scholar] [CrossRef]
- Carmon, T.; Uzdin, R.; Pigier, C.; Musslimani, Z.H.; Segev, M.; Nepomnyashchy, A. Rotating propeller solitons. Phys. Rev. Lett. 2001, 87, 143901. [Google Scholar] [CrossRef]
- Laskin, N. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 2000, 268, 298–305. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Quantum Mechanics; World Scientific: Singapore, 2018. [Google Scholar]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef]
- Stickler, B.A. Potential condensed-matter realization of space-fractional quantum mechanics: The one-dimensional Lévy crystal. Phys. Rev. E 2013, 88, 012120. [Google Scholar] [CrossRef]
- Pinsker, F.; Bao, W.; Zhang, Y.; Ohadi, H.; Dreismann, A.; Baumberg, J.J. Fractional quantum mechanics in polariton condensates with velocity-dependent mass. Phys. Rev. B 2015, 92, 195310. [Google Scholar] [CrossRef]
- Secchi, S.; Squassina, M. Soliton dynamics for fractional Schrödinger equations. Appl. Anal. 2014, 93, 1702–1729. [Google Scholar] [CrossRef]
- Malomed, B.A. Optical solitons and vortices in fractional media: A mini-review of recent results. Photonics 2021, 8, 353. [Google Scholar] [CrossRef]
- Agrawal, O.P. Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A Math. Theor. 2007, 40, 6287–6303. [Google Scholar] [CrossRef]
- Cai, M.; Li, C.P. On Riesz derivative. Fract. Calc. Appl. Anal. 2019, 22, 287–301. [Google Scholar] [CrossRef]
- Kwasnicki, M. Ten equivalent definitions of the fractional Laplace operators. Fract. Calc. Appl. Anal. 2017, 20, 7–51. [Google Scholar] [CrossRef]
- Navickas, Z.; Telksnys, T.; Marcinkevicius, R.; Ragulskis, M. Operator-based approach for the construction of analytical soliton solutions to nonlinear fractional-order differential equations. Chaos Solitons Fractals 2017, 104, 625–634. [Google Scholar] [CrossRef]
- Li, P.; Malomed, B.A.; Mihalache, D. Vortexsolitons in fractional nonlinear Schrödinger equation with the cubic-quintic nonlinearity. Chaos Solitons Fract. 2020, 137, 109783. [Google Scholar]
- Li, P.; Malomed, B.A.; Mihalache, D. Metastablesoliton necklaces supported by fractional diffraction and competing nonlinearities. Opt. Exp. 2020, 28, 34472–34488. [Google Scholar]
- Li, P.; Li, R.; Dai, C. Existence, symmetry breaking bifurcation and stability of two-dimensional optical solitons supported by fractional diffraction. Opt. Exp. 2021, 29, 3193–3210. [Google Scholar] [CrossRef] [PubMed]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 126401. [Google Scholar] [CrossRef]
- Giovanazzi, S.; Görlitz, A.; Pfau, T. Tuning the dipolar interaction in quantum gases. Phys. Rev. Lett. 2003, 89, 130401. [Google Scholar] [CrossRef]
- Micheli, A.; Pupillo, G.; Büchler, H.P.; Zoller, P. Cold polar molecules in two-dimensional traps: Tailoring interactions with external fields for novel quantum phases. Phys. Rev. A 2007, 76, 043604. [Google Scholar] [CrossRef]
- Pedri, P.; Santos, L. Two-dimensional bright solitons in dipolar Bose-Einstein condensates. Phys. Rev. Lett. 2005, 95, 200404. [Google Scholar] [CrossRef]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Vortex solitons in dipolar Bose-Einstein condensates. Phys. Rev. A 2008, 78, 043614. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Chuang, Y.-L.; Lin, C.-Y.; Wu, C.-M.; Li, Y.; Malomed, B.A.; Lee, R.-K. Magic tilt angle for stabilizing two-dimensional solitons by dipole-dipole interactions. Phys. Rev. A 2017, 96, 043631. [Google Scholar]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Anisotropic solitons in dipolar Bose-Einstein condensates. Phys. Rev. Lett. 2008, 100, 090406. [Google Scholar] [CrossRef]
- Köberle, P.; Zajec, D.; Wunner, G.; Malomed, B.A. Creating two-dimensional bright solitons in dipolar Bose-Einstein condensates. Phys. Rev. A 2012, 85, 023630. [Google Scholar] [CrossRef]
- Eichler, R.; Zajec, D.; Köberle, P.; Main, J.; Wunner, G. Collisions of anisotropic two-dimensional bright solitons in dipolar Bose-Einstein condensates. Phys. Rev. A 2012, 86, 053611. [Google Scholar]
- Young-S, L.E.; Adhikari, S.K. Deep inelastic collision of two-dimensional anisotropic dipolar condensate solitons. Comm. Nonlin. Sci. Num. Sim. 2022, 106, 106094. [Google Scholar]
- Zhao, Y.; Lei, Y.-B.; Xu, Y.-X.; Xu, S.-L.; Triki, H.; Biswas, A.; Zhou, Q. Vector spatiotemporal solitons and their memory features in cold Rydberg gases. Chin. Phys. Lett. 2022, 39, 034202. [Google Scholar] [CrossRef]
- Burnett, B.R.J.K.; Scott, T.F. Theory of an output coupler for Bose-Einstein condensed atoms. Phys. Rev. Lett. 1997, 78, 1607–1611. [Google Scholar]
- Bookjans, E.M.; Vinit, A.; Raman, C. Quantum Phase Transition in an Antiferromagnetic Spinor Bose-Einstein Condensate. Phys. Rev. Lett. 2011, 107, 195306. [Google Scholar] [CrossRef]
- Li, K.; Deng, L.; Hagley, E.W.; Payne, M.G.; Zhan, M.S. Matter-wave self-imaging by atomic center-of-mass motion induced interference. Phys. Rev. Lett. 2008, 101, 250401. [Google Scholar] [CrossRef]
- Zhu, J.; Dong, G.; Shneider, M.N.; Zhang, W. Strong local-field effect on the dynamics of a dilute atomic gas irradiated by two counterpropagating optical fields: Beyond standard optical lattices. Phys. Rev. Lett. 2011, 106, 210403. [Google Scholar] [CrossRef]
- Dong, G.; Zhu, J.; Zhang, W.; Malomed, B.A. Photon-atomic solitons in a Bose-Einstein condensate trapped in a soft optical lattice. Phys. Rev. Lett. 2013, 110, 250401. [Google Scholar] [CrossRef]
- Qin, J.; Dong, G.; Malomed, B.A. Hybrid matter-wave-microwave solitons produced by the local-field effect. Phys. Rev. Lett. 2015, 115, 023901. [Google Scholar] [CrossRef]
- Qin, J.; Dong, G.; Malomed, B.A. Stable giant vortex annuli in microwave-coupled atomic condensates. Phys. Rev. A 2016, 94, 053611. [Google Scholar] [CrossRef]
- Radzihovsky, L.; Sheehy, D.E. Imbalanced Feshbach-resonant Fermi gases. Rep. Prog. Phys. 2010, 73, 076501. [Google Scholar] [CrossRef]
- Comparat, D.; Fioretti, A.; Stern, G.; Dimova, E.; Tolra, B.; Pillet, P. Optimized production of large Bose-Einstein condensates. Phys. Rev. A 2006, 73, 043410. [Google Scholar] [CrossRef]
- van der Stam, K.M.R.; van Ooijen, E.D.; Meppelink, R.; Vogels, J.M.; van der Straten, P. Large atom number Bose-Einstein condensate of sodium. Rev. Sci. Instr. 2007, 78, 013102. [Google Scholar] [CrossRef]
- Caplan, R.M.; Carretero-Gonzalez, R.; Kevrekidis, P.G.; Malomed, B.A. Existence, stability, and scattering of bright vortices in the cubic-quintic nonlinear Schrödinger equation. Math. Comput. Simul. 2012, 82, 1150–1171. [Google Scholar] [CrossRef]
- Brtka, M.; Gammal, A.; Malomed, B.A. Hidden vorticity in binary Bose-Einstein condensates. Phys. Rev. A 2010, 82, 053610. [Google Scholar] [CrossRef]
- Pego, R.L.; Warchall, H.A. Spectrally stable encapsulated vortices for nonlinear Schrödinger equations. J. Nonlinear Sci. 2002, 12, 347–394. [Google Scholar] [CrossRef]
- Quiroga-Teixeiro, M.; Michinel, H. Stable azimuthal stationary state in quintic nonlinear optical media. J. Opt. Soc. Am. B 1997, 14, 2004–2009. [Google Scholar] [CrossRef]
- Borovkova, O.V.; Kartashov, Y.V.; Malomed, B.A.; Torner, L. Algebraic bright and vortex solitons in defocusing media. Opt. Lett. 2011, 36, 3088–3090. [Google Scholar] [CrossRef]
- Borovkova, O.V.; Kartashov, Y.V.; Torner, L.; Malomed, B.A. Bright solitons from defocusing nonlinearities. Phys. Rev. E 2011, 84, 035602(R). [Google Scholar] [CrossRef]
- Driben, R.; Kartashov, Y.V.; Malomed, B.A.; Meier, T.; Torner, L. Soliton gyroscopes in media with spatially growing repulsive nonlinearity. Phys. Rev. Lett. 2014, 112, 020404. [Google Scholar] [CrossRef]
- Sudharsan, J.B.; Radha, R.; Fabrelli, H.; Gammal, A.; Malomed, B.A. Stable multiple vortices in collisionally inhomogeneous attractive Bose-Einstein condensates. Phys. Rev. A 2015, 92, 053601. [Google Scholar] [CrossRef]
- Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef]
- Minovich, A.E.; Klein, A.E.; Neshev, D.N.; Pertsch, T.; Kivshar, Y.S.; Christodoulides, D.N. Airy plasmons: Non-diffracting optical surface waves. Laser Photonics Rev. 2013, 8, 221–232. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Paltoglou, V.; von Klitzing, W. Accelerating and abruptly autofocusing matter waves. Phys. Rev. A 2013, 87, 043637. [Google Scholar] [CrossRef]
- Zhang, P.; Li, T.; Zhu, J.; Zhu, X.; Yang, S.; Wang, Y.; Yin, X.; Zhang, X. Generation of acoustic self-bending and bottle beams by phase engineering. Nat. Commun. 2014, 5, 4316. [Google Scholar] [CrossRef]
- Clerici, M.; Hu, Y.; Lassonde, P.; Milian, C.; Couairon, A.; Christodoulides, D.N.; Chen, Z.; Razzari, L.; Vidal, F.; Legare, F.; et al. Laser-assisted guiding of electric discharges around objects. Sci. Adv. 2015, 1, e1400111. [Google Scholar] [CrossRef]
- Voloch-Bloch, N.; Lereah, Y.; Lilach, Y.; Gover, A.; Arie, A. Generation of electron Airy beams. Nature 2013, 494, 331–335. [Google Scholar] [CrossRef]
- Fu, S.; Tsur, Y.; Zhou, J.; Shemer, L.; Arie, A. Propagation dynamics of Airy water-wave pulses. Phys. Rev. Lett. 2015, 115, 034501. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
- Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photonics 2009, 3, 395–398. [Google Scholar] [CrossRef]
- Jia, S.; Lee, J.; Fleischer, J.W.; Siviloglou, G.A.; Christodoulides, D.N. Diffusion-trapped Airy beams in photorefractive media. Phys. Rev. Lett. 2010, 104, 253904. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, S.; Zhang, P.; Lou, C.; Xu, J.; Chen, Z. Persistence and breakdown of Airy beams driven by an initial nonlinearity. Opt. Lett. 2010, 35, 3952–3954. [Google Scholar] [CrossRef]
- Kaminer, I.; Segev, M.; Christodoulides, D.N. Self-accelerating self-trapped optical beams. Phys. Rev. Lett. 2011, 106, 213903. [Google Scholar] [CrossRef]
- Lotti, A.; Faccio, D.; Couairon, A.; Papazoglou, D.G.; Panagiotopoulos, P.; Abdollahpour, D.; Tzortzakis, S. Stationary nonlinear Airy beams. Phys. Rev. A 2011, 84, 021807. [Google Scholar] [CrossRef]
- Fattal, Y.; Rudnick, A.; Marom, D.M. Soliton shedding from Airy pulses in Kerr media. Opt. Exp. 2011, 18, 17298–17307. [Google Scholar] [CrossRef]
- Batz, S.; Peschel, U. Diametrically driven self-accelerating pulses in a photonic crystal fiber. Phys. Rev. Lett. 2013, 110, 193901. [Google Scholar] [CrossRef]
- Wimmer, M.; Regensburger, A.; Bersch, C.; Miri, M.-A.; Batz, S.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Optical diametric drive acceleration through action-reaction symmetry breaking. Nat. Phys. 2013, 9, 780–784. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Interactions of solitons with positive and negative masses: Shuttle motion and coacceleration. Phys. Rev. E 2019, 99, 022216. [Google Scholar] [CrossRef]
- Qin, J.; Liang, Z.; Malomed, B.A.; Dong, G. Tail-free self-accelerating solitons and vortices. Phys. Rev. A 2019, 99, 023610. [Google Scholar] [CrossRef]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wachtler, F.; Santos, L.; Ferlaino, F. Quantum-fluctuation-driven crossover from a dilute Bose-Einstein condensate to a macrodroplet in a dipolar quantum fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of quantum droplets in a strongly dipolar Bose gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Bottcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef]
- Cidrim, A.; dos Santos, F.E.; Henn, E.A.; Macrí, T. Vortices in self-bound dipolar droplets. Phys. Rev. A 2018, 98, 023618. [Google Scholar] [CrossRef]
- Gligorić, G.; Maluckov, A.; Stepić, M.; Hadžievski, L.; Malomed, B.A. Two-dimensional discrete solitons in dipolar Bose-Einstein condensates. Phys. Rev. A 2010, 81, 013633. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Fan, Z.; Pang, W.; Fu, S.; Malomed, B.A. Two-dimensional dipolar gap solitons in free space with spin-orbit coupling. Phys. Rev. A 2017, 95, 063613. [Google Scholar] [CrossRef]
- Malomed, B.A. Potential of interaction between two- and three-dimensional solitons. Phys. Rev. E 1998, 58, 7928–7933. [Google Scholar] [CrossRef]


| S | S | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 3 | 41 | |||||
| 1 | 11 | 4 | 57 | ||||
| 2 | 28 | 5 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malomed, B.A. Two-Dimensional Solitons in Nonlocal Media: A Brief Review. Symmetry 2022, 14, 1565. https://doi.org/10.3390/sym14081565
Malomed BA. Two-Dimensional Solitons in Nonlocal Media: A Brief Review. Symmetry. 2022; 14(8):1565. https://doi.org/10.3390/sym14081565
Chicago/Turabian StyleMalomed, Boris A. 2022. "Two-Dimensional Solitons in Nonlocal Media: A Brief Review" Symmetry 14, no. 8: 1565. https://doi.org/10.3390/sym14081565
APA StyleMalomed, B. A. (2022). Two-Dimensional Solitons in Nonlocal Media: A Brief Review. Symmetry, 14(8), 1565. https://doi.org/10.3390/sym14081565






