Improved LightGBM-Based Framework for Electric Vehicle Lithium-Ion Battery Remaining Useful Life Prediction Using Multi Health Indicators
Abstract
:1. Introduction
- (1)
- To improve prediction accuracy and avoid low training efficiency caused by HIs. This paper proposes a LightGBM-based RUL prediction framework, which derives the multi HIs extraction and an improved RUL prediction model.
- (2)
- The extracted HIs can be mainly divided into indirect HIs (i.e., resistances from EIS and loss modes from IC-DV curves) and direct HIs (i.e., OCV and temperature). To adapt to multi HIs, the loss function of the LightGBM model is improved by the adaptive loss.
- (3)
- To obtain the optimal performance, the parameters of the model are optimized by the hyperparameter optimization method. The proposed framework is validated by the database from a battery aging and performance testing experimental system. The performance of the proposed framework under different numbers of HIs is also analyzed.
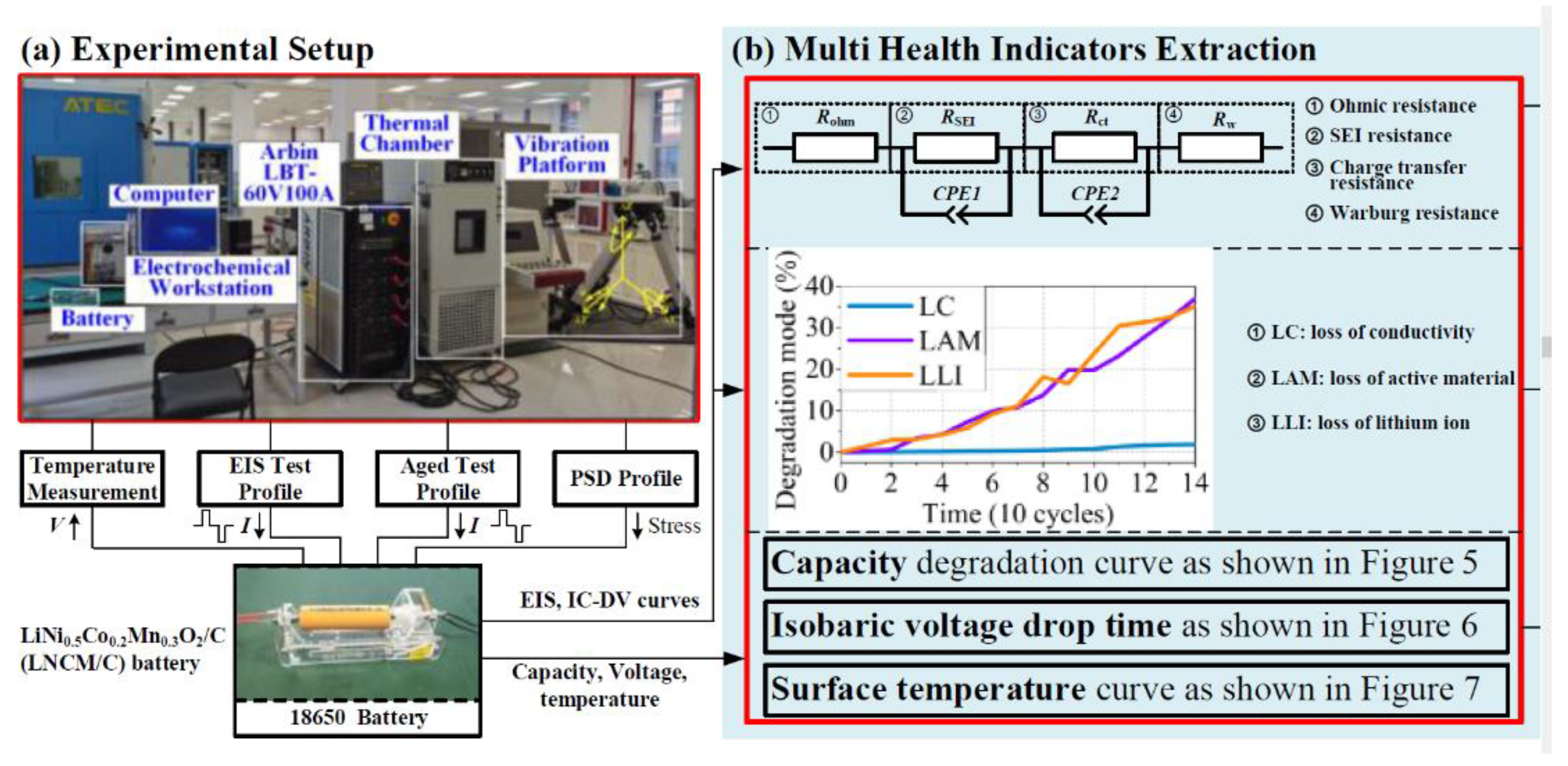
2. Multi Health Indicators Extraction
2.1. Multi Health Indicators Extraction
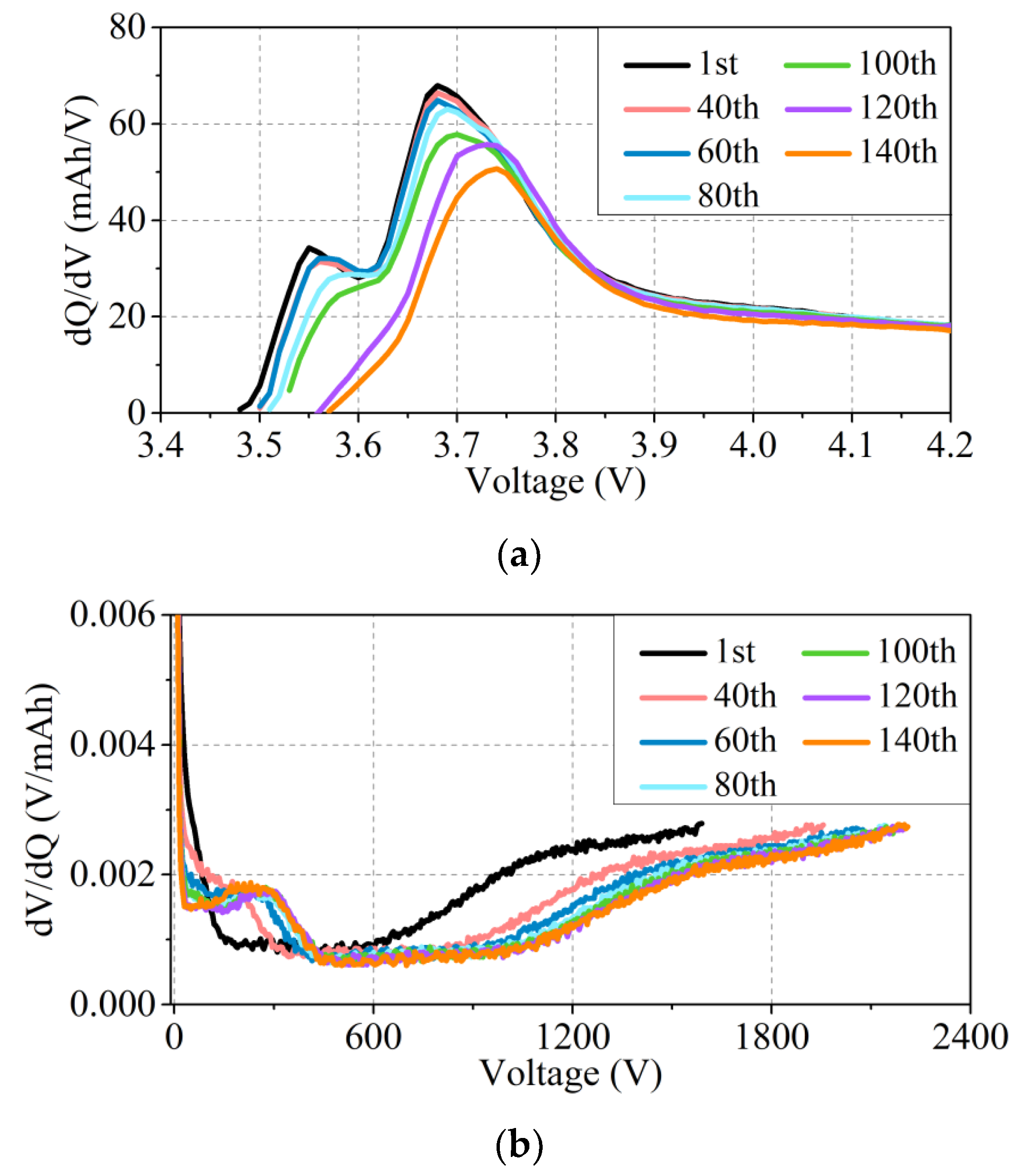
2.1.1. HIs Extracted from IC-DV Curves
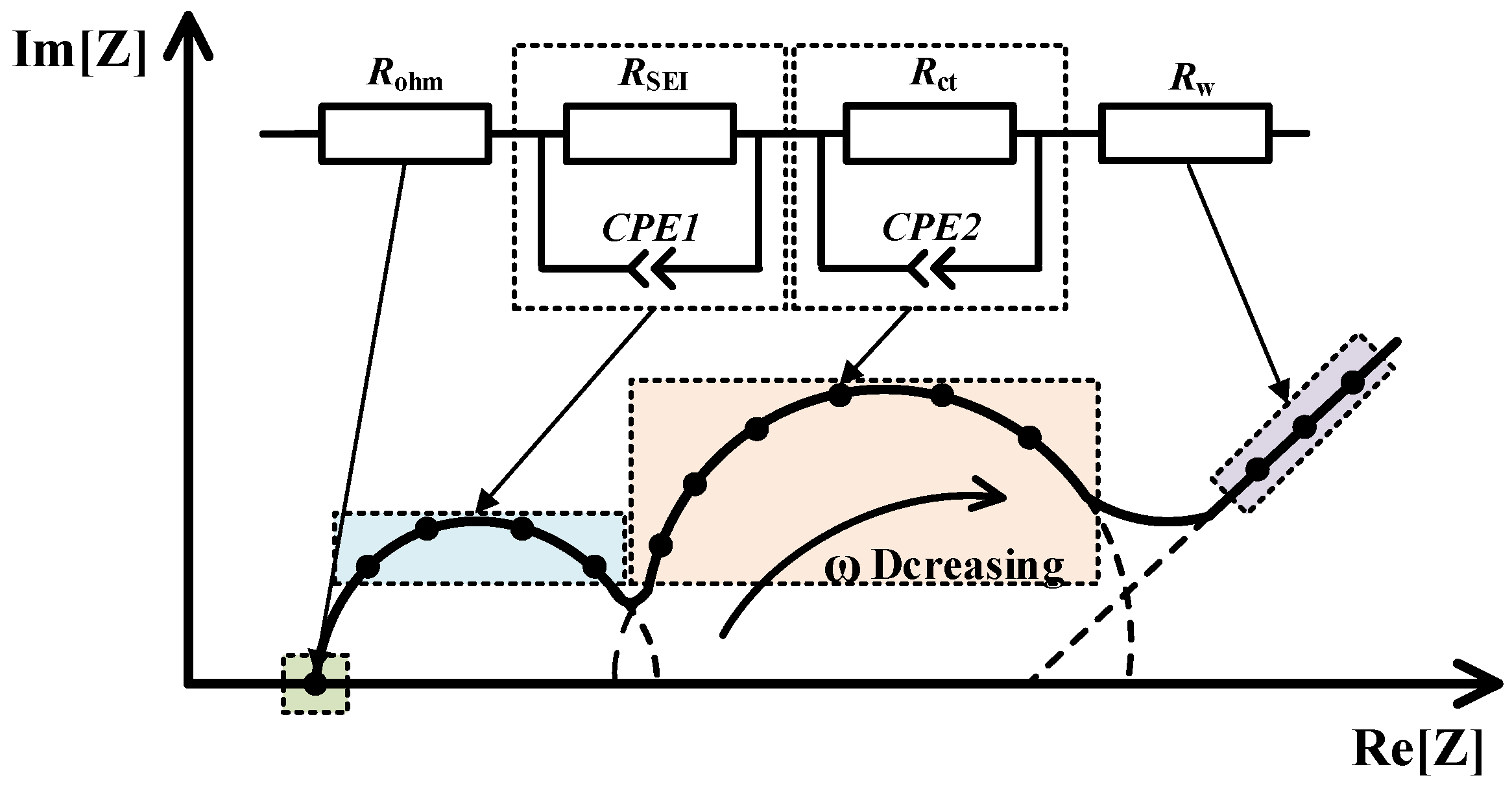
2.1.2. HIs Extracted from EIS
2.1.3. Other HIs Extracted from OCV and Temperature
2.2. Experimental Setup
2.2.1. Experimental System
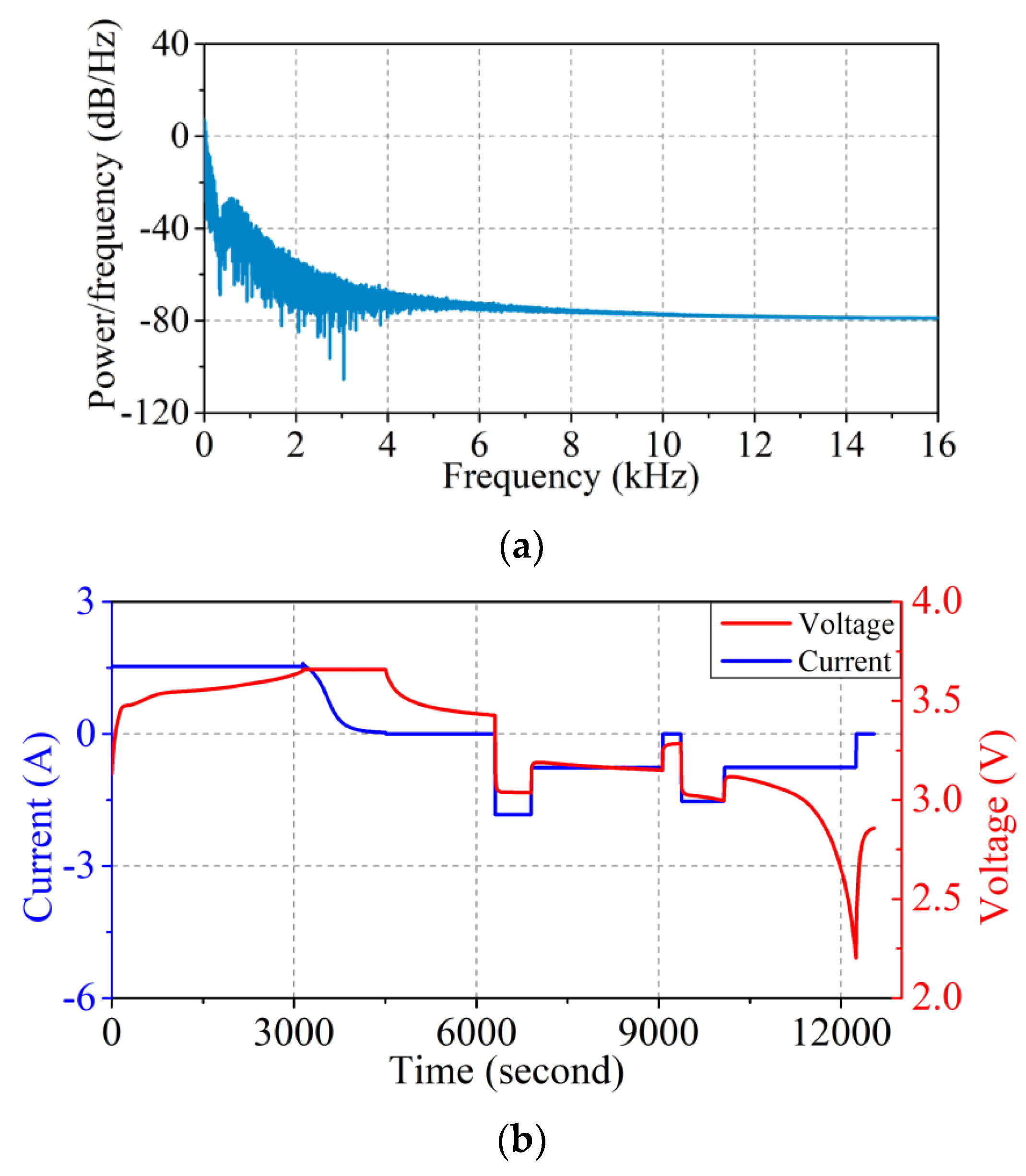
2.2.2. Experimental Profile
3. Improved LightGBM-Based RUL Prediction Framework
3.1. Improved LightGBM
3.2. The Proposed RUL Prediction Framework
4. Validation and Discussion
4.1. Experimental Results Analysis
4.1.1. IC-DV Curves
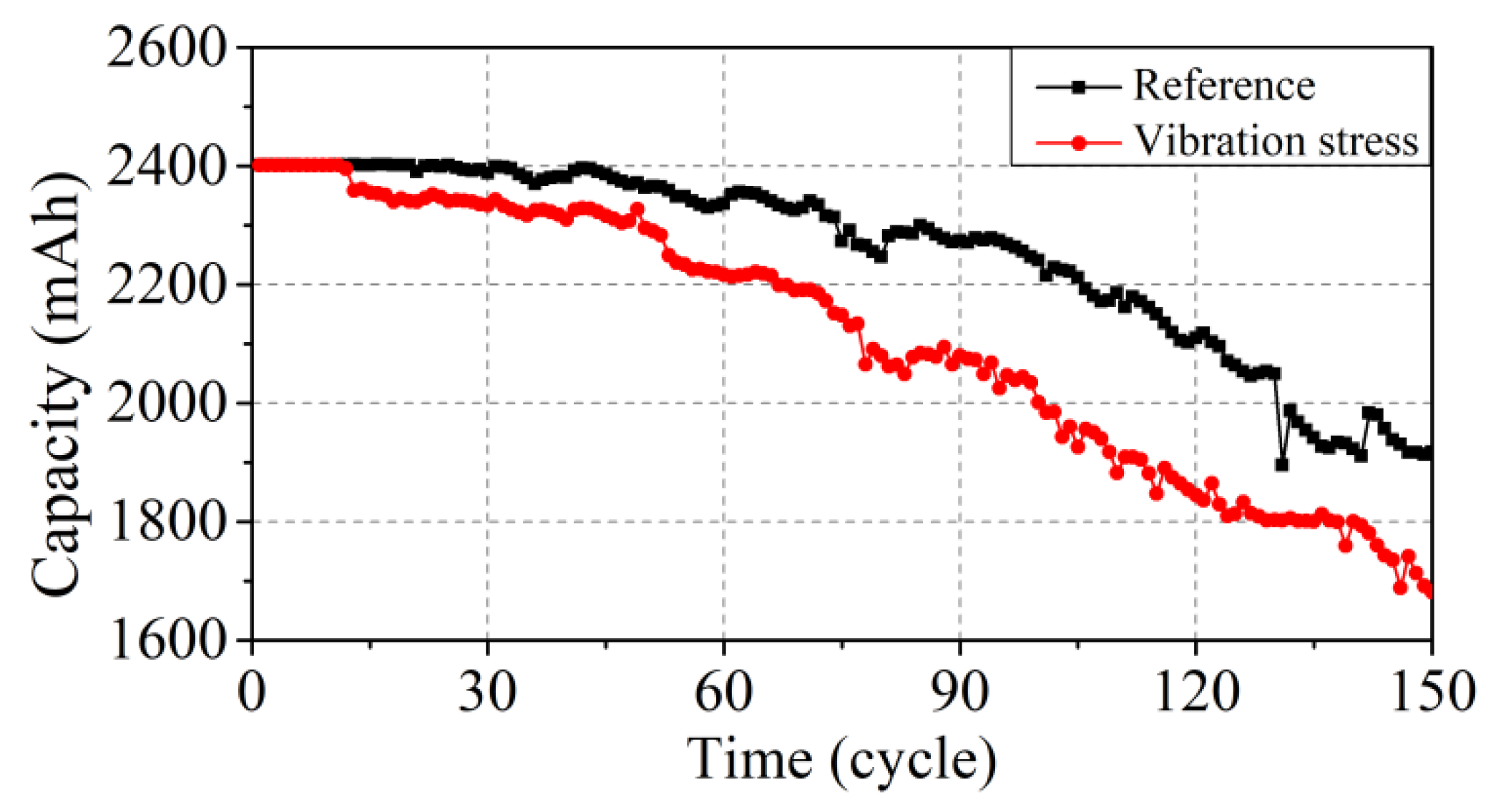
4.1.2. Capacity Degradation Curve
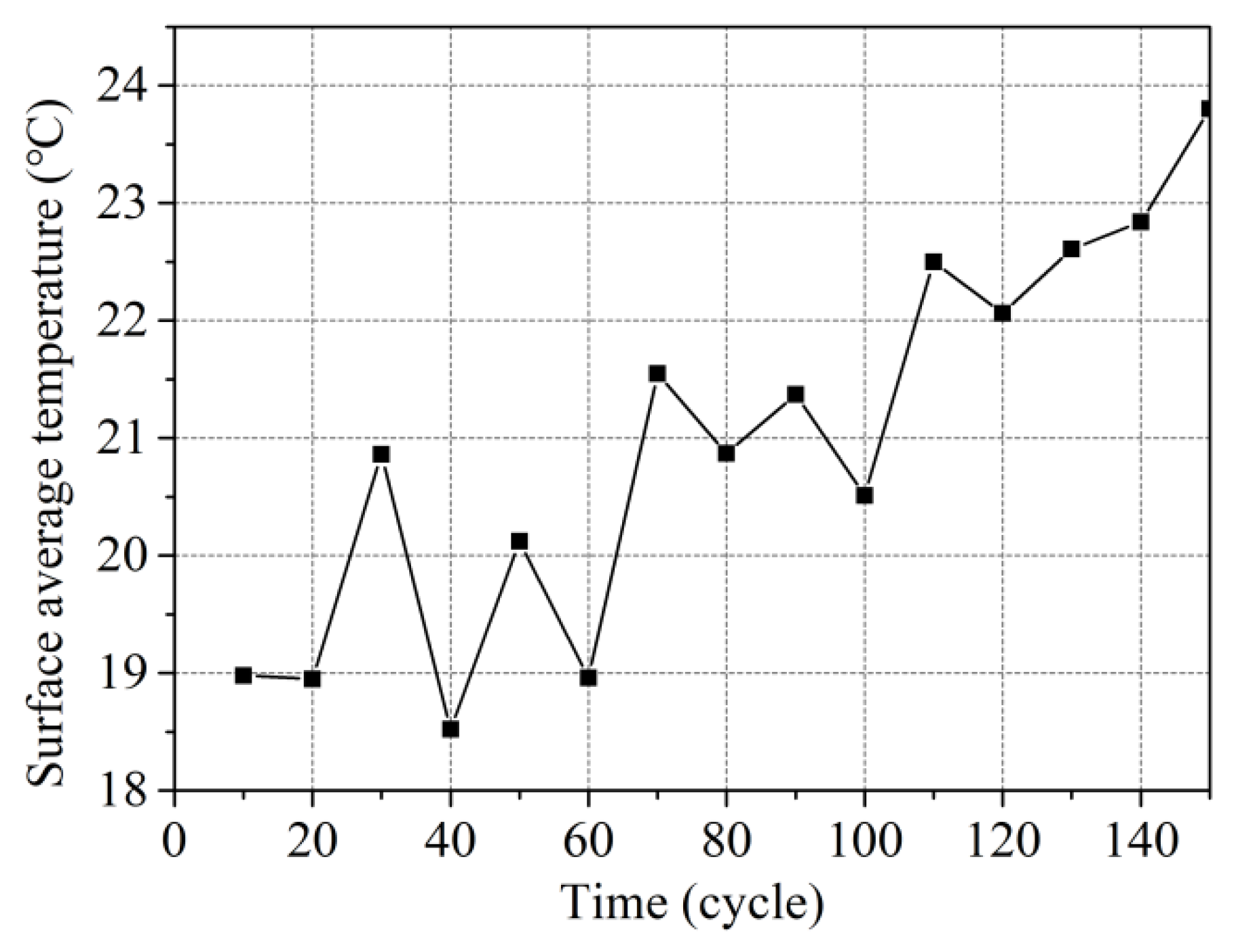
4.1.3. Isobaric Voltage Drop Time and Surface Temperature
4.2. Analysis of Health Indicators
4.2.1. Loss Modes
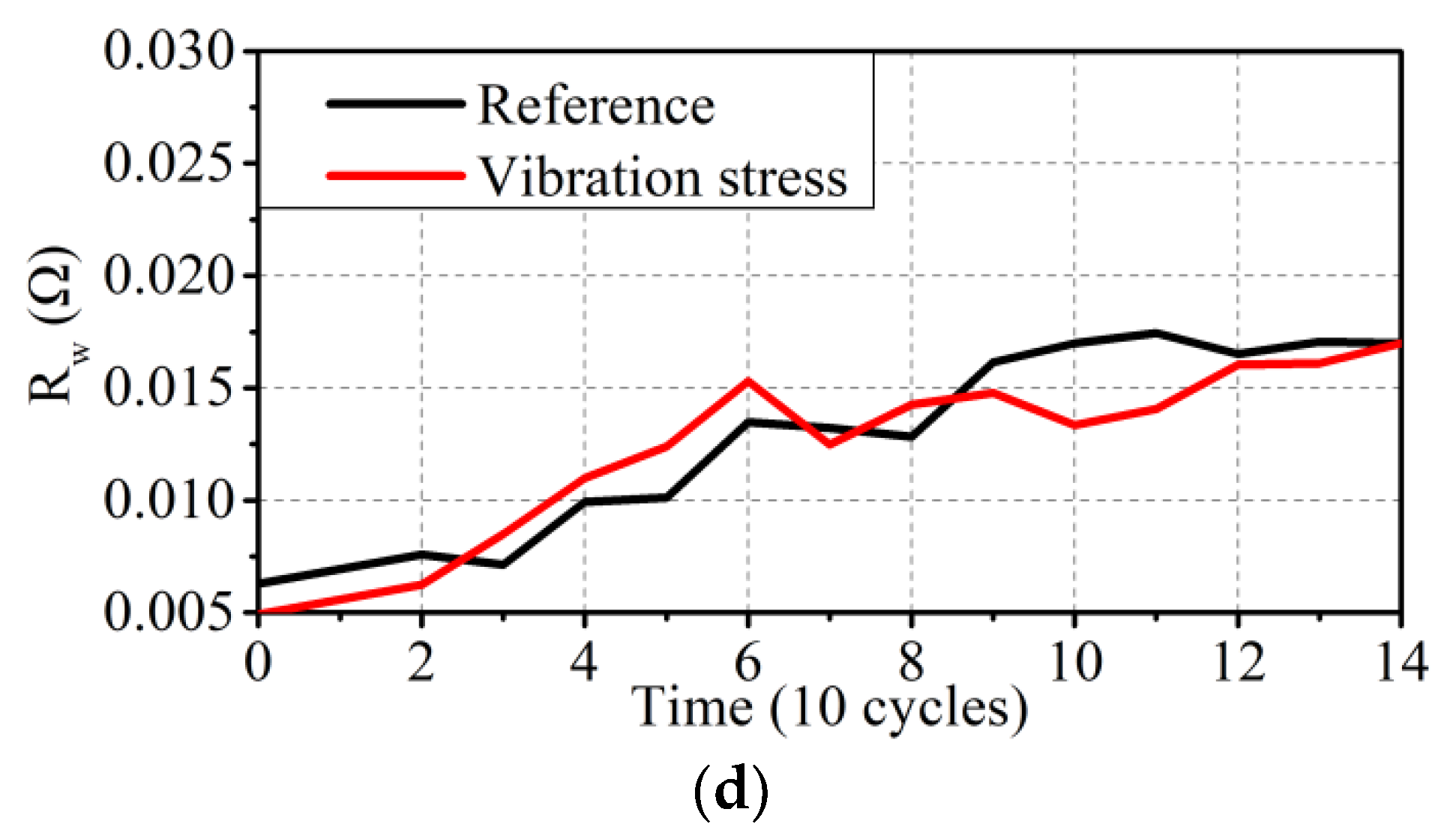
4.2.2. Four Types of Resistances
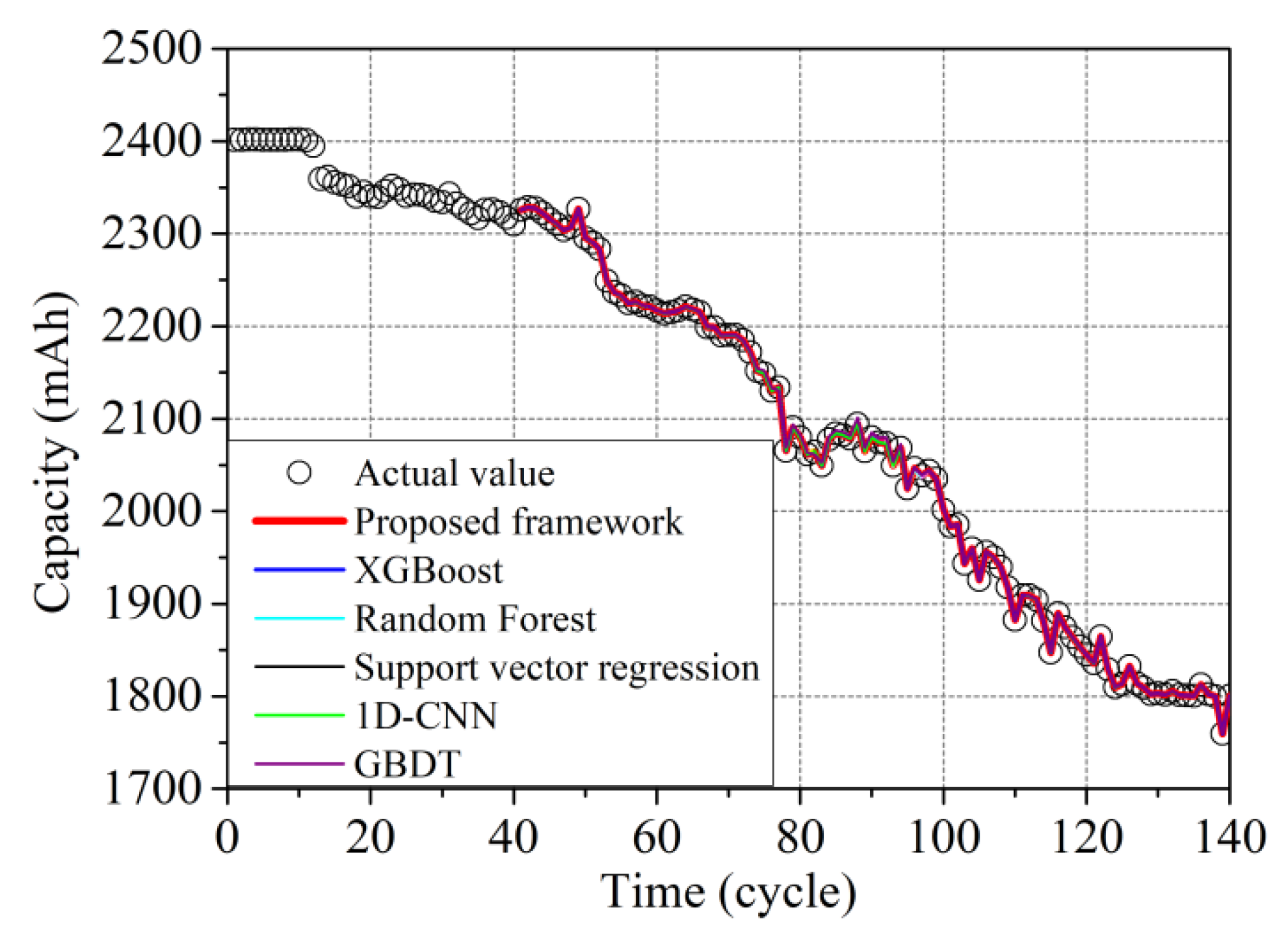
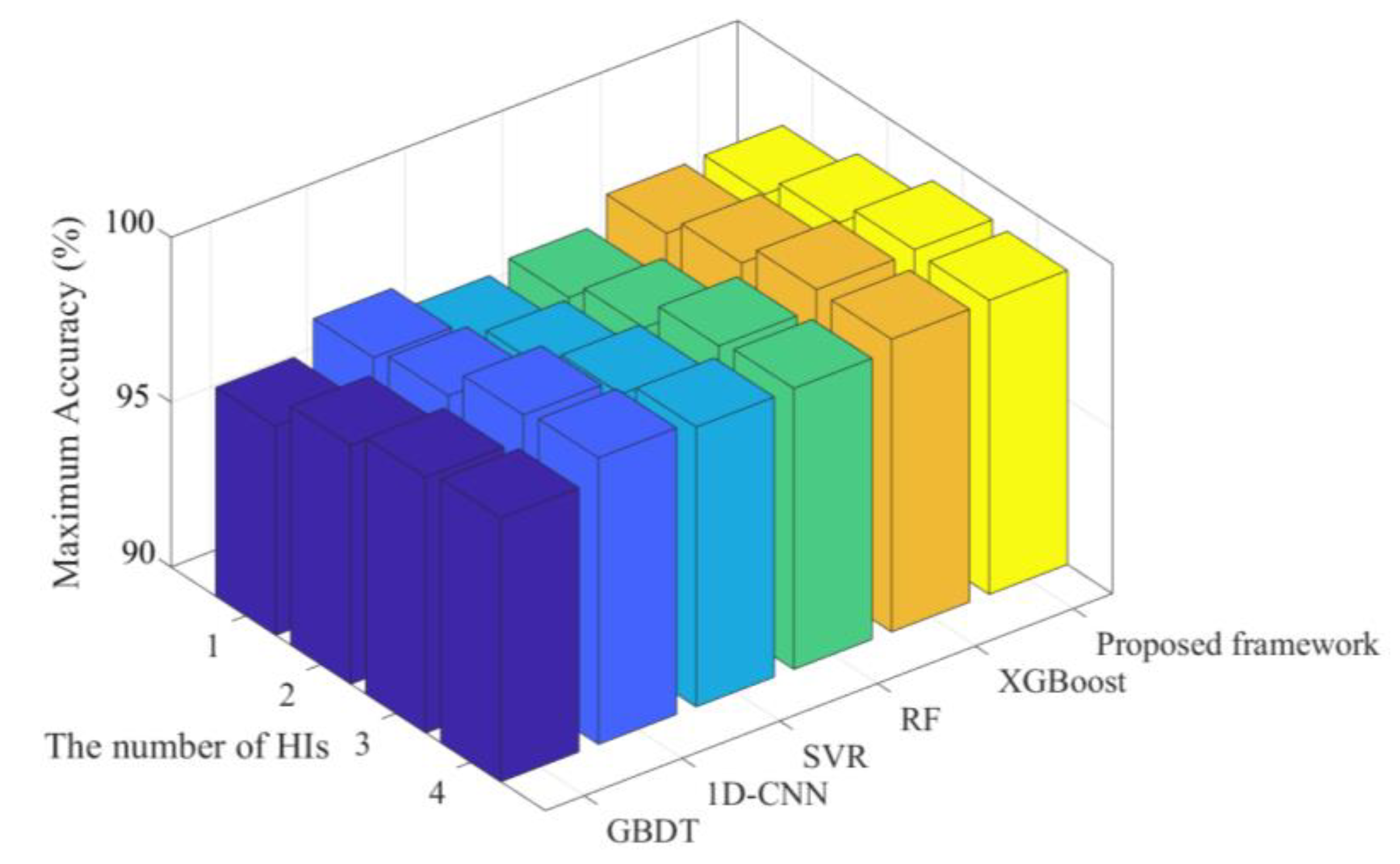
4.3. Validation of the Proposed Framework
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Terms | Abbreviations |
| Electric vehicle | EV |
| Remaining useful life | RUL |
| Light gradient boosting machine | LightGBM |
| Electrochemical impedance spectroscopy | EIS |
| Incremental capacity-differential voltage | IC-DV |
| Health indicator | HI |
| State of health | SOH |
| State of charge | SOC |
| Open circuit voltage | OCV |
| Loss of conductivity | LC |
| Loss of active material | LAM |
| Loss of lithium ion | LLI |
| Gradient boosting decision tree | GBDT |
| One-dimensional convolutional neural networks | 1D-CNN |
| Support vector regression | SVR |
| Random forest | RF |
| Extreme gradient boosting | XGBoost |
| End of life | EOL |
References
- Hu, X.; Liu, W.; Lin, X.; Xie, Y.; Foley, A.; Hu, L. A control-oriented electrothermal model for pouch-type electric vehicle batteries. IEEE Trans. Power Electron. 2021, 5, 5530–5544. [Google Scholar] [CrossRef]
- Nurdiawati, A.; Agrawal, T.K. Creating a circular EV battery value chain: End-of-life strategies and future perspective. Resour. Conser. Recycl. 2022, 185, 106484. [Google Scholar] [CrossRef]
- Meng, J.; Store, D.; Ricco, M.; Luo, G.; Teodorescu, R. A simplified model-based state-of-charge estimation approach for lithium-ion battery with dynamic linear model. IEEE Trans. Ind. Electron. 2019, 66, 7717–7727. [Google Scholar] [CrossRef]
- Sulzer, V.; Mohtat, P.; Aitio, A.; LEE, S.; Yeh, Y.T.; Steinbacher, F.; Khan, M.U.; Lee, J.W.; Siegel, J.B.; Stefanopoulou, A.J.; et al. The challenge and opportunity of battery lifetime prediction from field data. Joule 2021, 5, 1934–1955. [Google Scholar] [CrossRef]
- Qiu, Y.; Sun, J.; Shang, Y.; Wang, D. A fault diagnosis and prognosis method for lithium-ion batteries based on a nonlinear autoregressive exogenous neural network and boxplot. Symmetry 2021, 13, 1714. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Hu, J.; Sun, Q.; Ye, Z.; Zhou, Q. Joint modeling of degradation and lifetime data for RUL prediction of deteriorating products. IEEE Trans. Ind. Inform. 2021, 7, 4521–4531. [Google Scholar] [CrossRef]
- Sadabadi, K.K.; Jin, X.; Rizzoni, G. Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health. J. Power Sources 2021, 481, 228861. [Google Scholar] [CrossRef]
- Wang, Q.; He, Y.; Shen, J.; Hu, S.; Ma, Z. State of charge-dependent polynomial equivalent circuit modeling for electrochemical impedance spectroscopy of lithium-ion batteries. IEEE Trans. Power Electron. 2018, 33, 8449–8460. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion bat-teries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Feng, H.; Song, D. A health indicator extraction based on surface temperature for lithium-ion batteries remaining useful life prediction. J. Energy Storage 2021, 34, 102118. [Google Scholar] [CrossRef]
- Bai, L.; Cui, L.; Zhang, Z.; Xu, L.; Wang, Y.; Hancock, E.R. Entropic dynamic time warping kernels for co-evolving financial time series analysis. IEEE Trans. Neural Netw. Learn. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Xu, L.; Hu, X.; Zhang, Y.; Yi, J.; Yu, Y.; Xiao, X.; Yu, Y. A highly sensitive and precise temperature sensor based on optoelectronic oscillator. Optics Commun. 2021, 483, 126625. [Google Scholar] [CrossRef]
- Li, W.; Jiao, Z.; Xiao, Q.; Meng, J.; Mu, Y.; Jia, H.; Teodorescu, R.; Blaabjerg, F. A study on performance characterization considering six- degree-of-freedom vibration stress and aging stress for electric vehicle battery under driving conditions. IEEE Access 2019, 7, 112180–112190. [Google Scholar] [CrossRef]
- Adam, S.A.; Jalil, N.A.A.; Rezali, K.A.M.; Ng, Y.G. The effect of posture and vibration magnitude on the vertical vibration transmissibility of tractor suspension system. Int. J. Ind. Ergonom. 2020, 80, 103014. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pccht, M. Battery lifetime prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, D.; Zhang, H.; Zhang, W.; Chen, J. Application of relative entropy and gradient boosting decision tree to fault prognosis in electronic circuits. Symmetry 2018, 10, 495. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Stroe, D.; Huang, X.; Peng, J.; Liu, T.; Teodorescu, R. An automatic weak learner formulation for lithium-ion battery state of health estimation. IEEE Trans. Ind. Electron. 2022, 3, 2659–2668. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Lu, S.; Wang, J.; Zhang, X. Remaining useful life prediction of lithium-ion batteries using support vector regression optimized by artificial bee colony. IEEE Trans. Veh. Technol. 2019, 10, 9543–9553. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Lithium-ion battery remaining useful life prediction with Box-Cox transformation and monte carlo simulation. IEEE Trans. Ind. Electron. 2018, 2, 1585–1597. [Google Scholar] [CrossRef]
- Li, W.; Jiao, Z.; Du, L.; Fan, W.; Zhu, Y. An indirect RUL prognosis for lithium-ion battery under vibration stress using Elman neural network. Int. J. Hydrogen Energy 2019, 44, 12270–12276. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Xu, F.; Huang, Z.; Tsui, K.L. Lifespan prediction of lithium-ion batteries based on various extracted features and gradient boosting regression tree model. J. Power Sources 2020, 476, 228654. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y. Data-driven online health estimation of Li-ion batteries using a novel energy-based health indicator. IEEE Trans. Energy Convers. 2020, 35, 1715–1718. [Google Scholar] [CrossRef]
- Xiao, Q.; Jiao, Z.; Mu, Y.; Lu, W.; Jia, H. LightGBM based remaining useful life prediction of electric vehicle lithium-ion battery under driving conditions. Trans. China Electrotech. Soc. 2021, 36, 5176–5185. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Hossain Lipu, M.S.; Hussain, A.; Saad, M.H.M. Multi-channel profile based artificial neural network approach for remaining useful life prediction of electric vehicle lithium-ion batteries. Energies 2021, 14, 7521. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Wang, S.; Liu, Q.; Liu, H.; Zhou, H.; Tang, J. Multiple indicators-based health diagnostics and prognostics for energy storage technologies using fuzzy comprehensive evaluation and improved multivariate grey model. IEEE Trans. Power Electron. 2021, 36, 12309–12320. [Google Scholar] [CrossRef]
- Fernandez, C.P.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A comparison between electrochemical impedance spectroscopy and incremental capacity-differential voltage as Li-ion diagnostic techniques to identify and quantify the effects of degradation modes within battery management systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Qin, T.; Zeng, S.; Guo, J.; Skaf, Z. State of health estimation of Li-ion batteries with regeneration phenomena: A similar rest time-based prognostic framework. Symmetry 2017, 9, 4. [Google Scholar] [CrossRef]
- Jin, S.; Sui, X.; Huang, X.; Wang, S.; Teodorescu, R.; Stroe, D.-I. Overview of machine learning methods for lithium-ion battery remaining useful lifetime prediction. Electronics 2021, 10, 3126. [Google Scholar] [CrossRef]
- Chen, J.; Ren, D.; Hsu, H.; Wang, L.; He, X.; Zhang, C.; Feng, X.; Ouyang, M. Investigating the thermal runaway features of lithium-ion batteries using a thermal resistance network model. Appl. Energy 2021, 295, 117038. [Google Scholar] [CrossRef]
- Berg, P.; Spielbaauer, M.; Tillinger, M.; Merkel, M.; Jossen, A. Durability of lithium-ion 18650 cells under random vibration load with respect to the inner cell design. J. Energy Storage 2020, 31, 101499. [Google Scholar] [CrossRef]
- Braganca, H.; Colonna, J.G.; Oliveira, H.A.B.F.; Souto, E. How validation methodology influences human activity recognition mobile systems. Sensors 2022, 22, 2360. [Google Scholar] [CrossRef] [PubMed]
- Bhavsar, K.; Vakharia, V.; Chauddhari, R.; Vora, J.; Pimenov, D.Y.; Giasin, K. A comparative study to predict bearing degradation using discrete wavelet transform (DWT), tabular generative adversarial networks (TGAN) and machine learning models. Machines 2022, 10, 176. [Google Scholar] [CrossRef]




| Specifications | Parameters |
|---|---|
| Positive electrode | LiNi0.5Co0.2Mn0.3O2 |
| Negative electrode | Graphite |
| Nominal capacity | 2.4 Ah |
| Lower/upper cutoff voltage | 3.0 V/4.2 V |
| Parameters | Value |
|---|---|
| Acceleration effective value | 0.238031 g |
| Speed effective value | 8.684691 cm/s |
| Displacement effective value | 4.253971 mm |
| Acceleration peak value | 0.714093 g |
| Speed peak value | 26.0541 cm/s |
| Displacement peak value | 25.5238 mm |
| Parameters | Value |
|---|---|
| The proposed method | ‘bagging_fraction’: 0.56, ‘num_threads’: 2 |
| XGBoost | ‘feature_fraction’: 0.112, ‘max_depth’: 18, |
| GBDT | ‘lambda_l1′: 0.0001, ‘lambda_l2′: 0.0511 |
| RF | ‘learning_rate’: 0.0511, ‘num_leaves’: 46 |
| SVR | ‘min_data_in_leaf’: 34, ‘num_trees’: 588 |
| 1D-CINN | ‘min_sum_hessian_in_leaf’: 0.0511 |
| The proposed method | ‘alpha’: 0.0512, ‘learning_rate’: 0.0510 |
| XGBoost | ‘min_child_weight’: 4, ‘n_estimators’: 550 |
| GBDT | ‘max_depth’: 20, ‘subsample’: 0.59 |
| RF | ‘num_threads’: 2, ‘gamma’: 0.0, ‘lambda’: 0.0511 |
| SVR | ‘alpha’: 0.9, ‘min_samples_leaf’: 57 |
| 1D-CINN | (16,1) Convolution layer = 2, (64,1) Convolution layer = 2, activative function = ‘ReLu’, pooling layer = 1 |
| Model | Prediction Time (Second) | Prediction Accuracy (%) |
|---|---|---|
| GBDT | 4.324 | 98.007 |
| 1D-CNN | 47.381 | 98.692 |
| SVR | 80.333 | 98.490 |
| RF | 852.075 | 98.524 |
| XGBoost | 24.912 | 98.881 |
| Proposed framework | 15.728 | 98.922 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Xiao, Q.; Jin, Y.; Mu, Y.; Meng, J.; Zhang, T.; Jia, H.; Teodorescu, R. Improved LightGBM-Based Framework for Electric Vehicle Lithium-Ion Battery Remaining Useful Life Prediction Using Multi Health Indicators. Symmetry 2022, 14, 1584. https://doi.org/10.3390/sym14081584
Liu H, Xiao Q, Jin Y, Mu Y, Meng J, Zhang T, Jia H, Teodorescu R. Improved LightGBM-Based Framework for Electric Vehicle Lithium-Ion Battery Remaining Useful Life Prediction Using Multi Health Indicators. Symmetry. 2022; 14(8):1584. https://doi.org/10.3390/sym14081584
Chicago/Turabian StyleLiu, Huiqiao, Qian Xiao, Yu Jin, Yunfei Mu, Jinhao Meng, Tianyu Zhang, Hongjie Jia, and Remus Teodorescu. 2022. "Improved LightGBM-Based Framework for Electric Vehicle Lithium-Ion Battery Remaining Useful Life Prediction Using Multi Health Indicators" Symmetry 14, no. 8: 1584. https://doi.org/10.3390/sym14081584






