Dynamic Response Analysis of an Offshore Converter Platform with Valve Towers under Seismic Excitation
Abstract
:1. Introduction
2. Materials and Methods
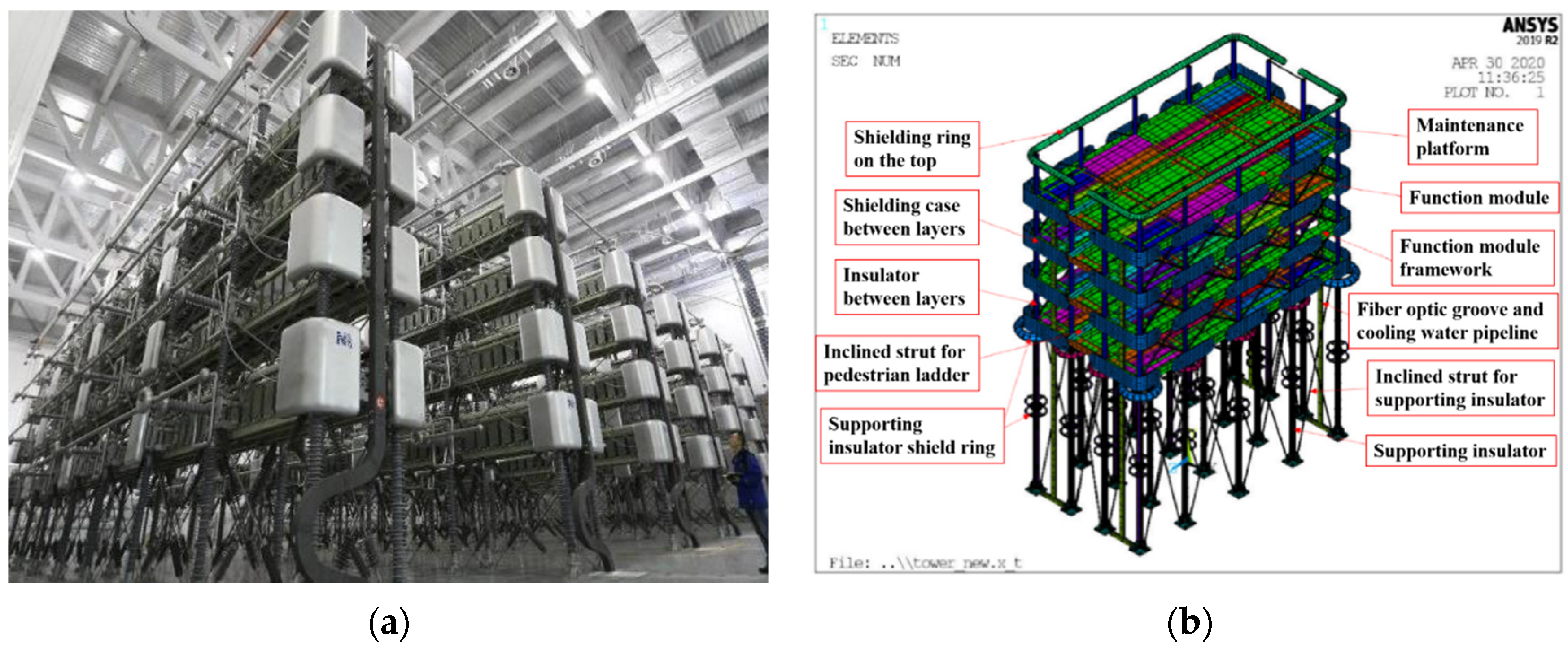
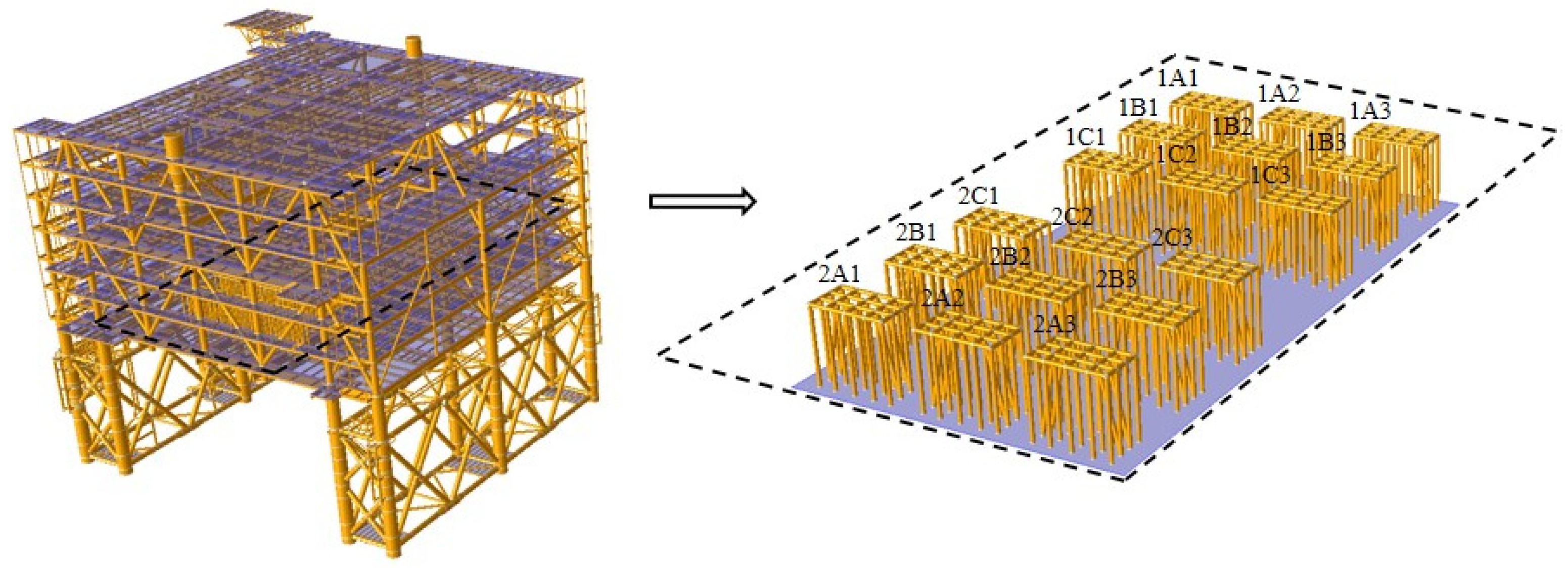
2.1. Numerical Model
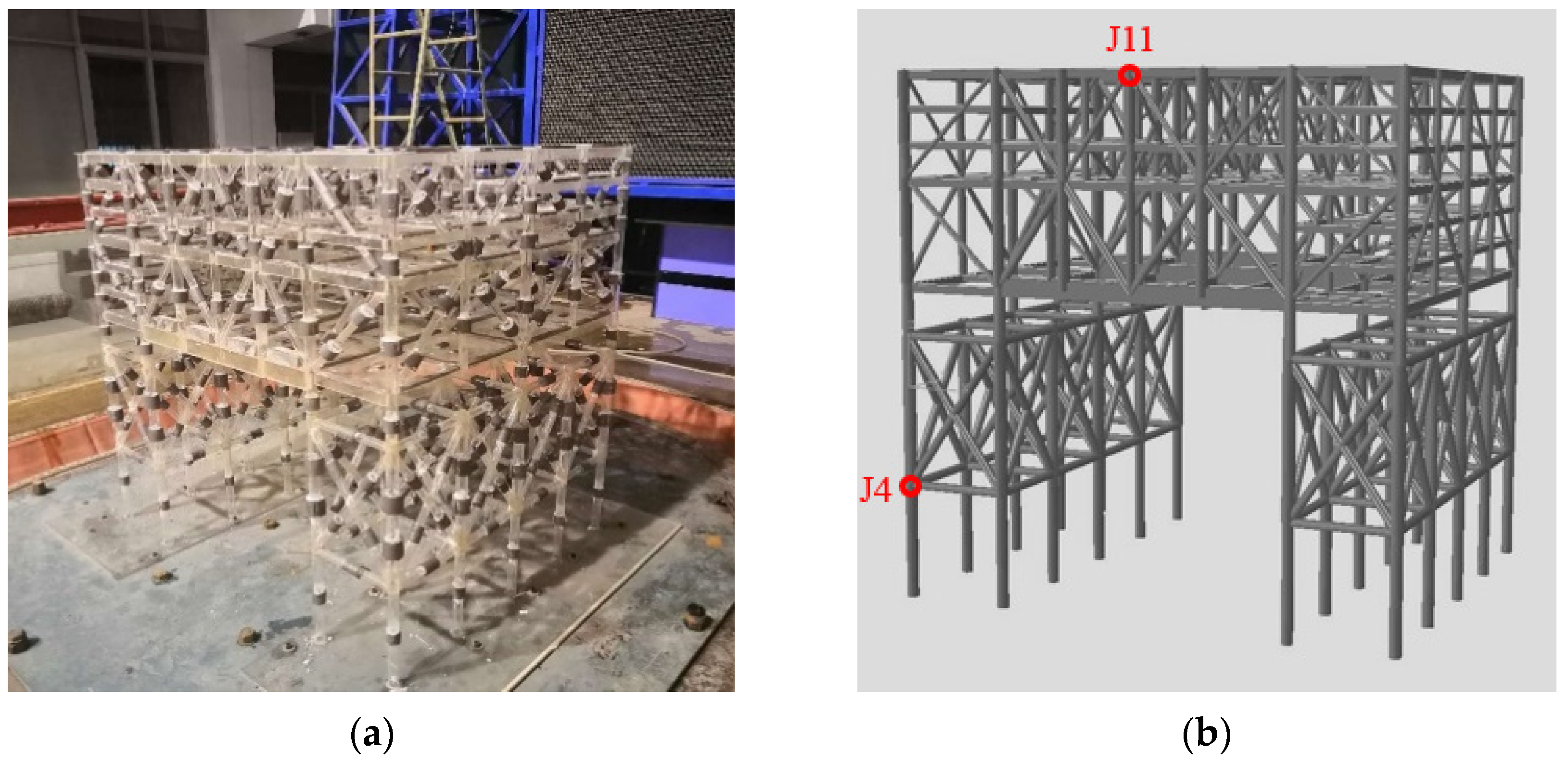
2.2. Experimental Validation
2.3. Evaluation of Valve Tower Effect
3. Results
3.1. Model and Modality
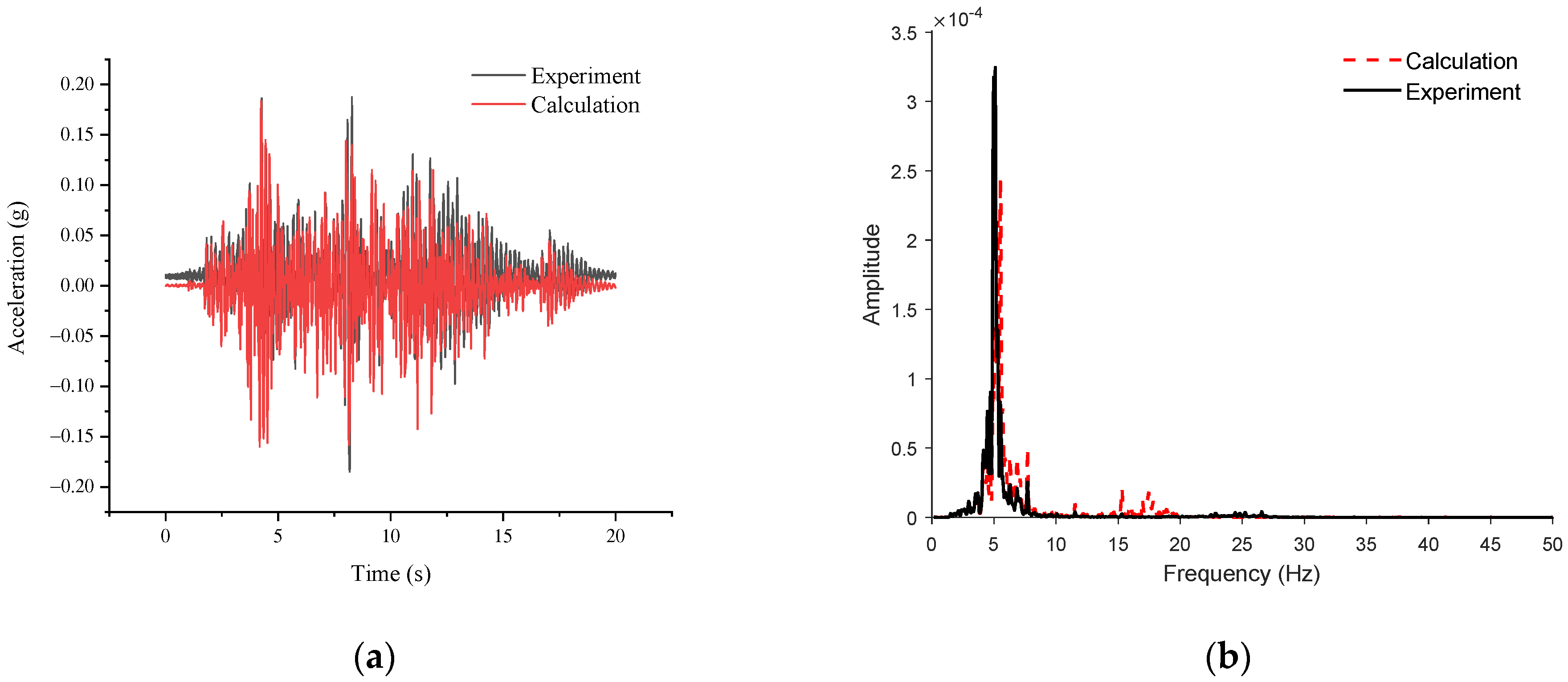
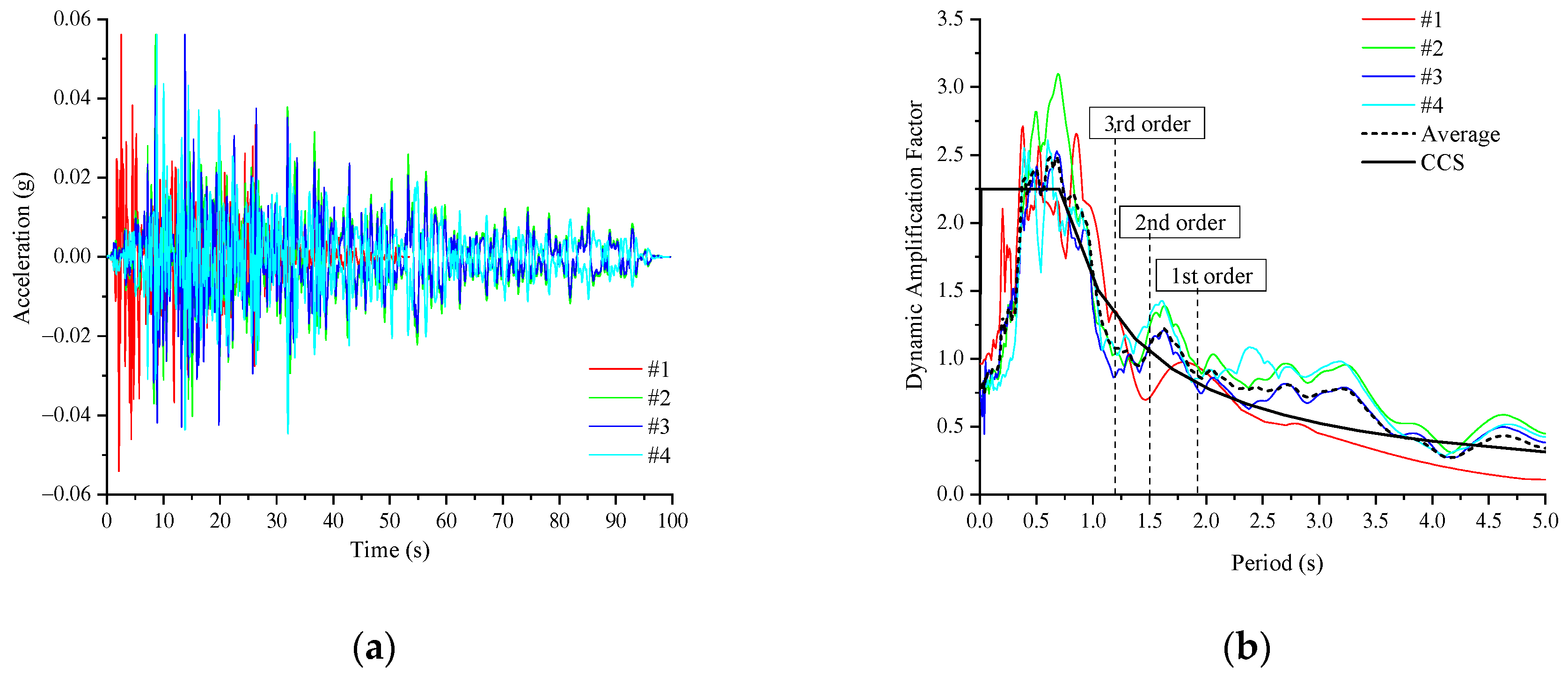
3.2. Inputs for Time-History and Response
4. Discussion
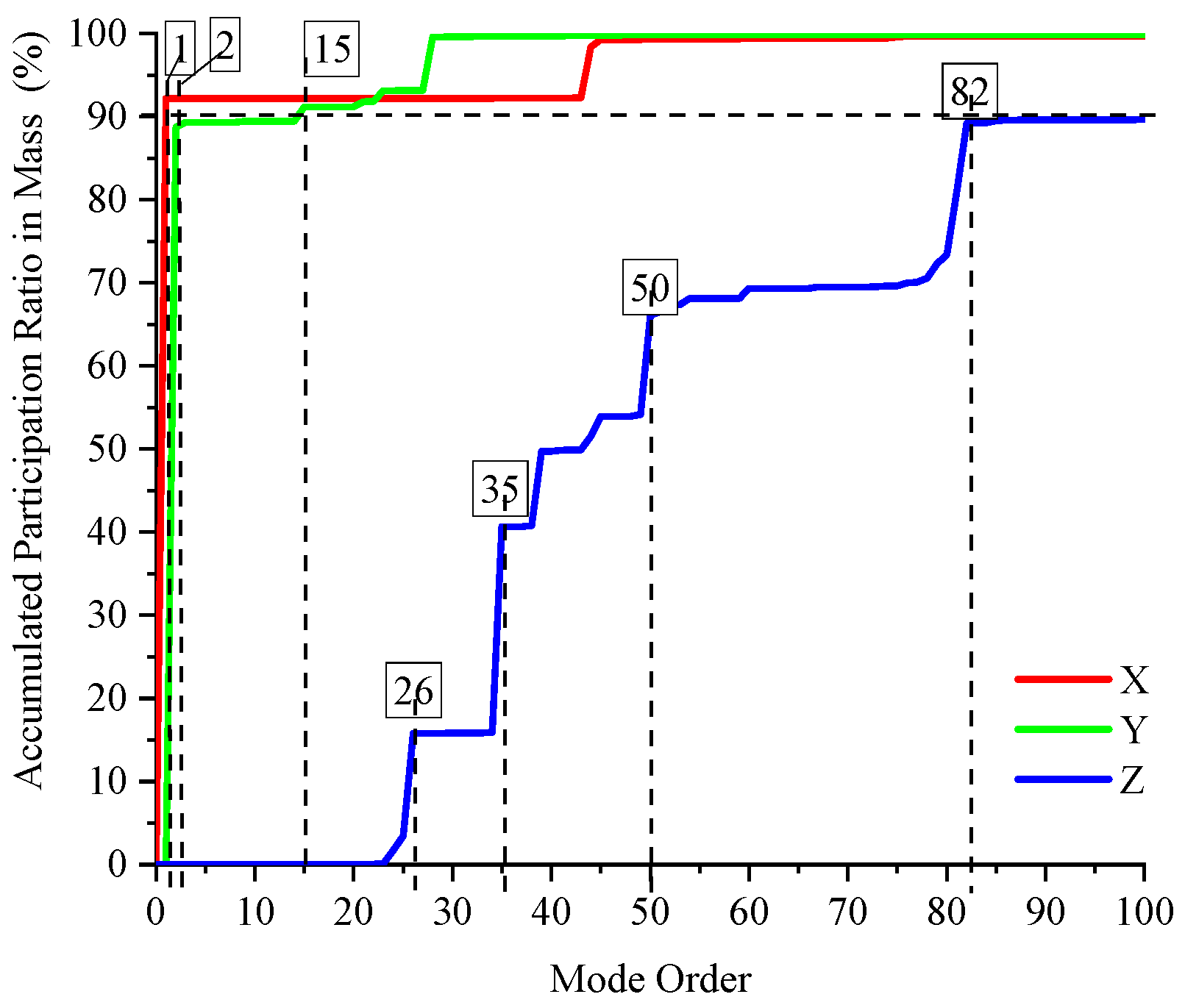
4.1. Mode Truncation Analysis
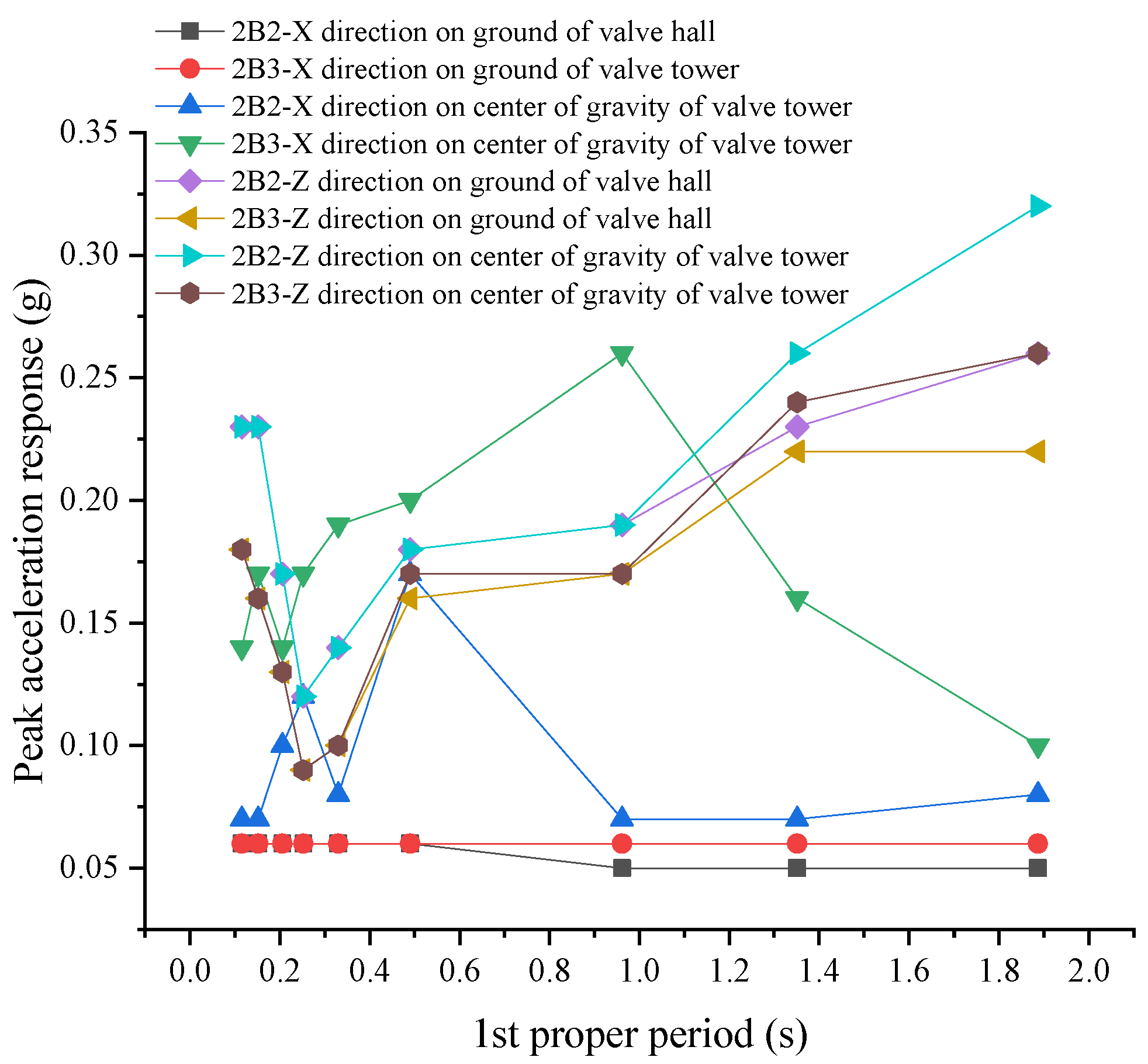
4.2. Stiffness of the Valve Tower
4.3. Foundation Dimension
4.4. Summary and Optimization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Soares-Ramos, E.P.P.; De Oliveira-Assis, L.; Sarrias-Mena, R.; Fernández-Ramírez, L.M. Current status and future trends of offshore wind power in Europe. Energy 2020, 202, 117787. [Google Scholar] [CrossRef]
- Mitra, P.; Zhang, L.-D.; Harnefors, L. Offshore wind integration to a weak grid by VSC-HVDC links using power-synchronization control: A case study. IEEE Trans. Power Deliv. 2014, 29, 453–461. [Google Scholar] [CrossRef]
- Rehana, R.; Nand, K.; Mohanty, S.R. Off-shore wind farm development: Present status and challenges. Renew. Sustain. Energy Rev. 2014, 29, 780–792. [Google Scholar]
- Kalair, A.; Abas, N.; Khan, N. Comparative study of HVAC and HVDC transmission systems. Renew. Sustain. Energy Rev. 2016, 59, 1653–1675. [Google Scholar] [CrossRef]
- Ruddy, J.; Meere, R.; O’Donnell, T. Low frequency AC transmission for offshore wind power: A review. Renew. Sustain. Energy Rev. 2016, 56, 75–86. [Google Scholar] [CrossRef]
- Mahfouz, M.M.A.; El-Sayed, M.A.H. One-end protection algorithm for offshore wind farm HVDC transmission based on travelling waves and cross-alienation. Electr. Power Syst. Res. 2020, 185, 106355. [Google Scholar] [CrossRef]
- Xie, L.-J.; Yao, L.-Z.; Fan, C.; Li, Y.; Liang, S. Coordinate control strategy for stability operation of offshore wind farm integrated with diode-rectifier HVDC. Glob. Energy Interconnect. 2020, 3, 205–216. [Google Scholar] [CrossRef]
- Gou, R. Research on 1100 kV/5500 A ultra-high voltage thyristor valve key technology and its application. IEEE Trans. Power Deliv. 2019, 34, 1052410533. [Google Scholar] [CrossRef]
- Zhu, R.; Lin, N.; Dinavahi, V.; Liang, G. An accurate and fast method for con-ducted EMI modeling and simulation of MMC-Based HVdc converter station. IEEE Trans. Power Deliv. 2020, 35, 4689–4702. [Google Scholar] [CrossRef]
- Liu, X.; Chen, M.; Liang, C.-J.; Tang, H.; Zhang, Q.-G. Investigation on distribution of electro-thermal coupled field and improved design of +1100 kV converter valve-side bushing. IET Sci. Meas. Technol. 2020, 14, 188–197. [Google Scholar] [CrossRef]
- Yang, Z.-Y.; Xie, Q.; Zhou, Y.; Mosalam, K.M. Seismic performance and restraint system of suspended 800 kV thyristor valve. Eng. Struct. 2018, 169, 179–187. [Google Scholar] [CrossRef]
- He, C.; Xie, Q.; Yang, Z.-Y.; Xue, S.-T. Seismic performance evaluation and improvement of ultra-high voltage wall bushing-valve hall system. J. Constr. Steel Res. 2019, 154, 123–133. [Google Scholar] [CrossRef]
- Bang, S.; Kim, H.-S.; Koo, J.-H.; Lee, B.-W. Consideration of the insulation design method on a ±200 kV converter valve unit in an HVDC converter hall. Energies 2021, 14, 2296. [Google Scholar] [CrossRef]
- Liu, F.-S.; Li, H.-J. A two-step mode shape expansion method for offshore jacket structures with physical meaningful modelling errors. Ocean Eng. 2013, 63, 26–34. [Google Scholar] [CrossRef]
- Liu, F.-S.; Li, H.-J.; Li, W.; Wang, B. Experiment study of improved modal strain energy method for damage localization in jacket-type offshore wind turbines. Renew. Energy 2014, 72, 174–181. [Google Scholar] [CrossRef]
- Chen, J.-L.; Zhan, G.-Y.; Zhao, Y. Application of spherical tuned liquid damper in vibration control of wind turbine due to earthquake excitations. Struct. Des. Tall Spec. Build. 2016, 25, 431–443. [Google Scholar] [CrossRef]
- Chen, J.-L.; Li, J.-W.; Wang, D.-W.; Feng, Y.-Q. Seismic response analysis of steel-concrete hybrid wind turbine tower. J. Vib. Control 2021, 1–14. [Google Scholar] [CrossRef]
- Ekstrom, A.; Eklund, L. HVDC thyristor valve development. IEEE Trans. Power Electron. 1987, PE-2, 177–185. [Google Scholar] [CrossRef]
- Larder, R.A.; Gallagher, R.P.; Nilsson, B. Innovative seismic design aspects of the intermountain power project converter stations. IEEE Trans. Power Deliv. 1989, 4, 1708–1714. [Google Scholar] [CrossRef]
- Enblom, R.; Coad, J.N.O.; Berggren, S. Design of HVDC converter station equipment subject to severe seismic performance requirements. IEEE Trans. Power Deliv. 1993, 8, 1766–1772. [Google Scholar] [CrossRef]
- Lan, D.-N.; Li, J.; Xu, Q.; Chen, J.-Y. Influence of the offshore electrical platform on the dynamic responses of converter valve under sea waves and earthquakes. Ships Offshore Struct. 2021, 16, 1–14. [Google Scholar] [CrossRef]
- Tondl, A.; Nabergoj, R. Dynamic absorbers for an externally excited pendulum. J. Sound Vib. 2000, 234, 611–624. [Google Scholar] [CrossRef]
- La, V.D. Semi-active on-off damping control of a dynamic vibration absorber using Coriolis force. J. Sound Vib. 2012, 331, 3429–3436. [Google Scholar] [CrossRef]
- Sun, Z.-Z.; Bi, C.-W.; Zhao, S.-X.; Dong, G.-H.; Yu, H.-F. Experimental analysis on dynamic responses of an electrical platform for an offshore wind farm under earthquake load. J. Mar. Sci. Eng. 2019, 7, 279. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.-X.; Bi, C.-W.; Sun, Z.-Z. Engineering analysis of the dynamic characteristics of an electrical jacket platform of an offshore wind farm under seismic loads. Appl. Ocean Res. 2021, 112, 102692. [Google Scholar] [CrossRef]
- Sun, Z.-Z.; Yu, Y.; Wang, H.-K.; Huang, S.-S.; Chen, J.-F. Dynamic response analysis of offshore converter station based on Vector Form Intrinsic Finite Element (VFIFE) method. J. Mar. Sci. Eng. 2022, 10, 749. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Bi, C.-W.; Wu, G.-Y.; Zhao, S.-X.; Dong, G.-H. Laboratory experimental investigation on the hydrodynamic responses of an extra-large electrical platform in wave and storm conditions. Water 2019, 11, 2042. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, X.; Li, W.; Liu, F.; Hancock, C. Time-frequency extraction model based on variational mode decomposition and Hilbert-Huang transform for offshore oil platforms using MIMU data. Symmetry 2021, 13, 1443. [Google Scholar] [CrossRef]
- DNVGL-ST-0145; Offshore Substations. DNV GL AS: Norge, Oslo, 2020.
- ISO 19901-3; Petroleum and Natural Gas Industries-Specific Requirements for Offshore Structures-Part 3: Topsides Structure. Interantional Organisation for Standardisation: Geneva, Switzerland, 2014.
- Hansteen, O.E.; Bell, K. On the accuracy of mode superposition analysis in structural dynamics. Earthq. Eng. Struct. Dyn. 1979, 7, 405–411. [Google Scholar] [CrossRef]
- Günay, S.; Mosalam, K.M. Seismic performance evaluation of high-voltage disconnect switches using real-time hybrid simulation: II. Parametric study. Earthq. Eng. Struct. Dyn. 2014, 43, 1223–1237. [Google Scholar] [CrossRef]
- Zhang, B.L.; Han, Q.L.; Zhang, X.M. Recent advances in vibration control of offshore platforms. Nonlinear Dyn. 2017, 89, 755–771. [Google Scholar] [CrossRef]
- Cao, Y.; He, E.; Furrer, M. Whipping effect of the seismic response of unbraced tied arch bridges. In Proceedings of the IABSE Conference–Structural Engineering: Providing Solutions to Global Challenges, Geneva, Switzerland, 23–25 September 2015; IABSE Rep. 105. pp. 1679–1686. [Google Scholar]
- Yang, L.J.; Liu, D.W.; Guo, Z.L.; Li, J.; Dai, B.H. Engineering mechanics in whipping effect of high-rise building. Appl. Mech. Mater. 2014, 540, 173–176. [Google Scholar]






| Measuring Point | Earthquake Ground Motion | Acceleration Response (g) | ||
|---|---|---|---|---|
| X | Y | Z | ||
| Center of foundation of valve tower 2B2 | #1 | 0.05 | 0.05 | 0.19 |
| #2 | 0.05 | 0.07 | 0.16 | |
| #3 | 0.05 | 0.06 | 0.15 | |
| #4 | 0.05 | 0.07 | 0.16 | |
| Average | 0.05 | 0.06 | 0.17 | |
| Center of gravity of valve tower 2B3 | #1 | 0.26 | 0.10 | 0.17 |
| #2 | 0.21 | 0.12 | 0.16 | |
| #3 | 0.22 | 0.11 | 0.15 | |
| #4 | 0.17 | 0.13 | 0.16 | |
| Average | 0.22 | 0.12 | 0.16 | |
| Node No. | N | |||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 21 | 26 | 35 | 50 | 82 | 100 | ||
| X-direction | F088 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| F108 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.06 | |
| V088 | 0.06 | 0.06 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | |
| V108 | 0.06 | 0.06 | 0.12 | 0.20 | 0.26 | 0.26 | 0.26 | |
| Z-direction | F088 | 0.02 | 0.02 | 0.06 | 0.12 | 0.18 | 0.19 | 0.19 |
| F108 | 0.02 | 0.02 | 0.04 | 0.09 | 0.16 | 0.17 | 0.17 | |
| V088 | 0.02 | 0.02 | 0.06 | 0.12 | 0.19 | 0.20 | 0.19 | |
| V108 | 0.02 | 0.02 | 0.04 | 0.09 | 0.17 | 0.17 | 0.17 | |
| Parameter | Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Modulus of elasticity | 0.25E | 0.50E | 1.0E | 4.0E | 9.0E | 16E | 25E | 50E | 100E | |
| First-order frequency (Hz) | 0.53 | 0.74 | 1.04 | 2.05 | 3.03 | 3.97 | 4.87 | 6.59 | 8.68 | |
| X-direction | F088 | 0.05 | 0.05 | 0.05 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 |
| F108 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | |
| V088 | 0.08 | 0.07 | 0.07 | 0.17 | 0.08 | 0.12 | 0.10 | 0.07 | 0.07 | |
| V108 | 0.10 | 0.16 | 0.26 | 0.20 | 0.19 | 0.17 | 0.14 | 0.17 | 0.14 | |
| Z-direction | F088 | 0.26 | 0.23 | 0.19 | 0.18 | 0.14 | 0.12 | 0.17 | 0.23 | 0.23 |
| F108 | 0.22 | 0.22 | 0.17 | 0.16 | 0.10 | 0.09 | 0.13 | 0.16 | 0.18 | |
| V088 | 0.32 | 0.26 | 0.19 | 0.18 | 0.14 | 0.12 | 0.17 | 0.23 | 0.23 | |
| V108 | 0.26 | 0.24 | 0.17 | 0.17 | 0.10 | 0.09 | 0.13 | 0.16 | 0.18 | |
| Parameter | Value | ||||||
|---|---|---|---|---|---|---|---|
| Dimension of the foundation steel | H120 × 40 | H150 × 50 | H180 × 60 | H220 × 80 | H250 × 90 | B300 × 100 | |
| X-direction | F088 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| F108 | 0.06 | 0.05 | 0.06 | 0.06 | 0.06 | 0.05 | |
| V088 | 0.07 | 0.08 | 0.08 | 0.07 | 0.07 | 0.09 | |
| V108 | 0.26 | 0.24 | 0.23 | 0.22 | 0.21 | 0.19 | |
| Z-direction | F088 | 0.19 | 0.20 | 0.21 | 0.21 | 0.21 | 0.20 |
| F108 | 0.17 | 0.17 | 0.18 | 0.18 | 0.18 | 0.17 | |
| V088 | 0.19 | 0.21 | 0.22 | 0.22 | 0.22 | 0.21 | |
| V108 | 0.17 | 0.18 | 0.19 | 0.19 | 0.19 | 0.18 | |
| Response/Sensitivity Factor | Truncated Mode N | Stiffness of the Valve Tower E | Dimension of the Foundation Steel D | ||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Trend | Sensitivity | Trend | Sensitivity | Trend | ||
| Foundation of the central valve tower | Horizontal | Weak | - | Weak | - | Weak | - |
| Vertical | Strong | Positively correlated | Strong | Trending to a minimum | Weak | - | |
| Foundation of the marginal valve tower | Horizontal | Weak | - | Weak | - | Weak | - |
| Vertical | Strong | Positively correlated | Strong | Trending to a minimum | Weak | - | |
| Center of gravity of the central valve tower | Horizontal | Weak | - | Weak | Trending to a maximum | Weak | - |
| Vertical | Strong | Positively correlated | Strong | Trending to a minimum | Weak | - | |
| Center of gravity of the marginal valve tower | Horizontal | Strong | Positively correlated | Strong | Trending to a maximum | Strong | Negatively correlated |
| Vertical | Strong | Positively correlated | Strong | Trending to a minimum | Weak | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zhao, S.; Bi, C.; Chen, Q.; Huang, S.; Chen, J. Dynamic Response Analysis of an Offshore Converter Platform with Valve Towers under Seismic Excitation. Symmetry 2022, 14, 1635. https://doi.org/10.3390/sym14081635
Sun Z, Zhao S, Bi C, Chen Q, Huang S, Chen J. Dynamic Response Analysis of an Offshore Converter Platform with Valve Towers under Seismic Excitation. Symmetry. 2022; 14(8):1635. https://doi.org/10.3390/sym14081635
Chicago/Turabian StyleSun, Zhenzhou, Shengxiao Zhao, Chunwei Bi, Qiupan Chen, Shanshan Huang, and Jiefeng Chen. 2022. "Dynamic Response Analysis of an Offshore Converter Platform with Valve Towers under Seismic Excitation" Symmetry 14, no. 8: 1635. https://doi.org/10.3390/sym14081635
APA StyleSun, Z., Zhao, S., Bi, C., Chen, Q., Huang, S., & Chen, J. (2022). Dynamic Response Analysis of an Offshore Converter Platform with Valve Towers under Seismic Excitation. Symmetry, 14(8), 1635. https://doi.org/10.3390/sym14081635





