The Dynamics of a Fractional-Order Mathematical Model of Cancer Tumor Disease
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. Models Description
2.2. Modelling Cancer Chemotherapy Effects Using the Caputo-Fractional Derivative
2.3. Modelling Cancer Tumor Based on the Cell’s Concentration
2.4. Method Description
- i.
- If 0 < ξ < 1 and then it is convergent;
- ii.
- If ξ > 1 and then it is divergent.
3. Numerical Simulation
3.1. Modelling Cancer Chemotherapy Effect Using the Caputo-Fractional Derivative
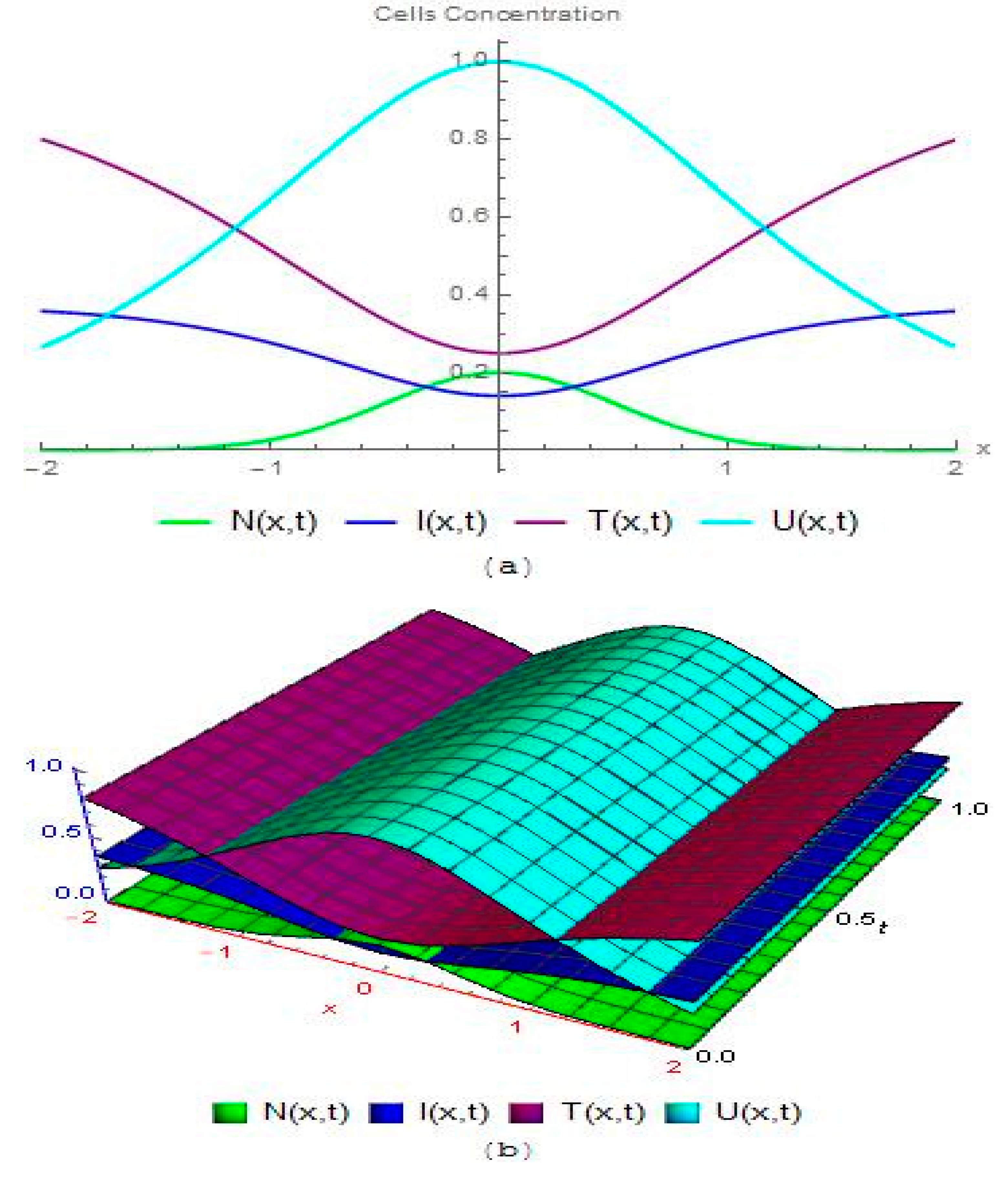
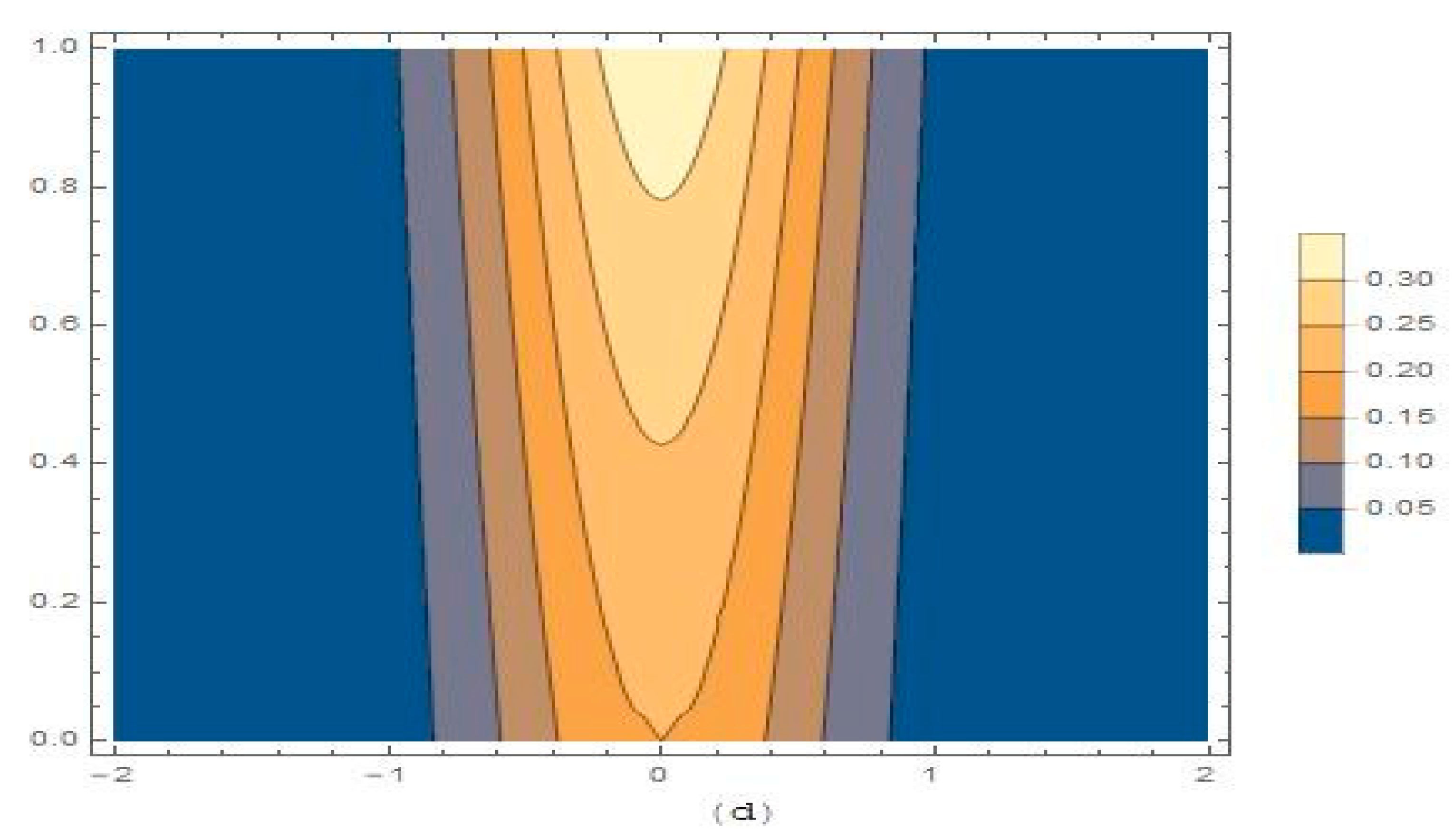
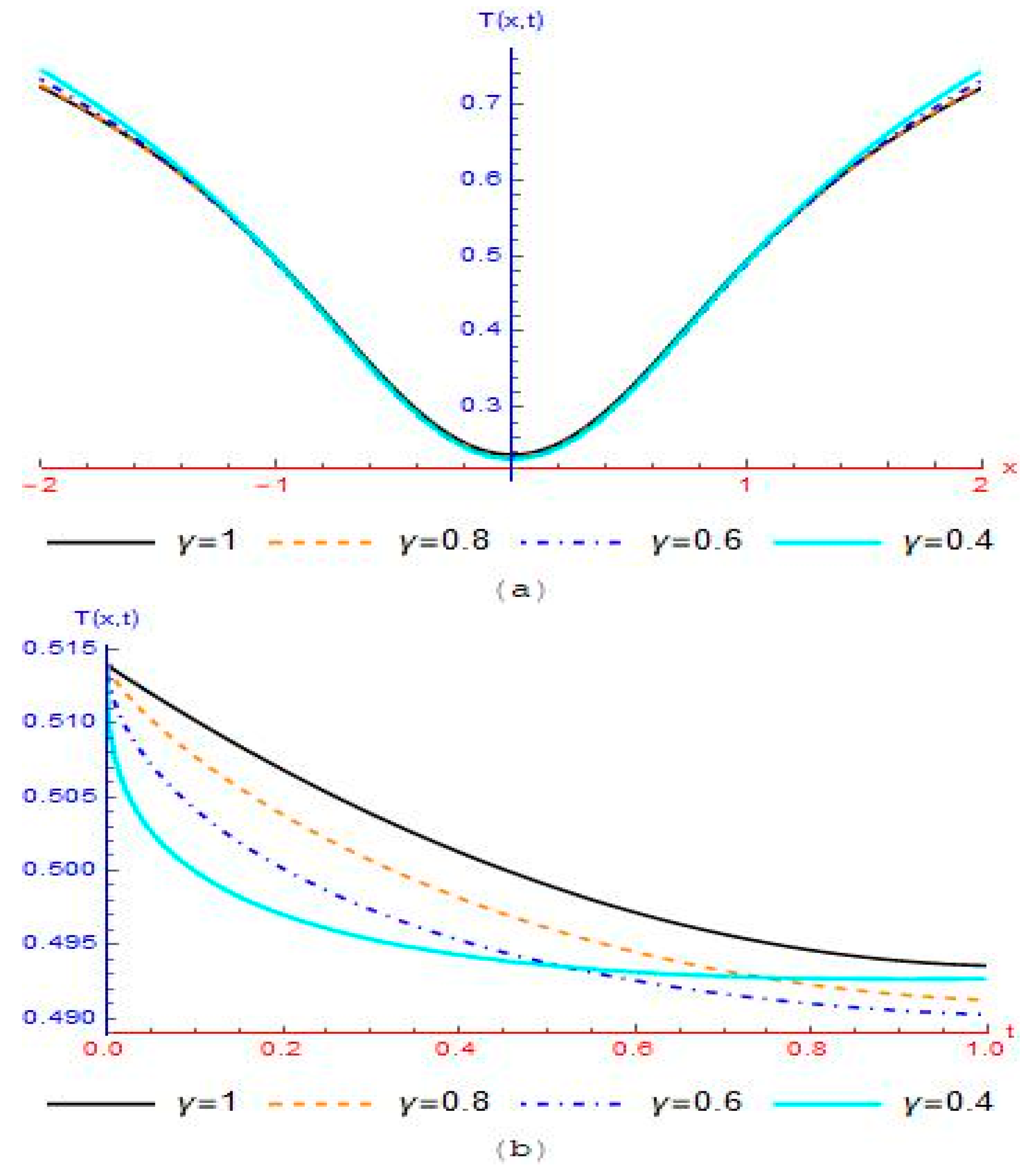
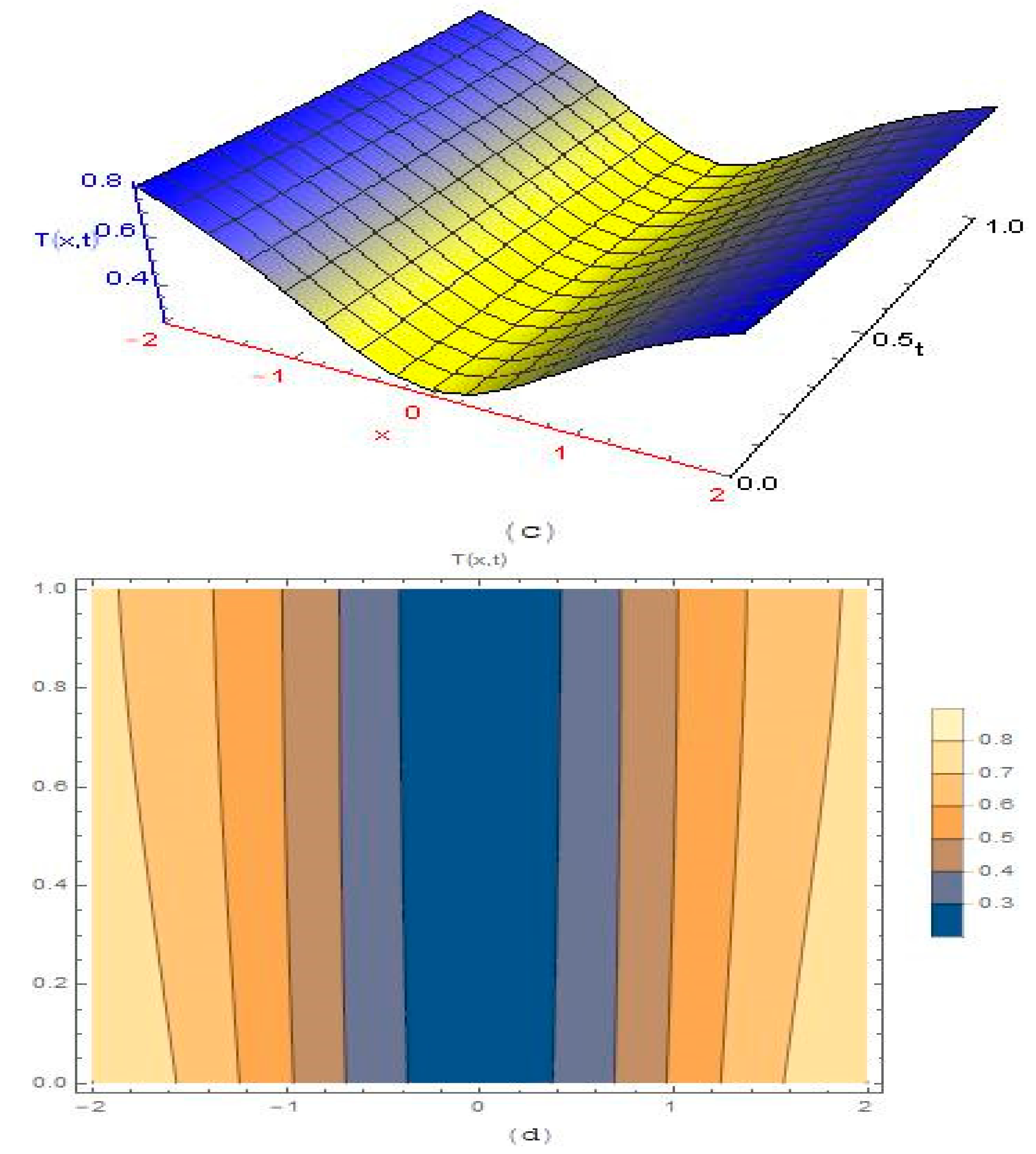
3.2. Modelling Cancer Tumor Based on Cells Concentration
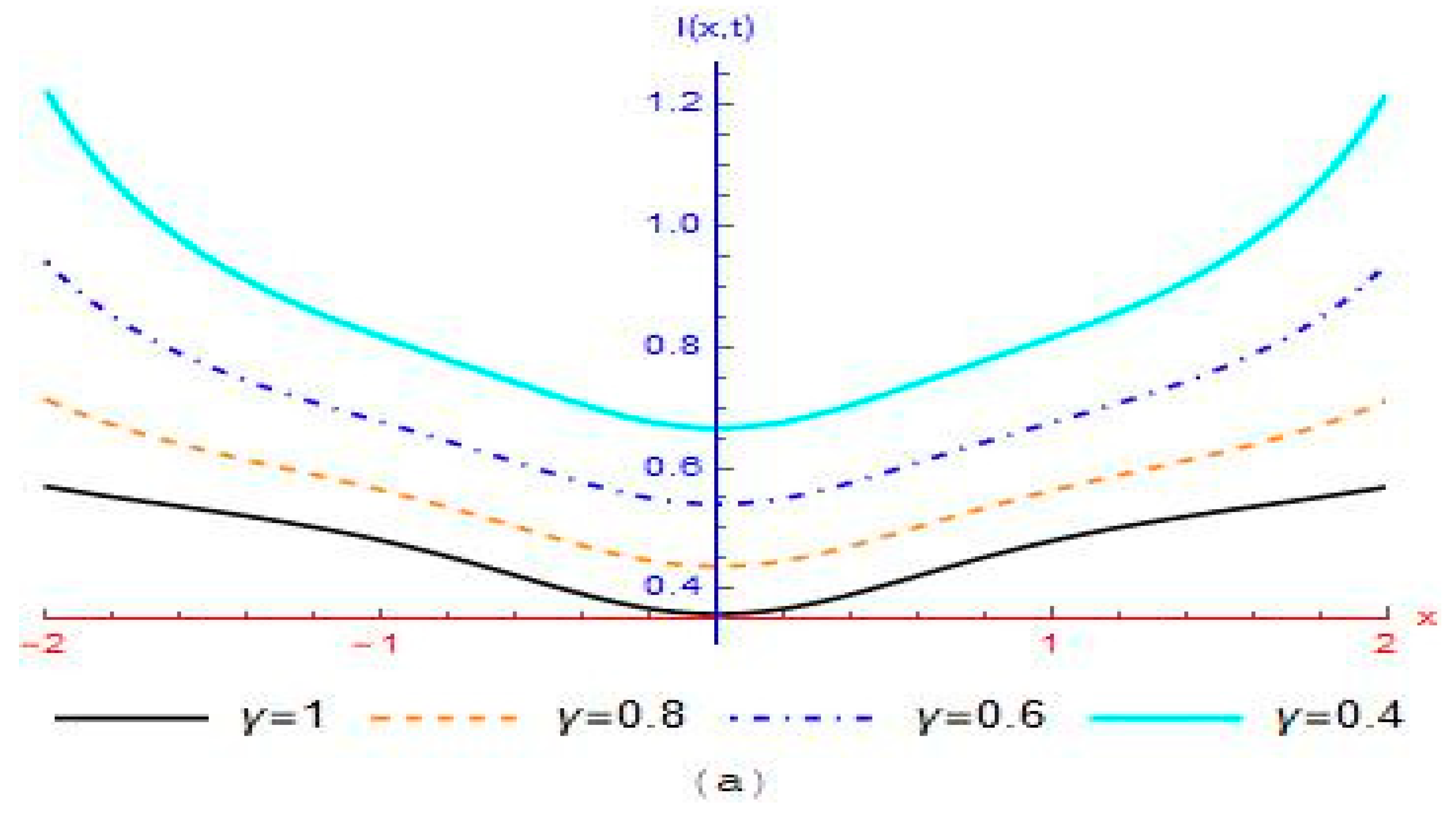
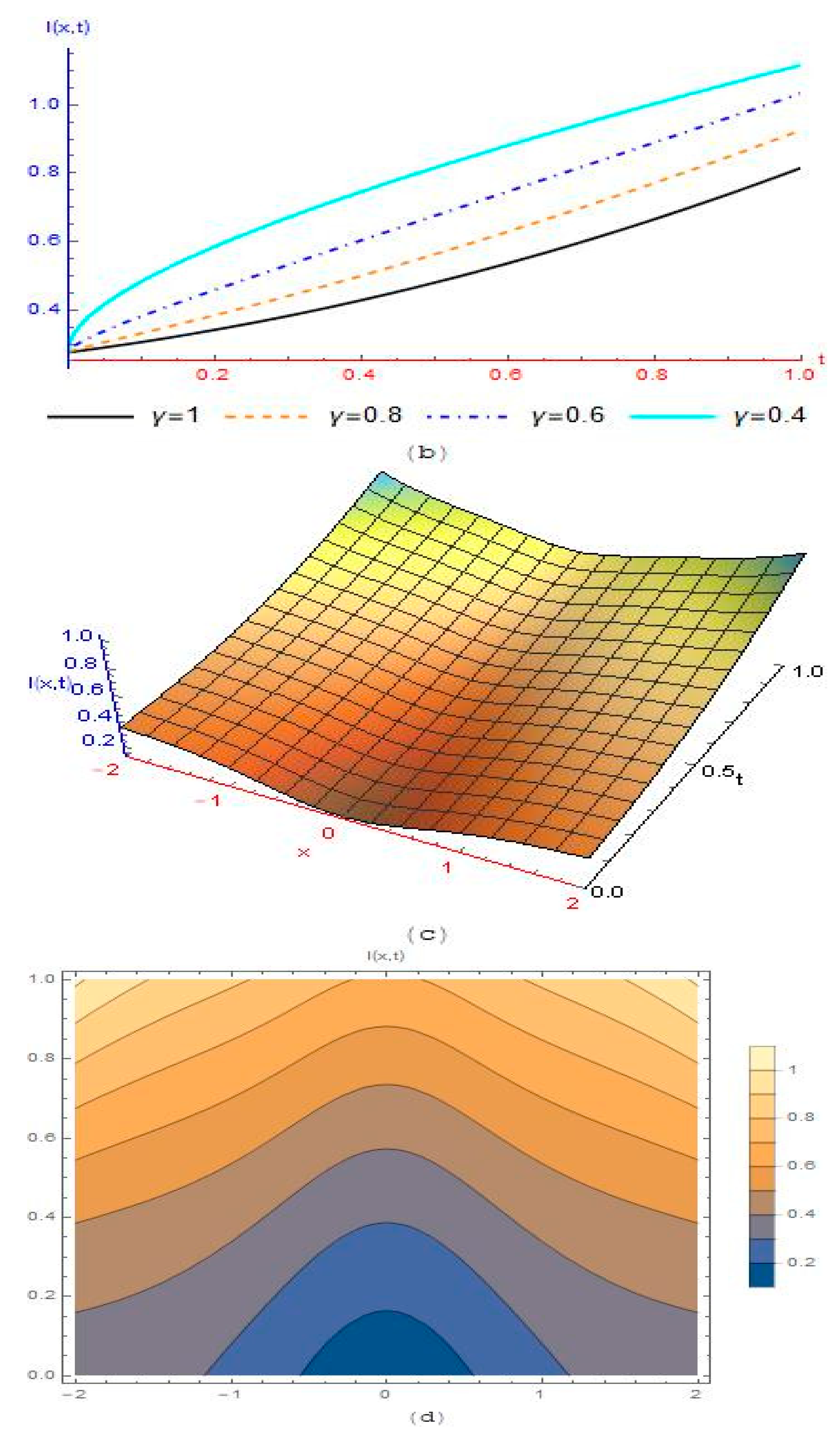
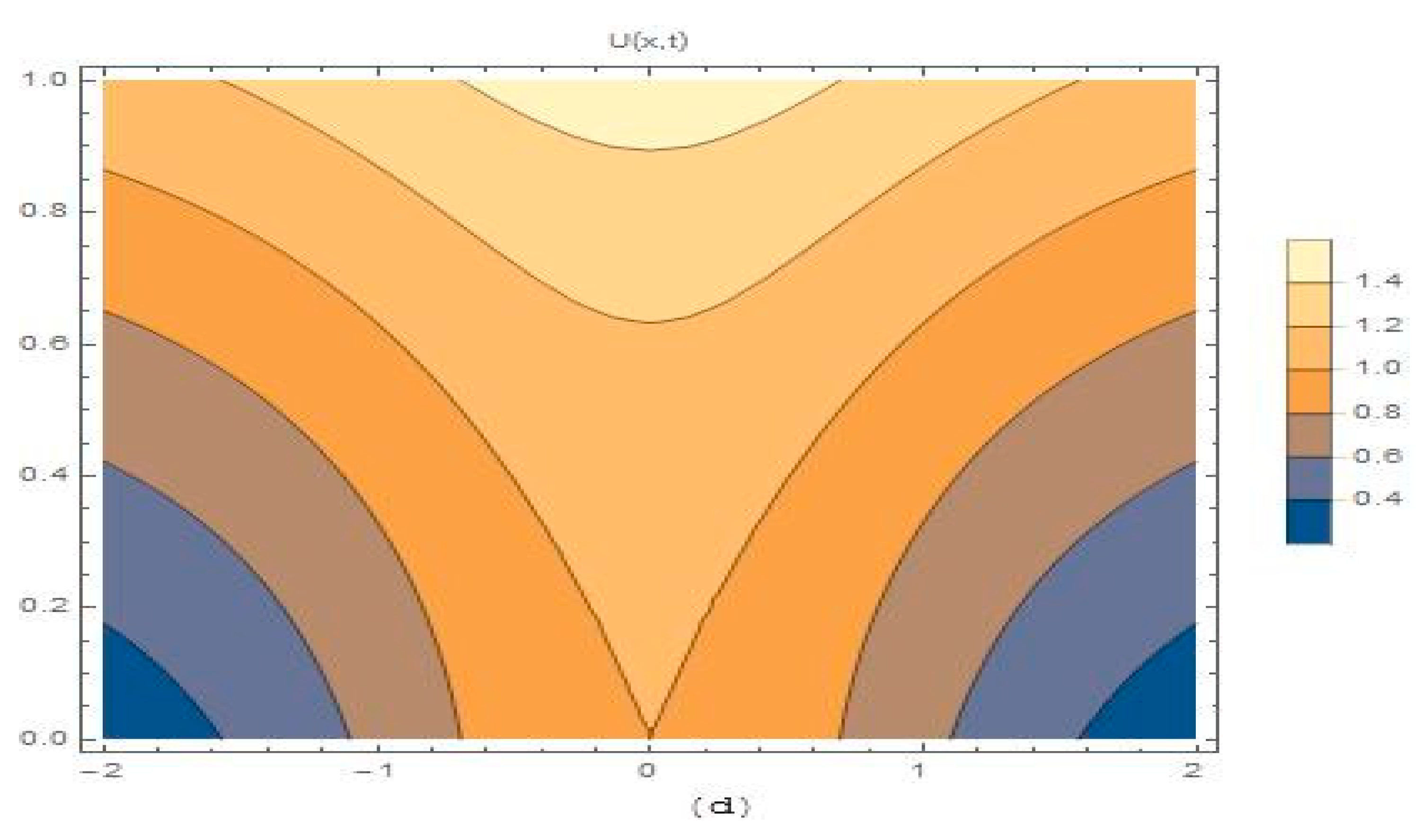
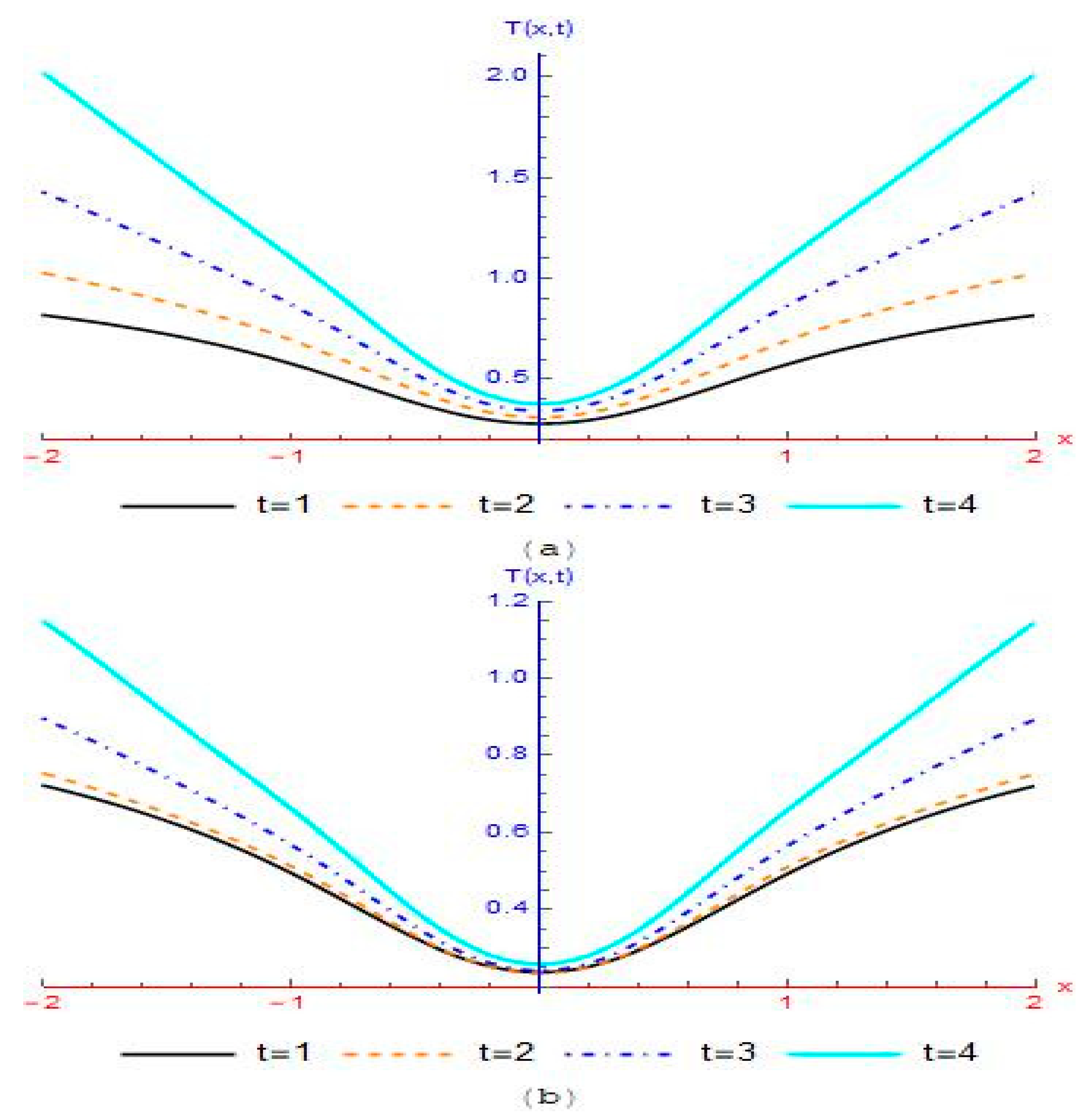
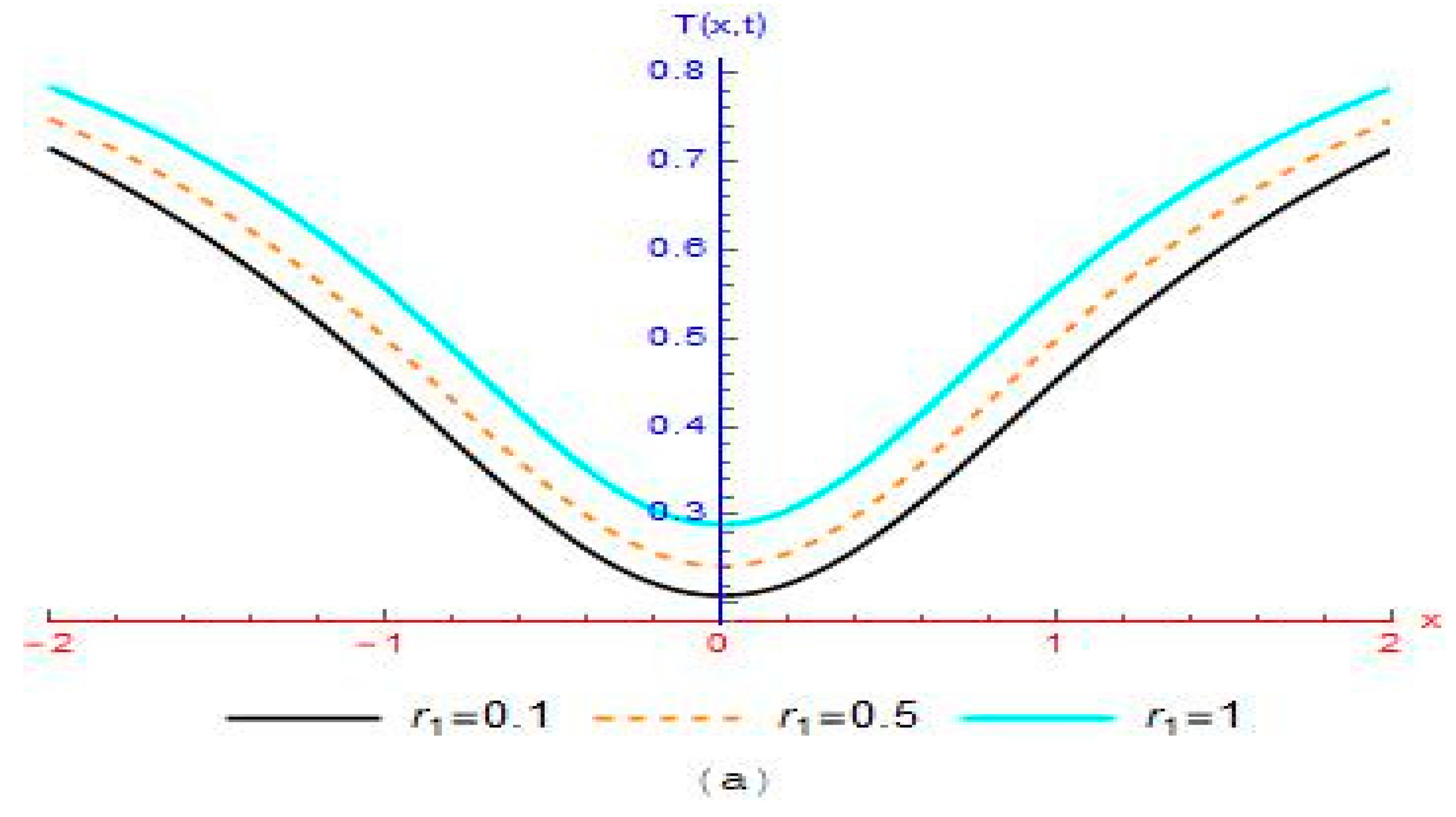
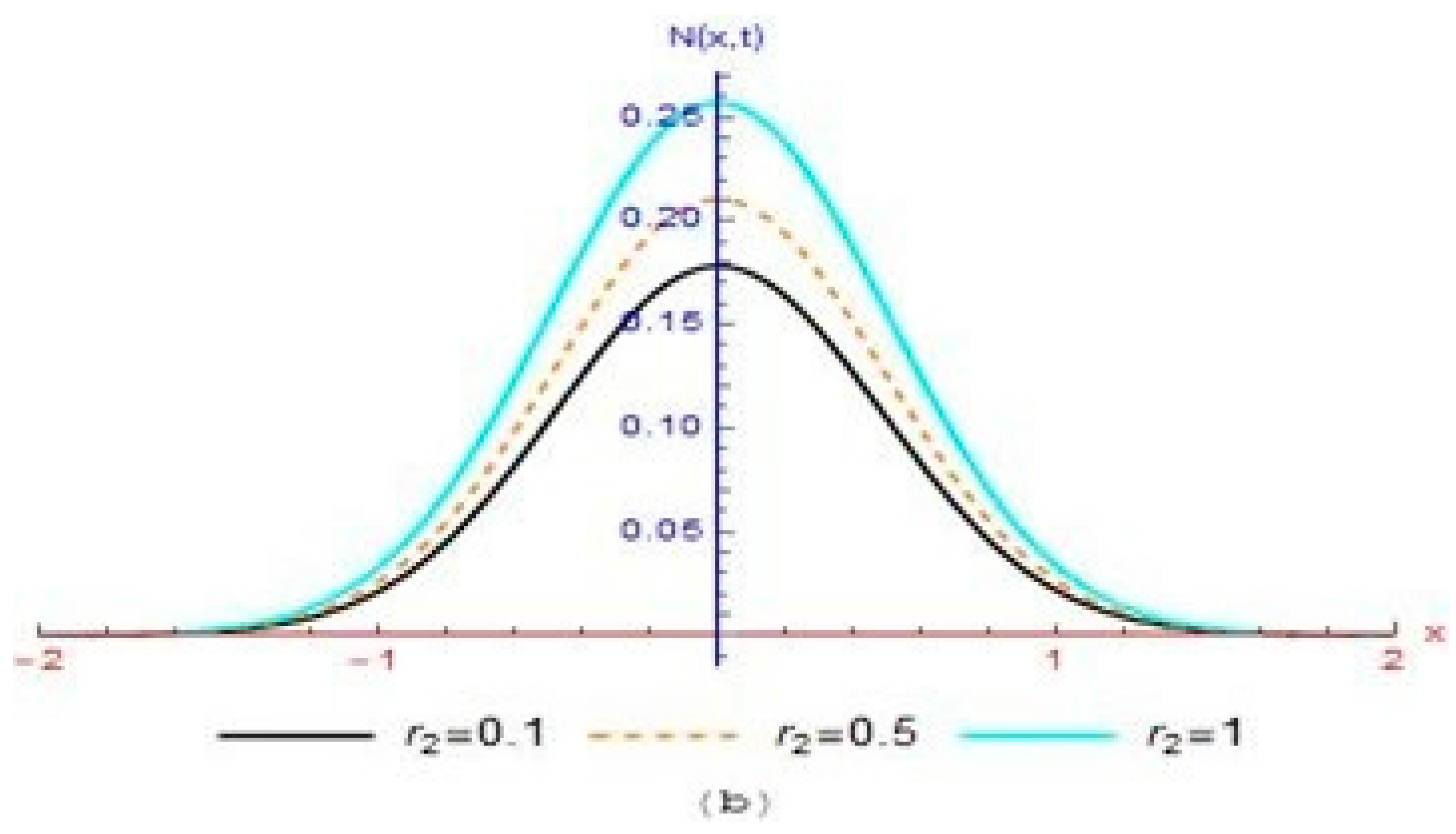
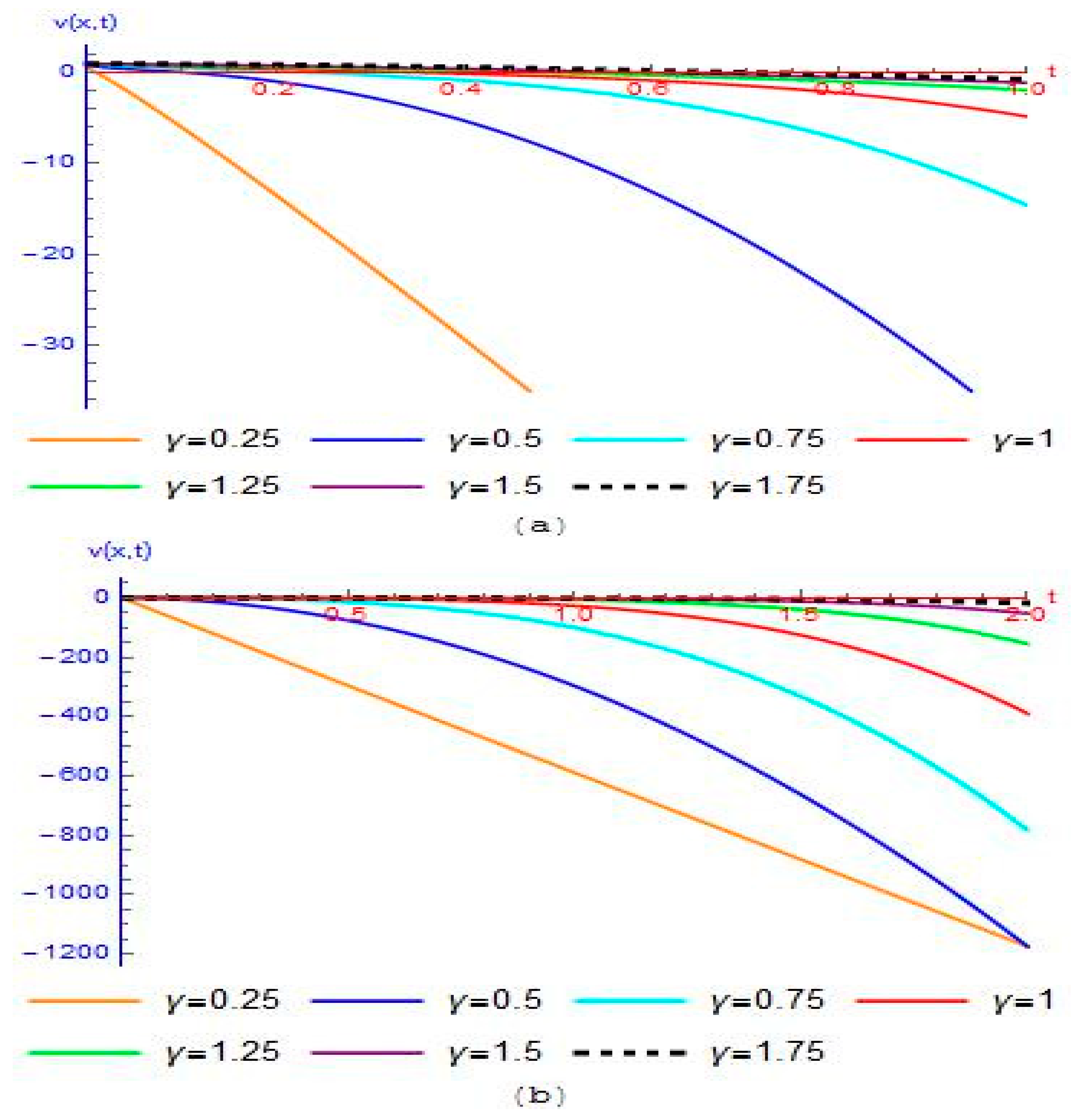
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ansarizadeh, F.; Singh, M.; Richards, D. Modelling of tumor cells regression in response to chemotherapeutic treatment. Appl. Math. Model. 2017, 48, 96–112. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus-a different approach to the analysis of viscoelastically damped structures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Ishteva, M.; Boyadjiev, L.; Scherer, R. On the Caputo operator of fractional calculus and C-Laguerre functions. Math. Sci. Res. J. 2005, 9, 161. [Google Scholar]
- Kuznetsov, V.A.; Knott, G.D. Modeling tumor regrowth and immunotherapy. Math. Comput. Model. 2001, 33, 1275–1287. [Google Scholar] [CrossRef]
- De Vladar, H.P.; González, J.A. Dynamic response of cancer under the influence of immunological activity and therapy. J. Theor. Biol. 2004, 227, 335–348. [Google Scholar] [CrossRef]
- D’Onofrio, A. Metamodeling tumor-immune system interaction, tumor evasion and immunotherapy. Math. Comput. Model. 2008, 47, 614–637. [Google Scholar] [CrossRef]
- Parish, C.R. Cancer immunotherapy: The past, the present and the future. Immunol. Cell Biol. 2003, 81, 106–113. [Google Scholar] [CrossRef]
- Attia, N.; Akgül, A.; Seba, D.; Nour, A. Reproducing kernel Hilbert space method for the numerical solutions of fractional cancer tumor models. Math. Methods Appl. Sci. 2020, 1–22. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013119. [Google Scholar] [CrossRef]
- Dokuyucu, M.A.; Celik, E.; Bulut, H.; Baskonus, H.M. Cancer treatment model with the Caputo-Fabrizio fractional derivative. Eur. Phys. J. Plus 2018, 133, 92. [Google Scholar] [CrossRef]
- Arfan, M.; Shah, K.; Ullah, A.; Shutaywi, M.; Kumam, P.; Shah, Z. On Fractional Order Model of Tumor Dynamics with Drug interventions under Nonlocal Fractional Derivative. Results Phys. 2021, 21, 103783. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, Y.; Kim, J. Mathematical model and its fast numerical method for the tumor growth. Math. Biosci. Eng. 2015, 12, 1173. [Google Scholar] [CrossRef] [PubMed]
- Kolev, M.; Zubik-Kowal, B. Numerical solutions for a model of tissue invasion and migration of tumour cells. Comput. Math. Methods Med. 2011, 2011, 452320. [Google Scholar] [CrossRef] [PubMed]
- Garrido, M.L.K.; Breitenbach, T.; Chudej, K.; Borzì, A. Modeling and numerical solution of a cancer therapy optimal control problem. Appl. Math. 2018, 9, 985–1004. [Google Scholar] [CrossRef]
- Yasir, M.; Ahmad, S.; Ahmed, F.; Aqeel, M.; Akbar, M.Z. Improved numerical solutions for chaotic-cancer-model. AIP Adv. 2017, 7, 015110. [Google Scholar] [CrossRef]
- Maddalena, L.; Ragni, S. Existence of solutions and numerical approximation of a non-local tumor growth model. Math. Med. Biol. A J. IMA 2020, 37, 58–82. [Google Scholar] [CrossRef]
- Sabir, Z.; Munawar, M.; Abdelkawy, M.A.; Raja, M.A.Z.; Ünlü, C.; Jeelani, M.B.; Alnahdi, A.S. Numerical Investigations of the Fractional-Order Mathematical Model Underlying Immune-Chemotherapeutic Treatment for Breast Cancer Using the Neural Networks. Fractal Fract. 2022, 6, 184. [Google Scholar] [CrossRef]
- Ahmed, N.; Shah, N.A.; Ali, F.; Vieru, D.; Zaman, F.D. Analytical Solutions of the Fractional Mathematical Model for the Concentration of Tumor Cells for Constant Killing Rate. Mathematics 2021, 9, 1156. [Google Scholar] [CrossRef]
- Bagheri, M.; Khani, A. Analytical Method for Solving the Fractional Order Generalized KdV Equation by a Beta-Fractional Derivative. Adv. Math. Phys. 2020, 2020, 8819183. [Google Scholar] [CrossRef]
- Fan, K.; Zhou, C. Mechanical Solving a Few Fractional Partial Differential Equations and Discussing the Effects of the Fractional Order. Adv. Math. Phys. 2020, 2020, 3758353. [Google Scholar] [CrossRef]
- Zhang, H.; Nadeem, M.; Rauf, A.; Hui, Z.G. A novel approach for the analytical solution of nonlinear time-fractional differential equations. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1069–1084. [Google Scholar] [CrossRef]
- Verma, P.; Kumar, M. An Analytical Solution of Linear/Nonlinear Fractional-Order Partial Differential Equations and with New Existence and Uniqueness Conditions. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2020, 92, 47–55. [Google Scholar] [CrossRef]
- Rehman, M.F.U.; Gu, Y.; Yuan, W. Exact Analytical Solutions of Nonlinear Fractional Liouville Equation by Extended Complex Method. Adv. Math. Phys. 2020, 2020, 8815363. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Baleanu, D.; Arif, M. Laplace decomposition for solving nonlinear system of fractional order partial differential equations. Adv. Differ. Equ. 2020, 2020, 375. [Google Scholar] [CrossRef]
- Singh, B.K. Fractional reduced differential transform method for numerical computation of a system of linear and nonlinear fractional partial differential equations. Int. J. Open Probl. Comput. Sci. Math. 2016, 9, 20–38. [Google Scholar] [CrossRef]
- Khalouta, A.; Kadem, A. A new modification of the reduced differential transform method for nonlinear fractional partial differential equations. J. Appl. Math. Comput. Mech. 2020, 19, 45–58. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Moshokoa, S.P.; Ariyan, V.M.; Tchier, F. Reduced differential transform method for partial differential equations within local fractional derivative operators. Adv. Mech. Eng. 2016, 8, 160. [Google Scholar] [CrossRef]
- Kumar, S.; Baleanu, D. A new numerical method for time fractional non-linear sharma-tasso-oliver equation and klein-Gordon equation with exponential kernel law. Front. Phys. 2020, 8, 136. [Google Scholar] [CrossRef]
- Albadarneh, R.B.; Zerqat, M.; Batiha, I.M. Numerical solutions for linear and non-linear fractional differential equations. Int. J. Pure Appl. Math. 2016, 106, 859–871. [Google Scholar] [CrossRef]
- Ali, K.K.; Mohamed, E.M.; Mohamed, E.M. A numerical technique for a general form of nonlinear fractional-order differential equations with the linear functional argument. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 83–91. [Google Scholar] [CrossRef]
- Jafari, H.; Gejji, V.D. Solving a system of nonlinear fractional differential equations using Adomian decomposition. J. Comput. Appl. Math. 2006, 196, 644–651. [Google Scholar] [CrossRef]
- Oyjinda, P.; Pochai, N. Numerical Simulation of an Air Pollution Model on Industrial Areas by Considering the Influence of Multiple Point Sources. Int. J. Differ. Equ. 2019, 2019, 2319831. [Google Scholar] [CrossRef]
- Bakkyaraj, T. Lie symmetry analysis of system of nonlinear fractional partial differential equations with Caputo fractional derivative. Eur. Phys. J. Plus 2020, 135, 1–17. [Google Scholar]
- Ibrahim, R.W.; Elobaid, R.M.; Obaiys, S.J. Symmetric conformable fractional derivative of complex variables. Mathematics 2020, 8, 363. [Google Scholar] [CrossRef]
- Iskenderoglu, G.; Kaya, D. Symmetry analysis of initial and boundary value problems for fractional differential equations in Caputo sense. Chaos Solitons Fractals 2020, 134, 109684. [Google Scholar] [CrossRef]
- Yang, Q.; Turner, I.; Liu, F. Analytical and numerical solutions for the time and space-symmetric fractional diffusion equation. ANZIAM J. 2008, 50, C800–C814. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Zaman, F.D. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Burgess, P.K.; Kulesa, P.M.; Murray, J.D.; Alvord, E.C., Jr. The interaction of growth rates and diffusion coefficients in a three-dimensional mathematical model of gliomas. J. Neuropathol. Exp. Neurol. 1997, 56, 704–713. [Google Scholar] [CrossRef]
- Moyo, S.; Leach, P.G.L. Symmetry methods applied to a mathematical model of a tumour of the brain. Proc. Inst. Math. NAS Ukr. 2004, 50, 204–210. [Google Scholar]
- Wise, S.M.; Lowengrub, J.S.; Frieboes, H.B.; Cristini, V. Three-dimensional multispecies nonlinear tumor growth—I: Model and numerical method. J. Theor. Biol. 2008, 253, 524–543. [Google Scholar] [CrossRef]






| Parameter | Description | Values |
|---|---|---|
| Fractional cell kill | 0.2, 0.3, 0.1 | |
| Carrying capacity | 1, 0.81 | |
| Competition term | 1, 0.55, 0.9, 1 | |
| Death rate | 0.2, 1 | |
| Per capita growth rate | 1.1, 1 | |
| Immune source rate | 0.33 | |
| Immune threshold rate | 0.3 | |
| Immune response rate | 0.2 | |
| Diffusion coefficients | 0.001, 0.001, 0.001, 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abaid Ur Rehman, M.; Ahmad, J.; Hassan, A.; Awrejcewicz, J.; Pawlowski, W.; Karamti, H.; Alharbi, F.M. The Dynamics of a Fractional-Order Mathematical Model of Cancer Tumor Disease. Symmetry 2022, 14, 1694. https://doi.org/10.3390/sym14081694
Abaid Ur Rehman M, Ahmad J, Hassan A, Awrejcewicz J, Pawlowski W, Karamti H, Alharbi FM. The Dynamics of a Fractional-Order Mathematical Model of Cancer Tumor Disease. Symmetry. 2022; 14(8):1694. https://doi.org/10.3390/sym14081694
Chicago/Turabian StyleAbaid Ur Rehman, Muhammad, Jamshad Ahmad, Ali Hassan, Jan Awrejcewicz, Witold Pawlowski, Hanen Karamti, and Fahad M. Alharbi. 2022. "The Dynamics of a Fractional-Order Mathematical Model of Cancer Tumor Disease" Symmetry 14, no. 8: 1694. https://doi.org/10.3390/sym14081694








