Searching for Orbits for a Mission to the Asteroid 2001SN263 Considering Errors in the Physical Parameters
Abstract
:1. Introduction
2. The Triple Asteroid 2001SN263
3. Description of the Problem
4. Equations of Motion
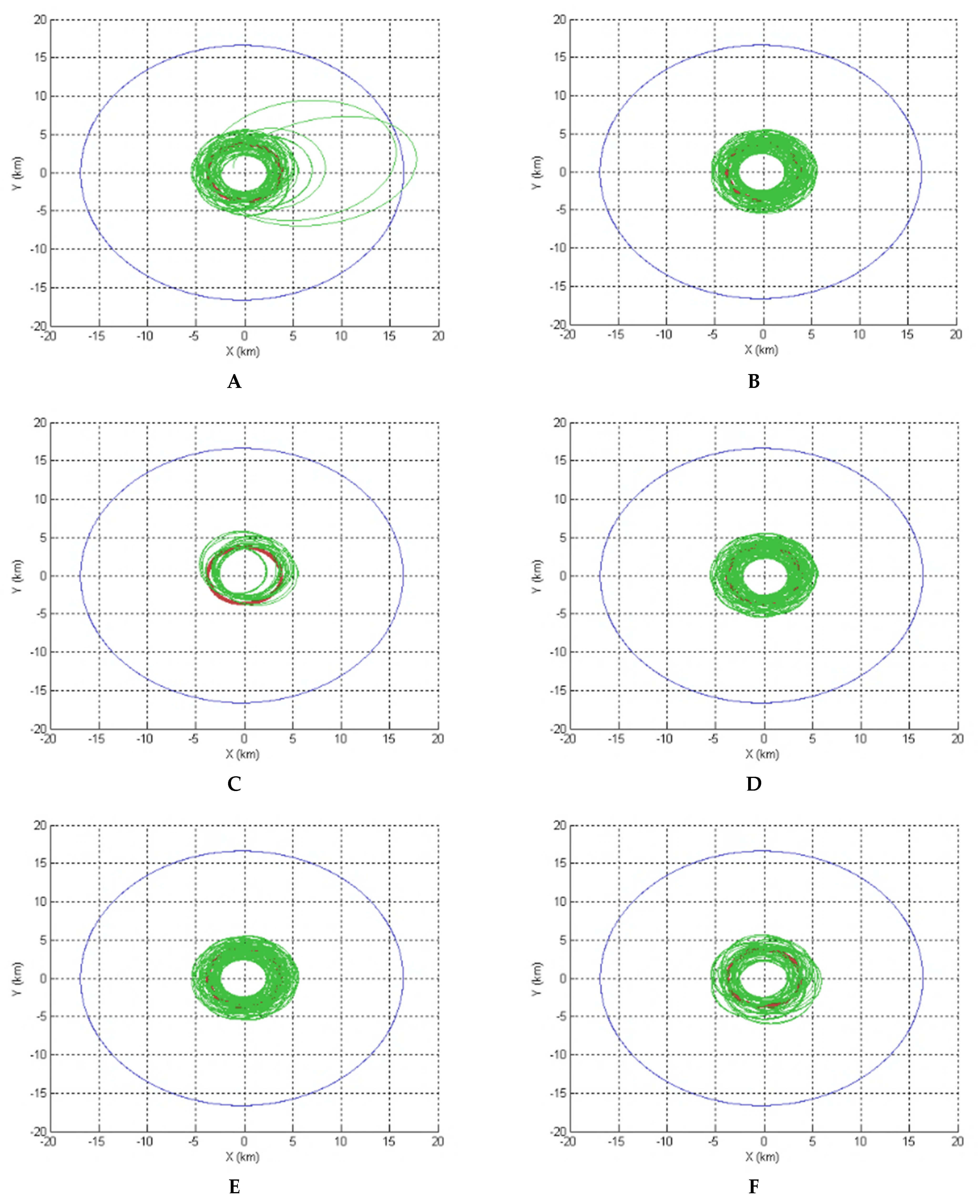
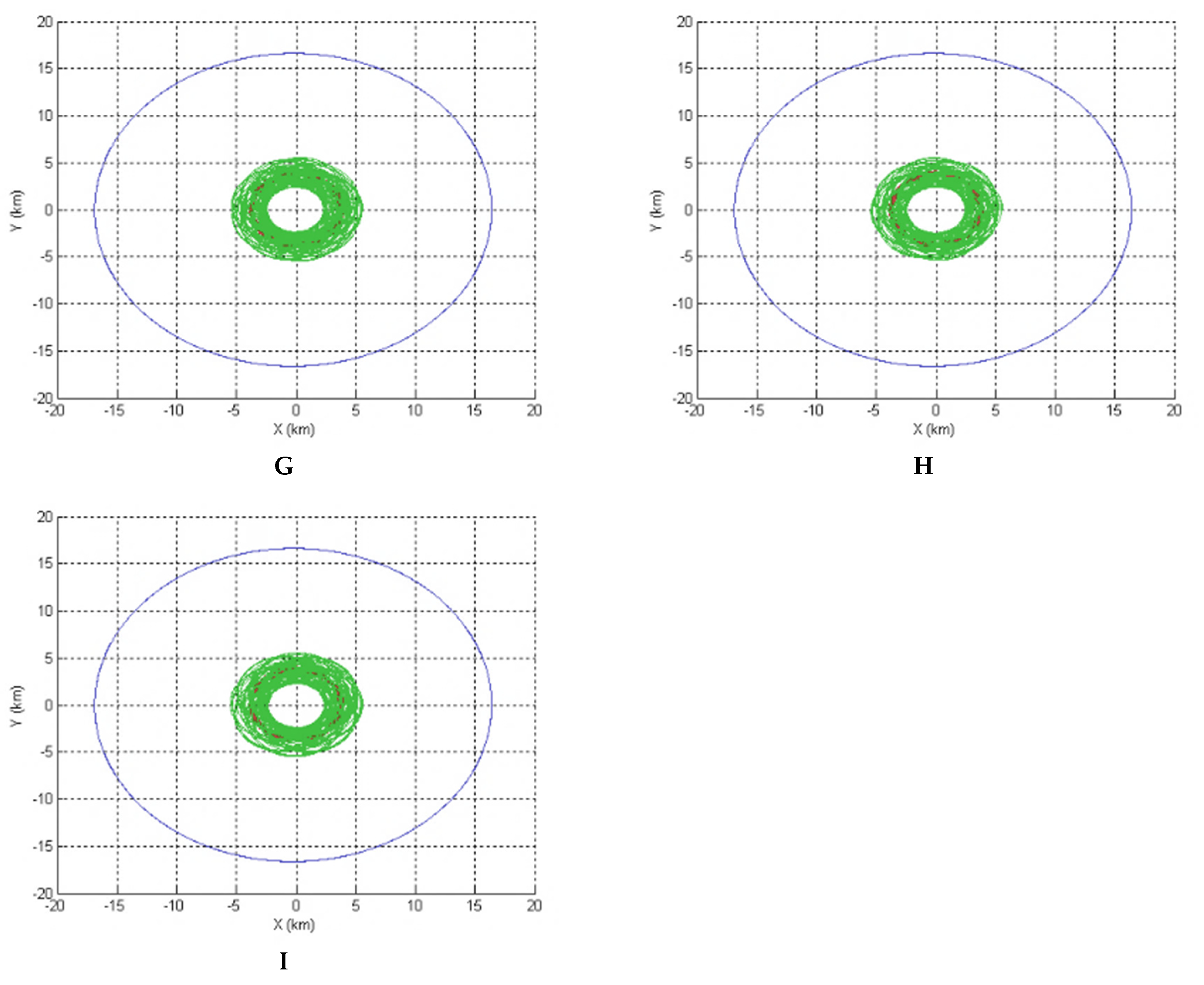
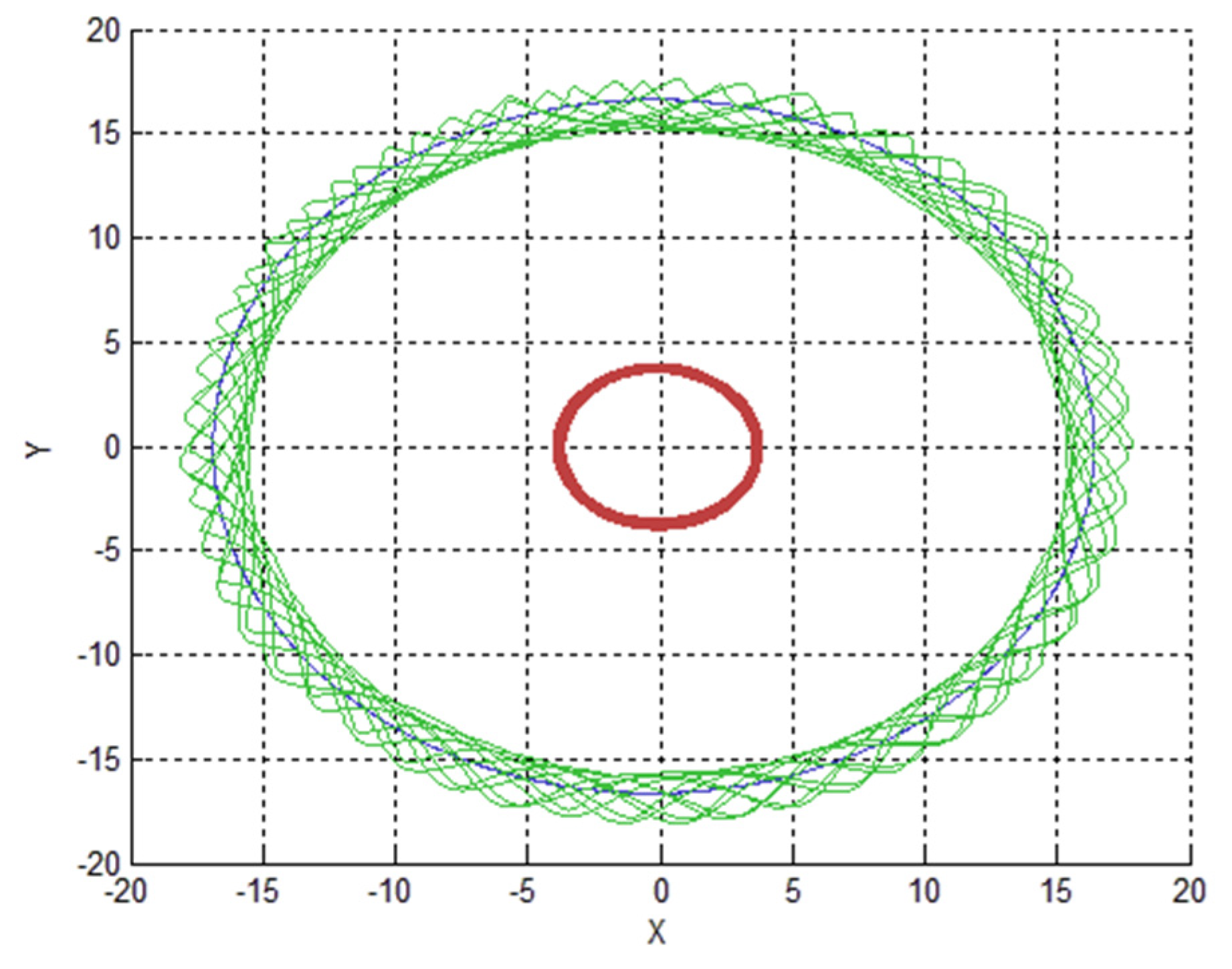
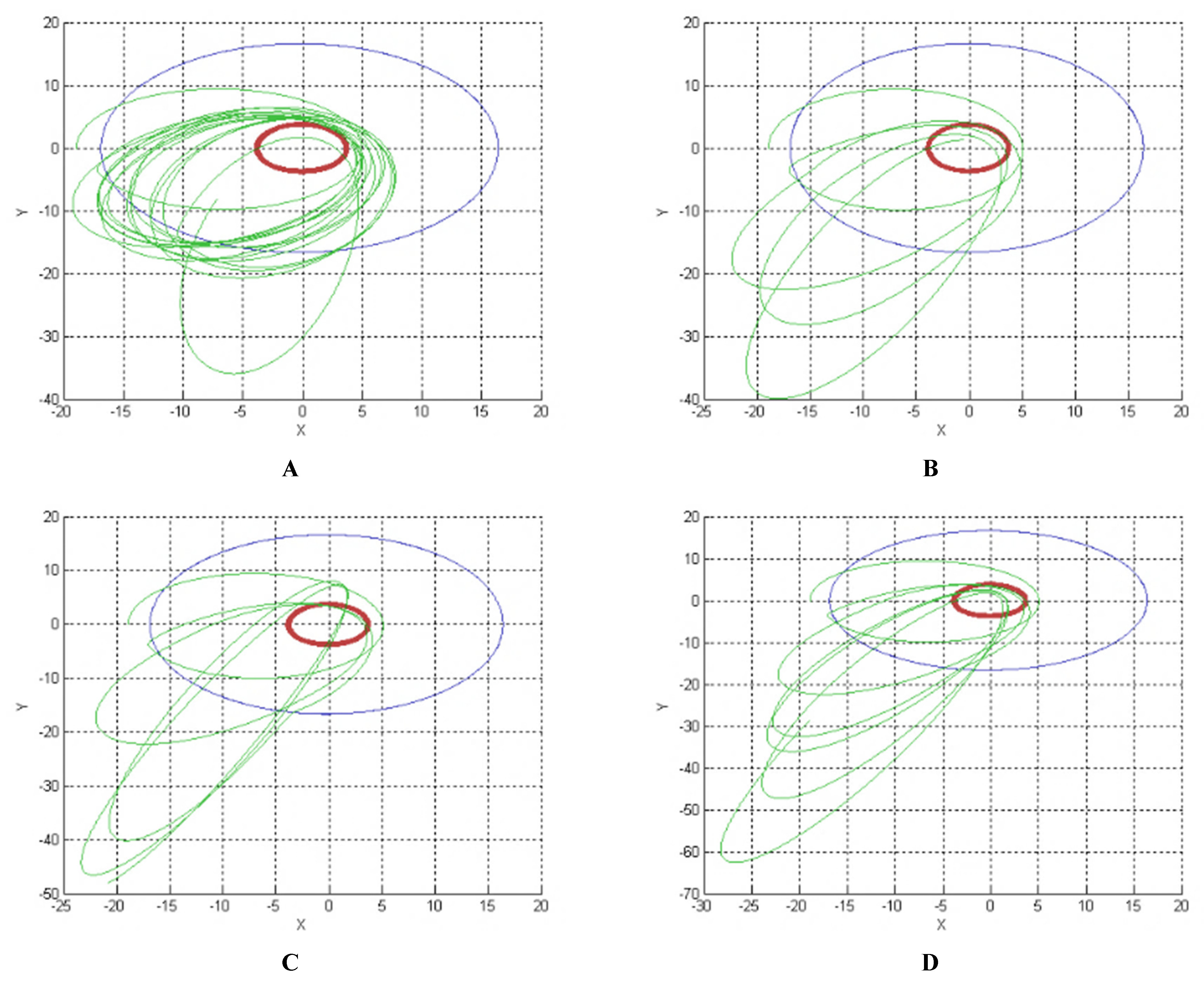
5. Results
5.1. A Good Option to Observe Alpha and Gamma
5.2. A Good Option to Observe Beta
5.3. An Option to Observe All the Three Bodies of the System
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Belton, M.J.S.; Veverka, J.; Thomas, P.; Helfenstein, P.; Simonelli, D.; Chapman, C.; Davies, M.E.; Greeley, R.; Greenberg, R.; Head, J.; et al. Galileo Encounter with 951 Gaspra: First pictures of an asteroid. Science 1992, 257, 1647. [Google Scholar] [CrossRef] [PubMed]
- Belton, M.J.; Chapman, C.R.; Klaasen, K.P.; Harch, A.P.; Thomas, P.C.; Veverka, J.; McEwen, A.S.; Pappalardo, R.T. Galileo’s Encounter with 243 Ida: Overview of the imaging experiment. Icarus 1996, 120, 1–19. [Google Scholar] [CrossRef]
- Binzel, R.P.; Rivkin, A.; Bus, S.J.; Sunshine, J.; Burbine, T.H. MUSES-C target asteroid (25143) 1998 SF36: A reddened ordinary chondrite. Meteorit. Planet. Sci. 2001, 36, 1167–1172. [Google Scholar] [CrossRef]
- Veverka, J.; Farquhar, B.B.; Robinson, M.J.; Thomas, P.C.; Murchie, S.; Harch, A.P.; Antreasian, P.G.; Chesley, S.R.; Miller, J.K.; Owen, W.M.; et al. The landing of the Near-Shoemaker spacecraft on asteroid 433 Eros. Nature 2001, 413, 390–393. [Google Scholar] [CrossRef]
- Miller, J.K.; Konopliv, A.S.; Antreasian, P.G.; Bordi, J.J.; Chesley, S.; Helfrich, C.E.; Owen, W.M.; Wang, T.C.; Williams, B.G.; Yeomans, D.K.; et al. Determination of shape, gravity and rotational state of asteroid 433 Eros. Icarus 2002, 155, 3–17. [Google Scholar] [CrossRef]
- Broschart, S.B.; Scheeres, D.J. Control of hovering spacecraft near small bodies: Application to asteroid 25143 Itokawa. J. Guid. Control Dyn. 2005, 28, 343–354. [Google Scholar] [CrossRef]
- Huntress, W.; Stetson, D.; Farquhar, R.; Zimmerman, J.; Clark, B.; O’Neil, W.; Bourke, R.; Foing, B. The next steps in exploring deep space—A cosmic study by the IAA. Acta Astronaut. 2006, 58, 304–377. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Fujiwara, A.; Kawaguchi, J. Hayabusa and its adventure around the tiny asteroid Itokawa. Proc. Int. Astron. Union 2006, 2, 323–324. [Google Scholar] [CrossRef]
- Brum, A.G.V.D.; Hetem, A., Jr.; Rêgo, I.D.S.; Francisco, C.P.F.; Fenili, A.; Madeira, F.; Da Cruz, F.C.; Assafin, M. Preliminary development plan of the ALR, the laser rangefinder for the Aster deep space mission to the 2001 SN263 asteroid. J. Aerosp. Tehchnol. Manag. 2011, 3, 331–338. [Google Scholar] [CrossRef]
- Jones, T.; Bellerose, J.; Lee, P.; Prettyman, T.; Lawrence, D.; Smith, P.; Gaffey, M.; Nolan, M.; Goldsten, J.; Thomas, P.; et al. Amor: Investigating The Triple Asteroid System 2001 SN263. AAS/Div. Planet. Sci. Meet. Abstr. #42 2010, 42, 49. Available online: https://ui.adsabs.harvard.edu/abs/2010DPS....42.4929J (accessed on 23 August 2022).
- Müller, T.G.; Ďurech, J.; Hasegawa, S.; Abe, M.; Kawakami, K.; Kasuga, T.; Kinoshita, D.; Kuroda, D.; Urakawa, S.; Okumura, S.; et al. Thermo-physical properties of 162173 (1999 JU3), a potential flyby and rendezvous target for interplanetary missions. Astron. Astrophys. 2011, 525, A145. [Google Scholar] [CrossRef] [Green Version]
- Tardivel, S.; Michel, P.; Scheeres, D.J. Deployment of a lander on the binary asteroid (175706) 1996 FG3, potential target of the European MarcoPolo-R sample return mission. Acta Astronaut. 2013, 89, 60–70. [Google Scholar] [CrossRef]
- Tsuda, Y.; Yoshikawa, M.; Abe, M.; Minamino, H.; Nakazawa, S. System design of the Hayabusa 2—Asteroid sample return mission to 199 JU3. Acta Astronaut. 2013, 91, 356–362. [Google Scholar] [CrossRef]
- Chesley, S.R.; Farnocchia, D.; Nolan, M.C.; Vokrouhlický, D.; Chodas, P.W.; Milani, A.; Spoto, F.; Rozitis, B.; Benner, L.A.; Bottke, W.F.; et al. Orbit and bulk density of the OSIRIS-REx target Asteroid (101955) Bennu. Icarus 2014, 235, 5–22. [Google Scholar] [CrossRef]
- Bottke, W.F.; Vokrouhlický, D.; Walsh, K.J.; Delbo, M.; Michel, P.; Lauretta, D.S.; Campins, H.; Connolly, H.C.; Scheeres, D.J.; Chelsey, S.R. In search of the source of asteroid (101955) Bennu: Applications of the stochastic YORP model. Icarus 2015, 247, 191–217. [Google Scholar] [CrossRef]
- NASA. Available online: https://www.nasa.gov/osiris-rex (accessed on 25 April 2017).
- Surovik, D.A.; Scheeres, D.J. Autonomous maneuver planning at small bodies via mission objective reachability analysis. In Proceedings of the 2014 AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 4–7 August 2014. [Google Scholar]
- Werner, R.A. The gravitational potential of a homogeneous polyhedron or don’t cut corners. Celest. Mech. Dyn. Astron. 1994, 59, 253–278. [Google Scholar] [CrossRef]
- Scheeres, D.J. Dynamics about uniformly rotating triaxial ellipsoids: Application to asteroids. Icarus 1994, 121, 225–238. [Google Scholar] [CrossRef]
- Scheeres, D.J. Orbital Motion in Strongly Perturbed Environments; Springer: Boulder, CO, USA, 2012; ISBN 978-3-642-03255-4. [Google Scholar]
- Scheeres, D.J. Orbit mechanics about asteroids and comets. J. Guid. Control Dyn. 2012, 35, 987–997. [Google Scholar] [CrossRef]
- Scheeres, D.J. Orbital mechanics about small bodies. Acta Astronaut. 2012, 72, 1–14. [Google Scholar] [CrossRef]
- Rossi, A.; Marzari, F.; Farinella, P. Orbital evolution around irregular bodies. Earth Planets Space 1999, 51, 1173–1180. [Google Scholar] [CrossRef]
- Scheeres, D.J.; Hu, W. Secular motion in a 2nd degree and order gravity field with no rotation. Celest. Mech. Dyn. Astron. 2001, 79, 183–200. [Google Scholar] [CrossRef]
- Bartczakk, P.; Breiter, S.; Jusiel, P. Ellipsoids, material points and material segments. Celest. Mech. Dyn. Astron. 2006, 96, 31–48. [Google Scholar] [CrossRef]
- Byram, S.M.; Scheeres, D.J. Stability of Sun-Synchronous Orbits in the Vicinity of a Comet. J. Guid. Control Dyn. 2009, 32, 1550–1559. [Google Scholar] [CrossRef]
- Shang, H.; Wu, X.; Cui, P. Periodic orbits in the doubly synchronous binary asteroid systems and their applications in space missions. Astrophys. Space Sci. 2014, 355, 69–87. [Google Scholar] [CrossRef]
- Yang, H.; Gong, S.; Baoyin, H. Two-impulse transfer orbits connecting equilibrium points of irregular-shaped asteroids. Astrophys. Space Sci. 2015, 357, 66. [Google Scholar] [CrossRef]
- Zeng, X.; Baoyin, H.; Li, J. Updated Rotating Mass Dipole with Oblateness of One Primary (II): Out-of-plane Equilibria and Their Stability. Astrophys. Space Sci. 2016, 361, 15. [Google Scholar] [CrossRef]
- Chanut, T.G.G.; Aljbaae, S.; Prado, A.F.B.A.; Carruba, V. Dynamics in the vicinity of (101955) Bennu: Solar radiation pressure effects in equatorial orbits. Mon. Not. R. Astron. Soc. 2017, 470, 2687–2701. [Google Scholar] [CrossRef]
- Almeida, A.K., Jr.; Oliveira, G.M.C.; Prado, A.F.B.A. Artificial equilibrium points and bi-impulsive maneuvers to observe 243 Ida. Chin. J. Aeronaut. 2021, 34, 410. [Google Scholar] [CrossRef]
- Araújo, R.A.N. O Sistema Triplo de Asteroides 2001SN263: Dinâmica Orbital e Estabilidade. Doctorate. Degree Thesis, INPE—National Institute for Space Research, São José dos Campos, Brazil, 2011. [Google Scholar]
- Fang, J.; Margot, J.L.; Brozovic, M.; Nolan, M.C.; Benner, L.A.M.; Taylor, P.A. Orbits of near-earth asteroid triple 2001SN263 and 1994 CC: Properties, origin, and evolution. Astron. J. 2011, 141, 154. [Google Scholar] [CrossRef]
- Araújo, R.A.N.; Winter, O.C.; Prado, A.F.B.A. Stable retrograde orbits around the triple system 2001 SN263. Mon. Not. R. Astron. Soc. 2015, 449, 4404. [Google Scholar] [CrossRef]
- Masago, B.Y.P.L.; Prado, A.; Chiaradia, A.P.M.; Gomes, V.M. Developing the Precessing Inclined Bi-Elliptical Four-Body Problem with Radiation Pressure” to search for orbits in the triple asteroid 2001SN263. Adv. Space Res. 2016, 57, 962–982. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, D.M.; Prado, A.F.B.A. Searching for Less-Disturbed Orbital Regions Around the Near-Earth Asteroid 2001 SN263. J. Spacecr. Rocket. 2019, 56, 1775–1785. [Google Scholar] [CrossRef]
- Cavalca, M.P.O.; Gomes, V.M.; Sanchez, D.M. Mid-range natural orbits around the triple asteroid 2001SN263. Eur. Phys. J. Spéc. Top. 2020, 229, 1557–1572. [Google Scholar] [CrossRef]
- Valvano, G.; Winter, O.C.; Sfair, R.; Oliveira, R.M.; Borderes-Motta, G. 2001 SN263—The contribution of their irregular shapes on the neighbourhood dynamics. Mon. Not. R. Astron. Soc. 2022, 515, 606–616. [Google Scholar] [CrossRef]
- Brum, A.G.V.D.; Schuindt, C.M. A Proposal of Optical Navigation for Deep Space Mission ASTER to Explore NEA 2001-SN263. J. Aerosp. Technol. Manag. 2022, 14. [Google Scholar] [CrossRef]
- Deienno, R.; Sanchez, D.M.; de Almeida Prado, A.F.B.; Smirnov, G. Satellite de-orbiting via controlled solar radiation pressure. Celest. Mech. Dyn. Astron. 2016, 126, 433–459. [Google Scholar] [CrossRef]
- Holman, M.J.; Wiegert, P.A. Long-term Stability of Planets in Binary Systems. Astron. J. 1999, 117, 621–628. [Google Scholar] [CrossRef]
- Hu, W.; Scheeres, D.J. Numerical determination of stability regions for orbital motion in uniformly rotating second degree and order gravity fields. Planet. Space Sci. 2004, 52, 685–692. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Wu, Y. Resonance Overlap is Responsible for Ejecting Planets in Binary Systems. Astrophys. J. Lett. 2006, 639, 423–431. [Google Scholar] [CrossRef]
- Nolan, M.C.; Howell, E.S.; Benner, L.A.M.; Ostro, S.J.; Giorgini, J.D.; Busch, M.W.; Carter, L.M.; Anderson, R.F.; Magri, C.; Campbell, D.B.; et al. Arecibo Radar Imaging of 2001SN263: A near-Earth triple asteroid system. Asteroids Comets Meteors 2008, 1405, 8258. [Google Scholar]
- de Almeida, A.K., Jr.; Prado, A.F.B.A. Comparisons between the circular restricted three-body and bi-circular four body problems for transfers between the two smaller primaries. Sci. Rep. 2022, 12, 4148. [Google Scholar] [CrossRef] [PubMed]
- Fieseler, P.D. A method for Solar Sailing in a low Earth Orbit. Acta Astronaut. 1988, 43, 531–541. [Google Scholar] [CrossRef]



| Body | Central Body | a | e | i | Period | Radius (km) | Mass (× 1010 kg) [33] |
|---|---|---|---|---|---|---|---|
| Alpha | Sun | 1.99 AU | 0.48 | 6.7° | 2.80 years | 1.30 | |
| Beta | Alpha | 16.633 km | 0.015 | 0.00° | 6.23 days | 0.39 | |
| Gamma | Alpha | 3.804 km | 0.016 | 13.87° | 0.69 days | 0.29 |
| Scenario | Symbol | Nomenclature |
|---|---|---|
| 1 | (+) (+) | mβ + error, mγ + error |
| 2 | (+) (0) | mβ + error, mγ without error |
| 3 | (+) (−) | mβ + error, mγ − error |
| 4 | (0) (+) | mβ without error, mγ + error |
| 5 | (0) (0) | mβ without error, mγ without error |
| 6 | (0) (−) | mβ without error, mγ − error |
| 7 | (−) (+) | mβ − error, mγ + error |
| 8 | (−) (0) | mβ − error, mγ without error |
| 9 | (−) (−) | mβ − error, mγ − error |
| Orbits with the Spacecraft Starting in the Periapsis (Same Side Orbits) |
|---|
| -2: Orbit internal to Gamma in resonance 3:4 |
| -3: Orbit internal to Gamma in resonance 4:5 |
| -4: Orbit external to Gamma in resonance 3:1 |
| Orbits with the spacecraft starting in the apoapsis (same side orbits) |
| -5: Orbit internal to Beta in resonance 1:2 |
| -12: Orbit external to Gamma in resonance 4:3 |
| -15: Orbit external to Gamma in resonance 7:5 |
| Orbit with the spacecraft starting in the periapsis (opposite side orbits) |
| -18: Orbit internal to Gamma in resonance 5:6 |
| Orbit with the spacecraft starting in the apoapsis (opposite side orbits) |
| -20: Orbit external to Gamma in resonance 6:5 |
| Orbit with the spacecraft starting in the periapsis (same side orbits with i = 13.87°) |
| -22: Orbit internal to Gamma in resonance 3:4 |
| Orbits with the spacecraft starting in the apoapsis (same side orbits with i = 13.87°) |
| -25: Orbit internal to Beta in resonance 1:2 |
| -27: Orbit internal to Beta in resonance 3:5 |
| -31: Orbit external to Gamma in resonance 7:2 |
| Orbit with the spacecraft starting in the periapsis (same side orbits with i = 90°) |
| -38: Orbit internal to Gamma in resonance 3:4 |
| Orbit with the spacecraft starting in the apoapsis (same side orbits with i = 90°) |
| -42: Orbit internal to Beta in resonance 2:3 |
| -52: Orbit external to Gamma in resonance 8:5 |
| Orbits with the spacecraft starting in the apoapsis (same side orbits with i = 180°) |
| -59: Orbit internal to Beta in resonance 3:5 |
| -60: Orbit internal to Beta in resonance 4:7 |
| -61: Orbit internal to Beta in resonance 5:9 |
| Family 1—Positive Errors in the Mass of Beta | ||||||
|---|---|---|---|---|---|---|
| Observation Times (Days) | ||||||
| Positive Errors in the Mass of Gamma | No Errors in the Mass of Gamma | Negative Errors in the Mass of Gamma | ||||
| Orbit | True Anomaly 0° | True Anomaly 180° | True Anomaly 0° | True Anomaly 180° | True Anomaly 0° | True Anomaly 180° |
| 2 | ||||||
| R1 | 6.95 | 9.62 | 18.57 | 18.57 | 10.23 | 10.23 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 5.88 | 8.47 | 13.20 | 13.20 | 6.98 | 6.98 |
| 3 | ||||||
| R1 | 3.53 | 6.72 | 62.50 | 62.50 | 10.44 | 14.76 |
| R2 | 1.49 | 0.84 | 0 | 0 | 0 | 0 |
| R3 | 7.21 | 5.67 | 43.07 | 43.06 | 8.06 | 12.72 |
| 4 | ||||||
| R1 | 6.50 | 6.48 | 4.94 | 6.02 | 13.34 | 4.72 |
| R2 | 0 | 0 | 0 | 1.36 | 0 | 0.62 |
| R3 | 7.87 | 5.62 | 6.74 | 6.99 | 15.84 | 5.93 |
| 5 | ||||||
| R1 | 0 | 0 | 0 | 0 | 0 | 0 |
| R2 | 62.50 | 62.50 | 62.50 | 62.50 | 62.50 | 62.50 |
| R3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | ||||||
| R1 | 3.55 | 3.61 | 25.86 | 25.87 | 12.62 | 16.51 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 4.65 | 4.96 | 30.07 | 30.07 | 13.85 | 18.22 |
| 15 | ||||||
| R1 | 6.34 | 7.19 | 18.65 | 15.36 | 6.16 | 13.41 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 6.64 | 5.60 | 21.73 | 18.28 | 6.70 | 9.60 |
| 18 | ||||||
| R1 | 28.54 | 25.41 | 11.83 | 12.44 | 20.68 | 17.55 |
| R2 | 0.87 | 0 | 0 | 0 | 0 | 0 |
| R3 | 9.25 | 8.46 | 8.13 | 8.45 | 17.10 | 11.56 |
| 20 | ||||||
| R1 | 52.40 | 52.41 | 51.78 | 51.71 | 14.55 | 14.55 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 12.77 | 12.76 | 15.32 | 15.36 | 5.51 | 5.50 |
| 22 | ||||||
| R1 | 1.86 | 1.86 | 62.50 | 62.50 | 6.03 | 6.03 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 1.45 | 1.45 | 43.31 | 43.33 | 4.04 | 4.04 |
| 25 | ||||||
| R1 | 0 | 0 | 7.50 | 1.65 | 0.09 | 0 |
| R2 | 1.84 | 1.84 | 2.65 | 2.66 | 2.48 | 2.77 |
| R3 | 0 | 0 | 7.71 | 0.46 | 0.41 | 0.48 |
| 27 | ||||||
| R1 | 10.56 | 7.06 | 1.87 | 13.37 | 11.29 | 1.66 |
| R2 | 1.48 | 4.33 | 2.65 | 1.75 | 2.21 | 5.65 |
| R3 | 9.93 | 7.94 | 2.79 | 14.84 | 11.85 | 2.55 |
| 31 | ||||||
| R1 | 0 | 0 | 0 | 1.33 | 0.09 | 0.09 |
| R2 | 2.01 | 2.01 | 6.68 | 6.32 | 1.92 | 1.92 |
| R3 | 3.16 | 3.17 | 1.33 | 2.35 | 1.21 | 1.21 |
| 38 | ||||||
| R1 | 5.78 | 5.78 | 7.07 | 7.07 | 6.32 | 6.32 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 2.64 | 2.64 | 3.23 | 3.23 | 3.36 | 3.36 |
| 42 | ||||||
| R1 | 0.90 | 0.93 | 1.91 | 1.66 | 1.62 | 1.61 |
| R2 | 0.71 | 0.31 | 0.46 | 0.30 | 0.33 | 0.34 |
| R3 | 1.16 | 1.95 | 1.95 | 1.59 | 1.46 | 1.38 |
| 52 | ||||||
| R1 | 8.09 | 11.34 | 12.86 | 13.03 | 14.36 | 12.06 |
| R2 | 0.78 | 0 | 0.49 | 0.47 | 0.16 | 0.43 |
| R3 | 6.94 | 9.56 | 10.41 | 10.08 | 10.78 | 9.79 |
| 59 | ||||||
| R1 | 0.79 | 0.79 | 1.16 | 1.16 | 0.66 | 0.69 |
| R2 | 0.97 | 0.99 | 0.88 | 0.88 | 1.00 | 1.00 |
| R3 | 0.71 | 0.57 | 1.32 | 0.95 | 0.70 | 0.60 |
| 60 | ||||||
| R1 | 0.11 | 0.11 | 0.10 | 0.10 | 0.09 | 0.09 |
| R2 | 0.17 | 0.17 | 0.16 | 0.16 | 0.17 | 0.17 |
| R3 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 |
| 61 | ||||||
| R1 | 0.14 | 0.14 | 0.14 | 0.14 | 0.13 | 0.13 |
| R2 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
| R3 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 |
| Family 2—No Errors in the Mass of Beta | ||||||
|---|---|---|---|---|---|---|
| Observation Times (Days) | ||||||
| Positive Errors in the Mass of Gamma | No Errors in the Mass of Gamma | Negative Errors in the Mass of Gamma | ||||
| Orbit | True Anomaly 0° | True Anomaly 180° | True Anomaly 0° | True Anomaly 180° | True Anomaly 0° | True Anomaly 180° |
| 2 | ||||||
| R1 | 3.52 | 2.91 | 25.13 | 40.69 | 10.22 | 10.22 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 3.75 | 3.02 | 18.50 | 25.02 | 6.97 | 6.97 |
| 3 | ||||||
| R1 | 3.42 | 3.41 | 62.50 | 62.50 | 4.43 | 4.43 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 3.51 | 3.22 | 43.07 | 43.07 | 2.66 | 2.66 |
| 4 | ||||||
| R1 | 21.18 | 6.60 | 6.86 | 18.00 | 1.53 | 1.53 |
| R2 | 0 | 0 | 0 | 0 | 2.27 | 2.63 |
| R3 | 20.63 | 7.60 | 5.92 | 20.61 | 1.98 | 1.98 |
| 5 | ||||||
| R1 | 0 | 0 | 0 | 0 | 0 | 0 |
| R2 | 62.50 | 62.50 | 62.50 | 62.50 | 62.50 | 62.50 |
| R3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | ||||||
| R1 | 2.74 | 3.02 | 25.83 | 25.82 | 7.26 | 8.80 |
| R2 | 0 | 1.14 | 0 | 0 | 0 | 0 |
| R3 | 4.67 | 5.04 | 30.39 | 30.40 | 7.05 | 8.59 |
| 15 | ||||||
| R1 | 5.96 | 9.52 | 24.27 | 24.26 | 11.90 | 42.46 |
| R2 | 0 | 0 | 0 | 0 | 0.24 | 0 |
| R3 | 5.03 | 7.56 | 27.15 | 27.15 | 12.79 | 31.33 |
| 18 | ||||||
| R1 | 9.66 | 12.08 | 35.73 | 11.36 | 6.19 | 6.19 |
| R2 | 0 | 0 | 0.69 | 0 | 0 | 0 |
| R3 | 5.36 | 5.83 | 16.51 | 5.99 | 2.64 | 2.64 |
| 20 | ||||||
| R1 | 52.19 | 52.20 | 36.18 | 35.00 | 32.56 | 24.10 |
| R2 | 0 | 0 | 0.43 | 0 | 0 | 0 |
| R3 | 12.33 | 12.32 | 12.61 | 11.63 | 12.65 | 12.39 |
| 22 | ||||||
| R1 | 1.86 | 1.86 | 62.50 | 62.50 | 6.03 | 6.03 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 1.46 | 1.46 | 43.03 | 43.02 | 4.06 | 4.05 |
| 25 | ||||||
| R1 | 2.71 | 2.73 | 6.86 | 2.40 | 2.36 | 2.33 |
| R2 | 1.42 | 0.99 | 0.88 | 0 | 0.55 | 0.55 |
| R3 | 1.48 | 1.43 | 7.58 | 1.71 | 1.25 | 2.68 |
| 27 | ||||||
| R1 | 0 | 0 | 5.51 | 5.64 | 0 | 0 |
| R2 | 2.22 | 2.20 | 4.58 | 4.55 | 2.32 | 2.32 |
| R3 | 0.51 | 0.50 | 4.27 | 5.06 | 0.32 | 0.32 |
| 31 | ||||||
| R1 | 4.55 | 10.91 | 4.32 | 5.39 | 1.62 | 11.24 |
| R2 | 5.80 | 1.15 | 1.59 | 2.23 | 4.48 | 1.38 |
| R3 | 5.08 | 8.69 | 5.17 | 5.65 | 3.31 | 11.43 |
| 38 | ||||||
| R1 | 6.61 | 6.61 | 8.12 | 8.13 | 6.71 | 6.71 |
| R2 | 0 | 0 | 0.32 | 0.37 | 0 | 0 |
| R3 | 3.05 | 3.05 | 4.43 | 4.40 | 3.81 | 3.80 |
| 42 | ||||||
| R1 | 1.87 | 1.87 | 2.16 | 2.18 | 1.88 | 1.88 |
| R2 | 0.69 | 0.69 | 0.34 | 0.34 | 0.78 | 0.78 |
| R3 | 1.06 | 1.04 | 0.88 | 1.01 | 1.34 | 1.34 |
| 52 | ||||||
| R1 | 6.53 | 5.57 | 9.15 | 5.00 | 13.73 | 11.90 |
| R2 | 0.34 | 0.44 | 0 | 0 | 0 | 0.31 |
| R3 | 4.57 | 4.31 | 8.23 | 4.03 | 9.84 | 9.57 |
| 59 | ||||||
| R1 | 2.39 | 2.39 | 1.88 | 1.86 | 2.14 | 2.14 |
| R2 | 2.55 | 2.56 | 2.68 | 2.68 | 2.89 | 2.93 |
| R3 | 2.83 | 2.83 | 2.62 | 2.61 | 3.57 | 3.55 |
| 60 | ||||||
| R1 | 2.65 | 2.67 | 2.27 | 1.65 | 0.69 | 0.69 |
| R2 | 1.01 | 0.64 | 1.53 | 1.07 | 0.35 | 0.35 |
| R3 | 2.08 | 1.97 | 2.35 | 1.34 | 0.54 | 0.54 |
| 61 | ||||||
| R1 | 0.69 | 0.80 | 2.48 | 2.52 | 0.15 | 0.15 |
| R2 | 2.58 | 2.66 | 1.39 | 1.33 | 0.17 | 0.17 |
| R3 | 2.79 | 2.75 | 1.52 | 1.90 | 0.25 | 0.25 |
| Family 3—Negative Errors in the Mass of Beta | ||||||
|---|---|---|---|---|---|---|
| Observation Times (Days) | ||||||
| Positive Errors in the Mass of Gamma | No Errors in the Mass of Gamma | Negative Errors in the Mass of Gamma | ||||
| Orbit | True Anomaly 0° | True Anomaly 180° | True Anomaly 0° | True Anomaly 180° | True Anomaly 0° | True Anomaly 180° |
| 2 | ||||||
| R1 | 2.85 | 2.98 | 18.55 | 18.55 | 10.22 | 10.22 |
| R2 | 0.65 | 0.72 | 0 | 0 | 0 | 0 |
| R3 | 2.46 | 2.49 | 13.17 | 13.17 | 6.97 | 6.96 |
| 3 | ||||||
| R1 | 5.59 | 3.82 | 62.50 | 62.50 | 4.42 | 4.41 |
| R2 | 1.44 | 0 | 0 | 0 | 0 | 0 |
| R3 | 5.61 | 3.95 | 43.06 | 43.07 | 2.65 | 2.64 |
| 4 | ||||||
| R1 | 2.59 | 24.33 | 22.45 | 3.60 | 5.97 | 4.85 |
| R2 | 0 | 0 | 0 | 0.68 | 0.51 | 0.57 |
| R3 | 3.10 | 23.88 | 22.49 | 5.25 | 5.53 | 5.24 |
| 5 | ||||||
| R1 | 0 | 0 | 0 | 0 | 0 | 0 |
| R2 | 62.50 | 62.50 | 62.50 | 62.50 | 62.50 | 62.50 |
| R3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | ||||||
| R1 | 1.97 | 3.05 | 25.80 | 25.78 | 22.53 | 4.16 |
| R2 | 0.49 | 0.49 | 0 | 0 | 0 | 1.65 |
| R3 | 3.22 | 5.37 | 30.39 | 30.37 | 23.71 | 5.23 |
| 15 | ||||||
| R1 | 3.84 | 3.84 | 23.95 | 23.95 | 18.00 | 17.38 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 4.08 | 4.08 | 26.53 | 26.53 | 17.25 | 17.99 |
| 18 | ||||||
| R1 | 7.27 | 6.48 | 10.67 | 27.67 | 45.54 | 9.66 |
| R2 | 0 | 0 | 0.24 | 0 | 0 | 0 |
| R3 | 3.76 | 2.98 | 5.98 | 18.11 | 20.09 | 5.58 |
| 20 | ||||||
| R1 | 52.27 | 52.27 | 51.56 | 51.57 | 52.55 | 51.72 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 12.79 | 12.80 | 14.95 | 14.95 | 17.37 | 18.03 |
| 22 | ||||||
| R1 | 1.86 | 1.86 | 62.50 | 62.50 | 6.02 | 6.02 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 1.46 | 1.46 | 42.82 | 42.83 | 4.10 | 4.09 |
| 25 | ||||||
| R1 | 0.39 | 0.75 | 1.87 | 2.21 | 0.99 | 1.04 |
| R2 | 1.60 | 1.89 | 0.62 | 0.45 | 2.44 | 2.47 |
| R3 | 1.89 | 1.95 | 2.55 | 2.28 | 1.65 | 1.66 |
| 27 | ||||||
| R1 | 0 | 0 | 0 | 0 | 0 | 0 |
| R2 | 1.68 | 2.11 | 1.62 | 1.62 | 1.34 | 1.34 |
| R3 | 0.43 | 0.43 | 0.36 | 0.36 | 0.35 | 0.35 |
| 31 | ||||||
| R1 | 0.99 | 2.45 | 7.28 | 6.89 | 7.26 | 7.26 |
| R2 | 0.57 | 2.12 | 2.13 | 4.45 | 1.40 | 1.40 |
| R3 | 1.60 | 2.33 | 5.30 | 5.31 | 4.40 | 4.40 |
| 38 | ||||||
| R1 | 7.97 | 7.97 | 8.49 | 8.27 | 8.14 | 8.14 |
| R2 | 0 | 0 | 0.09 | 0 | 0 | 0 |
| R3 | 4.38 | 4.38 | 4.27 | 4.02 | 5.02 | 5.03 |
| 42 | ||||||
| R1 | 1.79 | 1.78 | 2.20 | 2.42 | 1.58 | 1.58 |
| R2 | 1.45 | 1.44 | 0.69 | 0.52 | 0.03 | 0.04 |
| R3 | 0.70 | 0.85 | 1.01 | 0.94 | 0.11 | 0.11 |
| 52 | ||||||
| R1 | 1.81 | 1.81 | 7.33 | 5.76 | 18.28 | 18.36 |
| R2 | 0 | 0 | 0 | 0 | 0 | 0 |
| R3 | 1.68 | 1.68 | 7.53 | 5.46 | 13.27 | 13.98 |
| 59 | ||||||
| R1 | 0.78 | 0.77 | 0.31 | 0.31 | 0.25 | 0.25 |
| R2 | 3.05 | 3.05 | 2.84 | 2.84 | 2.68 | 2.68 |
| R3 | 2.96 | 2.97 | 2.93 | 2.93 | 2.76 | 2.76 |
| 60 | ||||||
| R1 | 3.11 | 3.21 | 3.11 | 3.02 | 2.65 | 2.64 |
| R2 | 2.97 | 2.82 | 2.99 | 2.92 | 3.13 | 3.14 |
| R3 | 2.85 | 2.99 | 3.17 | 3.11 | 2.99 | 2.99 |
| 61 | ||||||
| R1 | 3.14 | 3.15 | 2.55 | 2.51 | 2.82 | 2.82 |
| R2 | 1.62 | 1.48 | 1.61 | 1.71 | 2.09 | 2.08 |
| R3 | 2.80 | 2.86 | 2.41 | 2.40 | 2.40 | 2.58 |
| Scenario | Observational Times (Days) | ||
|---|---|---|---|
| True Anomaly 0° | True Anomaly 180° | ||
| (+) (+) | R1 | 52.40 | 52.41 |
| R3 | 12.77 | 12.76 | |
| (+) (0) | R1 | 51.78 | 51.71 |
| R3 | 15.32 | 15.36 | |
| (+) (−) | R1 | 14.55 | 14.55 |
| R3 | 5.51 | 5.50 | |
| (0) (+) | R1 | 52.19 | 52.20 |
| R3 | 12.33 | 12.32 | |
| (0) (0) | R1 | 36.18 | 35.00 |
| R3 | 12.61 | 11.63 | |
| (0) (−) | R1 | 32.56 | 24.10 |
| R3 | 12.65 | 12.39 | |
| (−) (+) | R1 | 52.27 | 52.27 |
| R3 | 12.79 | 12.80 | |
| (−) (0) | R1 | 51.56 | 51.57 |
| R3 | 14.95 | 14.95 | |
| (−) (−) | R1 | 52.55 | 51.72 |
| R3 | 17.37 | 18.03 | |
| Scenario (+) (+) | R1 | 0.79 | 0.79 |
| R2 | 0.97 | 0.99 | |
| R3 | 0.71 | 0.57 | |
| Scenario (+) (0) | R1 | 1.16 | 1.16 |
| R2 | 0.88 | 0.88 | |
| R3 | 1.32 | 0.95 | |
| Scenario (+) (−) | R1 | 0.66 | 0.69 |
| R2 | 1.00 | 1.00 | |
| R3 | 0.70 | 0.60 | |
| Scenario (0) (+) | R1 | 2.39 | 2.39 |
| R2 | 2.55 | 2.56 | |
| R3 | 2.83 | 2.83 | |
| Scenario (0) (−) | R1 | 2.14 | 2.14 |
| R2 | 2.89 | 2.93 | |
| R3 | 3.57 | 3.55 | |
| Scenario (−) (+) | R1 | 0.78 | 0.77 |
| R2 | 3.05 | 3.05 | |
| R3 | 2.96 | 2.97 | |
| Scenario (−) (0) | R1 | 0.31 | 0.31 |
| R2 | 2.84 | 2.84 | |
| R3 | 2.93 | 2.93 | |
| Scenario (−) (−) | R1 | 0.25 | 0.25 |
| R2 | 2.68 | 2.68 | |
| R3 | 2.76 | 2.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Almeida Junior, A.K.; Mescolotti, B.Y.P.M.; Chiaradia, A.P.M.; Gomes, V.M.; de Almeida Prado, A.F.B. Searching for Orbits for a Mission to the Asteroid 2001SN263 Considering Errors in the Physical Parameters. Symmetry 2022, 14, 1789. https://doi.org/10.3390/sym14091789
de Almeida Junior AK, Mescolotti BYPM, Chiaradia APM, Gomes VM, de Almeida Prado AFB. Searching for Orbits for a Mission to the Asteroid 2001SN263 Considering Errors in the Physical Parameters. Symmetry. 2022; 14(9):1789. https://doi.org/10.3390/sym14091789
Chicago/Turabian Stylede Almeida Junior, Allan Kardec, Bruna Yukiko Pinheiro Masago Mescolotti, Ana Paula Marins Chiaradia, Vivian M. Gomes, and Antonio Fernando Bertachini de Almeida Prado. 2022. "Searching for Orbits for a Mission to the Asteroid 2001SN263 Considering Errors in the Physical Parameters" Symmetry 14, no. 9: 1789. https://doi.org/10.3390/sym14091789





