Black String Bounce to Traversable Wormhole
Abstract
:1. Introduction
2. Simpson-Visser Regularization for a Black String
2.1. Tensors and Curvature Invariants
2.2. Black String Momentum–Energy Tensor and Energy Conditions
3. Applications of the Regular Solution of a Black String
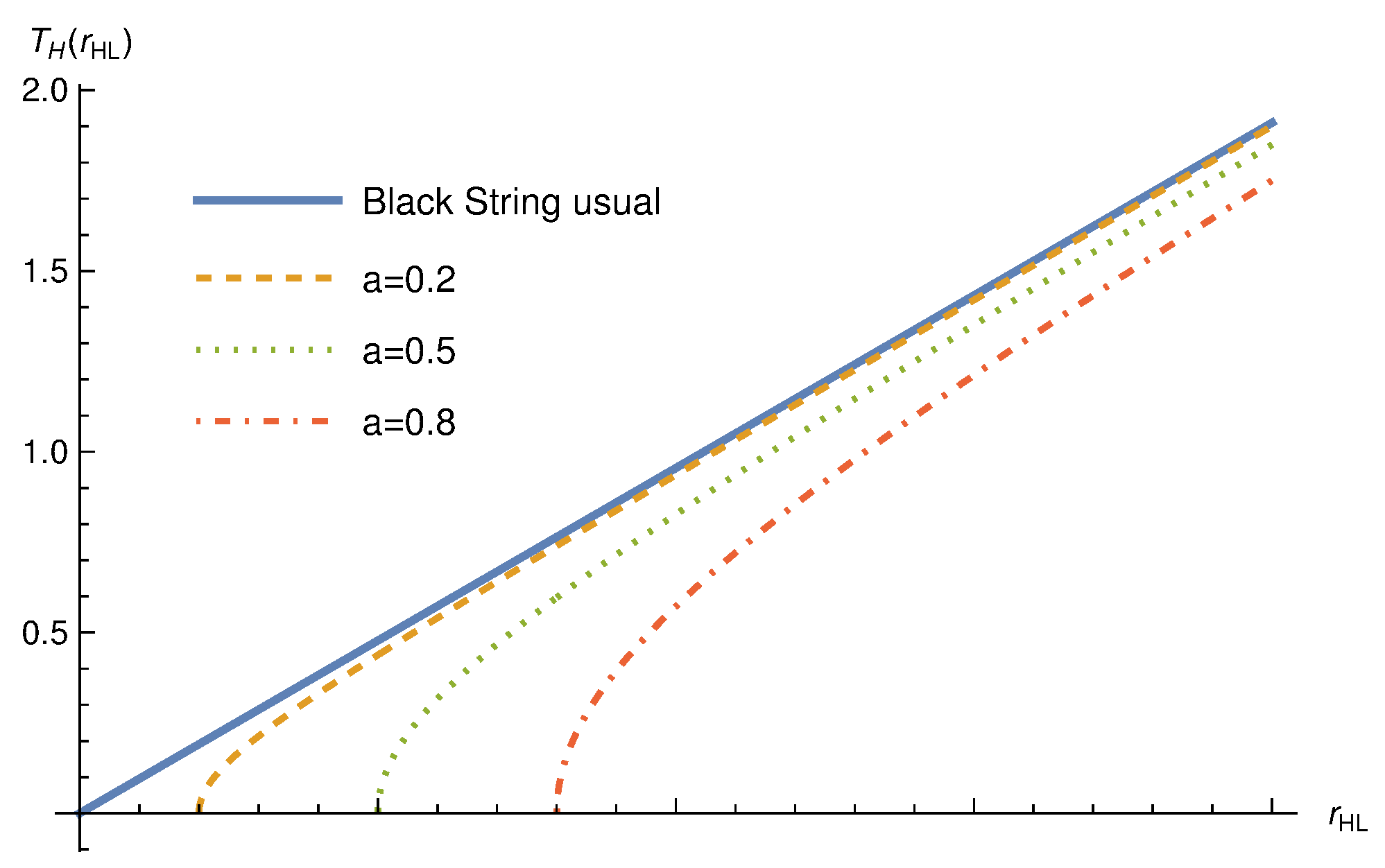
3.1. Regular Black String Thermodynamics
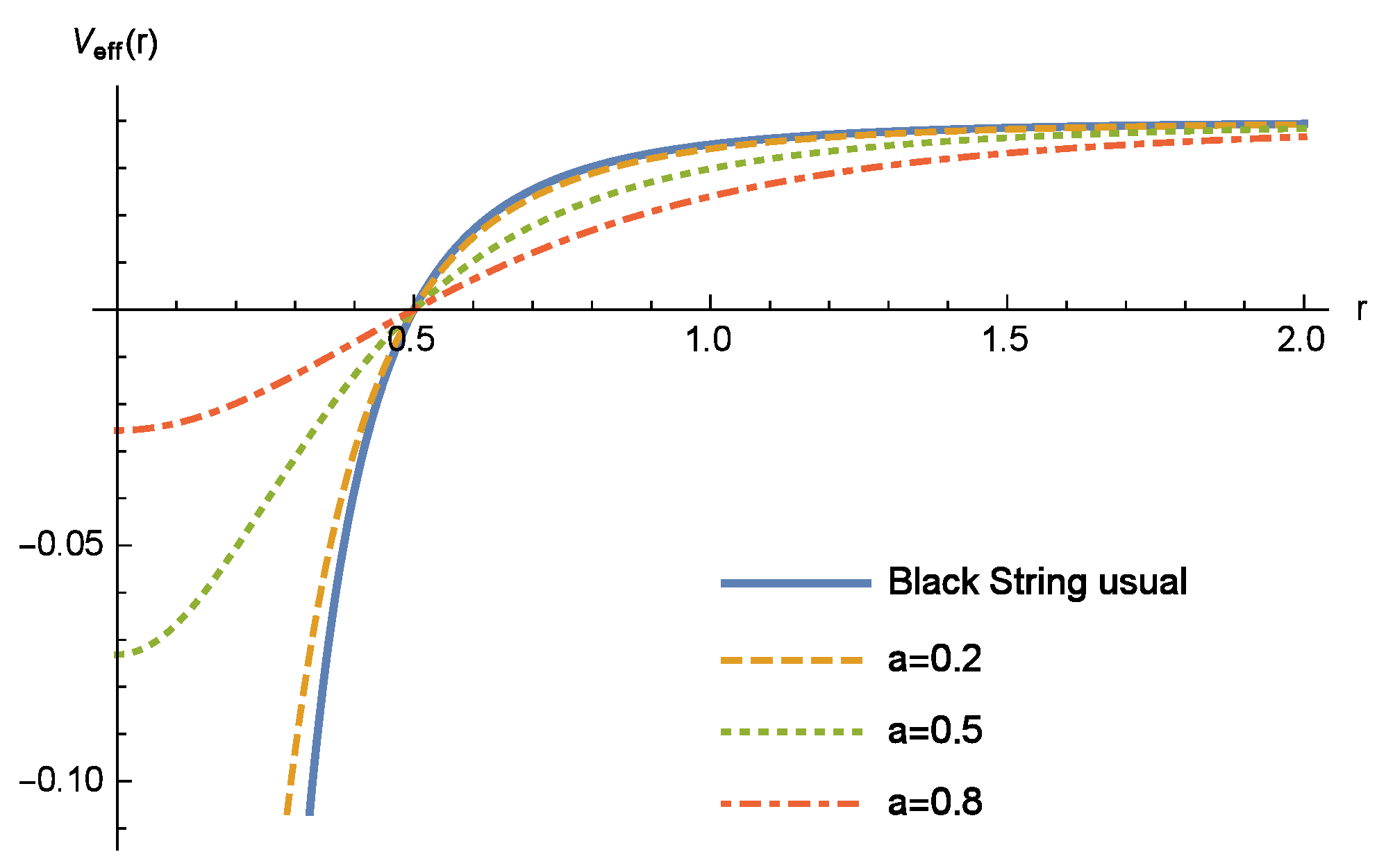
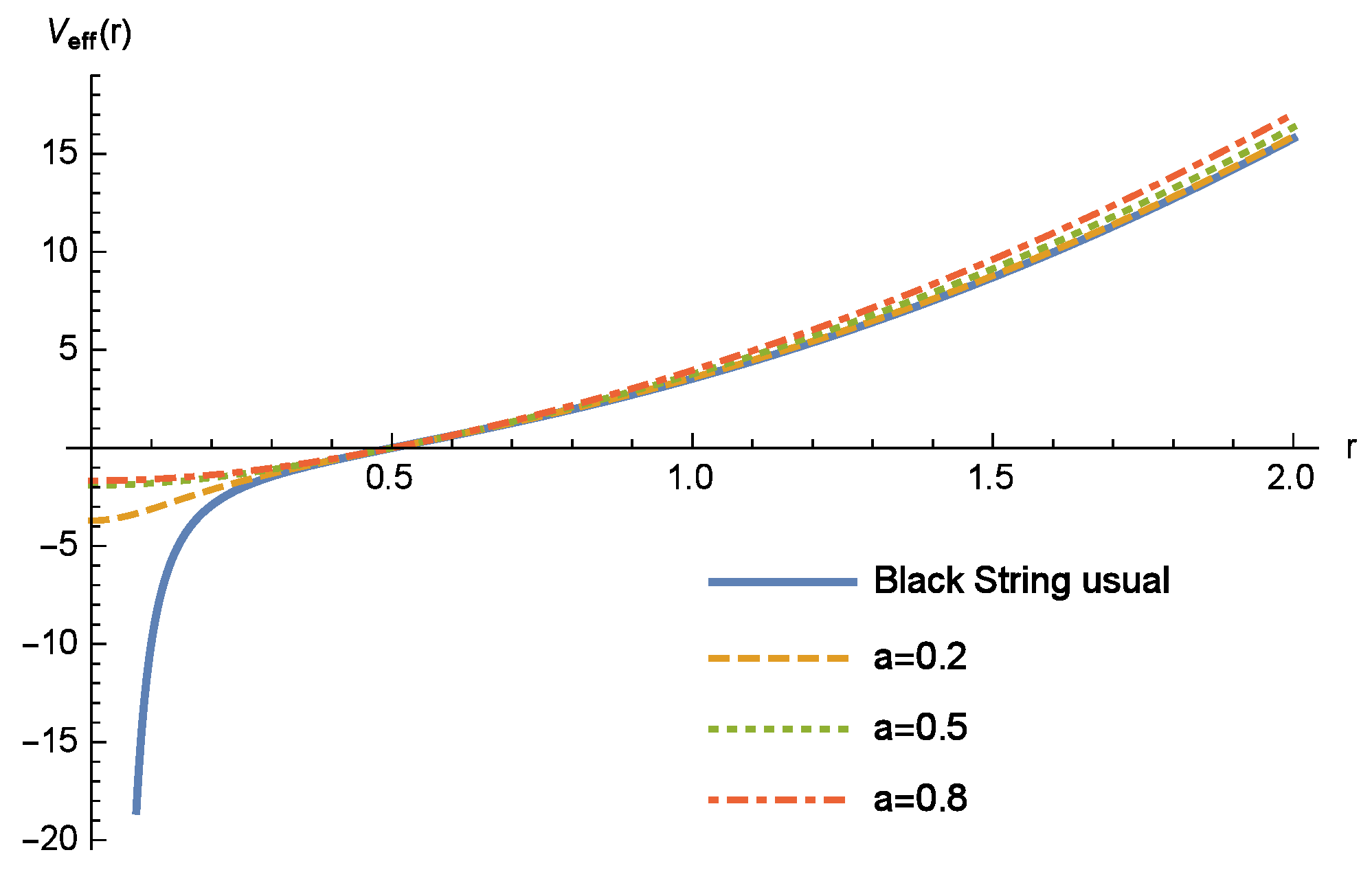
3.2. Circular Orbits in the Regular Black String
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; AIP Press: New York, NY, USA, 1995. [Google Scholar]
- Lemos, J.P.S. Cylindrical black hole in general relativity. Phys. Lett. B 1995, 353, 46–51. [Google Scholar] [CrossRef] [Green Version]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D. et al. [Event Horizon Telescope] First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azuly, R. [Event Horizon Telescope]. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Abbott, B.P. et al. [LIGO Scientific and Virgo] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P. et al. [LIGO Scientific and Virgo] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vilenkin, A. Cosmic Strings and Domain Walls. Phys. Rept. 1985, 121, 263–315. [Google Scholar] [CrossRef]
- Carballo-Rubio, R.; Filippo, F.D.; Liberati, S.; Pacilio, C.; Visser, M. On the viability of regular black holes. J. High Energy Phys. 2018, 07, 023. [Google Scholar] [CrossRef] [Green Version]
- Jayawiguna, B.N. Thermodynamics of regular Kerr-Sen black hole. J. Phys. Conf. Ser. 2022, 2165, 012016. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and Evaporation of Nonsingular Black Holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [Green Version]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. J. Cosmol. Astropart. Phys. 2019, 2, 42. [Google Scholar] [CrossRef] [Green Version]
- Morris, M.S.; Thorne, K.S. Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef] [Green Version]
- Junior Lima, H.C.D.; Crispino, L.C.B.; Cunha, P.V.P.; Herdeiro, C.A.R. Can different black holes cast the same shadow? Phys. Rev. D 2021, 103, 084040. [Google Scholar] [CrossRef]
- Simpson, A. From black-bounce to traversable wormhole, and beyond. arXiv 2021, arXiv:2110.05657. [Google Scholar]
- Bambhaniya, P.; Jusufi, S.K.K.; Joshi, P.S. Thin accretion disk in the Simpson-Visser black-bounce and wormhole spacetimes. Phys. Rev. D 2022, 105, 023021. [Google Scholar] [CrossRef]
- Terno, D.R. Inaccessibility of traversable wormholes. Phys. Rev. D 2022, 106, 044035. [Google Scholar] [CrossRef]
- Junior, E.L.B.; Rodrigues, M.E. Black-Bounce in f(T) Gravity. arXiv 2022, arXiv:2203.03629. [Google Scholar]
- Islam, S.U.; Kumar, J.; Ghosh, S.G. Strong gravitational lensing by rotating Simpson-Visser black holes. J. Cosmol. Astropart. Phys. 2021, 10, 013. [Google Scholar] [CrossRef]
- Nascimento, J.R.; Petrov, A.Y.; Porfirio, P.J.; Soares, A.R. Gravitational lensing in black-bounce spacetimes. Phys. Rev. D 2020, 102, 044021. [Google Scholar] [CrossRef]
- Tsukamoto, N. Gravitational lensing in the Simpson-Visser black-bounce spacetime in a strong deflection limit. Phys. Rev. D 2021, 103, 024033. [Google Scholar] [CrossRef]
- Övgün, A. Weak Deflection Angle of Black-bounce Traversable Wormholes Using Gauss-Bonnet Theorem in the Dark Matter Medium. Turk. J. Phys. 2020, 44, 465–471. [Google Scholar] [CrossRef]
- Chataignier, L.; Kamenshchik, A.Y.; Tronconi, A.; Venturi, G. Regular black holes, universes without singularities, and phantom-scalar field transitions. arXiv 2022, arXiv:2208.02280. [Google Scholar]
- Bronnikov, K.A. Black bounces, wormholes, and partly phantom scalar fields. Phys. Rev. D 2022, 106, 064029. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Vrba, J. Epicyclic Oscillations around Simpson–Visser Regular Black Holes and Wormholes. Universe 2021, 7, 279. [Google Scholar] [CrossRef]
- Churilova, M.S.; Stuchlik, Z. Ringing of the regular black-hole/wormhole transition. Class. Quant. Grav. 2020, 37, 075014. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Liu, D.; Xu, Z.; Long, Z.W. Echoes from black bounces surrounded by the string cloud. arXiv 2022, arXiv:2210.12641. [Google Scholar]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Visinelli, L.; Afrin, M.; Allahyari, A.; Bambhaniya, P.; Dey, D.; Ghosh, S.G.; Joshi, P.S.; et al. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A*. arXiv 2022, arXiv:2205.07787. [Google Scholar]
- Lobo, F.S.N.; Rodrigues, M.E.; Silva, M.V.d.S.; Simpson, A.; Visser, M. Novel black-bounce spacetimes: Wormholes, regularity, energy conditions, and causal structure. Phys. Rev. D 2021, 103, 084052. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; The University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Alencar, G.; Muniz, C.R. Thermodynamic Properties of Static and Rotating Unparticle Black Holes. J. Cosmol. Astropart. Phys. 2018, 3, 040. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, I.D.D.; Furtado, J.; Landim, R.R.; Alencar, G. Horizon Fractalization in Black Strings Ungravity. arXiv 2022, arXiv:2209.14793. [Google Scholar]
- Rayimbaev, J.; Demyanova, A.; Camci, U.; Abdujabbarov, A.; Ahmedov, B. Dynamics of charged and magnetized particles around cylindrical black holes immersed in external magnetic field. Int. J. Mod. Phys. D 2021, 30, 2150019. [Google Scholar] [CrossRef]
- Nilton, M.; Alencar, G. Black Strings in Asymptotically Safe Gravity. arXiv 2022, arXiv:2211.02581. [Google Scholar]
- Furtado, J.; Alencar, G. BTZ Black-bounce to Traversable Wormhole. Universe 2022, 8, 625. [Google Scholar] [CrossRef]
- Jefremov, P.I.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Innermost stable circular orbits of spinning test particles in Schwarzschild and Kerr space-times. Phys. Rev. D 2015, 91, 124030. [Google Scholar] [CrossRef]

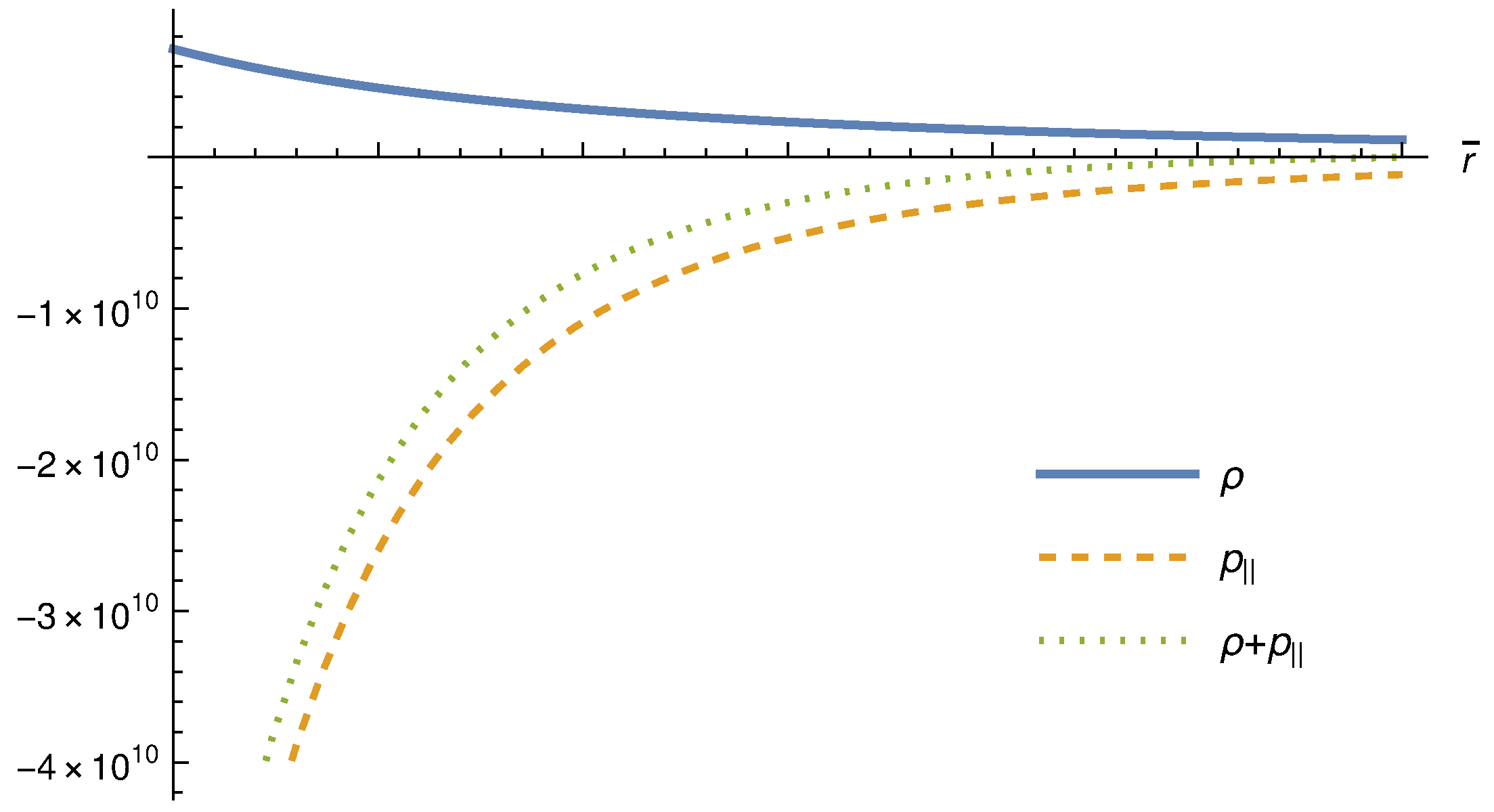

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, A.M.; de Alencar Filho, G.M.; Furtado Neto, J.S. Black String Bounce to Traversable Wormhole. Symmetry 2023, 15, 150. https://doi.org/10.3390/sym15010150
Lima AM, de Alencar Filho GM, Furtado Neto JS. Black String Bounce to Traversable Wormhole. Symmetry. 2023; 15(1):150. https://doi.org/10.3390/sym15010150
Chicago/Turabian StyleLima, Arthur Menezes, Geová Maciel de Alencar Filho, and Job Saraiva Furtado Neto. 2023. "Black String Bounce to Traversable Wormhole" Symmetry 15, no. 1: 150. https://doi.org/10.3390/sym15010150
APA StyleLima, A. M., de Alencar Filho, G. M., & Furtado Neto, J. S. (2023). Black String Bounce to Traversable Wormhole. Symmetry, 15(1), 150. https://doi.org/10.3390/sym15010150





