Stochastic Solitons in Birefringent Fibers for Biswas–Arshed Equation with Multiplicative White Noise via Itô Calculus by Modified Extended Mapping Method
Abstract
:1. Introduction
2. Preliminaries
3. Stochastic Solitons and Other Solutions
- Case 1:
- .
- Set 1:
- Set 2:
- Set 3:
- (1.1,1)
- If , then,represent bright solitons.
- (1.1,2)
- If , then,orrepresent singular periodic wave solutions.
- (1.1,3)
- If then,represent rational solutions.
- (1.2,1)
- If , then,represent dark solitons.
- (1.2,2)
- If , then,orrepresent periodic wave solutions.
- (1.2,3)
- If then,represent rational solutions.
- Case 2:
- .
- Set 1:
- Set 2:
- Set 3:
- Set 4:
- Set 5:
- Set 6:
- Set 7:
- (2.1,1)
- If , then,represent dark solitons.
- (2.1,2)
- If then,represent periodic solutions.
- (2.2,1)
- If , then,represent singular solitons.
- (2.2,2)
- If then,represent periodic solutions.
- (2.3,1)
- If , then,represent singular solitons.
- (2.3,2)
- If then,represent periodic solutions.
- (2.4,1)
- If , then,represent singular solitons.
- (2.2,2)
- If then,represent periodic solutions.
- (2.5,1)
- If , then,represent singular solitons.
- (2.5,2)
- If then,represent periodic solutions.
- (2.6,1)
- If , then,represent singular solitons.
- (2.6,2)
- If then,represent periodic solutions.
- represent periodic solutions.
- Case 3:
- If, we set ,
- (3.1)
- If , then,represent combo singular-bright solitons.
- (3.2)
- If then,represent periodic solutions.
- (3.3)
- If then,represent periodic solutions.
- Case 4:
- If we set ,
- Case 5:
- .
- Set 1:
- Set 2:
- Set 3:
- Set 4:
- (5.1,1)
- If , then,represent dark solitons.
- (5.1,2)
- If , then,represent singular solitons.
- (5.2,1)
- If , then,represent singular solitons.
- (5.2,2)
- If , thenrepresent combo bright–dark solitons.
- (5.3,1)
- If , then,represent singular solitons.
- (5.3,2)
- If , then,represent periodic solutions.
- (5.4,1)
- If , then,represent singular solitons.
- (5.4,2)
- If , then,represent periodic solutions.
- Case 6:
- If we set ,
- Case 7:
- .
- Set 1:
- Set 2:
- Set 3:
- (7.1,1)
- If , then,orrepresent Jacobi elliptic function solutions.If we take , then,orrepresent periodic solutions.
- (7.1,2)
- If , then,represent Jacobi elliptic function solutions.If we take , then,represent dark solitons.
- (7.1,3)
- If , then,If we take , then,represent dark solitons.
- (7.1,4)
- If , then,represent Jacobi elliptic function solutions.
- (7.2,1)
- If then,orrepresent periodic solutions.
- (7.2,2)
- If , then,represent dark solitons.
- (7.3,1)
- If then,represent periodic solutions.
- (7.3,2)
- If , then,represent dark solitons.
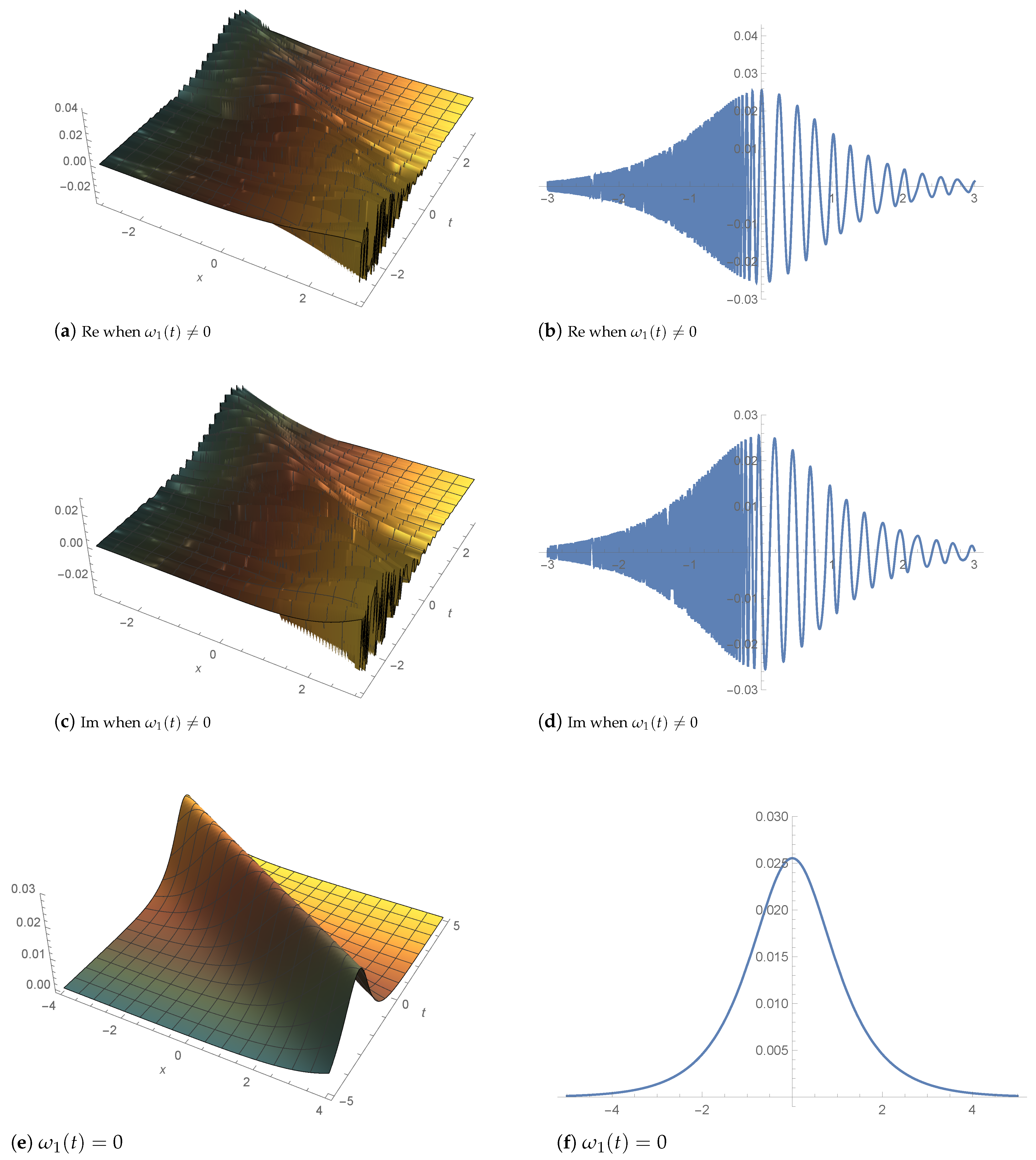
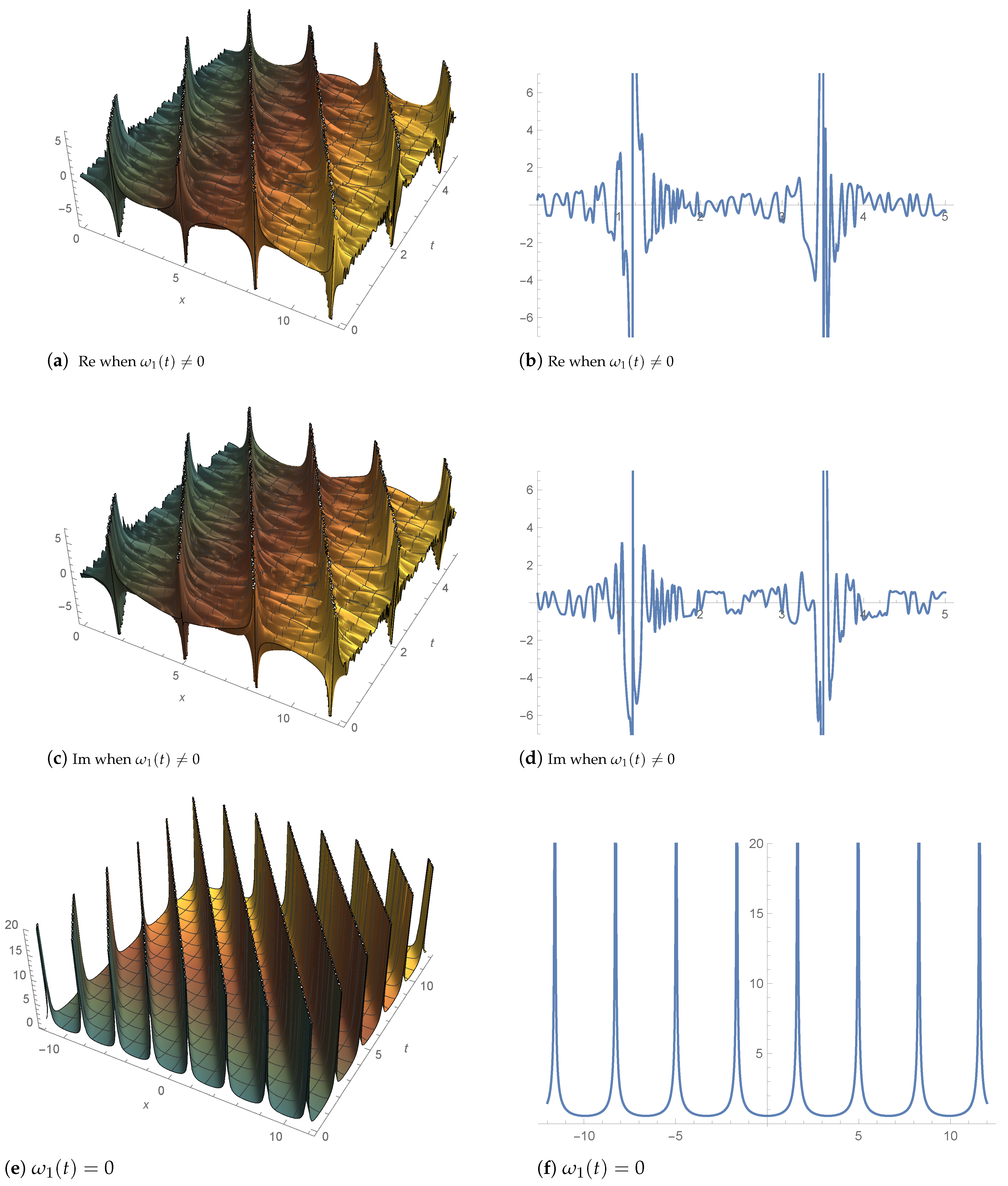
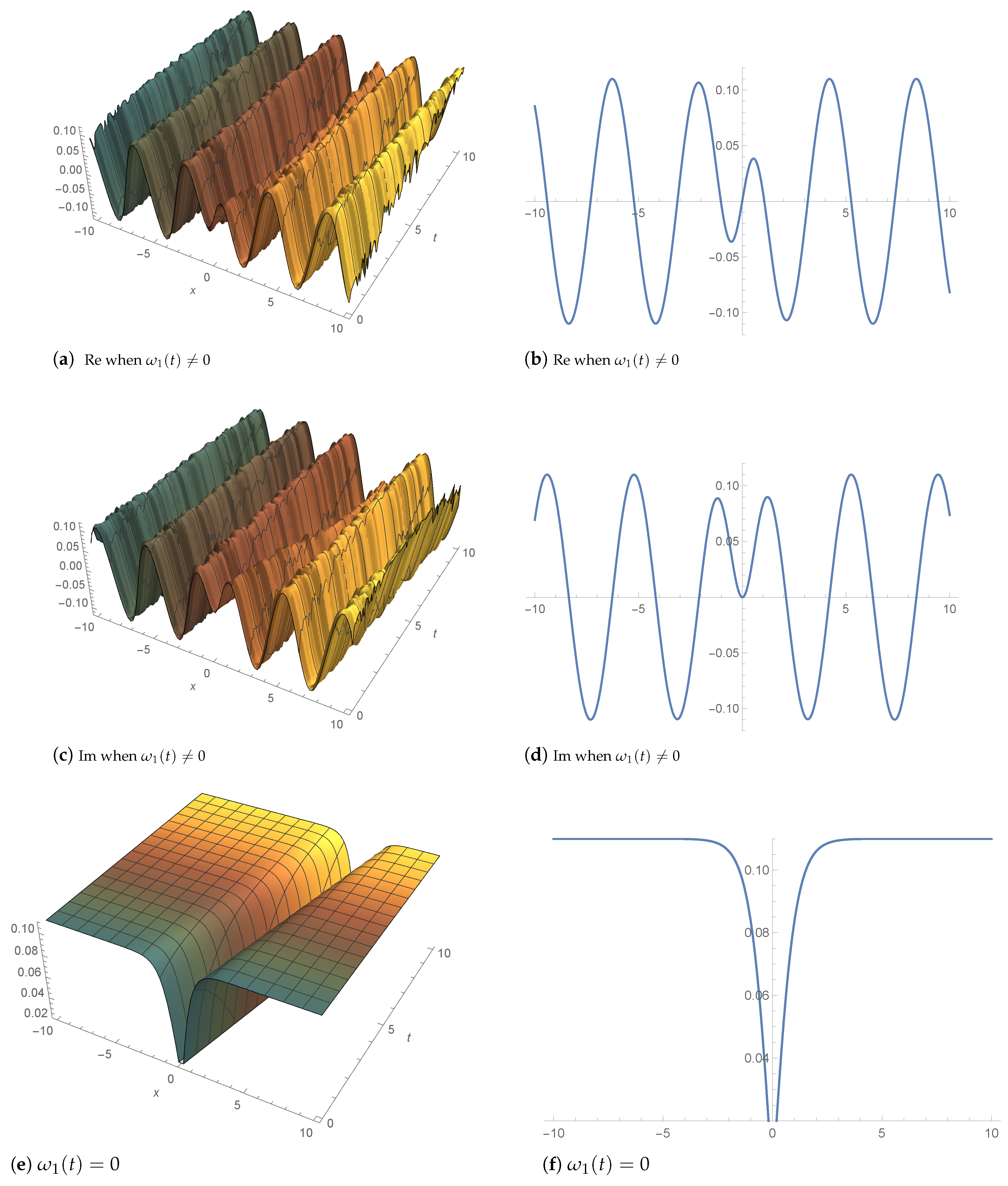
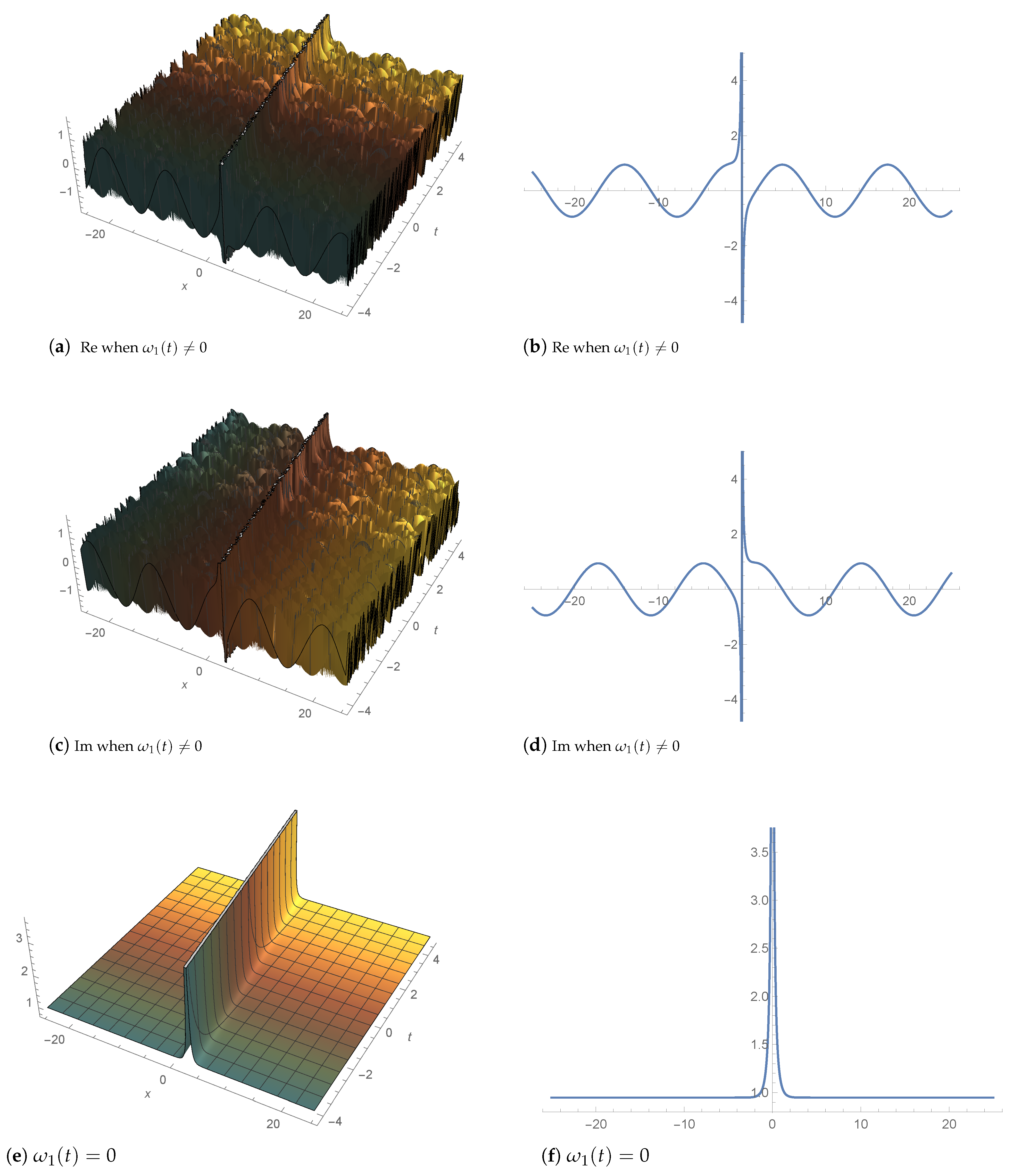
4. Graphic Illustration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hyder, A.A.; Soliman, A.H. Analytical manner for abundant stochastic wave solutions of extended KdV equation with conformable differential operators. Math. Methods Appl. Sci. 2022, 45, 8600–8612. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.; Sohaly, M.A. On the new wave solutions to the MCH equation. Indian J. Phys. 2019, 93, 903–911. [Google Scholar] [CrossRef]
- Oh, T.; Okamoto, M. Comparing the stochastic nonlinear wave and heat equations: A case study. Electron. J. Probab. 2021, 26, 1–44. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Stationary solitons of the generalized nonlinear Schrödinger equation with nonlinear dispersion and arbitrary refractive index. Appl. Math. Lett. 2022, 128, 107888. [Google Scholar] [CrossRef]
- Ahmed, K.K.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Soliton Solutions and Other Solutions for Kundu–Eckhaus Equation with Quintic Nonlinearity and Raman Effect Using the Improved Modified Extended Tanh-Function Method. Mathematics 2022, 10, 4203. [Google Scholar] [CrossRef]
- Bekir, A.; Zahran, E. Three distinct and impressive visions for the soliton solutions to the higher-order nonlinear Schrodinger equation. Optik 2021, 228, 166157. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Modulation stability and dispersive optical soliton solutions of higher order nonlinear Schrödinger equation and its applications in mono-mode optical fibers. Superlattices Microstruct. 2018, 113, 419–429. [Google Scholar] [CrossRef]
- Rasheed, N.M.; Al-Amr, M.O.; Az-Zo’bi, E.A.; Tashtoush, M.A.; Akinyemi, L. Stable optical solitons for the Higher-order Non-Kerr NLSE via the modified simple equation method. Mathematics 2021, 9, 1986. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of the generalized nonlinear Schrödinger equation with Kerr nonlinearity and dispersion of unrestricted order. Mathematics 2022, 10, 3409. [Google Scholar] [CrossRef]
- Hendi, A.A.; Ouahid, L.; Kumar, S.; Owyed, S.; Abdou, M.A. Dynamical behaviors of various optical soliton solutions for the Fokas–Lenells equation. Mod. Phys. Lett. B 2021, 35, 2150529. [Google Scholar] [CrossRef]
- Ozisik, M. On the optical soliton solution of the (1+1)-dimensional perturbed NLSE in optical nano-fibers. Optik 2022, 250, 168233. [Google Scholar] [CrossRef]
- Tozar, A.; Tasbozan, O.; Kurt, A. Optical soliton solutions for the (1+1)-dimensional resonant nonlinear Schröndinger’s equation arising in optical fibers. Opt. Quantum Electron. 2021, 53, 316. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Gómez-Aguilar, J.F. Soliton solutions of the Sasa–Satsuma equation in the monomode optical fibers including the beta-derivatives. Optik 2020, 224, 165425. [Google Scholar] [CrossRef]
- Owyed, S.; Abdou, M.A.; Abdel-Aty, A.H.; Ray, S.S. New optical soliton solutions of nolinear evolution equation describing nonlinear dispersion. Commun. Theor. Phys. 2019, 71, 1063. [Google Scholar] [CrossRef]
- Younis, M.; Seadawy, A.R.; Baber, M.Z.; Husain, S.; Iqbal, M.S.; Rizvi, S.T.R.; Baleanu, D. Analytical optical soliton solutions of the Schrödinger-Poisson dynamical system. Results Phys. 2021, 27, 104369. [Google Scholar] [CrossRef]
- Ali, K.K.; Wazwaz, A.M.; Osman, M.S. Optical soliton solutions to the generalized nonautonomous nonlinear Schrödinger equations in optical fibers via the sine-Gordon expansion method. Optik 2020, 208, 164132. [Google Scholar] [CrossRef]
- Rabie, W.B.; Seadawy, A.R.; Ahmed, H.M. Highly dispersive Optical solitons to the generalized third-order nonlinear Schrödinger dynamical equation with applications. Optik 2021, 241, 167109. [Google Scholar] [CrossRef]
- Bilal, M.; Ren, J.; Younas, U. Stability analysis and optical soliton solutions to the nonlinear Schrödinger model with efficient computational techniques. Opt. Quantum Electron. 2021, 53, 406. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Ullah, N.; Akinyemi, L.; Shah, A.; Mirhosseini-Alizamin, S.M.; Chu, Y.M.; Ahmad, H. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov’s method. Results Phys. 2021, 24, 104179. [Google Scholar] [CrossRef]
- Savaissou, N.; Gambo, B.; Rezazadeh, H.; Bekir, A.; Doka, S.Y. Exact optical solitons to the perturbed nonlinear Schrödinger equation with dual-power law of nonlinearity. Opt. Quantum Electron. 2020, 52, 318. [Google Scholar] [CrossRef]
- Mostafa, E.; Rezazadeh, H. The first integral method for Wu-Zhang system with conformable time fractional derivative. Calcolo 2016, 53, 475–485. [Google Scholar]
- Rezazadeh, H.; Younis, M.; Eslami, M.; Bilal, M.; Younas, U. New exact traveling wave solutions to the (2+1)-dimensional Chiral nonlinear Schröndinger equation. Math. Model. Nat. Phenom. 2021, 16, 1–15. [Google Scholar] [CrossRef]
- Ma, W.X. Soliton solutions by means of Hirota bilinear forms. Partial Differ. Equ. Appl. Math. 2022, 5, 100220. [Google Scholar] [CrossRef]
- Ma, W.X. Nonlocal PT-symmetric integrable equations and related Riemann–Hilbert problems. Partial Differ. Equ. Appl. Math. 2021, 4, 100190. [Google Scholar] [CrossRef]
- Ma, W.X. Integrable nonlocal nonlinear Schrödinger equations associated with so (3, ). Proc. Am. Math. Soc. Ser. B 2022, 9, 1–11. [Google Scholar] [CrossRef]
- Ma, W.X. A multi-component integrable hierarchy and its integrable reductions. Phys. Lett. A 2022, 128575. [Google Scholar] [CrossRef]
- Ma, W.X. Reduced Non-Local Integrable NLS Hierarchies by Pairs of Local and Non-Local Constraints. Int. J. Appl. Comput. Math. 2022, 8, 206. [Google Scholar] [CrossRef]
- Bo, W.B.; Wang, R.R.; Liu, W.; Wang, Y.Y. Symmetry breaking of solitons in the PT-symmetric nonlinear Schrödinger equation with the cubic–quintic competing saturable nonlinearity. Chaos. Interdiscip. J. Nonlinear Sci. 2022, 32, 093104. [Google Scholar] [CrossRef] [PubMed]
- Bo, W.B.; Liu, W.; Wang, Y.Y. Symmetric and antisymmetric solitons in the fractional nonlinear schrödinger equation with saturable nonlinearity and PT-symmetric potential.Stability and dynamics. Optik 2022, 255, 168697. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I. Self-steepening, Raman scattering and self-phase modulation-interactions via the perturbed Chen–Lee–Liu equation with an extra dispersion. Modulation insability and spectral analysis. Opt. Quantum Electron. 2022, 54, 426. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I. Longitudinal-transverse soliton chains analog to heisenberg ferromagnetic spin chains in (2+1) dimensional with biquadrant interactions. Opt. Quantum Electron. 2022, 54, 479. [Google Scholar] [CrossRef]
- Khan, S.; Biswas, A.; Zhou, Q.; Adesanya, S.; Alfiras, M.; Belic, M. Stochastic perturbation of optical solitons having anti-cubic nonlinearity with bandpass filters and multi-photon absorption. Optik 2019, 178, 1120–1124. [Google Scholar] [CrossRef]
- He, T.; Wang, Y.Y. Dark-multi-soliton and soliton molecule solutions of stochastic nonlinear Schrödinger equation in the white noise space. Appl. Math. Lett. 2021, 121, 107405. [Google Scholar] [CrossRef]
- Arshed, S.; Raza, N.; Javid, A.; Baskonus, H.M. Chiral solitons of (2+1)-dimensional stochastic chiral nonlinear Schrödinger equation. Int. J. Geom. Methods Mod. Phys. 2021, 19, 2250149. [Google Scholar] [CrossRef]
- Secer, A. Stochastic optical solitons with multiplicative white noise via Itô calculus. Optik 2022, 268, 169831. [Google Scholar] [CrossRef]
- Yin, H.M.; Tian, B.; Chai, J.; Wu, X.Y. Stochastic soliton solutions for the (2+1)-dimensional stochastic Broer–Kaup equations in a fluid or plasma. Appl. Math. Lett. 2018, 82, 126–131. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Alngar, M.E.M. Optical solitons in birefringent fibers with Biswas-Arshed equation having multiplicative noise via Itô calculus using two integration algorithms. Optik 2022, 262, 169322. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D.; Saleem, M.S. Elliptic function solutions, modulation instability and optical solitons analysis of the paraxial wave dynamical model with Kerr media. Opt. Quantum Electron. 2021, 53, 7. [Google Scholar] [CrossRef]
- Samir, I.; Badra, N.; Ahmed, H.M.; Arnous, A.H.; Ghanem, A.S. Solitary wave solutions and other solutions for Gilson–Pickering equation by using the modified extended mapping method. Results Phys. 2022, 36, 105427. [Google Scholar] [CrossRef]
- Saleh, R.; Mabrouk, S.M.; Wazwaz, A.M. Lie symmetry analysis of a stochastic gene evolution in double-chain deoxyribonucleic acid system. Waves Random Complex Media 2022, 32, 2903–2917. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhojilan, Y.; Ahmed, H.M.; Rabie, W.B. Stochastic Solitons in Birefringent Fibers for Biswas–Arshed Equation with Multiplicative White Noise via Itô Calculus by Modified Extended Mapping Method. Symmetry 2023, 15, 207. https://doi.org/10.3390/sym15010207
Alhojilan Y, Ahmed HM, Rabie WB. Stochastic Solitons in Birefringent Fibers for Biswas–Arshed Equation with Multiplicative White Noise via Itô Calculus by Modified Extended Mapping Method. Symmetry. 2023; 15(1):207. https://doi.org/10.3390/sym15010207
Chicago/Turabian StyleAlhojilan, Yazid, Hamdy M. Ahmed, and Wafaa B. Rabie. 2023. "Stochastic Solitons in Birefringent Fibers for Biswas–Arshed Equation with Multiplicative White Noise via Itô Calculus by Modified Extended Mapping Method" Symmetry 15, no. 1: 207. https://doi.org/10.3390/sym15010207
APA StyleAlhojilan, Y., Ahmed, H. M., & Rabie, W. B. (2023). Stochastic Solitons in Birefringent Fibers for Biswas–Arshed Equation with Multiplicative White Noise via Itô Calculus by Modified Extended Mapping Method. Symmetry, 15(1), 207. https://doi.org/10.3390/sym15010207





