Simulation Studies on the Dissipative Modified Kawahara Solitons in a Complex Plasma

Abstract

In this work, a damped modified Kawahara equation (mKE) with cubic nonlinearity and two dispersion terms including the third- and fifth-order derivatives is analyzed. We employ an effective semi-analytical method to achieve the goal set for this study. For this purpose, the ansatz method is implemented to find some approximate solutions to the damped mKE. Based on the proposed method, two different formulas for the analytical symmetric approximations are formally obtained. The derived formulas could be utilized for studying all traveling waves described by the damped mKE, such as symmetric solitary waves (SWs), shock waves, cnoidal waves, etc. Moreover, the energy of the damped dressed solitons is derived. Furthermore, the obtained approximations are used for studying the dynamics of the dissipative dressed (modified Kawahara (mK)) dust-ion acoustic (DIA) solitons in an unmagnetized collisional superthermal plasma consisting of inertia-less superthermal electrons and inertial cold ions as well as immobile negative dust grains. Numerically, the impact of the collisional parameter that arises as a result of taking the ion-neutral collisions into account and the electron spectral index on the profile of the dissipative structures are examined. Finally, the analytical and numerical approximations using the finite difference method (FDM) are compared in order to confirm the high accuracy of the obtained approximations. The achieved results contribute to explaining the mystery of several nonlinear phenomena that arise in different plasma physics, nonlinear optics, shallow water waves, oceans, and seas, and so on.

1. Introduction

The study of differential equations (DEs) (e.g., ordinary, partial, linear, nonlinear, etc.) is interesting and inevitable. The significance of DEs is paramount for understanding how nature works, as it helps in modeling a vast number of problems in engineering, physics, chemistry, biology, medicine, etc. This enables us to understand how scientific phenomena behave and how to manifest the precise details of nature and to control its behavior [1,2]. There are many equations that have greatly succeeded in explaining the mechanism of solitary wave propagation in various physical models [3,4,5,6]. An example is the third- and/or fifth-order Korteweg–de Vries (KdV) equation $\left({\partial }_{\tau }\varphi +a\varphi {\partial }_{\zeta }\varphi +b{\partial }_{\zeta }^3\varphi =0\right)$, which is considered one of the most famous equations of the twenty-first century due to its great role in modeling many nonlinear phenomena that arise in electrical circuits, seas, oceans, nonlinear optics, shallow water waves, in addition to plasma physics [7,8]. The KdV equation succeeded in describing the mechanism of propagation of many nonlinear structures (e.g., solitons) in various fields of science, especially in plasma, seas, and oceans. However, the KdV equation sometimes fails to model the nonlinear structures at some physical values of the parameters related to the model under consideration, which are called ‘critical parameters’. At these critical parameters, the coefficient of the nonlinear term “a” disappears, and the KdV equation becomes unsuitable for modeling nonlinear structures. Accordingly, many researchers have derived another high-order nonlinearity evolution equation to describe the nonlinear structures at the critical values of plasma compositions, which is called the ‘modified KdV (mKdV) equation’: ${\partial }_{\tau }\varphi +c{\varphi }^2{\partial }_{\zeta }\varphi +b{\partial }_{\zeta }^3\varphi =0$, where c represents the coefficient of the cubic nonlinear term. However, sometimes both KdV and mKdV equations fail to describe the nonlinear waves near/close to the critical values of some plasma compositions. Therefore, many authors have come up with another evolution equation, known as the ‘Extended/Gardner KdV (EKdV) equation’: ${\partial }_{\tau }\varphi +\left(a\varphi +c{\varphi }^2\right){\partial }_{\zeta }\varphi +b{\partial }_{\zeta }^3\varphi =0$, which has succeeded in modeling many nonlinear waves near/close to the critical values of some plasma compositions.

It is noted that the aforementioned equations are called the ‘family of the third-order dispersion KdV equation’ or the ‘KdV-type equation’. On the contrary, there is another form of the KdV-type equation of a fifth-order dispersion term, which is called the ‘fifth-order KdV-type (fKdV-type) equation’ or sometimes the ‘Kawahara-type equation’, which includes the following family of the Kawahara equation (KE) [9,10,11,12,13]:

$$\begin{array}{cc}\hfill \mathrm{damped}\mathrm{KE}& :{\partial }_{\tau }\varphi +a\varphi {\partial }_{\zeta }\varphi +B{\partial }_{\zeta }^3\varphi -d{\partial }_{\zeta }^5\varphi =0,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathrm{damped}\mathrm{KE}& :{\partial }_{\tau }\varphi +a\varphi {\partial }_{\zeta }\varphi +B{\partial }_{\zeta }^3\varphi -d{\partial }_{\zeta }^5\varphi +R\varphi =0,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \mathrm{nonplanar}\mathrm{KE}& :{\partial }_{\tau }\varphi +a\varphi {\partial }_{\zeta }\varphi +B{\partial }_{\zeta }^3\varphi -d{\partial }_{\zeta }^5\varphi +\frac{m}{2\tau }\varphi =0,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathrm{nonplanar}\mathrm{damped}\mathrm{KE}& :{\partial }_{\tau }\varphi +a\varphi {\partial }_{\zeta }\varphi +B{\partial }_{\zeta }^3\varphi -d{\partial }_{\zeta }^5\varphi +\left(R+\frac{m}{2\tau }\right)\varphi =0,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathrm{modified}\mathrm{KE}\left(\mathrm{mKE}\right)& :{\partial }_{\tau }\varphi +A{\varphi }^2{\partial }_{\zeta }\varphi +B{\partial }_{\zeta }^3\varphi -d{\partial }_{\zeta }^5\varphi =0.\hfill \end{array}$$

(5)

Many other forms, such as forced KE, forced mKE, Gardner/Extended KE (EKE), and forced EKE, have been studied and solved using a variety of analytical and numerical approaches. Here, “a” and “B” are the coefficients of the quadratic nonlinear term and the third-order dispersion term, respectively. However, the parameter “d” is the coefficient of the fifth-order dispersion term, and $\varphi \equiv \varphi \left(\zeta ,\tau \right).$ The family of the fifth-order dispersion term has many applications in several branches of science, such as capillary-gravity water waves, waves in plasma physics [14,15,16], shallow water waves (WWs), WWs with surface tension, and many other applications [17,18,19,20,21]. Due to the importance of this family in modeling many nonlinear physical problems, it has been analyzed and solved using several analytical and numerical techniques, e.g., the tanh method (TM) [22,23,24], tanh–coth method [22], a direct algebraic method [25], the homotopy analysis method (HAM) [26], sine–cosine [27], mesh-free method [28], septic B-spline collocation method [29], and so on [30]. For instance, Wazwaz [31] used many exact methods, including TM, extended TM, and sine–cosine method, to find a series of analytical solutions to the mKE using the sine–cosine method, the tanh method, and the ansatz method based on hyperbolic functions for analyzing and solving the mKE. Moreover, the homogeneous balance method (HBM) [32] has been employed for solving KE, and the authors [32] compared the obtained results with the ($G^{\prime }/G$)-expansion method solution and the F-expansion method solutions. Additionally, Gepreel et al. [33] used the improved general mapping deformation technique to find some exact analytic solutions to some nonlinear PDEs, such as the planar mKE. In addition, both the homotopy perturbation method (HPM) and the variational iteration method (VIM) [34] have been professionally applied to analyze the mKE and some related equations of the fifth-order dispersion term. The authors of [34] compared the numerical solutions of the VIM and HPM methods and the exact solutions to the mKE. The authors of [34] found that both VIM and HPM are characterized by their high accuracy and efficiency and ease of processing that many other numerical methods do not furnish. Biazar et al. [35] used both the VIM and Adomian decomposition method (ADM) to find some analytical approximations for both KE and mKE. Additionally, the KE has been solved numerically using the optimal homotopy asymptotic technique (OHAT) [36,37]. Further, the authors of [36] compared the solution obtained via the OHAT and the exact solution to this equation using VIM, HPM, and Variational HPM (VHPM) and found that the solution obtained using OHAT has higher accuracy than some of the indicated methods. Moreover, the OHAT [37] has been applied to determine an approximate solution to the mKE. Recently, El-Tantawy [13] used TM, the ansatz method based on the trigonometric, the Weierrtrass, and the Jacobi elliptic functions for deriving exact solutions to both mKE and EKE.

All the aforementioned studies focused on analyzing the family of differential equations that have a fifth-order dispersion term, including KE, mKE, EKE, etc., that support exact analytical solutions. However, there are many physical effects that if taken into account, such as the viscosity, collision, etc., eventually lead to some evolutionary equations with the fifth-order dispersion term with no exact analytical solution. For example, we report the case of the collision of charged particles with each other or neutral particles within some plasma systems. In this case, the fluid equations of the plasma model under study can be reduced to the family of damped Kawahara-type equations in order to study the properties of the nonlinear dissipative waves that propagate in a plasma model [38,39,40]. Further, if the geometrical effects are considered, then the set of fluid equations are reduced to the family of a completely non-integrable nonplanar (cylindrical and spherical) KE [11]. The families of the damped Kawahara-type equation, nonplanar Kawahara-type equation, and nonplanar damped Kawahara-type equation do not support exact solutions and must be solved using some numerical or semi-analytical methods. For instance, the non-integrable nonplanar damped KE (4) has been solved analytically using the ansatz method to derive semi-analytical solutions with high accuracy in order to study the properties of nonplanar dissipative Kawahara solitary and cnoidal waves in superthermal dusty plasma [12]. Further, the authors of [12] derived a general formula for the nonplanar dressed soliton energy. Sometimes, the collisional force between the charged particles cannot be neglected in some types of plasma compositions [41,42,43,44,45], especially cold plasma. Further, at certain values of plasma parameters, the nonlinear quadratic term disappears, so this forces us to search for higher-order nonlinearity orders to be able to describe the physical phenomenon at these values. Accordingly, the following new evolutionary equation, which is called ’damped mKE’ is obtained:

$${\partial }_{\tau }\psi +A{\psi }^2{\partial }_{\zeta }\psi +B{\partial }_{\zeta }^3\psi -d{\partial }_{\zeta }^5\psi +R\psi =0,$$

(6)

where $\psi \equiv \psi \left(\zeta ,\tau \right)$, and R indicates the coefficient of the linear term that arises as a result of taking the collisional force between the charged and neutral plasma particles into account.

Equation (6) is used to describe large but finite amplitudes of dissipative nonlinear waves at some critical plasma compositions or any other fluid model described by this equation. To our knowledge and based on a comprehensive and thorough survey, this is the first analysis of the damped mKE using a semi-analytical approach. Thus, the main objective of the present investigation is to derive semi-analytical solutions/analytical approximations to Equation (6) using the ansatz method [10,11,12]. Moreover, the finite difference method (FDM) is applied to find numerical approximations for comparison with the semi-analytical solutions. Further, the global maximum residual error (GMRE) for all obtained approximations is estimated to confirm the effectiveness of all obtained approximations:

$$L_R={\left.\mathrm{FindMaximum}\right|}_{\mho }\left|{\partial }_{\tau }\psi +A{\psi }^2{\partial }_{\zeta }\psi +B{\partial }_{\zeta }^3\psi -d{\partial }_{\zeta }^5\psi +R\psi \right|,$$

(7)

where $\mho \in \left[{\zeta }_i,{\zeta }_f\right]\times \left[{\tau }_i,{\tau }_f\right]$ represents the whole study domain.

The second objective of this investigation is to derive a formula for the energy of the damped modified Kawahara soliton and prove that it is not conserved due to the existence of the damping term. Further, we prove that the obtained formula of the damped modified Kawahara soliton energy can recover the energy of the conserved case. The third objective is to use all obtained semi-analytical solutions in order to study the distinctive characteristics of the damped (dissipative) modified Kawahara solitary waves (SWs) in a super-thermal dusty plasma composed of fluid inertial cold ions and superthermal electrons in addition to the immobile negative dust grains.

The paper is structured as follows: in Section 2, the anstaz method is carried out for analyzing the damped mKE in order to find semi-analytical solutions to the damped mKE (6). All derived semi-analytical solutions are implemented to find the dissipative modified Kawahara SWs, as illustrated in Section 3. For the physical application, the reductive perturbation method (RPM) is used for reducing the fluid equations of a superthermal dusty plasma to a damped mKE (6). After that, the impact of the plasma parameters on the profile (including the width and the amplitude) of the dissipative modified Kawahara solitons is discussed in Section 4. In Section 5, we briefly summarize the most important results we obtained.

2. The Anstaz Method for Analyzing the Damped mKE

Since the damped mKE (6) cannot be solved analytically via exact analytical methods due to the existence of the collisional term, in this section, we try to determine semi-analytical solutions to this equation using one of the semi-analytical methods that give good results with this type of non-integrable equation. Thus, the anstaz method is applied to find symmetric approximations to the damped mKE (6). This method is summarized as follows:

• We assume the solution of the damped mKE (6) is in the form

  $$\psi (\zeta ,\tau )=F_1\varphi \left(\zeta F_2,F_3\right)\equiv F_1{\varphi }_F.$$

  (8)
  Here, $F_1\equiv F_1\left(\tau \right)$, $F_2\equiv F_2\left(\tau \right)$, and $F_3\equiv F_3\left(\tau \right)$ are, respectively, time-dependent functions related to the temporal amplitude, inverted width, and wave velocity of the damped structures. Remember that for $F_{1,2}=1$ and $F_3=t$, the planar undamped case is recovered. Further, the function $\varphi \left(\zeta ,\tau \right)$ indicates the exact solution to the mKE (5).
• Inserting Equation (8) into the damped mKE (6), the following values of ${\partial }_{\zeta }^n\psi$ and ${\partial }_{\tau }\psi$ $\left(n=1,3,5\right)$ are obtained:

  $$\left\{\begin{array}{c}{\partial }_{\zeta }\psi =F_1{F}_2{\partial }_{\zeta }{\varphi }_F,\\ {\partial }_{\zeta }^3\psi =F_1{F}_2^3{\partial }_{\zeta }^3{\varphi }_F,\\ {\partial }_{\zeta }^5\psi =F_1{F}_2^5{\partial }_{\zeta }^5{\varphi }_F,\end{array}\right.$$

  (9)

  and

  $${\partial }_{\tau }\psi ={\dot{F}}_1{\varphi }_F+F_1\left[\zeta {\dot{F}}_2{\partial }_{\zeta }{\varphi }_F+{\dot{F}}_3\left(-A{\varphi }_F^2{\partial }_{\zeta }{\varphi }_F-B{\partial }_{\zeta }^3{\varphi }_F+d{\partial }_{\zeta }^5{\varphi }_F\right)\right].$$

  (10)
• Substituting the values of ${\partial }_{\zeta }^n\psi$ and ${\partial }_{\tau }\psi$ into the damped mKE (6) and reorganizing all terms, the following residual equation is obtained:

  $$Q_1{\partial }_{\zeta }^5{\varphi }_F+Q_2{\partial }_{\zeta }^3{\varphi }_F+Q_3{\varphi }_F^2{\partial }_{\zeta }{\varphi }_F+Q_4{\partial }_{\zeta }{\varphi }_F+Q_5{\varphi }_F=0,$$

  (11)

  with

  $$\left(\begin{array}{c}{Q}_1\\ Q_2\\ Q_3\\ Q_4\\ Q_5\end{array}\right)=\left(\begin{array}{c}\left(d\right)F_1\left(-F_2^5+{\dot{F}}_3\right),\\ B{F}_1\left(F_2^3-{\dot{F}}_3\right)\\ A{F}_1\left(F_1^2{F}_2-{\dot{F}}_3\right),\\ \zeta F_1{\dot{F}}_2,\\ {\dot{F}}_1+F_{1}R,\end{array}\right)$$

  where ${\dot{F}}_i\equiv {\partial }_{\tau }{F}_i$$\left(i=1,2,3\right).$
• Now, for $Q_i=0$$\left(i=1,2,3,5\right)$, we get the following system of differential equations:

  $$\begin{array}{cc}\hfill {\dot{F}}_1+F_{1}R& =0,\hfill \end{array}$$

  (12)

  $$\begin{array}{cc}\hfill F_1^2{F}_2-{\dot{F}}_3& =0,\hfill \end{array}$$

  (13)

  $$\begin{array}{cc}\hfill -F_2^5+{\dot{F}}_3& =0,\hfill \end{array}$$

  (14)

  $$\begin{array}{cc}\hfill F_2^3-{\dot{F}}_3& =0.\hfill \end{array}$$

  (15)
• Solving Equation (12) by using the initial condition (IC) $F_1\left({\tau }_0\right)=1$, the following value of $F_1$ is obtained:

  $$F_1=e^{R\left({\tau }_0-\tau \right)}.$$

  (16)
• It is clear from Equations (14) and (15) that there are two independent ODEs in $\left(F_2,F_3\right)$ in addition to Equation (13) which means that there are two values for $\left(F_2,F_3\right)$ that should be determined. By solving Equations (13) and (14) together, we get the first values for $\left(F_2,F_3\right).$ Further, by solving Equations (13) and (15) together, we get the second values for $\left(F_2,F_3\right)$. Inserting the value of $F_1,$ given in Equation (16), into Equation (13), yields

  $$\left(e^{2R\left({\tau }_0-\tau \right)}{F}_2-{\dot{F}}_3\right)=0.$$

  (17)
• For the first values of $\left(F_2,F_3\right)$: inserting Equation (14) $\left({\dot{F}}_3=F_2^5\right)$ into (17) yields

  $$\left(e^{2R\left({\tau }_0-\tau \right)}{F}_2-F_2^5\right)=0$$

  (18)

  and by solving Equation (18), we get

  $$F_2=e^{\frac{R}{2}\left({\tau }_0-\tau \right)}.$$

  (19)
  To find the value of $F_3$ corresponding to the value of $F_2$ given in Equation (19), we must solve Equation (14) using both IC $F_3{|}_{\tau ={\tau }_0}=0$ and the value of $F_2$ given in Equation (19), which leads to

  $$F_3=\frac{2}{5R}\left(1-e^{\frac{5R}{2}\left({\tau }_0-\tau \right)}\right),$$

  (20)
  It is obvious that the values of $\left(F_2,F_3\right)$ given in Equations (19) and (20) can be recovered in many cases, which is discussed later.
• For the second values of $\left(F_2,F_3\right)$: Equation (15) $\left({\dot{F}}_3=F_2^3\right)$ is inserted into (17) to get

  $$\left(e^{2R\left({\tau }_0-\tau \right)}{F}_2-F_2^3\right)=0$$

  (21)

  and by solving Equation (21), the following new value of $F_2$ is obtained

  $$F_2=e^{R\left({\tau }_0-\tau \right)}.$$

  (22)
  Now, by replacing the new value of $F_2$, given in Equation (22), into Equation (15), and using the IC $F_3{|}_{\tau ={\tau }_0}=0$, we finally get

  $$F_3=\frac{1}{3R}\left(1-e^{3R\left({\tau }_0-\tau \right)}\right),$$

  (23)
• By inserting both the first and second values of $\left(F_2,F_3\right)$ as well as the value of $F_1$ given in Equation (16) into the ansatz solution (8), the following two general approximate solutions of the damped mKE (6) are obtained:

  $${\psi }_1(\zeta ,\tau )=e^{R\left({\tau }_0-\tau \right)}\varphi \left[\zeta e^{\frac{R}{2}\left({\tau }_0-\tau \right)},\frac{2}{5R}\left(1-e^{\frac{5R}{2}\left({\tau }_0-\tau \right)}\right)\right],$$

  (24)

  and

  $${\psi }_2(\zeta ,\tau )=e^{R\left({\tau }_0-\tau \right)}\varphi \left[\zeta e^{R\left({\tau }_0-\tau \right)},\frac{1}{3R}\left(1-e^{3R\left({\tau }_0-\tau \right)}\right)\right].$$

  (25)

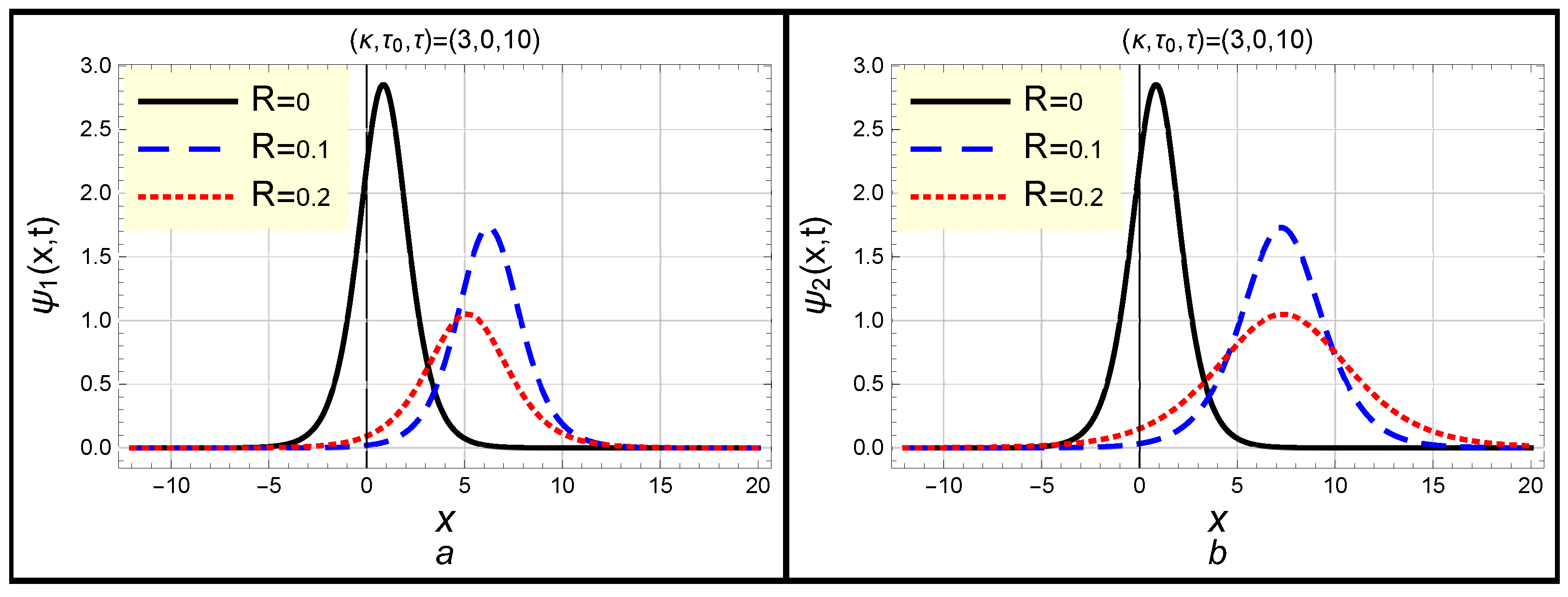
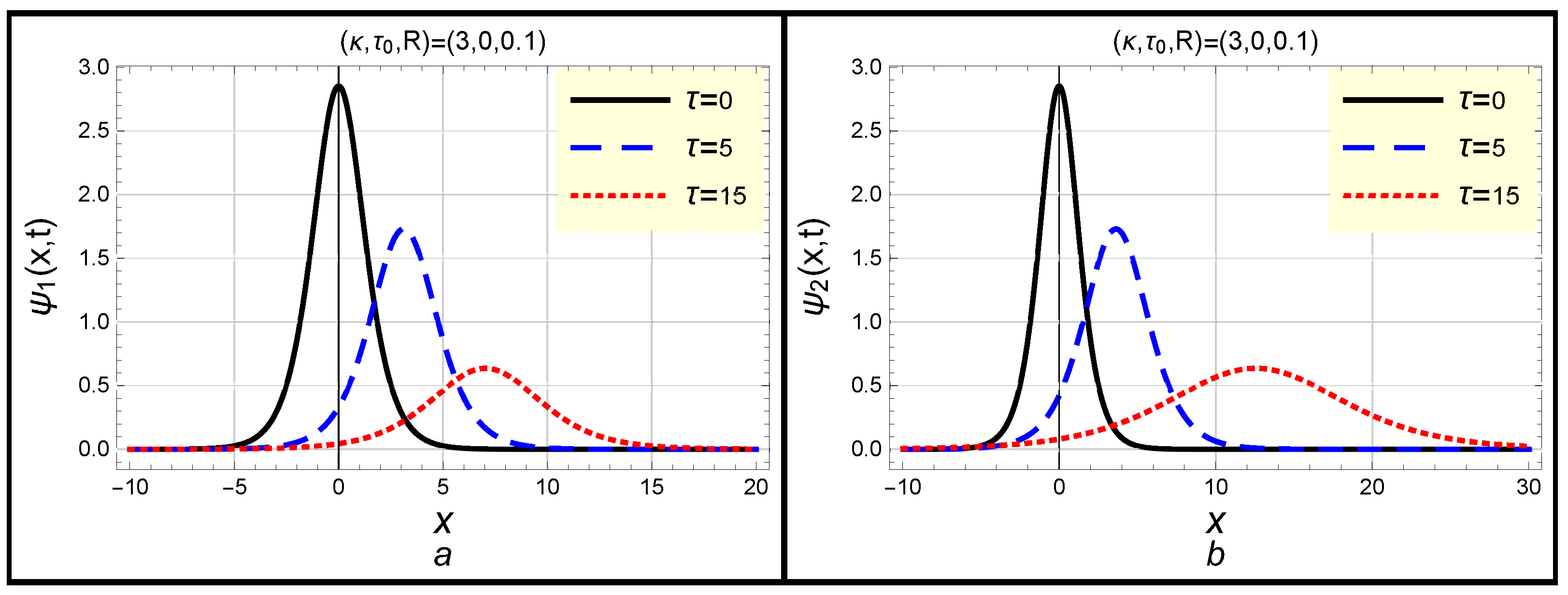
3. Dissipative Modified Kawahara Solitons and Their Energy

To find the dissipative SWs of the damped mKE (6), firstly, we need the exact soliton solution to the mKE (5). As we demonstrated in the introductory section, the mKE (5) has been solved using different analytical and numerical techniques. One of the symmetric exact dressed soliton solutions of the mKE (5) reads [13]

$$\varphi (\zeta ,\tau )={\varphi }_{max}{sech}^2\left[W\left(\zeta -\frac{4B^2}{25d}\tau \right)\right].$$

(26)

Here, ${\varphi }_{max}=\frac{3B}{\sqrt{10Ad}}$ is the maximum amplitude of the SWs, while $W=\frac{1}{2}\sqrt{\frac{B}{5d}}$ gives the inverse width of the SWs. Now, to obtain the dissipative dressed soliton solution of the damped mKE (6), we should insert Equation (26) into the general approximations (24) and (25):

$${\psi }_1(\zeta ,\tau )={\varphi }_{max}{e}^{R\left({\tau }_0-\tau \right)}{sech}^2\left[W\left(\zeta e^{\frac{R}{2}\left({\tau }_0-\tau \right)}-\frac{4B^2}{25d}\frac{2}{5R}\left(1-e^{\frac{5R}{2}\left({\tau }_0-\tau \right)}\right)\right)\right],$$

(27)

and

$${\psi }_2(\zeta ,\tau )={\varphi }_{max}{e}^{R\left({\tau }_0-\tau \right)}{sech}^2\left[W\left(\zeta e^{R\left({\tau }_0-\tau \right)}-\frac{4B^2}{25d}\frac{1}{3R}\left(1-e^{3R\left({\tau }_0-\tau \right)}\right)\right)\right].$$

(28)

In the following section, the semi-analytical solutions (27) and (28) are applied to study the properties of the dissipative modified Kawahara solitons that can be generated in an electronegative dusty plasmas.

To find the energy of the dissipative modified Kawahara soliton, we first determine the planar modified Kawahara soliton energy and prove that it is conserved (does not change with time). The energy of the modified Kawahara soliton can be obtained using the following conservation law:

$$\begin{array}{cc}\hfill I& ={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\varphi {\partial }_{\tau }\varphi {\partial }_{\zeta }={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\frac{1}{2}{\partial }_{\tau }{\varphi }^2{\partial }_{\zeta }={\partial }_{\tau }\left({\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\frac{1}{2}{\varphi }^2{\partial }_{\zeta }\right)={\partial }_{\tau }{E}_{mKE}\hfill \\ \hfill & =-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\varphi \left(A{\varphi }^2{\partial }_{\zeta }\varphi +B{\partial }_{\zeta }^3\varphi -d{\partial }_{\zeta }^5\varphi \right){\partial }_{\zeta }\hfill \\ \hfill & =-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\left(A{\varphi }^3{\partial }_{\zeta }\varphi +B\varphi {\partial }_{\zeta }^3\varphi -d\varphi {\partial }_{\zeta }^5\varphi \right){\partial }_{\zeta }\hfill \\ \hfill & =-A{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\left({\varphi }^3{\partial }_{\zeta }\varphi \right){\partial }_{\zeta }-B{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\left(\varphi {\partial }_{\zeta }^3\varphi \right){\partial }_{\zeta }+d{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\left(\varphi {\partial }_{\zeta }^5\varphi \right){\partial }_{\zeta }\hfill \\ \hfill & =0.\hfill \end{array}$$

(29)

Thus, the planar modified Kawahara SWs energy is conserved and is given by

$$\begin{array}{cc}\hfill E_{mKE}& =\frac{1}{2}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{\varphi }^2{\partial }_{\zeta }=\frac{1}{2}{\varphi }_{max}^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{sech}^4\left[W\left(\zeta -\frac{4B^2}{25d}\tau \right)\right]{\partial }_{\zeta }\hfill \\ \hfill & =\frac{2}{3}\frac{{\varphi }_{max}^2}{W}.\hfill \end{array}$$

(30)

We shall now proceed to derive the energy of the dissipative modified Kawahara soliton. As we proved above, the modified Kawahara soliton energy is conserved, i.e., ${\partial }_{\tau }{E}_0=0$. On the other side, since all physical quantities (amplitude, width, and velocity) associated with these waves change with time, their energy becomes unconserved, i.e., ${\partial }_{\tau }{E}_R\left(\tau \right)\ne 0$. The value of $E_R\left(\tau \right)$ can be obtained as follows:

$$\begin{array}{cc}\hfill {\partial }_{\tau }{E}_R\left(\tau \right)& ={\partial }_{\tau }\left({\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\frac{1}{2}{\psi }^2{\partial }_{\zeta }\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\psi {\partial }_{\tau }\psi {\partial }_{\zeta }\hfill \\ \hfill & =-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\psi \left(A{\psi }^2{\partial }_{\zeta }\psi +B{\partial }_{\zeta }^3\psi -d{\partial }_{\zeta }^5\psi +R\psi \right){\partial }_{\zeta }\hfill \\ \hfill & =-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\left(A{\psi }^3{\partial }_{\zeta }\psi +B\psi {\partial }_{\zeta }^3\psi -d\psi {\partial }_{\zeta }^5\psi +R{\psi }^2\right){\partial }_{\zeta }\hfill \\ \hfill & =-2R{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\frac{1}{2}{\psi }^2{\partial }_{\zeta }=-2R{E}_R\left(\tau \right).\hfill \end{array}$$

(31)

By integrating Equation (31) once over $\tau$, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \int }\frac{{\partial }_{\tau }{E}_R\left(\tau \right)}{E_R\left(\tau \right)}& =-2{\displaystyle \int }R{\partial }_{\tau }+cc\Rightarrow \hfill \\ \hfill ln\left(E_R\left(\tau \right)\right)& =-2R\tau +cc.\hfill \end{array}$$

(32)

To determine the value of the integration constant $cc$, we use the IC $E_R\left({\tau }_0\right)=E_0$, which leads to

$$cc=ln\left(E_0\right)+2R{\tau }_0.$$

(33)

Inserting Equation (33) into Equation (32), we get

$$\begin{array}{cc}\hfill ln\left(E_R\left(\tau \right)\right)& =-2R\tau +ln\left(E_0\right)+2R{\tau }_0\hfill \\ \hfill & \Rightarrow ln\left(\frac{E_R\left(\tau \right)}{E_0}\right)=2R\left({\tau }_0-\tau \right)\hfill \\ \hfill & \Rightarrow E_R\left(\tau \right)=E_0{e}^{2R\left({\tau }_0-\tau \right)}.\hfill \end{array}$$

(34)

It is noticed that the Kawahara soliton energy is a function of time and decays with the increase of time, which confirms that the energy of the soliton is not conserved. It is noteworthy that for $R=0$, the conserved soliton energy of the mKE is recovered as

$$E_R\left(\tau \right)=E_0.$$

(35)

4. Dissipative Modified Kawahara Solitons in a Dusty Plasma

Now, we can apply the analytical approximations (24) and (25) for studying the dissipative dust-ion acoustic modified Kawahara solitons in a collisional super-thermal complex plasma consisting of inertialess superthermal electrons and inertial cold ions in addition to stationary negative dust grains to preserve the neutrality condition. In this model, the ion-neutral collisions are considered. Thus, the set of normalized fluid equations that govern the dynamics of dust-ion acoustic waves (DIAWs) are given by: [46]

The continuity equation of the positive ions:

$${\partial }_t{n}_i+{\partial }_x\left(n_i{u}_i\right)=0,$$

(36)

the momentum equation of the positive ions:

$${\partial }_t{u}_i+u_i{\partial }_x{u}_i+\upsilon u_i-{\partial }_x\phi =0,$$

(37)

and Poission’s equation:

$${\partial }_x^2\phi +n_i-n_e-{\alpha }_d=0,$$

(38)

while the superthermal electrons’ normalized density $n_e$ is given by:

$$\begin{array}{cc}\hfill n_e& =\mu {\left[1-\frac{\phi }{\kappa -\frac{3}{2}}\right]}^{-\kappa +\frac{1}{2}}\hfill \\ \hfill & =\mu \left(1+{\alpha }_1\phi +{\alpha }_2{\phi }^2+{\alpha }_3{\phi }^3+\cdots \right),\hfill \end{array}$$

(39)

with

$$\begin{array}{cc}\hfill {\alpha }_1& =\frac{(2\kappa -1)}{\left(2\kappa -3\right)},\hfill \\ \hfill {\alpha }_2& =\frac{(2\kappa -1)(2\kappa +1)}{2{(2\kappa -3)}^2}\hfill \\ \hfill {\alpha }_3& =\frac{(2\kappa -1)(2\kappa +1)(2\kappa +3)}{6{(2\kappa -3)}^3}.\hfill \end{array}$$

Equations (36)–(39) are written in the dimensionless form, i.e., the dependent quantities $\left(n_i,u_i,\phi ,n_e\right)$ and independent variables $\left(\upsilon ,x,t\right)$ are written in normalized form. Here, $u_i$ and $n_i$ indicate the normalized velocity and density of the positive ions, respectively, $\varphi$ expresses the normalized wave potential, $\upsilon$ is the normalized ion-neutral collisional frequency, while $\left(x,t\right)$ represent the scaled space-time independent variables [46]. Here, $\kappa$ indicates the spectral index of the superthermal electron distribution $\left(1.5<\kappa \right)$, $\mu$ and ${\alpha }_d$ are, respectively, the electron and negative dust concentrations that satisfy the following neutrality condition: $\mu =1-{\alpha }_d$.

The RPM is implemented to reduce the fluid Equations (36)–(39) to an evolution equation governing the propagation of nonlinear structures that can be created in the present plasma model. Accordingly, the following, stretched to the independent variables, are considered:

$$\left(\zeta ,\tau ,\upsilon \right)=\left(\epsilon \left(x-V_{ph}t\right),{\epsilon }^{3}t,{\epsilon }^3{\upsilon }_0\right),$$

(40)

while the following expansion of the dependent quantities are as follows:

$$Y\left(x,t\right)=Y^{\left(0\right)}+\sum _{j=1}^{\infty }{\epsilon }^j{Y}^{\left(j\right)}\left(\zeta ,\tau \right)$$

(41)

with

$$\begin{array}{cc}\hfill Y\left(x,t\right)& \equiv \left[n_i,u_i,\phi \right],\hfill \\ \hfill Y^{\left(j\right)}\left(\zeta ,\tau \right)& \equiv \left[n_i^{\left(j\right)},u_i^{\left(j\right)},{\phi }^{\left(j\right)}\right],\hfill \\ \hfill Y^{\left(0\right)}& \equiv \left[1,0,0\right],\hfill \end{array}$$

where $V_{ph}$ expresses the normalized phase velocity of DIAWs, and $\epsilon$ is a small real parameter ($\epsilon <<1$).

Inserting Equations (40) and (41) into Equations (36)–(39) and rearranging all terms, we get reduced equations with different orders of $\epsilon$. For the lowest-orders of $\epsilon$, the first-order quantities $\left(n_i^{\left(1\right)},u_i^{\left(1\right)}\right)$ and the normalized phase velocity $V_{ph}$ are obtained:

$$n_i^{\left(1\right)}=\frac{1}{V_{ph}}{u}_i^{\left(1\right)}=\frac{1}{V_{ph}^2}{\phi }^{\left(1\right)}\mathrm{and}{V}_{ph}=\frac{1}{\sqrt{{\alpha }_1}}.$$

(42)

For the next-order to $\epsilon$, we get the second-order quantities $\left(n_i^{\left(2\right)},u_i^{\left(2\right)}\right)$ as follows:

$$\left\{\begin{array}{c}{n}_i^{\left(2\right)}=\frac{1}{V_{ph}^4}\left(\frac{3}{2}{\phi }^{\left(1\right)2}+V_{ph}^2{\phi }^{\left(2\right)}\right),\\ u_i^{\left(2\right)}=\frac{1}{V_{ph}^3}\left(\frac{1}{2}{\phi }^{\left(1\right)2}+V_{ph}^2{\phi }^{\left(2\right)}\right).\end{array}\right.$$

(43)

In addition, Poisson’s equation gives us

$$\frac{1}{V_{ph}}\left(2{\alpha }_2{V}_{ph}^4-3\right){\phi }^{\left(1\right)2}+2V_{ph}\left({\alpha }_1{V}_{ph}^2-1\right){\phi }^{\left(2\right)}=0.$$

(44)

In Equation (44), the coefficient of the second term represents the dispersion relation, i.e., $\left({\alpha }_1{V}_{ph}^2-1\right)=0$, while the coefficient of the first term represents the coefficient of the quadratic nonlinear term in the damped KdV equation, which must vanish (i.e., $2{\alpha }_2{V}_{ph}^4-3=0$) to get the damped mKdV equation. Now, by solving $\left(2{\alpha }_2{V}_{ph}^4-3\right)=0$, the critical value of dust concentration ${\alpha }_{dc}$ is obtained:

$${\alpha }_{dc}=\frac{4}{3}\frac{(\kappa -1)}{\left(2\kappa -1\right)}.$$

(45)

Note here that the value of ${\alpha }_{dc}$ must satisfy the neutrality condition: $\mu =1-{\alpha }_{dc}$.

For the next-higher order to $\epsilon$, we get

$$\begin{array}{cc}\hfill & {\partial }_{\tau }{n}_i^{\left(1\right)}+{\partial }_{\zeta }\left(n_i^{\left(1\right)}{u}_i^{\left(2\right)}\right)+{\partial }_{\zeta }\left(n_i^{\left(2\right)}{u}_i^{\left(1\right)}\right)-V_{ph}{\partial }_{\zeta }{n}_i^{\left(3\right)}+{\partial }_{\zeta }{u}_i^{\left(3\right)}=0\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & {\upsilon }_0{u}_i^{\left(1\right)}+{\partial }_{\tau }{u}_i^{\left(1\right)}+{\partial }_{\zeta }\left(u_i^{\left(1\right)}{u}_i^{\left(2\right)}\right)-V_{ph}{\partial }_{\zeta }{u}_i^{\left(3\right)}+{\partial }_{\zeta }{\phi }^{\left(3\right)}=0,\hfill \end{array}$$

(47)

while Poission’s equation gives us:

$$n_i^{\left(3\right)}-{\alpha }_3{\phi }^{\left(1\right)3}-2{\alpha }_2{\phi }^{\left(1\right)}{\phi }^{\left(2\right)}-{\alpha }_1{\phi }^{\left(3\right)}+{\partial }_{\zeta }^2{\phi }^{\left(1\right)}=0.$$

(48)

Solving Equations (46)–(48) and taking the fifth-order derivative/perturbation into consideration, the following damped mKE is obtained:

$${\partial }_{\tau }\psi +A{\psi }^2{\partial }_{\zeta }\psi +B{\partial }_{\zeta }^3\psi -d{\partial }_{\zeta }^5\psi +R\psi =0,$$

(49)

with

$$A=\frac{1}{4{\lambda }^3}\left(15-6{\alpha }_3{\lambda }^6\right)\mathrm{and}B=\frac{{\lambda }^3}{2},$$

(50)

where $R={\upsilon }_0/2$ denotes the coefficient of the damping term and $\psi \equiv {\phi }^{\left(1\right)}$.

Before proceeding to analyze the effect of plasma parameters on the dissipative modified Kawahara solitons, we should study the impact of the electron spectral index $\kappa$ and the collisional frequency R on the dressed soliton energy $E_R\left(\tau \right)$. Figure 1 demonstrates the relation between the parameters $\left(\kappa ,R\right)$ and the energy $E_R\left(\tau \right).$ One can see that the energy $E_R\left(\tau \right)$ increases (decreases) with the increase in $\kappa$ (R). We can deduce an important result from this analysis: as long as the energy $E_R\left(\tau \right)$ of the dressed dissipative soliton decreases with a specific parameter, this, in turn, leads to a decrease in the speed and nonlinearity of the dressed soliton, and therefore, it works to reduce the amplitude of the dressed soliton and vice versa.

Now, we can study the impact of the physical parameters $\left(\kappa ,R\right)$ on the properties of the symmetric dissipative dressed solitons using the two approximations (27) and (28). Figure 2 exhibits the effect of the ion-neutral collisional frequency R on the profiles of the dissipative dressed solitons using the two approximations (27) and (28). We can observe that by increasing R, the dissipative dressed soliton amplitude decreases. A similar trend is observed as time goes on, as illustrated in Figure 3, i.e., the dissipative dressed soliton amplitude decays over time. It is important to note here that for ultrafine values of ${\upsilon }_0/R$, the nonlinearity of the DIA dissipative dressed solitons increases, which leads to the enhancement of the soliton amplitude, and the profile of the dissipative dressed solitons becomes identical to the planar dressed solitons. Figure 4 is considered for investigating the impact of the electron spectral index $\kappa$ on the profile of the DIA dissipative dressed solitons. It is found that the amplitude of the dressed solitons increases with $\kappa$, which means that the dressed soliton nonlinearity and energy increase with increasing $\kappa$ (this result is confirmed above during analyzing the soliton energy). Moreover, the GMRE $L_R$ is estimated for $\left(\kappa ,R,d\right)=\left(2,0.1,0.1\right)$, as shown in

Table 1. In this table, the residual error $L_R$ is estimated for all obtained approximations.

Approximation	${\mathit{L}}_{\mathit{R}}$
Approx. (27)	0.0205979
Approx. (28)	0.0399192
FDM Approx.	0.0206002
Mathematica	0.0607945

.

It is observed from Table 1 and Figure 5 that there is almost complete harmony between all semi-analytical solutions and numerical solutions using FDM, but there are some minor differences in the accuracy of each them. As shown in Table 1, the accuracy of the first formula for the semi-analytical solution (24) or (27) is better than both the second formula for the semi-analytical solution (25) or (28) and the FDM numerical approximation. Furthermore, the obtained results are compared with numerical solutions using Wolfram Mathematica. It is noticed that the semi-analytical solutions (27) and (28) as well as the FDM numerical approximations are better than the numerical solutions using Wolfram Mathematica. In general, the obtained semi-analytical solutions are characterized by high-accuracy and are more stable over a long period of time. Moreover, we analyzed the damped mKE (49) numerically using HPM, but unfortunately, this method gave a bad result over a long period of time; in addition, the accuracy of its approximations was not good due to the existence of the damping term. Thus, we did not add these results here.

5. Conclusions

The damped modified Kawahara equation (mKE) was analyzed via an ansatz method to find semi-analytical symmetric solutions. After applying the proposed method, two general semi-analytical solutions were formally derived. All derived symmetric approximations can recover all traveling wave solutions to the mKE. As an example to the derived approximations, the dissipative modified Kawahara solitary wave solution was obtained. Moreover, a generic energy formula of the dissipative dressed solitons was derived. Further, the dust-ion acoustic (DIA) dissipative solitons in a superthermal plasma were studied using the derived approximations. The effects of the collisional frequency R and the electron spectral index $\kappa$ on the profile of the dissipative dressed solitons were studied and discussed. It was found that the two parameters have an opposite effect on the soliton profile, i.e., the dissipative dressed soliton amplitude increases (decreases) with increasing $\kappa$ (R). Further, the accuracy of both analytical and numerical approximations was investigated by estimating the global maximum residual error along the whole study domain. We observed that numerical approximation using the finite difference method (FDM) is better than approximation (25) or (28). The current study can contribute to studying the mechanisms of various nonlinear phenomena that arise in several plasma models, nonlinear optics, fluid mechanics, etc.

Future work: Due to the importance of fractional differential equations [47] in explaining many mysterious phenomena, we will employ some effective methods for analyzing the damped fractional Kawahara-type equation and some linked fractional equations with the fifth-order dispersion term.