Transport Barriers in Geophysical Flows: A Review
Abstract
:1. Introduction
2. Elliptic Barriers around Vortices and Their Destruction
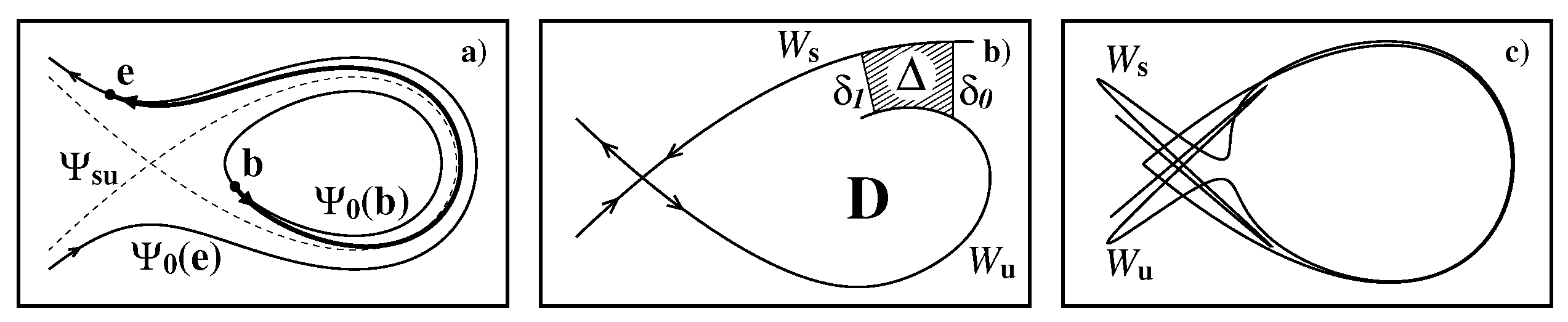
2.1. Chaotic Advection and Stable and Unstable Manifolds
2.2. Simple Model with a Fixed-Point Vortex in a Time-Periodic Flow
3. Detection of Elliptic Barriers for Eddies
3.1. The Problem of Identifying Eddy Boundaries
3.2. The LCS Method for Detecting Eddy Boundaries and Elliptic Barriers
3.3. Atmospheric Flows
4. Identification and Destruction of Parabolic Barriers in Zonal Jets
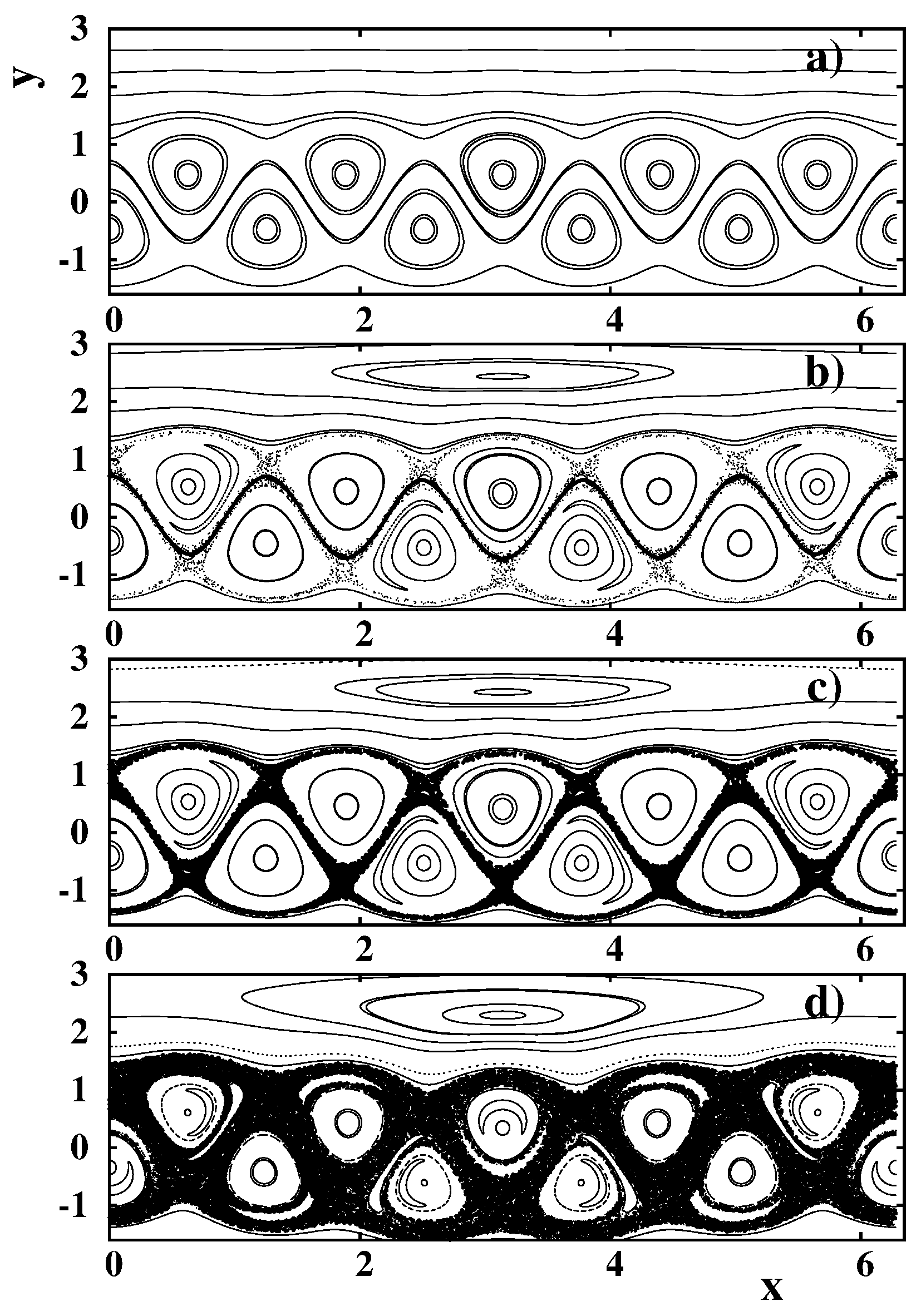
4.1. Model of a Zonal Jet with Rossby Waves
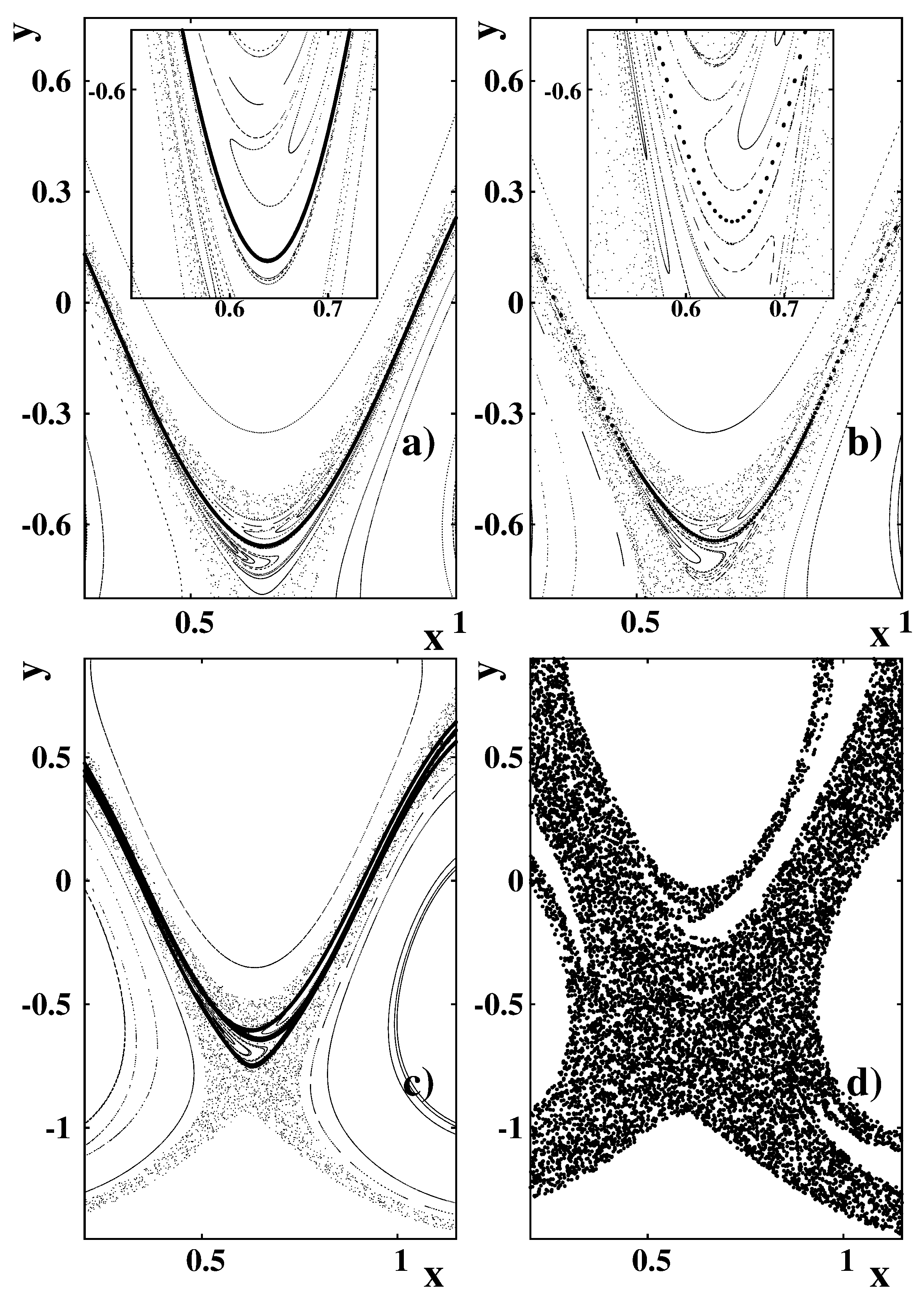
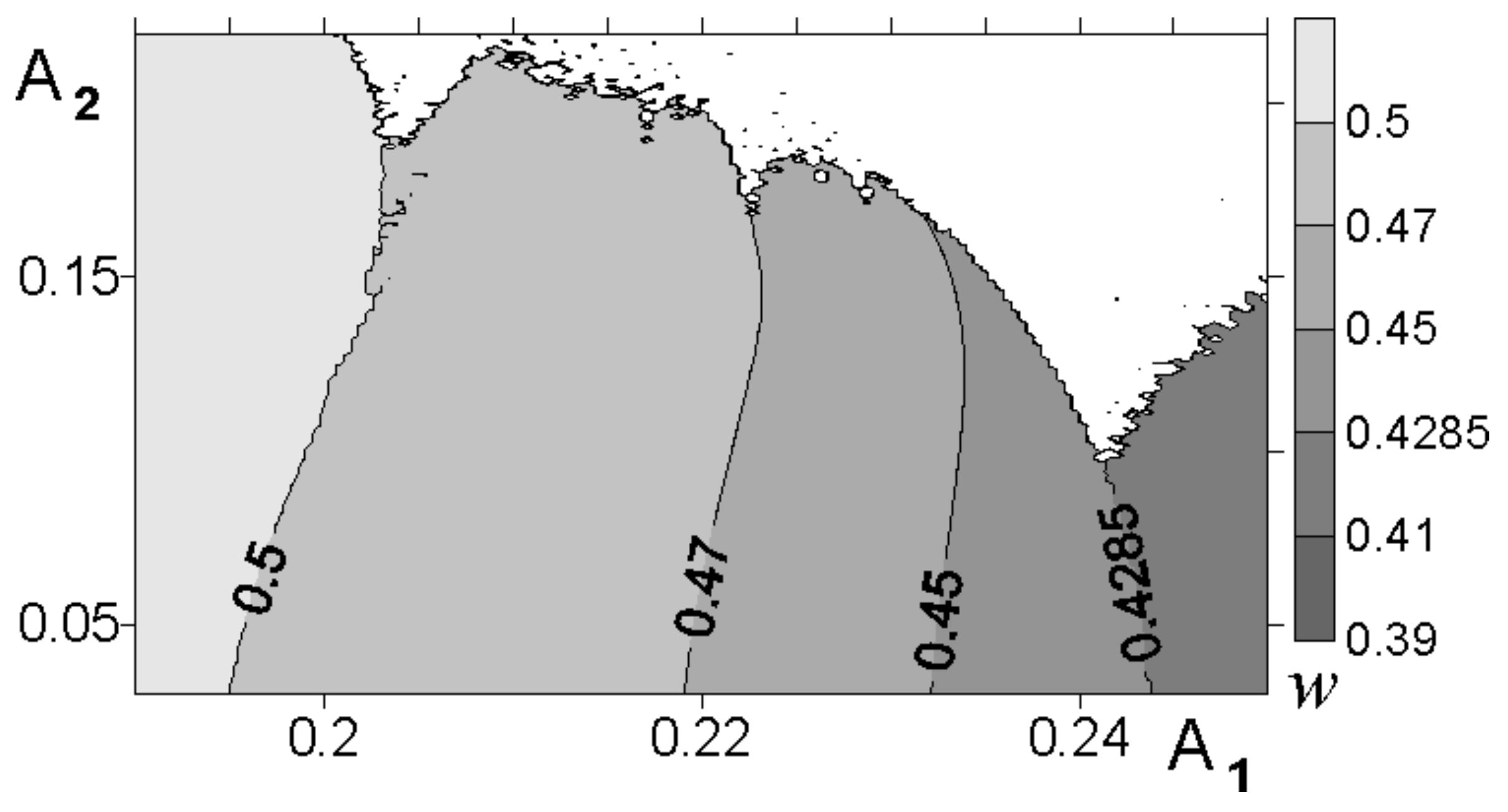
4.2. Chaotic Cross-Jet Transport
5. Hyperbolic Barriers in Geophysical Flows and Their Extraction
5.1. Identification of Hyperbolic Barriers Using Lagrangian Coherent Structures
5.2. Some Remarks on the Simulation of Transport and Mixing Processes in Satellite-Derived Velocity Fields
- Bicubic interpolation of the velocity components in space, and time interpolation using third-order Lagrangian polynomials, conducted independently of each other.
- Substituting the interpolated velocity values in Equation (16), which are integrated using the fourth order Runge–Kutta method.
- Calculating the relevant Lagrangian indicators and representing their values on a geographic map of the study region.
5.3. Lyapunov Exponents as Lagrangian Diagnostics
6. The Role of Barriers in Tracer Transport
6.1. Oil Spill Dispersal
6.2. Radioactive Tracers
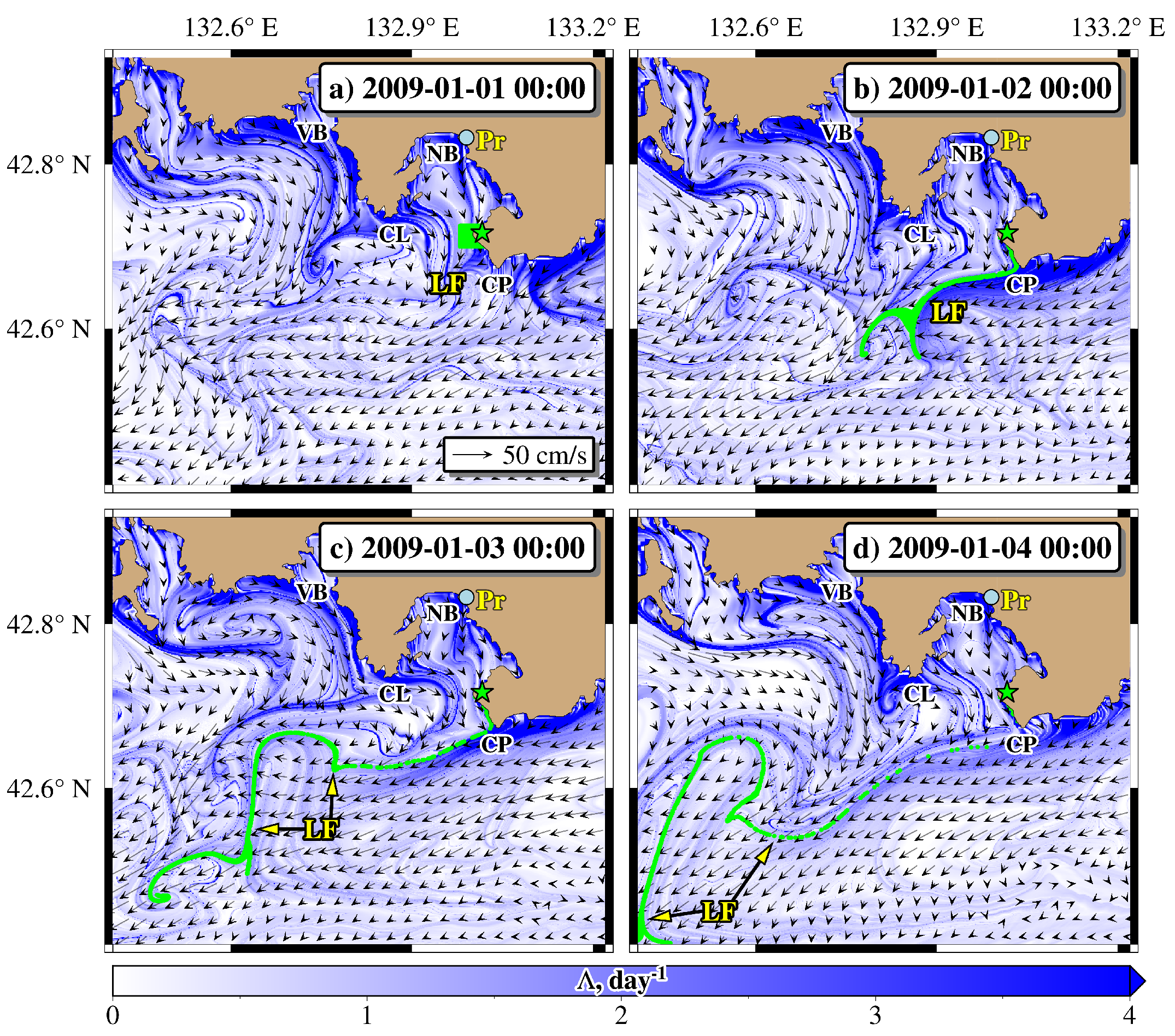
6.3. Cross-Shelf and Coastal Barriers
6.4. Transport Barriers in Advection of Plankton
7. Barriers in 3D Flows
8. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TB | transport barrier |
| LCS | Lagrangian coherent structure |
| ETB | elliptic transport barrier |
| PTB | parabolic transport barrier |
| HTB | hyperbolic transport barrier |
| VAVD | Lagrangian-averaged vorticity deviation |
| CJT | cross-jet transport |
| CIC | central invariant curve |
| FTLE | finite-time Lyapunov exponent |
| FSLE | finite-size Lyapunov exponent |
References
- Arnold, V.I.; Kozlov, V.V.; Neishtadt, A.I. Mathematical Aspects of Classical and Celestial Mechanics, 3rd ed.; Encyclopaedia of Mathematical Sciences; Springer: New York, NY, USA, 2006; Volume 3, p. XIII, 505. [Google Scholar] [CrossRef]
- Wiggins, S. Chaotic Transport in Dynamical Systems; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 1992; Volume 2, p. 301. [Google Scholar] [CrossRef]
- Meiss, J.D. Symplectic maps, variational principles, and transport. Rev. Mod. Phys. 1992, 64, 795–848. [Google Scholar] [CrossRef]
- Prants, S.V.; Uleysky, M.Y.; Budyansky, M.V. Lagrangian Oceanography: Large-Scale Transport and Mixing in the Ocean; Physics of Earth and Space Environments; Springer: Berlin/Heidelberg, Germany, 2017; p. XIV, 273. [Google Scholar] [CrossRef]
- Boffetta, G.; Lacorata, G.; Redaelli, G.; Vulpiani, A. Detecting barriers to transport: A review of different techniques. Phys. D Nonlinear Phenom. 2001, 159, 58–70. [Google Scholar] [CrossRef]
- d’Ovidio, F.; Fernández, V.; Hernández-García, E.; López, C. Mixing structures in the Mediterranean Sea from finite-size Lyapunov exponents. Geophys. Res. Lett. 2004, 31, L17203. [Google Scholar] [CrossRef]
- Budyansky, M.; Uleysky, M.; Prants, S. Chaotic scattering, transport, and fractals in a simple hydrodynamic flow. J. Exp. Theor. Phys. 2004, 99, 1018–1027. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Geodesic theory of transport barriers in two-dimensional flows. Phys. D Nonlinear Phenom. 2012, 241, 1680–1702. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures from approximate velocity data. Phys. Fluids 2002, 14, 1851–1861. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Haller, G. A variational theory of hyperbolic Lagrangian Coherent Structures. Phys. D Nonlinear Phenom. 2011, 240, 574–598. [Google Scholar] [CrossRef]
- Aref, H. Stirring by chaotic advection. J. Fluid Mech. 1984, 143, 1–21. [Google Scholar] [CrossRef]
- Aref, H. The development of chaotic advection. Phys. Fluids 2002, 14, 1315–1325. [Google Scholar] [CrossRef]
- Kozlov, V. Symmetries, Topology and Resonances in Hamiltonian Mechanics; UdGU: Izhevsk, Russia, 1995; p. 432. (In Russian) [Google Scholar]
- Budyansky, M.V.; Prants, S.V. A mechanism of chaotic mixing in an elementary deterministic flow. Tech. Phys. Lett. 2001, 27, 508–510. [Google Scholar] [CrossRef]
- Zaslavsky, G.M. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Zhmur, V.V.; Ryzhov, E.A.; Koshel, K.V. Ellipsoidal vortex in a nonuniform flow: Dynamics and chaotic advections. J. Mar. Res. 2011, 69, 435–461. [Google Scholar] [CrossRef]
- Koshel, K.V.; Ryzhov, E.A.; Zhmur, V.V. Diffusion-affected passive scalar transport in an ellipsoidal vortex in a shear flow. Nonlinear Process. Geophys. 2013, 20, 437–444. [Google Scholar] [CrossRef]
- Koshel, K.V.; Ryzhov, E.A. Parametric resonance in the dynamics of an elliptic vortex in a periodically strained environment. Nonlinear Process. Geophys. 2017, 24, 1–8. [Google Scholar] [CrossRef]
- Izrailsky, Y.G.; Koshel, K.V.; Stepanov, D.V. Determination of optimal excitation frequency range in background flows. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 013107. [Google Scholar] [CrossRef]
- Koshel, K.V.; Sokolovskiy, M.A.; Davies, P.A. Chaotic advection and nonlinear resonances in an oceanic flow above submerged obstacle. Fluid Dyn. Res. 2008, 40, 695–736. [Google Scholar] [CrossRef]
- Ryzhov, E.A.; Koshel’, K.V. Chaotic transport and mixing of a passive admixture by vortex flows behind obstacles. Izv. Atmos. Ocean. Phys. 2010, 46, 184–191. [Google Scholar] [CrossRef]
- Owen, R.W. Fronts and Eddies in the Sea: Mechanisms, Interactions and Biological Effects. In Analysis of Marine Ecosystems; Longhurst, A.R., Ed.; Academic Press Inc.: London, UK, 1981; pp. 197–233. [Google Scholar]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Prants, S.V. Trench Eddies in the Northwest Pacific: An Overview. Izv. Atmos. Ocean. Phys. 2021, 57, 341–353. [Google Scholar] [CrossRef]
- Zhao, D.; Xu, Y.; Zhang, X.; Huang, C. Global chlorophyll distribution induced by mesoscale eddies. Remote Sens. Environ. 2021, 254, 112245. [Google Scholar] [CrossRef]
- Xia, Q.; Li, G.; Dong, C. Global Oceanic Mass Transport by Coherent Eddies. J. Phys. Oceanogr. 2022, 52, 1111–1132. [Google Scholar] [CrossRef]
- Ueno, H.; Bracco, A.; Barth, J.A.; Budyansky, M.V.; Hasegawa, D.; Itoh, S.; Kim, S.Y.; Ladd, C.; Lin, X.; Park, Y.G.; et al. Review of oceanic mesoscale processes in the North Pacific: Physical and biogeochemical impacts. Prog. Oceanogr. 2023, 212, 102955. [Google Scholar] [CrossRef]
- Dugan, J.P.; Mied, R.P.; Mignerey, P.C.; Schuetz, A.F. Compact, intrathermocline eddies in the Sargasso Sea. J. Geophys. Res. Oceans 1982, 87, 385–393. [Google Scholar] [CrossRef]
- Gordon, A.L.; Giulivi, C.F.; Lee, C.M.; Furey, H.H.; Bower, A.; Talley, L. Japan/East Sea Intrathermocline Eddies. J. Phys. Oceanogr. 2002, 32, 1960–1974. [Google Scholar] [CrossRef]
- Hormazabal, S.; Combes, V.; Morales, C.E.; Correa-Ramirez, M.A.; Di Lorenzo, E.; Nuñez, S. Intrathermocline eddies in the coastal transition zone off central Chile (31–41∘ S). J. Geophys. Res. Ocean. 2013, 118, 4811–4821. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Filyushkin, B.N.; Carton, X.J. Dynamics of intrathermocline vortices in a gyre flow over a seamount chain. Ocean Dyn. 2013, 63, 741–760. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Dynamics of Vortex Structures in a Stratified Rotating Fluid; Atmospheric and Oceanographic Sciences Library; Springer International Publishing: New York, NY, USA, 2014; Volume 47. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Verron, J. Finite-core hetons: Stability and interactions. J. Fluid Mech. 2000, 423, 127–154. [Google Scholar] [CrossRef]
- Sokolovskiy, M.A.; Carton, X.J. Baroclinic multipole formation from heton interaction. Fluid Dyn. Res. 2010, 42, 045501. [Google Scholar] [CrossRef]
- Carton, X.J. Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 2001, 22, 179–263. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics, Physical and Numerical Aspects, 2nd ed.; International Geophysics; Academic Press: Cambridge, MA, USA, 2011; Volume 101. [Google Scholar]
- Jorba, A.; Simo, C. On Quasi-Periodic Perturbations of Elliptic Equilibrium Points. SIAM J. Math. Anal. 1996, 27, 1704–1737. [Google Scholar] [CrossRef]
- Peacock, T.; Haller, G. Lagrangian coherent structures: The hidden skeleton of fluid flows. Phys. Today 2013, 66, 41–47. [Google Scholar] [CrossRef]
- Haller, G.; Hadjighasem, A.; Farazmand, M.; Huhn, F. Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 2016, 795, 136–173. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Dong, C.; Nencioli, F.; Liu, Y.; McWilliams, J.C. An Automated Approach to Detect Oceanic Eddies From Satellite Remotely Sensed Sea Surface Temperature Data. IEEE Geosci. Remote. Sens. Lett. 2011, 8, 1055–1059. [Google Scholar] [CrossRef]
- Le Vu, B.; Stegner, A.; Arsouze, T. Angular Momentum Eddy Detection and Tracking Algorithm (AMEDA) and Its Application to Coastal Eddy Formation. J. Atmos. Ocean. Technol. 2018, 35, 739–762. [Google Scholar] [CrossRef]
- Wang, Y.; Beron-Vera, F.J.; Olascoaga, M.J. The life cycle of a coherent Lagrangian Agulhas ring. J. Geophys. Res. Ocean. 2016, 121, 3944–3954. [Google Scholar] [CrossRef]
- Fu, L.L. Pattern and velocity of propagation of the global ocean eddy variability. J. Geophys. Res. Ocean. 2009, 114, C11017. [Google Scholar] [CrossRef]
- Abdalla, S.; Kolahchi, A.A.; Ablain, M.; Adusumilli, S.; Bhowmick, S.A.; Alou-Font, E.; Amarouche, L.; Andersen, O.B.; Antich, H.; Aouf, L.; et al. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef]
- Prants, S.V.; Budyansky, M.V.; Uleysky, M.Y. How Eddies Gain, Retain, and Release Water: A Case Study of a Hokkaido Anticyclone. J. Geophys. Res. Ocean. 2018, 123, 2081–2096. [Google Scholar] [CrossRef]
- Budyansky, M.V.; Prants, S.V.; Uleysky, M.Y. Odyssey of Aleutian eddies. Ocean Dyn. 2022, 72, 455–476. [Google Scholar] [CrossRef]
- Udalov, A.; Budyansky, M.; Prants, S. A census and properties of mesoscale Kuril eddies in the altimetry era. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2023, 200, 104129. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, C.; Guan, Y.; Chen, D.; McWilliams, J.; Nencioli, F. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2012, 68, 54–67. [Google Scholar] [CrossRef]
- Liu, T.; Abernathey, R. A global Lagrangian eddy dataset based on satellite altimetry. Earth Syst. Sci. Data 2023, 15, 1765–1778. [Google Scholar] [CrossRef]
- Abernathey, R.; Haller, G. Transport by Lagrangian Vortices in the Eastern Pacific. J. Phys. Oceanogr. 2018, 48, 667–685. [Google Scholar] [CrossRef]
- McIntyre, M.; Palmer, T. The ‘surf zone’ in the stratosphere. J. Atmos. Terr. Phys. 1984, 46, 825–849. [Google Scholar] [CrossRef]
- Bowman, K.P. Large-scale isentropic mixing properties of the Antarctic polar vortex from analyzed winds. J. Geophys. Res. 1993, 98, 23013–23027. [Google Scholar] [CrossRef]
- Shepherd, T.G. Transport in the Middle Atmosphere. J. Meteorol. Soc. Jpn. Ser. II 2007, 85, 165–191. [Google Scholar] [CrossRef]
- Manney, G.L.; Santee, M.L.; Rex, M.; Livesey, N.J.; Pitts, M.C.; Veefkind, P.; Nash, E.R.; Wohltmann, I.; Lehmann, R.; Froidevaux, L.; et al. Unprecedented Arctic ozone loss in 2011. Nature 2011, 478, 469–475. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T. Chaotic mixing of tracer and vorticity by modulated travelling Rossby waves. Geophys. Astrophys. Fluid Dyn. 1991, 58, 285–319. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T.; Yang, H. Global Chaotic Mixing on Isentropic Surfaces. J. Atmos. Sci. 1993, 50, 2462–2480. [Google Scholar] [CrossRef]
- Joseph, B.; Legras, B. Relation between Kinematic Boundaries, Stirring, and Barriers for the Antarctic Polar Vortex. J. Atmos. Sci. 2002, 59, 1198–1212. [Google Scholar] [CrossRef]
- de la Cámara, A.; Mancho, A.M.; Ide, K.; Serrano, E.; Mechoso, C.R. Routes of Transport across the Antarctic Polar Vortex in the Southern Spring. J. Atmos. Sci. 2012, 69, 741–752. [Google Scholar] [CrossRef]
- Olascoaga, M.J.; Brown, M.G.; Beron-Vera, F.J.; Koçak, H. Brief communication “Stratospheric winds, transport barriers and the 2011 Arctic ozone hole”. Nonlinear Process. Geophys. 2012, 19, 687–692. [Google Scholar] [CrossRef]
- Bower, A.S. A Simple Kinematic Mechanism for Mixing Fluid Parcels across a Meandering Jet. J. Phys. Oceanogr. 1991, 21, 173–180. [Google Scholar] [CrossRef]
- Samelson, R.M. Fluid Exchange across a Meandering Jet. J. Phys. Oceanogr. 1992, 22, 431–444. [Google Scholar] [CrossRef]
- Raynal, F.; Wiggins, S. Lobe dynamics in a kinematic model of a meandering jet. I. Geometry and statistics of transport and lobe dynamics with accelerated convergence. Phys. D Nonlinear Phenom. 2006, 223, 7–25. [Google Scholar] [CrossRef]
- Prants, S.V.; Budyansky, M.V.; Uleysky, M.Y.; Zaslavsky, G.M. Chaotic mixing and transport in a meandering jet flow. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 033117. [Google Scholar] [CrossRef]
- Uleysky, M.Y.; Budyansky, M.V.; Prants, S.V. Genesis and bifurcations of unstable periodic orbits in a jet flow. J. Phys. A Math. Theor. 2008, 41, 215102. [Google Scholar] [CrossRef]
- Koshel’, K.V.; Prants, S.V. Chaotic advection in the ocean. Phys.-Uspekhi 2006, 49, 1151–1178. [Google Scholar] [CrossRef]
- del Castillo-Negrete, D.; Morrison, P.J. Chaotic transport by Rossby waves in shear flow. Phys. Fluids A Fluid Dyn. 1993, 5, 948–965. [Google Scholar] [CrossRef]
- Rypina, I.I.; Brown, M.G.; Beron-Vera, F.J.; Koçak, H.; Olascoaga, M.J.; Udovydchenkov, I.A. On the Lagrangian Dynamics of Atmospheric Zonal Jets and the Permeability of the Stratospheric Polar Vortex. J. Atmos. Sci. 2007, 64, 3595–3610. [Google Scholar] [CrossRef]
- Haynes, P.H.; Poet, D.A.; Shuckburgh, E.F. Transport and Mixing in Kinematic and Dynamically Consistent Flows. J. Atmos. Sci. 2007, 64, 3640–3651. [Google Scholar] [CrossRef]
- Uleysky, M.Y.; Budyansky, M.V.; Prants, S.V. Mechanism of destruction of transport barriers in geophysical jets with Rossby waves. Phys. Rev. E 2010, 81, 017202. [Google Scholar] [CrossRef] [PubMed]
- Uleysky, M.Y.; Budyansky, M.V.; Prants, S.V. Chaotic transport across two-dimensional jet streams. J. Exp. Theor. Phys. 2010, 111, 1039–1049. [Google Scholar] [CrossRef]
- Sommeria, J.; Meyers, S.D.; Swinney, H.L. Laboratory model of a planetary eastward jet. Nature 1989, 337, 58–61. [Google Scholar] [CrossRef]
- Solomon, T.H.; Holloway, W.J.; Swinney, H.L. Shear flow instabilities and Rossby waves in barotropic flow in a rotating annulus. Phys. Fluids A Fluid Dyn. 1993, 5, 1971–1982. [Google Scholar] [CrossRef]
- Kuo, H.l. Dynamic instability of two-dimensional nondivergent flow in a barotropic atmosphere. J. Meteorol. 1949, 6, 105–122. [Google Scholar] [CrossRef]
- Budyansky, M.V.; Uleysky, M.Y.; Prants, S.V. Detection of barriers to cross-jet Lagrangian transport and its destruction in a meandering flow. Phys. Rev. E 2009, 79, 056215. [Google Scholar] [CrossRef]
- Shinohara, S.; Aizawa, Y. The Breakup Condition of Shearless KAM Curves in the Quadratic Map. Prog. Theor. Phys. 1997, 97, 379–385. [Google Scholar] [CrossRef]
- Behringer, R.P.; Meyers, S.D.; Swinney, H.L. Chaos and mixing in a geostrophic flow. Phys. Fluids A Fluid Dyn. 1991, 3, 1243–1249. [Google Scholar] [CrossRef]
- Haller, G. Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Phys. D Nonlinear Phenom. 2001, 149, 248–277. [Google Scholar] [CrossRef]
- Prants, S.V.; Budyansky, M.V.; Ponomarev, V.I.; Uleysky, M.Y. Lagrangian study of transport and mixing in a mesoscale eddy street. Ocean Model. 2011, 38, 114–125. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Michel, J.; Fingas, M. Oil Spills: Causes, Consequences, Prevention, and Countermeasures. In Fossil Fuels; Crawley, G.M., Ed.; World Scientific: Singapore, 2016; Volume 1, Chapter 7; pp. 159–201. [Google Scholar] [CrossRef]
- Varlamov, S.M.; Yoon, J.H.; Hirose, N.; Kawamura, H.; Shiohara, K. Simulation of the oil spill processes in the Sea of Japan with regional ocean circulation model. J. Mar. Sci. Technol. 1999, 4, 94–107. [Google Scholar] [CrossRef]
- Ono, J.; Ohshima, K.I.; Uchimoto, K.; Ebuchi, N.; Mitsudera, H.; Yamaguchi, H. Particle-tracking simulation for the drift/diffusion of spilled oils in the Sea of Okhotsk with a three-dimensional, high-resolution model. J. Oceanogr. 2013, 69, 413–428. [Google Scholar] [CrossRef]
- Qiao, F.; Wang, G.; Yin, L.; Zeng, K.; Zhang, Y.; Zhang, M.; Xiao, B.; Jiang, S.; Chen, H.; Chen, G. Modelling oil trajectories and potentially contaminated areas from the Sanchi oil spill. Sci. Total. Environ. 2019, 685, 856–866. [Google Scholar] [CrossRef]
- Korotenko, K.; Mamedov, R.; Kontar, A.; Korotenko, L. Particle tracking method in the approach for prediction of oil slick transport in the sea: Modelling oil pollution resulting from river input. J. Mar. Syst. 2004, 48, 159–170. [Google Scholar] [CrossRef]
- Prants, S.V.; Budyansky, M.V.; Fayman, P.A.; Uleysky, M.Y.; Didov, A.A. Lagrangian Oil Spill Simulation in Peter the Great Bay (Sea of Japan) with a High-Resolution ROMS Model. Pure Appl. Geophys. 2023, 180, 551–568. [Google Scholar] [CrossRef]
- Olascoaga, M.J.; Haller, G. Forecasting sudden changes in environmental pollution patterns. Proc. Natl. Acad. Sci. USA 2012, 109, 4738–4743. [Google Scholar] [CrossRef]
- Duran, R.; Beron-Vera, F.J.; Olascoaga, M.J. Extracting quasi-steady Lagrangian transport patterns from the ocean circulation: An application to the Gulf of Mexico. Sci. Rep. 2018, 8, 5218. [Google Scholar] [CrossRef] [PubMed]
- Fifani, G.; Baudena, A.; Fakhri, M.; Baaklini, G.; FaugÚre, Y.; Morrow, R.; Mortier, L.; d’Ovidio, F. Drifting Speed of Lagrangian Fronts and Oil Spill Dispersal at the Ocean Surface. Remote Sens. 2021, 13, 4499. [Google Scholar] [CrossRef]
- Prants, S.V.; Uleysky, M.Y.; Budyansky, M.V. Numerical simulation of propagation of radioactive pollution in the ocean from the Fukushima Dai-ichi nuclear power plant. Dokl. Earth Sci. 2011, 439, 1179–1182. [Google Scholar] [CrossRef]
- Tsumune, D.; Tsubono, T.; Aoyama, M.; Hirose, K. Distribution of oceanic 137Cs from the Fukushima Dai-ichi Nuclear Power Plant simulated numerically by a regional ocean model. J. Environ. Radioact. 2012, 111, 100–108. [Google Scholar] [CrossRef]
- Rossi, V.; Sebille, E.V.; Gupta, A.S.; Garçon, V.; England, M.H. Multi-decadal projections of surface and interior pathways of the Fukushima Cesium-137 radioactive plume. Deep Sea Res. Part I Oceanogr. Res. Pap. 2013, 80, 37–46. [Google Scholar] [CrossRef]
- Budyansky, M.V.; Goryachev, V.A.; Kaplunenko, D.D.; Lobanov, V.B.; Prants, S.V.; Sergeev, A.F.; Shlyk, N.V.; Uleysky, M.Y. Role of mesoscale eddies in transport of Fukushima-derived cesium isotopes in the ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2015, 96, 15–27. [Google Scholar] [CrossRef]
- Prants, S.V.; Budyansky, M.V.; Uleysky, M.Y. Lagrangian simulation and tracking of the mesoscale eddies contaminated by Fukushima-derived radionuclides. Ocean Sci. 2017, 13, 453–463. [Google Scholar] [CrossRef]
- Budyansky, M.; Fayman, P.; Uleysky, M.; Prants, S. The impact of circulation features on the dispersion of radionuclides after the nuclear submarine accident in Chazhma Bay (Japan Sea) in 1985: A retrospective Lagrangian simulation. Mar. Pollut. Bull. 2022, 177, 113483. [Google Scholar] [CrossRef]
- Sarkisov, A.A.; Vysotskii, V.L.; Pripachkin, D.A. Reconstruction of the Radioactive Contamination Occurring in the Environment in Primorskii Krai as a Result of a Nuclear Accident on a Submarine in Bukhta Chazhma. At. Energy 2020, 127, 159–165. [Google Scholar] [CrossRef]
- Brink, K. Cross-Shelf Exchange. Annu. Rev. Mar. Sci. 2016, 8, 59–78. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-Frequency Radar Observations of Ocean Surface Currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef]
- Lekien, F.; Coulliette, C.; Mariano, A.J.; Ryan, E.H.; Shay, L.K.; Haller, G.; Marsden, J. Pollution release tied to invariant manifolds: A case study for the coast of Florida. Phys. D Nonlinear Phenom. 2005, 210, 1–20. [Google Scholar] [CrossRef]
- Olascoaga, M.J.; Rypina, I.I.; Brown, M.G.; Beron-Vera, F.J.; Koçak, H.; Brand, L.E.; Halliwell, G.R.; Shay, L.K. Persistent transport barrier on the West Florida Shelf. Geophys. Res. Lett. 2006, 33, L22603. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Weisberg, R.H.; Niiler, P.; Sturges, W.; Johnson, W. Lagrangian circulation and forbidden zone on the West Florida Shelf. Cont. Shelf Res. 1999, 19, 1221–1245. [Google Scholar] [CrossRef]
- Olascoaga, M.J.; Beron-Vera, F.J.; Brand, L.E.; Koçak, H. Tracing the early development of harmful algal blooms on the West Florida Shelf with the aid of Lagrangian coherent structures. J. Geophys. Res. Ocean. 2008, 113, C12014. [Google Scholar] [CrossRef] [PubMed]
- Prants, S.V.; Ponomarev, V.I.; Budyansky, M.V.; Uleysky, M.Y.; Fayman, P.A. Lagrangian analysis of mixing and transport of water masses in the marine bays. Izv. Atmos. Ocean. Phys. 2013, 49, 82–96. [Google Scholar] [CrossRef]
- Enrile, F.; Besio, G.; Stocchino, A.; Magaldi, M.; Mantovani, C.; Cosoli, S.; Gerin, R.; Poulain, P. Evaluation of surface Lagrangian transport barriers in the Gulf of Trieste. Cont. Shelf Res. 2018, 167, 125–138. [Google Scholar] [CrossRef]
- Gildor, H.; Fredj, E.; Steinbuck, J.; Monismith, S. Evidence for Submesoscale Barriers to Horizontal Mixing in the Ocean from Current Measurements and Aerial Photographs. J. Phys. Oceanogr. 2009, 39, 1975–1983. [Google Scholar] [CrossRef]
- Landsberg, J.H. The Effects of Harmful Algal Blooms on Aquatic Organisms. Rev. Fish. Sci. 2002, 10, 113–390. [Google Scholar] [CrossRef]
- Hutchinson, G.E. The Paradox of the Plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- Károlyi, G.; Péntek, A.; Scheuring, I.; Tél, T.; Toroczkai, Z. Chaotic flow: The physics of species coexistence. Proc. Natl. Acad. Sci. USA 2000, 97, 13661–13665. [Google Scholar] [CrossRef] [PubMed]
- Bracco, A.; Provenzale, A.; Scheuring, I. Mesoscale vortices and the paradox of the plankton. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2000, 267, 1795–1800. [Google Scholar] [CrossRef] [PubMed]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Loisel, H. Seasonal distribution and succession of dominant phytoplankton groups in the global ocean: A satellite view. Glob. Biogeochem. Cycles 2008, 22, GB3001. [Google Scholar] [CrossRef]
- d’Ovidio, F.; De Monte, S.; Alvain, S.; Dandonneau, Y.; Levy, M. Fluid dynamical niches of phytoplankton types. Proc. Natl. Acad. Sci. USA 2010, 107, 18366–18370. [Google Scholar] [CrossRef]
- Sulman, M.H.M.; Huntley, H.S.; Lipphardt, B.L.; Kirwan, A.D. Leaving flatland: Diagnostics for Lagrangian coherent structures in three-dimensional flows. Phys. D Nonlinear Phenom. 2013, 258, 77–92. [Google Scholar] [CrossRef]
- Mancho, A.M.; Wiggins, S.; Curbelo, J.; Mendoza, C. Lagrangian descriptors: A method for revealing phase space structures of general time dependent dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3530–3557. [Google Scholar] [CrossRef]
- Bettencourt, J.H.; López, C.; Hernández-García1, E. Characterization of coherent structures in three-dimensional turbulent flows using the finite-size Lyapunov exponent. J. Phys. A Math. Theor. 2013, 46, 254022. [Google Scholar] [CrossRef]
- Blazevski, D.; Haller, G. Hyperbolic and elliptic transport barriers in three-dimensional unsteady flows. Phys. D Nonlinear Phenom. 2014, 273–274, 46–62. [Google Scholar] [CrossRef]
- Tang, W.; Mathur, M.; Haller, G.; Hahn, D.C.; Ruggiero, F.H. Lagrangian Coherent Structures near a Subtropical Jet Stream. J. Atmos. Sci. 2010, 67, 2307–2319. [Google Scholar] [CrossRef]
- Bettencourt, J.H.; Lopez, C.; Hernandez-Garcia, E. Oceanic three-dimensional Lagrangian coherent structures: A study of a mesoscale eddy in the Benguela upwelling region. Ocean Model. 2012, 51, 73–83. [Google Scholar] [CrossRef]
- Bettencourt, J.; López, C.; Hernández-García, E.; Montes, I.; Sudre, J.; Dewitte, B.; Paulmier, A.; Garçon, V. Boundaries of the Peruvian oxygen minimum zone shaped by coherent mesoscale dynamics. Nat. Geosci. 2015, 8, 937–940. [Google Scholar] [CrossRef]
- Bettencourt, J.H.; Rossi, V.; Hernández-García, E.; Marta-Almeida, M.; López, C. Characterization of the structure and cross-shore transport properties of a coastal upwelling filament using three-dimensional finite-size Lyapunov exponents. J. Geophys. Res. Ocean. 2017, 122, 7433–7448. [Google Scholar] [CrossRef]
- Curbelo, J.; GarcÃa-Garrido, V.J.; Mechoso, C.R.; Mancho, A.M.; Wiggins, S.; Niang, C. Insights into the three-dimensional Lagrangian geometry of the Antarctic polar vortex. Nonlinear Process. Geophys. 2017, 24, 379–392. [Google Scholar] [CrossRef]
- Madrid, J.A.J.; Mancho, A.M. Distinguished trajectories in time dependent vector fields. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 013111. [Google Scholar] [CrossRef]
- Prants, S. Marine life at Lagrangian fronts. Prog. Oceanogr. 2022, 204, 102790. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prants, S. Transport Barriers in Geophysical Flows: A Review. Symmetry 2023, 15, 1942. https://doi.org/10.3390/sym15101942
Prants S. Transport Barriers in Geophysical Flows: A Review. Symmetry. 2023; 15(10):1942. https://doi.org/10.3390/sym15101942
Chicago/Turabian StylePrants, Sergey. 2023. "Transport Barriers in Geophysical Flows: A Review" Symmetry 15, no. 10: 1942. https://doi.org/10.3390/sym15101942



