This section includes all concepts and techniques used in this research work.
3.1. Mathematical Model of the CVRP
The CVRP is shown to be an NP-hard problem [
27]. The CVRP is associated with a set of pathways related to a fleet of vehicles that starts from one depot. However, the multi-depot CVRP is associated with a set of pathways related to fleet of vehicles that starts from some depots with a specified number of clients (or customers) in various geographical locations. It includes a maximal load capacity for all vehicles. The CVRP is a variation of the vehicle routing problem (VRP) that includes the capacity constraints associated with all vehicles. In this context, the main objective of both VRP and CVRP is to minimize the total traveling costs (or distance). The route design considers visiting each customer by a single vehicle such that all customer demand is fulfilled.
- (i)
The uniformed vehicle fleet needs to originate from a single station (or depot);
- (ii)
Every order by a customer cannot be separated and must be served by only one vehicle.
The CVRP is described as a problem that aims to determine the optimal route that can visit each customer and satisfy their demands, subject to different constraints. All components in the CVRP are described as follows: a complete graph
where
is the number of nodes,
denotes a set of nodes (customers), and
represents edges that connect the nodes.
is the distance matrix among the nodes including a depot while the Euclidean distance between two nodes
I and
j can be calculated as
. It must be noted that every edge
is related to the cost
,
. The distance and cost matrices are related to E. The function
is the cost function and node 0 represents the depot and the demand of the depot is
. The remaining nodes represent the customers and every customer
i has a non-negative demand and the function
represents the demand function;
m is the number of vehicles that are identical and present in the depot [
37] based on the additional constraint that the total demand of a route cannot surpass the vehicle capacity ([
19,
38]).
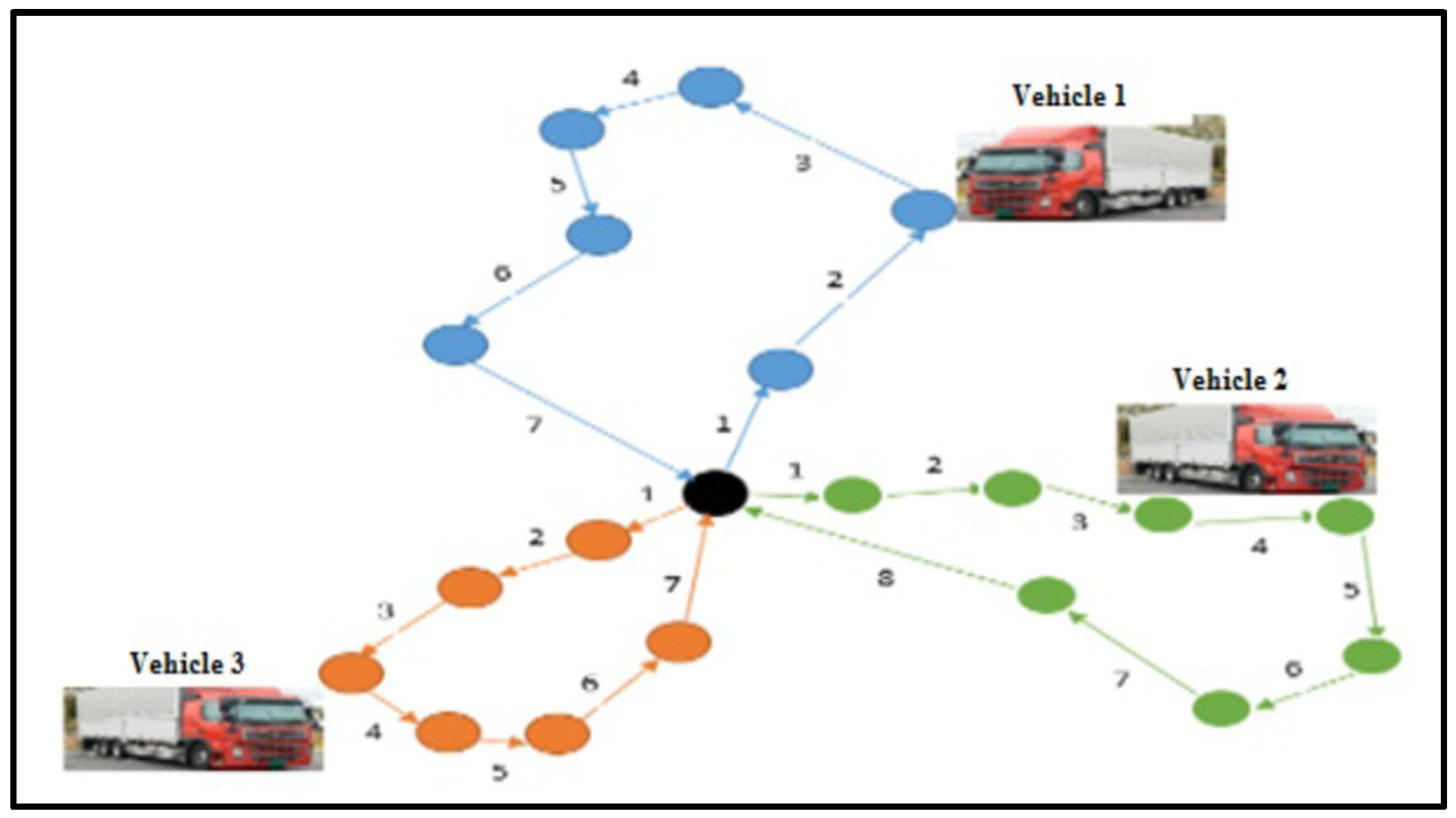
Figure 1 depicts an example of routes for the CVRP with three vehicles as follows.
- (A)
Assumptions
- (i)
Customer demand,, is known 0 < qi ≤ Q;
- (ii)
Limited vehicle capacity.
- (B)
Variables and parameters
- (i)
V: A set of customers is represented as V = {v0, v1, v2, …, vn} where n is the number of customers;
- (ii)
cij: Transportation cost from nodes (customers) i to j;
- (iii)
D: Length of the route (total distance that is travelled by the vehicle) should not surpass a particular defined constraint;
- (iv)
Q: Capacity of each vehicle;
- (v)
m: Number of vehicles;
- (vi)
v0: Main distribution centre refers to the depot node where a tour starts and ends;
- (vii)
K: Set of identical vehicles; K = {k0, k1, k2, …, km} is based on the main distribution centre, v0.
Dantzig and Ramser [
1] proposed the first mathematical model for the CVRP ([
6,
39]) which is described below:
Based on the following constraints:
Equation (1) describes the objective functions used for minimizing the total distance travelled by a vehicle under constraint as shown in (2)–(8). Constraint (3) ensures that the number of vehicles entering a customer is the same as the number of vehicles leaving the same customer. Constraints (4) and (5) are applied for observing the customers who receive the service only once. On the other hand, Constraints (6) and (7) ensure that each vehicle that is used starts and ends at a depot and travels only once to offer its service. The main equation that is used for solving the CVRP problem is presented in (8) where it assigns the vehicle’s capacity for transporting different items. The sub-tour elimination constraints (9) guarantee that the solution contains no sub-tour.
3.4. Proposed Enhanced Ant Colony System (EACS) Algorithm
The ACS algorithm consists of four main steps—initialization, solution creation, local search, and pheromone update. The steps of the EACS algorithm are presented by proposing an enhancement mechanism based on the subpaths that achieve finding the best solutions for the proposed objectives. The enhancement is made in the step of building the solution which is characterized by the transition of the ant through the transitional equation that has a significant impact on achieving a balance between exploitation and exploration mechanisms. In the same context, this equation has been enhanced by using two mechanisms. The first one is related to the diversification by introducing a new term that supports the exploration mechanism of the transition equation from node to node. The second one is related to the intensification by selecting the best subpaths previously saved in a table that supports the exploitation mechanism for the transitional equation from node to subpath. The steps of our proposed EACS are as follows.
Step I (Initialization): Initialize the pheromone primary matrix, distance matrix, number of ants that are to be used, and control parameters—α, β, ρ, τ0, , (Q ≥ 0). The total demand of items carried by each vehicle must not surpass the vehicle’s capacity, Q. is the inverse of the distance between nodes i and j. The initial pheromone amount for every edge (i, j) depends on the following function: where represents the initial value describing the pheromone effect and refers to the cost generated by the KNN.
Step II: (i) (Solution creation): The transition rule equation used in the ACS algorithm was significant as it allowed the algorithm structure to enhance the solutions. This was attributed to the fact that based on the traditional formulation mentioned in
Table 1, the ants move from one node to the other. Hence, it should be properly used for improving the transition and preventing any incorrect move to an unacceptable node since it could lead to a waste of effort and prove to be expensive. The transition rule is enhanced by using the two formulations described in
Table 1.
After improving the transition rule, Step 1 implements the transition rule node by node for deriving new solutions. On the other hand, the second formulation was dependent on the movement between the node to subpaths for generating solutions. The first formulation is dependent on the subpaths because it helps in diversifying the solutions when travelling from one node to the next after the addition of a new term that supports the exploration mechanism since all terms in the initial transition rule support the exploitation mechanism implemented for this purpose. Then, all subpaths are saved after each iteration in the table while the repetitive subpaths are excluded for improving the diversification. Thereafter, the second formulation is applied in the intensification mechanism after determining the best solution while travelling from the node to the subpath. The best subpaths are stored after every iteration in different tables wherein all subpaths are utilized rather than depending on the nodes (i.e., the conventional formulation). The paths initiate at a particular node and stop at different specified nodes. The total distance and total pheromone concentration are calculated. Moreover, determine the amount of pheromone that is saved for every subpath of the path. Then, the transition rule is applied after they are considered as a single edge. The enhancement in the transition rule depends on the transition between the nodes or the transition to the subpath in the following manner (Equation (10)):
Here,
is the transition equation of node-by-node,
is the transition equation from node to subpath,
h is the coefficient for utilizing the subpaths, and
is a random number. In the traditional transitional rule, a tour is carried out from one node to another wherein each ant successively adds new nodes until it visits all nodes. Here, if the ant
k is present at node
i, it moves to the next node,
j, from the set of legal nodes,
U (i.e., the set of unvisited nodes). The justification for suggesting this enhancement is because the ACS algorithm suffers from a lack of diversity so there is a need for improving the transitional rule which has derived from a set of terms with its associated coefficients that has been enhanced by most related studies ([
44,
45]) that used the terms to support exploitation. While this research work introduced a new term
for this transitional rule in the enhanced ACS algorithm through which the passage of the same subpaths that were visited in previous solutions is avoided, this supports the exploration mechanism and, thus, the diversity is increased. The transitional rule became the following (Equation (11)):
Here,
,
is the maximum number of continuously visited nodes from the beginning of the solution
k that exist partly or completely on one of the recorded previous subpaths so that the more the number of nodes in the chosen subpath
increases, the value of
decreases. Therefore, the probability of choosing it later decreases and the probability of exploring other subpaths then increases. Furthermore, (
i,
l) refers to the edge;
l is the city that was not yet visited by ant
k. If
, the exploitation mechanism was selected; however, if
, the exploration was selected.
is the random variable that is specified based on the probability transition rule between different nodes
[
38] that was applied on the subpaths in the following manner (Equation (12)):
Here,
is amount of pheromone on the edge
,
is the inverse of the distance between nodes
i and
j,
ξij is the savings between nodes
i and
j, and
α,
β,
γ, and
δ are the control parameters. In the mechanism of building the solution by using the subpaths, we convert the terms of the transitional equation so that it depends on the subpaths and not on the edges as we select the best subpaths to build the solution sequentially. The transition rule based on subpaths is given as below (Equation (13)):
Here,
is the random variable that is defined based on the probability of the transition rule from the node to a subpath
which is applied according to the subpaths in the following manner (Equation (14)):
Here, G represents the set of nodes of the subpaths that start at node i. Between the start and end nodes, these subpaths include many other unvisited nodes. These subpaths have a common feature where they start at one node and differ in other nodes and end at a different node while travelling between different paths.
Step II: (ii) (Local pheromone update): It includes the update of local pheromone to limit its concentration for exploring unused routes to produce different solutions and avoids the fall in a locally optimal, thus making the route less attractive for the next ants. Equation (15) shows the process of this stage.
Here,
is a parameter, known as the evaporation coefficient, whose value is described in
Table 2.
=
represents the primary pheromone level of edges and
is the length of the tour generated by the KNN.
Step III: (Local search): In this section, the nodes are changed to enhance the route of all vehicles and, hence, to enhance the solutions that have been built by all ants through improving the quality of the solution of every ant. Alternatively, when utilizing the local search, the best local enhanced solutions might have a major chance to find the best solution. So, the local search is utilized for improving the solutions. Although this can be conducted in many ways, the most popular techniques include the use of two-opt and three-opt local search methods. In the two-opt method, two edges are eliminated from the tour and then the eliminated two edges are reconnected. The two edges can only be reconnected such that the validity of the tour is guaranteed and it is shorter. It is seen that the three-opt algorithm is operated similarly; however, rather than eliminating two edges, the algorithm removes three edges. This means that there are two techniques of reconnecting the three edges. In this study, we focused on using the large CVRP data, hence, we apply the three-opt technique for completing their subtour and k-opt was applied to various subpaths derived based on the experience of subpaths from the earlier iterations. This considered the installation of node 1 at last in every subpath. This ensures the enhancement of the best picture of the paths. In this phase, we apply the local search technique for improving the best solutions and thereby improving the best subpaths. This experience can help in successive iterations. This could be maximized after improving the subpaths where we can use them for global update.
Step IV: (Global pheromone update): A global update is carried out after every iteration wherein the pheromone values are updated based on the solution quality in the existing iteration. It can be performed by decreasing the pheromone values for all solutions using the evaporation procedure. This increases the pheromone value which helps in deriving the best solutions. On the other hand, in the EACS algorithm, the best elitist ants present in the iteration can lay the pheromone compound on the ribs where they travelled. A global updating rule may be described as follows (Equation (16)).
where
where
= ranking index,
refers to the increased trail level on the edge (
i,
j) that are affected by
best ant,
= tour length of
best ant,
represents the increase in the trail level on the edge (
i,
j) triggered by elitist ants,
= no. of elitist ants,
= tour length of the best solution, and
t = iteration counter while
∈ (0, 1] is the parameter used for regulating the decrease in
The global update section collects all experience of the earlier iterations and updates the pheromone level of the best solution using another coefficient that differs from other coefficients used for the specific solutions that were not as effective as the elitist solutions. In the algorithm proposed in this study, the experience of the distinctive subpaths derived using the earlier iterations was retained for their later use. They could be used for developing solutions that were based on the experience of paths and helped in generating better results in less time. The pseudocode of the proposed EACS algorithm was presented as in Algorithm 1.
| Algorithm 1: EACS algorithm |
![Symmetry 15 02020 i001]() |