The Influence of Increased Electron Energy Spread on the Radiation of the Second Harmonic in Free Electron Lasers
Abstract
:1. Introduction
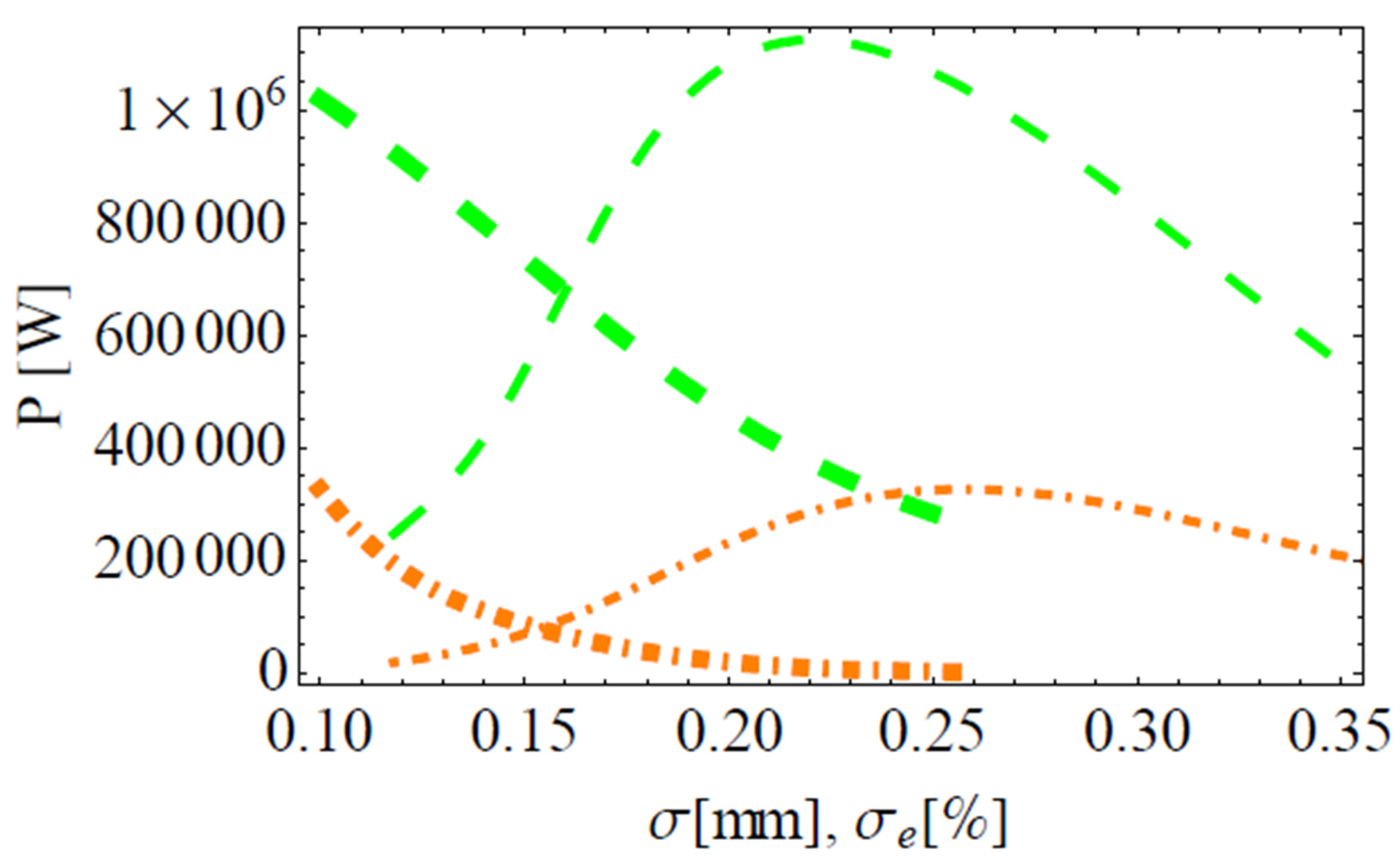
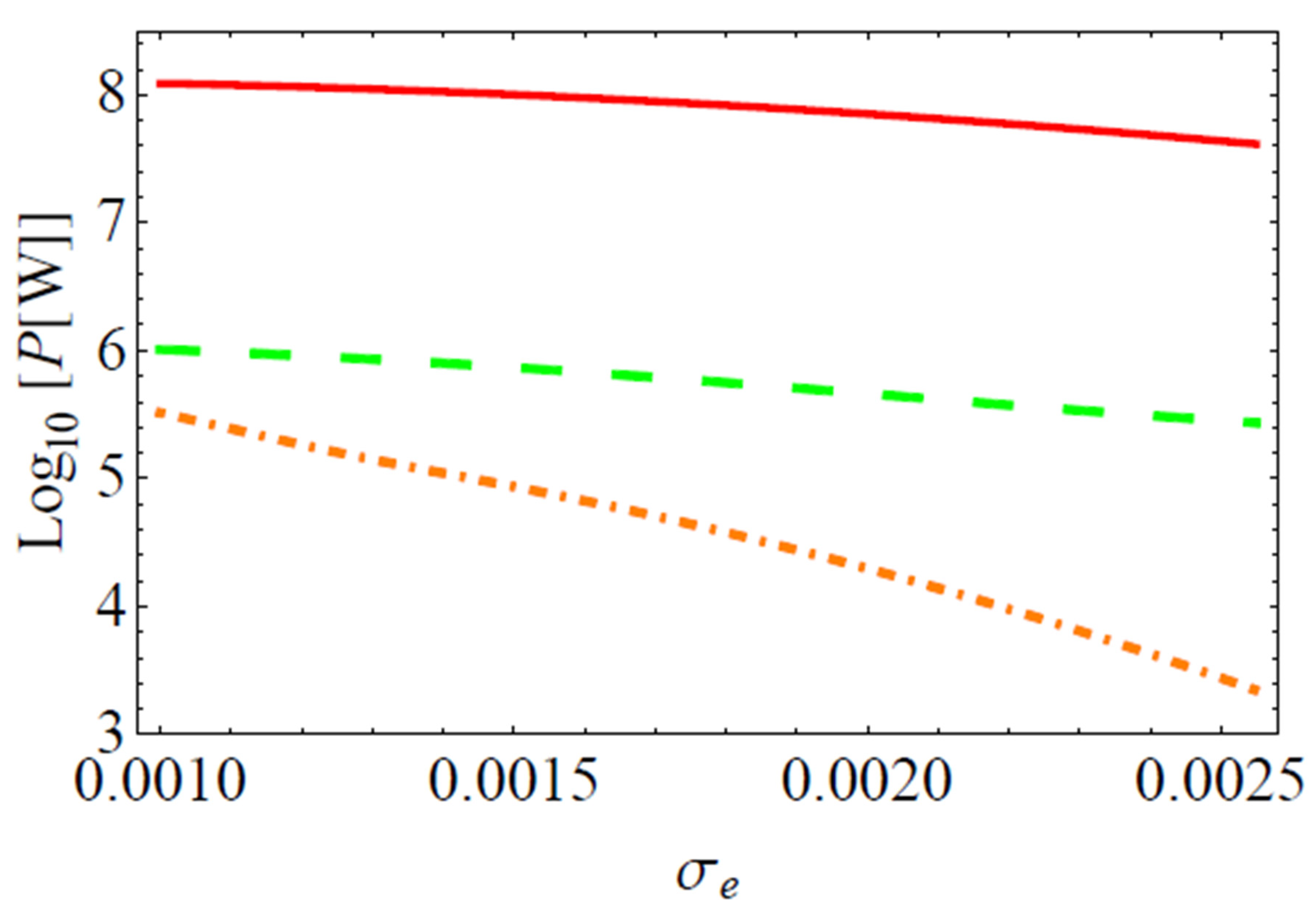
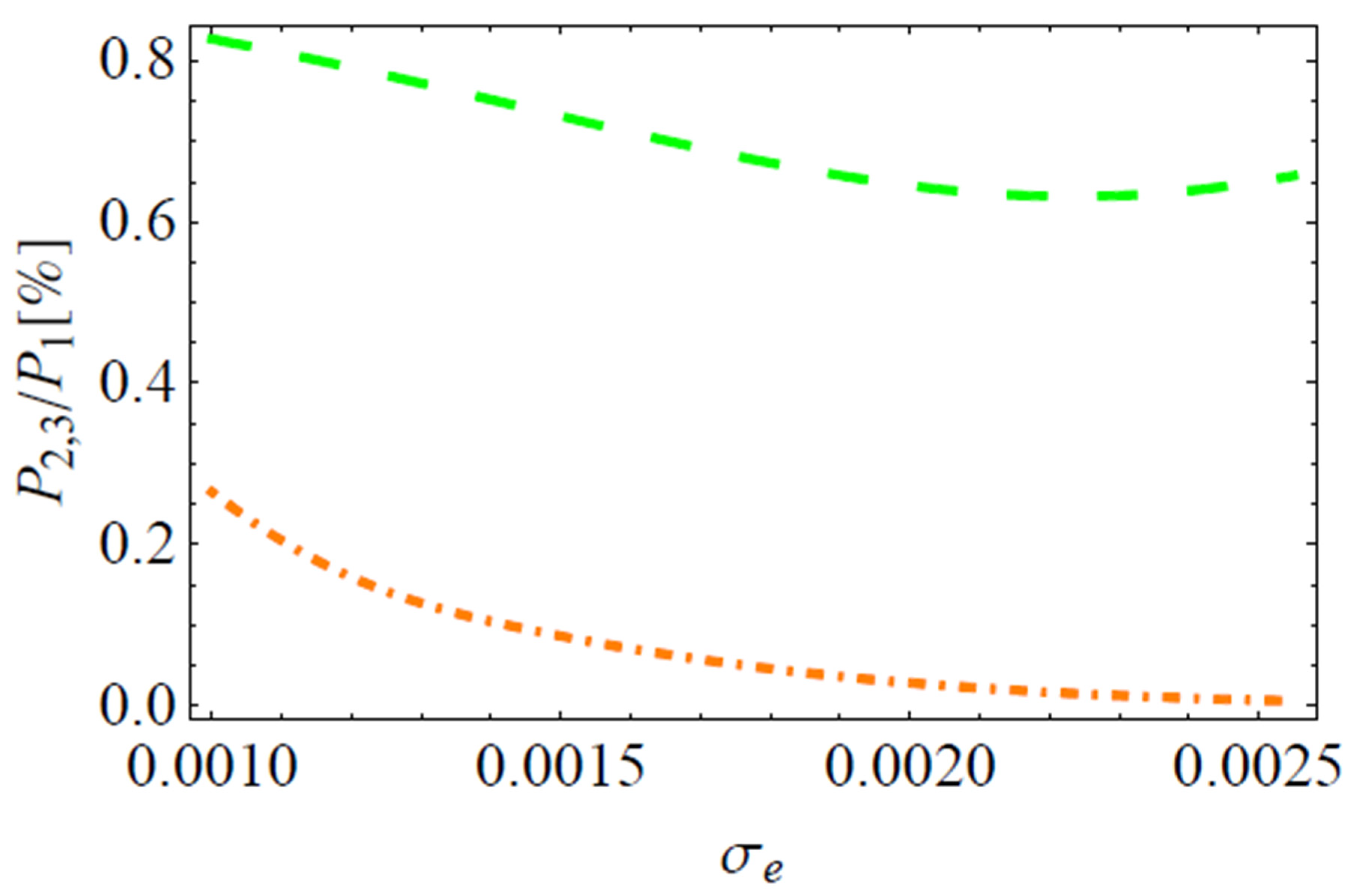
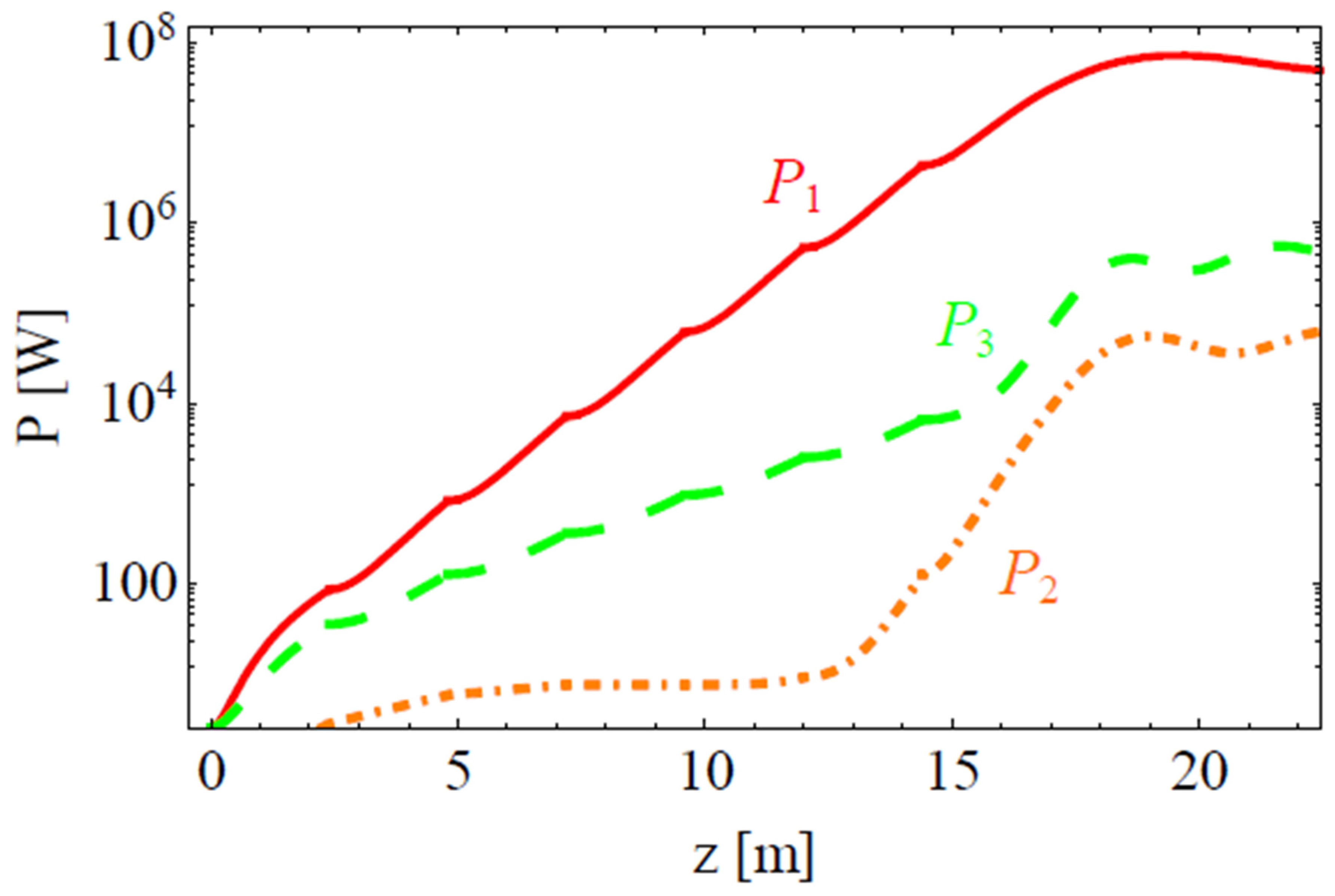
2. Results and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faatz, B.; Braune, M.; Hensler, O.; Honkavaara, K.; Kammering, R.; Kuhlmann, M.; Ploenjes, E.; Roensch-Schulenburg, J.; Schneidmiller, E.; Schreiber, S.; et al. The FLASH Facility: Advanced Options for FLASH2 and Future Perspectives. Appl. Sci. 2017, 7, 1114. [Google Scholar] [CrossRef]
- Schneidmiller, E.A.; Faatz, B.; Kuhlmann, M.; Rönsch-Schulenburg, J.; Schreiber, S.; Tischer, M.; Yurkov, M.V. First operation of a harmonic lasing self-seeded free electron laser. Phys. Rev. Accel. Beams 2017, 20, 020705. [Google Scholar] [CrossRef]
- Altarelli, M.; Brinkmann, R.; Chergui, M.; Decking, W.; Dobson, B.; Düsterer, S.; Grübel, G.; Graeff, W.; Graafsma, H.; Hajdu, J.; et al. (Eds.) XFEL: The European X-ray Free-Electron Laser—Technical Design Report; DESY 2006-097; DESY: Hamburg, Germany, 2006. [Google Scholar]
- Altarelli, M. The European X-ray free-electron laser facility in Hamburg. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2011, 269, 2845–2849. [Google Scholar] [CrossRef]
- Tschentscher, T.; Bressler, C.; Grünert, J.; Madsen, A.; Mancuso, A.P.; Meyer, M.; Scherz, A.; Sinn, H.; Zastrau, U. Photon Beam Transport and Scientific Instruments at the European XFEL. Appl. Sci. 2017, 7, 592. [Google Scholar] [CrossRef]
- Schneidmiller, E.A.; Yurkov, M.V. An overview of the radiation properties of the European XFEL. In Proceedings of the FEL 2014 Conference, Basel, Switzerland, 5–29 August 2014. [Google Scholar]
- Schneidmiller, E.A.; Yurkov, M.V. Photon Beam Properties at the European XFEL. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/42/096/42096439.pdf (accessed on 1 July 2023).
- Togashi, T.; Takahashi, E.J.; Midorikawa, K.; Aoyama, M.; Yamakawa, K.; Sato, T.; Iwasaki, A.; Owada, S.; Okino, T.; Yamanouchi, K.; et al. Extreme ultraviolet free electron laser seeded with high-order harmonic of Ti:sapphire laser. Opt. Express 2010, 19, 317–324. [Google Scholar] [CrossRef]
- Kang, H.-S.; Min, C.-K.; Heo, H.; Kim, C.; Yang, H.; Kim, G.; Nam, I.; Baek, S.Y.; Choi, H.-J.; Mun, G.; et al. Hard X-ray free-electron laser with femtosecond-scale timing jitter. Nat. Photonics 2017, 11, 708–713. [Google Scholar] [CrossRef]
- Yang, H.; Kim, G.; Kang, H.-S. First saturation of 14.5 keV free electron laser at PAL-XFEL. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2018, 911, 51–54. [Google Scholar] [CrossRef]
- Hong, J.; Han, J.-H.; Park, S.; Jung, Y.; Kim, D.; Kang, H.-S.; Pflueger, J. A study on low emittance injector and undulator for PAL-XFEL. High Power Laser Sci. Eng. 2015, 3, e21. [Google Scholar] [CrossRef]
- Ko, I.S.; Kang, H.-S.; Heo, H.; Kim, C.; Kim, G.; Min, C.-K.; Yang, H.; Baek, S.Y.; Choi, H.-J.; Mun, G.; et al. Construction and Commissioning of PAL-XFEL Facility. Appl. Sci. 2017, 7, 479. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Emma, P. First lasing of the LCLS X-ray FEL at 1.5 Å, TH3PBI01. In Proceedings of the 23rd Conference PAC09, Vancouver, BC, Canada, 4–8 May 2009. [Google Scholar]
- Huang, Z.; Reiche, S. Generation of GW-level, sub-Angstrom radiation in the LCLS using a second-harmonic radiator. In Proceedings of the FEL 2004 Conference, Trieste, Italy, 29 August–3 September 2004; p. 201. [Google Scholar]
- Ratner, D.; Brachmann, A.; Decker, F.J.; Ding, Y.; Dowell, D.; Emma, P.; Fisher, A.; Frisch, J.; Gilevich, S.; Huang, Z.; et al. Second and third harmonic measurements at the linac coherent light source. Phys. Rev. Spéc. Top. Accel. Beams 2011, 14, 060701. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray Free Electron Laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Abela, R.; Beaud, P.; van Bokhoven, J.A.; Chergui, M.; Feurer, T.; Haase, J.; Ingold, G.; Johnson, S.L.; Knopp, G.; Lemke, H.; et al. Perspective: Opportunities for ultrafast science at SwissFEL. Struct. Dyn. 2017, 4, 061602. [Google Scholar] [CrossRef] [PubMed]
- Juranić, P.; Rehanek, J.; Arrell, C.A.; Pradervand, C.; Ischebeck, R.; Erny, C.; Heimgartner, P.; Gorgisyan, I.; Thominet, V.; Tiedtke, K.; et al. SwissFEL Aramis beamline photon diagnostics. J. Synchrotron Radiat. 2018, 25, 1238–1248. [Google Scholar] [CrossRef] [PubMed]
- Juranić, P.; Rehanek, J.; Arrell, C.A.; Pradervand, C.; Cassar, A.; Calvi, M.; Ischebeck, R.; Erny, C.; Heimgartner, P.; Gorgisyan, I.; et al. SwissFEL Aramis beamline photon diagnostics. Erratum. J. Synchrotron Radiat. 2019, 26, 906. [Google Scholar] [CrossRef] [PubMed]
- Abela, R.; Alarcon, A.; Alex, J.; Arrell, C.; Arsov, V.; Bettoni, S.; Bopp, M.; Bostedt, C.; Braun, H.-H.; Calvi, M.; et al. The SwissFEL soft X-ray free-electron laser beamline: Athos. J. Synchrotron Rad. 2019, 26, 1073–1084. [Google Scholar] [CrossRef] [PubMed]
- Prat, E.; Abela, R.; Aiba, M.; Alarcon, A.; Alex, J.; Arbelo, Y.; Arrell, C.; Arsov, V.; Bacellar, C.; Beard, C.; et al. A compact and cost-effective hard X-ray free-electron laser driven by a high-brightness and low-energy electron beam. Nat. Photon. 2020, 14, 748–754. [Google Scholar] [CrossRef]
- Inoue, I.; Osaka, T.; Hara, T.; Tanaka, T.; Inagaki, T.; Fukui, T.; Goto, S.; Inubushi, Y.; Kimura, H.; Kinjo, R.; et al. Generation of narrow-band X-ray free-electron laser via reflection self-seeding. Nat. Photon. 2019, 13, 319–322. [Google Scholar] [CrossRef]
- Owada, S.; Nakajima, K.; Togashi, T.; Kayatama, T.; Yabashi, M. Single-shot arrival timing diagnostics for a soft X-ray free-electron laser beamline at SACLA. J. Synchrotron Rad. 2018, 25, 282. [Google Scholar] [CrossRef]
- Tetsuya, I.; Hideki, A.; Takao, A.; Yoshihiro, A.; Noriyoshi, A.; Teruhiko, B.; Hiroyasu, E.; Kenji, F.; Toru, F.; Yukito, F.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photon. 2012, 6, 540–544. [Google Scholar]
- Available online: http://xfel.riken.jp/eng/users/bml02-11.html (accessed on 1 July 2023).
- Ego, H.; Asaka, T.; Fujita, T.; Fukui, T.; Hosoda, N.; Inagaki, T.; Kobayashi, K.; Kondo, C.; Maesaka, H.; Masuda, T.; et al. RF System of the SPring-8 Upgrade Project. In Proceedings of the IPAC2016, Busan, Korea, 8–13 May 2016; pp. 414–416. [Google Scholar]
- Iwai, E.; Inoue, I.; Maesaka, H.; Inagaki, T.; Yabashi, M.; Hara, T.; Tanaka, H. Spectral-brightness optimization of an X-ray free-electron laser by machine-learning-based tuning. J. Synch. Rad. 2023, 30, 1048–1053. [Google Scholar] [CrossRef]
- Tono, K.; Hara, T.; Yabashi, M.; Tanaka, H. Multiple-beamline operation of SACLA. J. Synchrotron Rad. 2019, 26, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Tono, K.; Togashi, T.; Inubushi, Y.; Sato, T.; Katayama, T.; Ogawa, K.; Ohashi, H.; Kimura, H.; Takahashi, S.; Takeshita, K.; et al. Beamline, experimental stations and photon beam diagnostics for the hard x-ray free electron laser of SACLA. New J. Phys. 2013, 15, 083035. [Google Scholar] [CrossRef]
- Biedron, S.G.; Dejus, R.J.; Huang, Z.; Milton, S.V.; Sajaev, V.; Berg, W.; Borland, M.; DenHartog, P.K.; Erdmann, M.; Fawley, W.M.; et al. Measurements of nonlinear har-monic generation at the Advanced Photon Source’s SASE FEL. Nucl. Instrum. Meth. Phys. Res. A 2002, 483, 94–100. [Google Scholar] [CrossRef]
- Milton, S.V.; Gluskin, E.; Arnold, N.D.; Benson, C.; Berg, W.; Biedron, S.G.; Borland, M.; Chae, Y.C.; Dejus, R.J.; Den Hartog, P.K.; et al. Exponential Gain and Saturation of a Self-AmpliÞed Spontaneous Emission Free-Electron Laser. Science 2000, 292, 2037–2041. [Google Scholar] [CrossRef] [PubMed]
- Alfonso, F.; Maya, K. Elettra-Sincrotrone Trieste: Present and future. Eur. Phys. J. Plus 2023, 79, 138. [Google Scholar]
- Xiao, R.; Chen, K.; Shi, Y.; Chen, C. Toward 80% Efficiency in a Super Klystron-Like Relativistic Backward Wave Oscillator With Second and Third Harmonic Coaxial-Premodulation Cavity. IEEE Trans. Electron Devices 2023, 70, 2521–25251. [Google Scholar] [CrossRef]
- Kuznetsov, S.V.; Sedov, V.S.; Martyanov, A.K.; Batygov, S.C.; Vakalov, D.S.; Boldyrev, K.N.; Tiazhelov, I.A.; Popovich, A.F.; Pasternak, D.G.; Bland, H.; et al. Cerium-doped gadolinium-scandium-aluminum garnet powders: Synthesis and use in X-ray luminescent diamond composites. Ceram. Int. 2022, 48, 12962–12970. [Google Scholar] [CrossRef]
- Sedov, V.; Kuznetsov, S.; Kamenskikh, I.; Martyanov, A.; Vakalov, D.; Savin, S.; Rubtsova, E.; Tarala, V.; Omelkov, S.; Kotlov, A.; et al. Diamond composite with embedded YAG:Ce nanoparticles as a source of fast X-ray luminescence in the visible and near-IR range. Carbon 2021, 174, 52–58. [Google Scholar] [CrossRef]
- Kuznetsov, S.V.; Yasyrkina, D.S.; Valiev, D.T.; Stepanov, S.A.; Alexandrov, A.A.; Batygov, S.K.; Voronov, V.V.; Konyushkin, V.A.; Nakladov, A.N.; Ermakova, J.A.; et al. Spectral and Cathodoluminescence Decay Characteristics of the Ba1−xCexF2+x (x = 0.3–0.4) Solid Solution Synthesized by Precipitation from Aqueous Solutions and Fusion. Photonics 2023, 10, 1057. [Google Scholar] [CrossRef]
- Kuznetsov, S.V.; Ermakova, Y.A.; Boldyrev, K.N.; Sedov, V.S.; Alexandrov, A.A.; Voronov, V.V.; Batygov, S.K.; Rezaeva, A.D.; Drobysheva, A.R.; Tabachkova, N.Y. Single-phase nanopowders of Sr0.85-xBaxEu0.15F2.15: Investigation of structure and X-ray luminescent properties. Ceram. Int. 2023, 49, 39189–39195. [Google Scholar] [CrossRef]
- Wu, L.; Patankar, S.; Morimoto, T.; Nair, N.L.; Thewalt, E.; Little, A.; Analytis, J.G.; Moore, J.E.; Orenstein, J. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 2016, 13, 350–355. [Google Scholar] [CrossRef]
- Nuriya, M.; Fukushima, S.; Momotake, A.; Shinotsuka, T.; Yasui, M.; Arai, T. Multimodal two-photon imaging using a second harmonic generation-specific dye. Nat. Commun. 2016, 7, 11557. [Google Scholar] [CrossRef] [PubMed]
- Campagnola, P.J.; Loew, L.M. Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms. Nat. Biotechnol. 2003, 21, 1356–1360. [Google Scholar] [CrossRef] [PubMed]
- Boyd, G.; Bridges, T.; Burkhardt, E. Up-Conversion of 10.6 p Radiation to the Visible and Second Harmonic Generation in HgS. IEEE J. Quantum Electron. 1968, 4, 515. [Google Scholar] [CrossRef]
- Bhar, G.C.; Das, S.; Vodopyanov, K.L. Nonlinear optical laser devices using GaSe. Appl. Phys. B Laser Opt. 1995, 61, 187–190. [Google Scholar] [CrossRef]
- Csonka, P.L.; Kroo, N. Methods to generate femto- and attosecond electron and X-ray pulses. Nucl. Instrum. Methods Phys. Res. Sect. A 1996, 376, 283–290. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Fedorov, I. Spontaneous and Stimulated Undulator Radiation in Symmetric and Asymmetric Multi-Periodic Magnetic Fields. Symmetry 2021, 13, 135. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Effect of the 3rd undulator field harmonic on spontaneous and stimulated undulator radiation. J. Synchrotron Rad. 2019, 26, 1481. [Google Scholar] [CrossRef]
- Zhukovsky, K. Analysis of the spectral properties of free electron lasers in X-ray and other bands. Radiat. Phys. Chem. 2021, 189, 109698. [Google Scholar] [CrossRef]
- Zhukovsky, K. Theoretical analysis of the radiation properties of some major x-ray free electron lasers. Ann. Phys. 2021, 533, 2100091. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Fedorov, I. On the Generation of Even Harmonics in Planar and Elliptical Undulators of Free Electron Lasers. Mosc. Univ. Phys. Bull. 2022, 77, 11. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Undulator and free-electron laser radiation with field harmonics and off-axis effects taken into account analytically. Phys. Uspekhi 2021, 64, 304–316. [Google Scholar] [CrossRef]
- Zhukovsky, K. On the possibilities of amplification and radiation of harmonics in modern X-ray free electron lasers. Opt. Laser Technol. 2021, 143, 107296. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Theoretical Analysis of Radiation Properties of X-ray Free-Electron Lasers. Radiophys. Quantum Electron. 2022, 65, 88–117. [Google Scholar] [CrossRef]
- Prakash, B.; Huse, V.; Gehlot, M.; Mishra, G. Analysis of spectral properties of harmonic undulator radiation of an electromagnet undulator. Optik 2016, 127, 1639. [Google Scholar] [CrossRef]
- Attwood, D. Soft X-rays and Extreme Ultraviolet Radiation; Cambridge University Press: Cambridge, UK, 1999; Chapter 5. [Google Scholar]
- Kitamura, H. Polarization of Undulator Radiation. Jpn. J. Appl. Phys. 1980, 19, L185–L188. [Google Scholar] [CrossRef]
- Vinokurov; Levichev, E.B. Undulators and wigglers for the production of radiation and other applications. Phys. Uspekhi 2015, 58, 850. [Google Scholar] [CrossRef]
- Alferov, D.F.; Bashmakov, Y.A.; Cherenkov, P.A. Radiation from relativistic electrons in a magnetic undulator. Sov. Phys. Uspekhi 1989, 32, 200. [Google Scholar] [CrossRef]
- Zhukovsky, K. JETP, On the Possibility of Controlling the Second Harmonic Radiation of the Free Electron Laser Using the Second Harmonic of the Undulator Field. J. Exp. Theor. Phys. 2023, 137, 271. [Google Scholar] [CrossRef]
- Tanaka, T.; Kitamura, H. SPECTRA: A synchrotron radiation calculation code. J. Synchrotron Rad. 2001, 8, 1221–1228. [Google Scholar] [CrossRef]
- Tanaka, T. Numerical methods for characterization of synchrotron radiation based on the Wigner function method. Phys. Rev. ST Accel. Beams 2014, 17, 060702. [Google Scholar] [CrossRef]
- Tanaka, T. Coherent mode decomposition using mixed Wigner functions of Hermite–Gaussian beams. Opt. Lett. 2017, 42, 1576. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T. Universal representation of undulator phase errors. Phys. Rev. Accel. Beams 2018, 21, 110704. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Fedorov, I.; Gubina, N. Theoretical analysis of the influence of electron beam parameters on the harmonic powers in free electron lasers. Opt. Laser Technol. 2023, 159, 108972. [Google Scholar] [CrossRef]
- McNeil BW, J.; Thompson, N.R. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814. [Google Scholar] [CrossRef]
- Pellegrini, C.; Marinelli, A.; Reiche, S. The physics of x-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 015006. [Google Scholar] [CrossRef]
- Margaritondo, G. Synchrotron light: A success story over six decades. Riv. Nuovo Cimento. 2017, 40, 411–471. [Google Scholar]
- Huang, Z.; Kim, K.-J. Review of X-ray free-electron laser theory. Phys. Rev. Spéc. Top. Accel. Beams 2007, 10, 034801. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Three-dimensional analysis of harmonic generation in high-gain free-electron lasers. Phys. Rev. E 2000, 62, 7295–7308. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Nonlinear harmonic generation of coherent amplification and self-amplified spontaneous emission. Nucl. Instrum. Methods Phys. Res. Sect. A 2001, 475, 112. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.; Yurkov, M. The Physics of Free Electron Lasers; Springer-Verlag: Berlin/Heidelberg, Germany, 2000; 470p. [Google Scholar]
- Colson, W. Theory of high-gain free-electron lasers. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 393, 82–85. [Google Scholar] [CrossRef]
- Freund, H.P.; O’Shea, P.G.; Biedron, S.G. Nonlinear harmonic generation in free-electron lasers. IEEE J. Quantum Electron. 2000, 36, 275. [Google Scholar] [CrossRef]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Giannessi, L. Seeding and Harmonic Generation in Free-Electron Lasers. In Synchrotron Light Sources and Free-Electron Lasers; Jaeschke, E.J., Khan, S., Schneider, J.R., Hastings, J.B., Eds.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Dattoli, G.; Giannessi, L.; Ottaviani, P.L.; Ronsivalle, C. Semi-analytical model of self-amplified spontaneous-emission free-electron lasers, including diffraction and pulse-propagation effects. J. Appl. Phys. 2004, 95, 3206–3210. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Nonlinear harmonic generation in high-gain free-electron lasers. J. Appl. Phys. 2005, 97, 113102. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Booklet for FEL Desing: A Collection of Practical Formulae; ENEA Report RT/2007/40/FIM; ENEA: Frascati, Italy, 2007. [Google Scholar]
- Dattoli, G.; Di Palma, E.; Licciardi, S.; Sabia, E. Free Electron Laser High Gain Equation and Harmonic Generation. Appl. Sci. 2020, 11, 85. [Google Scholar] [CrossRef]
- Xie, M. Exact and variational solutions of 3D eigenmodes in high gain FELs. Nucl. Instrum. Methods Phys. Res. Sect. A 2000, 445, 59. [Google Scholar] [CrossRef]
- Xie, M. Design Optimization for an X-Ray Free Electron Laser Driven by SLAC Linac. In Proceedings of the 1995 Particle Accelerator Conference, Dallas, TX, USA, 1–5 May 1995; IEEE: Piscataway, NJ, USA, 1995; p. 183. [Google Scholar]
- Zhukovsky, K.V. Analytical Description of Nonlinear Harmonic Generation Close to the Saturation Region in Free Electron Lasers. Mosc. Univ. Phys. Bull. 2019, 74, 480–487. [Google Scholar] [CrossRef]
- Zhukovsky, K. On the second harmonic generation in X-ray FELs. EPL 2023, 141, 45002. [Google Scholar] [CrossRef]
- Zhukovsky, K.; Kalitenko, A. Phenomenological and numerical analysis of power evolution and bunching in single-pass X-ray FELs. J. Synchrotron Radiat. 2019, 26, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Gianessi, L. Overview of Perseo, a system for simulating FEL dynamics in Mathcad. In Proceedings of the 28th International Free Electron Laser Conference (FEL 2006), Berlin, Germany, 27 August–1 September 2006; pp. 91–94. [Google Scholar]
- Freund, H.P.; van der Slot, P.J.M. Variable polarization states in free-electron lasers. J. Phys. Commun. 2021, 5, 085011. [Google Scholar] [CrossRef]
- Geloni, G.; Saldin, E.; Schneidmiller, E.; Yurkov, M. Exact solution for second harmonic generation in XFELs. Opt. Commun. 2007, 271, 207–218. [Google Scholar] [CrossRef]
- Saldin, E.; Geloni, G.; Schneidmiller, E.; Yurkov, M.V. Misconceptions regarding Second Harmonic Generation in X-ray Free-Electron Lasers. Nucl. Instrum. Methods Phys. Res. Sect. A 2005, 539, 499. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhukovsky, K. The Influence of Increased Electron Energy Spread on the Radiation of the Second Harmonic in Free Electron Lasers. Symmetry 2023, 15, 2180. https://doi.org/10.3390/sym15122180
Zhukovsky K. The Influence of Increased Electron Energy Spread on the Radiation of the Second Harmonic in Free Electron Lasers. Symmetry. 2023; 15(12):2180. https://doi.org/10.3390/sym15122180
Chicago/Turabian StyleZhukovsky, Konstantin. 2023. "The Influence of Increased Electron Energy Spread on the Radiation of the Second Harmonic in Free Electron Lasers" Symmetry 15, no. 12: 2180. https://doi.org/10.3390/sym15122180
APA StyleZhukovsky, K. (2023). The Influence of Increased Electron Energy Spread on the Radiation of the Second Harmonic in Free Electron Lasers. Symmetry, 15(12), 2180. https://doi.org/10.3390/sym15122180





