Parameter Identification in Metabolic Reaction Networks by Means of Multiple Steady-State Measurements
Abstract
1. Introduction
- –
- First of all, the alternative estimation reduces to solve a nonlinear system which reveals to be actually polynomial w.r.t. the unknown parameters, provided that the kinetic laws are chosen among the standard widespread kinetic mechanisms, as mass-action, or Michaelis-Menten, or the convenience rate law proposed by [5]. Conversely, the classical time-dependent identification leads to the solution of a nonlinear system which is usually non-polynomial.
- –
- The alternative approach requires a lower number of measurements than the classical one, and the required measurements are metabolite concentrations at steady state, which are easier to be obtained w.r.t. time-course measurements.
- –
- The proposed steady-state estimation approach becomes easier when both metabolite concentrations and fluxes (usually determined by constraint-based techniques, [13]) are known, even though this complete knowledge concerns only a subsystem of the considered network. Indeed, in this case, we can split the identification into two steps: (1) identification of the subsystem parameters, exploiting both fluxes and metabolite concentrations; (2) identification of the kinetic parameters of the whole network, using only the available concentration measurements and the subsystem parameter values estimated in the previous step, entering this second estimation round as a priori knowledge. The complexity of the identification is highly reduced in this way. In particular, in step (1) the system complexity is reduced by decoupling the problem into smaller and simpler subproblems related to the single reactions. This decomposition highlights modular and symmetrical properties of the algebraic system, which are extremely relevant as they reduce the computational burden of the identification task, and allow us to further reduce the number of required steady-state measurements (which is a non-negligible aspect, especially for large-scale networks). Moreover, in this case, the local result given in Section 4 becomes global for many simple kinetic mechanisms, as in the case of mass-action or one-to-one bidirectional Michaelis–Menten.
2. Mathematical Models of Metabolic Networks
3. Kinetic Parameter Identification in Metabolic Networks
- the nonlinear system (13) reduces to a polynomial system with respect to the kinetic parameters, for any chosen kinetic mechanism among the standard ones (mass-action, MM, convenience, etc.). In fact, system (13) is a linear combination of reaction rates of the kinds given by Equations (5)–(8); when such rate laws are rational, each balance equation of system (13) can be transformed into a polynomial multiplying by the denominators of the related rate laws, which are always strictly positive (as they are given by 1 plus non-negative terms). Conversely, the nonlinear system (12) is usually non-polynomial;
- the required measurements are metabolite concentrations at steady-state, which are easier to be obtained w.r.t. time-course measurements;
4. Parameters Identifiability Conditions
4.1. Unknown Fluxes
4.2. Known Fluxes
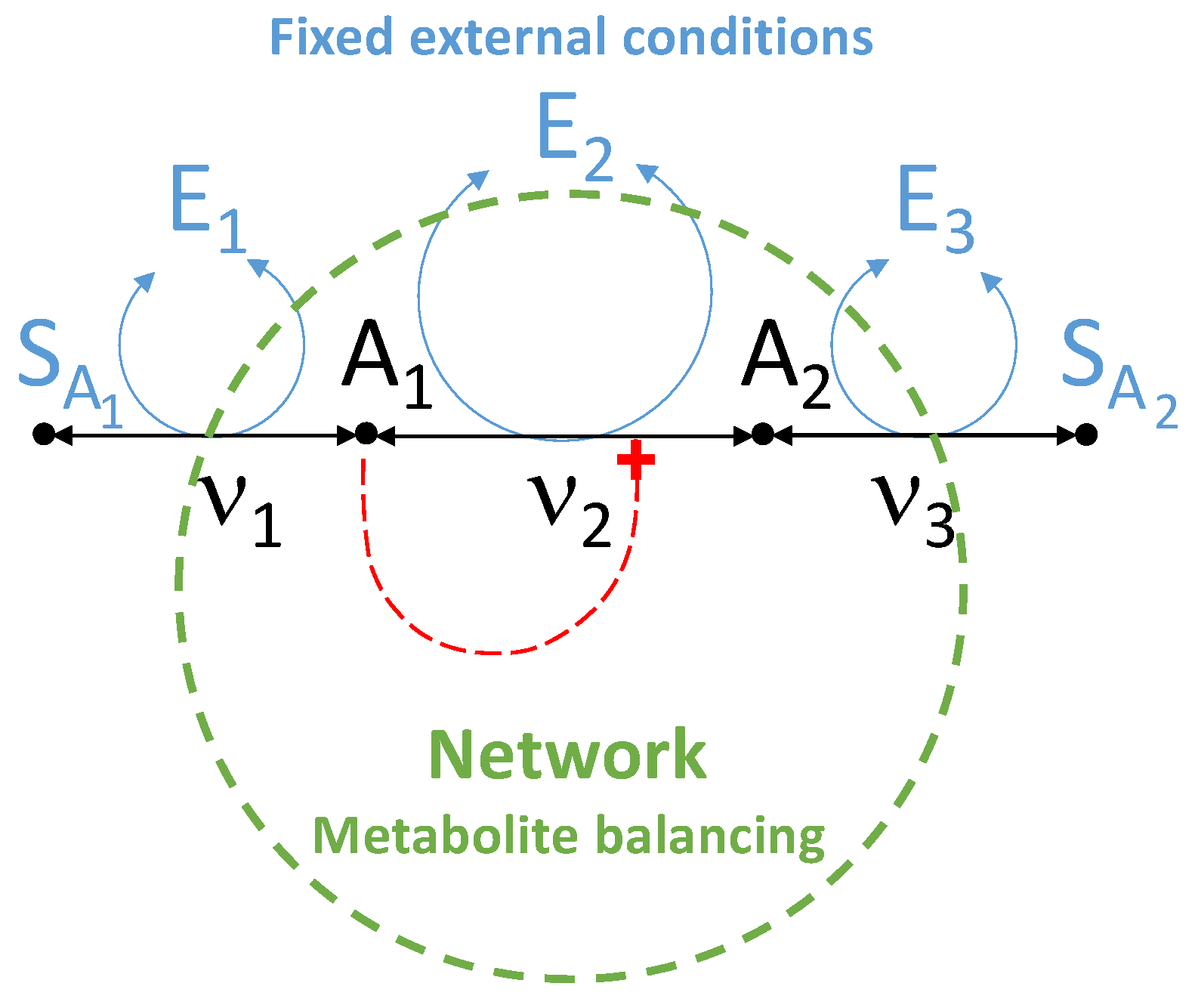
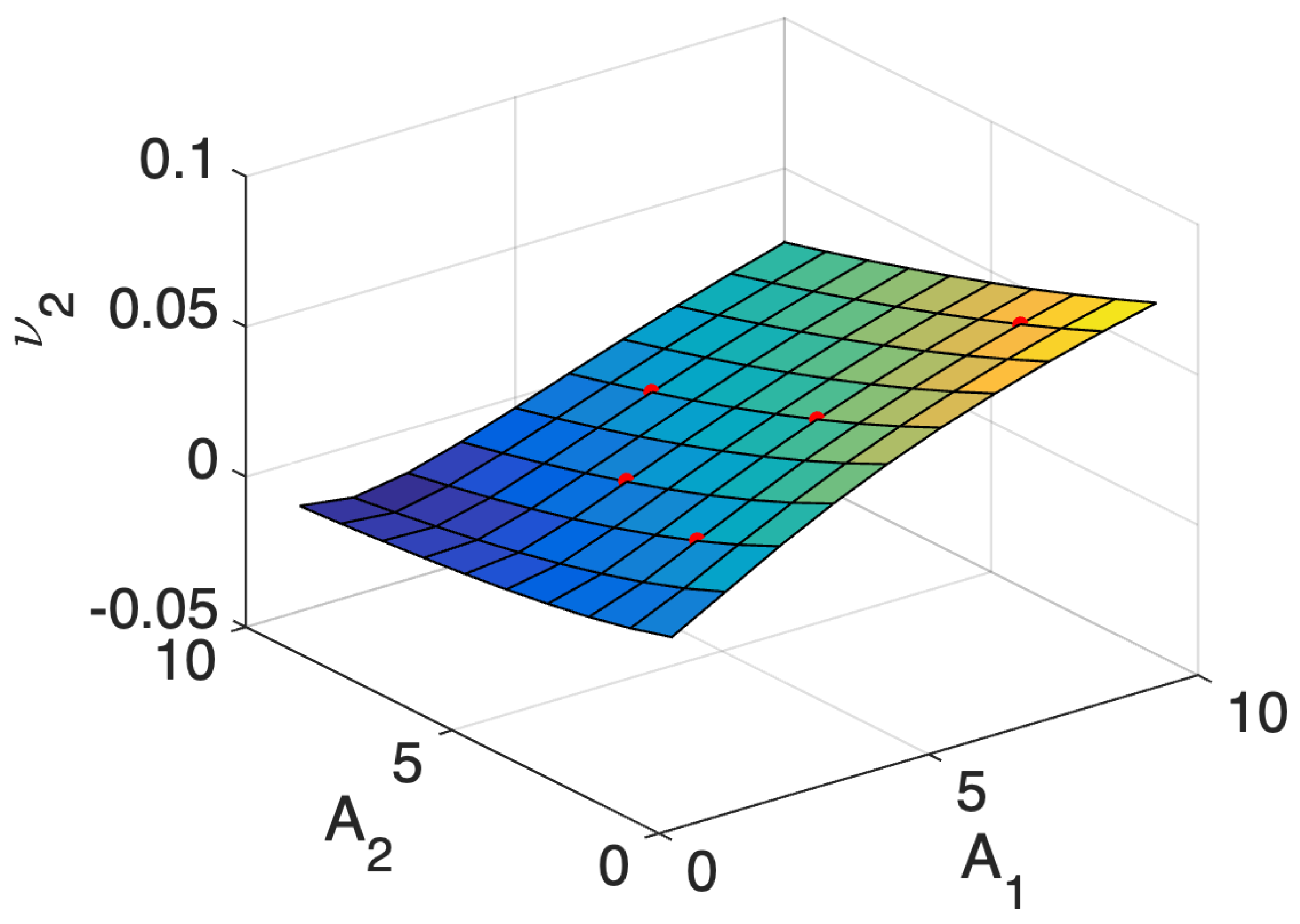
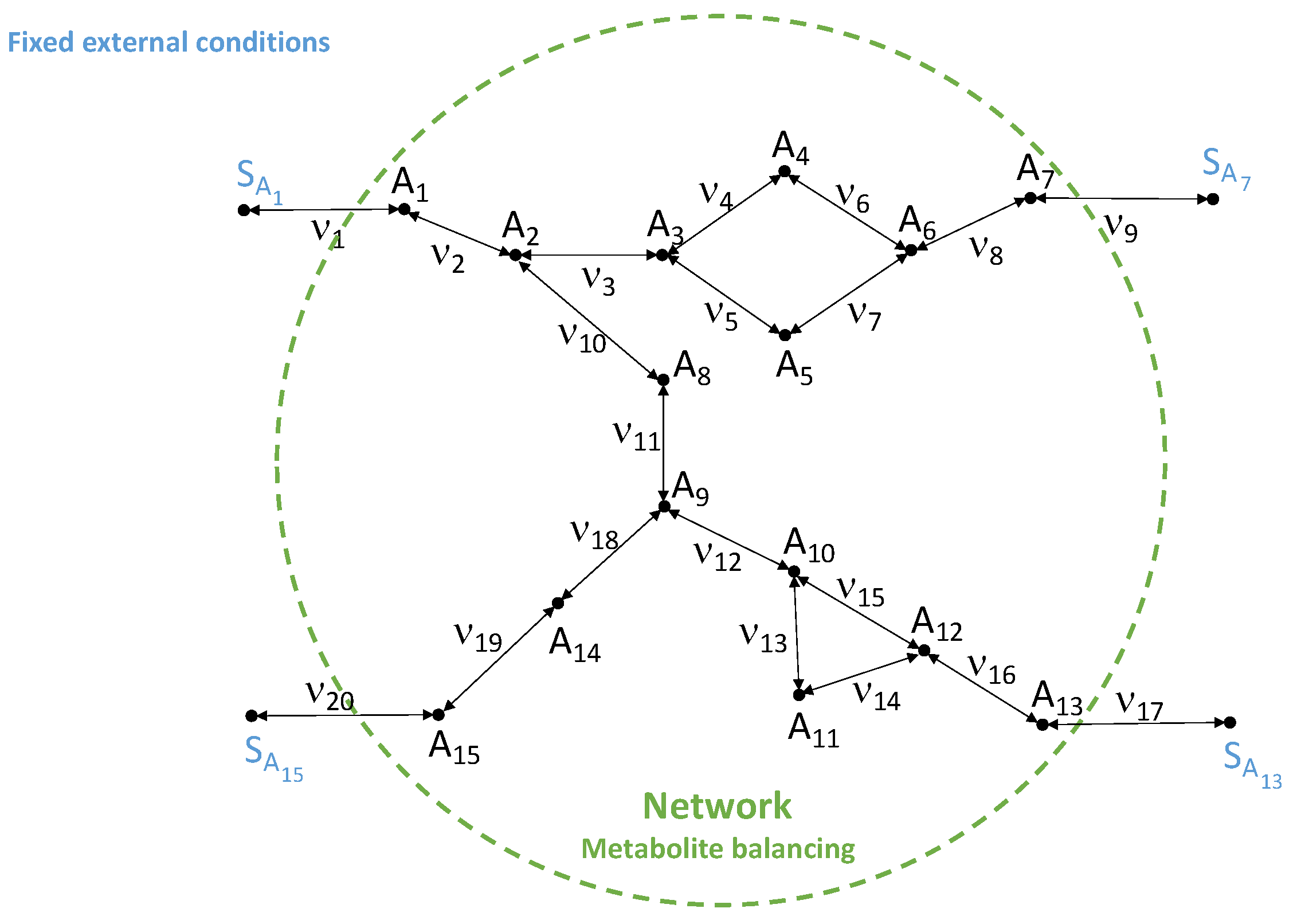
5. Examples
5.1. Comparison of the Estimation Methods Using an Illustrative Example
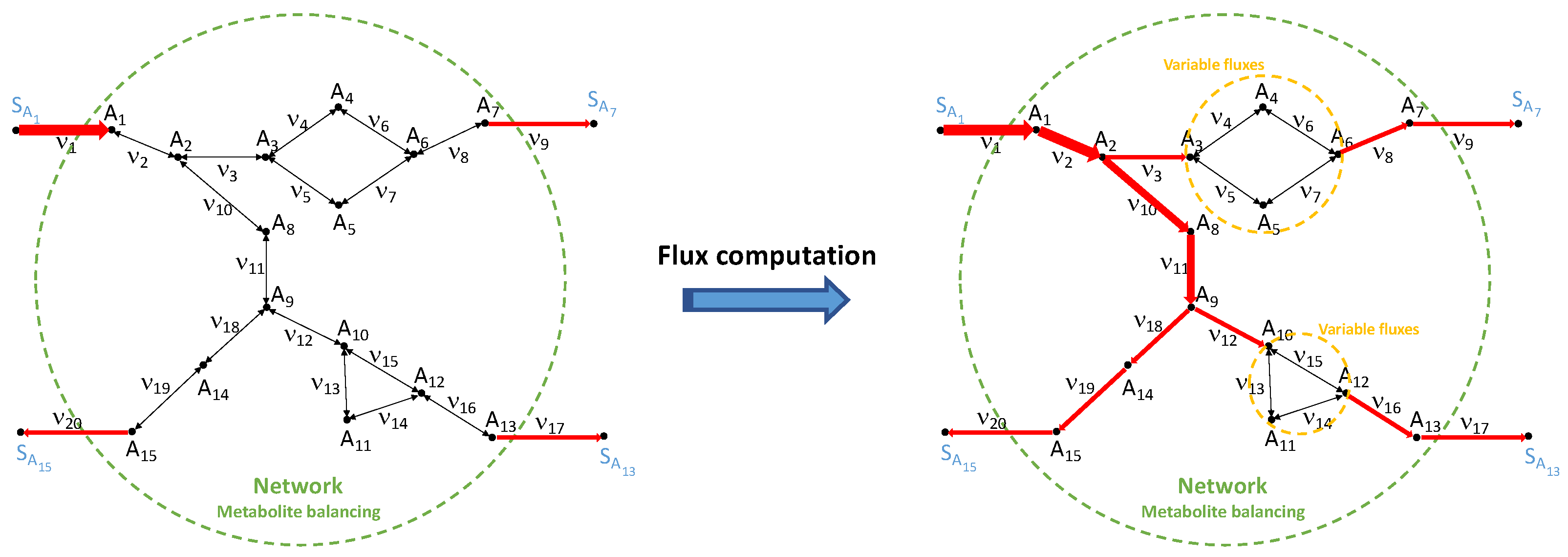
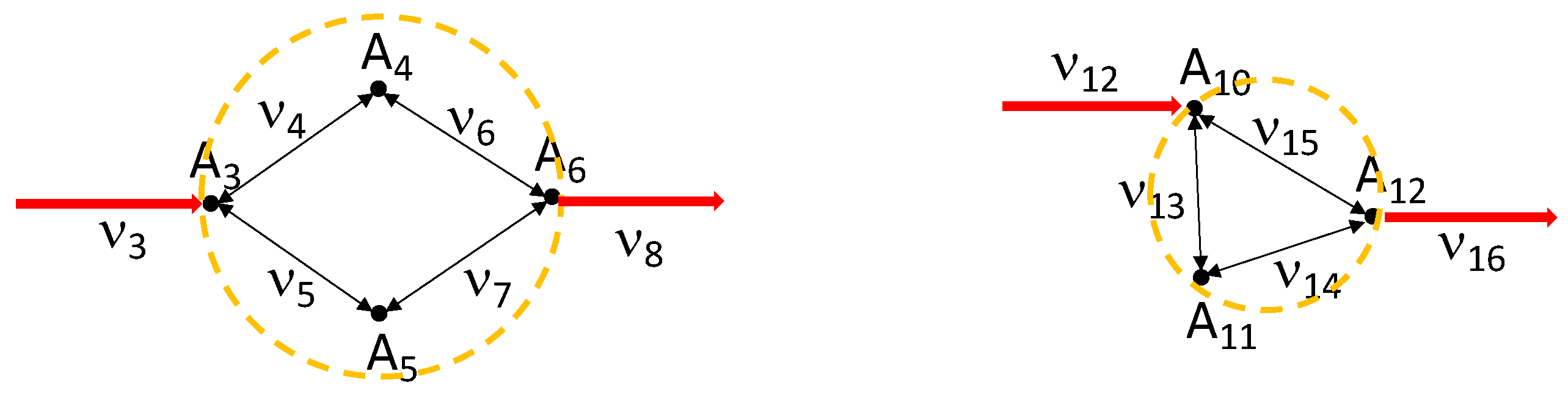
5.2. Two-Step Decomposition of the Alternative Estimation When Fluxes Are Partially Known
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saa, P.A.; Nielsen, L.K. Formulation, construction and analysis of kinetic models of metabolism: A review of modelling frameworks. Biotechnol. Adv. 2017, 35, 981–1003. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, R.U.; Edwards, J.S.; Palsson, B.Ø. Escherichia coli K-12 undergoes adaptive evolution to achieve Silico predicted optimal growth. Nature 2002, 420, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Schuetz, R.; Zamboni, N.; Zampieri, M.; Heinemann, M.; Sauer, U. Multidimensional optimality of microbial metabolism. Science 2012, 336, 601–604. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Donizelli, M.; Rodriguez, N.; Dharuri, H.; Endler, L.; Chelliah, V.; Li, L.; He, E.; Henry, A.; Stefan, M.I.; et al. BioModels Database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010, 4, 92. [Google Scholar] [CrossRef] [PubMed]
- Liebermeister, W.; Klipp, E. Bringing metabolic networks to life: Convenience rate law and thermodynamic constraints. Theor. Biol. Med. Model. 2006, 3, 41. [Google Scholar] [CrossRef] [PubMed]
- Liebermeister, W.; Klipp, E. Bringing metabolic networks to life: Integration of kinetic, metabolic, and proteomic data. Theor. Biol. Med. Model. 2006, 3, 42. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.O. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3, 121. [Google Scholar] [CrossRef] [PubMed]
- Herrgard, M.J.; Swainston, N.; Dobson, P.; Dunn, W.B.; Arga, K.Y.; Arvas, M.; Blüthgen, N.; Borger, S.; Costenoble, R.; Heinemann, M.; et al. A consensus yeast metabolic network reconstruction obtained from a community approach to systems biology. Nat. Biotechnol. 2008, 26, 1155–1160. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Palsson, B.Ø. The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat. Biotechnol. 2008, 26, 659–667. [Google Scholar] [CrossRef] [PubMed]
- Tran, L.M.; Rizk, M.L.; Liao, J.C. Ensemble modeling of metabolic networks. Biophys. J. 2008, 95, 5606–5617. [Google Scholar] [CrossRef] [PubMed]
- Lubitz, T.; Schulz, M.; Klipp, E.; Liebermeister, W. Parameter Balancing in Kinetic Models of Cell Metabolism. J. Phys. Chem. B 2010, 114, 16298–16303. [Google Scholar] [CrossRef] [PubMed]
- Stanford, N.J.; Lubitz, T.; Smallbone, K.; Klipp, E.; Mendes, P.; Liebermeister, W. Systematic Construction of Kinetic Models from Genome-Scale Metabolic Networks. PLoS ONE 2013, 8, e79195. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Klipp, E.; Liebermeister, W.; Wierling, C.; Kowald, A.; Lehrach, H.; Herwig, R. (Eds.) Systems Biology: A Textbook; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Noor, E.; Flamholz, A.; Bar-Even, A.; Davidi, D.; Milo, R.; Liebermeister, W. The protein cost of metabolic fluxes: Prediction from enzymatic rate laws and cost minimization. PLoS Comput. Biol. 2016, 12, e1005167. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Wiechert, W. 13C metabolic flux analysis. Metab. Eng. 2001, 3, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Quek, L.E.; Wittmann, C.; Nielsen, L.K.; Kromer, J.O. OpenFLUX: Efficient modelling software for 13C-based metabolic flux analysis. Microb. Cell Factories 2009, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Weitzel, M.; Noh, K.; Dalman, T.; Niedenfuhr, S.; Stute, B.; Wiechert, W. 13CFLUX2—High-performance software suite for 13C-metabolic flux analysis. Bioinformatics 2013, 29, 143–145. [Google Scholar] [CrossRef] [PubMed]
- Young, J.D. INCA: A computational platform for isotopically non-stationary metabolic flux analysis. Bioinformatics 2014, 30, 1333–1335. [Google Scholar] [CrossRef] [PubMed]
- Allendoerfer, C.B. (Ed.) Calculus of Several Variables and Differentiable Manifolds; Macmillan: New York, NY, USA, 1974. [Google Scholar]
- Ross, J.; Nyström, D.W. Differentiability of the argmin function and a minimum principle for semiconcave subsolutions. arXiv 2018, arXiv:1808.04402. [Google Scholar]

| Kinetic Mechanism | Number of Parameters | Kinetic Parameters | Equation |
|---|---|---|---|
| One-to-One Mass Action | 2 | , | (5) |
| One-to-One Michaelis Menten | 4 | , , , | (7) |
| -to- Convenience Rate | , , | ||
| , | (8) | ||
| Regulation module | 1 | (or ) | (9) |
| Kinetic Parameter | True Value |
|---|---|
| 0.0344 | |
| 0.7655 | |
| 0.4617 | |
| 6.9483 | |
| 0.4387 | |
| 0.7952 | |
| 0.9713 | |
| 3.1710 | |
| 7.4484 | |
| 0.3816 | |
| 0.1869 | |
| 7.2346 | |
| 9.5022 |
| 6.0405 | 17.1430 | 9.2908 | 10.1628 | 4.6702 |
| 15.7836 | 6.1016 | 20.6447 | 9.3868 | 7.6004 |
| 4.0000 | 9.0000 | 6.0000 | 6.0000 | 3.0000 |
| 6.0000 | 3.0000 | 8.0000 | 4.0000 | 3.0000 |
| 0.0048 | 0.0515 | 0.0103 | 0.0287 | 0.0109 |
| 0.0048 | 0.0515 | 0.0103 | 0.0287 | 0.0109 |
| 0.0048 | 0.0515 | 0.0103 | 0.0287 | 0.0109 |
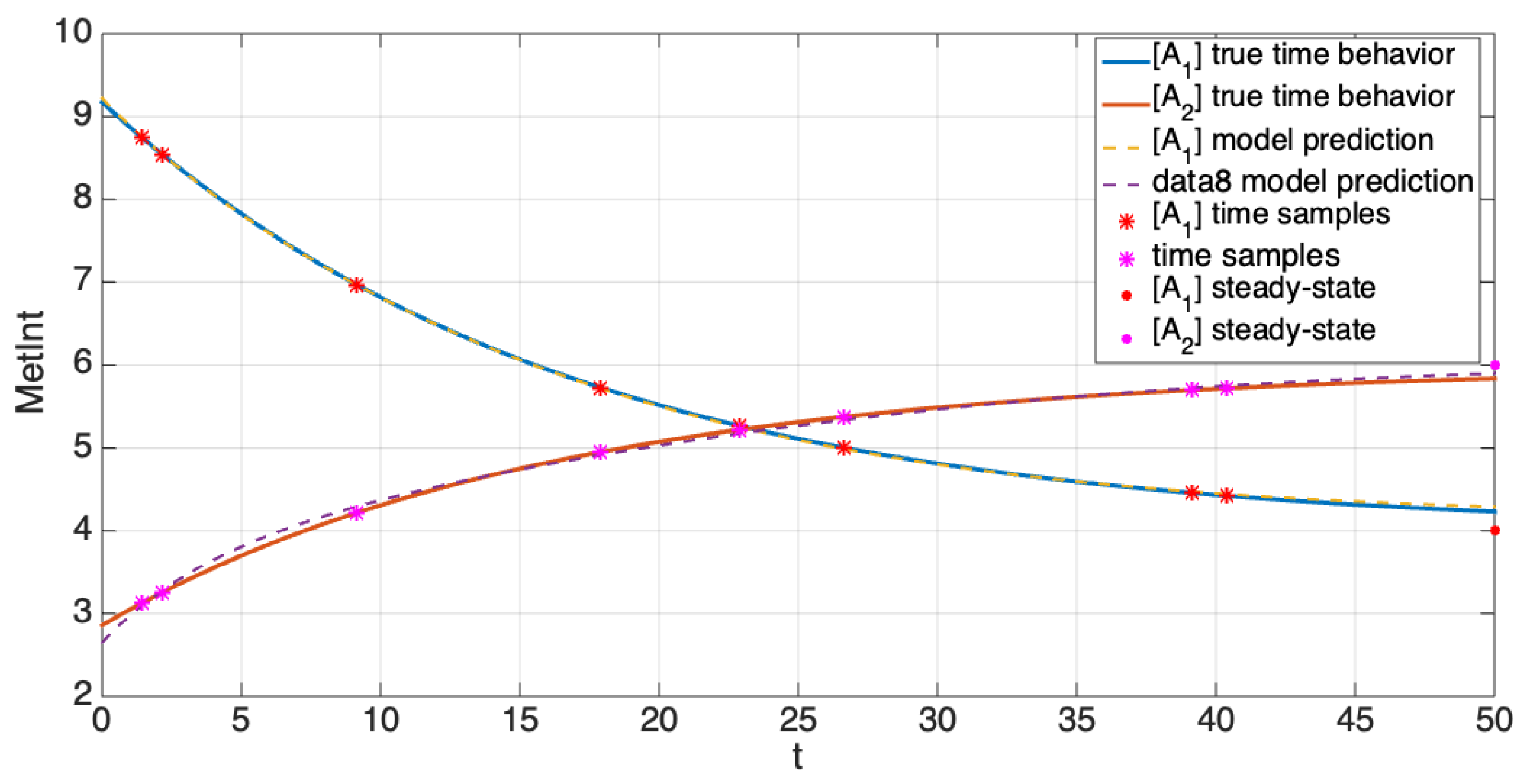
| 1.4526 | 8.7401 | 3.1321 |
| 2.1789 | 8.5371 | 3.2593 |
| 9.1551 | 6.9667 | 4.2182 |
| 17.9051 | 5.7270 | 4.9502 |
| 22.9051 | 5.2644 | 5.2205 |
| 26.6551 | 5.0000 | 5.3753 |
| 39.1551 | 4.4558 | 5.6979 |
| 40.4051 | 4.4213 | 5.7188 |
| Kinetic Parameter | |||
|---|---|---|---|
| 0.0344 | 0.0344 | 0.2137 | |
| 0.7655 | 0.7655 | 0.3171 | |
| 0.4617 | 0.4617 | 6.7456 | |
| 6.9483 | 6.9483 | 2.2505 | |
| 0.4387 | 0.4387 | 3.8292 | |
| 0.7952 | 0.7952 | 6.4673 | |
| 0.9713 | 0.9713 | 6.4887 | |
| 3.1710 | 3.1710 | 0.1928 | |
| 7.4484 | 7.4484 | 6.6438 | |
| 0.3816 | 0.3816 | 1.9562 | |
| 0.1869 | 0.1869 | 0.8278 | |
| 7.2346 | 7.2346 | 6.4133 | |
| 9.5022 | 9.5022 | 3.7288 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palombo, G.; Borri, A.; Papa, F.; Papi, M.; Palumbo, P. Parameter Identification in Metabolic Reaction Networks by Means of Multiple Steady-State Measurements. Symmetry 2023, 15, 368. https://doi.org/10.3390/sym15020368
Palombo G, Borri A, Papa F, Papi M, Palumbo P. Parameter Identification in Metabolic Reaction Networks by Means of Multiple Steady-State Measurements. Symmetry. 2023; 15(2):368. https://doi.org/10.3390/sym15020368
Chicago/Turabian StylePalombo, Giovanni, Alessandro Borri, Federico Papa, Marco Papi, and Pasquale Palumbo. 2023. "Parameter Identification in Metabolic Reaction Networks by Means of Multiple Steady-State Measurements" Symmetry 15, no. 2: 368. https://doi.org/10.3390/sym15020368
APA StylePalombo, G., Borri, A., Papa, F., Papi, M., & Palumbo, P. (2023). Parameter Identification in Metabolic Reaction Networks by Means of Multiple Steady-State Measurements. Symmetry, 15(2), 368. https://doi.org/10.3390/sym15020368








