Non-Trivial Band Topology Criteria for Magneto-Spin–Orbit Graphene
Abstract
:1. Introduction
2. Model Hamiltonian
- The kinetic energy that is evaluated to account only for the principal (nearest-neighbor) hopping;
- The Rashba spin–orbit term reflecting the interaction between graphene and a high-Z substrate;
- The collinear sublattice magnetization term (the magnetization direction is ).
3. Results
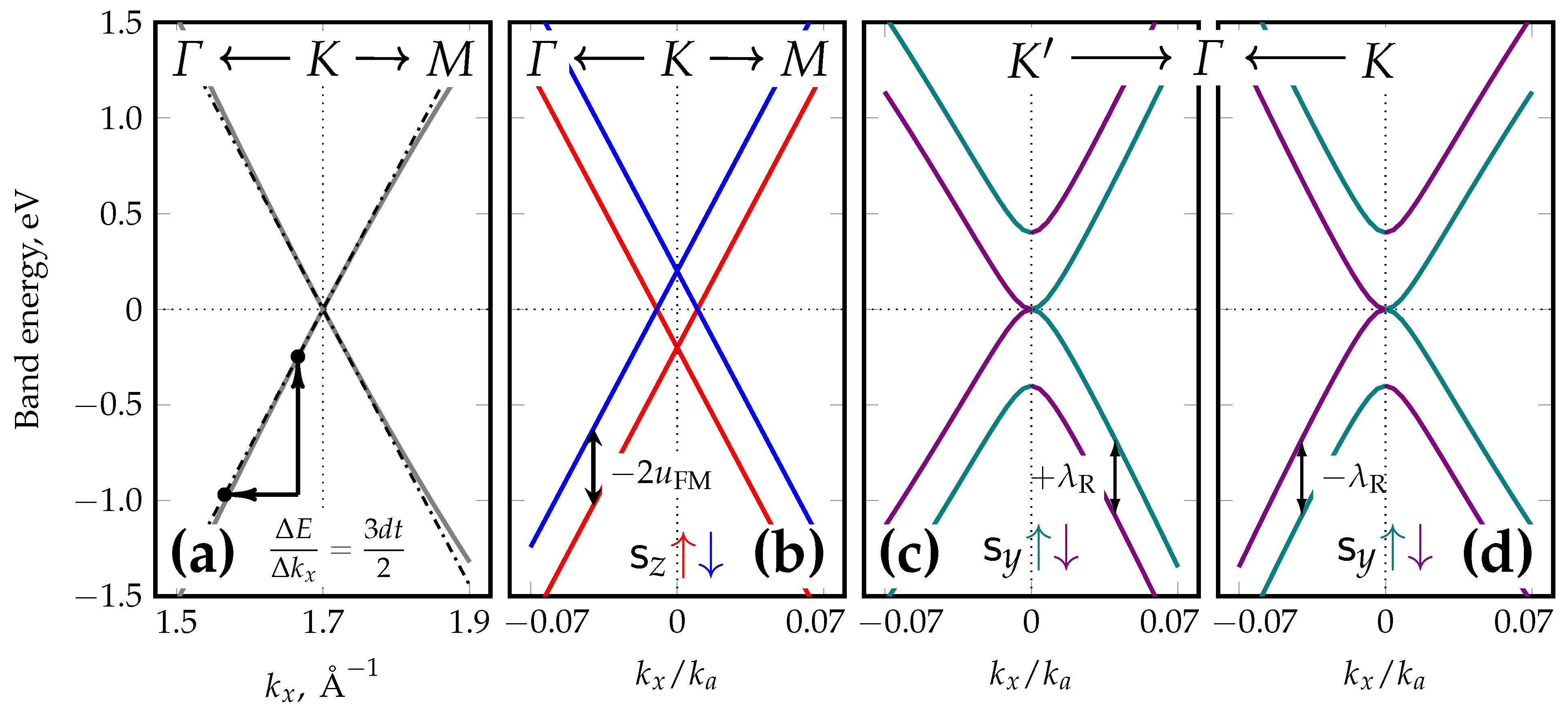
3.1. In-Plane Magnetized Graphene with Rashba Interaction
3.2. Out-of-Plane Magnetized Graphene with Rashba Interaction
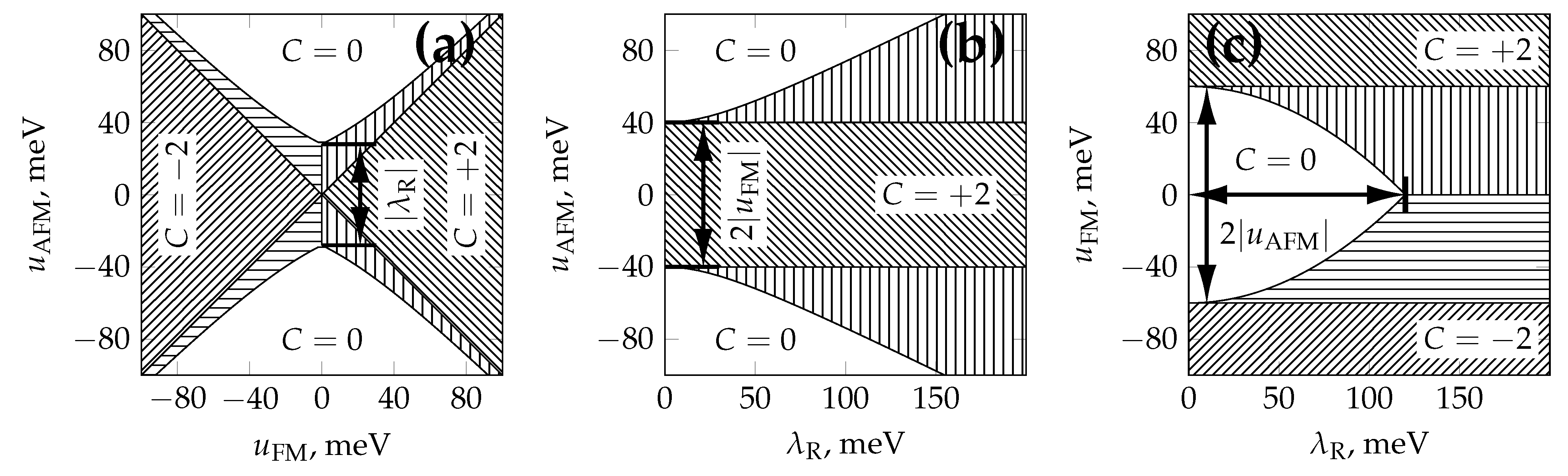
- The condition defines an FM-dominated case where the band structure at both valleys is gapped and inverted ( inversion is evident in Figure 3d,e), and the band structure is always characterized by two Dirac rings per valley. The total Chern number is ; the system is always topologically nontrivial with the valley gap of magnitudewhere the gap center explicitly depends on the valley. The global gap is .
- If the value in the AFM-dominated case is sufficiently large, a band inversion manifests itself at both valleys. The critical value is defined by a zero gap in Equation (9) and is equal to
4. Discussion
4.1. In-Plane Magnetized Graphene with Rashba Interaction
4.2. Out-of-Plane Magnetized Graphene with Rashba Interaction
4.3. Multiparametric Topological Phase Diagrams
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARPES | Angle-resolved photoelectron spectroscopy |
| spin-ARPES | Spin- and angle-resolved photoelectron spectroscopy |
| DFT | Density functional theory |
| STM | Scanning tunnel microscopy |
| QAHE | Quantum anomalous Hall effect |
| FM | Ferromagnetism, ferromagnetic coupling |
| AFM | Antiferromagnetism, antiferromagnetic coupling |
| FIM | Ferrimagnetism, combination of FM and AFM couplings |
| VB | Valence band |
| CB | Conduction band |
| DR | Dirac ring |
Appendix A. Model Geometry
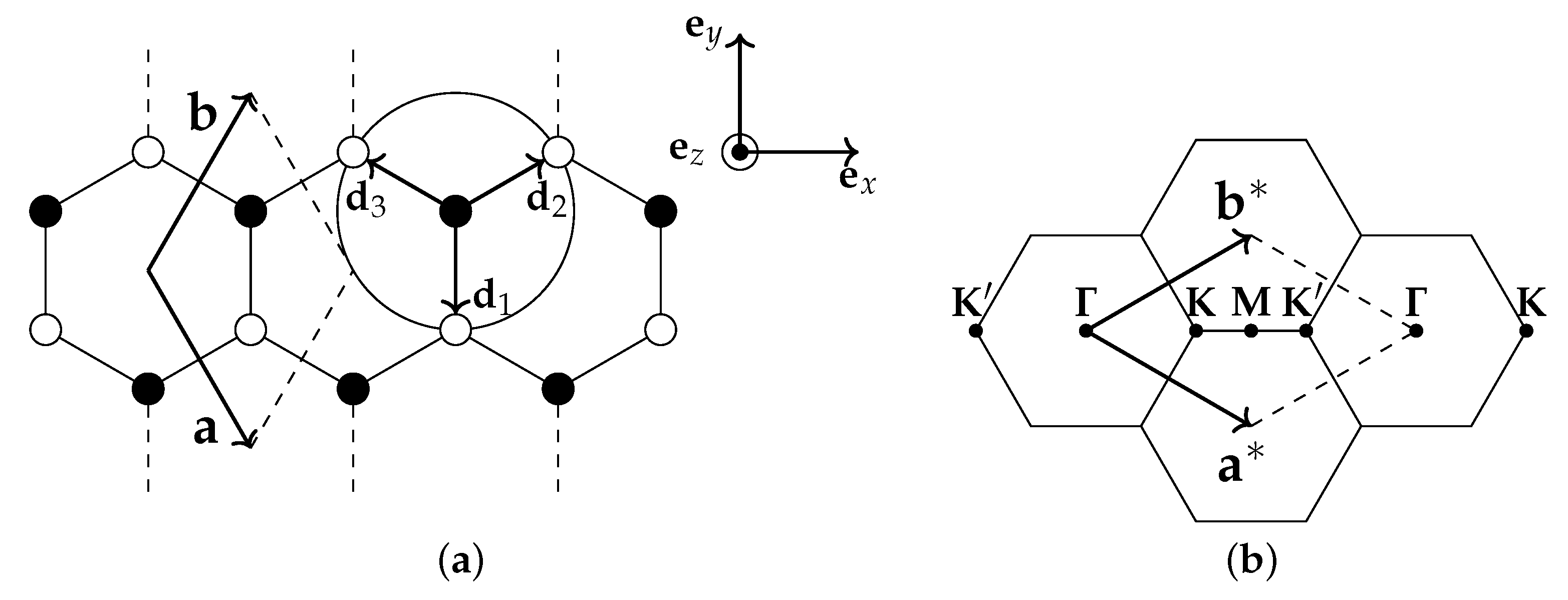
Appendix B. Graphene with One Kind of Interactions
Appendix B.1. Principal Hopping Integral
Appendix B.2. Standard Rashba Splitting
| Valley | K | |
|---|---|---|
| Upper VB, spin | ||
| Lower VB, spin | ||
| Signed splitting |
Appendix B.3. Valley Gap
- If , the resulting band dispersion consists of two completely spin-polarized standard graphene dispersions split by (see Figure 1b). The eigenvectors match those for pristine graphene, but the energy eigenvalues are
- If , the spin-degenerate bands with a gap of magnitude are given by (see Figure 3b)These bands have a meron-like [51] pseudospin texture where the pseudospin vector is directed along . In particular, it is directed along at the Dirac points (where ), which signals a complete sublattice localization of the corresponding electronic states.
- If both and are nonzero, then a ferrimagnetic configuration is established giving the band dispersionswith the spin-splitting of . When the sublattice magnetizations are -aligned, FM interaction dominates, and the corresponding band structure has an FM-like character (see Figure 3c). Conversely, another FIM case presents when the moments are -aligned; AFM interaction then dominates (see Figure 3h) and a finite gap ofopens up. The presence of a sufficiently large band gap on ARPES spectra is a clear sign that a significant AFM interaction is involved if no other sources of sublattice symmetry breaking are evident.
Appendix C. Valence and Conduction Band Hamiltonians
References
- Chowdhury, T.; Sadler, E.C.; Kempa, T.J. Progress and Prospects in Transition-Metal Dichalcogenide Research Beyond 2D. Chem. Rev. 2020, 120, 12563–12591. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Tang, C.S.; Zheng, Y.; Gao, J.; Wu, J.; Zhang, H.; Chhowalla, M.; Chen, W.; Wee, A.T.S. Recent developments in 2D transition metal dichalcogenides: Phase transition and applications of the (quasi-)metallic phases. Chem. Soc. Rev. 2021, 50, 10087–10115. [Google Scholar] [CrossRef]
- Habib, M.R.; Wang, W.; Khan, A.; Khan, Y.; Obaidulla, S.M.; Pi, X.; Xu, M. Theoretical Study of Interfacial and Electronic Properties of Transition Metal Dichalcogenides and Organic Molecules Based van der Waals Heterostructures. Adv. Theory Simulat. 2020, 3, 2000045. [Google Scholar] [CrossRef]
- Mu, H.; Yu, W.; Yuan, J.; Lin, S.; Zhang, G. Interface and surface engineering of black phosphorus: A review for optoelectronic and photonic applications. Mater. Futur. 2022, 1, 012301. [Google Scholar] [CrossRef]
- Burch, K.S.; Mandrus, D.; Park, J.G. Magnetism in two-dimensional van der Waals materials. Nature 2018, 563, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Tang, F.; Ji, J.; Zhang, W.; Vishwanath, A.; Po, H.C.; Wan, X. Two-dimensional topological materials discovery by symmetry-indicator method. Phys. Rev. B 2019, 100, 195108. [Google Scholar] [CrossRef] [Green Version]
- Weiss, N.O.; Zhou, H.; Liao, L.; Liu, Y.; Jiang, S.; Huang, Y.; Duan, X. Graphene: An Emerging Electronic Material. Adv. Mater. 2012, 24, 5782–5825. [Google Scholar] [CrossRef]
- Falkovsky, L.A. Optical properties of graphene. J. Phys. Conf. Ser. 2008, 129, 012004. [Google Scholar] [CrossRef] [Green Version]
- Wimmer, M.; Adagideli, I.D.I.M.C.; Berber, S.M.C.; Tománek, D.; Richter, K. Spin Currents in Rough Graphene Nanoribbons: Universal Fluctuations and Spin Injection. Phys. Rev. Lett. 2008, 100, 177207. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.H.; Nikolić, B.K.; Chang, C.R. Inverse quantum spin Hall effect generated by spin pumping from precessing magnetization into a graphene-based two-dimensional topological insulator. Phys. Rev. B 2010, 81, 035428. [Google Scholar] [CrossRef]
- Han, W.; McCreary, K.; Pi, K.; Wang, W.; Li, Y.; Wen, H.; Chen, J.; Kawakami, R. Spin transport and relaxation in graphene. J. Magn. Magn. Mater. 2012, 324, 369–381. [Google Scholar] [CrossRef] [Green Version]
- Rybkina, A.A.; Rybkin, A.G.; Adamchuk, V.K.; Marchenko, D.; Varykhalov, A.; Barriga, J.S.; Shikin, A.M. The graphene/Au/Ni interface and its application in the construction of a graphene spin filter. Nanotechnology 2013, 24, 295201. [Google Scholar] [CrossRef] [PubMed]
- Rybkina, A.A.; Rybkin, A.G.; Klimovskikh, I.I.; Skirdkov, P.N.; Zvezdin, K.A.; Zvezdin, A.K.; Shikin, A.M. Advanced graphene recording device for spin–orbit torque magnetoresistive random access memory. Nanotechnology 2020, 31, 165201. [Google Scholar] [CrossRef] [PubMed]
- Kamalakar, M.V.; Groenveld, C.; Dankert, A.; Dash, S. Long distance spin communication in chemical vapour deposited graphene. Nat. Commun. 2015, 6, 6766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zatko, V.; Dubois, S.M.M.; Godel, F.; Galbiati, M.; Peiro, J.; Sander, A.; Carretero, C.; Vecchiola, A.; Collin, S.; Bouzehouane, K.; et al. Almost Perfect Spin Filtering in Graphene-Based Magnetic Tunnel Junctions. ACS Nano 2022, 16, 14007–14016. [Google Scholar] [CrossRef] [PubMed]
- Konschuh, S.; Gmitra, M.; Fabian, J. Tight-binding theory of the spin-orbit coupling in graphene. Phys. Rev. B 2010, 82, 245412. [Google Scholar] [CrossRef] [Green Version]
- Rashba, E.I. Graphene with structure-induced spin-orbit coupling: Spin-polarized states, spin zero modes, and quantum Hall effect. Phys. Rev. B 2009, 79, 161409. [Google Scholar] [CrossRef] [Green Version]
- Shikin, A.M.; Rybkina, A.A.; Rybkin, A.G.; Klimovskikh, I.I.; Skirdkov, P.N.; Zvezdin, K.A.; Zvezdin, A.K. Spin current formation at the graphene/Pt interface for magnetization manipulation in magnetic nanodots. Appl. Phys. Lett. 2014, 105, 042407. [Google Scholar] [CrossRef]
- Shikin, A.M.; Rybkin, A.G.; Marchenko, D.; Rybkina, A.A.; Scholz, M.R.; Rader, O.; Varykhalov, A. Induced spin–orbit splitting in graphene: The role of atomic number of the intercalated metal and π–d hybridization. New J. Phys. 2013, 15, 013016. [Google Scholar] [CrossRef] [Green Version]
- Klimovskikh, I.I.; Otrokov, M.M.; Voroshnin, V.Y.; Sostina, D.; Petaccia, L.; Di Santo, G.; Thakur, S.; Chulkov, E.V.; Shikin, A.M. Spin–Orbit Coupling Induced Gap in Graphene on Pt(111) with Intercalated Pb Monolayer. ACS Nano 2017, 11, 368–374. [Google Scholar] [CrossRef]
- Marchenko, D.; Varykhalov, A.; Sánchez-Barriga, J.; Seyller, T.; Rader, O. Rashba splitting of 100 meV in Au-intercalated graphene on SiC. Appl. Phys. Lett. 2016, 108, 172405. [Google Scholar] [CrossRef] [Green Version]
- Otrokov, M.M.; Klimovskikh, I.I.; Calleja, F.; Shikin, A.M.; Vilkov, O.; Rybkin, A.G.; Estyunin, D.; Muff, S.; Dil, J.H.; de Parga, A.L.V.; et al. Evidence of large spin-orbit coupling effects in quasi-free-standing graphene on Pb/Ir(111). 2D Mater. 2018, 5, 035029. [Google Scholar] [CrossRef]
- Zhizhin, E.; Varykhalov, A.; Rybkin, A.; Rybkina, A.; Pudikov, D.; Marchenko, D.; Sánchez-Barriga, J.; Klimovskikh, I.; Vladimirov, G.; Rader, O.; et al. Spin splitting of Dirac fermions in graphene on Ni intercalated with alloy of Bi and Au. Carbon 2015, 93, 984–996. [Google Scholar] [CrossRef]
- Marchenko, D.; Varykhalov, A.; Scholz, M.R.; Bihlmayer, G.; Rashba, E.I.; Rybkin, A.; Shikin, A.M.; Rader, O. Giant Rashba splitting in graphene due to hybridization with gold. Nat. Commun. 2012, 3, 1232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rybkin, A.G.; Rybkina, A.A.; Otrokov, M.M.; Vilkov, O.Y.; Klimovskikh, I.I.; Petukhov, A.E.; Filianina, M.V.; Voroshnin, V.Y.; Rusinov, I.P.; Ernst, A.; et al. Magneto-Spin–Orbit Graphene: Interplay between Exchange and Spin–Orbit Couplings. Nano Lett. 2018, 18, 1564–1574. [Google Scholar] [CrossRef] [PubMed]
- Rybkin, A.G.; Tarasov, A.V.; Rybkina, A.A.; Usachov, D.Y.; Petukhov, A.E.; Eryzhenkov, A.V.; Pudikov, D.A.; Gogina, A.A.; Klimovskikh, I.I.; Di Santo, G.; et al. Sublattice Ferrimagnetism in Quasifreestanding Graphene. Phys. Rev. Lett. 2022, 129, 226401. [Google Scholar] [CrossRef]
- Weser, M.; Rehder, Y.; Horn, K.; Sicot, M.; Fonin, M.; Preobrajenski, A.B.; Voloshina, E.N.; Goering, E.; Dedkov, Y.S. Induced magnetism of carbon atoms at the graphene/Ni(111) interface. Appl. Phys. Lett. 2010, 96, 012504. [Google Scholar] [CrossRef] [Green Version]
- Voroshnin, V.; Tarasov, A.; Bokai, K.; Chikina, A.; Senkovskiy, B.; Ehlen, N.; Usachov, D.; Grüneis, A.; Krivenkov, M.; Sánchez-Barriga, J.; et al. Direct Spectroscopic Evidence of Magnetic Proximity Effect in MoS2 Monolayer on Graphene/Co. ACS Nano 2022, 16, 7448–7456. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Dubois, S.M.M.; Zatko, V.; Galbiati, M.; Godel, F.; Martin, M.B.; Weatherup, R.S.; Petroff, F.; Fert, A.; et al. Spin filtering by proximity effects at hybridized interfaces in spin-valves with 2D graphene barriers. Nat. Commun. 2020, 11, 5670. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Zhang, Z.; Lai, S.; Tan, Q.; Gao, W.b. Magnetic Proximity Effect in Graphene/CrBr3 van der Waals Heterostructures. Adv. Mater. 2020, 32, 1908498. [Google Scholar] [CrossRef] [PubMed]
- Karpiak, B.; Cummings, A.W.; Zollner, K.; Vila, M.; Khokhriakov, D.; Hoque, A.M.; Dankert, A.; Svedlindh, P.; Fabian, J.; Roche, S.; et al. Magnetic proximity in a van der Waals heterostructure of magnetic insulator and graphene. 2D Mater. 2019, 7, 015026. [Google Scholar] [CrossRef]
- Kaverzin, A.A.; Ghiasi, T.S.; Dismukes, A.H.; Roy, X.; van Wees, B.J. Spin injection by spin–charge coupling in proximity induced magnetic graphene. 2D Mater. 2022, 9, 045003. [Google Scholar] [CrossRef]
- Varykhalov, A.; Sánchez-Barriga, J.; Shikin, A.M.; Biswas, C.; Vescovo, E.; Rybkin, A.; Marchenko, D.; Rader, O. Electronic and Magnetic Properties of Quasifreestanding Graphene on Ni. Phys. Rev. Lett. 2008, 101, 157601. [Google Scholar] [CrossRef]
- Jacobsen, J.; Pleth Nielsen, L.; Besenbacher, F.; Stensgaard, I.; Lægsgaard, E.; Rasmussen, T.; Jacobsen, K.W.; Nørskov, J.K. Atomic-Scale Determination of Misfit Dislocation Loops at Metal-Metal Interfaces. Phys. Rev. Lett. 1995, 75, 489–492. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015–2018. [Google Scholar] [CrossRef] [Green Version]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voloshina, E.; Dedkov, Y. Realistic Large-Scale Modeling of Rashba and Induced Spin–Orbit Effects in Graphene/High-Z-Metal Systems. Adv. Theory Simulat. 2018, 1, 1800063. [Google Scholar] [CrossRef]
- Sławińska, J.; Cerdá, J.I. Complex spin texture of Dirac cones induced via spin-orbit proximity effect in graphene on metals. Phys. Rev. B 2018, 98, 075436. [Google Scholar] [CrossRef] [Green Version]
- Sławińska, J.; Cerdá, J.I. Spin–orbit proximity effect in graphene on metallic substrates: Decoration versus intercalation with metal adatoms. New J. Phys. 2019, 21, 073018. [Google Scholar] [CrossRef]
- Takenaka, H.; Sandhoefner, S.; Kovalev, A.A.; Tsymbal, E.Y. Magnetoelectric control of topological phases in graphene. Phys. Rev. B 2019, 100, 125156. [Google Scholar] [CrossRef]
- López, A.; Colmenárez, L.; Peralta, M.; Mireles, F.; Medina, E. Proximity-induced spin-orbit effects in graphene on Au. Phys. Rev. B 2019, 99, 085411. [Google Scholar] [CrossRef] [Green Version]
- Peralta, M.; Medina, E.; Mireles, F. Proximity-induced exchange and spin-orbit effects in graphene on Ni and Co. Phys. Rev. B 2019, 99, 195452. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Sun, Q.; Jena, P. Valley-Polarized Quantum Anomalous Hall Effect in Ferrimagnetic Honeycomb Lattices. Phys. Rev. Lett. 2017, 119, 046403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Offidani, M.; Ferreira, A. Anomalous Hall Effect in 2D Dirac Materials. Phys. Rev. Lett. 2018, 121, 126802. [Google Scholar] [CrossRef] [Green Version]
- Zou, J.; Yuan, Y.; Kang, J. Spin and spin-valley Hall effects in a honeycomb lattice with antiferromagnetism and spin-orbit couplings. Phys. Lett. A 2019, 383, 3162–3166. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, F. Realization of an Antiferromagnetic Superatomic Graphene: Dirac Mott Insulator and Circular Dichroism Hall Effect. Nano Lett. 2021, 21, 230–235. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Yan, Z.; Li, Z.; Xu, X.; Zhang, Z.; Niu, Q.; Qiao, Z. Large Rashba Spin-Orbit Coupling and High-Temperature Quantum Anomalous Hall Effect in Re-Intercalated Graphene/CrI3 Heterostructure. arXiv 2022, arXiv:2203.16429. [Google Scholar]
- Qiao, Z.; Ren, W.; Chen, H.; Bellaiche, L.; Zhang, Z.; MacDonald, A.H.; Niu, Q. Quantum Anomalous Hall Effect in Graphene Proximity Coupled to an Antiferromagnetic Insulator. Phys. Rev. Lett. 2014, 112, 116404. [Google Scholar] [CrossRef] [Green Version]
- Phong, V.T.; Walet, N.R.; Guinea, F. Effective interactions in a graphene layer induced by the proximity to a ferromagnet. 2D Mater. 2017, 5, 014004. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Z.; Jiang, H.; Li, X.; Yao, Y.; Niu, Q. Microscopic theory of quantum anomalous Hall effect in graphene. Phys. Rev. B 2012, 85, 115439. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Xiao, M.; Guo, Y.; Yuan, L.; Fan, S. Meron Spin Textures in Momentum Space. Phys. Rev. Lett. 2020, 124, 106103. [Google Scholar] [CrossRef] [PubMed]
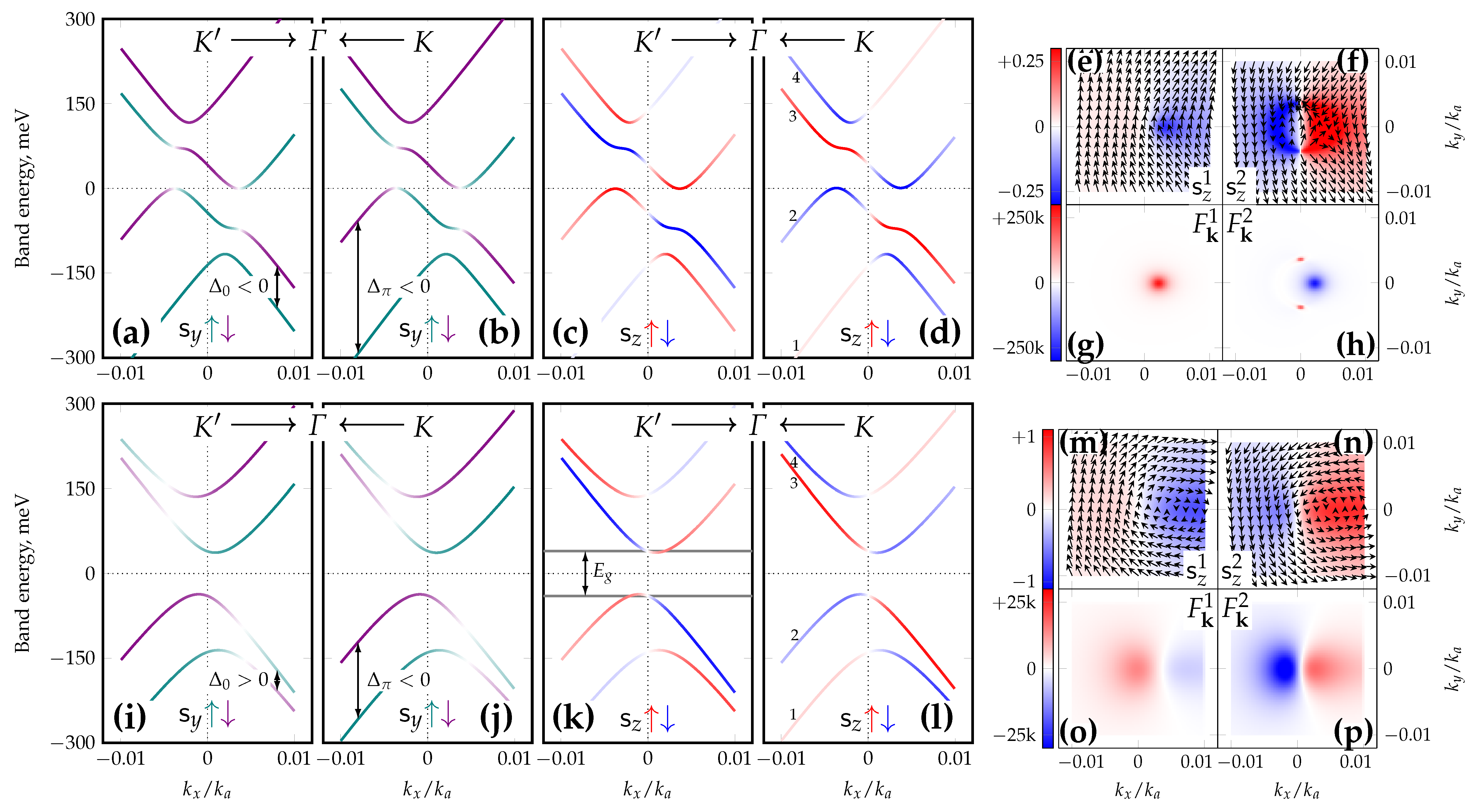

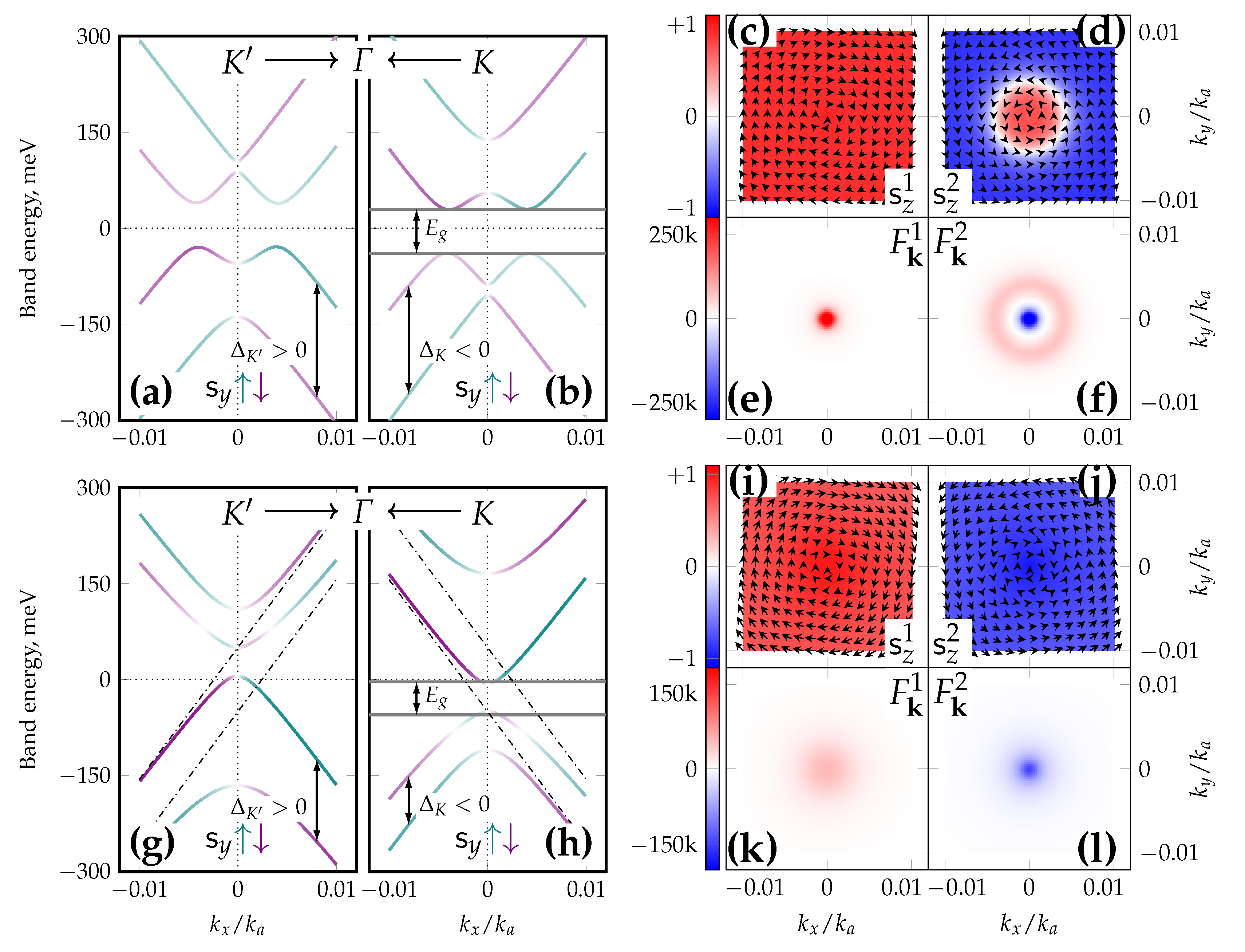

| Spin Ordering, Gap | > | |
|---|---|---|
| persistent, gapless (Figure 2a,b) | invertible, gapless | |
| persistent, gapped | invertible, gapped (Figure 2i,j) |
| Valley | K | |
|---|---|---|
| Upper VB, spin | ||
| Lower VB, spin | ||
| Signed splitting (4) | ||
| Upper VB, spin | ||
| Lower VB, spin | ||
| FM-dominated case, | ||
| Gap value | zero | |
| Upper VB maximum | 0 | 0 |
| Lower CB minimum | 0 | 0 |
| AFM-dominated case, | ||
| Gap value (6) | ||
| Upper VB maximum | ||
| Lower CB minimum | ||
| Valley | K | |
|---|---|---|
| Upper VB, spin | ||
| Lower VB, spin | ||
| Signed splitting (15) | ||
| Upper VB, spin | ||
| Lower VB, spin | ||
| FM-dominated case, | Always topological | |
| Gap value | see (8) | |
| Gap center | ||
| Upper VB maximum | ||
| Lower CB minimum | ||
| AFM-dominated case, | Trivial, | , see (10) |
| Gap value | see (9) | |
| Upper VB maximum | ||
| Lower CB minimum | ||
| Topological, simple | , see (11) | |
| Gap value | see (9), sign reversed | |
| Upper VB maximum | ||
| Lower CB minimum | ||
| Topological, Dirac ring | ||
| Gap value | see (12) | |
| Upper VB maximum | ||
| Lower CB minimum | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eryzhenkov, A.V.; Tarasov, A.V.; Shikin, A.M.; Rybkin, A.G. Non-Trivial Band Topology Criteria for Magneto-Spin–Orbit Graphene. Symmetry 2023, 15, 516. https://doi.org/10.3390/sym15020516
Eryzhenkov AV, Tarasov AV, Shikin AM, Rybkin AG. Non-Trivial Band Topology Criteria for Magneto-Spin–Orbit Graphene. Symmetry. 2023; 15(2):516. https://doi.org/10.3390/sym15020516
Chicago/Turabian StyleEryzhenkov, Alexander V., Artem V. Tarasov, Alexander M. Shikin, and Artem G. Rybkin. 2023. "Non-Trivial Band Topology Criteria for Magneto-Spin–Orbit Graphene" Symmetry 15, no. 2: 516. https://doi.org/10.3390/sym15020516






