Numerical Method for Solving Fractional Order Optimal Control Problems with Free and Non-Free Terminal Time
Abstract
:1. Introduction
2. Main Problem
- Case I: Non-Free Terminal Time
- Case II: Free Terminal Time
3. Preliminary
3.1. Basic Definitions of the Fractional Derivatives and (FOCDS) with Free and Non-Free Terminal Time
- (i)
- Let and . The fractional definition of f using the Riemann–Liouville derivative for is defined by:
3.2. Hooke and Jeeves Direct Search Method Analysis
3.2.1. Algorithm of Hooke and Jeeves Method
- Set k = 0;
- Choose an initial point and indicate the variable increments with for, where the factor of step reduction is a > 1, and the termination parameter is ;
- Use as the base point for an experimental move. Consider the result of the exploratory maneuver to be X. Set and proceed to Step 4 if the exploratory move is successful; otherwise, proceed to Step 3;
- Is If so, terminate; otherwise, set A= A/a for and go to Step 3;
- Perform the pattern move after setting k = k+1: ;
- Perform another exploratory move using as the base point. Let the result be ;
- Is If so, go to Step 5; otherwise, go to Step 4.
3.2.2. The Convergence of Hooke and Jeeves Method
4. The Numerical Method
4.1. Proposed Algorithm
- Algorithm of non-free terminal time (FOC) problem:
- Choose a suitable approximated base.
- Construct an approximated solution of (FOC),
- In case the differential equation in Equation (2) is given as explicit formula in the control function then we have to evaluate the function ;
- Substitute the approximated formulas of the functions and in Equation (1);
- Use a suitable minimizing search methods such as the Hooke and Jeeves method to find the minimal parameter(s) in Equation (1).
- Algorithm of free terminal time (FOC) problem:
- Perform steps 1–4 in the previous algorithm;
- Use suitable minimizing search methods such as the Hooke and Jeeves method to find the best parameters (minimal) including the parameter T in Equation (1).
4.2. Dual Discreet Problem
- Algorithm of non-free terminal time (FOC) problem:
- From the differential equation in Equation (2), we obtain the control function as a function , then, we have to evaluate the function ;
- From Equation (1), we obtain the optimal problem Minimum in case of the free terminal time (FOC) problem, and Minimum in case of the non-free terminal time (FOC) problem.
where T is free parameter.
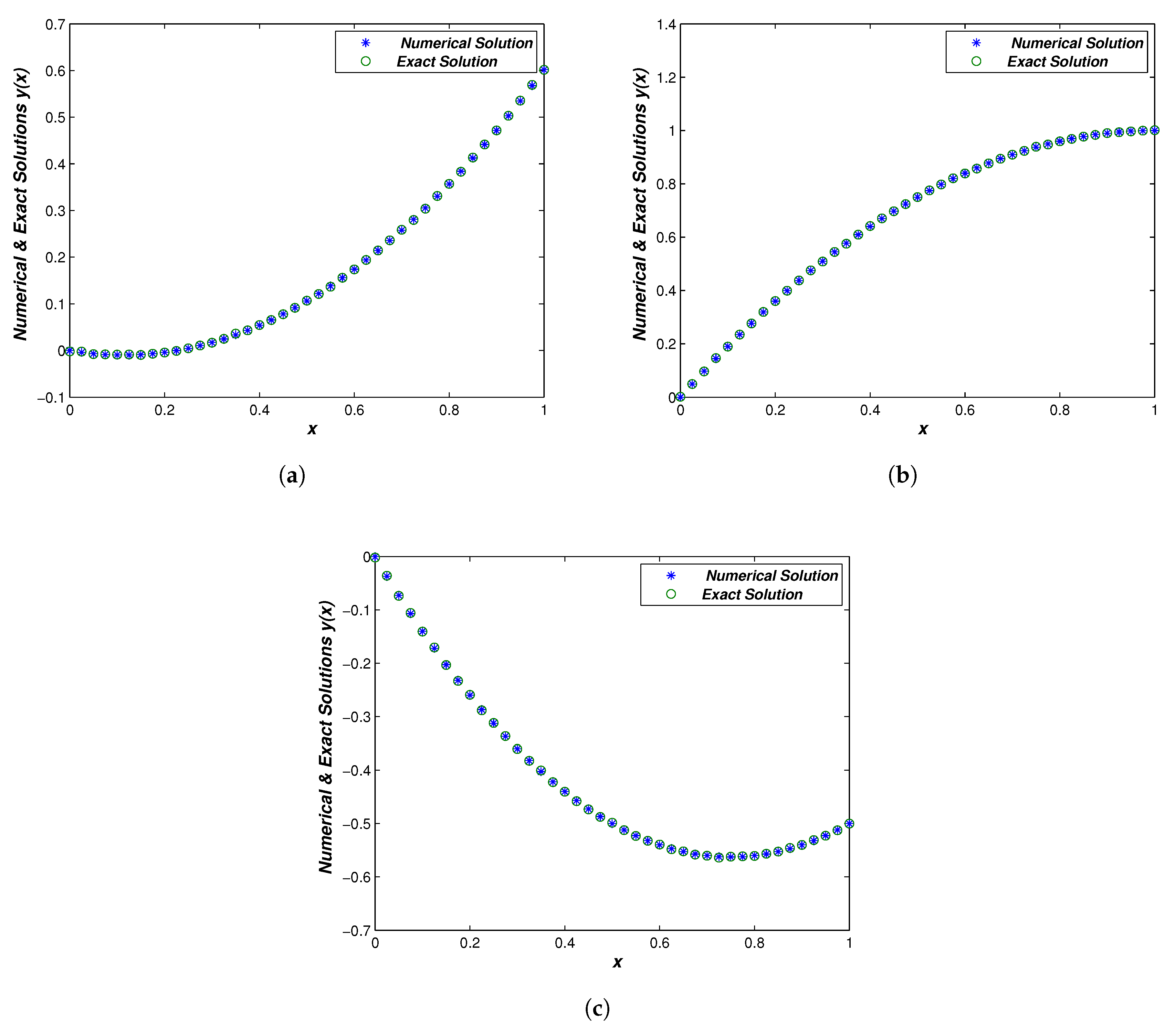
5. Implementations (Numerical Examples)
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Longuski, J.M.; Guzmán, J.J.; Prussing, J.E. Optimal Control with Aerospace Applications; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Agrawal, O.P. A formulation and numerical scheme for fractional optimal control problems. J. Vib. Control. 2008, 14, 1291–1299. [Google Scholar] [CrossRef]
- Sweilam, N.; Hassan, A.-A.; Tamer, M.; Hoppe, R.H.W. Numerical solution of some types of fractional optimal control problems. Sci. World J. 2013, 2013, 306237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhrawy, A.H.; Doha, E.H.; Baleanu, D.; Ezz-Eldien, S.S.; Abdelkawy, M.A. An accurate numerical technique for solving fractional optimal control problems. Differ. Equ. 2015, 15, 23. [Google Scholar]
- Akbarian, T.; Keyanpour, M. A new approach to the numerical solution of fractional order optimal control problems. Appl. Appl. Math. 2013, 8, 523–534. [Google Scholar]
- Bhrawy, A.H.; Doha, E.H.; Tenreiro Machado, J.A.; Ezz-Eldien, S.S. An efficient numerical scheme for solving multi-dimensional fractional optimal control problems with a quadratic performance index. Asian J. Control 2015, 17, 2389–2402. [Google Scholar] [CrossRef] [Green Version]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. An efficient Legendre spectral tau matrix formulation for solving fractional subdiffusion and reaction subdiffusion equations. J. Comput. Nonlinear Dyn. 2015, 10, 021019. [Google Scholar] [CrossRef]
- Liu, J.; Hou, G. Numerical solutions of the space-and time-fractional coupled Burgers equations by generalized differential transform method. Appl. Math. Comput. 2011, 217, 7001–7008. [Google Scholar] [CrossRef]
- Lotfi, A.; Dehghan, M.; Yousefi, S.A. A numerical technique for solving fractional optimal control problems. Comput. Math. Appl. 2011, 62, 1055–1067. [Google Scholar] [CrossRef] [Green Version]
- Pooseh, S.; Almeida, R.; Torres, D.F.M. A numerical scheme to solve fractional optimal control problems. Conf. Pap. Sci. 2013, 2013, 165298. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Li, C. Fractional difference/finite element approximations for the time–space fractional telegraph equation. Appl. Math. Comput. 2012, 219, 2975–2988. [Google Scholar] [CrossRef]
- Mechee, M.S.; Senu, N. Numerical Study of Fractional Differential Equations of Lane-Emden Type by Method of Collocation; Scientific Research Publishing: Wuhan, China, 2012. [Google Scholar]
- Zhou, H.; Tian, W.Y.; Deng, W. Quasi-compact finite difference schemes for space fractional diffusion equations. J. Sci. Comput. 2013, 56, 45–66. [Google Scholar] [CrossRef] [Green Version]
- Bhrawy, A.H.; Doha, E.H.; Ezz-Eldien, S.S.; Van Gorder, R.A. A new Jacobi spectral collocation method for solving 1 + 1 fractional Schrödinger equations and fractional coupled Schrödinger systems. Eur. Phys. J. Plus 2014, 129, 1–21. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Ezz-Eldien, S.S.; Doha, E.H.; Abdelkawy, M.A.; Baleanu, D. Solving fractional optimal control problems within a Chebyshev–Legendre operational technique. Int. J. Control 2017, 90, 1230–1244. [Google Scholar] [CrossRef]
- Yousefi, S.A.; Lotfi, A.; Dehghan, M. The use of a Legendre multiwavelet collocation method for solving the fractional optimal control problems. J. Vib. Control. 2011, 17, 2059–2065. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Ezz-Eldien, S.S. A new Legendre operational technique for delay fractional optimal control problems. Calcolo 2016, 53, 521–543. [Google Scholar] [CrossRef]
- Heydari, M.H.; Hooshmandasl, M.R.; Mohammadi, F. Legendre wavelets method for solving fractional partial differential equations with Dirichlet boundary conditions. Appl. Math. Comput. 2014, 234, 267–276. [Google Scholar] [CrossRef]
- Khan, R.A.; Khalil, H. A new method based on legendre polynomials for solution of system of fractional order partial differential equations. Int. J. Comput. Math. 2014, 91, 2554–2567. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Ajami, T.M. Legendre spectral-collocation method for solving some types of fractional optimal control problems. J. Adv. Res. 2015, 6, 393–403. [Google Scholar] [CrossRef] [Green Version]
- Sweilam, N.H.; Nagy, A.M.; El-Sayed, A.A. Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation. Chaos Solitons Fractals 2015, 73, 141–147. [Google Scholar] [CrossRef]
- Almeida, R.; Torres, D.F.M. A discrete method to solve fractional optimal control problems. Nonlinear Dyn. 2015, 80, 1811–1816. [Google Scholar] [CrossRef] [Green Version]
- Suárez, J.I.; Vinagre, B.M.; Chen, Y. A fractional adaptation scheme for lateral control of an AGV. J. Vib. Control 2008, 14, 1499–1511. [Google Scholar] [CrossRef]
- Pinto, C.; Tenreiro Machado, J.A. Fractional dynamics of computer virus propagation. Math. Probl. Eng. 2014, 2014, 476502. [Google Scholar] [CrossRef] [Green Version]
- Pooseh, S.; Almeida, R.; Torres, D.F.M. Fractional order optimal control problems with free terminal time. arXiv 2013, arXiv:1302.1717. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Tajadodi, H. Fractional order optimal control problems via the operational matrices of Bernstein polynomials. UPB Sci. Bull. 2014, 76, 115–128. [Google Scholar]
- Jesus, I.S.; Tenreiro, M.J.A. Fractional control of heat diffusion systems. Nonlinear Dyn. 2008, 54, 263–282. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, W.M.; El-Khazali, R. Fractional-order dynamical models of love. Chaos Solitons Fractals 2007, 33, 1367–1375. [Google Scholar] [CrossRef]
- David, S.A.; Linares, J.L.; Pallone, E.M.J.A. Fractional order calculus: Historical apologia, basic concepts and some applications. Rev. Bras. Ensino Física 2011, 33, 4302. [Google Scholar] [CrossRef]
- Bohannan, G.W. Analog fractional order controller in temperature and motor control applications. J. Vib. Control. 2008, 14, 1487–1498. [Google Scholar] [CrossRef]
- Joshi, H.J.; Brajesh, K. 2D dynamic analysis of the disturbances in the calcium neuronal model and its implications in neurodegenerative disease. Cogn. Neurodynam. 2022, 1–12. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.-Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons: Hoboken, NJ, USA, 1991; Volume 17. [Google Scholar]
- Zhao, Y.; Li, Y.; Liu, H. Fractional-order Iterative Learning Control with Nonuniform Trial Lengths. Int. J. Control. Autom. Syst. 2022, 20, 3167–3176. [Google Scholar] [CrossRef]
- Matt, C.; Hess, T.; Benlian, A. Digital transformation strategies. Bus. Inf. Syst. Eng. 2015, 57, 339–343. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Zhang, F.; Liu, H. Iterative learning control of fractional-order linear systems with nonuniform pass lengths. Trans. Inst. Meas. Control. 2022, 44, 3071–3080. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, Y. Fibonacci wavelets and Galerkin method to investigate fractional optimal control problems with bibliometric analysis. J. Vib. Control. 2021, 27, 1778–1792. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Shaher, O.I.; Mahmoudi, M.; Mechee, M.S. Numerical Method for Solving Fractional Order Optimal Control Problems with Free and Non-Free Terminal Time. Symmetry 2023, 15, 624. https://doi.org/10.3390/sym15030624
Al-Shaher OI, Mahmoudi M, Mechee MS. Numerical Method for Solving Fractional Order Optimal Control Problems with Free and Non-Free Terminal Time. Symmetry. 2023; 15(3):624. https://doi.org/10.3390/sym15030624
Chicago/Turabian StyleAl-Shaher, Oday I., M. Mahmoudi, and Mohammed S. Mechee. 2023. "Numerical Method for Solving Fractional Order Optimal Control Problems with Free and Non-Free Terminal Time" Symmetry 15, no. 3: 624. https://doi.org/10.3390/sym15030624
APA StyleAl-Shaher, O. I., Mahmoudi, M., & Mechee, M. S. (2023). Numerical Method for Solving Fractional Order Optimal Control Problems with Free and Non-Free Terminal Time. Symmetry, 15(3), 624. https://doi.org/10.3390/sym15030624




