Traversable Wormhole Solutions Admitting Noether Symmetry in
Abstract
:1. Introduction
2. Basic Formalism of Theory
- Null energy constraint
- Strong energy constraint
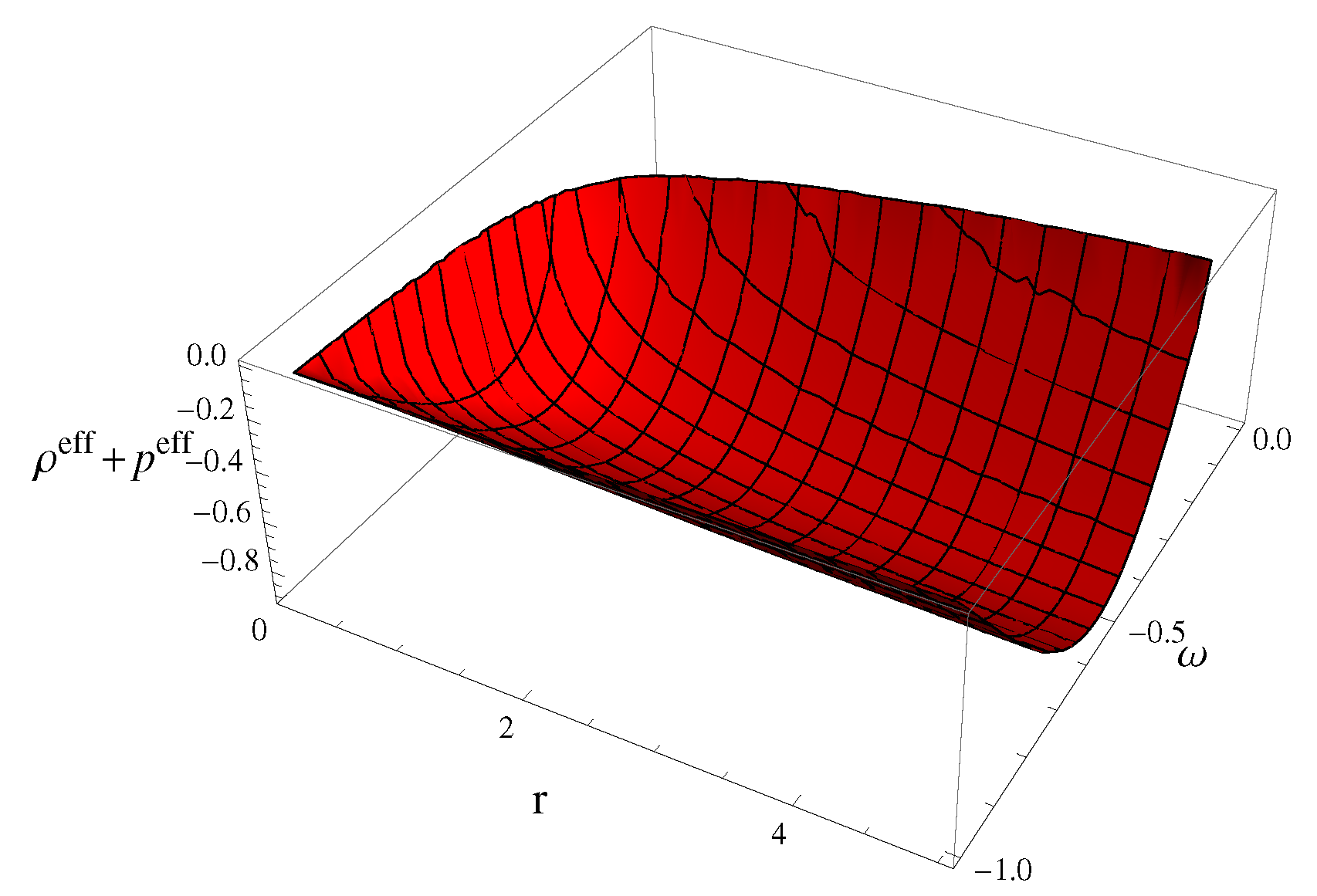
- Dominant energy constraint
- Weak energy constraint
3. Noether Symmetry Approach
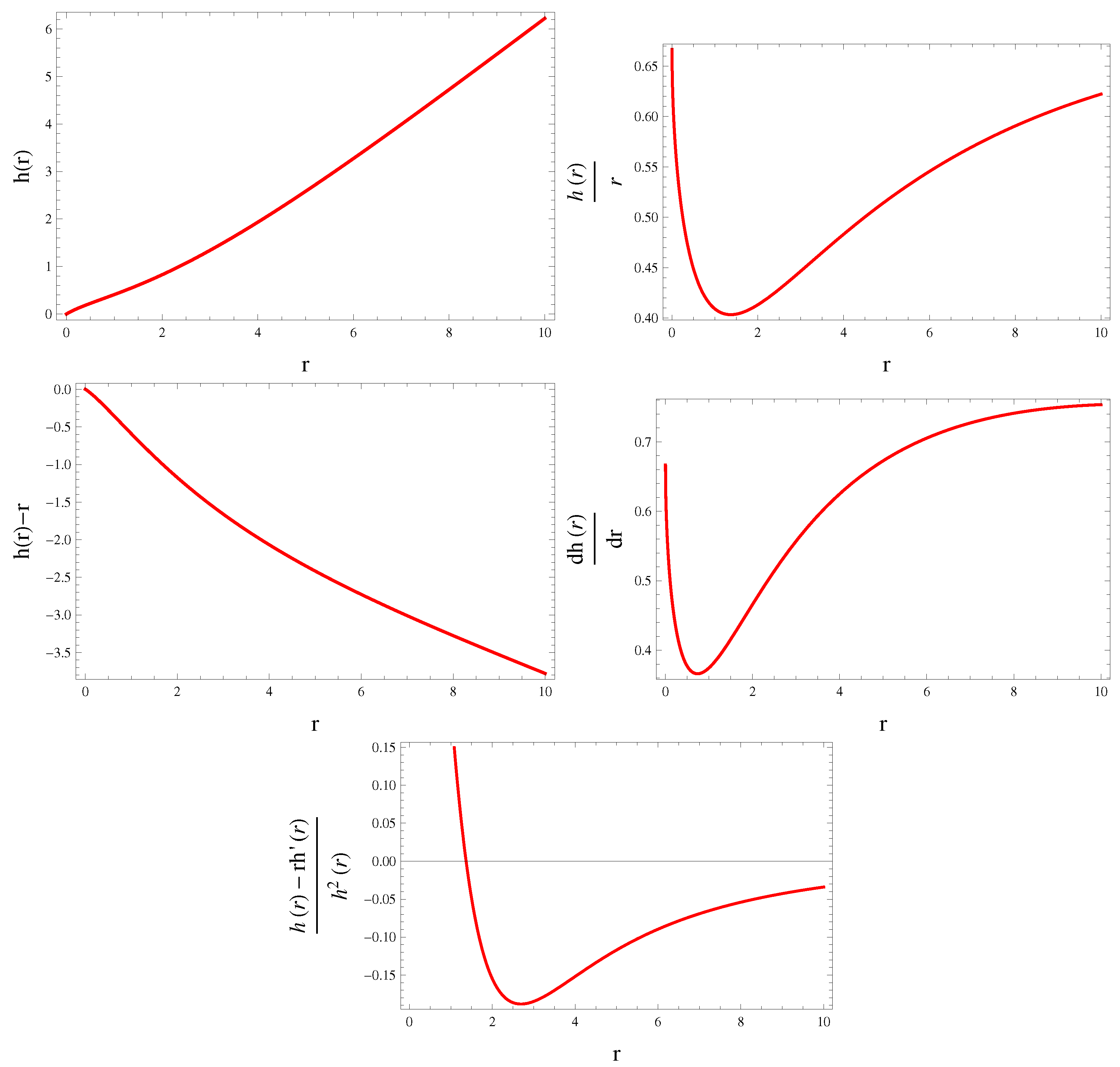
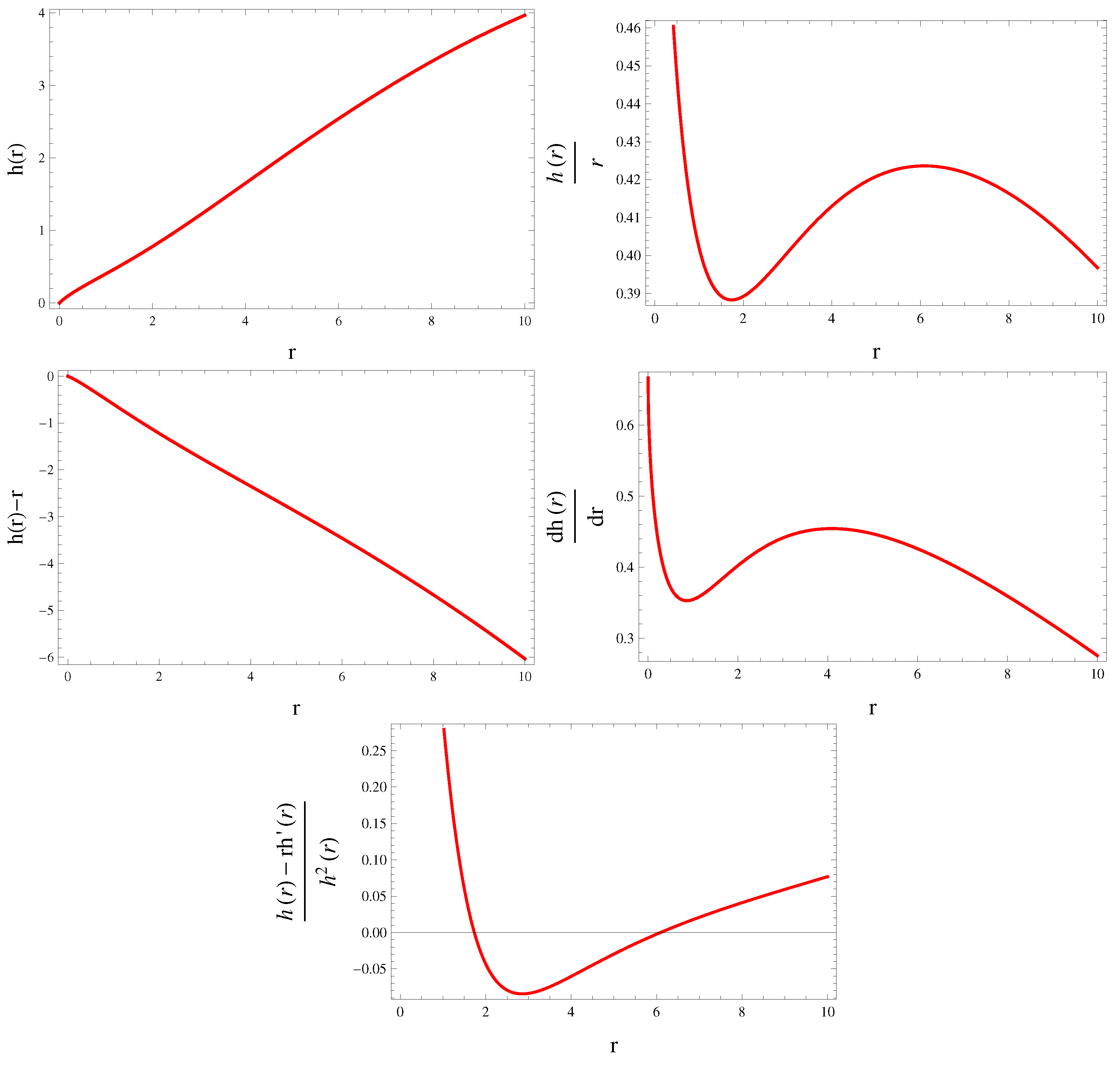
4. Exact Solutions
4.1. Dust Case
- Case I:
- Case II:
4.2. Non-Dust Case
- Case I:
- Case II:
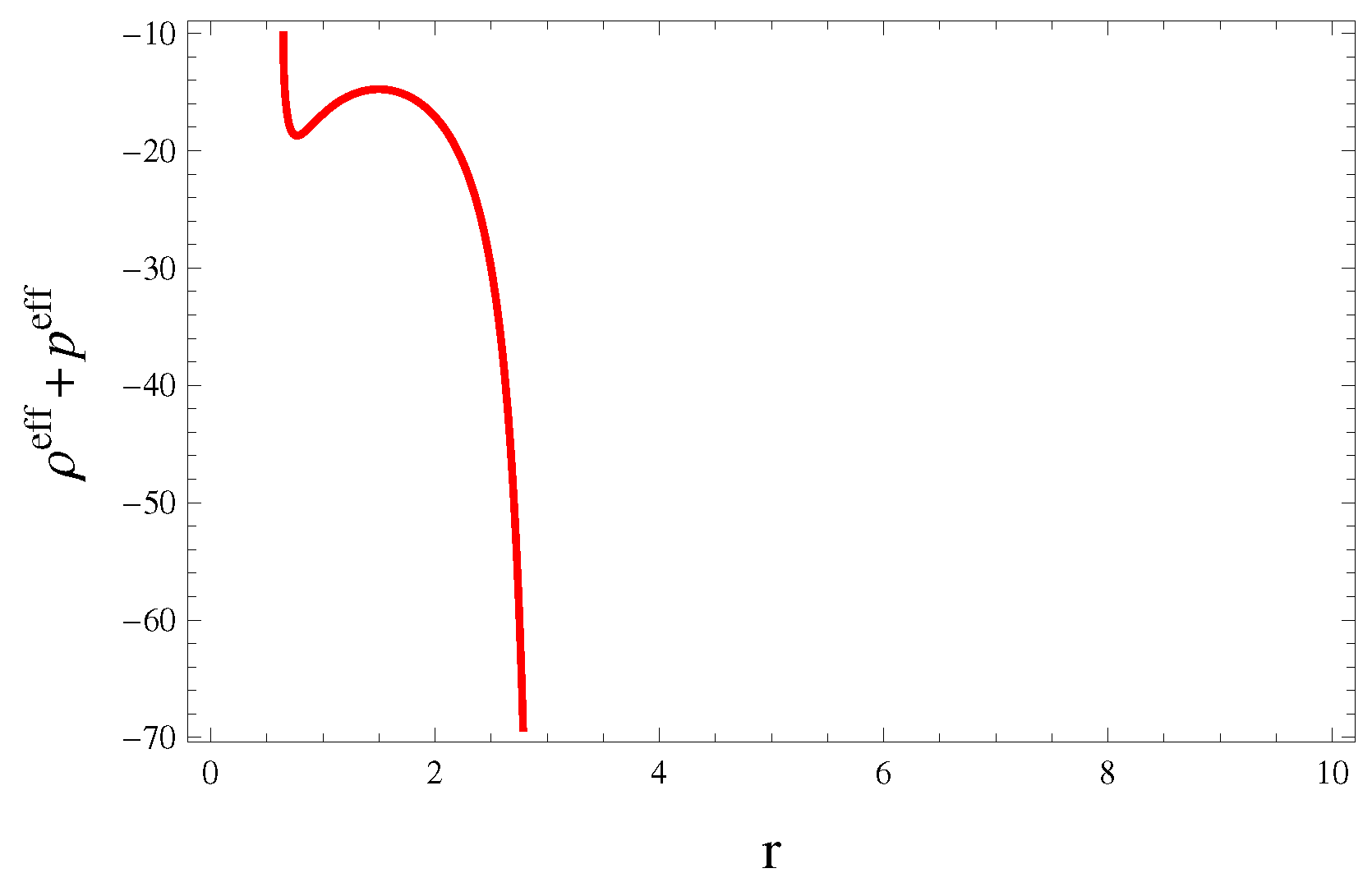
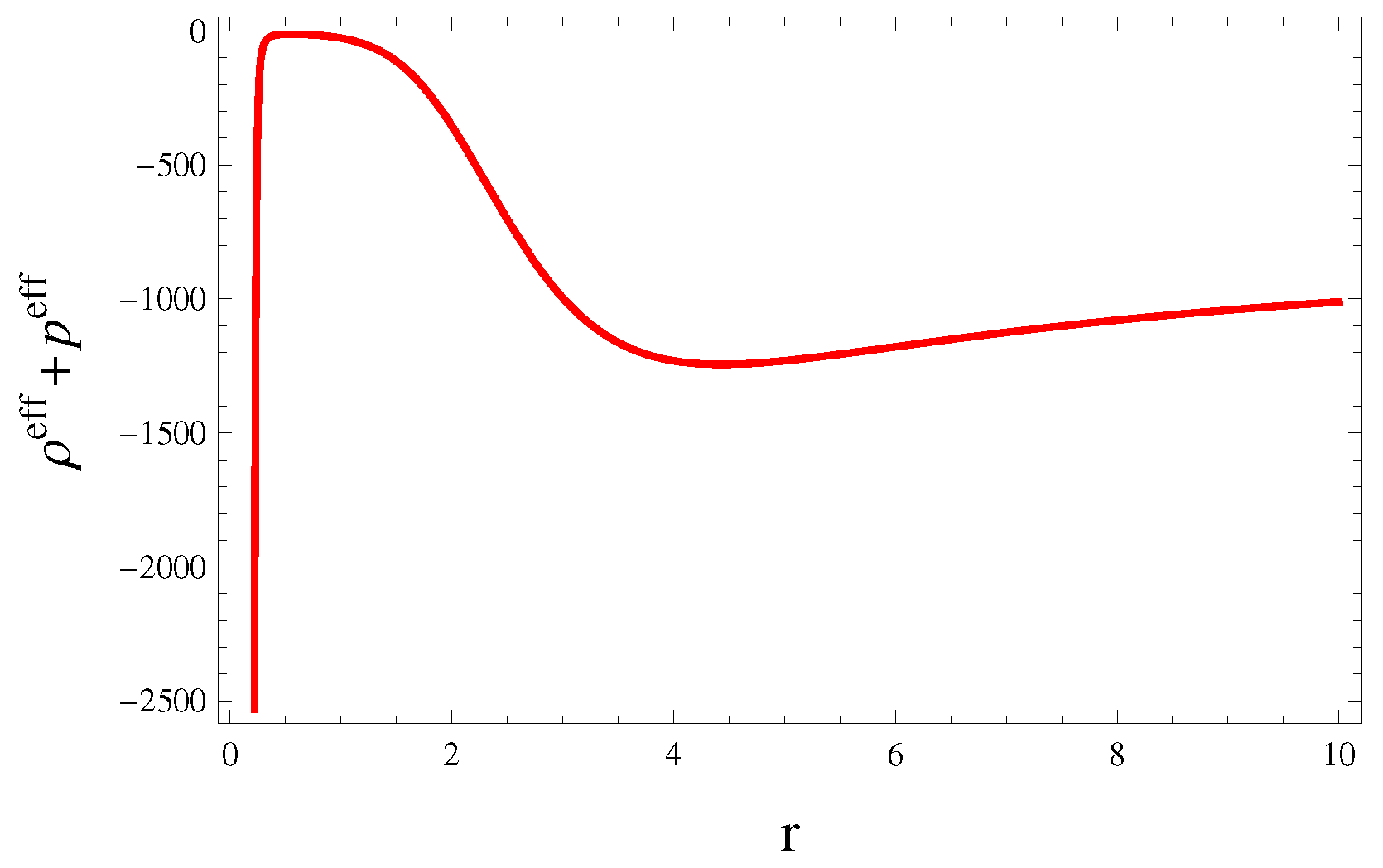
5. Stability Analysis
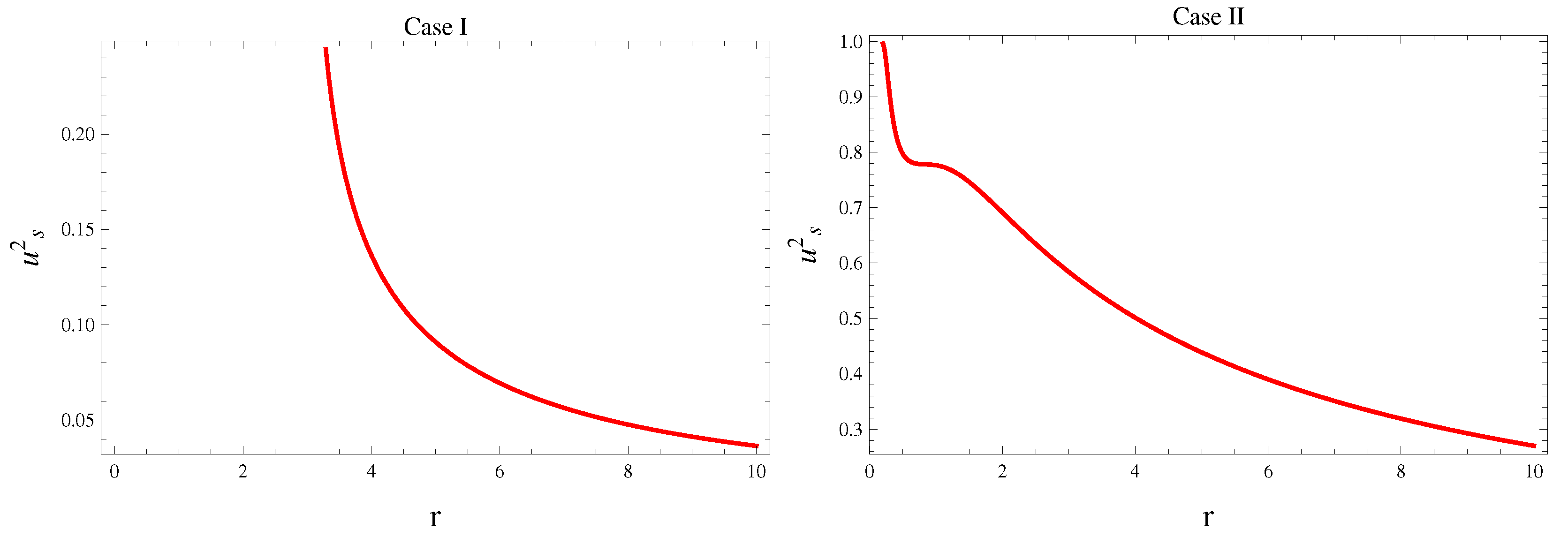
5.1. Causality Condition
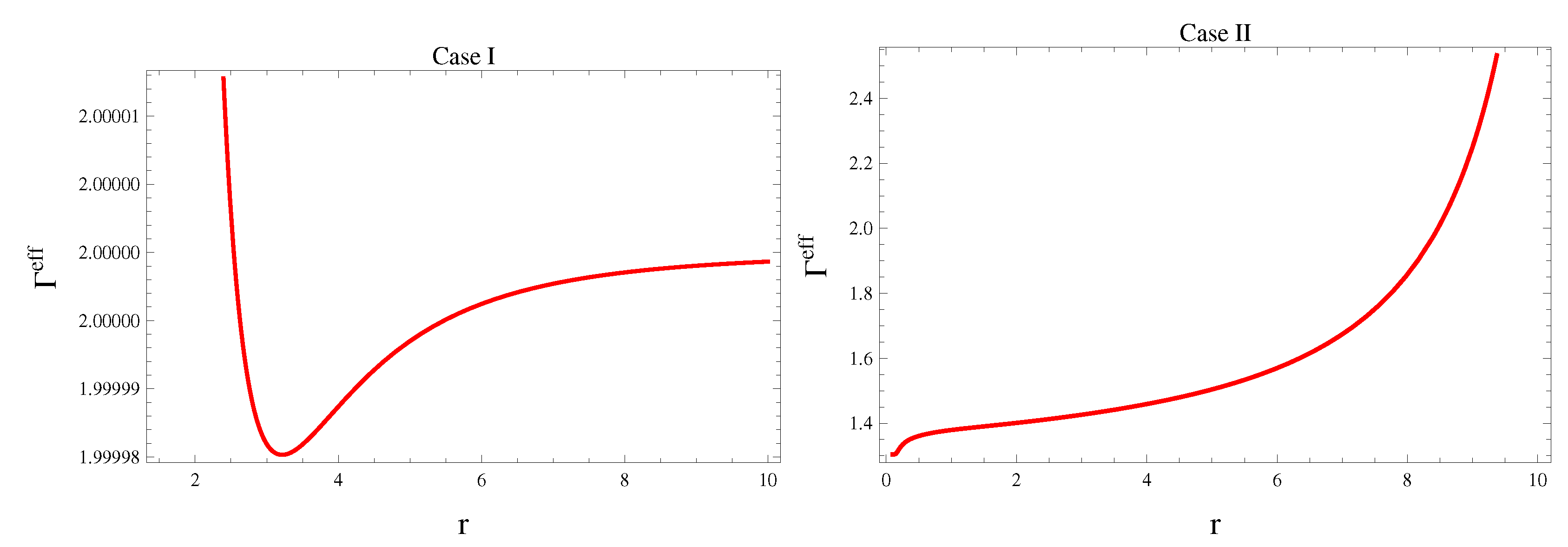
5.2. Adiabatic Index
6. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 1–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Lobo, F.S.; Nojiri, S.I.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Gul, M.Z. Study of charged spherical collapse in f(G,T) gravity. Eur. Phys. J. Plus 2018, 133, 345. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamics of cylindrical collapse in f(G,T) gravity. Chin. J. phys. 2019, 57, 329–337. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamics of perfect fluid collapse in f(G,T) gravity. Int. J. Mod. Phys. D 2019, 28, 1950054. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Stellar structures admitting Noether symmetries in f(R,T) gravity. Mod. Phys. Lett. A 2021, 36, 2150214. [Google Scholar] [CrossRef]
- Katirci, N.; Kavuk, M. Gravity and Cardassian-like expansion as one of its consequences. Eur. Phys. J. Plus 2014, 129, 163. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Sahoo, P.K. Temporally varying universal gravitational constant and speed of light in energy-momentum squared gravity. Eur. Phys. J. Plus 2020, 135, 86. [Google Scholar] [CrossRef]
- Singh, K.N.; Banerjee, A.; Maurya, S.K.; Rahaman, F.; Pradhan, A. Color-flavor locked quark stars in energy-momentum squared gravity. Phys. Dark Universe 2021, 31, 100774. [Google Scholar] [CrossRef]
- Nazari, E. Light bending and gravitational lensing in energy-momentum-squared gravity. Phys. Rev. D 2022, 105, 104026. [Google Scholar] [CrossRef]
- Roshan, M.; Shojai, F. Energy-momentum squared gravity. Phys. Rev. D 2016, 94, 044002. [Google Scholar] [CrossRef] [Green Version]
- Board, C.V.; Barrow, J.D. Cosmological models in energy-momentum-squared gravity. Phys. Rev. D 2017, 96, 123517. [Google Scholar] [CrossRef] [Green Version]
- Akarsu, O.; Katirci, N.; Kumar, S. Cosmic acceleration in a dust only Universe via energy-momentum powered gravity. Phys. Rev. D 2018, 2018 97, 024011. [Google Scholar] [CrossRef] [Green Version]
- Akarsu, O.; Katirci, N.; Kumar, S.; Nunes, R.C.; Sami, M. Cosmological implications of scale-independent energy-momentum squared gravity: Pseudo nonminimal interactions in dark matter and relativistic relics. Phys. Rev. D 2018, 98, 063522. [Google Scholar] [CrossRef] [Green Version]
- Ranjit, C.; Rudra, P.; Kundu, S. Constraints on Energy-Momentum Squared Gravity from cosmic chronometers and Supernovae Type Ia data. Ann. Phys. 2021, 428, 168432. [Google Scholar] [CrossRef]
- Sharif, M.; Naz, S. Gravastars with Karmarkar condition in f(R,T2) gravity. Int. J. Mod. Phys. D 2022, 31, 2240008. [Google Scholar] [CrossRef]
- Chen, C.Y.; Chen, P. Eikonal black hole ringings in generalized energy-momentum squared gravity. Phys. Rev. D 2020, 101, 064021. [Google Scholar] [CrossRef] [Green Version]
- Akarsu, O.; Barrow, J.D.; Uzun, N.M. Screening anisotropy via energy-momentum squared gravity: ΛCDM model with hidden anisotropy. Phys. Rev. D 2020, 102, 124059. [Google Scholar] [CrossRef]
- Kazemi, A.; Roshan, M.; De Martino, I.; De Laurentis, M. Jeans analysis in energy-momentum-squared gravity. Eur. Phys. J. C 2020, 80, 150. [Google Scholar] [CrossRef]
- Rudra, P.; Pourhassan, B. Thermodynamics of the apparent horizon in the generalized energy-momentum-squared cosmology. Phys. Dark Universe 2021, 33, 100849. [Google Scholar] [CrossRef]
- Nazari, E.; Sarvi, F.; Roshan, M. Generalized energy-momentum-squared gravity in the Palatini formalism. Phys. Rev. D 2020, 102, 064016. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Stability of the closed Einstein universe in energy-momentum squared gravity. Phys. Scr. 2021, 96, 105001. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Effects of f(R,T2) gravity on the stability of anisotropic perturbed Einstein Universe. Pramana J. Phys. 2022, 96, 153. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamics of spherical collapse in energy-momentum squared gravity. Int. J. Mod. Phys. A 2021, 36, 2150004. [Google Scholar] [CrossRef]
- Gul, M.Z.; Sharif, M. Dynamical analysis of charged dissipative cylindrical collapse in energy-momentum squared gravity. Universe 2021, 7, 154. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Study of stellar structures in f(R,TμνTμν) theory. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250012. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamics of charged anisotropic spherical collapse in energy-momentum squared gravity. Chin. J. Phys. 2021, 71, 365–374. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Role of energy-momentum squared gravity on the dynamics of charged dissipative plane symmetric collapse. Mod. Phys. Lett. A 2022, 37, 2250005. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bhatti, M.Z.; Farwa, U. Evolution of axially and reflection symmetric source in energy-momentum squared gravity. Eur. Phys. J. Plus 2022, 137, 1–22. [Google Scholar] [CrossRef]
- Khodadi, M.; Firouzjaee, J.T. A survey of strong cosmic censorship conjecture beyond Einstein’s gravity. Phys. Dark Universe 2022, 37, 101084. [Google Scholar] [CrossRef]
- Flamm, L. Beitrge zur Einsteinschen gravitationstheorie. Phys. Z. 1916, 17, 448–454. [Google Scholar]
- Einstein, A.; Rosen, N. The particle problem in the general theory of relativity. Phys. Rev. 1935, 48, 73. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geons. Phys. Rev. 1955, 97, 511. [Google Scholar] [CrossRef]
- Fuller, R.W.; Wheeler, J.A. Causality and multiply connected spacetime. Phys. Rev. 1962, 128, 919. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef] [Green Version]
- Kashargin, P.E.; Sushkov, S.V. Slowly rotating wormholes: The first-order approximation. Gravit. Cosmol. 2008, 14, 80–85. [Google Scholar] [CrossRef]
- Eiroa, E.F.; Simeone, C. Brans-Dicke cylindrical wormholes. Phys. Rev. D 2010, 82, 084039. [Google Scholar] [CrossRef] [Green Version]
- Dzhunushaliev, V.; Folomeev, V.; Singleton, D.; Myrzakulov, R. Linear stability of spherically symmetric and wormhole solutions supported by the sine-Gordon ghost scalar field. Phys. Rev. D 2010, 82, 045032. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, P.H.F.D.; Alencar, G.; Jardim, I.C.; Landim, R.R. On the Traversable Yukawa-Casimir Wormholes. Symmetry 2023, 15, 383. [Google Scholar] [CrossRef]
- Noether, E. Invariante Variationsprobleme. Tramp. Th. Stat, Phys. 1918, 1, 189–207. [Google Scholar]
- Jamil, M.; Mahomed, F.M.; Momeni, D. Noether symmetry approach in f(R)- tachyon model. Phys. Lett. B 2011, 702, 315–319. [Google Scholar] [CrossRef] [Green Version]
- Basilakos, S.; Tsamparlis, M.; Paliathanasis, A. Using the Noether symmetry approach to probe the nature of dark energy. Phys. Rev. D 2011, 83, 103512. [Google Scholar] [CrossRef] [Green Version]
- Paliathanasis, A.; Tsamparlis, M.; Basilakos, S. Constraints and analytical solutions of f(R) theories of gravity using Noether symmetries. Phys. Rev. D 2011, 84, 123514. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M.; Odintsov, S.D. Hamiltonian dynamics and Noether symmetries in extended gravity cosmology. Eur. Phys. J. C 2012, 72, 1–21. [Google Scholar] [CrossRef]
- Hussain, I.; Jamil, M.; Mahomed, F.M. Noether gauge symmetry approach in f(R) gravity. Astrophys. Space Sci. 2012, 337, 373–377. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Dialektopoulos, K.F. Noether symmetries in Gauss-Bonnet-teleparallel cosmology. Eur. Phys. J. C 2016, 76, 1–6. [Google Scholar]
- Motavali, H.; Golshani, M. Exact solutions for cosmological models with a scalar field. Int. J. Mod. Phys. D 2002, 17, 375–381. [Google Scholar] [CrossRef] [Green Version]
- Vakili, B. Noether symmetry in f(R) cosmology. Phys. Lett. B 2008, 664, 16–20. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; Piedipalumbo, E.; Rubano, C.; Scudellaro, P. Noether symmetry approach in phantom quintessence cosmology. Phys. Rev. D 2009, 80, 104030. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; Stabile, A.; Troisi, A. Spherical symmetry in f(R)-gravity. Class. Quantum Grav. 2008, 25, 085004. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M.; Stabile, A. Axially symmetric solutions in f (R)-gravity. Class. Quantum Grav. 2010, 27, 165008. [Google Scholar] [CrossRef] [Green Version]
- Shamir, M.F.; Jhangeer, A.; Bhatti, A.A. Conserved quantities in f(R) gravity via Noether symmetry. Chin. Phys. Lett. 2012, 29, 080402. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Ali, S.; Momeni, D.; Myrzakulov, R. Bianchi type I cosmology in generalized Saez-Ballester theory via Noether gauge symmetry. Eur. Phys. J. C 2012, 72, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Momeni, D.; Myrzakulov, R.; Gudekli, E. Cosmological viable mimetic f(R) and f(R,T) theories via Noether symmetry. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550101. [Google Scholar] [CrossRef] [Green Version]
- Shamir, M.F.; Ahmad, M. Noether symmetry approach in f(G,T) gravity. Eur. Phys. J. C 2017, 77, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Shamir, M.F.; Ahmad, M. Some exact solutions in f(G,T) gravity via Noether symmetries. Mod. Phys. Lett. A 2017, 32, 1750086. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Gul, M.Z. Noether symmetry approach in energy-momentum squared gravity. Phys. Scr. 2020, 96, 025002. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Noether symmetries and anisotropic universe in energy-momentum squared gravity. Phys. Scr. 2021, 96, 125007. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Viable wormhole solutions in energy-momentum squared gravity. Eur. Phys. J. Plus 2021, 136, 503. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Compact stars admitting noether symmetries in energy-momentum squared gravity. Adv. Astron. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Scalar field cosmology via Noether symmetries in energy-momentum squared gravity. Chin. J. Phys. 2022, 80, 58–73. [Google Scholar] [CrossRef]
- Lobo, F.S.; Oliveira, M.A. Wormhole geometries in f(R) modified theories of gravity. Phys. Rev. D 2009, 80, 104012. [Google Scholar] [CrossRef] [Green Version]
- Mazharimousavi, S.H.; Halilsoy, M. Necessary conditions for having wormholes in f(R) gravity. Mod. Phys. Lett. A 2016, 31, 1650203. [Google Scholar] [CrossRef] [Green Version]
- Bahamonde, S.; Camci, U.; Capozziello, S.; Jamil, M. Scalar-tensor teleparallel wormholes by Noether symmetries. Phys. Rev. D 2016, 94, 084042. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Ahmad, Y. Static spherically symmetric wormholes in f(R,T) gravity. Eur. Phys. J. C 2016, 76, 444. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Nawazish, I. Wormhole geometry and Noether symmetry in f(R) gravity. Ann. Phys. 2018, 389, 283–305. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Shah, S.A.A.; Bamba, K. New Holographic Dark Energy Model in Brans-Dicke Theory. Symmetry 2018, 10, 153. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Saba, S. Tsallis holographic dark energy in f(G,T) gravity. Symmetry 2019, 11, 92. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, G.; Shamir, M.F.; Ashraf, A.; Xia, T.C. Noncommutative wormholes solutions with conformal motion in the background of f(G,T) gravity. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050103. [Google Scholar] [CrossRef]
- Shamir, M.F.; Fayyaz, I. Traversable wormhole solutions in f(R) gravity via Karmarkar condition. Eur. Phys. J. C 2020, 80, 1102. [Google Scholar] [CrossRef]
- Hassan, Z.; Mustafa, G.; Sahoo, P.K. Wormhole solutions in symmetric teleparallel gravity with noncommutative geometry. Symmetry 2021, 13, 1260. [Google Scholar] [CrossRef]
- Malik, A.; Mofarreh, F.; Zia, A.; Ali, A. Traversable wormhole solutions in the f(R) theories of gravity under the Karmarkar condition. Chin. Phys. C 2022, 46, 095104. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Maartens, R.; MacCallum, M.A.H. Relativistic Cosmology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Cataldo, M.; Liempi, L.; Rodriguez, P. Static spherically symmetric wormholes with isotropic pressure. Phys. Lett. B 2016, 757, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Gyulchev, G.; Nedkova, P.; Tinchev, V.; Yazadjiev, S. On the shadow of rotating traversable wormholes. Eur. Phys. J. C 2018, 78, 544. [Google Scholar] [CrossRef]
- Abreu, H.; Hernandez, H.; Nunez, L.A. Sound speeds, cracking and the stability of self-gravitating anisotropic compact objects. Class. Quantum Grav. 2007, 24, 4631. [Google Scholar] [CrossRef]
- Heintzmann, H.; Hillebrandt, W. Neutron stars with an anisotropic equation of state-mass, redshift and stability. Astron. Astrophys. 1975, 38, 51–55. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef] [Green Version]
- Shamir, M.F.; Ahmad, M. Emerging anisotropic compact stars in f(G,T) gravity. Eur. Phys. J. C 2017, 77, 674. [Google Scholar] [CrossRef]
- Deb, D.; Chowdhury, S.R.; Ray, S.; Rahaman, F.; Guha, B.K. Relativistic model for anisotropic strange stars. Ann. Phys. 2017, 387, 239–252. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Siddiqa, A. Study of stellar structures in f(R,T) gravity. Int. J. Mod. Phys. D 2018, 27, 1850065. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Anisotropic compact stars with Karmarkar condition in energy-momentum squared gravity. Gen. Relativ. Gravit. 2023, 55, 10. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Role of f(R,T2) theory on charged compact stars. Phys. Scr. 2023, 98, 035030. [Google Scholar]
- Sharif, M.; Gul, M.Z. Study of charged anisotropic Karmarkar stars in f(R,T2) theory. Fortschritte Phys. 2023, 2023, 2200184. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gul, M.Z.; Sharif, M.
Traversable Wormhole Solutions Admitting Noether Symmetry in
Gul MZ, Sharif M.
Traversable Wormhole Solutions Admitting Noether Symmetry in
Gul, Muhammad Zeeshan, and Muhammad Sharif.
2023. "Traversable Wormhole Solutions Admitting Noether Symmetry in
Gul, M. Z., & Sharif, M.
(2023). Traversable Wormhole Solutions Admitting Noether Symmetry in







