Variability of Elastic Properties of Two-Layered Tubes from Six-Constant Tetragonal Crystals
Abstract
1. Introduction
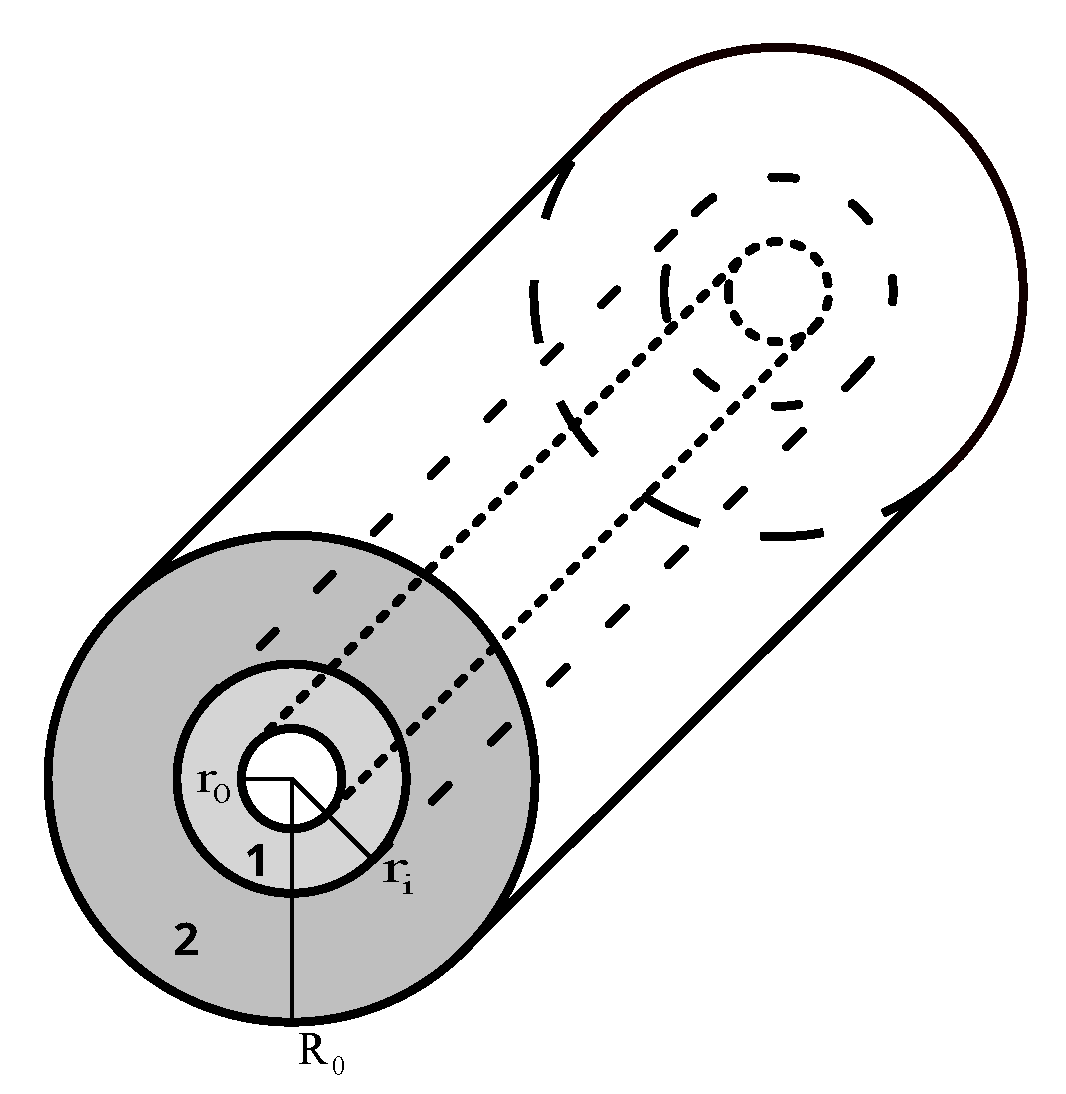
2. Two-Layered Tubes from Six-Constant Tetragonal Crystals under Longitudinal Tension
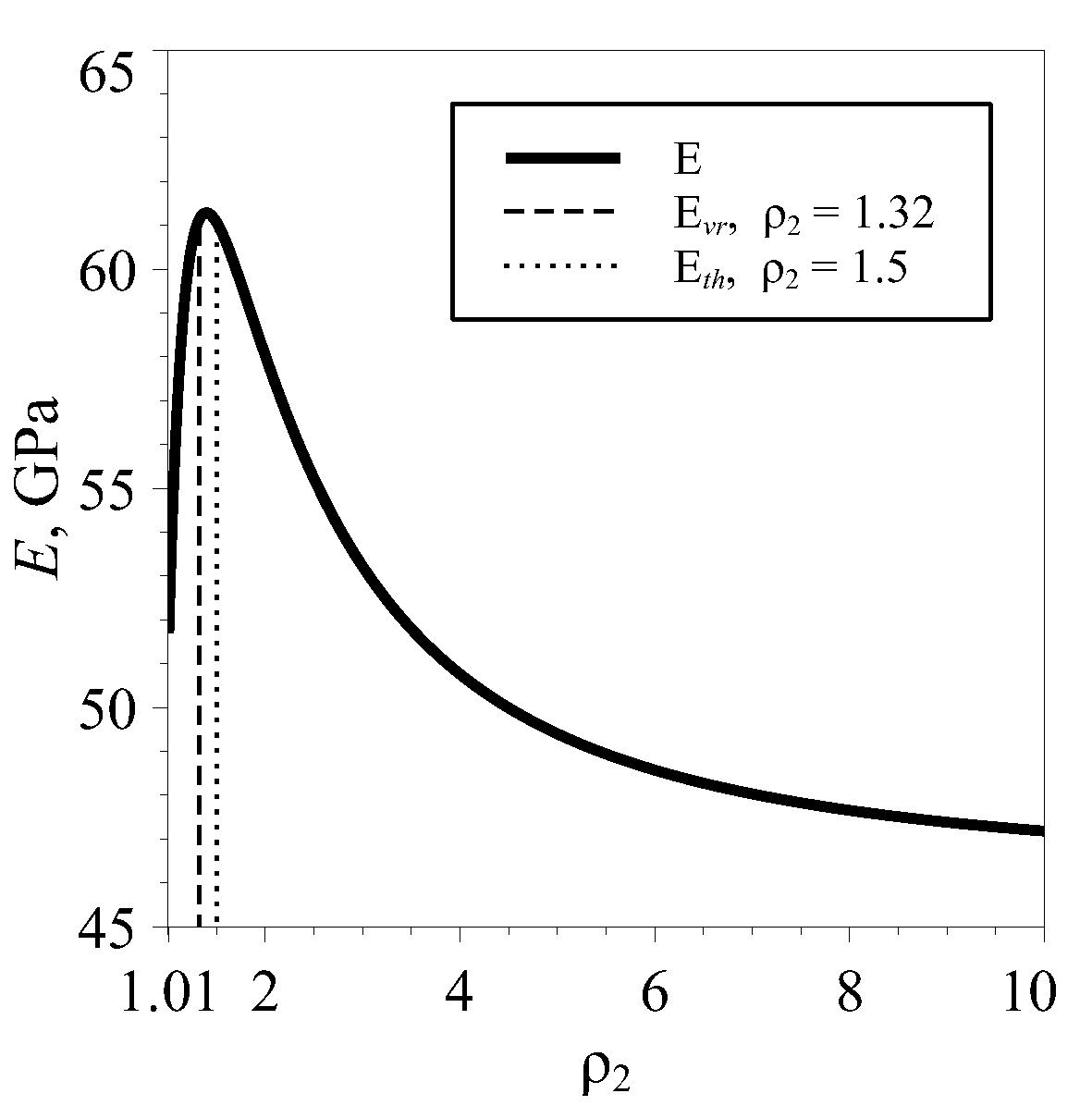
3. Elastic Properties of Two-Layered Six-Constant Tetragonal Tubes with Equal Thicknesses and Volumes of Layers
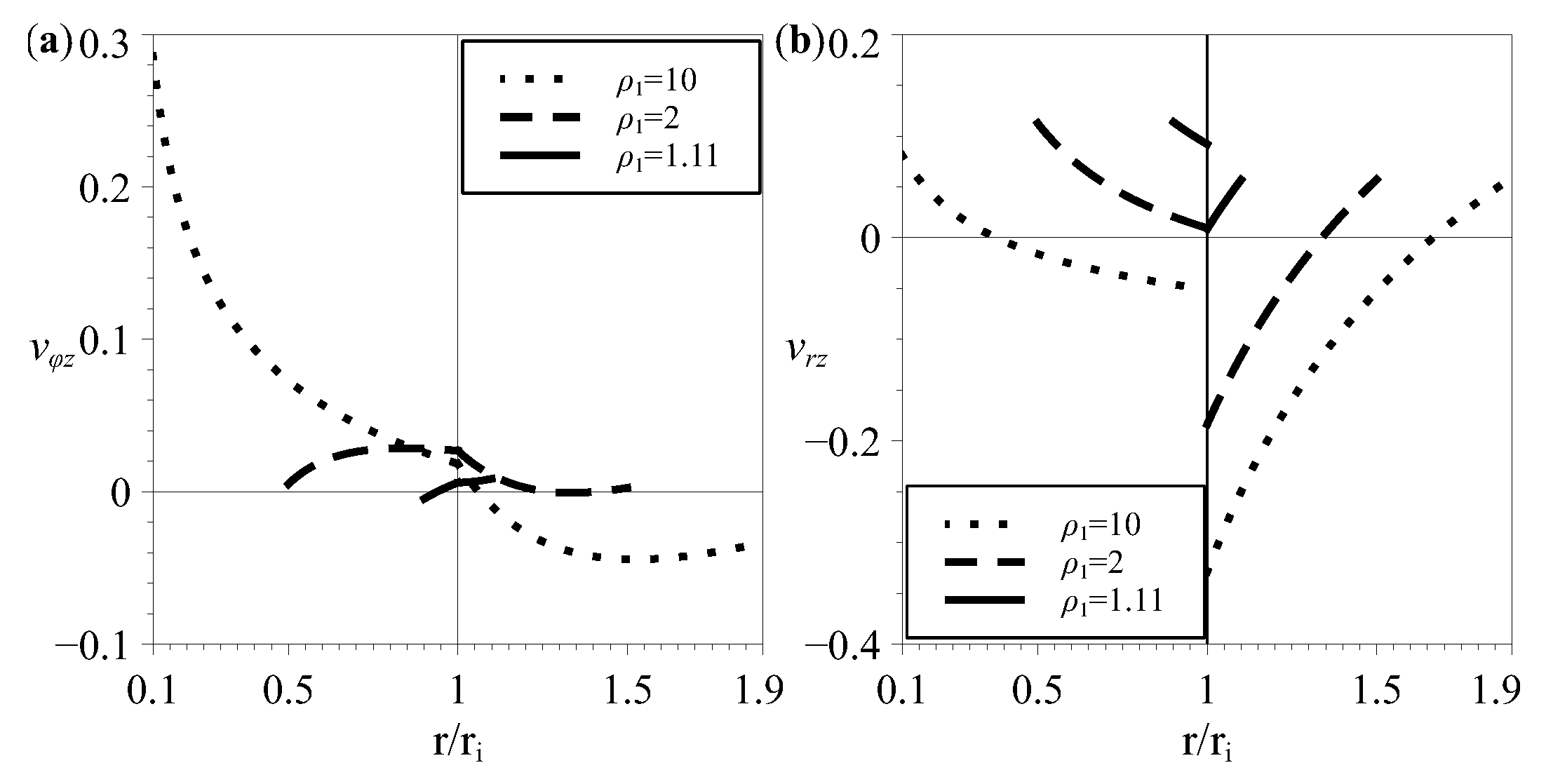
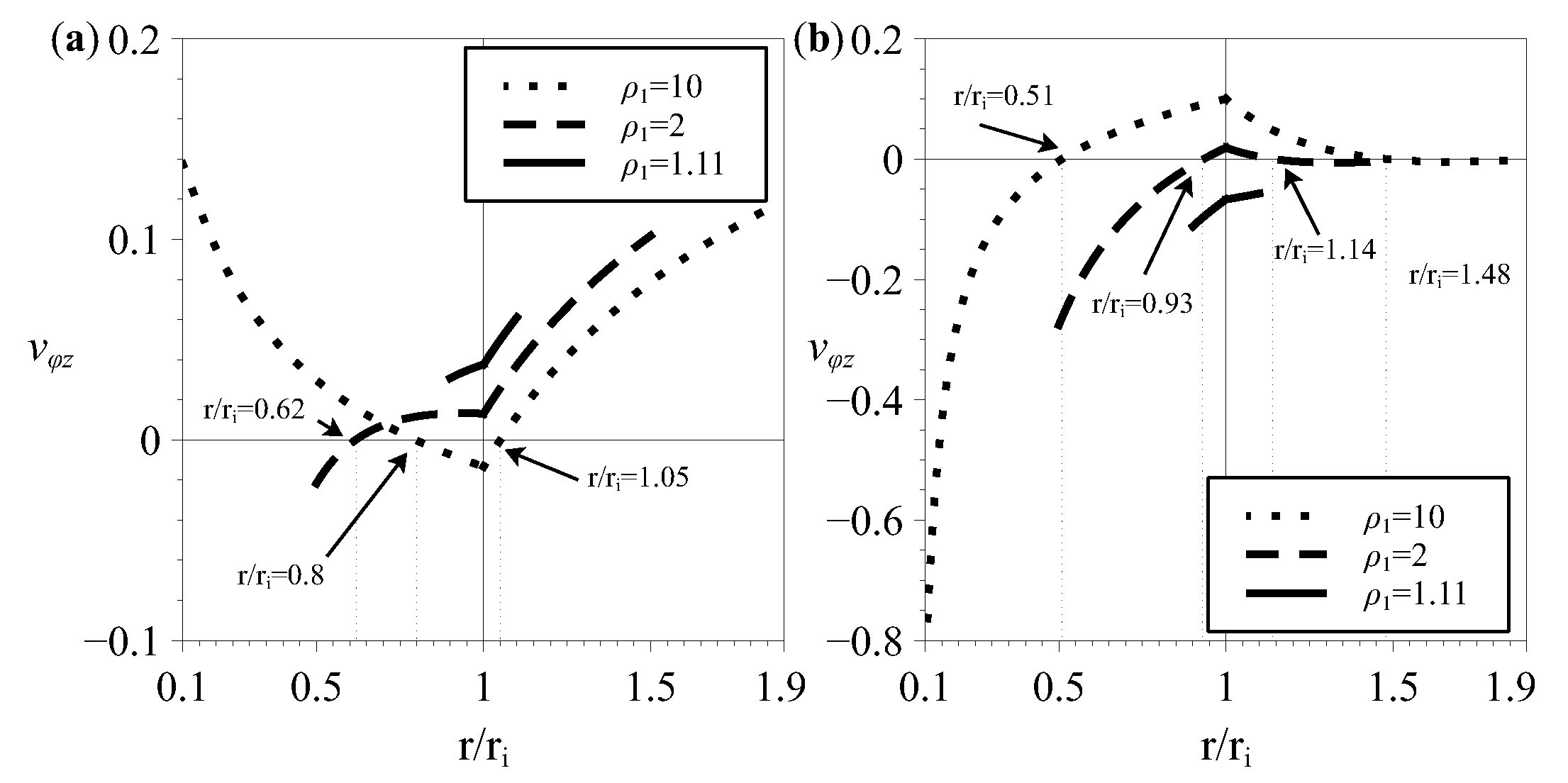
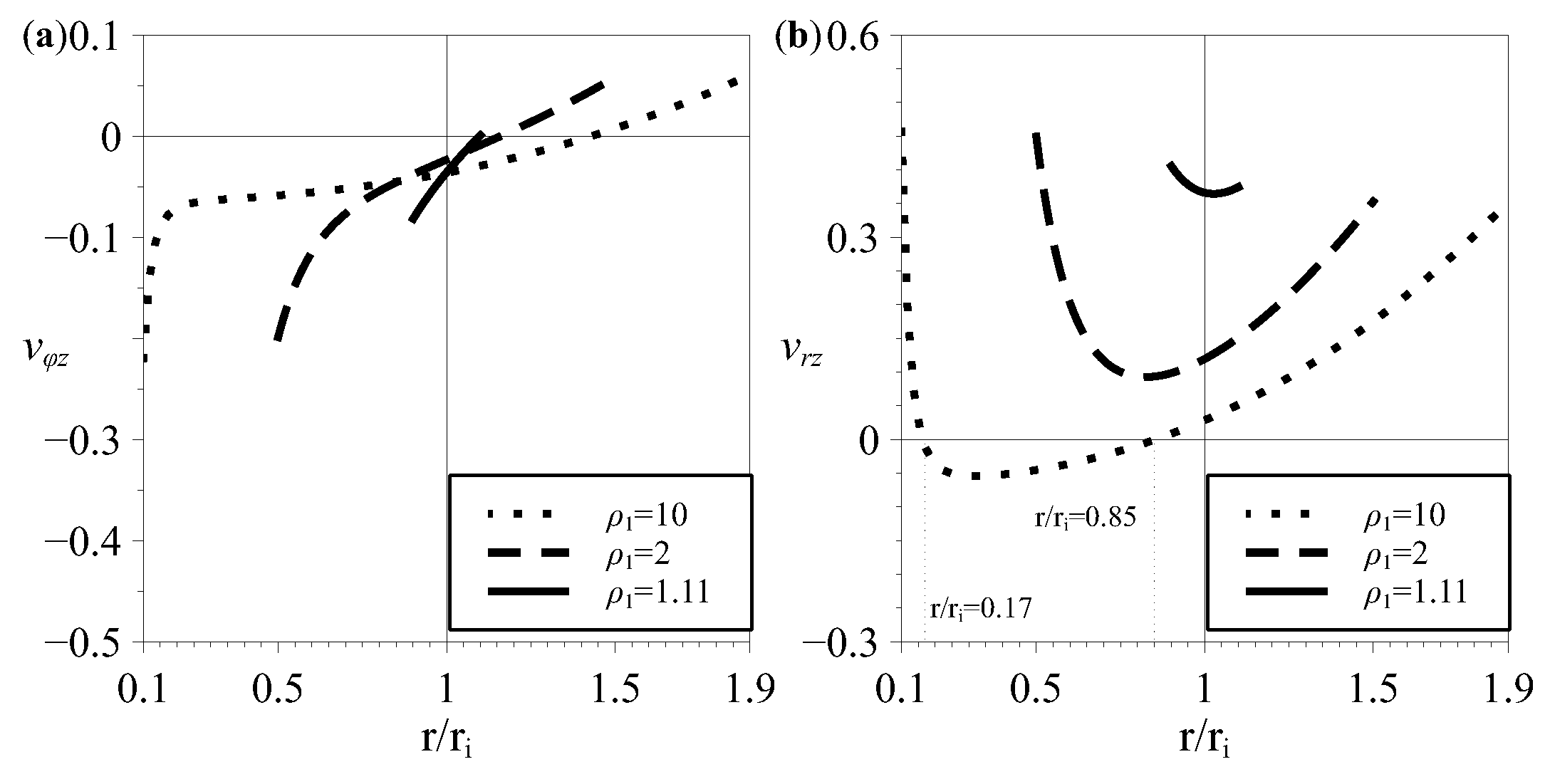
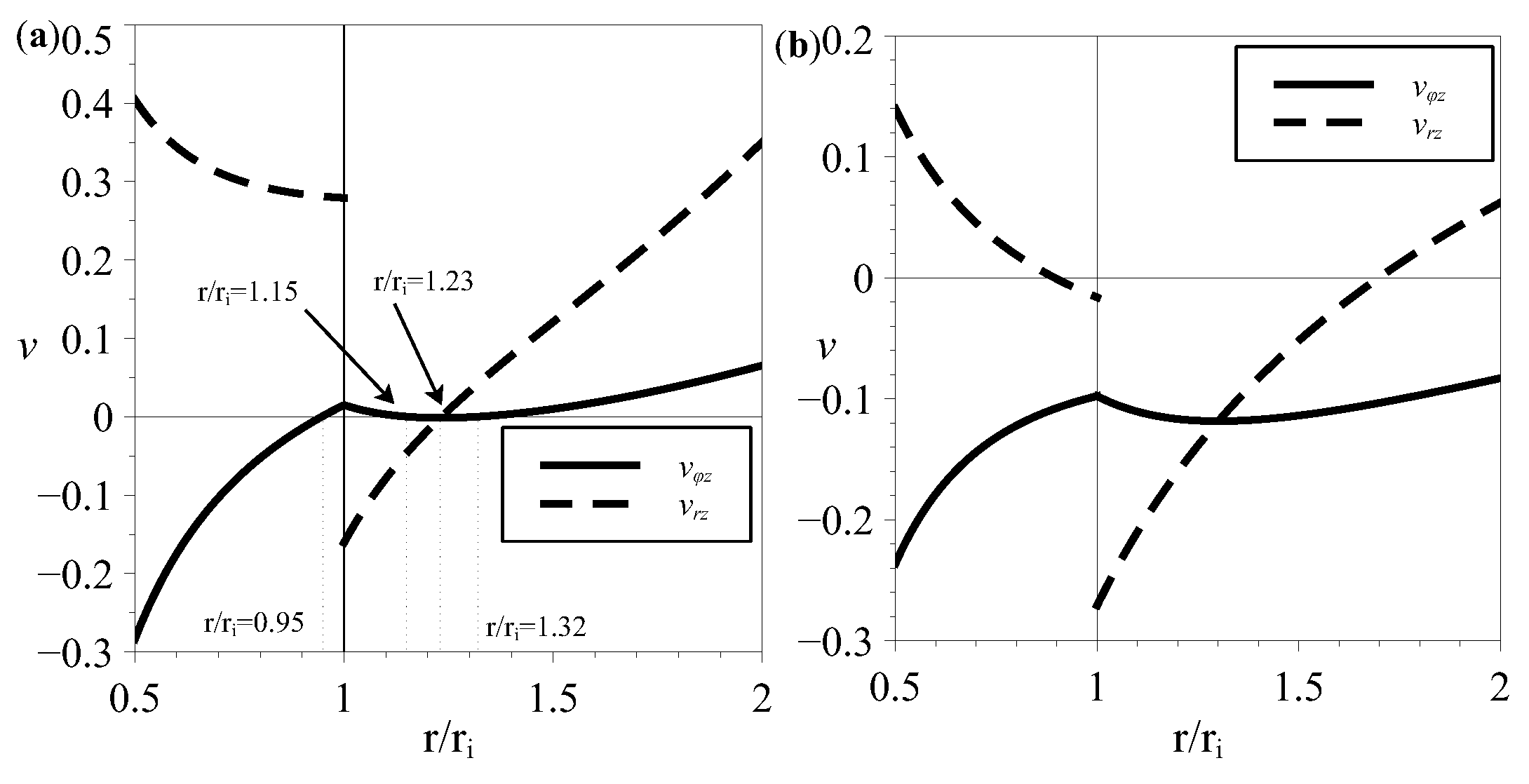
4. Effective Properties Variability for Two-Layered Tubes from Six-Constant Tetragonal Crystals with Arbitrary Thicknesses of Layers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Solution to the Problem of Longitudinal Tension of Two-Layered Tubes from Six-Constant Tetragonal Crystals
References
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge Unviersity Press: Cambridge, UK, 1892; Volume 1. [Google Scholar]
- Simmons, G.; Birch, F. Elastic Constants of Pyrite. J. Appl. Phys. 1963, 34, 2736–2738. [Google Scholar] [CrossRef]
- Benbattouche, N.; Saunders, G.A.; Lambson, E.F.; Honle, W. The dependences of the elastic stiffness moduli and the Poisson ratio of natural iron pyrites FeS2 upon pressure and temperature. J. Phys. D Appl. Phys. 1989, 22, 670–675. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. J. Mater. Sci. 1988, 23, 4406–4414. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi B 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Bellis, M.L.D. Auxetic anti-tetrachiral materials: Equivalent elastic properties and frequency band-gaps. Compos. Struct. 2015, 131, 530–544. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi B 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. Auxetic behaviour from rotating rhombi. Phys. Status Solidi B 2008, 245, 2395–2404. [Google Scholar] [CrossRef]
- Larsen, U.; Signund, O.; Bouwsta, S. Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio. J. Microelectromech. Syst. 1997, 6, 99–106. [Google Scholar] [CrossRef]
- Lim, T.C. Metamaterial honeycomb with sign-toggling expansion coefficients that manifests an Islamic mosaic pattern at the Alhambra Palace. Adv. Compos. Hybrid. Mater. 2021, 4, 966–978. [Google Scholar] [CrossRef]
- Lim, T.C. Adjustable positive and negative hygrothermal expansion metamaterial inspired by the Maltese cross. R. Soc. Open Sci. 2021, 8, 210593. [Google Scholar] [CrossRef]
- Nedoushan, R.J.; An, Y.; Yu, W.R.; Abghary, M.J. Novel triangular auxetic honeycombs with enhanced stiffness. Compos. Struct. 2021, 277, 114605. [Google Scholar] [CrossRef]
- Lim, T.C. Metamaterial with sign-toggling thermal expansivity inspired by Islamic motifs in Spain. J. Sci. Adv. Mater. Devices 2022, 7, 100401. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafström, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Paczkiewicz, T.; Pruchnik, M.; Wolski, S. Slowness surfaces and energy focusing patterns of auxetic cubic media. Comput. Meth. Sci. Technol. 2004, 10, 183–195. [Google Scholar] [CrossRef]
- Tokmakova, S.P. Stereographic projections of Poisson’s ratio in auxetic crystals. Phys. Status Solidi B 2005, 242, 721–729. [Google Scholar] [CrossRef]
- Norris, A.N. Poisson’s ratio in cubic materials. Proc. R. Soc. A 2006, 462, 3385–3405. [Google Scholar] [CrossRef]
- Paszkiewicz, T.; Wolski, S. Anisotropic properties of mechanical characteristics and auxeticity of cubic crystalline media. Phys. Status Solidi B 2007, 244, 966–977. [Google Scholar] [CrossRef]
- Paszkiewicz, T.; Wolski, S. Elastic properties of cubic crystals: Every’s versus Blackman’s diagram. J. Phys. Conf. Ser. 2008, 104, 012038. [Google Scholar] [CrossRef]
- Brańka, A.C.; Heyes, D.M.; Wojciechowski, K.W. Auxeticity of cubic materials. Phys. Status Solidi B 2009, 246, 2063–2071. [Google Scholar] [CrossRef]
- Brańka, A.C.; Heyes, D.M.; Wojciechowski, K.W. Auxeticity of cubic materials under pressure. Phys. Status Solidi B 2010, 248, 96–104. [Google Scholar] [CrossRef]
- Hughes, T.P.; Marmier, A.; Evans, K.E. Auxetic frameworks inspired by cubic crystals. Int. J. Solids Struct. 2010, 47, 1469–1476. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Cubic auxetics. Dokl. Phys. 2011, 56, 399–402. [Google Scholar] [CrossRef]
- Brańka, A.C.; Heyes, D.M.; Maćkowiak, S.; Pieprzyk, S.; Wojciechowski, K.W. Cubic materials in different auxetic regions: Linking microscopic to macroscopic formulations. Phys. Status Solidi B 2012, 249, 1373–1378. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Relation of Poisson’s ratio on average with Young’s modulus. Auxetics on average. Dokl. Phys. 2012, 57, 174–178. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Classification of cubic auxetics. Phys. Status Solidi B 2013, 250, 2038–2043. [Google Scholar] [CrossRef]
- Krasavin, V.V.; Krasavin, A.V. Auxetic properties of cubic metal single crystals. Phys. Status Solidi B 2014, 251, 2314–2320. [Google Scholar] [CrossRef]
- Ho, D.T.; Park, S.D.; Kwon, S.Y.; Han, T.S.; Kim, S.Y. Negative Poisson’s ratio in cubic materials along principal directions. Phys. Status Solidi B 2016, 253, 1288–1294. [Google Scholar] [CrossRef]
- Lisovenko, D.S.; Baimova, J.A.; Rysaeva, L.K.; Gorodtsov, V.A.; Rudskoy, A.I.; Dmitriev, S.V. Equilibrium diamond-like carbon nanostructures with cubic anisotropy: Elastic properties. Phys. Status Solidi B 2016, 253, 1295–1302. [Google Scholar] [CrossRef]
- Epishin, A.I.; Lisovenko, D.S. Extreme values of the Poisson’s ratio of cubic crystals. Tech. Phys. 2016, 61, 1516–1524. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S. Auxetics among Materials with Cubic Anisotropy. Mech. Solids. 2020, 55, 461–474. [Google Scholar] [CrossRef]
- Epishin, A.I.; Lisovenko, D.S. Influence of the Crystal Structure and Type of Interatomic Bond on the Elastic Properties of Monatomic and Diatomic Cubic Crystals. Mech. Solids. 2022, 57, 1344–1358. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Pigłowski, P.M.; Hyżorek, K.; Wojciechowski, K.W. Enhanced auxeticity in Yukawa systems due to introduction of nanochannels in [001]-direction. Smart Mater. Struct. 2016, 25, 054007. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Kowalik, M.; Wojciechowski, K.W. Influence of nanochannels on Poisson’s ratio of degenerate crystal of hard dimers. Phys. Status Solidi B 2016, 253, 1324–1330. [Google Scholar] [CrossRef]
- Pigłowski, P.M.; Wojciechowski, K.W.; Tretiakov, K.V. Partial auxeticity induced by nanoslits in the Yukawa crystal. Phys. Status Solidi RRL 2016, 10, 566–569. [Google Scholar] [CrossRef]
- Pigłowski, P.; Narojczyk, J.; Poźniak, A.; Wojciechowski, K.; Tretiakov, K. Auxeticity of Yukawa Systems with Nanolayers in the (111) Crystallographic Plane. Materials 2017, 10, 1338. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Pigłowski, P.M.; Narojczyk, J.W.; Wojciechowski, K.W. Selective enhancement of auxeticity through changing a diameter of nanochannels in Yukawa systems. Smart Mater. Struct. 2018, 27, 115021. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Pigłowski, P.M.; Narojczyk, J.W.; Bilski, M.; Wojciechowski, K.W. High Partial Auxeticity Induced by Nanochannels in [111]-Direction in a Simple Model with Yukawa Interactions. Materials 2018, 11, 2550. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W. Poisson’s Ratio of the f.c.c. Hard Sphere Crystals with Periodically Stacked (001)-Nanolayers of Hard Spheres of Another Diameter. Materials 2019, 12, 700. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V.; Smardzewski, J.; Scarpa, F.; Piglowski, P.M.; Kowalik, M.; Imre, A.R.; Bilski, M. Auxetic Properties of a f.c.c. Crystal of Hard Spheres with an Array of [001]-Nanochannels Filled by Hard Spheres of Another Diameter (Phys. Status Solidi B 1/2019). Phys. Status Solidi B 2019, 256, 1970012. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Smardzewski, J.; Imre, A.R.; Grima, J.N.; Bilski, M. Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter. Materials 2021, 14, 3008. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Bilski, M.; Grima, J.N.; Kędziora, P.; Morozow, D.; Rucki, M.; Wojciechowski, K.W. Removing Auxetic Properties in f.c.c. Hard Sphere Crystals by Orthogonal Nanochannels with Hard Spheres of Another Diameter. Materials 2022, 15, 1134. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Tretiakov, K.V.; Wojciechowski, K.W. Poisson’s Ratio of f.c.c. Hard-Sphere Crystals with Cubic Supercells Containing Four Nanochannels Filled by Hard Spheres of Another Diameter. Phys. Status Solidi B 2022, 259, 2200464. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Pigłowski, P.M.; Wojciechowski, K.W. Auxeticity modifications and unit cell doubling in Yukawa fcc crystals with [001]-nanochannels filled by hard spheres. Smart Mater. Struct. 2023, 32, 025008. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Negative Poisson’s ratio for cubic crystals and nano/microtubes. Phys. Mesomech. 2014, 17, 97–115. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Negative Poisson’s ratio for six-constant tetragonal nano/microtubes. Phys. Status Solidi B 2015, 252, 1580–1586. [Google Scholar] [CrossRef]
- Bryukhanov, I.A.; Gorodtsov, V.A.; Lisovenko, D.S. Chiral Fe nanotubes with both negative Poisson’s ratio and Poynting’s effect. Atomistic simulation. J. Phys. Condens. Matter 2019, 31, 475304. [Google Scholar] [CrossRef] [PubMed]
- Bryukhanov, I.A.; Volkov, M.A.; Gorodtsov, V.A.; Lisovenko, D.S. Elastic Properties of Chiral Metallic Nanotubes Formed from Cubic Crystals. Phys. Mesomech. 2021, 24, 464–474. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Two-layer tubes from cubic crystals. Dokl. Phys. 2016, 61, 604–610. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Longitudinal elastic tension of two-layered plates from isotropic auxetics-nonauxetics and cubic crystals. Eur. J. Mech. A. Solids 2017, 63, 122–127. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Thin Homogeneous Two-Layered Plates of Cubic Crystals with Different Layer Orientation. Phys. Mesomech. 2019, 22, 261–268. [Google Scholar] [CrossRef]
- Volkov, M.A.; Gorodtsov, V.A.; Fadeev, E.P.; Lisovenko, D.S. Stretching of chiral tubes obtained by rolling-up plates of cubic crystals with various orientations. J. Mech. Mater. Struct. 2021, 16, 139–157. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S. Tension of thin two-layered plates of hexagonal crystals. Compos. Struct. 2019, 209, 453–459. [Google Scholar] [CrossRef]
- Nelson, D.F. (Ed.) Second and Higher Order Elastic Constants. In Landolt-Börnstein—Group III Condensed Matter; Springer: Berlin/Heidelberg, Germany, 1992; Volume 29a. [Google Scholar] [CrossRef]



| Material | |||
|---|---|---|---|
| Ba2Si2TiO8, sE | 136 | 0.26 | −0.32 |
| CsH2AsO4 | 51.5 | 0.01 | 0.03 |
| CsNiF3 | 34.4 | 0.45 | 0.06 |
| CoF2 | 50.3 | 0.64 | 0.15 |
| CoPt | 175 | 0.43 | 0.32 |
| In-17 at% Pb | 20.4 | 0.33 | 0.45 |
| In-10 at% Tl | 4.46 | 0.43 | 0.53 |
| In-15 at% Tl | 3.76 | 0.50 | 0.46 |
| FeGe2 | 209 | −0.04 | 0.39 |
| LuAsO4 | 244 | −0.02 | 0.32 |
| HgI2 | 24.4 | −0.11 | 0.80 |
| Hg2I2 | 1.85 | 0.88 | 0.03 |
| PdPb2 | 677 | 0.38 | 0.35 |
| RbH2AsO4 | 43.9 | −0.37 | 0.08 |
| Sn | 23.6 | 0.76 | 0.10 |
| TiO2 | 147 | 0.59 | 0.13 |
| WSi2 | 403 | 0.25 | 0.11 |
| ZrSiO4 | 377 | 0.07 | 0.28 |
| Zr2Ni | 46.3 | 0.76 | 0.15 |
| Tube | , GPa | , GPa | |||
|---|---|---|---|---|---|
| Sn–RbH2AsO4 | 1.11 | 51.5 | 1.17 | 50.9 | 1.16 |
| CoPt–FeGe2 | 1.11 | 206 | 0.98 | 205 | 0.98 |
| PdPb2–Sn | 1.11 | 337 | 0.50 | 354 | 0.52 |
| LuAsO4–Hg2I2 | 1.11 | 120 | 0.49 | 126 | 0.52 |
| Sn–RbH2AsO4 | 2 | 51.9 | 1.18 | 49.0 | 1.12 |
| Hg2I2–RbH2AsO4 | 2 | 34.2 | 0.78 | 29.8 | 0.68 |
| RbH2AsO4–Hg2I2 | 2 | 22.6 | 0.52 | 27.3 | 0.62 |
| LuAsO4–RbH2AsO4 | 2 | 125 | 0.51 | 149 | 0.61 |
| FeGe2–LuAsO4 | 2 | 233 | 0.95 | 228 | 0.93 |
| Sn–RbH2AsO4 | 10 | 51.7 | 1.18 | 48.0 | 1.09 |
| CsNiF3–RbH2AsO4 | 10 | 48.6 | 1.11 | 46.5 | 1.06 |
| In–15 at% Tl-Hg2I2 | 10 | 3.76 | 1.00 | 3.61 | 0.96 |
| LuAsO4–FeGe2 | 10 | 224 | 0.91 | 233 | 0.95 |
| Sn–FeGe2 | 10 | 168 | 0.80 | 129 | 0.62 |
| PdPb2–In-15 at% Tl | 10 | 189 | 0.28 | 340 | 0.50 |
| Tube | ||||
|---|---|---|---|---|
| RbH2AsO4–Zr2Ni | 68.5 | 1.48 | 1.34 | 1.18 |
| Zr2Ni–RbH2AsO4 | 67.9 | 1.47 | 1.01 | 1.01 |
| HgI2–Sn | 31.0 | 1.27 | 1.15 | 1.09 |
| Sn–HgI2 | 31.0 | 1.27 | 1.01 | 1.02 |
| RbH2AsO4–CoF2 | 63.6 | 1.26 | 1.25 | 1.19 |
| CoF2–RbH2AsO4 | 63.3 | 1.26 | 1.01 | 1.01 |
| HgI2–Zr2Ni | 49.5 | 1.07 | 1.84 | 2 |
| Zr2Ni–HgI2 | 47.5 | 1.03 | 2 | 1.01 |
| PdPb2–WSi2 | 670 | 0.99 | 2 | 1.01 |
| TiO2–In-17 at% Pb | 146 | 0.99 | 2 | 1.01 |
| RbH2AsO4–Hg2I2 | 43.3 | 0.99 | 2 | 1.01 |
| WSi2–FeGe2 | 399 | 0.99 | 2 | 1.01 |
| ZrSiO4–CoPt | 373 | 0.99 | 2 | 1.01 |
| ZrSiO4–TiO2 | 373 | 0.99 | 2 | 1.01 |
| LuAsO4–Zr2Ni | 242 | 0.99 | 2 | 1.01 |
| FeGe2–CoF2 | 207 | 0.99 | 2 | 1.01 |
| WSi2–CoPt | 398 | 0.99 | 2 | 1.01 |
| PdPb2–Hg2I2 | 659 | 0.97 | 2 | 1.01 |
| PdPb2–In-15 at% Tl | 659 | 0.97 | 2 | 1.01 |
| Tube | ||||
|---|---|---|---|---|
| In-15 at% Tl-RbH2AsO4 | 2 | 2 | 0.5 | |
| In-15 at% Tl–LuAsO4 | 2 | 2 | 0.5 | |
| In-15 at% Tl–FeGe2 | 2 | 2 | 0.5 | |
| HgI2–LuAsO4 | 2 | 2 | 0.5 | |
| FeGe2–RbH2AsO4 | 1.01 | 2 | 1.0 | |
| WSi2–RbH2AsO4 | 1.01 | 2 | 1.0 | |
| HgI2–Sn | 2 | 1.01 | 0.5 | |
| FeGe2–LuAsO4 | 1.55 | 2 | 0.65 | |
| Sn–LuAsO4 | 1.49 | 2 | 0.67 | |
| CoF2–LuAsO4 | 1.34 | 2 | 0.75 | |
| FeGe2–Hg2I2 | 2 | 1.01 | 0.5 | |
| CoF2–ZrSiO4 | 1.62 | 2 | 0.62 | |
| Zr2Ni–CsH2AsO4 | 0.02 | 1.01 | 2 | 1.45 |
| CoPt–CsH2AsO4 | 0.03 | 1.01 | 2 | 1.55 |
| CsH2AsO4–Zr2Ni | 0.04 | 2 | 1.01 | 0.61 |
| CsH2AsO4–WSi2 | 0.04 | 2 | 1.01 | 0.68 |
| Tube | ||||
|---|---|---|---|---|
| PdPb2–FeGe2 | 2 | 2 | 1 | |
| TiO2–FeGe2 | 2 | 2 | 1 | |
| CoPt–FeGe2 | 2 | 2 | 1 | |
| CoF2–RbH2AsO4 | 2 | 2 | 1 | |
| TiO2–CsH2AsO4 | 1.76 | 2 | 1 | |
| Zr2Ni–HgI2 | 1.90 | 2 | 1 | |
| Sn–HgI2 | 2 | 2 | 1 | |
| RbH2AsO4–TiO2 | 0.01 | 1.28 | 2 | 1 |
| RbH2AsO4–HgI2 | 0.02 | 2 | 2 | 0.78 |
| RbH2AsO4–CsH2AsO4 | 0.03 | 1.01 | 2 | 1.68 |
| TiO2–WSi2 | 0.06 | 1.94 | 1.77 | 1 |
| CoF2–WSi2 | 0.07 | 1.30 | 1.01 | 1 |
| HgI2–FeGe2 | 0.13 | 2 | 2 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volkov, M.A.; Gorodtsov, V.A.; Lisovenko, D.S. Variability of Elastic Properties of Two-Layered Tubes from Six-Constant Tetragonal Crystals. Symmetry 2023, 15, 685. https://doi.org/10.3390/sym15030685
Volkov MA, Gorodtsov VA, Lisovenko DS. Variability of Elastic Properties of Two-Layered Tubes from Six-Constant Tetragonal Crystals. Symmetry. 2023; 15(3):685. https://doi.org/10.3390/sym15030685
Chicago/Turabian StyleVolkov, Mikhail A., Valentin A. Gorodtsov, and Dmitry S. Lisovenko. 2023. "Variability of Elastic Properties of Two-Layered Tubes from Six-Constant Tetragonal Crystals" Symmetry 15, no. 3: 685. https://doi.org/10.3390/sym15030685
APA StyleVolkov, M. A., Gorodtsov, V. A., & Lisovenko, D. S. (2023). Variability of Elastic Properties of Two-Layered Tubes from Six-Constant Tetragonal Crystals. Symmetry, 15(3), 685. https://doi.org/10.3390/sym15030685







