Numerical Simulation of the Effects of Reduced Gravity, Radiation and Magnetic Field on Heat Transfer Past a Solid Sphere Using Finite Difference Method
Abstract
1. Introduction
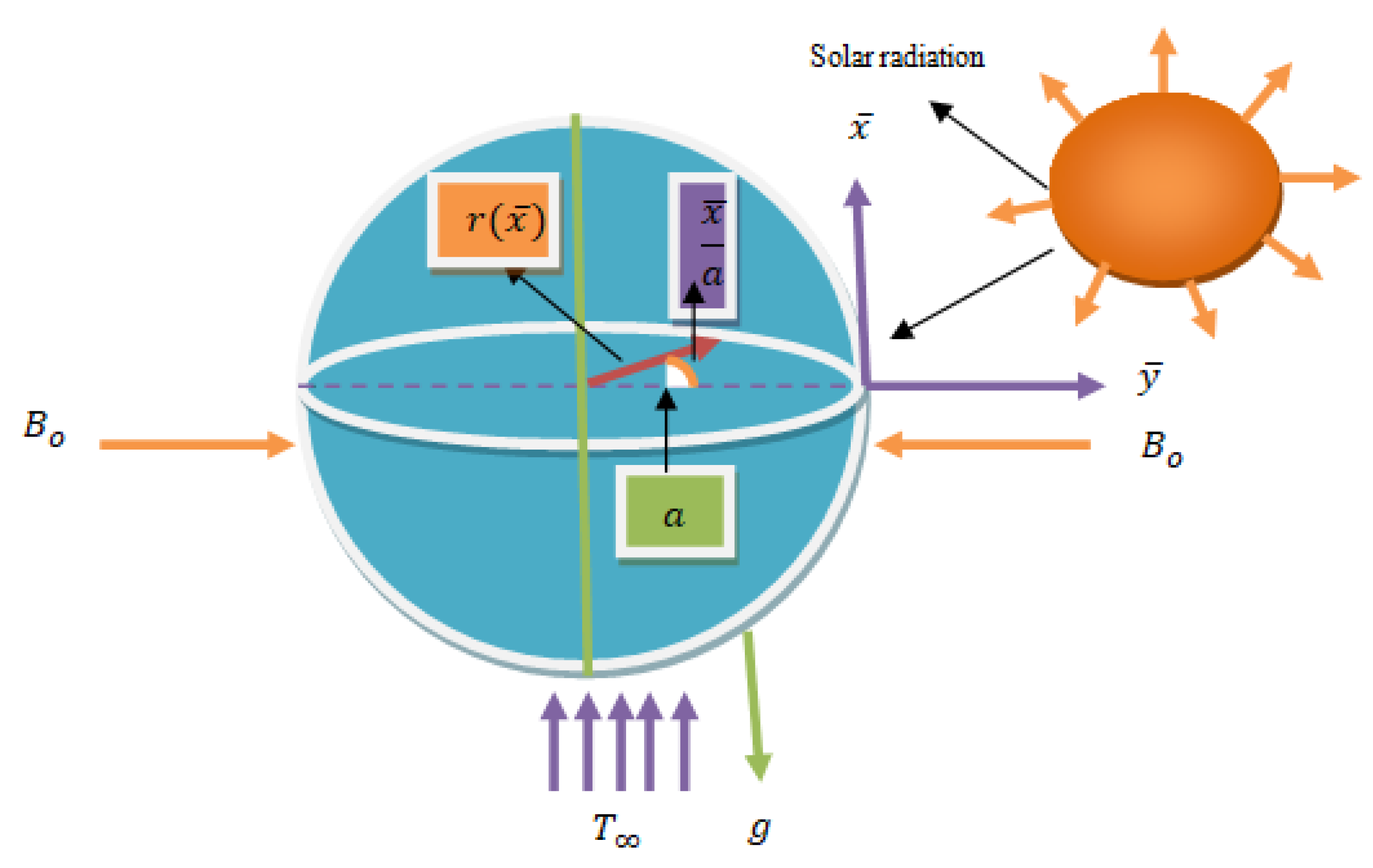
2. Problem Analysis
3. Dimensionless Variables
4. Solution Methodology
Method of Solution
5. Grid Independency Test and Numerical Model Verification
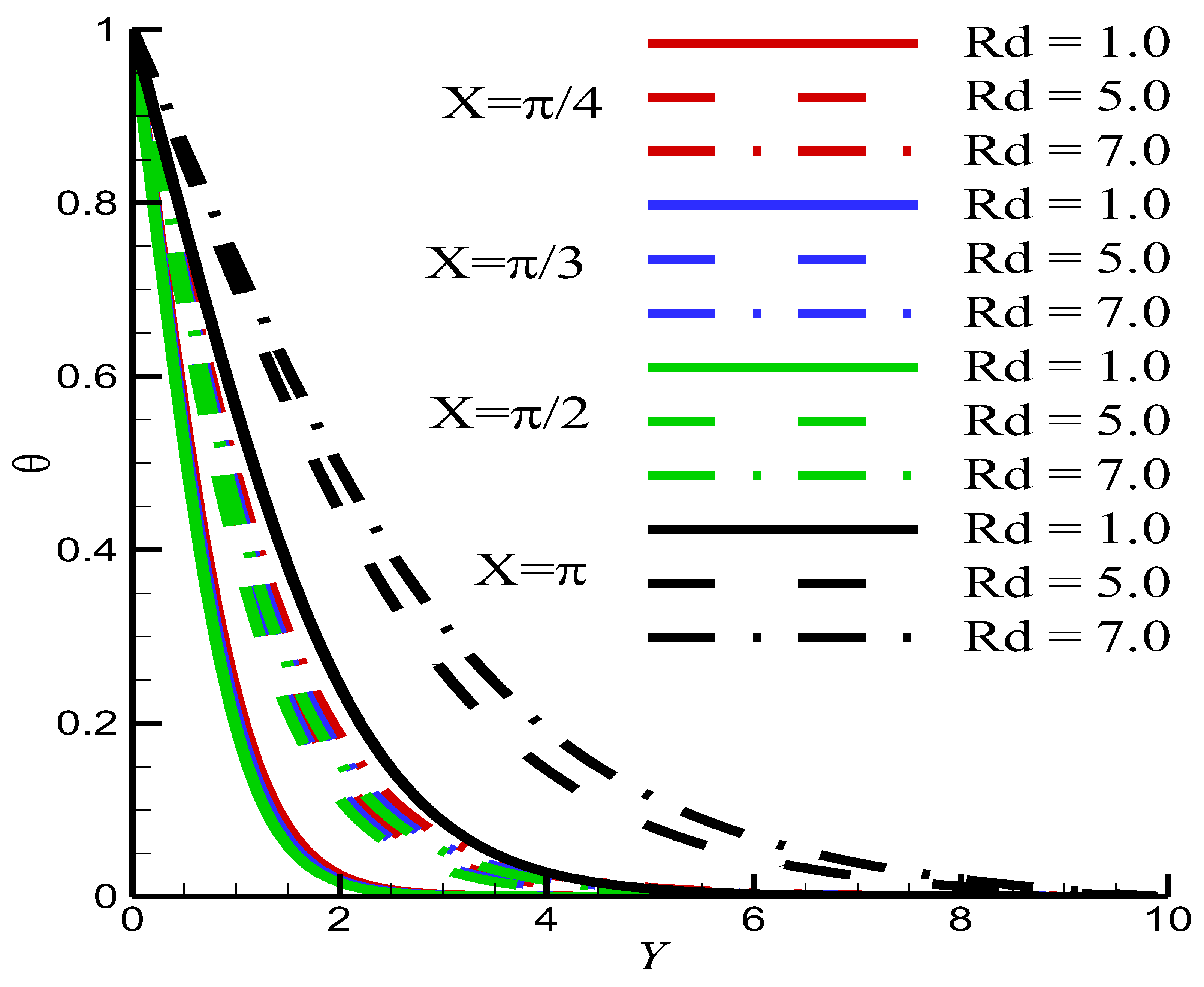
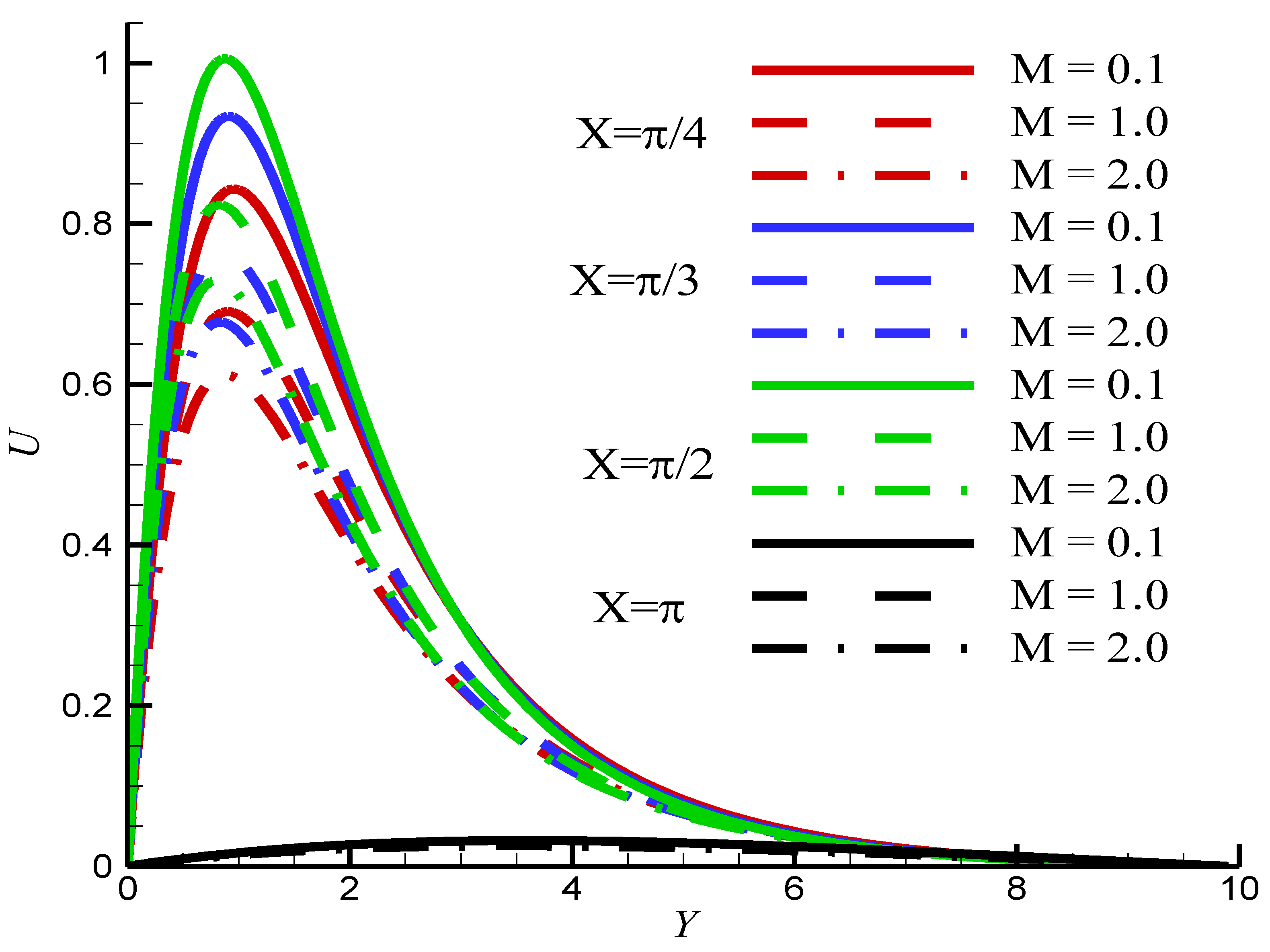
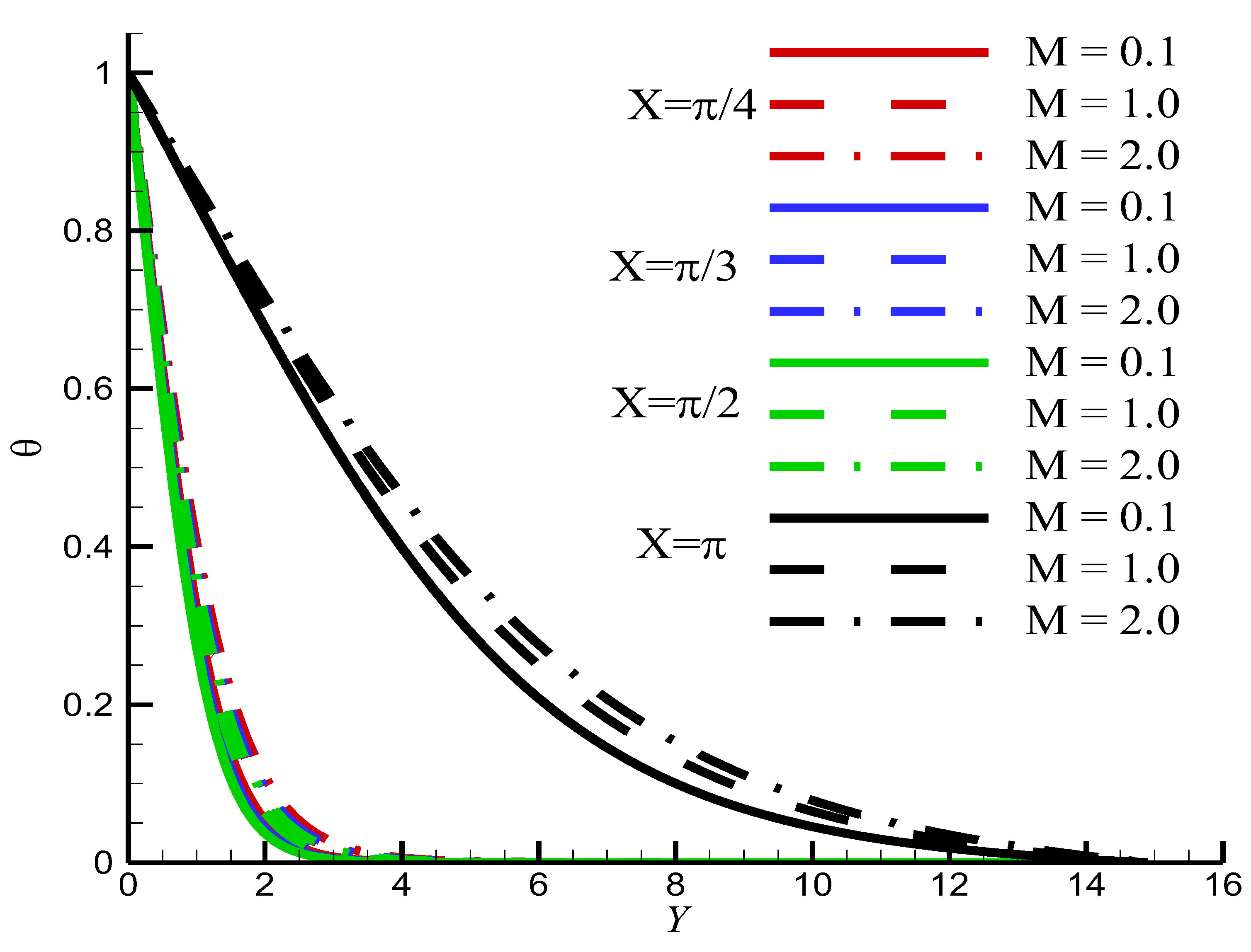
6. Results and Discussion
7. Conclusions
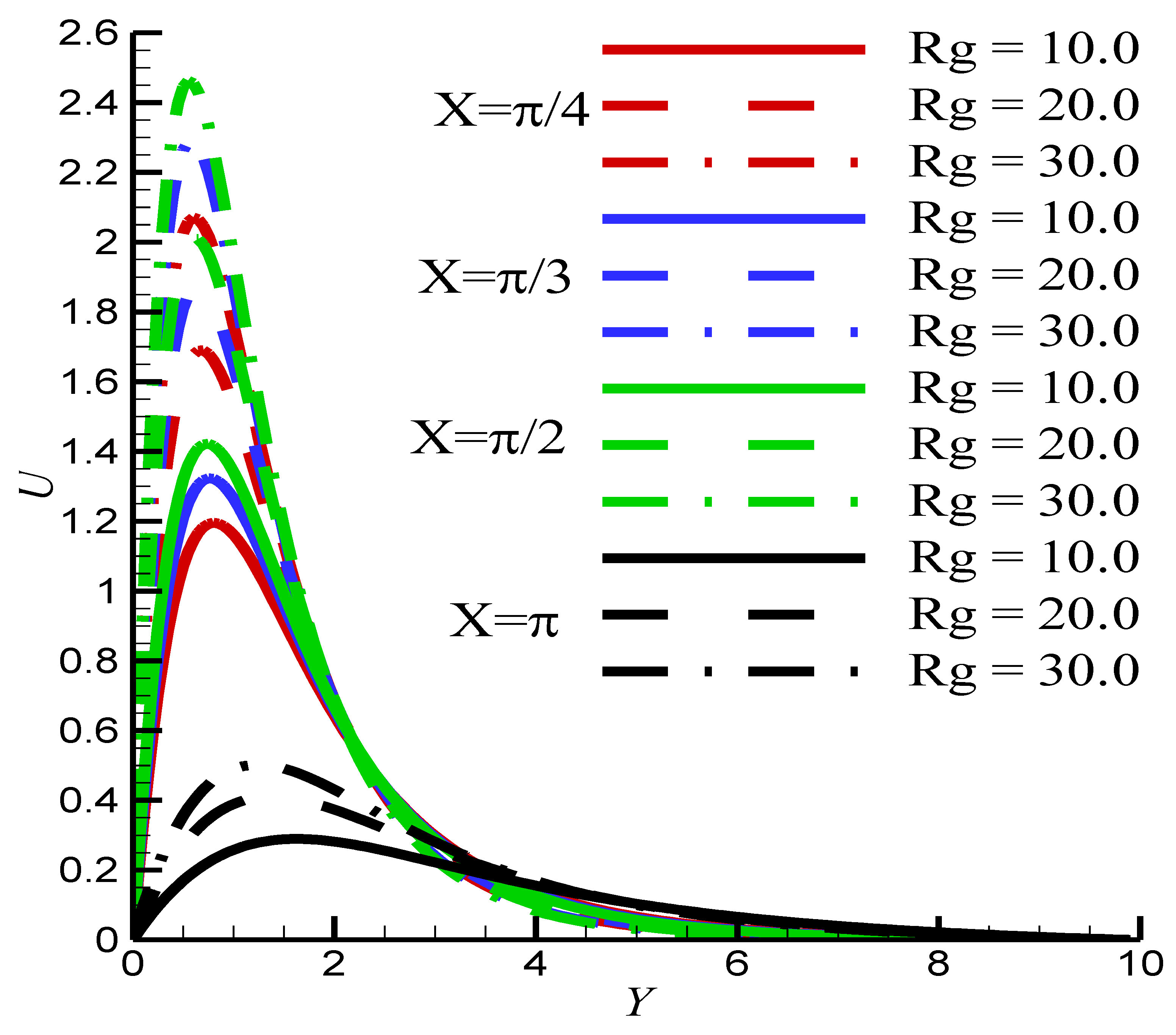
- When is increased, the velocity increases, and the temperature decreases due the enhancement of the buoyancy force.
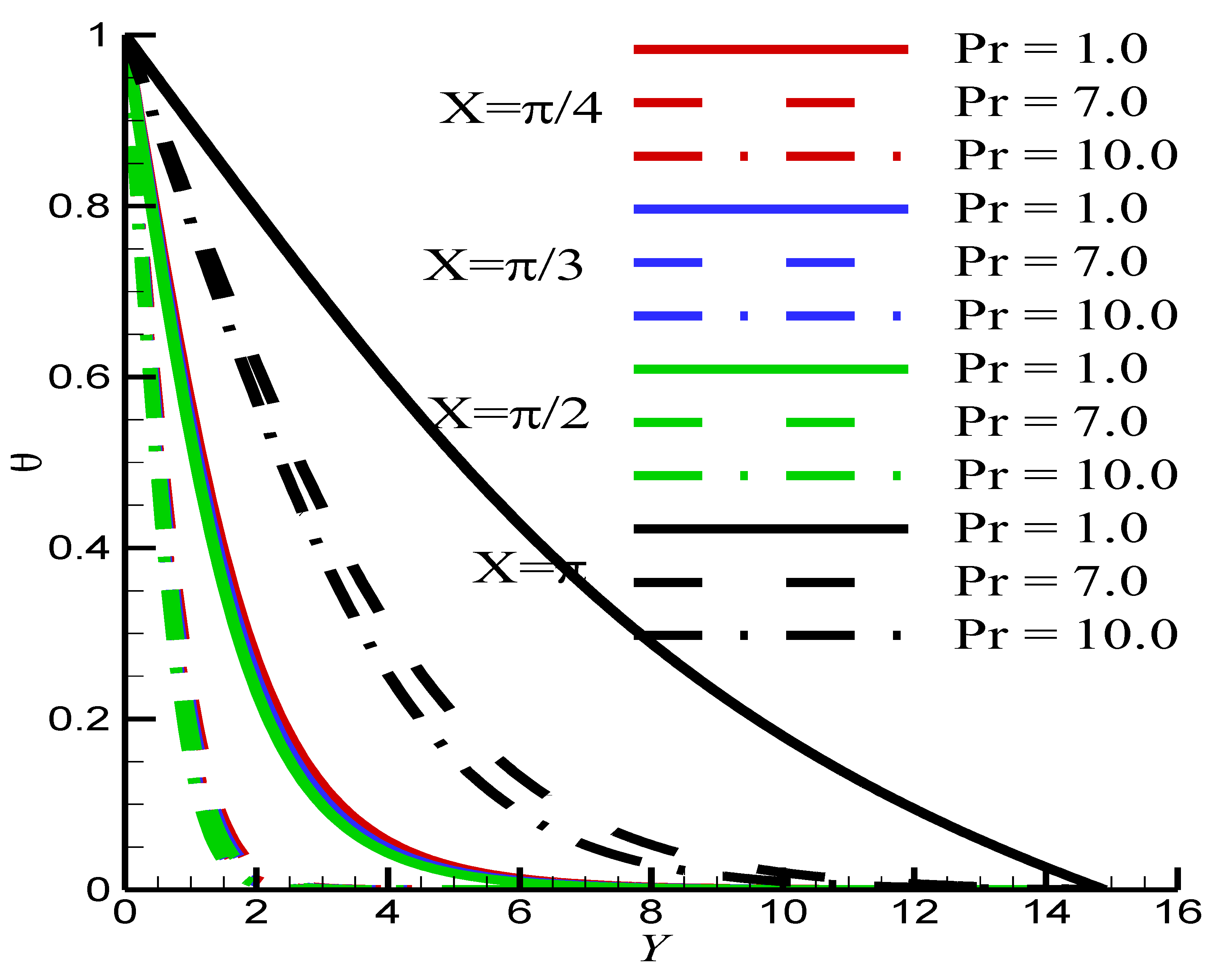
- The increase of Pr leads to the decrease of the velocity and temperature of the fluid, due to the increase of the viscosity.
- The application of an external magnetic field causes the reduction of the flow intensity and an augmentation of the temperature.
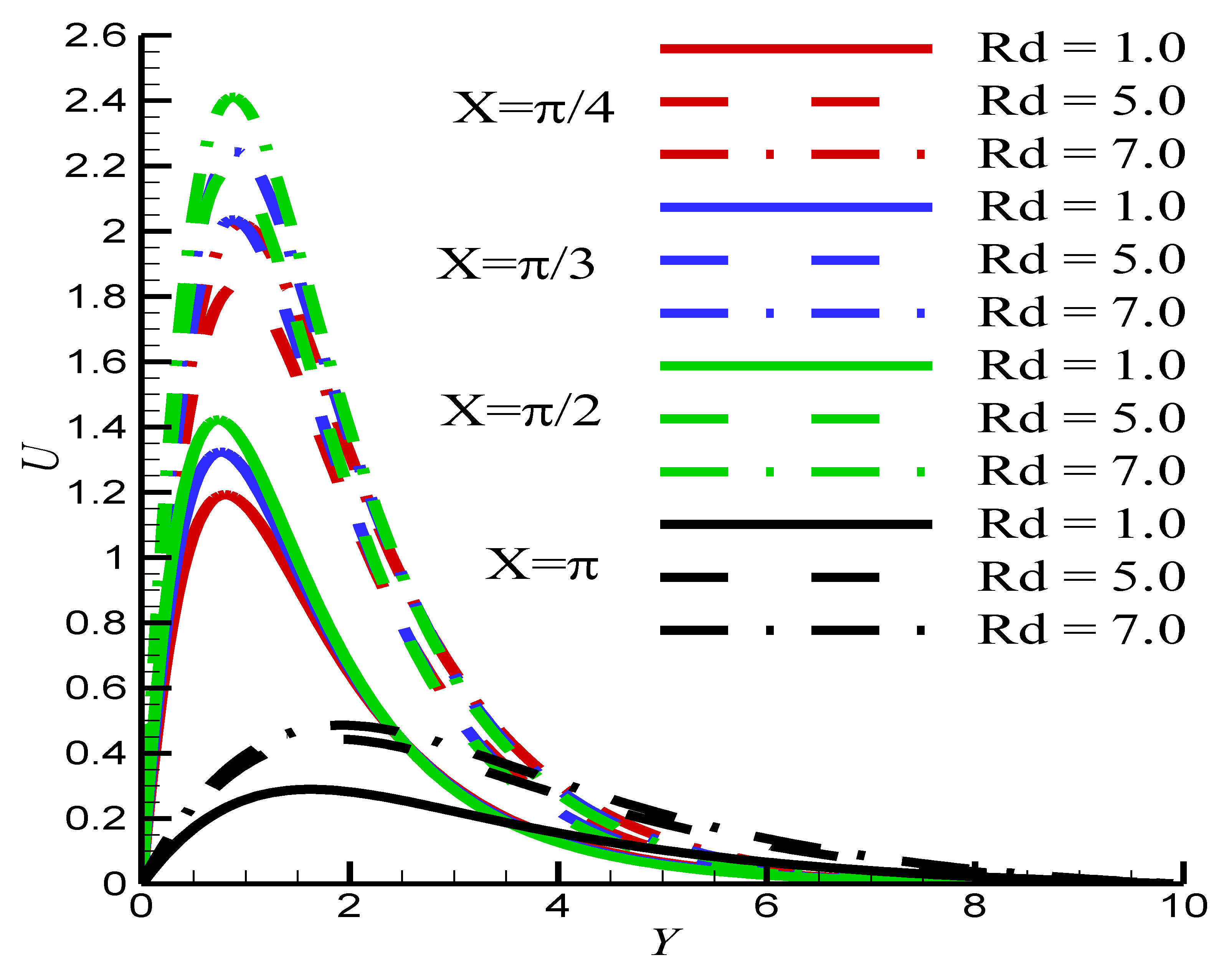
- The increase in cause an increase of the temperature and a reduction of the velocity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Potter, J.M.; Riley, N. Free convection from a heated sphere at large Grashof number. J. Fluid Mech. 1980, 100, 769–783. [Google Scholar] [CrossRef]
- Riley, N. The heat transfer from a sphere in free convective flow. Comput. Fluids 1986, 14, 225–237. [Google Scholar] [CrossRef]
- Kay, A.; Kuiken, H.K.; Merkin, J.H. Boundary-layer analysis of the thermal bar. J. Fluid Mech. 1995, 303, 253–278. [Google Scholar] [CrossRef]
- Ashraf, M.; Fatima, A.; Gorla, R.S.R. Periodic momentum and thermal boundary layer mixed convection flow around the surface of a sphere in the presence of viscous dissipation. Can. J. Phys. 2017, 95, 976–986. [Google Scholar] [CrossRef]
- Ashraf, M.; Fatima, A. Numerical simulation of the effect of transient shear stress and the rate of heat transfer around different positions of sphere in the presence of viscous dissipation. J. Heat Transf. 2018, 140, 701–702. [Google Scholar] [CrossRef]
- Ashraf, M.; Khan, A.; Gorla, R.S.R. Natural convection boundary layer flow of nanofluids around different stations of the sphere and into the plume above the sphere. Heat Transf. Asian Res. 2019, 48, 1127–1148. [Google Scholar] [CrossRef]
- Abbas, A.; Ashraf, M.; Chu, Y.; Zia, S.; Khan, I.; Nisar, K.S. Computational Study of the Coupled Mechanism of Thermophoretic Transportation and Mixed Convection Flow around the Surface of a Sphere. Molecules 2020, 25, 2694. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.; Muhammad, A. Combined effects of variable viscosity and thermophoretic transportation on mixed convection flow around the surface of a sphere. Therm. Sci. 2020, 24, 4089–4101. [Google Scholar] [CrossRef]
- Ashraf, M.; Abbas, A.; Ali, A.; Shah, Z.; Alrabaiah, H.; Bonyah, E. Numerical simulation of the combined effects of thermophoretic motion and variable thermal conductivity on free convection heat transfer. AIP Adv. 2020, 10, 085005. [Google Scholar] [CrossRef]
- Abbas, A.; Ashraf, M.; Chamkha, A.J. Combined effects of thermal radiation and thermophoretic motion on mixed convection boundary layer flow. Alex. Eng. J. 2021, 60, 3243–3252. [Google Scholar] [CrossRef]
- Ashraf, M.; Abbas, A.; Zia, S.; Chu, Y.M.; Khan, I.; Nisar, K.S. Computational analysis of the effect of nano particle material motion on mixed convection flow in the presence of heat generation and absorption. CMC Comput. Mater. Contin. 2020, 65, 1809–1823. [Google Scholar] [CrossRef]
- Ashraf, M.; Abbas, A.; Oztop, H.F.; Nisar, K.S.; Khan, I. Computations of mixed convection slip flow around the surface of a sphere: Effects of thermophoretic transportation and viscous dissipation. Heat Transf. 2021, 50, 7349–7362. [Google Scholar] [CrossRef]
- Ahmad, U.; Ashraf, M.; Abbas, A.; Rashad, A.M.; Nabwey, H.A. Mixed convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. Sci. Rep. 2021, 11, 12907. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.; Ijaz, I.; Ashraf, M.; Ahmad, H. Combined effects of variable density and thermal radiation on MHD Sakiadis flow. Case Stud. Therm. Eng. 2021, 28, 101640. [Google Scholar] [CrossRef]
- Rashad, A.M.; Chamkha, A.J.; Modather, M. Mixed convection boundary-layer flow past a horizontal circular cylinder embedded in a porous medium filled with a nanofluid under convective boundary conditions. Comput. Fluids 2013, 86, 380–388. [Google Scholar] [CrossRef]
- Khan, A.; Ashraf, M.; Rashad, A.M.; Nabwey, H.A. Impact of Heat Generation on Magneto Nanofluid Free Convection Flow About Sphere In The Plume Region. Mathematics 2020, 8, 2010. [Google Scholar] [CrossRef]
- Bulinda, V.M.; Kang’ethe, G.P.; Kiogora, P.R. Magnetohydrodynamics Free Convection Flow of Incompressible Fluids over Corrugated Vibrating Bottom Surface with Hall Currents and Heat and Mass Transfers. J. Appl. Math. 2020, 2020, 2589760. [Google Scholar] [CrossRef]
- Molla, M.M.; Rahman, A.; Rahman, L.T. Natural convection flow from an isothermal sphere with temperature dependent thermal conductivity. J. Nav. Archit. Mar. Eng. 2005, 2, 53–64. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. MHD natural convection of Sodium Alginate Casson nanofluid over a solid sphere. Results Phys. 2020, 16, 102818. [Google Scholar] [CrossRef]
- Jenifer, A.S.; Saikrishnan, P.; Lewis, R.W. Unsteady MHD Mixed Convection Flow of Water over a Sphere with Mass Transfer. J. Appl. Comput. Mech. 2021, 7, 935–943. [Google Scholar]
- Ahmad, U.; Ashraf, M.; Al-Zubaidi, A.; Ali, A.; Saleem, S. Effects of temperature dependent viscosity and thermal conductivity on natural convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. PLoS ONE 2021, 16, e0252485. [Google Scholar] [CrossRef]
- Salleh, M.Z.; Nazar, R.; Pop, I. Mixed convection boundary layer flow about a solid sphere with Newtonian heating. Arch. Mech. 2010, 62, 283–303. [Google Scholar]
- Molla, M.; Hossain, A. Effects of chemical reaction, heat and mass diffusion in natural convection flow from an isothermal sphere with temperature dependent viscosity. Eng. Comput. 2006, 23, 840–857. [Google Scholar] [CrossRef]
- Chamkha, A. Non-Darcy natural convection of a nanofluid about a permeable vertical cone embedded in a porous medium. Int. J. Microscale Nanoscale Therm. 2012, 4, 99–114. [Google Scholar]
- Chamkha, A.J.; Aly, A.M.; Raizah, Z.A.S. Double-Diffusion MHD free convective flow along a sphere in the presence of a homogeneous chemical reaction and Soret and Dufour effects. Appl. Comput. Math. 2017, 6, 34. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Gregg, J.L. Details of Exact Low Prandtl Number Boundary-Layer Solutions for Forced and for Free Convection; No. NASA-MEMO-2-27-59E; NASA: Washington, DC, USA, 1959. [Google Scholar]
- Zhang, L.; Zhang, X.; Peng, S.; Yan, Z.; Liang, Y.; Yan, B.; Li, Q. Thermal-mechanical coupling propagation and transient thermal fracture in multilayer coatings. Heat Transf. Res. 2017, 48, 935–954. [Google Scholar] [CrossRef]
- Liu, L.; Li, Q.; Ju, F.; Dong, X.; Yu, X. Numerical simulation and analysis of the vertical and double pipe soil-air heat exchanger. Therm. Sci. 2019, 23, 3905–3916. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Ahmed, S.; Shah, M.A. Analysis of bio-convective MHD Blasius and Sakiadis flow with Cattaneo-Christov heat flux model and chemical reaction. Chin. J. Phys. 2022, 77, 1963–1975. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Iqbal, T.; Zulqarnain, R.M.; Javid, M. A comparative study of unsteady MHD Falkner–Skan wedge flow for non-Newtonian nanofluids considering thermal radiation and activation energy. Chin. J. Phys. 2022, 77, 1625–1638. [Google Scholar] [CrossRef]
- Ali, L.; Wang, Y.; Ali, B.; Liu, X.; Din, A.; Al Mdallal, Q. The function of nanoparticle’s diameter and Darcy-Forchheimer flow over a cylinder with effect of magnetic field and thermal radiation. Case Stud. Therm. Eng. 2021, 28, 101392. [Google Scholar] [CrossRef]
- Abbas, A.; Ahmad, H.; Mumtaz, M.; Ilyas, A.; Hussan, M. MHD dissipative micropolar fluid flow past stretching sheet with heat generation and slip effects. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Abbas, A.; Jeelani, M.B.; Alnahdi, A.S.; Ilyas, A. MHD Williamson Nanofluid Fluid Flow and Heat Transfer Past a Non-Linear Stretching Sheet Implanted in a Porous Medium: Effects of Heat Generation and Viscous Dissipation. Processes 2022, 10, 1221. [Google Scholar] [CrossRef]
- Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Significance of Chemical Reaction and Lorentz Force on Third-Grade Fluid Flow and Heat Transfer with Darcy–Forchheimer Law over an Inclined Exponentially Stretching Sheet Embedded in a Porous Medium. Symmetry 2022, 14, 779. [Google Scholar] [CrossRef]
- Abbas, A.; Jeelani, M.B.; Alharthi, N.H. Darcy–Forchheimer Relation Influence on MHD Dissipative Third-Grade Fluid Flow and Heat Transfer in Porous Medium with Joule Heating Effects: A Numerical Approach. Processes 2022, 10, 906. [Google Scholar] [CrossRef]
- Abbas, A.; Noreen, A.; Ali, M.A.; Ashraf, M.; Alzahrani, E.; Marzouki, R.; Goodarzi, M. Solar radiation over a roof in the presence of temperature-dependent thermal conductivity of a Casson flow for energy saving in buildings. Sustain. Energy Technol. Assess. 2022, 53, 102606. [Google Scholar] [CrossRef]
- Abbas, A.; Jeelani, M.B.; Alharthi, N.H. Magnetohydrodynamic Effects on Third-Grade Fluid Flow and Heat Transfer with Darcy–Forchheimer Law over an Inclined Exponentially Stretching Sheet Embedded in a Porous Medium. Magnetochemistry 2022, 8, 61. [Google Scholar] [CrossRef]
- Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Convective Heat and Mass Transfer in Third-Grade Fluid with Darcy–Forchheimer Relation in the Presence of Thermal-Diffusion and Diffusion-Thermo Effects over an Exponentially Inclined Stretching Sheet Surrounded by a Porous Medium: A CFD Study. Processes 2022, 10, 776. [Google Scholar] [CrossRef]
- Ashraf, M.; Ilyas, A.; Ullah, Z.; Abbas, A. Periodic magnetohydrodynamic mixed convection flow along a cone embedded in a porous medium with variable surface temperature. Ann. Nucl. Energy 2022, 175, 109218. [Google Scholar] [CrossRef]
- Ullah, Z.; Bilal, M.; Sarris, I.E.; Hussanan, A. MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis. Symmetry 2022, 14, 2421. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Shahid, A.; Sarris, I.E.; Bég, O.A. Spectral relaxation computation of Maxwell fluid flow from a stretching surface with quadratic convection and non-Fourier heat flux using Lie symmetry transformations. Int. J. Mod. Phys. B 2022, 37, 2350082. [Google Scholar] [CrossRef]
- Maranna, T.; Sneha, K.N.; Mahabaleshwar, U.S.; Sarris, I.E.; Karakasidis, T.E. An Effect of Radiation and MHD Newtonian Fluid over a Stretching/Shrinking Sheet with CNTs and Mass Transpiration. Appl. Sci. 2022, 12, 5466. [Google Scholar] [CrossRef]
- Punith Gowda, R.J.; Sarris, I.E.; Naveen Kumar, R.; Kumar, R.; Prasannakumara, B.C. A Three-Dimensional Non-Newtonian Magnetic Fluid Flow Induced Due to Stretching of the Flat Surface with Chemical Reaction. J. Heat Transf. 2022, 144, 113602. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Sarris, I.E.; Karakasidis, T.E. The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Appl. Sci. 2022, 12, 5081. [Google Scholar] [CrossRef]


| No. of Grid Points | ||
|---|---|---|
| 25.0 | 2.01299 | 0.79793 |
| 50.0 | 2.12478 | 0.77268 |
| 100.0 | 2.15249 | 0.76919 |
| 200.0 | 2.15950 | 0.76891 |
| 250.0 | 2.16036 | 0.76892 |
| 500.0 | 2.16150 | 0.76894 |
| Sparrow & Gregg [26] | Present | |
|---|---|---|
| 0.03 | 0.93841 | 0.93740 |
| 0.02 | 0.95896 | 0.95870 |
| 0.008 | 0.99550 | 0.99400 |
| = 0.1 | = 1.0 | = 5.0 | = 10.0 | = 0.1 | = 1.0 | = 5.0 | = 10.0 | |
| 0.10860 | 0.64508 | 2.16368 | 3.63897 | 0.16210 | 0.28475 | 0.42706 | 0.50809 | |
| 0.14868 | 0.86768 | 2.90589 | 4.886676 | 0.17741 | 0.31446 | 0.47131 | 0.56063 | |
| 0.19412 | 1.12016 | 3.74840 | 6.30307 | 0.19241 | 0.34257 | 0.51314 | 0.61033 | |
| 0.00013 | 0.00135 | 0.00701 | 0.01477 | 0.10090 | 0.09991 | 0.09515 | 0.08816 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.; Ashraf, M.; Sarris, I.E.; Ghachem, K.; Labidi, T.; Kolsi, L.; Ahmad, H. Numerical Simulation of the Effects of Reduced Gravity, Radiation and Magnetic Field on Heat Transfer Past a Solid Sphere Using Finite Difference Method. Symmetry 2023, 15, 772. https://doi.org/10.3390/sym15030772
Abbas A, Ashraf M, Sarris IE, Ghachem K, Labidi T, Kolsi L, Ahmad H. Numerical Simulation of the Effects of Reduced Gravity, Radiation and Magnetic Field on Heat Transfer Past a Solid Sphere Using Finite Difference Method. Symmetry. 2023; 15(3):772. https://doi.org/10.3390/sym15030772
Chicago/Turabian StyleAbbas, Amir, Muhammad Ashraf, Ioannis E. Sarris, Kaouther Ghachem, Taher Labidi, Lioua Kolsi, and Hafeez Ahmad. 2023. "Numerical Simulation of the Effects of Reduced Gravity, Radiation and Magnetic Field on Heat Transfer Past a Solid Sphere Using Finite Difference Method" Symmetry 15, no. 3: 772. https://doi.org/10.3390/sym15030772
APA StyleAbbas, A., Ashraf, M., Sarris, I. E., Ghachem, K., Labidi, T., Kolsi, L., & Ahmad, H. (2023). Numerical Simulation of the Effects of Reduced Gravity, Radiation and Magnetic Field on Heat Transfer Past a Solid Sphere Using Finite Difference Method. Symmetry, 15(3), 772. https://doi.org/10.3390/sym15030772










