Application of Fixed-Point Results to Integral Equation through F-Khan Contraction

Abstract

In this article, we establish fixed point results by defining the concept of $\mathbf{F}$-Khan contraction of an orthogonal set by modifying the symmetry of usual contractive conditions. We also provide illustrative examples to support our results. The derived results have been applied to find analytical solutions to integral equations. The analytical solutions are verified with numerical simulation.

1. Introduction

The French mathematician Fréchet [1] introduced the notion of metric space. The Banach contraction principle presents a constructive way of obtaining a unique solution for models containing various forms of differential and integral equations. Several researchers extend this notion in multiple directions (see [2,3,4,5], and references therein). In fact, several modifications of the Banach contraction principle were generated from contraction conditions involving rational expressions. Khan [3] created one of the most significant works in this field.

In recent years, Piri et al. [6] presented some fixed-point results of F-Khan-type self-mappings on complete metric spaces. Wardowski [7] gave a beautiful fixed point result in a different way to extend the Banach contraction theorem. He proposed a new contraction known as the $\mathbf{F}$-contraction and developed a fixed-point result as an extension of the Banach contraction principle in a method distinct from previously established results from the literature. For some recent works on $\mathbf{F}$-contraction, authors can refer to [8,9].

The concept of an orthogonal in metric spaces was introduced by Gordji et al. [10]. The fixed-point results in generalized OMSs (orthogonal metric spaces) were proven by many researchers; see [11,12,13,14,15,16,17,18,19,20]. In 2022, Aiman et al. [21] initiated orthogonality in Brianciari metric spaces and proved some fixed point results. In this paper, we introduce the new idea of an orthogonal $\mathbf{F}$-Khan contraction to prove fixed-point result in the setting of orthogonal complete metric spaces. The derived results are supplemented with suitable examples, and the result is applied to find an analytical solution to the integral equation. A comparison between the analytical and numerical solutions is also discussed.

The paper is organized as follows. In Section 2, we review some preliminary concepts including certain definitions and monographs which are very vital to this study. In Section 3, we present the main results and establish a fixed point result. In Section 4, the derived results have been applied to find analytical solutions to integral equations.

2. Preliminaries

The metric space concept was introduced by Fréchet [1] as follows:

Definition 1

([1]). Let $\mathbb{H}$ be a non-void set. A function $\mathsf{\Lambda }:\mathbb{H}\times \mathbb{H}\to {\mathbb{R}}^{+}$ is said to be a metric on $\mathbb{H}$, if for all $\kappa ,\tau ,\rho \in \mathbb{H}$, the following conditions hold:

(Λ₁)

$\mathsf{\Lambda }(\kappa ,\tau )\ge 0$ and $\mathsf{\Lambda }(\kappa ,\tau )=0$ if and only if $\kappa =\tau$,

(Λ₂)

$\mathsf{\Lambda }(\kappa ,\tau )=\mathsf{\Lambda }(\tau ,\kappa )$,

(Λ₃)

$\mathsf{\Lambda }(\kappa ,\tau )\le \mathsf{\Lambda }(\kappa ,\rho )+\mathsf{\Lambda }(\rho ,\tau )$.

Then, we say that $(\mathbb{H},\mathsf{\Lambda })$ is a metric space.

Definition 2

([7]). Let $(\mathbb{H},\mathsf{\Lambda })$ be a metric space. A mapping $\mathcal{S}:\mathbb{H}\to \mathbb{H}$ is called an $\mathbf{F}$-contraction on $(\mathbb{H},\mathsf{\Lambda })$, if there exists $\mathfrak{F}\in \mathbf{F}$ and $\mu \in (0,\infty )$ s.t.

$$\begin{array}{c}\hfill \forall \kappa ,\tau \in \mathbb{H},\left[\mathsf{\Lambda }\right(\mathcal{S}\kappa ,\mathcal{S}\tau )>0\Rightarrow \mu +\mathfrak{F}(\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau ))\le \mathfrak{F}(\mathsf{\Lambda }(\kappa ,\tau )\left)\right].\end{array}$$

Definition 3

([7]). Let ${\mathbf{F}}_{\mathfrak{k}}$ be the family of all increasing functions $\mathfrak{F}:(0,\infty )\to \mathbb{R}$; that is, for all $\kappa ,\tau \in (0,\infty )$, if $\kappa <\tau$, then $\mathfrak{F}\left(\kappa \right)<\mathfrak{F}\left(\tau \right)$.

Gordji et al. [10] proposed orthogonal sets and generalized Banach fixed point theorems in 2017. The results are as follows:

Definition 4

([10]). Let $\mathbb{H}$ be a non-void set and $\perp \subseteq \mathbb{H}\times \mathbb{H}$ be a binary relation. If ⊥ holds, we obtain the following axioms:

$$\begin{array}{c}\hfill \exists {\kappa }_0\in \mathbb{H}:(\forall \kappa \in \mathbb{H},\kappa \perp {\kappa }_0)or(\forall \kappa \in \mathbb{H},{\kappa }_0\perp \kappa ),\end{array}$$

then, $(\mathbb{H},\perp )$ is called an orthogonal set.

Definition 5

([10]). Let $(\mathbb{H},\perp )$ be an orthogonal set ($O_s$). A sequence $\left\{{\kappa }_{\vartheta }\right\}$ is called an orthogonal sequence if

$$\begin{array}{c}\hfill (\forall \vartheta \in \mathbb{N},{\kappa }_{\vartheta }\perp {\kappa }_{\vartheta +1})or(\forall \vartheta \in \mathbb{N},{\kappa }_{\vartheta +1}\perp {\kappa }_{\vartheta }).\end{array}$$

Definition 6

([10]). The triplet $(\mathbb{H},\perp ,\mathsf{\Lambda })$ is known as an OMS if $(\mathbb{H},\perp )$ is an $O_s$ and $(\mathbb{H},\perp )$ is a metric space.

Definition 7

([10]). Let $(\mathbb{H},\perp ,\mathsf{\Lambda })$ be an OMS. Then, a mapping $\mathsf{\Lambda }:\mathbb{H}\to \mathbb{H}$ is said to be orthogonally continuous in $\kappa \in \mathbb{H}$, if for each orthogonal-sequence $\left\{{\kappa }_{\vartheta }\right\}$ in $\mathbb{H}$ with ${\kappa }_{\vartheta }\to \kappa$ as $\vartheta \to \infty$, we have $\mathsf{\Lambda }\left({\kappa }_{\vartheta }\right)\to \mathsf{\Lambda }\left(\kappa \right)$ as $\vartheta \to \infty$.

Definition 8.

Let $\left\{{\kappa }_{\vartheta }\right\}$ be a sequence in $\mathbb{H}$. Then, the sequence $\left\{{\kappa }_{\vartheta }\right\}$ is called a Cauchy orthogonal-sequence if for every $\epsilon >0$, ∃ a ${\vartheta }_0(>0)\in \mathbb{N}$ such that $\mathsf{\Lambda }({\kappa }_{\vartheta },{\kappa }_{\mathfrak{j}})<\epsilon \forall \vartheta ,\mathfrak{j}>{\vartheta }_0$. i.e., $\underset{\vartheta ,\mathfrak{j}\to \infty }{lim}\mathsf{\Lambda }({\kappa }_{\vartheta },{\kappa }_{\mathfrak{j}})=0$.

Definition 9

([10]). Let $(\mathbb{H},\perp ,\mathsf{\Lambda })$ be an OMS. Then, $\mathbb{H}$ is called an orthogonal complete if every orthogonal Cauchy sequence is convergent.

Definition 10

([10]). Let $(\mathbb{H},\perp )$ be $O_s$. A mapping $\mathsf{\Lambda }:\mathbb{H}\to \mathbb{H}$ is known as orthogonal-preserving (Shortly $O_p$), if $\mathsf{\Lambda }\kappa \perp \mathsf{\Lambda }\tau$ whenever $\kappa \perp \tau$.

3. Main Results

In this section, we propose the concept of $\mathbf{F}$-Khan contraction of orthogonal set and we prove the fixed point result for these contraction mappings in the setting of OMS.

Definition 11.

Let $(\mathbb{H},\perp ,\mathsf{\Lambda })$ be an orthogonal complete metric space. A mapping $\mathcal{S}:\mathbb{H}\to \mathbb{H}$ is said to be an orthogonal $\mathbf{F}$-Khan-contraction if there exist $\mu \in (0,\infty )$ and $\mathfrak{F}\in {\mathbf{F}}_{\mathfrak{k}}$ s.t. for all $\kappa ,\tau \in \mathbb{H}$ with $\tau \perp \kappa$, if $max\left\{\mathsf{\Lambda }\right(\kappa ,\mathcal{S}\tau ),\mathsf{\Lambda }(\mathcal{S}\kappa ,\tau \left)\right\}\ne 0$, then $\mathcal{S}\kappa \ne \mathcal{S}\tau$ and

$$\begin{array}{c}\hfill \mu +\mathfrak{F}(\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )\le \mathfrak{F}\left(\frac{\mathsf{\Lambda }(\kappa ,\mathcal{S}\kappa )\mathsf{\Lambda }(\kappa ,\mathcal{S}\tau )+\mathsf{\Lambda }(\tau ,\mathcal{S}\tau )\mathsf{\Lambda }(\tau ,\mathcal{S}\kappa )}{max\left\{\mathsf{\Lambda }\right(\kappa ,\mathcal{S}\tau ),\mathsf{\Lambda }(\mathcal{S}\kappa ,\tau \left)\right\}}\right),\end{array}$$

(1)

and for all $\kappa ,\tau \in \mathbb{H}$ with $\mathcal{S}\tau \perp \kappa$ or $\mathcal{S}\kappa \perp \tau$, if $max\left\{\mathsf{\Lambda }\right(\kappa ,\mathcal{S}\tau ),\mathsf{\Lambda }(\mathcal{S}\kappa ,\tau \left)\right\}=0$, then $\mathcal{S}\kappa =\mathcal{S}\tau$.

Theorem 1.

Let $(\mathbb{H},\perp ,\mathsf{\Lambda })$ be an orthogonal-CMS and $\mathcal{S}$ be a self-mapping on $\mathbb{H}$ satisfying the following axioms:

1. 

$\mathcal{S}$ is an orthogonal preserving;

2. 

$\mathcal{S}$ is an orthogonal-$\mathbf{F}$-Khan contraction;

3. 

$\mathcal{S}$ is an orthogonal-continuous.

Then, $\mathcal{S}$ has a UFP (unique fixed point) ${\kappa }^{*}\in \mathbb{H}$.

Proof. 

Since $(\mathbb{H},\perp )$ is an $O_s$,

$$\begin{array}{c}\hfill \exists {\kappa }_0\in \mathbb{H}:(\forall \kappa \in \mathbb{H},\kappa \perp {\kappa }_0)\mathrm{or}(\forall \kappa \in \mathbb{H},{\kappa }_0\perp \kappa ).\end{array}$$

It follows that ${\kappa }_0\perp \mathcal{S}{\kappa }_0$ or $\mathcal{S}{\kappa }_0\perp {\kappa }_0$. Let

$$\begin{array}{c}\hfill {\kappa }_1:=\mathcal{S}{\kappa }_0,{\kappa }_2:=\mathcal{S}{\kappa }_1={\mathcal{S}}^2{\kappa }_0\dots \dots ,{\kappa }_{\vartheta +1}:=\mathcal{S}{\kappa }_{\vartheta }={\mathcal{S}}^{\vartheta +1}{\kappa }_0,\end{array}$$

(2)

for all $\vartheta \in \mathbb{N}\cup \left\{0\right\}$. If there exists ${\vartheta }_0\in \mathbb{N}$ s.t. $\mathsf{\Lambda }({\kappa }_{{\vartheta }_0},{\kappa }_{{\vartheta }_0+1})=0$, then ${\kappa }_{{\vartheta }_0+1}={\kappa }_{{\vartheta }_0}$; hence, the proof is complete. That is $\mathcal{S}$ has a fixed point.

• Now, we take ${\kappa }_{\vartheta }\ne {\kappa }_{\vartheta +1}\forall \vartheta \in \mathbb{N}$. Suppose that $\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\ne 0,\forall \vartheta \in \mathbb{N}$. Then, from (1), we obtain

$$\begin{array}{cc}\hfill \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\right)& <\mu +\mathfrak{F}\left(\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta })\right)\hfill \\ & \le \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta -1})\mathsf{\Lambda }({\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta })+\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta -1})}{max\{\mathsf{\Lambda }({\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta }),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta -1},{\kappa }_{\vartheta })\}}\right)\hfill \\ & =\mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta -1})\right).\hfill \end{array}$$

(3)

Since $\mathfrak{F}\in {\mathfrak{F}}_{\mathfrak{k}}$, from (3), we have

$$\begin{array}{c}\hfill \mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })<\mathsf{\Lambda }({\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta -1}),\forall \vartheta \in \mathbb{N}.\end{array}$$

Therefore ${\left\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\right\}}_{\vartheta \in \mathbb{N}}$ is a strictly non-increasing sequence of non-negative real numbers, and hence

$$\begin{array}{c}\hfill \underset{\vartheta \to \infty }{lim}\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })=\gamma \ge 0.\end{array}$$

Since ${\left\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\right\}}_{\vartheta \in \mathbb{N}}$ is a positive strictly non-increasing sequence, for every $\vartheta \in \mathbb{N}$, we have

$$\begin{array}{c}\hfill \mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\ge \gamma .\end{array}$$

(4)

Now, we assume that $\gamma =0$. Arguing by contradiction, suppose that $\gamma >0$. From (4) and $\mathfrak{F}\in {\mathbf{F}}_{\mathfrak{k}}$, we have

$$\begin{array}{cc}\hfill \mathfrak{F}\left(\gamma \right)& \le \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\right)\le \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_{\vartheta -1},\mathcal{S}{\kappa }_{\vartheta -1})\right)-\mu \hfill \\ & \le \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_{\vartheta -2},\mathcal{S}{\kappa }_{\vartheta -2})\right)-2\mu \hfill \\ & \le \dots \dots \le \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_0,\mathcal{S}{\kappa }_0)\right)-\vartheta \mu ,\forall \vartheta \in \mathbb{N}.\hfill \end{array}$$

(5)

Since $\mathbb{H}\left(\gamma \right)\in \mathbb{R}$ and $\underset{\vartheta \to \infty }{lim}\mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_0,\mathcal{S}{\kappa }_0)\right)-\vartheta \mu =-\infty$, there exists ${\vartheta }_1\in \mathbb{N}$ such that

$$\begin{array}{c}\hfill \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_0,\mathcal{S}{\kappa }_0)\right)-\vartheta \mu <\mathfrak{F}\left(\gamma \right),\forall \vartheta >{\vartheta }_1.\end{array}$$

(6)

It follows from (5) and (6) that

$$\begin{array}{c}\hfill \mathfrak{F}\left(\gamma \right)\le \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }_0,\mathcal{S}{\kappa }_0)\right)-\vartheta \mu <\mathfrak{F}\left(\gamma \right),\forall \vartheta >{\vartheta }_1.\end{array}$$

This is a contradiction. Therefore, we have

$$\begin{array}{c}\hfill \underset{\vartheta \to \infty }{lim}\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })=0.\end{array}$$

(7)

Now, we assume, ${\left\{{\kappa }_{\vartheta }\right\}}_{\vartheta =1}^{\infty }$ is an orthogonal Cauchy sequence. We claim that there exists $ϵ>0$; the sequences ${\left\{\mathcal{P}\left(\vartheta \right)\right\}}_{\vartheta =1}^{\infty },{\left\{\mathcal{Q}\left(\vartheta \right)\right\}}_{\vartheta =1}^{\infty }\in \mathbb{N}$ s.t.

$$\begin{array}{c}\hfill \mathcal{P}\left(\vartheta \right)>\mathcal{Q}\left(\vartheta \right)>\vartheta ,\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\ge ϵ,\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)-1},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})<ϵ.\end{array}$$

(8)

By triangular inequality, we have

$$\begin{array}{c}\hfill \mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\le \mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)}).\end{array}$$

It follows from (7) and (8) that

$$\begin{array}{c}\hfill ϵ\le lim\underset{\vartheta \to \infty }{inf}\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}).\end{array}$$

So, there exists ${\vartheta }_2\in \mathbb{N}$ s.t. for all $\vartheta \ge {\vartheta }_2,\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})>\frac{ϵ}{2}$. Therefore,

$$\begin{array}{c}\hfill max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}>\frac{ϵ}{2},\forall \vartheta \ge {\vartheta }_2.\end{array}$$

(9)

Again by triangular inequality, we have

$$\begin{array}{c}\hfill \mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\le \mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})+\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)}).\end{array}$$

From (7) and (8) we obtain,

$$\begin{array}{c}\hfill ϵ\le lim\underset{\vartheta \to \infty }{inf}\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}).\end{array}$$

There exists ${\vartheta }_3\in \mathbb{N}$ s.t. for all $\vartheta \ge {\vartheta }_3,$

$$\begin{array}{c}\hfill \mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})>\frac{ϵ}{2}.\end{array}$$

(10)

Since $\mathfrak{F}\in {\mathbf{F}}_{\mathfrak{k}}$, from (1), (9) and (10), for all $\vartheta \ge max\{{\vartheta }_2,{\vartheta }_3\}$, we have

$$\begin{array}{cc}\hfill \mu +\mathfrak{F}(\frac{ϵ}{2})& \le \mu +\mathfrak{F}\left(\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\right)\hfill \\ & \le \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}\right).\hfill \end{array}$$

(11)

From (9), for $\vartheta \ge {\vartheta }_2$,

$$\begin{array}{cc}\hfill 0& \le \frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}\hfill \\ & =\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}+\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}\hfill \\ & \le \frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})}{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})}+\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})}\hfill \\ & =\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}).\hfill \end{array}$$

(12)

It follows from (7) and (12) and sandwich theorem that

$$\begin{array}{c}\hfill \underset{\vartheta \to \infty }{lim}\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}=0.\end{array}$$

So there exists ${\vartheta }_4\in \mathbb{N}$ s.t. for all $\vartheta >{\vartheta }_4$,

$$\begin{array}{c}\hfill \frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}<\frac{ϵ}{2}.\end{array}$$

Since $\mathfrak{F}\in {\mathbf{F}}_{\mathfrak{k}}$, for all $\vartheta >{\vartheta }_4$, we have

$$\begin{array}{c}\hfill \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}\right)\le \mathfrak{F}\left(\frac{ϵ}{2}\right).\end{array}$$

(13)

From (11) and (13), for all $\vartheta \ge max\{{\vartheta }_2,{\vartheta }_3,{\vartheta }_4\}$, we obtain

$$\begin{array}{cc}\hfill \mu +\mathfrak{F}(\frac{ϵ}{2})& \le \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})+\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\mathsf{\Lambda }({\kappa }_{\mathcal{Q}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)})}{max\{\mathsf{\Lambda }({\kappa }_{\mathcal{P}\left(\vartheta \right)},\mathcal{S}{\kappa }_{\mathcal{Q}\left(\vartheta \right)}),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\mathcal{P}\left(\vartheta \right)},{\kappa }_{\mathcal{Q}\left(\vartheta \right)})\}}\right)\hfill \\ & \le \mathfrak{F}(\frac{ϵ}{2}),\hfill \end{array}$$

which is a contradiction. By Completeness of $(\mathbb{H},\mathsf{\Lambda })$, therefore, there exists $\left\{{\kappa }_{\vartheta }\right\}\to {\kappa }^{\star }\in \mathbb{H}$ such that

$$\begin{array}{c}\hfill \underset{\vartheta \to \infty }{lim}\mathsf{\Lambda }({\kappa }_{\vartheta },{\kappa }^{\star })=0\mathrm{and}\underset{\vartheta \to \infty }{lim}\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })=\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star }).\end{array}$$

(14)

Now, we consider $\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })=0$. We assume that $\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })>0$ and consider the following two cases:

• for all $\vartheta \in \mathbb{N}$, there exists $j_{\vartheta }\in \mathbb{N},j_{\vartheta }>j_{\vartheta -1},j_0=1$ and ${\kappa }_{j_{\vartheta +1}}=\mathcal{S}{\kappa }^{\star };$
• for all $\vartheta \in \mathbb{N},\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })>0$.

In the first case, from (14) we have

$$\begin{array}{c}\hfill {\kappa }^{\star }=\underset{\vartheta \to \infty }{lim}{\kappa }_{j_{\vartheta +1}}=\mathcal{S}{\kappa }^{\star }.\end{array}$$

In the second case, $\forall \vartheta \in \mathbb{N}$, we have

$$\begin{array}{c}\hfill max\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },{\kappa }^{\star })\}>0.\end{array}$$

So from (1), we have

$$\begin{array}{c}\hfill \mu +\mathfrak{F}\left(\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })\right)\le \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })+\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }_{\vartheta })}{max\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },{\kappa }^{\star })\}}\right).\end{array}$$

(15)

On the other hand, from (7) and (14), we have

$$\begin{array}{c}\hfill \underset{\vartheta \to \infty }{lim}\frac{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })+\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }_{\vartheta })}{max\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },{\kappa }^{\star })\}}=0.\end{array}$$

Since $\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })>0$, so there exists ${\vartheta }_5\in \mathbb{N}$ s.t. $\vartheta \ge {\vartheta }_5,$

$$\begin{array}{c}\hfill \frac{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })+\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }_{\vartheta })}{max\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },{\kappa }^{\star })\}}<\frac{1}{2}\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star }).\end{array}$$

Therefore

$$\begin{array}{cc}\hfill \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }_{\vartheta })\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })+\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }_{\vartheta })}{max\{\mathsf{\Lambda }({\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },{\kappa }^{\star })\}}\right)& \le \mathfrak{F}\left(\frac{1}{2}\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\right),\hfill \end{array}$$

(16)

for all $\vartheta \ge {\vartheta }_5$.

• It follows from (15) and (16), we have

$$\begin{array}{c}\hfill \mu +\mathfrak{F}\left(\mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })\right)\le \mathfrak{F}\left(\frac{1}{2}\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\right),\forall \vartheta \ge {\vartheta }_5.\end{array}$$

Hence

$$\begin{array}{c}\hfill \mathsf{\Lambda }(\mathcal{S}{\kappa }_{\vartheta },\mathcal{S}{\kappa }^{\star })\le \frac{1}{2}\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star }),\forall \vartheta \ge {\vartheta }_5.\end{array}$$

From (14), we obtain

$$\begin{array}{c}\hfill \mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\le \frac{1}{2}\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star }),\end{array}$$

which is a contradiction. Therefore, ${\kappa }^{\star }=\mathcal{S}{\kappa }^{\star }$. Now, we prove that $\mathcal{S}$ has a UFP. Now, we consider ${\tau }^{\star }$ is another fixed point of $\mathcal{S}$ in $\mathbb{H}$ s.t. $\mathsf{\Lambda }({\kappa }^{\star },{\tau }^{\star })>0$. Therefore

$$\begin{array}{c}\hfill max\{\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\tau }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }^{\star },{\tau }^{\star })\}>0.\end{array}$$

From (1),

$$\begin{array}{cc}\hfill \mathfrak{F}\left(\mathsf{\Lambda }({\kappa }^{\star },{\tau }^{\star })\right)& =\mathfrak{F}\left(\mathsf{\Lambda }(\mathcal{S}{\kappa }^{\star },\mathcal{S}{\tau }^{\star })\right)<\mu +\mathfrak{F}\left(\mathsf{\Lambda }(\mathcal{S}{\kappa }^{\star },\mathcal{S}{\tau }^{\star })\right)\hfill \\ & \le \mathfrak{F}\left(\frac{\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\tau }^{\star })+\mathsf{\Lambda }({\tau }^{\star },\mathcal{S}{\tau }^{\star })\mathsf{\Lambda }({\tau }^{\star },\mathcal{S}{\kappa }^{\star })}{max\{\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\tau }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }^{\star },{\tau }^{\star })\}}\right).\hfill \end{array}$$

Since

$$\begin{array}{c}\hfill \frac{\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\kappa }^{\star })\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\tau }^{\star })+\mathsf{\Lambda }({\tau }^{\star },\mathcal{S}{\tau }^{\star })\mathsf{\Lambda }({\tau }^{\star },\mathcal{S}{\kappa }^{\star })}{max\{\mathsf{\Lambda }({\kappa }^{\star },\mathcal{S}{\tau }^{\star }),\mathsf{\Lambda }(\mathcal{S}{\kappa }^{\star },{\tau }^{\star })\}}=0,\end{array}$$

which is a contradiction and hence ${\kappa }^{\star }={\tau }^{\star }$. This completes the proof. □

Example 1.

Let $\mathbb{H}=[0,1]$ and $\mathsf{\Lambda }:\mathbb{H}\times \mathbb{H}\to {\mathbb{R}}^{+}$ be defined by

$$\begin{array}{c}\hfill \mathsf{\Lambda }(\kappa ,\tau )=|\kappa -\tau |.\end{array}$$

Define ⊥ on $\mathbb{H}$ by $\kappa \perp \tau$ iff $\kappa ,\tau \ge 0$. Then, it is easy to prove that $(\mathbb{H},\perp ,\mathsf{\Lambda })$ is an O-complete metric space. Define the mapping $\mathcal{S}:\mathbb{H}\to \mathbb{H}$ by

$$\mathcal{S}\left(\kappa \right)=\left\{\begin{array}{cc}\frac{\kappa }{4},\hfill & \kappa \in [0,1)\hfill \\ \frac{1}{6},\hfill & \kappa =1.\hfill \end{array}\right.$$

Clearly, $\mathcal{S}$ is an $O_p$ and an orthogonal continuous. Define the function $\mathbf{F}\left(r\right)=lnr$, for $r\in {\mathbb{R}}^{+}$. Then, we have

$$\begin{array}{c}\hfill \wr +\mathbf{F}\left(\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )\right)\le \mathbf{F}\left(\mathsf{\Lambda }(\kappa ,\tau )\right)\iff ln\left(\frac{\mathsf{\Lambda }(\kappa ,\tau )}{\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )}\right)\ge \wr ,\end{array}$$

for all $\kappa ,\tau \in \mathbb{H}$. First, we can observe that

$$\begin{array}{cc}\hfill \mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )>0,\frac{1}{2}\mathsf{\Lambda }(\kappa ,\mathcal{S}\kappa )& <\mathsf{\Lambda }(\kappa ,\tau )\iff \left\{\right(\kappa =1and\tau =0)\hfill \\ \hfill & \vee (\kappa =0and\tau =1)\vee (\kappa <\tau <1)\vee (\tau \le \kappa <1)\}.\hfill \end{array}$$

For $\kappa =1and\tau =0$, we have $\mathsf{\Lambda }(\kappa ,\tau )=1$ and

$$\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )=\mathsf{\Lambda }\left(\frac{1}{6},\mathcal{S}\tau \right)=\left\{\begin{array}{cc}\frac{1}{6},\hfill & \tau \in [0,\frac{1}{2}]\hfill \\ \frac{\tau }{6},\hfill & \tau \in (\frac{1}{2},1)\hfill \\ \frac{1}{6},\hfill & \tau =1.\hfill \end{array}\right.$$

Hence, we have

$$\frac{\mathsf{\Lambda }(\kappa ,\tau )}{\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )}=\left\{\begin{array}{cc}6,\hfill & \tau \in [0,\frac{1}{2}]\hfill \\ \frac{6}{\tau },\hfill & \tau \in (\frac{1}{2},1)\hfill \\ 6,\hfill & \tau =1.\hfill \end{array}\right.$$

(17)

For $\kappa =0and\tau =1$, we have $\mathsf{\Lambda }(\kappa ,\tau )=1$ and

$$\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )=\mathsf{\Lambda }\left(\mathcal{S}\kappa ,\frac{1}{6}\right)=\left\{\begin{array}{cc}\frac{1}{6},\hfill & \kappa \in [0,\frac{1}{2}]\hfill \\ \frac{\kappa }{6},\hfill & \kappa \in (\frac{1}{2},1).\hfill \end{array}\right.$$

Hence, we have

$$\frac{\mathsf{\Lambda }(\kappa ,\tau )}{\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )}=\left\{\begin{array}{cc}6,\hfill & \kappa \in [0,\frac{1}{2}]\hfill \\ \frac{6}{\kappa },\hfill & \kappa \in (\frac{1}{2},1).\hfill \end{array}\right.$$

(18)

For $\kappa <\tau <1$, we have $\mathsf{\Lambda }(\kappa ,\tau )=|\kappa -\tau |$ and $\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )=\mathsf{\Lambda }(\frac{\kappa }{4},\frac{\tau }{4})=\frac{|\kappa -\tau |}{4}$. Hence, we have

$$\begin{array}{c}\hfill \frac{\mathsf{\Lambda }(\kappa ,\tau )}{\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )}=4.\end{array}$$

(19)

For $\tau \le \kappa <1$, we have $\mathsf{\Lambda }(\kappa ,\tau )=|\kappa -\tau |$ and $\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )=\mathsf{\Lambda }(\frac{\kappa }{4},\frac{\tau }{4})=\frac{|\kappa -\tau |}{4}$. Hence, we have

$$\begin{array}{c}\hfill \frac{\mathsf{\Lambda }(\kappa ,\tau )}{\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )}=4.\end{array}$$

(20)

From (17)–(20), we have if $0<\wr \le ln4$, then $ln\left(\frac{\mathsf{\Lambda }(\kappa ,\tau )}{\mathsf{\Lambda }(\mathcal{S}\kappa ,\mathcal{S}\tau )}\right)\ge \wr$. Thus,

$$\begin{array}{cc}\hfill \wr +\mathbf{F}\left(\mathsf{\Lambda }\right(\mathcal{S}\kappa ,\mathcal{S}\tau \left)\right)& \le \mathbf{F}\left(\mathsf{\Lambda }\right(\kappa ,\tau \left)\right).\hfill \end{array}$$

Therefore, $\mathcal{S}$ satisfies all the conditions of Theorem 1 with $0<\wr \le ln4$. Thus, $\mathcal{S}$ has a UFP.

4. Application

Let $\mathcal{F}=C\left(\right[0,\mathbb{H}],\mathbb{R})$ be the set of all real-valued continuous functions with domain $[0,\mathbb{H}]$. Consider the integral equation

$$\begin{array}{c}\hfill \mu (\ell )={\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )ϝ(\tau ,\mu \left(\tau \right))d\tau ,\ell \in [0,\mathbb{H}],\end{array}$$

(21)

where

(a)

$ϝ:[0,\mathbb{H}]\times \mathbb{R}\to \mathbb{R}$ is continuous;

(b)

$\Sigma :[0,\mathbb{H}]\times [0,\mathbb{H}]$ is continuous and measurable at $\tau \in [0,\mathbb{H}]$, ∀$\ell \in [0,\mathbb{H}]$;

(c)

$\Sigma (\ell ,\tau )\ge 0$, for all $\ell ,\tau \in [0,\mathbb{H}]$ and ${\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )d\tau \le 1$, for all $\ell \in [0,\mathbb{H}]$.

Theorem 2.

Assume that the conditions $\left(a\right)$–$\left(c\right)$ hold. Suppose that there exists $\wp >0$ s.t.

$$\begin{array}{cc}\hfill \left|ϝ\right(\ell ,\mu (\ell ))-ϝ(\ell ,ð(\ell )\left)\right|& \le e^{-\wp }|\mu (\ell )-ð(\ell )|,\hfill \end{array}$$

for every $\ell \in [0,\mathbb{H}]$ and for all $\mu ,ð\in C\left(\right[0,\mathbb{H}],\mathbb{R})$. Then, the Equation (21) has a unique solution in $C\left(\right[0,\mathbb{H}],\mathbb{R})$.

Proof. 

Let $\mathcal{F}=\{w\in C([0,\mathbb{H}],\mathbb{R}):w(\rho )>0,\mathrm{for}\mathrm{all}\rho \in [0,\mathbb{H}\left]\right\}$. Define the orthogonality relation ⊥ on $\mathcal{F}$ by

$$\begin{array}{c}\hfill \mu \perp ð\iff \mu \left(\rho \right)ð\left(\rho \right)\ge \mu \left(\rho \right)or\mu \left(\rho \right)ð\left(\rho \right)\ge ð\left(\rho \right),\mathrm{for}\mathrm{all}\rho \in [0,\mathbb{H}].\end{array}$$

Define a mapping $\mathsf{\Lambda }:\mathcal{F}\times \mathcal{F}\to [0,\infty )$ by

$$\begin{array}{c}\hfill \mathsf{\Lambda }(\mu ,ð)=\left|\mu \right(\ell )-ð(\ell \left)\right|,\end{array}$$

for all $\mu ,ð\in \mathcal{F}$. Thus, $(\mathcal{F},\perp ,\mathsf{\Lambda })$ is an OMS and also an orthogonal complete metric space. Define $\mathcal{S}:\mathcal{F}\to \mathcal{F}$ by

$$\begin{array}{c}\hfill \mathcal{S}\mu (\ell )={\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )ϝ(\tau ,\mu (\ell )),\ell \in [0,\mathbb{H}].\end{array}$$

Now, we prove that $\mathcal{S}$ is an $O_p$. For every $\mu ,ð\in \mathcal{F}$ with $\mu \perp ð,\rho \in I$, we get

$$\begin{array}{c}\hfill \mathcal{S}\mu (\ell )={\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )ϝ(\tau ,\mu (\ell ))\ge 1.\end{array}$$

It follows that $\left[\right(\mathcal{S}\mu \left)\right(\rho \left)\right]\left[\right(\mathcal{S}ð\left)\right(\rho \left)\right]\ge (\mathcal{S}ð)\left(\rho \right)$ and so $\left(\mathcal{S}\mu \right)\left(\rho \right)\perp (\mathcal{S}ð)\left(\rho \right)$. Then, $\mathcal{S}$ is an $O_p$.

• Next, we assume that $\mathcal{S}$ is an orthogonal $\mathbf{F}$-Khan contraction. Let $\mu ,ð\in \mathcal{F}$ with $\mu \perp ð$. Suppose that $\mathcal{S}\left(\mu \right)\ne \mathcal{S}(ð)$. For every $\ell \in [0,\mathbb{H}]$, we have

$$\begin{array}{cc}\hfill \mathsf{\Lambda }(\mathcal{S}\mu ,\mathcal{S}ð)=\left|\mathcal{S}\mu \right(\ell )-\mathcal{S}ð(\ell \left)\right|& ={\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )|ϝ(\tau ,\mu \left(\tau \right))-ϝ(\tau ,ð\left(\tau \right))|d\tau \hfill \\ \hfill & \le {\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )e^{-\wp }|\mu (\ell )-ð(\ell ))d\tau \hfill \\ \hfill & =e^{-\wp }|\mu (\ell )-ð(\ell )|{\int }_0^{\mathbb{H}}\Sigma (\ell ,\tau )d\tau \hfill \\ \hfill & \le e^{-\wp }|\mu (\ell )-ð(\ell )|\hfill \\ \hfill & =e^{-\wp }\mathsf{\Lambda }(\mu ,ð).\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill \wp +ln\left(\mathsf{\Lambda }(\mathcal{S}\mu ,\mathcal{S}ð)\right)\le ln\left(\mathsf{\Lambda }(\mu ,ð)\right).\end{array}$$

Taking $\mathbf{F}(\ell )=ln(\ell )$, we obtain

$$\begin{array}{c}\hfill \wp +\mathbf{F}\left(\mathsf{\Lambda }(\mathcal{S}\mu ,\mathcal{S}ð)\right)\le \mathbf{F}\left(\mathsf{\Lambda }(\mu ,ð)\right).\end{array}$$

for all $\mu ,ð\in \mathcal{F}$. Therefore, by Theorem 1, $\mathcal{S}$ has a UFP. Hence there is a unique solution for (21). □

Example 2.

Consider the integral equation

$${\int }_0^{t}cos(t-s)\kappa \left(s\right)ds=tsint.$$

(22)

From (22) with exact solution $\kappa \left(t\right)=2sin\left(t\right)$, for $0\le t<1$.

Table 1. Comparison of exact solution and approximation solutions.

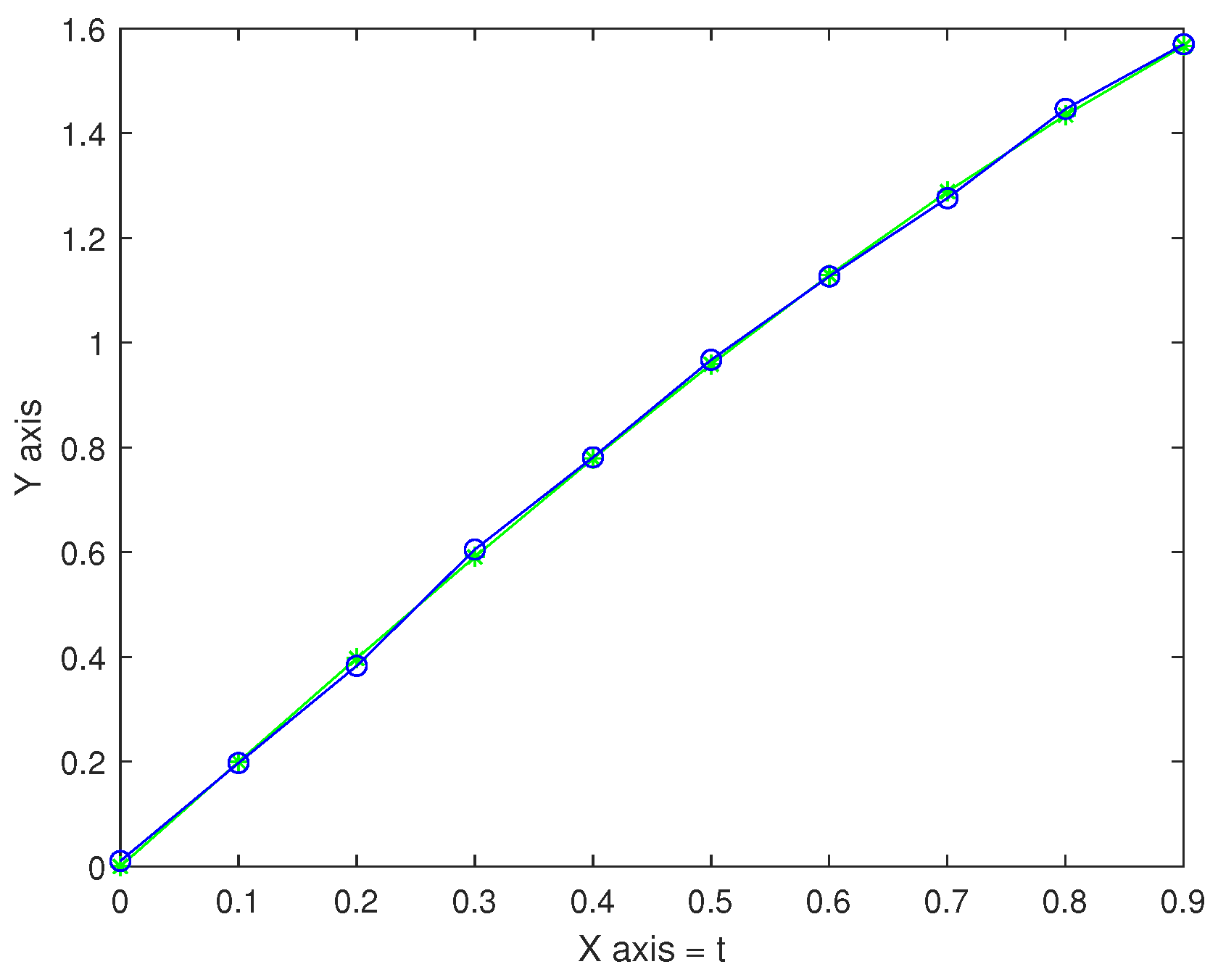
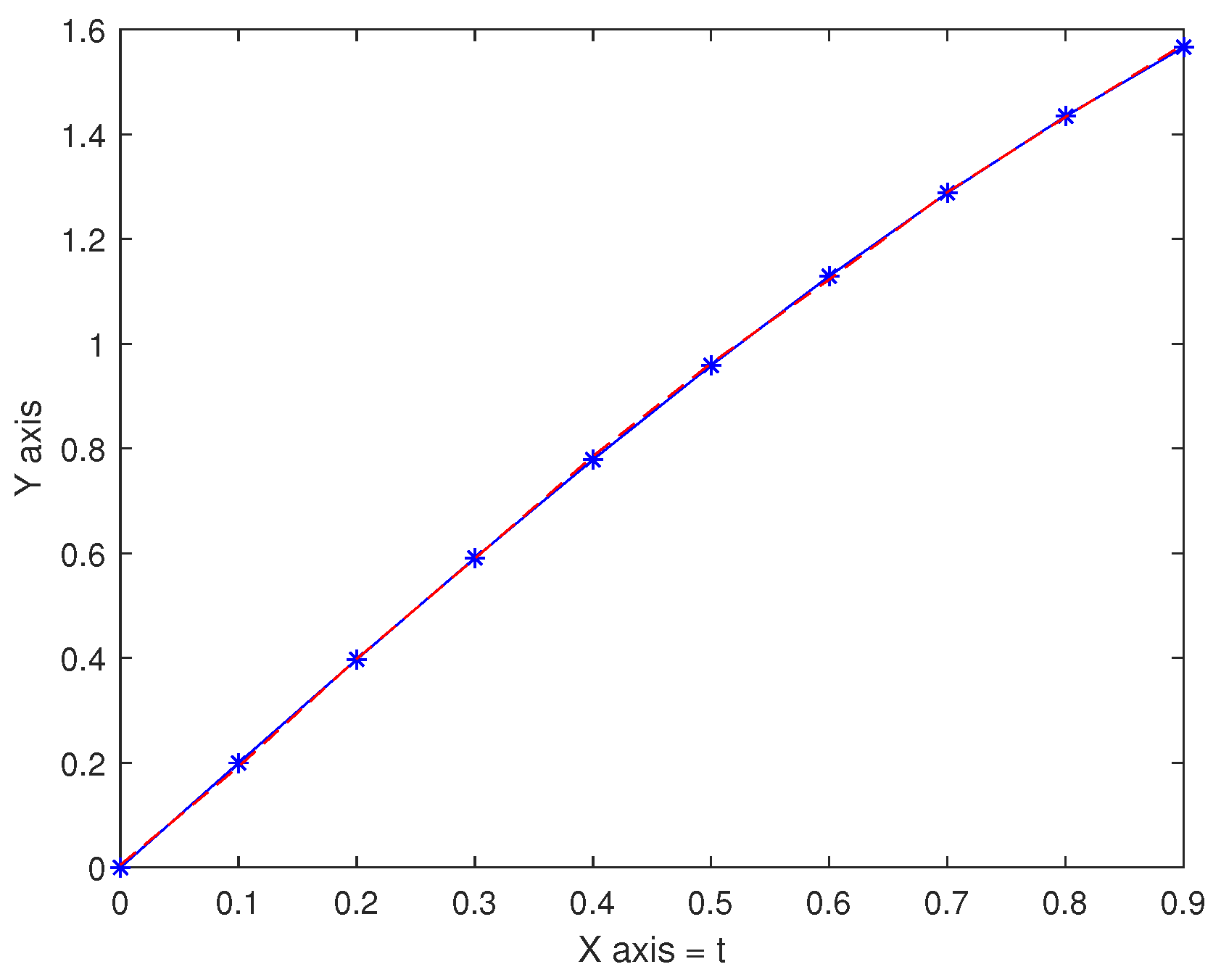
t	Exact Solution	Approximation Solution (m = 64)	Approximation Solution (m = 128)
0.0	0	0.010417	0.005208
0.1	0.199667	0.197570	0.192399
0.2	0.397339	0.382942	0.398412
0.3	0.591040	0.605205	0.589930
0.4	0.778837	0.781174	0.785758
0.5	0.958851	0.967335	0.963098
0.6	1.129285	1.126666	1.122812
0.7	1.288435	1.276056	1.289847
0.8	1.434712	1.446451	1.433200
0.9	1.566654	1.569934	1.572171

shows the numerical value.

Figure 1 and Figure 2 show that the error between the approximation and exact solution is also relatively very small.

Example 3.

Consider the integral equation

$$\begin{array}{c}\hfill \kappa \left(\mathfrak{t}\right)=1-\kappa -{\displaystyle \frac{{\kappa }^2}{2}}+{\int }_0^1(\kappa -\mathfrak{s})\delta \mathfrak{s}.\end{array}$$

Here, $1-\kappa -{\displaystyle \frac{{\kappa }^2}{2}}$ is not an orthogonal continuous function on $(0,1)$. The following table compares analytical and numerical solutions.

Table 2. Comparison of approximation and exact solution.

${\mathit{\kappa }}_{\mathit{j}}$	Approximation Solution	Exact Solution	Error
0.05	0.95	0.94875	0.00125
0.15	0.85	0.83875	0.01125
0.25	0.75	0.71875	0.03125
0.35	0.65	0.58875	0.06125
0.45	0.55	0.44875	0.10125
0.55	0.45	0.29875	0.15125
0.65	0.35	0.13875	0.21125
0.75	0.25	−0.03125	0.28125
0.85	0.15	−0.21125	0.36125
0.95	0.05	−0.40125	0.45125

shows that the error between the approximation and exact solution is also relatively small, and Figure 3 shows the comparison of approximation and exact solution with h = 0.1.

5. Conclusions

In this article, we demonstrated the existence of fixed point theorem for orthogonal $\mathbf{F}$-Khan contractions of an orthogonal CMS. The derived results have been applied to find the solution to the integral equation. We have also compared the analytical and numerical solutions for the integral equation and found that the margin of error was minimal.

Recently, Özgür et al. [22,23,24,25,26] introduced the fixed-circle problem considered for metric and some generalized metric spaces. It is an interesting open problem to study the fixed-circle problem and obtained Branciari metric space results on complete Branciari metric spaces. More generally, it will be also an open problem to use appropriate contractive conditions for the existence and uniqueness of theorems for fixed circles of self-mappings on metric spaces with geometric interpretation.