Deformation Characteristics Analysis of Temporary Support in Unsymmetrical Loading Tunnel Excavation under Composite Support
Abstract
:1. Introduction
2. Engineering Background and Excavation Method
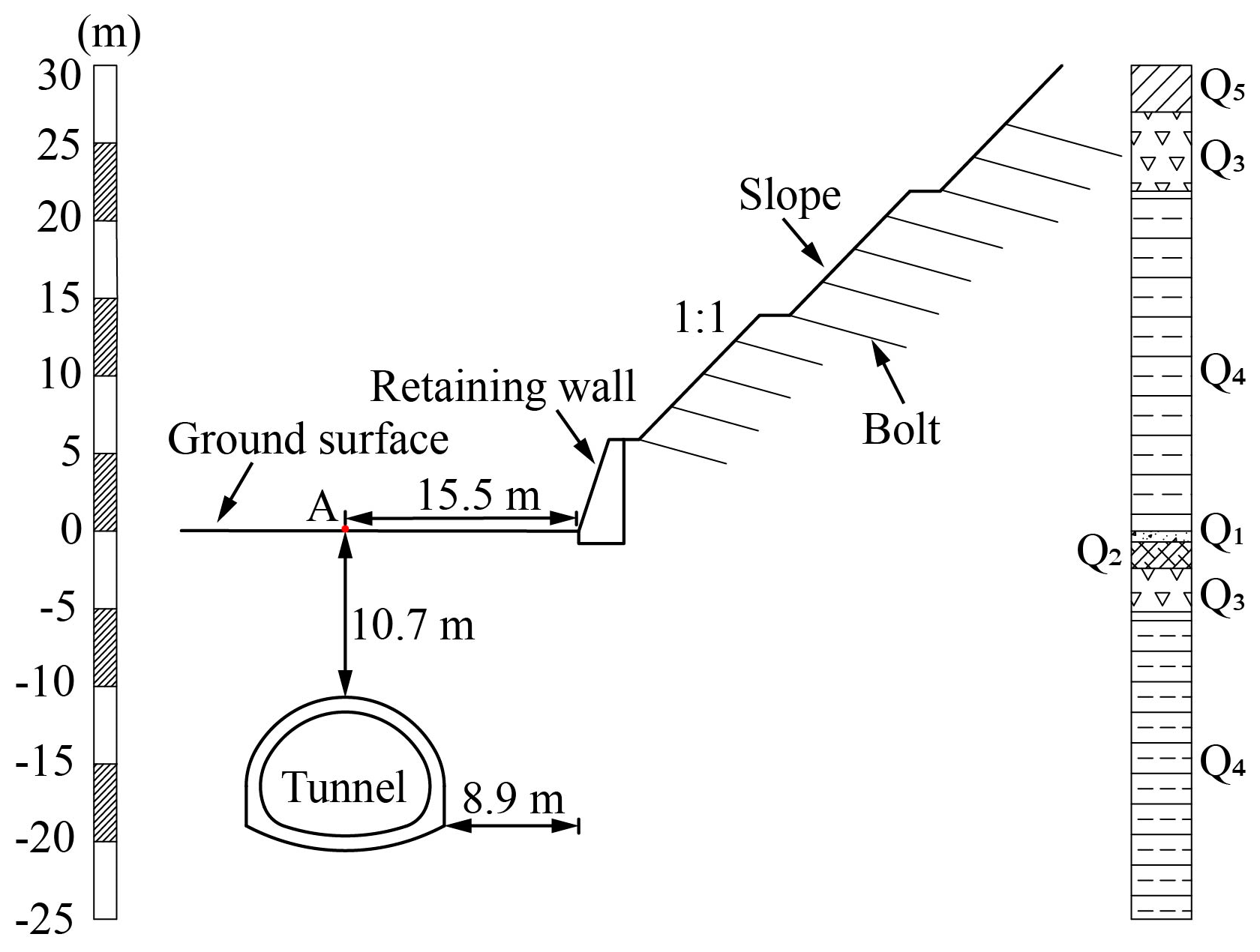
2.1. Engineering Geology
2.2. Excavation Method of Shallow-Buried Large-Section Tunnel
3. Mechanical Analysis of Supporting Structure
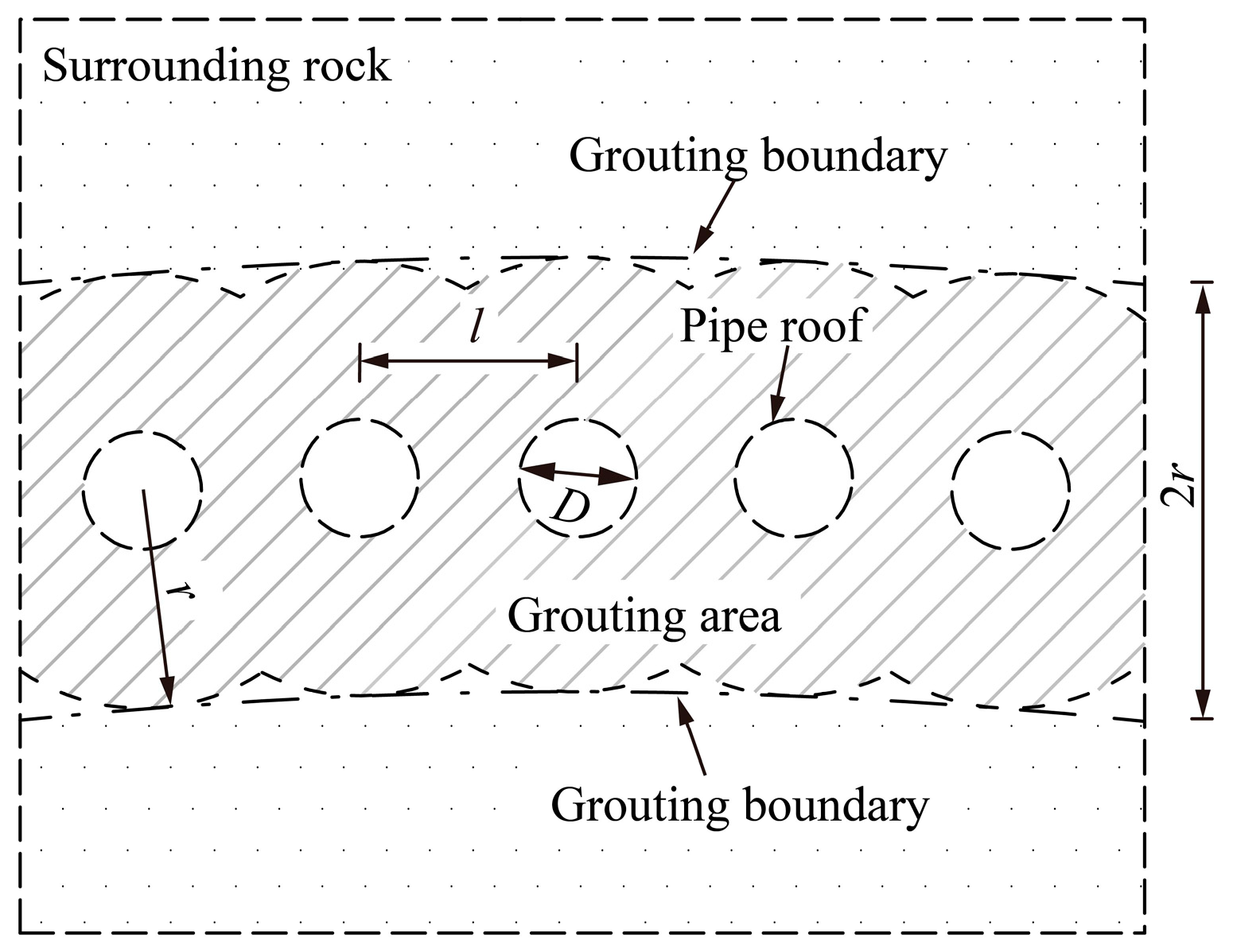
3.1. Pipe Roof
| Eg | is the equivalent elastic modulus of the grouting steel pipe, |
| γg | is the equivalent weight of the grouting steel pipe, |
| E1 | is the elastic modulus of the steel pipe, E1 = 210 GPa, |
| I1 | is the moment of inertia of the steel pipe section, I1 = 1.77 × 10−6 m4, |
| γ1 | is the weight of the steel pipe, γ1 = 78.5 kN/m3, |
| A1 | is the cross-sectional area of the steel pipe, A1 =1.31 × 10−3 m2, |
| E2 | is the elastic modulus of the cement mortar, E2 = 2.8 × 104 MPa, |
| I2 | is the moment of inertia of the filling cement mortar section, I2 = 4.91 × 10−6 m4, |
| γ2 | is the weight of the cement mortar, γ2 = 20.0 kN/m3, |
| A2 | is the cross-sectional area of the filling cement mortar, A2 = 7.85 × 10−3 m2. |
| E | is the elastic modulus of the grouting reinforcement area, |
| E0 | is the elastic modulus of the stratum, E0 = 59.4 MPa, |
| Sg | is the cross-sectional area of the grouting steel pipe, Sg = A1 + A2 = 9.16 × 10−3 m2, |
| Sc | is the cross-sectional area of the support section, Sc = l × 2r = 0.4 m2. |
3.2. Steel Grid Support
| P | is the structural support resistance, |
| K | is the supporting stiffness of the structure, |
| u | is the radial displacement of the structure. |
| E | is the equivalent elastic modulus of the steel grid, |
| t | is the structural thickness of the steel grid, |
| v | is the Poisson’s ratio of the steel grid, |
| R | is the equivalent radius of the tunnel. |
| σc | is the equivalent yield stress of the steel grid, |
| σs | is the yield strength of the steel grid, |
| Es | is the elastic modulus of the steel grid, |
| As | is the cross-sectional area of the steel grid, |
| A | is the equivalent rectangular cross-sectional area, |
| Is | is the moment of inertia of the section, |
| I | is the moment of inertia of the equivalent rectangular section. |
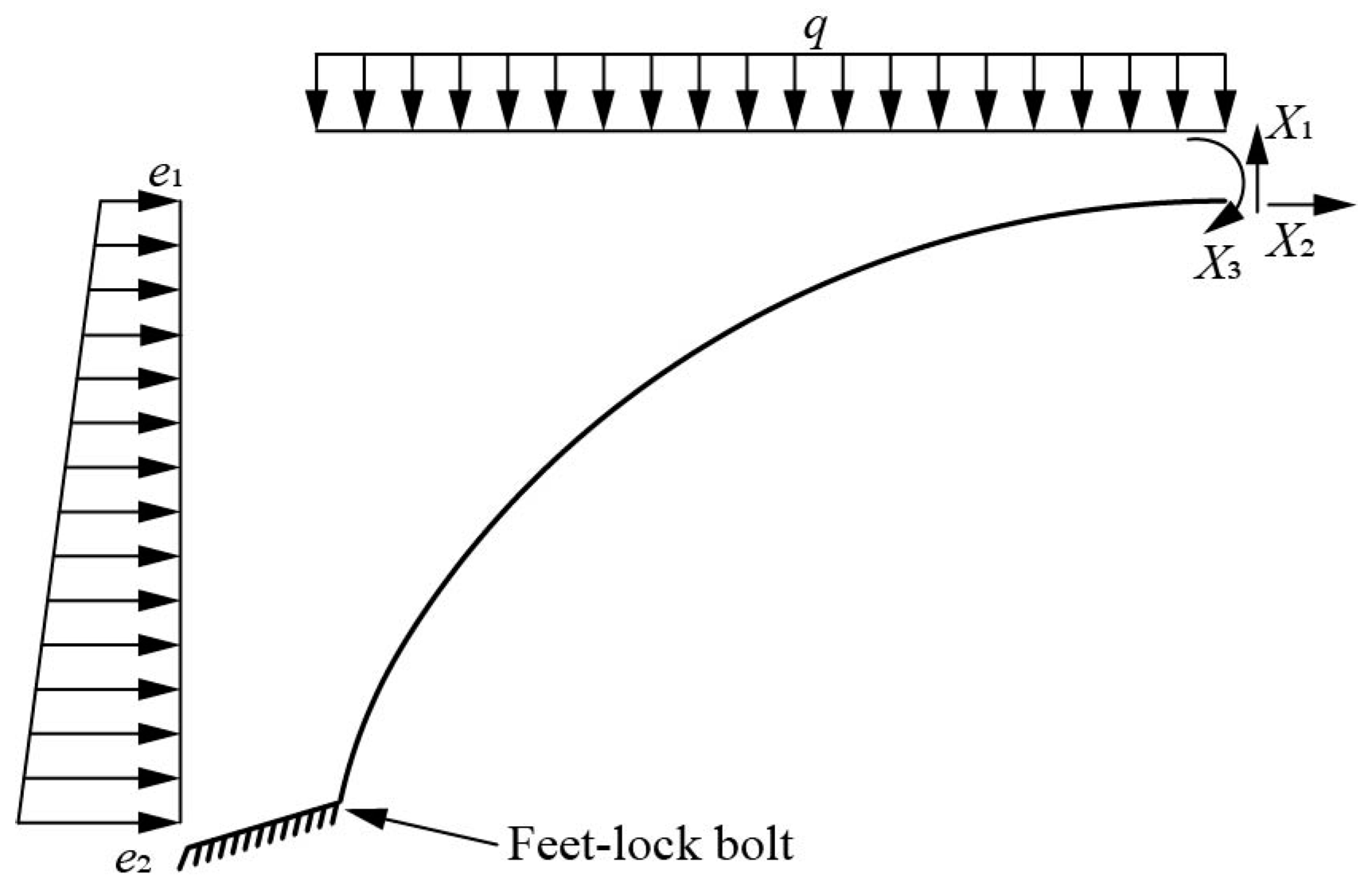
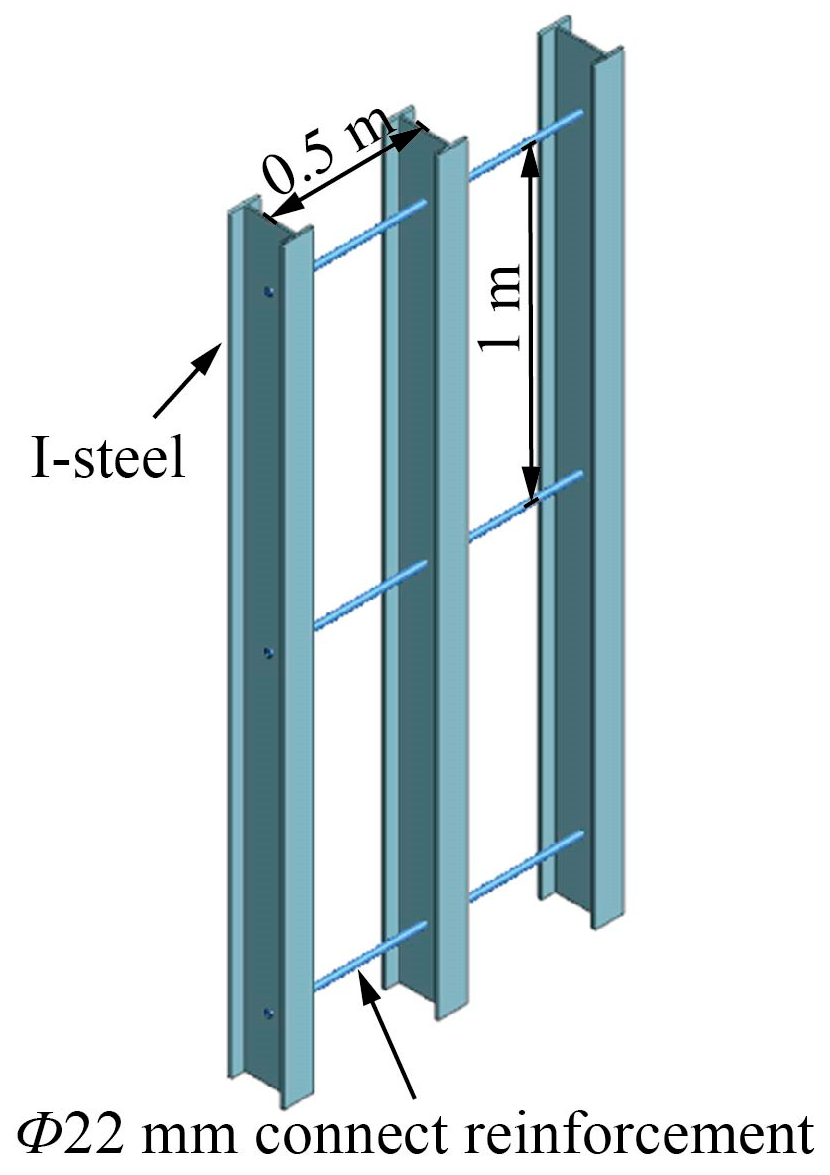
3.3. Temporary Steel Support
4. Numerical Analysis
4.1. Model Building
4.2. Fundamental Assumption
- (1)
- Each geological layer, pipe roof grouting and solid are regarded as homogeneous and isotropic media.
- (2)
- The deformation and failure of the tunnel surrounding rock, temporary steel support, and pipe roof grouting conform to the classical elastic–plastic theory.
- (3)
- Without considering the influence of disturbance caused by tunnel excavation on the structure itself and the effect of tectonic stress, only considering the influence of self-weight on the structure itself. The initial horizontal stress is calculated by using the surrounding rock gravity in MIDAS software, which can be expressed by Equation (9).
| σh | is the horizontal stress, |
| σv | is the vertical stress, |
| μ | is Poisson’s ratio. |
4.3. Constitutive Relation
| σ1 | is the first principal stress of the material, |
| σ2 | is the second principal stress of the material, |
| σ3 | is the third principal stress of the material, |
| σs | is the yield point of the material, and σs = 235 MPa, |
| K | is the shear yield strength of the material. |
| τ | is the shear stress on the shear plane, Pa, |
| σ | is the normal stress on the shear plane, |
| φ | is the internal friction angle, |
| σ1 | is the first principal stress, |
| σ3 | is the third principal stress. |
4.4. Calculated Parameters
4.5. Analysis Process
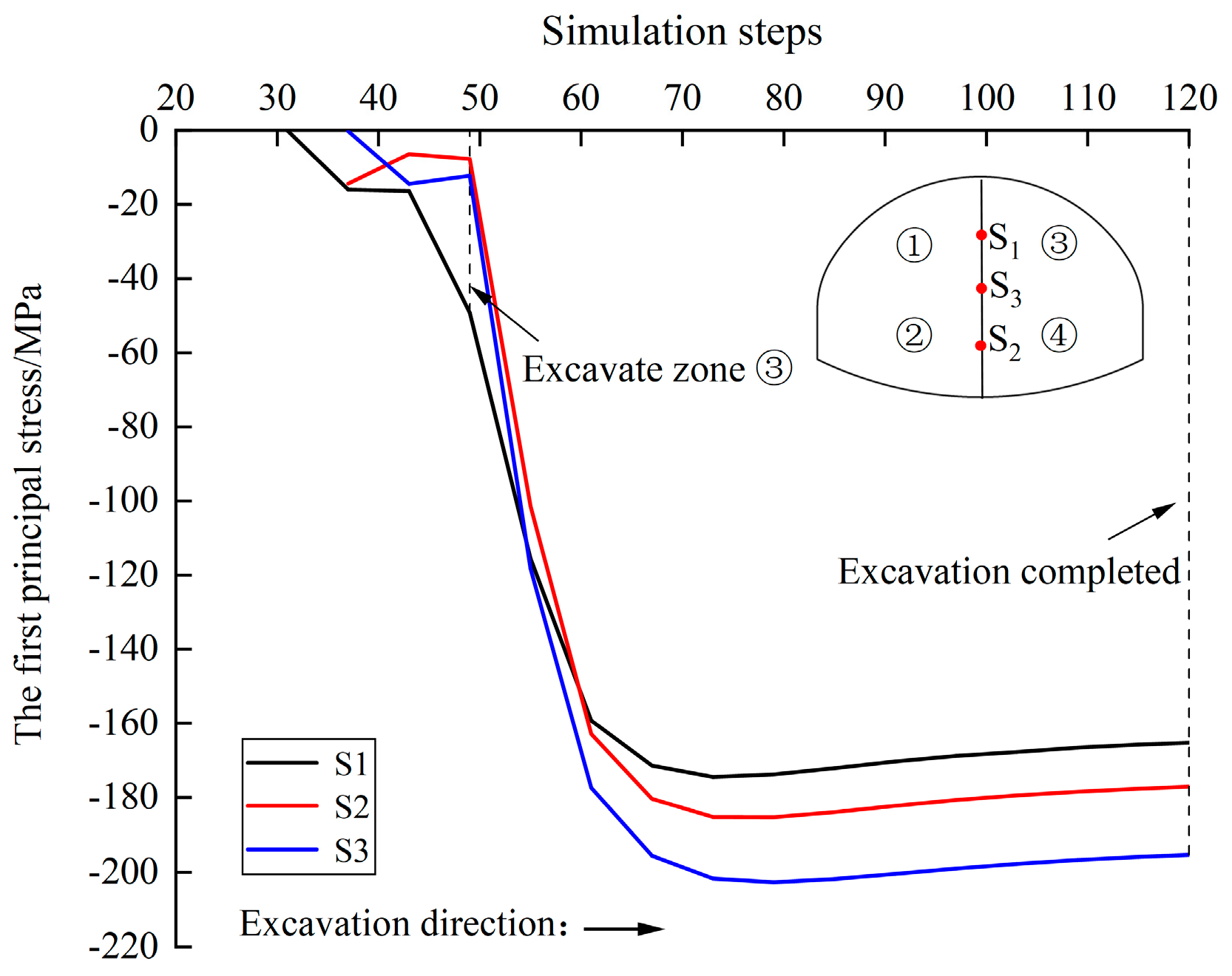
4.5.1. Surrounding Rock Stress
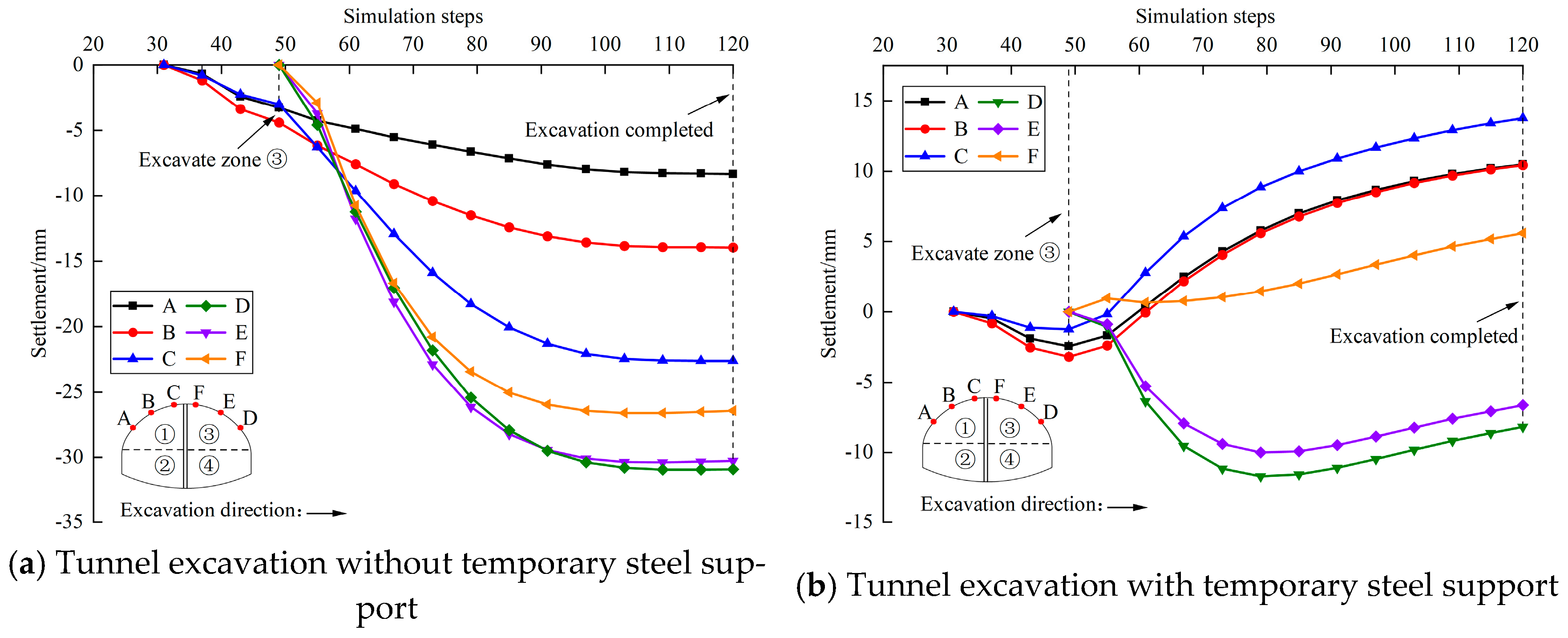
4.5.2. Displacement of Surrounding Rock
4.5.3. Analysis of Mechanical Characteristics in Temporary Steel Support
5. Field Monitoring
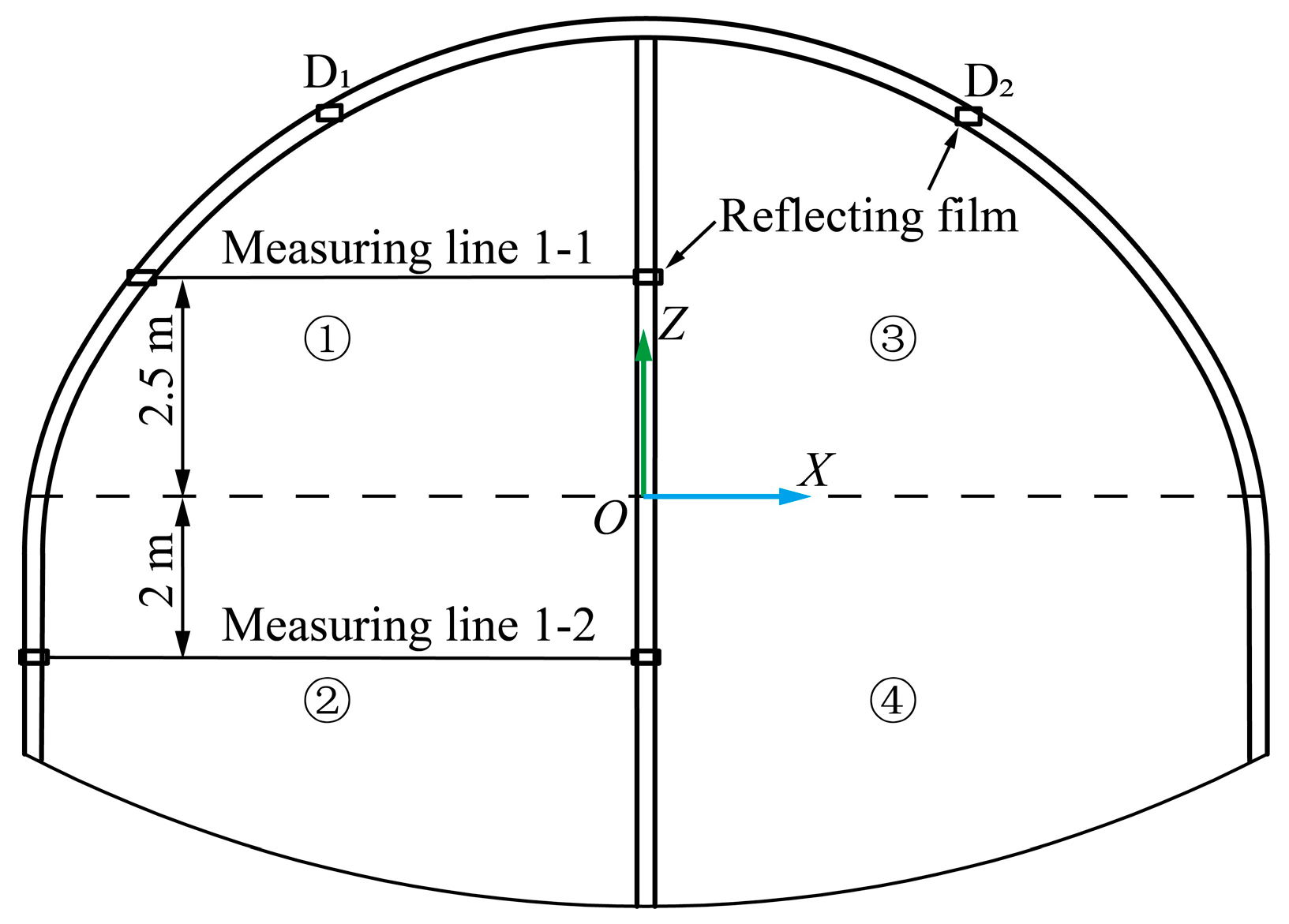
5.1. Measurement Method
5.2. Analysis of Monitoring Results
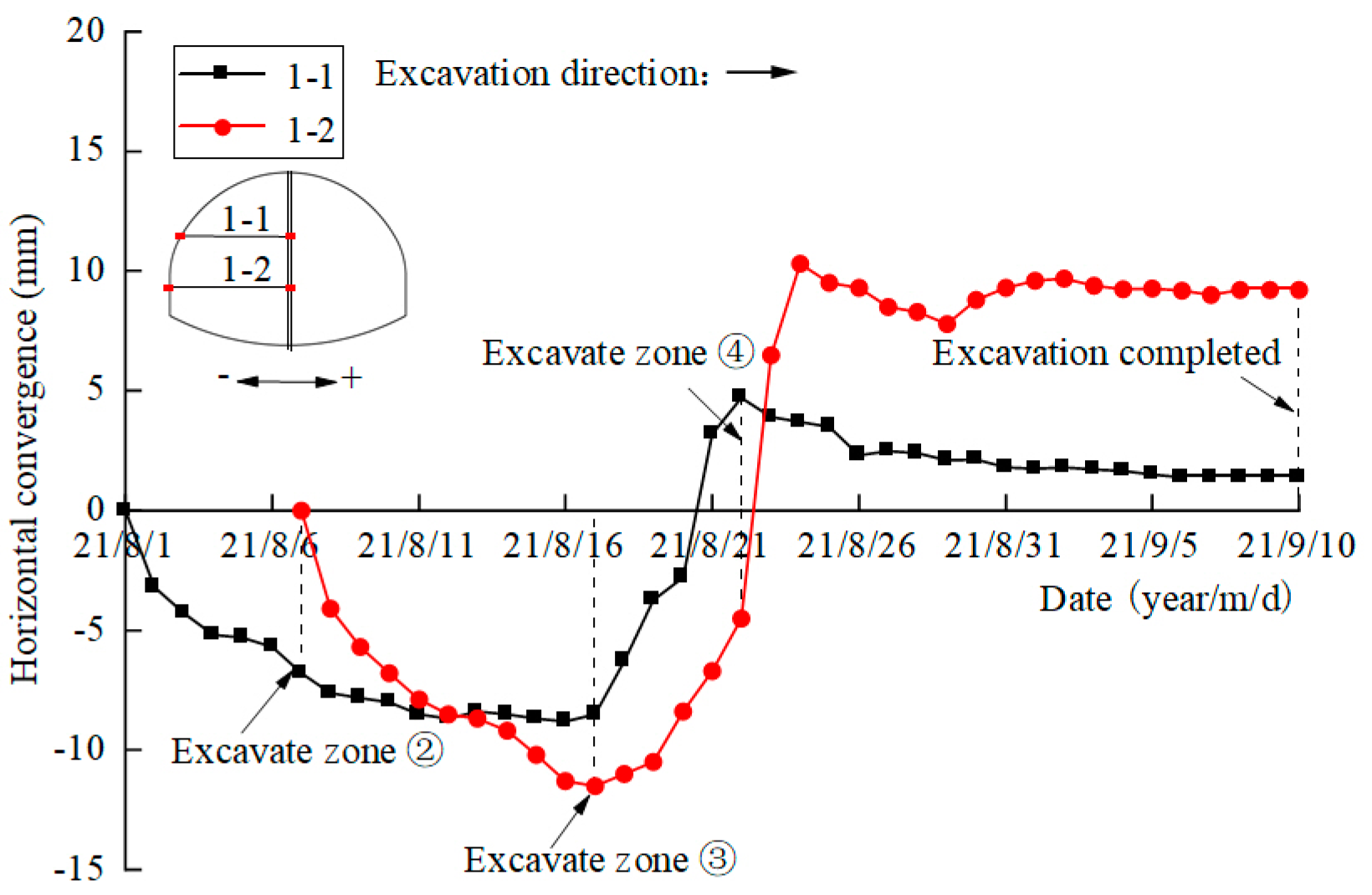
5.2.1. Horizontal Convergence
5.2.2. Spandrel Settlement
6. Conclusions
- (1)
- In the process of simulating tunnel excavation with or without temporary steel support, the stress distribution of the surrounding is basically the same. The existence of steel supports changes the maximum tensile stress of the left spandrel from 0.35 MPa to 0.16 MPa, a decrease of 54.3%. At the same time, the area of the tensile stress area is reduced, which is more conducive to the stability of the surrounding rock.
- (2)
- Affected by the slope bias and the excavation sequence, the maximum settlement of the surrounding rock is distributed on the right spandrel. The existence of temporary steel support makes the maximum settlement of surrounding rock change from −31.23 mm to −7.4 mm, and the bottom uplift change from 88.58 mm to 66.18 mm, which are reduced by 76.3% and 25.3%, respectively.
- (3)
- During the excavation process of the tunnel using the two-step CDM, the change law of the principal stress at the middle point of the temporary steel support of the upper and lower bench is basically the same, showing a “bench-type” phenomenon. Due to the phenomenon of stress concentration, the principal stress value at the joint of the temporary steel support of the upper and lower bench is the largest. Ji Xinbo et al. [39,40] have performed similar research and put forward some measures to enhance the stability of temporary steel supports, such as adding lateral supports or increasing the size of I-steels.
- (4)
- Tunnel excavation methods and excavation sequences have different effects on the deformation of temporary steel supports. When the excavation method (two-step CDM) is used in this paper, the deformation of the steel support on the upper bench undergoes four stages: convergence, expansion, convergence, and stabilization; and the deformation of the steel support on the lower bench undergoes five stages: convergence, expansion, convergence, expansion, and stabilization. However, when the tunnel is excavated by blasting [31,41], the failure process of the temporary steel support goes through four stages of development. Additionally, when adopting CRD excavation method [23], the deformation process is different. This paper enriches the deformation characteristics of temporary steel supports under different excavation methods.
- (5)
- There are some errors between the field monitoring data and the numerical simulation, but the variation law is basically the same, which verifies the rationality of the numerical simulation. The research results can provide guidance for similar engineering support.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.C.; Wong, R.C.K.; Li, S.C.; Qiao, L.P. Finite element analysis of long-term surface settlement above a shallow tunnel in soft ground. Tunn. Undergr. Space Technol. 2012, 30, 85–92. [Google Scholar] [CrossRef]
- Fang, Q.; Tai, Q.M.; Zhang, D.L.; Wong, L.N.Y. Ground surface settlements due to construction of closely-spaced twin tunnels with different geometric arrangements. Tunn. Undergr. Space Technol. 2016, 51, 144–151. [Google Scholar] [CrossRef]
- Dindarloo, S.R.; Siami-Irdemoosa, E. Maximum surface settlement based classification of shallow tunnels in soft ground. Tunn. Undergr. Space Technol. 2015, 49, 320–327. [Google Scholar] [CrossRef]
- Ocak, I. A new approach for estimating the transverse surface settlement curve for twin tunnels in shallow and soft soils. Environ. Earth Sci. 2014, 72, 2357–2367. [Google Scholar] [CrossRef]
- Xiao, J.Z.; Dai, F.C.; Wei, Y.Q.; Xing, Y.C.; Cai, H.; Xu, C. Analysis of mechanical behavior in a pipe roof during excavation of a shallow bias tunnel in loose deposits. Environ. Earth Sci. 2016, 75, 18. [Google Scholar] [CrossRef]
- Morovatdar, A.; Palassi, M.; Ashtiani, R.S. Effect of pipe characteristics in umbrella arch method on controlling tunneling-induced settlements in soft grounds. J. Rock Mech. Geotech. Eng. 2020, 12, 984–1000. [Google Scholar] [CrossRef]
- Aksoy, C.O.; Onargan, T. The role of umbrella arch and face bolt as deformation preventing support system in preventing building damages. Tunn. Undergr. Space Technol. 2010, 25, 553–559. [Google Scholar] [CrossRef]
- Li, D.B.; Zhao, D.; Liu, C.Y. Numerical simulation analysis of the construction mechanics in the process of tunnel excavation. In Proceedings of the International Conference on Green Building, Materials and Civil Engineering (GBMCE 2011), Shangri-La, China, 22–23 August 2011; Trans Tech Publications Ltd.: Shangri-La, China, 2011; pp. 1590–1595. [Google Scholar]
- Tan, Z.-S.; Meng, D.-X.; Shi, X.-D.; Ji, T.-G.; He, L.-C. Research on support system and construction method for large-section small spacing tunnel in loess. China J. Highw. Transp. 2015, 28, 82–97. [Google Scholar]
- Qing, J.; Shu-guang, S.; Tao, L.; Kang, W.; Rui-hai, G. Study on surrounding rock stability of small clear-distance twin highway tunnel with eight lanes. Geotech. Geol. Eng. 2019, 37, 593–598. [Google Scholar]
- Li, Z.Q.; Li, Z. Study on the blasting excavation method of urban shallow tunnel. In Proceedings of the 4th International Conference on Civil Engineering, Architecture and Building Materials (CEABM), Haikou, China, 24–25 May 2014; Trans Tech Publications Ltd.: Haikou, China, 2014; pp. 1051–1055. [Google Scholar]
- Bai, P. Settlement control techniques of the super-shallow buried large-span mined tunnel underneath an existing tunnel. Mod. Tunn. Technol. 2020, 57, 175–181. [Google Scholar]
- Kong, X.; Xia, C.; Qiu, Y.; Zhang, L.; Gong, J. Study of construction mechanical behavior of parallel-small spacing metro tunnels excavated by shield method and cross diaphragm(CRD)method in loess region. Rock Soil Mech. 2011, 32, 516–524. [Google Scholar]
- Yao, H.; Wang, W. Study of optimal proposal and field test for CRD excavation method of shallow-buried tunnel. J. Railway Sci. Eng. 2018, 15, 1509–1515. [Google Scholar]
- Weizhong, C.; Hongdan, Y.U.; Guo, X.; Haifeng, L.U.; Shanpo, J.I.A.; Guojun, W.U. Study on stabilities of surrounding rocks through weathered slot in xiamen subsea tunnel. Chin. J. Rock Mech. Eng. 2008, 27, 873–884. [Google Scholar]
- Li, P.F.; Zhao, Y.; Zhou, X.J. Displacement characteristics of high-speed railway tunnel construction in loess ground by using multi-step excavation method. Tunn. Undergr. Space Technol. 2016, 51, 41–55. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Z.; Chen, J.; Liu, W.; Chen, L.; Li, Y.; Wu, Y. Mechanical calculation model and research on construction mechanical behavior of middle diaphragm in upper bench cd method for super-large span tunnel. China J. Highw. Transp. 2020, 33, 235–248. [Google Scholar]
- Chen, L.J.; Zhang, Y.L.; Ma, Z.Y. Analytical approach for support mechanism of feet-lock pipe combined with steel frame in weak rock tunnels. KSCE J. Civ. Eng. 2016, 20, 2965–2980. [Google Scholar] [CrossRef]
- Luo, Y.B.; Chen, J.X.; Wang, H.Y.; Sun, P.L. Deformation rule and mechanical characteristics of temporary support in soil tunnel constructed by sequential excavation method. KSCE J. Civ. Eng. 2017, 21, 2439–2449. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.; Wang, S.; Wang, G.; Feng, J. Dynamic construction mechanical characteristics and application of combination support method of steel frame and rock wall. China J. Highw. Transp. 2019, 32, 132–142. [Google Scholar]
- Qiu, C.; Liu, B.; He, L.; Feng, S. Model test and in-situ monitoring of double-arch tunnel with integrated middle wall. Rock Soil Mech. 2012, 33, 2625–2631. [Google Scholar]
- Khan, U.H.; Mitri, H.S.; Jones, D. Full scale testing of steel arch tunnel supports. Int. J. Rock Mech. Min. Sci. 1996, 33, 219–232. [Google Scholar] [CrossRef]
- Luo, Y.B.; Chen, J.X.; Huang, P.; Tang, M.Q.; Qiao, X.; Liu, Q. Deformation and mechanical model of temporary support sidewall in tunnel cutting partial section. Tunn. Undergr. Space Technol. 2017, 61, 40–49. [Google Scholar] [CrossRef]
- Lai, J.X.; Zhang, G.L.; Liu, X.W. Mechanical analysis of construction process for shallow weaking surrounding rock multi-arch tunnel. In Proceedings of the International Conference on Fuzzy Systems and Neural Computing (FSNC 2011), Hong Kong, China, 20–21 February 2011; IEEE: Hong Kong, China, 2011; pp. 276–280. [Google Scholar]
- Liu, Y.Q.; Zhang, X.D.; Li, J.L.; Zhang, Z.H.; Zhang, H. Performance assessment of arch-shaped primary lining during construction in weak rock shallow-buried tunnel. KSCE J. Civ. Eng. 2019, 23, 433–443. [Google Scholar] [CrossRef]
- Haidong, G.; Gang, L.; Yanbing, G.; Peng, G. Stability analysis of the middle wall in process of double-arch tunnel construction. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 558, p. 032046. [Google Scholar]
- Zhongwei, W.; Ruihuai, Y.; Hongyan, G.; Ke, L. Study on key construction procedures of CRD method for Re Shuitang No.3 Tunnel. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 711, p. 012074. [Google Scholar]
- Zhang, W.J.; Li, W.T.; Yang, N.; Wang, Q.; Li, T.C.; Wang, G. Determination of the bearing capacity of a Concrete-filled Steel Tubular arch support for tunnel engineering: Experimental and theoretical studies. KSCE J. Civ. Eng. 2017, 21, 2932–2945. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, F.; Fang, Q. Study on mechanical characteristics and applicability of primary lining used in tunnel. Eng. Mech. 2014, 31, 78–84. [Google Scholar]
- Wang, W.; Pan, W.; Bian, J.; Gao, L. Optimization and application of the shallow-buried construction method for an urban underground road tunnel. Mod. Tunn. Technol. 2017, 54, 209–216. [Google Scholar]
- Hou, F.; Li, S.; Guan, X.; Jiang, Q.; Zhou, K.; Zhang, L.; Mou, B. Dynamic response and destruction mechanism of center diaphragm support wall under tunnel blasting. China J. Highw. Transp. 2019, 32, 109–117. [Google Scholar]
- Wang, W. Study on Mechanism and Support Effect of Pipe Roof in Shallow Soft Surrounding Rock Tunnel. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2022. [Google Scholar]
- Li, S.; Zhu, W.; Chen, W.; Li, S. Application of elasto-plastic large displacement finite element method to the study of deformation prediction of soft rock tunnel. Chin. J. Rock Mech. Eng. 2002, 21, 466–470. [Google Scholar]
- Jianxun, C.; Jiuchun, J.; Yanbin, L.U.O.; Mengshu, W. Mechanics characteristic analysis of support structure of loess tunnel entrance. China J. Highw. Transp. 2008, 21, 75–80. [Google Scholar]
- Zhu, Z.; Liu, X.; Zhang, Y. Study of excavation method for ultra-shallow-buried light railway station tunnels with large span. Chin. J. Rock Mech. Eng. 2005, 24, 290–295. [Google Scholar]
- Tang, X.J. Study on the Convergence-Confinement Method and Lts Application in Tunnel Construction. Ph.D. Thesis, Huazhong University of Science & Technology, Wuhan, China, 2009. [Google Scholar]
- GB/T 50266-2013; Standard for Test Methods of Engineering Rock Mass. China Planning Press: Beijing, China, 2013.
- GB/T 50218-2014; Engineering Classification Rock Mass. China Planning Press: Beijing, China, 2014.
- Ji, X.; Zhao, W.; Han, J.; Zhou, Y.; Yu, H. Parameter analysis considering the impacts of the support structure on ground settlement and inner force during center drift construction. Mod. Tunn. Technol. 2015, 52, 59–66. [Google Scholar]
- Zhang, W.; Qiao, X.; Luo, W.; Wang, Y.; Tian, G.; Ni, W.; Liu, W. Research on the optimization of the partition wall in the tunnel construction by the sub-excavation method. J. Lanzhou Univ. Technol. 2022, 48, 127–135. [Google Scholar]
- Guan, X.; Yang, N.; Zhang, W.; Li, M.; Liu, Z.; Wang, X.; Zhang, S. Vibration response and failure modes analysis of the temporary support structure under blasting excavation of tunnels. Eng. Fail. Anal. 2022, 136, 106188. [Google Scholar] [CrossRef]














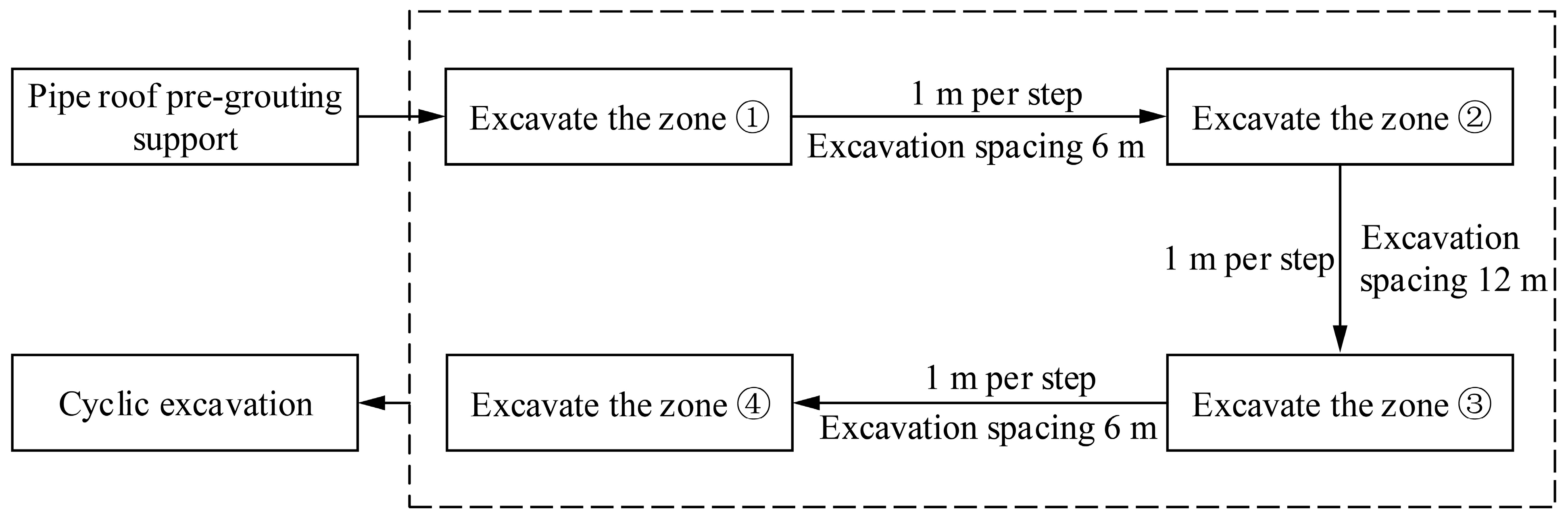
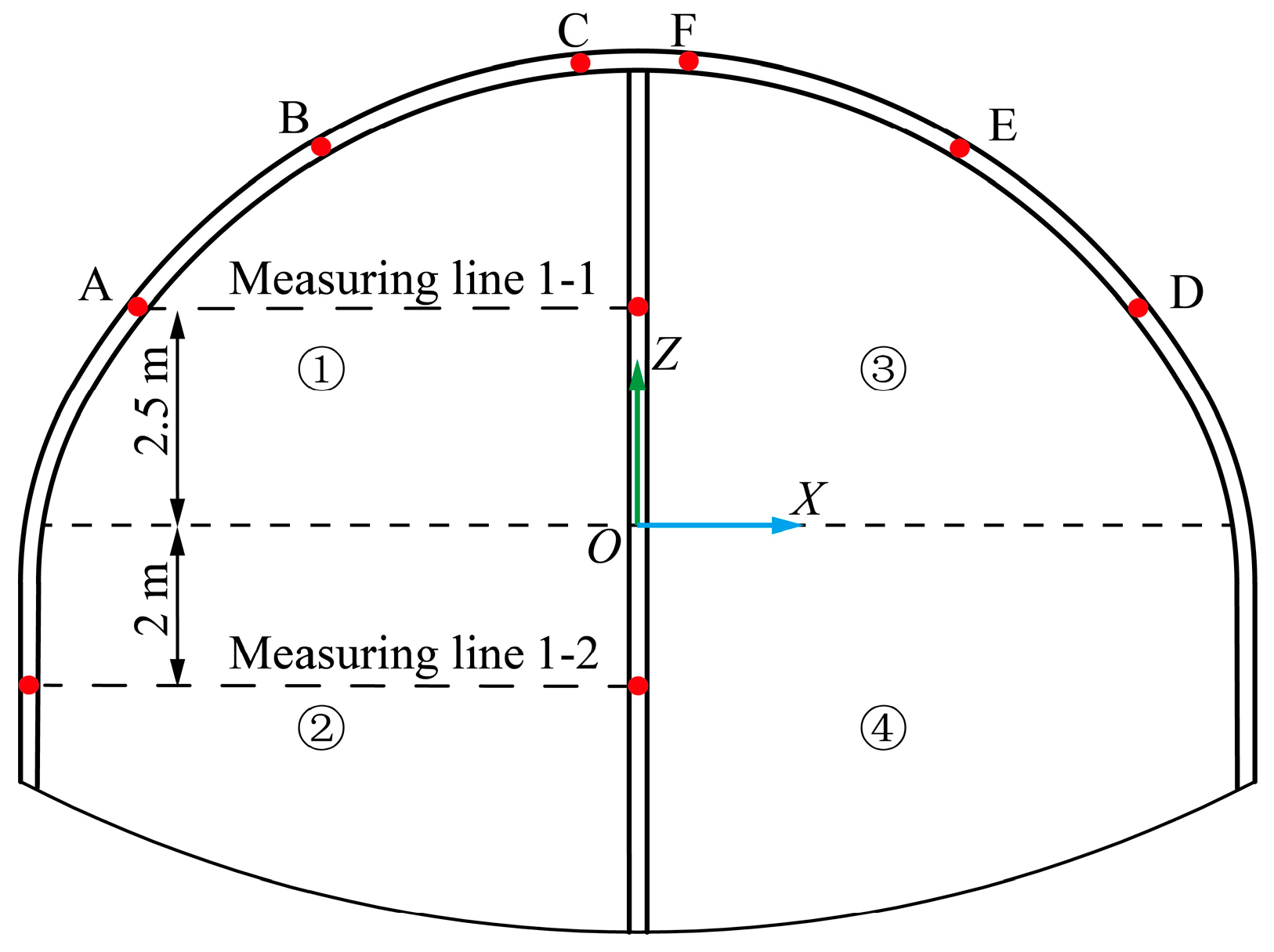
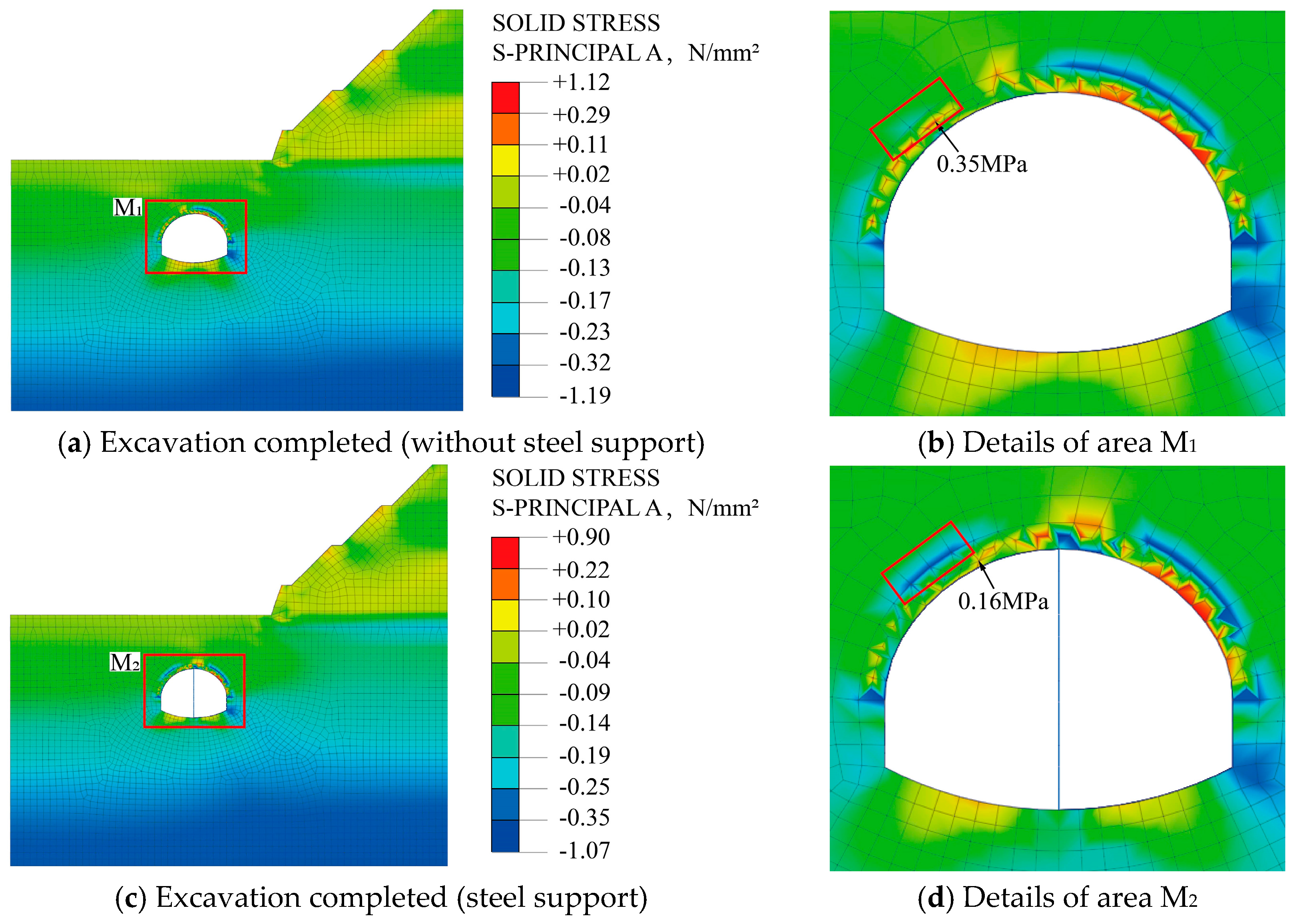

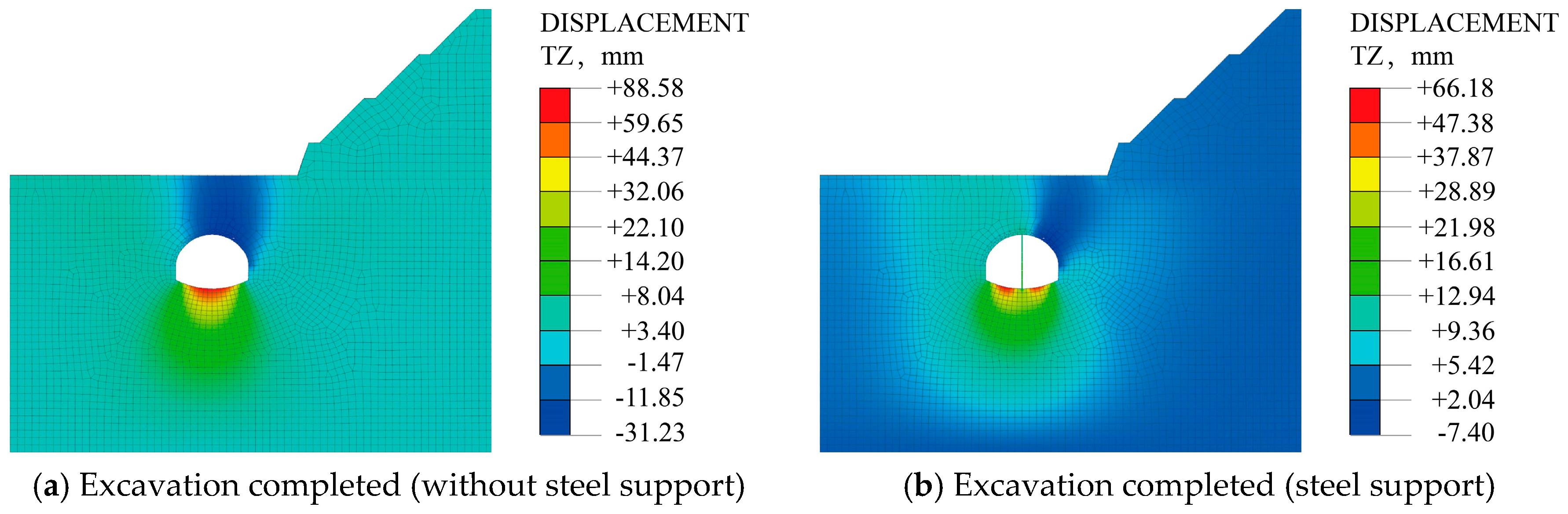




| Strata | Thickness/m | Representative Symbols |
|---|---|---|
| Subgrade filling | 0.7 | Q1 |
| Completely weathered mudstone | 1.7 | Q2 |
| Intensely weathered mudstone | 7.9 | Q3 |
| Moderately weathered calcareous mudstone | 67.4 | Q4 |
| Gravel-containing silty clay | 3.0 | Q5 |
| Materials | Diameter/mm | Elastic Modulus/GPa | Yield Strength/MPa |
|---|---|---|---|
| Anchors | 22 | 210 | 235 |
| Component | Size |
|---|---|
| Diameter of a single steel pipe | D = 108 mm |
| The thickness of a single steel pipe | δ = 4 mm |
| Length of a single steel pipe | L = 40 m |
| Circumferential spacing of a single steel pipe | L = 0.4 m |
| Material | E/MPa | µ | γ/kN·m−3 | c/kPa | φ/(°) |
|---|---|---|---|---|---|
| Grouting steel pipe | 76225 | 0.20 | 28.4 | ||
| Reinforcement area | 1805 | 0.30 | 21.0 | 200 | 28 |
| Type | Section Area/cm2 | Cross-Section Moment of Inertia/cm4 | Elastic Modulus/GPa | Yield Strength/MPa |
|---|---|---|---|---|
| Φ25 mm main reinforcement | 19.63 | 2954.45 | 210 | 400 |
| Φ14 mm connect reinforcement | 12.32 | 732.31 | 210 | 400 |
| Type | Section Area/cm2 | Cross-Section Moment of Inertia /cm4 | Elastic Modulus/GPa | Yield Strength /MPa |
|---|---|---|---|---|
| No. 18 I-steel | 30.43 | 1659.45 | 210 | 235 |
| Specimen | Diameter/mm | Failure Load/kN | Peak Stress/MPa | Poisson Ratio µ | Elastic Modulus/MPa |
|---|---|---|---|---|---|
| 1 | 54.7 | 99.734 | 42.4 | 0.188 | 54.527 |
| 2 | 54.7 | 107.324 | 45.7 | 0.315 | 69.333 |
| 3 | 54.7 | 94.974 | 40.4 | 0.188 | 54.305 |
| Material | E/MPa | µ | γ/kN·m−3 | c/kPa | φ/ (°) |
|---|---|---|---|---|---|
| Subgrade filling | 1.8 | 0.15 | 16.9 | 17 | 10 |
| Completely weathered mudstone | 4.5 | 0.30 | 20.5 | 28 | 16 |
| Intensely weathered mudstone | 9.1 | 0.20 | 20.4 | 28 | 27 |
| Moderately weathered calcareous mudstone | 59.4 | 0.23 | 24.0 | 150 | 33 |
| Gravel-containing silty clay | 20.0 | 0.25 | 19.0 | 39 | 20 |
| Reinforcement area | 1805 | 0.30 | 21.0 | 200 | 28 |
| Grouting steel pipe | 76,225 | 0.20 | 28.4 | ||
| Concrete | 28,000 | 0.20 | 23.0 | ||
| I-steel | 210,000 | 0.30 | 78.5 |
| Positions | Maximum/mm | Final Values/mm | Final Convergence Rates/mm·d−1 |
|---|---|---|---|
| Measuring line 1-1 | −11.5 | 1.4 | −0.1 |
| Measuring line 1-2 | −8.5 | 9.2 | 0.0 |
| Monitoring Points | Maximum/mm | Final Values/mm | Final Settlement Rates/mm·d−1 |
|---|---|---|---|
| D1 | −3.4 | 5.4 | 0.1 |
| D2 | −9.9 | -9.9 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Xiong, Y.; Li, S.; Zhou, X.; Li, Z. Deformation Characteristics Analysis of Temporary Support in Unsymmetrical Loading Tunnel Excavation under Composite Support. Symmetry 2023, 15, 830. https://doi.org/10.3390/sym15040830
Wang K, Xiong Y, Li S, Zhou X, Li Z. Deformation Characteristics Analysis of Temporary Support in Unsymmetrical Loading Tunnel Excavation under Composite Support. Symmetry. 2023; 15(4):830. https://doi.org/10.3390/sym15040830
Chicago/Turabian StyleWang, Kezhong, Yu Xiong, Sheng Li, Xin Zhou, and Zhikuan Li. 2023. "Deformation Characteristics Analysis of Temporary Support in Unsymmetrical Loading Tunnel Excavation under Composite Support" Symmetry 15, no. 4: 830. https://doi.org/10.3390/sym15040830
APA StyleWang, K., Xiong, Y., Li, S., Zhou, X., & Li, Z. (2023). Deformation Characteristics Analysis of Temporary Support in Unsymmetrical Loading Tunnel Excavation under Composite Support. Symmetry, 15(4), 830. https://doi.org/10.3390/sym15040830






