A Novel Strong S-Box Design Using Quantum Crossover and Chaotic Boolean Functions for Symmetric Cryptosystems
Abstract
1. Introduction
- (1)
- The proposed S-box is based on the combination of chaotic Boolean functions, classical genetic algorithm techniques, and the quantum crossover. The chaotic Lorenz system provides a source of randomness, while the Boolean functions and genetic algorithm techniques ensure the cryptographic strength of the generated S-box. Chaotic Boolean functions offer several advantages for their use in symmetric cryptography. They can generate pseudo-random sequences that have a high level of entropy, meaning that they appear random to an observer even if they are generated deterministically. Moreover, chaotic Boolean functions are computationally efficient, which is important in cryptography as encryption and decryption must be performed in real time. They can be implemented in hardware with low resources.
- (2)
- The quantum crossover is used to generate new bitstrings by combining bits from two parent bitstrings. This technique takes advantage of quantum parallelism to evaluate multiple-bit combinations simultaneously, which can lead to faster convergence and better exploration of the search space.
- (3)
- The classical two-point crossover technique helps to improve the permutation phase of the algorithm.
- (4)
- The present work offers a comprehensive and meticulous investigation of the randomness properties of the S-box. The randomness is evaluated by applying the NIST statistical test suite. The distribution of p-values was analyzed to ensure its uniformity, which is a measure of the randomness of the S-box’s output. The results of the statistical tests, combined with the uniformity of the distribution of p-values, provided a comprehensive evaluation of the S-box’s randomness and cryptographic security. By passing the NIST tests, the generated S-box is confirmed to have the desired randomness properties, making it suitable for use in symmetric cryptography.
- (5)
- This paper makes a significant contribution to the field of cryptography by providing a novel and efficient method for generating secure S-boxes, which can be easily adapted for use in various symmetric cryptosystems.
2. Related Work
3. Quantum Computing
3.1. Quantum Bit
3.2. Quantum Gates
4. Boolean Functions
4.1. Substitution Box
4.2. Non-Linearity
4.3. Cryptographic Properties
5. Classical Genetic Algorithm
| Algorithm 1 Classical Genetic Algorithm |
|
| Algorithm 2 Crossover and Mutation in Classical Genetic Algorithm |
|
6. Lorenz System
7. The Proposed Algorithm
7.1. Quantum Crossover
- Step 1.
- Initialize the quantum circuit: The number of qubits in the circuit is equal to twice the length of the classical chromosome A. The first half of the qubits corresponds to the qubits of the first parent A, and the second half corresponds to the qubits of the second parent B.
- Step 2.
- Apply the Hadamard gate to the qubits of parent A: The Hadamard gate initializes the qubits in a superposition of the 0 and 1 states, which is necessary for the quantum parallelism used in the crossover operation.
- Step 3.
- Apply the controlled-NOT (CNOT) gate to each pair of corresponding qubits of parents A and B: The CNOT gate flips the target qubit (the qubit in the second half) if the control qubit (the qubit in the first half) is in the 1 state.
- Step 4.
- Measure the qubits corresponding to parent A: The measurement collapses the superposition of the qubits into a classical bitstring c with a probability proportional to the amplitude of the state.
- Step 5.
- Decode the classical bitstring c into the corresponding child chromosome C: The classical bitstring c represents a part of the child chromosome C that is inherited from parent A, which is obtained by applying the XOR operation between c and parent A.
- Step 6.
- Output the parent chromosomes A and B and the child chromosome C.
| Algorithm 3 Quantum Bitstring Crossover |
| Require: Two classical parent bitstrings A and B of length n. Ensure: One child bitstring C of length n.
|
7.2. S-Box Generation Algorithm
- Step 1.
- Create eight chaotic Boolean functions using the following steps.
- Start with an empty binary sequence, SB.
- Using the initial value , iterate the first equation of the Lorenz system (Equation (5)) 50 times to eliminate the transient effect.
- Continue iterating the equation for 4096 times and, at each iteration, calculate the current state value, . Then, using Equation (6), obtain a binary value, x, and add it to SB.SB is a set of 512 eight-bitstrings.
- Perform the quantum crossover between every two consecutive bitstrings to obtain 256 new bitstrings.
- Divide these bitstrings into eight sets, each containing 256 elements. Each set represents a Boolean function.
Step 1 is shown in Figure 4. - Step 2.
- The process of creating an S-box involves transforming every bitstring generated in Step 1 into decimal values. As a result, 256 decimal values are generated to form the S-box.
- Step 3.
- The S-box must satisfy the requirement of bijectivity, which means that each output value must be unique. To ensure this, the S-box must undergo an adjustment process, the steps of which are as follows.
- Identify duplicates within the S-box and replace all duplicates except the first occurrence with −1.
- Create an array (V) of missing elements in the range of 0 to 255.
- Fill the missing elements (represented by −1) in the S-box with elements from the V array in sequence.
- Step 4.
- Generating crossover points: The proposed algorithm uses the two-point crossover operator for permutation. To determine the crossover points, the second equation of the Lorenz system (Equation (5)) is utilized, and the points are generated within the range from 0 to 255. The steps are illustrated in Algorithm 4.
- Given the initial value .
- Iterate the second equation of the Lorenz system (Equation (5)) to obtain the value of y.
- Use the value of to generate the crossover points within the range from 0 to 255 as follows.
- Repeat Steps 2 and 3 until the desired number of crossover points are generated.
Algorithm 4 Generating Crossover Points Using Lorenz System 1: procedureGenerate Crossover Points; 2: Input: Initial value , Desired number of crossover points N; 3: Output: Crossover points y; 4: Set ; 5: for to N do; 6: ▹ Iterate the second equation of the Lorenz system; 7: ▹ Generate the crossover points; 8: end for; 9: end procedure. - Step 5.
- Reshaping process: Transform the obtained S-box from a vector of 256 values into a 16 × 16 matrix. This process is used to visualize the S-box as a matrix, which can help with analyzing and understanding its properties. An example of transforming a vector of six values into a 2 × 3 matrix is illustrated in Figure 5.
- Step 6.
- Permutation phase: Perform the two-point crossover operator by utilizing the two points generated previously to swap the sequences of values between the points. The two random points would be selected in each pair of consecutive rows, and the values between these two points would be swapped between the two rows to generate a new offspring matrix. The process is illustrated in Figure 6.
- Step 7.
- The mutation step is applied by swapping the two crosspoints that were generated previously. This step is used to introduce variation and diversity into the S-box values.
- Step 8.
- This process is repeated several times to achieve the desired degree of randomness in the final S-box.
8. Experimental Results and Performance Analysis of the Generated S-Box
8.1. Bijectivity
8.2. Non-Linearity
8.3. Algebraic Immunity
8.4. BIC
9. Randomness Test of the S-Box
9.1. NIST Statistical Test Suite
- (1)
- Evaluates the quality of the S-box: The NIST tests evaluate the randomness and uniformity of the S-box, which are important properties for cryptographic applications.
- (2)
- Helps to detect flaws: By evaluating the output of an S-box against the requirements for randomness and uniformity, the NIST tests can help to identify any flaws in the design or implementation of the S-box.
- (3)
- Industry standard: The NIST statistical test suite is widely accepted as the industry standard for evaluating the randomness and uniformity of digital sequences. This means that the results of NIST tests are easily recognizable and interpretable by others in the field.
- (4)
- Comprehensive testing: The NIST suite consists of 15 statistical tests, which evaluate different aspects of randomness and uniformity. This comprehensive approach provides a thorough evaluation of the S-box.
- (5)
- Improved security: By ensuring that the S-box has good randomness and uniformity properties, the NIST tests help to improve the security of the cryptographic system that uses the S-box.
9.2. Uniform Distribution of p-Values
9.3. Results and Discussion
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rijmen, V. Efficient Implementation of the Rijndael S-Box; Katholieke Universiteit Leuven, Department of Electrical Engineering ESAT: Leuven, Belgium, 2000. [Google Scholar]
- Mister, S.; Adams, C. Practical S-box design. In Proceedings of the Workshop on Selected Areas in Cryptography, SAC, Kingston, ON, Canada, 1996; Volume 96, pp. 61–76. Available online: https://sacworkshop.org/SAC-history.html (accessed on 20 March 2023).
- Carlet, C.; Crama, Y.; Hammer, P.L. Boolean Functions for Cryptography and Error-Correcting Codes; Universiry of Paris: Paris, France, 2010. [Google Scholar]
- Zhang, R.; Cavalcante, H.L.d.S.; Gao, Z.; Gauthier, D.J.; Socolar, J.E.; Adams, M.M.; Lathrop, D.P. Boolean chaos. Phys. Rev. E 2009, 80, 045202. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Ding, Q. Construction of an S-box based on chaotic and bent functions. Symmetry 2021, 13, 671. [Google Scholar] [CrossRef]
- Tito-Corrioso, O.; Borges-Trenard, M.A.; Borges-Quintana, M.; Rojas, O.; Sosa-Gómez, G. Study of Parameters in the Genetic Algorithm for the Attack on Block Ciphers. Symmetry 2021, 13, 806. [Google Scholar] [CrossRef]
- Ahmed, H.A.; Zolkipli, M.F.; Ahmad, M. A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map. Neural Comput. Appl. 2019, 31, 7201–7210. [Google Scholar] [CrossRef]
- Ahmad, M.; Doja, M.N.; Beg, M.S. ABC optimization based construction of strong substitution-boxes. Wirel. Pers. Commun. 2018, 101, 1715–1729. [Google Scholar] [CrossRef]
- Akhtar, T.; Din, N.; Uddin, J. Substitution box design based on chaotic maps and cuckoo search algorithm. In Proceedings of the 2019 International Conference on Advanced Communication Technologies and Networking (CommNet), Rabat, Morocco, 12–14 April 2019; pp. 1–7. [Google Scholar]
- Guesmi, R.; Farah, M.A.B.; Kachouri, A.; Samet, M. A novel design of Chaos based S-Boxes using genetic algorithm techniques. In Proceedings of the 2014 IEEE/ACS 11th International Conference on Computer Systems and Applications (AICCSA), Doha, Qatar, 10–13 November 2014; pp. 678–684. [Google Scholar]
- Artuğer, F.; Özkaynak, F. An effective method to improve nonlinearity value of substitution boxes based on random selection. Inf. Sci. 2021, 576, 577–588. [Google Scholar] [CrossRef]
- Guesmi, R.; Farah, M.A.B.; Kachouri, A.; Samet, M. Chaos-based designing of a highly nonlinear S-box using Boolean functions. In Proceedings of the 2015 IEEE 12th International Multi-Conference on Systems, Signals & Devices (SSD15), Mahdia, Tunisia, 16–19 March 2015; pp. 1–5. [Google Scholar]
- Farah, M.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dyn. 2020, 99, 3041–3064. [Google Scholar] [CrossRef]
- Ahmad, M.; Ahmad, Z. Random search based efficient chaotic substitution box design for image encryption. Int. J. Rough Sets Data Anal. 2018, 5, 131–147. [Google Scholar] [CrossRef]
- Khan, M.; Asghar, Z. A novel construction of substitution box for image encryption applications with Gingerbreadman chaotic map and S 8 permutation. Neural Comput. Appl. 2018, 29, 993–999. [Google Scholar] [CrossRef]
- Mousavi, M.; Sadeghiyan, B. A new image encryption scheme with Feistel like structure using chaotic S-box and Rubik cube based P-box. Multimed. Tools Appl. 2021, 80, 13157–13177. [Google Scholar] [CrossRef]
- Ullah, A.; Jamal, S.S.; Shah, T. A novel scheme for image encryption using substitution box and chaotic system. Nonlinear Dyn. 2018, 91, 359–370. [Google Scholar] [CrossRef]
- Shafique, A. A new algorithm for the construction of substitution box by using chaotic map. Eur. Phys. J. Plus 2020, 135, 1–13. [Google Scholar] [CrossRef]
- Artuğer, F.; Özkaynak, F. A novel method for performance improvement of chaos-based substitution boxes. Symmetry 2020, 12, 571. [Google Scholar] [CrossRef]
- Zahid, A.H.; Arshad, M.J. An innovative design of substitution-boxes using cubic polynomial mapping. Symmetry 2019, 11, 437. [Google Scholar] [CrossRef]
- Usama, M.; Rehman, O.; Memon, I.; Rizvi, S. An efficient construction of key-dependent substitution box based on chaotic sine map. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719895957. [Google Scholar] [CrossRef]
- Alzaidi, A.A.; Ahmad, M.; Ahmed, H.S.; Solami, E.A. Sine-cosine optimization-based bijective substitution-boxes construction using enhanced dynamics of chaotic map. Complexity 2018, 2018, 9389065. [Google Scholar] [CrossRef]
- Lawnik, M.; Berezowski, M. New chaotic system: M-map and its application in chaos-based cryptography. Symmetry 2022, 14, 895. [Google Scholar] [CrossRef]
- Zhu, D.; Tong, X.; Zhang, M.; Wang, Z. A new S-box generation method and advanced design based on combined chaotic system. Symmetry 2020, 12, 2087. [Google Scholar] [CrossRef]
- Wan, P.Y.; Liao, T.L.; Yan, J.J.; Tsai, H.H. Discrete sliding mode control for chaos synchronization and its application to an improved El-Gamal cryptosystem. Symmetry 2019, 11, 843. [Google Scholar] [CrossRef]
- Khan, M. A novel image encryption scheme based on multiple chaotic S-boxes. Nonlinear Dyn. 2015, 82, 527–533. [Google Scholar] [CrossRef]
- Lambić, D. A novel method of S-box design based on discrete chaotic map. Nonlinear Dyn. 2017, 87, 2407–2413. [Google Scholar] [CrossRef]
- Islam, F.u.; Liu, G. Designing S-box based on 4D-4wing hyperchaotic system. 3D Res. 2017, 8, 1–9. [Google Scholar] [CrossRef]
- Gabr, M.; Younis, H.; Ibrahim, M.; Alajmy, S.; Khalid, I.; Azab, E.; Elias, R.; Alexan, W. Application of DNA Coding, the Lorenz Differential Equations and a Variation of the Logistic Map in a Multi-Stage Cryptosystem. Symmetry 2022, 14, 2559. [Google Scholar] [CrossRef]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. Rgb image encryption through cellular automata, s-box and the lorenz system. Symmetry 2022, 14, 443. [Google Scholar] [CrossRef]
- Xiao, G.Z.; Massey, J.L. A spectral characterization of correlation-immune combining functions. IEEE Trans. Inf. Theory 1988, 34, 569–571. [Google Scholar] [CrossRef]
- Pasalic, E. On Boolean Functions in Symmetric-Key Ciphers; Lund University: Lund, Sweden, 2003. [Google Scholar]
- Makhlin, Y.; Schön, G.; Shnirman, A. Quantum-state engineering with Josephson-junction devices. Rev. Mod. Phys. 2001, 73, 357. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 1995, 74, 4091. [Google Scholar] [CrossRef]
- Hanson, R.; Gywat, O.; Awschalom, D. Room-temperature manipulation and decoherence of a single spin in diamond. Phys. Rev. B 2006, 74, 161203. [Google Scholar] [CrossRef]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V.; Damski, B.; Sen, A.; Sen, U. Ultracold atomic gases in optical lattices: Mimicking condensed matter physics and beyond. Adv. Phys. 2007, 56, 243–379. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Gruska, J. Quantum Computing; McGraw-Hill: London, UK, 1999; Volume 2005. [Google Scholar]
- Barnum, H.; Bernstein, H.J.; Spector, L. A quantum circuit for OR. arXiv 1999, arXiv:quant-ph/9907056. [Google Scholar]
- Leier, A.; Banzhaf, W. Evolving Hogg’s quantum algorithm using linear-tree GP. In Proceedings of the Genetic and Evolutionary Computation—GECCO 2003: Genetic and Evolutionary Computation Conference, Chicago, IL, USA, 12–16 July 2003; pp. 390–400. [Google Scholar]
- Malossini, A.; Blanzieri, E.; Calarco, T. QGA: A quantum genetic algorithm. IEEE Trans. Neural Netw. Publ. IEEE Neural Netw. Counc. 2008, 12, 231–241. [Google Scholar]
- Malossini, A.; Blanzieri, E.; Calarco, T. Quantum genetic optimization. IEEE Trans. Evol. Comput. 2008, 12, 231–241. [Google Scholar] [CrossRef]
- Carlet, C.; Dalai, D.K.; Gupta, K.C.; Maitra, S. Algebraic immunity for cryptographically significant Boolean functions: Analysis and construction. IEEE Trans. Inf. Theory 2006, 52, 3105–3121. [Google Scholar] [CrossRef]
- Webster, A.; Tavares, S. On the design of S-boxes in Advances in Cryptology. In Proceedings of the CRYPTO’ 85, Santa Barbara, CA, USA, 18–22 August 1985. [Google Scholar]
- Biham, E.; Shamir, A. Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 1991, 4, 3–72. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Weisstein, E.W. Logistic Equation. 2003. Available online: https://mathworld.wolfram.com/ (accessed on 20 March 2023).
- Bouman, C.; Sauer, K. A generalized Gaussian image model for edge-preserving MAP estimation. IEEE Trans. Image Process. 1993, 2, 296–310. [Google Scholar] [CrossRef]
- Aharonov, D.; Kitaev, A.; Nisan, N. Quantum circuits with mixed states. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998; pp. 20–30. [Google Scholar]
- Wang, J.; Zhu, Y.; Zhou, C.; Qi, Z. Construction method and performance analysis of chaotic S-box based on a memorable simulated annealing algorithm. Symmetry 2020, 12, 2115. [Google Scholar] [CrossRef]
- Alshammari, B.M.; Guesmi, R.; Guesmi, T.; Alsaif, H.; Alzamil, A. Implementing a symmetric lightweight cryptosystem in highly constrained IoT devices by using a chaotic S-box. Symmetry 2021, 13, 129. [Google Scholar] [CrossRef]
- Tian, P.; Su, R. A Novel Virtual Optical Image Encryption Scheme Created by Combining Chaotic S-Box with Double Random Phase Encoding. Sensors 2022, 22, 5325. [Google Scholar] [CrossRef]
- Lambić, D. A new discrete-space chaotic map based on the multiplication of integer numbers and its application in S-box design. Nonlinear Dyn. 2020, 100, 699–711. [Google Scholar] [CrossRef]
- Hematpour, N.; Ahadpour, S.; Sourkhani, I.G.; Sani, R.H. A new steganographic algorithm based on coupled chaotic maps and a new chaotic S-box. Multimed. Tools Appl. 2022, 81, 39753–39784. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü.; Zengin, A.; Pehlivan, I.; Kaçar, S. A novel approach for strong S-Box generation algorithm design based on chaotic scaled Zhongtang system. Nonlinear Dyn. 2017, 87, 1081–1094. [Google Scholar] [CrossRef]
- Tong, X.; Liu, X.; Liu, J.; Zhang, M.; Wang, Z. A novel lightweight block encryption algorithm based on combined chaotic S-box. Int. J. Bifurc. Chaos 2021, 31, 2150152. [Google Scholar] [CrossRef]
- Hua, Z.; Li, J.; Chen, Y.; Yi, S. Design and application of an S-box using complete Latin square. Nonlinear Dyn. 2021, 104, 807–825. [Google Scholar] [CrossRef]
- Zheng, J.; Zeng, Q. An image encryption algorithm using a dynamic S-box and chaotic maps. Appl. Intell. 2022, 52, 15703–15717. [Google Scholar] [CrossRef]
- Özkaynak, F.; Çelik, V.; Özer, A.B. A new S-box construction method based on the fractional-order chaotic Chen system. Signal Image Video Process. 2017, 11, 659–664. [Google Scholar] [CrossRef]
- Jakimoski, G.; Kocarev, L. Chaos and cryptography: Block encryption ciphers based on chaotic maps. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 163–169. [Google Scholar] [CrossRef]
- Crocetti, L.; Nannipieri, P.; Di Matteo, S.; Fanucci, L.; Saponara, S. Review of Methodologies and Metrics for Assessing the Quality of Random Number Generators. Electronics 2023, 12, 723. [Google Scholar] [CrossRef]
- de la Fraga, L.G.; Ovilla-Martínez, B. Generating Even More Chaotic Instances in Hardware. Electronics 2023, 12, 332. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- Bassham, L.E., III; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. SP 800-22 Rev. 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
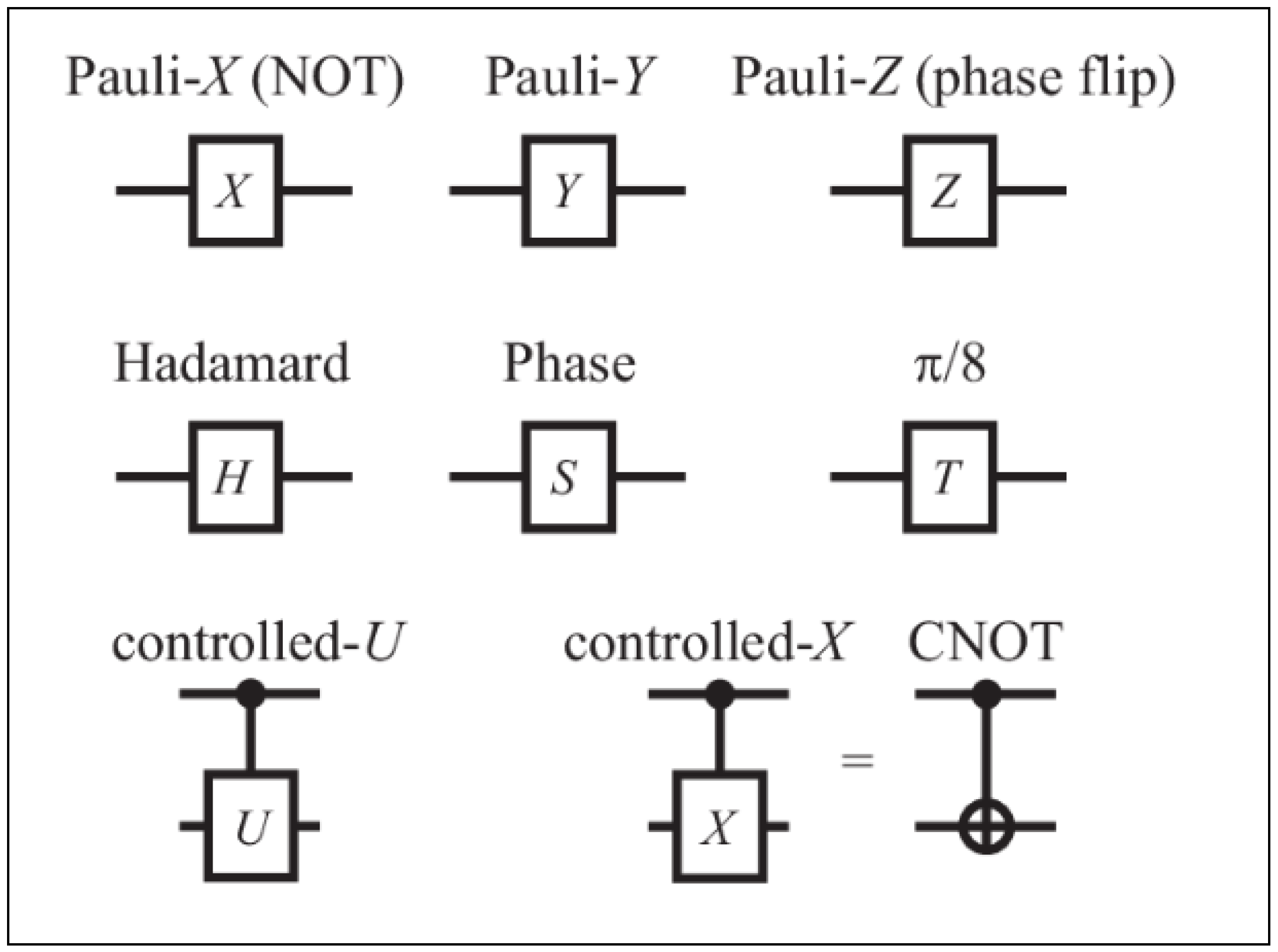







| Gate | Name | Operation |
|---|---|---|
| X | Pauli-X gate | Flips the state of a qubit |
| Y | Pauli-Y gate | Flips the state of a qubit and adds a phase of i |
| Z | Pauli-Z gate | Adds a phase of −1 to the state |
| H | Hadamard gate | Creates a superposition of and |
| CNOT | Controlled-NOT gate | Flips the second qubit if and only if the first qubit is |
| CCNOT | Toffoli gate | Flips the third qubit if and only if the first two qubits are both |
| SWAP | SWAP gate | Swaps the states of two qubits |
| S | Phase shift gate | Adds a phase of i to the state |
| T | Phase shift gate | Adds a phase of to the state |
| 232 | 3 | 228 | 222 | 125 | 243 | 219 | 176 | 199 | 107 | 7 | 217 | 250 | 205 | 229 | 139 |
| 30 | 168 | 35 | 32 | 147 | 73 | 6 | 104 | 233 | 118 | 151 | 126 | 53 | 206 | 169 | 183 |
| 51 | 150 | 245 | 157 | 209 | 138 | 12 | 246 | 148 | 84 | 85 | 113 | 154 | 77 | 105 | 23 |
| 207 | 255 | 64 | 254 | 92 | 96 | 115 | 57 | 74 | 190 | 31 | 208 | 127 | 119 | 130 | 93 |
| 149 | 180 | 102 | 203 | 72 | 25 | 238 | 241 | 242 | 143 | 173 | 109 | 225 | 239 | 197 | 80 |
| 54 | 175 | 153 | 195 | 152 | 67 | 18 | 4 | 81 | 170 | 49 | 13 | 99 | 9 | 66 | 79 |
| 61 | 135 | 71 | 230 | 94 | 45 | 75 | 46 | 165 | 116 | 122 | 194 | 134 | 68 | 19 | 158 |
| 191 | 237 | 26 | 8 | 37 | 163 | 252 | 251 | 27 | 234 | 184 | 86 | 117 | 98 | 215 | 40 |
| 69 | 41 | 70 | 188 | 58 | 36 | 196 | 38 | 214 | 218 | 48 | 161 | 224 | 177 | 167 | 189 |
| 11 | 16 | 100 | 244 | 213 | 223 | 227 | 62 | 192 | 17 | 132 | 247 | 145 | 235 | 226 | 124 |
| 156 | 24 | 78 | 87 | 200 | 171 | 29 | 82 | 160 | 159 | 253 | 178 | 39 | 111 | 42 | 221 |
| 112 | 202 | 65 | 14 | 89 | 182 | 249 | 60 | 33 | 212 | 108 | 166 | 123 | 131 | 142 | 187 |
| 21 | 0 | 140 | 231 | 155 | 103 | 114 | 186 | 15 | 162 | 56 | 43 | 34 | 91 | 101 | 95 |
| 106 | 88 | 10 | 110 | 146 | 120 | 90 | 128 | 97 | 198 | 47 | 248 | 236 | 20 | 55 | 144 |
| 83 | 28 | 141 | 210 | 50 | 137 | 5 | 172 | 133 | 179 | 164 | 204 | 136 | 129 | 185 | 216 |
| 193 | 76 | 22 | 211 | 1 | 201 | 2 | 174 | 44 | 59 | 121 | 63 | 220 | 181 | 240 | 52 |
| S-Box | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Avg. Non-Linearity |
|---|---|---|---|---|---|---|---|---|---|
| S-Box | 108 | 104 | 108 | 108 | 106 | 108 | 108 | 108 | 107 |
| S-Box | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Non-Linearity |
|---|---|---|---|---|---|---|---|---|---|
| AES S-box | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 |
| [12] | 108 | 110 | 110 | 108 | 106 | 106 | 106 | 110 | 108 |
| [51] | 108 | 108 | 108 | 104 | 106 | 110 | 108 | 110 | 108 |
| [10] | 106 | 108 | 110 | 106 | 110 | 106 | 106 | 108 | 107.5 |
| [52] | 108 | 108 | 106 | 108 | 106 | 106 | 108 | 106 | 107 |
| The generated S-box | 108 | 104 | 108 | 108 | 106 | 108 | 108 | 108 | 107 |
| [53] | 108 | 110 | 108 | 104 | 108 | 106 | 106 | 106 | 107 |
| [27] | 108 | 106 | 106 | 106 | 106 | 106 | 108 | 108 | 106.5 |
| [54] | 108 | 108 | 106 | 106 | 106 | 106 | 106 | 106 | 106.5 |
| [55] | 102 | 110 | 102 | 106 | 108 | 108 | 108 | 108 | 106.5 |
| [13] | 108 | 104 | 106 | 106 | 106 | 106 | 108 | 106 | 106.25 |
| [56] | 108 | 106 | 104 | 108 | 106 | 110 | 104 | 104 | 106 |
| [57] | 108 | 106 | 104 | 108 | 104 | 106 | 102 | 106 | 105.5 |
| [58] | 108 | 106 | 104 | 108 | 104 | 108 | 102 | 102 | 105.25 |
| [59] | 108 | 102 | 104 | 106 | 104 | 104 | 102 | 102 | 104 |
| [60] | 107 | 102 | 101 | 104 | 106 | 104 | 106 | 106 | 104.5 |
| [61] | 108 | 102 | 100 | 102 | 104 | 104 | 104 | 102 | 103.25 |
| 0.4075 | 0.50125 | 0.515625 | 0.484075 | 0.4075 | 0.515625 | 0.450125 | 0.484075 |
| 0.46875 | 0.515625 | 0.5625 | 0.484075 | 0.515625 | 0.515625 | 0.50125 | 0.5 |
| 0.46875 | 0.546875 | 0.546875 | 0.484075 | 0.46875 | 0.50125 | 0.50125 | 0.421875 |
| 0.515625 | 0.450125 | 0.515625 | 0.50125 | 0.5 | 0.50125 | 0.5 | 0.50125 |
| 0.46875 | 0.515625 | 0.515625 | 0.484075 | 0.515625 | 0.59075 | 0.515625 | 0.50125 |
| 0.50125 | 0.50125 | 0.4075 | 0.484075 | 0.5 | 0.546875 | 0.515625 | 0.4075 |
| 0.450125 | 0.484075 | 0.450125 | 0.515625 | 0.59075 | 0.5 | 0.46875 | 0.5 |
| 0.515625 | 0.4075 | 0.50125 | 0.515625 | 0.484075 | 0.515625 | 0.5 | 0.450125 |
| - | 106 | 106 | 106 | 106 | 102 | 100 | 106 |
| 106 | - | 106 | 104 | 104 | 104 | 102 | 104 |
| 104 | 106 | - | 104 | 104 | 104 | 106 | 106 |
| 106 | 102 | 104 | - | 104 | 106 | 104 | 106 |
| 106 | 104 | 104 | 104 | - | 104 | 104 | 106 |
| 100 | 104 | 104 | 106 | 104 | - | 102 | 100 |
| 102 | 102 | 106 | 104 | 104 | 102 | - | 96 |
| 106 | 104 | 106 | 106 | 106 | 96 | 100 | - |
| - | 0.4960 | 0.5000 | 0.5019 | 0.5097 | 0.5019 | 0.4824 | 0.5058 |
| 0.4960 | - | 0.5292 | 0.5117 | 0.4902 | 0.4980 | 0.5097 | 0.5136 |
| 0.5000 | 0.5292 | - | 0.5019 | 0.5058 | 0.5058 | 0.5234 | 0.5019 |
| 0.5019 | 0.5117 | 0.5019 | - | 0.5058 | 0.5156 | 0.5097 | 0.5234 |
| 0.5097 | 0.4902 | 0.5058 | 0.5058 | - | 0.4824 | 0.4843 | 0.4746 |
| 0.5019 | 0.4980 | 0.5058 | 0.5156 | 0.4824 | - | 0.5117 | 0.5156 |
| 0.4824 | 0.5097 | 0.5234 | 0.5097 | 0.4843 | 0.5117 | - | 0.4843 |
| 0.5058 | 0.5136 | 0.5019 | 0.5234 | 0.4746 | 0.5156 | 0.4843 | - |
| Statistic Tests | p-Value |
|---|---|
| Frequency (Monobit) test | 0.99366 |
| Frequency test within a block | 0.534109 |
| Runs test | 0.886973 |
| Test for the longest run of ones in a block | 0.99889 |
| Binary matrix rank test | 0.402188 |
| Discrete Fourier transform (Spectral) test | 0.166021 |
| Non-overlapping template matching test | Success |
| Overlapping template matching test | 0.867599 |
| Maurer’s “universal statistical” test | 0.895623 |
| Linear complexity test | 0.959774 |
| Serial test (1) | 0.772120 |
| Serial test (2) | 0.095163 |
| Approximate entropy test | 0.0900 |
| Cumulative sums | 0.658232 |
| Random excursions test | Success |
| Random excursions variant test | Success |
| Results | Pass |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaif, H.; Guesmi, R.; Kalghoum, A.; Alshammari, B.M.; Guesmi, T. A Novel Strong S-Box Design Using Quantum Crossover and Chaotic Boolean Functions for Symmetric Cryptosystems. Symmetry 2023, 15, 833. https://doi.org/10.3390/sym15040833
Alsaif H, Guesmi R, Kalghoum A, Alshammari BM, Guesmi T. A Novel Strong S-Box Design Using Quantum Crossover and Chaotic Boolean Functions for Symmetric Cryptosystems. Symmetry. 2023; 15(4):833. https://doi.org/10.3390/sym15040833
Chicago/Turabian StyleAlsaif, Haitham, Ramzi Guesmi, Anwar Kalghoum, Badr M. Alshammari, and Tawfik Guesmi. 2023. "A Novel Strong S-Box Design Using Quantum Crossover and Chaotic Boolean Functions for Symmetric Cryptosystems" Symmetry 15, no. 4: 833. https://doi.org/10.3390/sym15040833
APA StyleAlsaif, H., Guesmi, R., Kalghoum, A., Alshammari, B. M., & Guesmi, T. (2023). A Novel Strong S-Box Design Using Quantum Crossover and Chaotic Boolean Functions for Symmetric Cryptosystems. Symmetry, 15(4), 833. https://doi.org/10.3390/sym15040833








