Numerical Analysis of the Fractional-Order Belousov–Zhabotinsky System
Abstract
:1. Introduction
2. Basic Definitions
3. HPYTM
4. ETDM
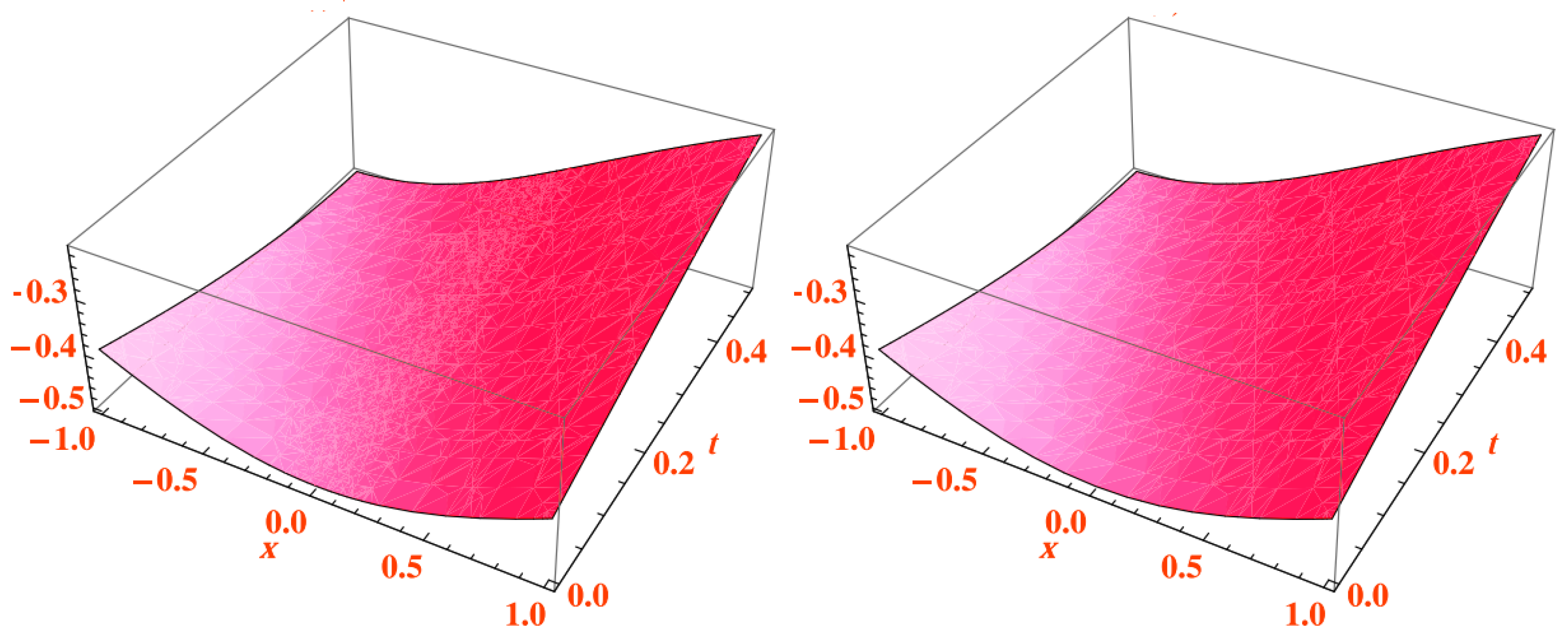
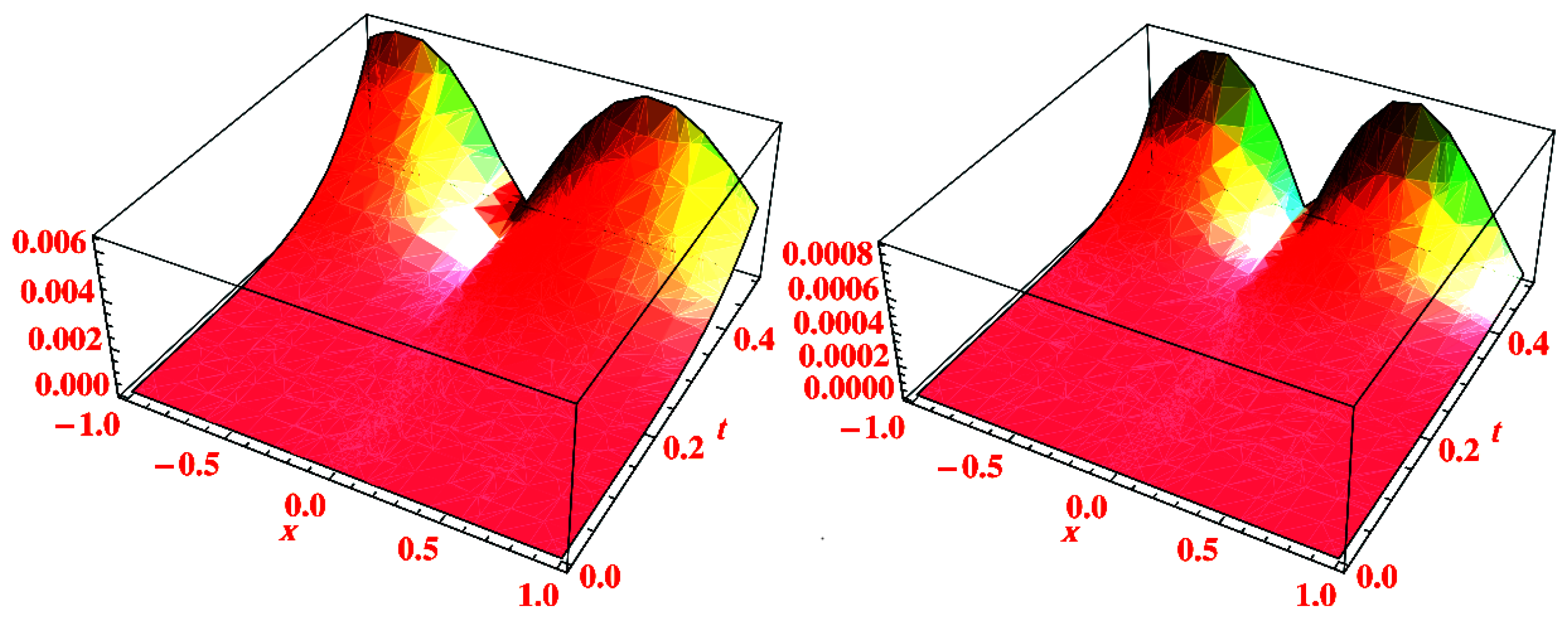
5. Applications
ETDM Result
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Subasi, M.; Araz, S.I. Numerical regularization of optimal control for the coefficient function in a wave equation. Iran. J. Sci. Technol. Trans. Sci. 2019, 43, 2325–2333. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. Analysis of a new partial integro-differential equation with mixed fractional operators. Chaos Solitons Fractals 2019, 127, 257–271. [Google Scholar]
- Goyal, M.; Baskonus, H.M.; Prakash, A. Regarding new positive, bounded and convergent numerical solution of nonlinear time fractional HIV/AIDS transmission model. Chaos Solitons Fractals 2020, 139, 110096. [Google Scholar] [CrossRef]
- Goyal, V.; Rani, N.; Gupta, D. A Solution Approach for Multi-Level Multi-Objective Quadratic Fractional Programming with Trapezoidal Fuzzy Numbers using Rouben Ranking Function. Int. J. Math. Eng. Manag. Sci. 2022, 7, 131. [Google Scholar] [CrossRef]
- Goyal, M.; Prakash, A.; Gupta, S. Numerical simulation for time-fractional nonlinear coupled dynamical model of romantic and interpersonal relationships. Pramana 2019, 92, 1–12. [Google Scholar]
- Li, C.; Zhao, J. A fractional nonlinear system of partial differential equations and its numerical simulation. J. Comput. Appl. Math. 2018, 327, 97–110. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Nonlaopon, K. Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques. Symmetry 2023, 15, 220. [Google Scholar] [CrossRef]
- Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Chung, J.D. A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform. Symmetry 2023, 15, 146. [Google Scholar]
- Yasmin, H. Application of Aboodh Homotopy Perturbation Transform Method for Fractional-Order Convection-Reaction-Diffusion Equation within Caputo and Atangana-Baleanu Operators. Symmetry 2023, 15, 453. [Google Scholar]
- Sheng, H.; Cong, R.; Yang, D.; Chen, R.; Wang, S.; Cui, Z. UrbanLF: A Comprehensive Light Field Dataset for Semantic Segmentation of Urban Scenes. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 7880–7893. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Kornilova, M.I.; Khakhalev, Y.A.; Generalov, D.A.; Simos, T.E.; Tsitouras, C. Fitted modifications of Runge-Kutta-Nystrom pairs of orders7(5) for addressing oscillatory problems. Math. Meth. Appl. Sci. 2022, 46, 273–282. [Google Scholar] [CrossRef]
- Sun, L.; Hou, J.; Xing, C.; Fang, Z. A Robust Hammerstein-Wiener Model Identification Method for Highly Nonlinear Systems. Processes 2022, 10, 2664. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Wu, J.H. Numerical solution of fractional nonlinear partial differential equations by a meshless method. J. Comput. Phys. 2008, 227, 9361–9377. [Google Scholar]
- Zhang, Y.; Liu, F.; Turner, I. A spectral method for solving fractional nonlinear partial differential equations. J. Comput. Phys. 2013, 240, 136–147. [Google Scholar]
- Al-Sawalha, M.M.; Ababneh, O.Y.; Shah, R.; Nonlaopon, K. Numerical analysis of fractional-order Whitham-Broer-Kaup equations with non-singular kernel operators. AIMS Math. 2023, 8, 2308–2336. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Shah, R.; Shah, N.A.; Dassios, I. A reliable technique for solving fractional partial differential equation. Axioms 2022, 11, 574. [Google Scholar] [CrossRef]
- Lu, S.; Guo, J.; Liu, S.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. An Improved Algorithm of Drift Compensation for Olfactory Sensors. Appl. Sci. 2022, 12, 9529. [Google Scholar] [CrossRef]
- Dang, W.; Guo, J.; Liu, M.; Liu, S.; Yang, B.; Yin, L.; Zheng, W. A Semi-Supervised Extreme Learning Machine Algorithm Based on the New Weighted Kernel for Machine Smell. Appl. Sci. 2022, 12, 9213. [Google Scholar] [CrossRef]
- Jin, H.Y.; Wang, Z.A. Global stabilization of the full attraction-repulsion Keller-Segel system. Discret. Contin. Dyn.-Syst. Ser. A 2020, 40, 3509–3527. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; Shah, S.A.; Haq, R.U. Fractional-order dynamics of the Belousov–Zhabotinsky reaction: A comprehensive review. Int. J. Dyn. Control. 2021, 1–29. [Google Scholar]
- Chen, Y.; Li, C.; Wei, G.W. Spatiotemporal chaos in fractional-order Belousov–Zhabotinsky systems. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 053111. [Google Scholar]
- Wei, G.W.; Chen, Y.; Li, C. Multistability and pattern formation in fractional-order Belousov–Zhabotinsky systems. Phys. Rev. E 2018, 97, 012211. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmin, H.; Alshehry, A.S.; Khan, A.; Shah, R.; Nonlaopon, K. Numerical Analysis of the Fractional-Order Belousov–Zhabotinsky System. Symmetry 2023, 15, 834. https://doi.org/10.3390/sym15040834
Yasmin H, Alshehry AS, Khan A, Shah R, Nonlaopon K. Numerical Analysis of the Fractional-Order Belousov–Zhabotinsky System. Symmetry. 2023; 15(4):834. https://doi.org/10.3390/sym15040834
Chicago/Turabian StyleYasmin, Humaira, Azzh Saad Alshehry, Asfandyar Khan, Rasool Shah, and Kamsing Nonlaopon. 2023. "Numerical Analysis of the Fractional-Order Belousov–Zhabotinsky System" Symmetry 15, no. 4: 834. https://doi.org/10.3390/sym15040834






