A Fractional-Order Density-Dependent Mathematical Model to Find the Better Strain of Wolbachia
Abstract
:1. Introduction
- When a -infected male mosquito mates with the wild female, the produced eggs will not hatch (CI).
- When a -infected female mates with a wild male, then the produced offspring will have infection (CI rescue).
- The failure of integer order systems to accurately predict certain phenomena is a widely recognized issue, and thus, the use of fractional-order systems is a natural extension in many fields. This article presents a novel 10-compartmental, fractional-order, density dependent mathematical model. Then, we checked the model’s eligibility by performing various mathematical analyses.
- A new parameter describing the CI mechanism in both the mosquito population and controlling the disease spread by reducing the population size of wild mosquitoes is introduced. Owing to this parameter’s inclusion, we are able to find the better strain in the sense of having perfect CI.
- In the existing literature, vaccination strategies are included while developing a model. However, we neglected the vaccination strategy because there exists a licensed vaccination called Dengvaxia (CYD-TDV), and five more are in trials. Regardless, WHO recommends these vaccines to people who have a history of dengue infection. Although there are four different stereotypes of dengue virus (DENV-1, DENV-2, DENV-3, DENV-4), the invented vaccinations are not able to control all four DENVs. They provide immunity against one and do not provide immunity against the other three. For this reason, there is a chance of having severe dengue infection by the remaining three variants. This aspect of vaccination is considered seriously and neglected in the vaccination strategy from the disease-controlling process.
- Our proposed model shows that when there is the existence of -infected mosquitoes, there is a notable change in the spread of disease. We derived the basic reproduction number of the disease and analyzed it at possible equilibrium points. The derived numerical results show that our releasing strategy is physically meaningful, and at some point, it works as a better strategy to control mosquito-borne diseases.
- Dynamical analysis of the proposed model is depicted as a time-series plot by numerically solving our model.
2. Methodology
- (i)
- First we propose a fractional-order mathematical model using Caputo fractional derivative to expose the interaction dynamics of -infected, -uninfected mosquitoes and humans. Moreover, the influences of imperfect maternal transmission and density-dependent death rates are considered in mosquito populations.
- (ii)
- To find the basic reproduction number, we used a next-generation method [50].
- (iii)
- The local stability of four cases of the disease-free equilibrium and three cases of endemic equilibrium are analyzed by finding determinants and traces of the corresponding Jacobian matrix (Routh–Hurwitz criterion).
- (iv)
- The global stability of the developed model is derived from linear matrix inequality theory and Lyapunov theory.
- (v)
- Numerical simulations to prove the effectiveness of the parameters used in the model formulations and to show how the system dynamics are influenced by various strains.
3. Preliminaries
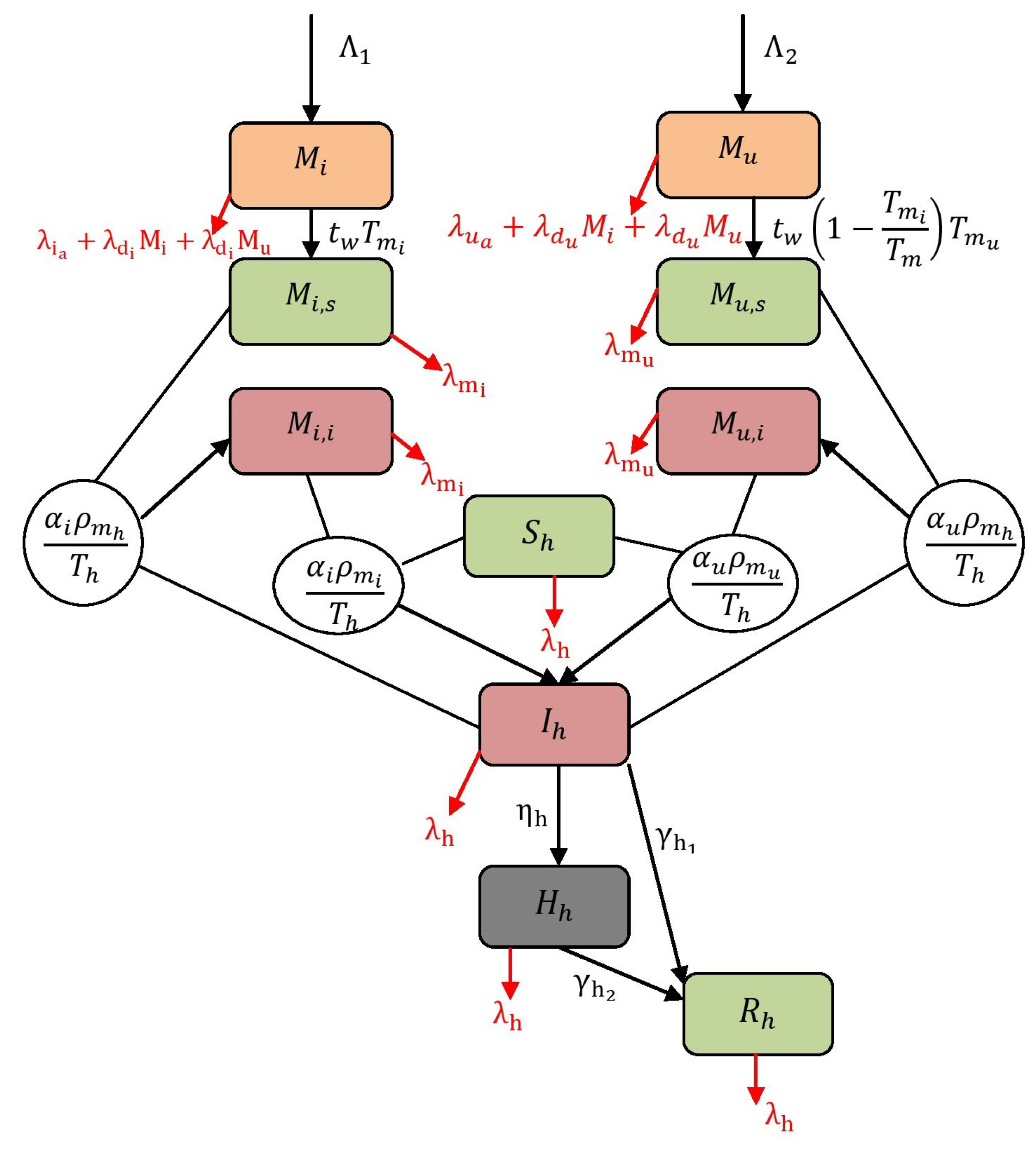
4. Model Formulation
- How does the release of -mosquitoes affect the wild mosquito population in the sense of reducing the lifespan, occupying the habitats, male feminization, and CI?
- What is the best strain to be used in the real world?
- How CI will influence the disease-spread dynamics?
- (H1)
- The three populations in the model are:
- Mi
- -infected mosquitoes (both laboratory-reared and offspring having after CI rescue).
- Mu
- Non- mosquitoes (both local and offspring produced by weak CI).
- H
- Human population.
In contrast to mosquitoes, which are believed to have a variable population size, humans have a steady population size. as, in contrast to a single human generation, mosquitoes have many generations over that period. - (H2)
- People of all ages and all genders make up the human population.
- (H3)
- The host population is monolithically intermingled. This implies that all individuals, irrespective of age, genetic development, sociocultural context, or geographic region, have almost the same pathogenic traits.
- (H4)
- Only mature females were taken into account for modeling. As they require a blood meal to warm and develop the eggs before they can lay eggs, only sexually active female mosquitoes will engage with people.
- (H5)
- Mosquitoes are divided into six groups representing the state variables: aquatic stage (eggs, larvae, pupae) of as and non- as . Adult female mosquitoes are divided into four groups: -infected and susceptible to virus—; -infectious (virus)—; non--infected and susceptible to virus—; and non--infected (virus)—. The human population is divided into four compartments as susceptible , infectious , hospitalized , and recovered . In both populations, we neglected the latent period (exposed) because the time span of latency is much smaller compared with the total life span of the human population and the mosquito population. Additionally, we assumed that and (function of time).
- (H6)
- All newborns are susceptible to the virus; there is no vertical transmission of the disease or heredity in the human population or mosquitoes.
- (H7)
- However, in the case of spread. there is vertical transmission and heredity in mosquitoes. Notably, there is no horizontal transmission of between mosquito and human population.
- (H8)
- A mosquito acquires an infection when it bites an infected individual, and a person who has been bitten by an infected mosquito contracts the infection as well. Male mosquitoes do not participate in this activity, since they solely feed on nectar.
- (H9)
- There is a chance to generate a density-dependent concurrence for food, habitats, etc., when we intentionally introduce -infected mosquitoes as eggs in the form of ’Zancu KIT’ and adult mosquitoes via drones, transportation, and manual release into mosquito-borne disease epidemic areas. This fact causes both and non- mosquitoes to die in a density-dependent manner.
- (H10)
- The parameter denotes the cytoplasmic incompatibility (CI) induced by . This CI will serve as a main component in reducing the population size of mosquitoes. As CI is the process that makes the males feminized and reduce the possibility of producing viable progeny. There exist many strains, such as , , , , and . Among these strains, the superinfected strain has the highest CI [55].
4.1. Integer-Order Model
4.2. Factional-Order Model—Caputo Sense
5. Fundamental Properties
5.1. Positivity of the Solution
5.2. Positive Invariant Region
6. Analysis of the Model
6.1. Basis Reproduction Number
6.1.1. Disease-Free Equilibrium:
- Annihilation of both wild and Wolbachia mosquitoes: If both mosquitoes are completely destructed, then the possible equilibrium point is
- Annihilation of Wild mosquito only: The equilibrium point when there is a successful replacement of wild mosquitoes by -infected mosquitoes is derived as
- Annihilation of Wolbachia-infected mosquitoes only: If the rate of an imperfect maternal transmission increases, then after some period, the sustainability of will be reduced to zero. For this zero -mosquitoes case, the equilibrium point is
- Co-existence of all wild and Wolbachia-infected mosquitoes with humans: An equilibrium point when all populations co-exist in a common environment is derived aswhere .
6.1.2. Endemic Equilibrium
- Successful replacement of wild mosquitoes by Wolbachia-infected mosquitoes: .
- Annihilation of Wolbachia-infected mosquitoes: .
- 1.
- Successful replacement of wild mosquitoes by -infected mosquitoes: That is, . Then, the model (2) is reduced as follows:By adding the first two equations and adding the last four equations, we obtainBy solving for , we obtain and .Let us equate the RHS of each equation in (6) to zero. After some manipulations, we obtain the following equilibrium point ():
- 2.
- Annihilation of -infected mosquitoes:Adding the first two equations, and adding the last four equations, we obtainBy solving for , we obtain and .Let us equate the RHS of each equation in (7) to zero. After some manipulations, we obtain the following equilibrium point ().
6.1.3. Basis Reproduction Number at Disease-Free Equilibrium
- (i)
- .
- (ii)
- .
- (iii)
- .
- (iv)
- .
6.1.4. Local Stability
- (i)
- The Jacobian at disease-free equilibrium :where .Here, if (i.e.,) and the trace of . Hence, by Routh Hurwitz’s theorem, our system at disease-free equilibrium point is locally asymptotically stable when .
- (ii)
- The Jacobian at disease-free equilibrium :Here, if (i.e.,) and the trace of . Hence, by Routh Hurwitz’s theorem, our system at disease-free equilibrium point is locally asymptotically stable when .
6.1.5. Global Stability: LMI Approach
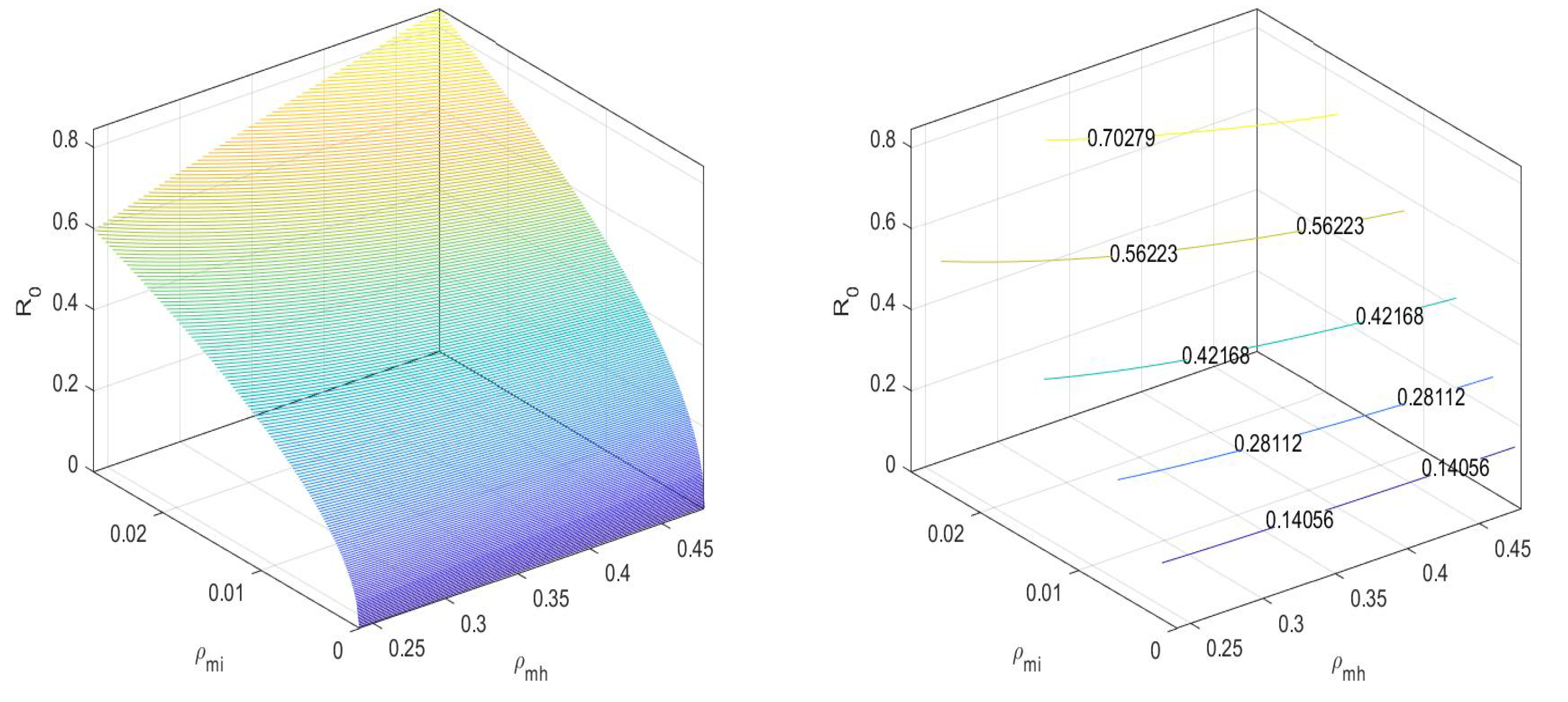
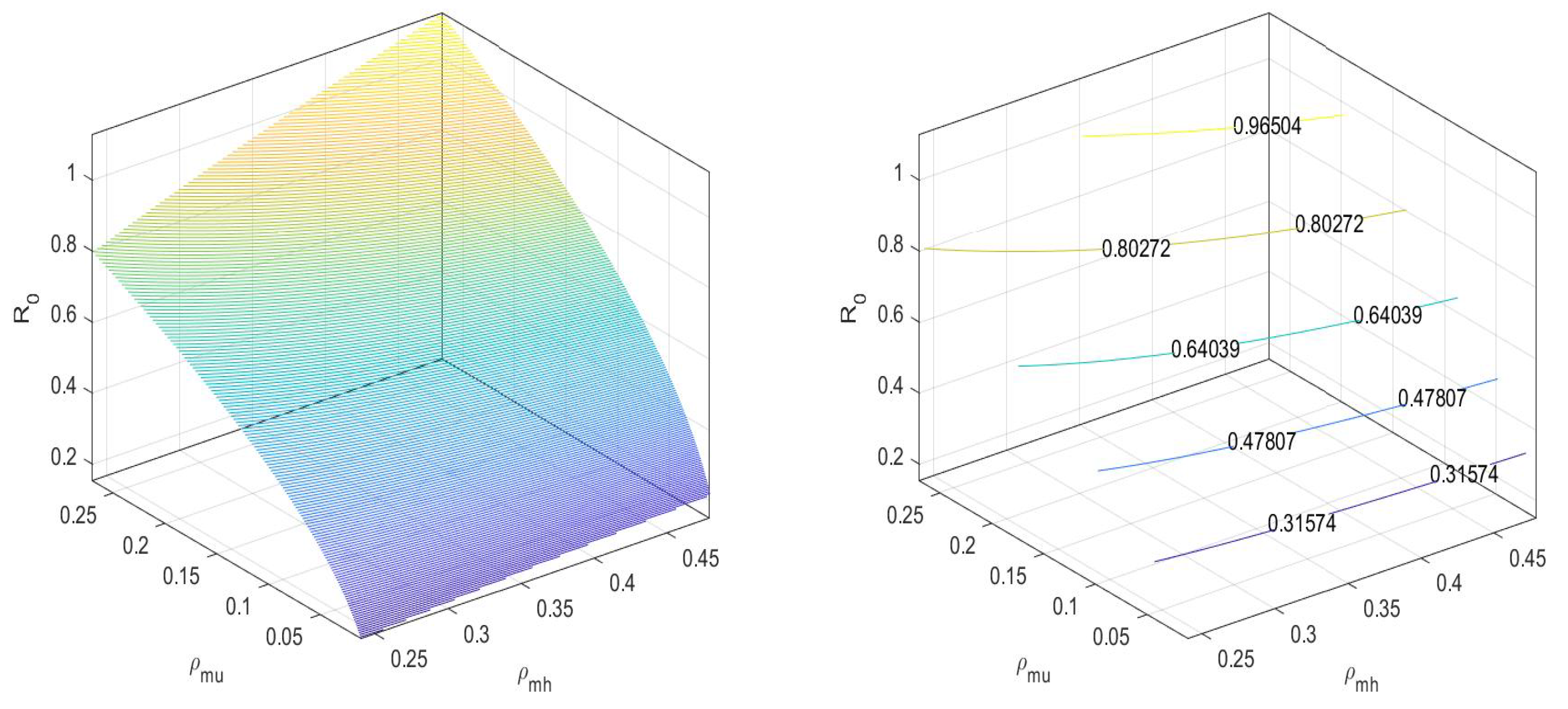
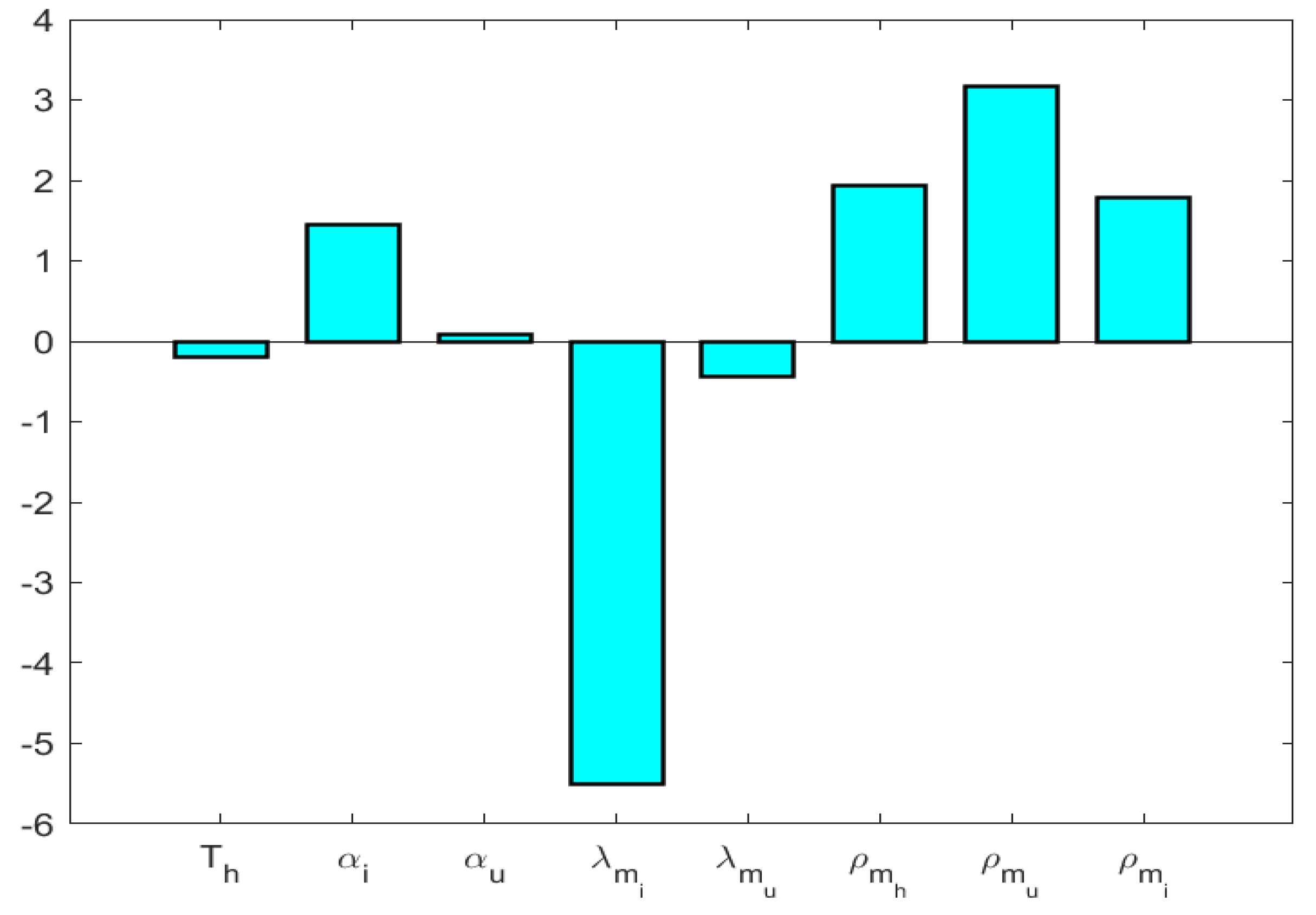
7. Sensitivity Analysis
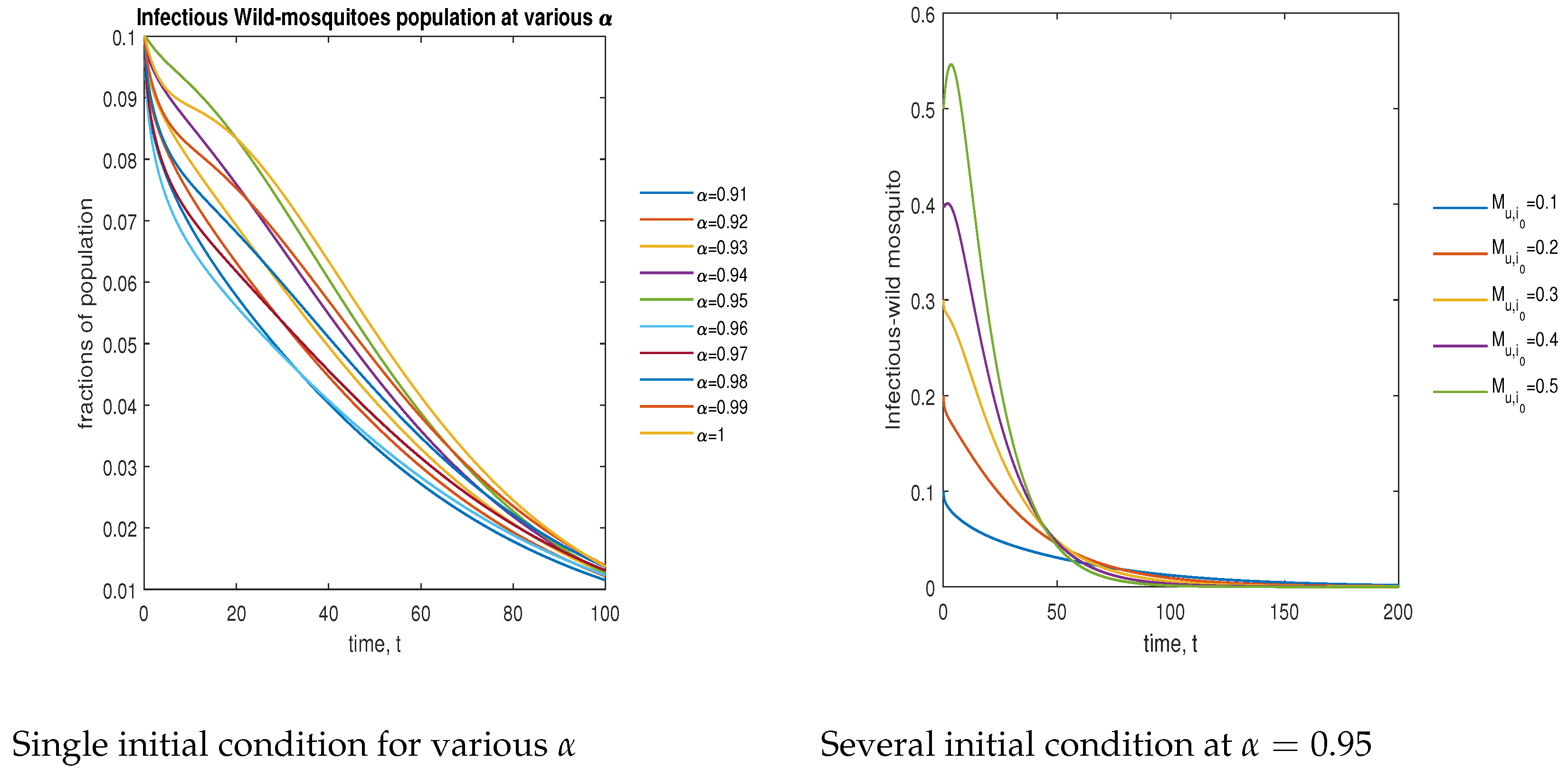
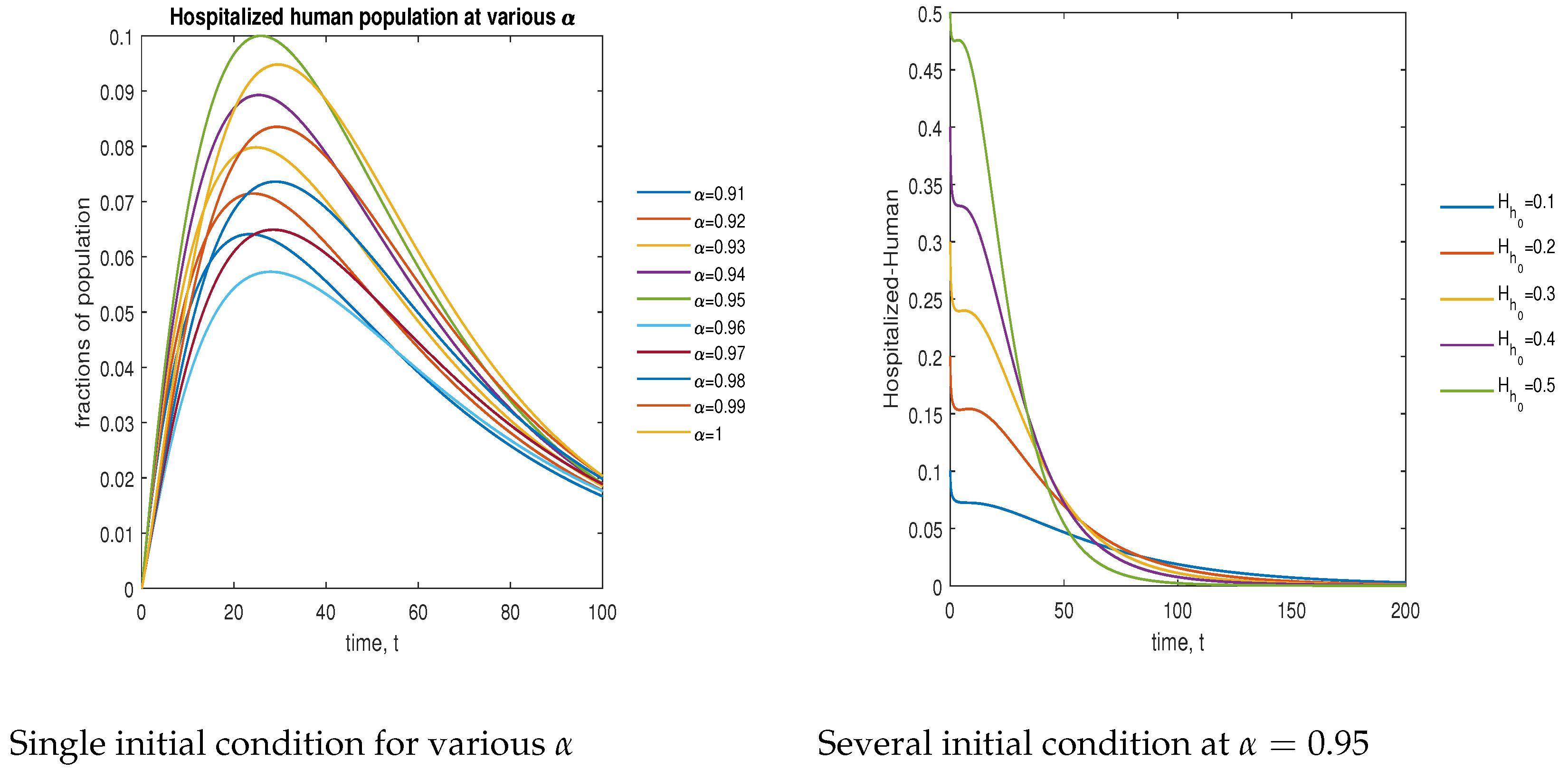
8. Numerical Simulation
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Cattarino, L.; Rodriguez-Barraquer, I.; Imai, N.; Cummings, D.A.T.; Ferguson, N.M. Mapping global variation in dengue transmission intensity. Sci. Transl. Med. 2020, 12, 105788. [Google Scholar] [CrossRef]
- Evelyn, M.; Murray, A.; Quam, M.B.; Wilder-Smith, A. Epidemiology of dengue: Past, present and future prospects. Clin. Epidemiol. 2013, 5, 299. [Google Scholar]
- Shepard, D.S.; Undurraga, E.A.; Halasa, Y.A.; Stanaway, J.D. The global economic burden of dengue: A systematic analysis. Lancet Infect. Dis. 2016, 16, 935–941. [Google Scholar] [CrossRef]
- Souza-Neto, J.A.; Powell, J.R.; Bonizzoni, M. Aedes Aegypti Vector Competence Stud. A Rev. Infection. Genet. Sel. Evol. 2019, 67, 191–209. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization, Vector-Borne Diseases Fact Sheet. Available online: https://www.who.int/news-room/fact-sheets/detail/vector-borne-diseases (accessed on 12 December 2022).
- Jose, S.A.; Raja, R.; Omede, B.I.; Agarwal, R.P.; Alzabut, J.; Cao, J.; Balas, V.E. Mathematical Modeling on Co-infection: Transmission Dynamics of Zika virus and Dengue fever. Nonlinear Dyn. 2022. [Google Scholar] [CrossRef]
- Baldacchino, F.; Caputo, B.; Chandre, F.; Drago, A.; Torre, A.D.; Montarsi, F.; Rizzoli, A. Control methods against invasive Aedes mosquitoes in Europe: A review. Pest Manag. Sci. 2015, 71, 1471–1485. [Google Scholar] [CrossRef] [PubMed]
- Somwang, P.; Yanola, J.; Suwan, W.; Walton, C.; Lumjuan, N.; Prapanthadara, L.A.; Somboon, P. Enzymes-based resistant mechanism in pyrethroid resistant and susceptible Aedes aegypti strains from northern Thailand. Parasitol. Res. 2011, 109, 531–537. [Google Scholar] [CrossRef]
- Silva, J.V.J., Jr.; Lopes, T.R.R.; de Oliveira-Filho, E.F.; Oliveira, R.A.S.; Duraes-Carvalho, R.; Gil, L.H.V.G. Current status, challenges and perspectives in the development of vaccines against yellow fever, dengue, Zika, and chikungunya viruses. Acta Trop. 2018, 182, 257–263. [Google Scholar] [CrossRef]
- Joubert, D.A.; Walker, T.; Carrington, L.B.; De Bruyne, J.T.; Kien, D.H.T.; Hoang, N.L.T.; Chau, N.V.V.; Iturbe-Ormaetxe, I.; Simmons, C.P.; O’Neill, S.L. Establishment of a Wolbachia superinfection in Aedes Aegypti Mosquitoes A Potential Approach Future Resist. Management. PLoS Pathog. 2016, 12, e1005434. [Google Scholar] [CrossRef] [PubMed]
- World Mosquito Program, How Wolbachia Method Works. Available online: https://www.worldmosquitoprogram.org/en/work/wolbachia-method (accessed on 12 December 2022).
- Xi, Z.; Khoo, C.C.; Dobson, S.L. Wolbachia establishment and invasion in an Aedes Aegypti Lab. Population. Science 2005, 310, 326–328. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, N.E.; Gerdtzen, Z.P.; Olivera-Nappa, A.; Salgado, J.C.; Concaa, C. Novel symbiotic genome-scale model reveals Wolbachia’s arboviral pathogen blocking mechanism in Aedes Aegypti. MBio 2021, 12, e01563-21. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Montgomery, B.L.; Popovici, J.; Iturbeormaetxe, I.; Johnson, P.H.; Muzzi, F.; Greenfield, M.; Durkan, M.; Leong, Y.S.; Dong, Y. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature 2011, 476, 454–457. [Google Scholar] [CrossRef] [PubMed]
- Crawford, J.E.; Clarke, D.W.; Criswell, V.; Desnoyer, M.; Cornel, D.; Deegan, B.; Gong, K.; Hopkins, K.C.; Howell, P.; Hyde, J.S.J.S. Efficient production of male Wolbachia-infected Aedes Aegypti Mosquitoes Enables Large-Scale Suppr. Wild Populations. Nat. Biotechnol. 2020, 38, 482–492. [Google Scholar] [CrossRef] [PubMed]
- Dianavinnarasi, J.; Raja, R.; Alzabut, J.; Niezabitowski, M.; Selvam, G.; Bagdasar, O. An LMI Approach-Based Mathematical Model to Control Aedes Aegypti Mosquitoes Popul. Via Biol. Control. Math. Probl. Eng. 2021, 2021, 5565949. [Google Scholar] [CrossRef]
- Dianavinnarasi, J.; Raja, R.; Alzabut, J.; Niezabitowski, M.; Bagdasar, O. Controlling Wolbachia transmission and invasion dynamics among Aedes aegypti population via impulsive control strategy. Symmetry 2021, 13, 434. [Google Scholar] [CrossRef]
- Pagendam, D.E.; Trewin, B.J.; Snoad, N.; Ritchie, S.A.; Hoffmann, A.A.; Staunton, K.M.; Paton, C.; Beebe, N. Modelling the Wolbachia incompatible insect technique: Strategies for effective mosquito population elimination. BMC Biol. 2020, 18, 161. [Google Scholar] [CrossRef]
- Jose, S.A.; Raja, R.; Dianavinnarasi, J.; Baleanu, D.; Jirawattanapanit, A. Mathematical Modeling of Chickenpox in Phuket: Efficacy of Precautionary Measures and Bifurcation Analysis. Biomed. Signal. Proces. 2023, 84, 104714. [Google Scholar] [CrossRef]
- Sadek, L.; Sadek, O.; Alaoui, H.T.; Abdo, M.S.; Shah, K.; Abdeljawad, T. Fractional Order Modeling of Predicting COVID-19 with Isolation and Vaccination Strategies in Morocco. CMES-Comput. Model. Eng. Sci. 2023, 136, 1931–1950. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Abdo, M.S.; Shah, K. Theoretical and numerical analysis for transmission dynamics of COVID-19 mathematical model involving Caputo-Fabrizio derivative. Adv. Differ. Equ. 2021, 2021, 1–17. [Google Scholar]
- Thirthar, A.A.; Abboubakar, H.; Khan, A.; Abdeljawad, T. Mathematical modeling of the COVID-19 epidemic with fear impact. AIMS Math. 2023, 8, 6447–6465. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M.; Avazzadeh, Z. Numerical investigation of variable-order fractional Benjamin–Bona–Mahony–Burgers equation using a pseudo-spectral method. Math Meth. Appl. Sci. 2021, 1–15. [Google Scholar] [CrossRef]
- Ghafoor, A.; Khan, N.; Hussain, M.; Ullah, R. A hybrid collocation method for the computational study of multi-term time fractional partial differential equations. Comput. Math. Appl. 2022, 128, 130–144. [Google Scholar] [CrossRef]
- Haq, S.; Ghafoor, A.; Hussain, M. Numerical solutions of variable order time fractional (1+1)- and (1+2)-dimensional advection dispersion and diffusion models. Appl. Math. Comput. 2019, 360, 107–121. [Google Scholar] [CrossRef]
- Barclay, H.J. The sterile insect release method on species with two-stage life cycles. Popul. Ecol. 1980, 21, 165–180. [Google Scholar] [CrossRef]
- Barclay, H.J.; Mackauer, M. The sterile insect release method for pest control: A density-dependent model. Environ. Entomol. 1980, 9, 810–817. [Google Scholar] [CrossRef]
- Barclay, H.J. Pest population stability under sterile releases. Popul. Ecol. 1982, 24, 405–416. [Google Scholar] [CrossRef]
- Barclay, H.J. Modeling incomplete sterility in a sterile release program: Interactions with other factors. Popul. Ecol. 2001, 43, 197–206. [Google Scholar] [CrossRef]
- Barclay, H.J. Mathematical models for the use of sterile insects, in Sterile Insect Technique. In Principles and Practice in Area-Wide Integrated Pest Management; Dyck, V.A., Hendrichs, J., Robinson, A.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 147–174. [Google Scholar]
- Dame, D.A.; Curtis, C.F.; Benedict, M.Q.; Robinson, A.S.; Knols, B.G. Historical applications of induced sterilization in field populations of mosquitoes. Malar. J. 2009, 8, S2. [Google Scholar] [CrossRef]
- Ranathunge, T.; Harishchandra, J.; Maiga, H.; Bouyer, J.; Gunawardena, Y.I.N.S.; Hapugoda, M. Development of the Sterile Insect Technique to control the dengue vector Aedes Aegypti (Linnaeus) Sri Lanka. PLoS ONE 2022, 17, e0265244. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Yan, R.; Feng, X. Existence and stability of two periodic solutions for an interactive wild and sterile mosquitoes model. J. Biol. Dyn. 2022, 16, 277–293. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Ai, S.; Li, J. Dynamics of mosquitoes populations with different strategies for releasing sterile mosquitoes. SIAP 2014, 74, 1786–1809. [Google Scholar] [CrossRef]
- Li, J. New revised simple models for interactive wild and sterile mosquito populations and their dynamics. J. Biol. Dyn. 2017, 11, 316–333. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Hickson, R.I.; Mercer, G.N. Modelling the introduction of Wolbachia into Aedes aegypti mosquitoes to reduce dengue transmission. ANZIAM J. 2012, 53, 213–227. [Google Scholar]
- Ndii, M.Z.; Hickson, R.I.; Allingham, D.; Mercer, G.N. Modelling the transmission dynamics of dengue in the presence of Wolbachia. Math. Biosci. 2015, 262, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Ndii, M.Z.; Allingham, D.; Hickson, R.I.; Glass, K. The effect of Wolbachia on dengue outbreaks when dengue is repeatedly introduced. Theor. Popul. Biol. 2016, 111, 9–15. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Allingham, D.; Hickson, R.I.; Glass, K. The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: Symmetric and asymmetric epidemiological characteristics. Epidemiol. Infect. 2016, 144, 2874–2882. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Wiraningsih, E.D.; Anggriani, N.; Supriatna, A.K. Dengue Fever-a Resilient Threat in the Face of Innovation: Mathematical Model as a Tool for the Control of Vector-Borne Diseases: Wolbachia Example; Intechopen: London, UK, 2018. [Google Scholar]
- Ndii, M.Z. Modelling the Use of Vaccine and Wolbachia on Dengue Transmission Dynamics. Infect. Dis. Trop. Med. 2020, 5, 78. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Messakh, J.J.; Djahi, B.S. Effects of vaccination on dengue transmission dynamics. JPCS 2020, 1490, 012048. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Supriatna, A.K. Stochastic Dengue Mathematical Model in the Presence of Wolbachia: Exploring the Disease Extinction. Nonlinear Dyn. Syst. Theory 2020, 20, 214–227. [Google Scholar]
- Su, Y.; Zheng, B.; Zou, X. Wolbachia Dynamics in Mosquitoes with Incomplete CI and Imperfect Maternal Transmission by a DDE System. Bull. Math. Biol. 2022, 84–95. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zheng, B. Modeling Wolbachia infection in mosquito population via discrete dynamical models. J. Differ. Equ. 2019, 25, 1549–1567. [Google Scholar] [CrossRef]
- Ai, S.; Li, J.; Yu, J.; Zheng, B. Stage-structured models for interactive wild and periodically and impulsively released sterile mosquitoes. Discret. Contin. Dyn. Syst. Ser. B 2022, 27, 3039–3052. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Ross, P.A.; Rasic, G. Wolbachia strains for disease control: Ecological and evolutionary considerations. Evol. Appl. 2015, 8, 751–768. [Google Scholar] [CrossRef]
- Van-Driessche, D.; Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. An Introduction to Fractiorlal Derivatives, Fractiorlal Differential Eqnations, to Methods of Their Solutiori and Some of Their Applications; Academic Press: London, UK, 1999. [Google Scholar]
- Caputo, M. Linear model of dissipation whose Q is almost frequency independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Wu, H.; Zhang, X.; Xue, S.; Wang, L.; Wang, Y. LMI conditions to global Mittag–Leffler stability of fractional-order neural networks with impulses. Neurocomputing 2016, 193, 148–154. [Google Scholar] [CrossRef]
- Ross, P.A.; Gu, X.; Robinson, K.L.; Yang, Q.; Cottingham, E.; Zhang, Y.; Yeap, H.L.; Xu, X.; Endersby-Harshman, N.M.; Hoffmann, A.A. A wAlbB Wolbachia Transinfection Displays Stable Phenotypic Effects across Divergent Aedes Aegypti Mosq. Backgrounds. Appl. Environ. Microbiol. 2021, 87, e0126421. [Google Scholar] [CrossRef]
- Walker, T.; Johnson, P.H.; Moreira, L.A.; Iturbe-Ormaetxe, I.; Frentiu, F.D.; McMeniman, C.J.; Leong, Y.S.; Dong, Y.; Axford, J.; Kriesner, P.; et al. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 2011, 476, 450–453. [Google Scholar] [CrossRef]
- Yang, H.M.; Macoris, M.L.G.; Galvani, K.C.; Andrighetti, M.T.M.; Wanderley, D.M.V. Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiol. Infect. 2009, 137, 1188–1202. [Google Scholar] [CrossRef] [PubMed]
- Scott, T.W.; Amerasinghe, P.H.; Morrison, A.C.; Lorenz, L.H.; Clark, G.G.; Strickman, D.; Kittayapong, P.; Edman, J.D. Longitudinal studies of Aedes Aegypti (Diptera: Culicidae) Thail. Puerto Rico: Blood Feed. Frequency. J. Med. Entomol. 2000, 37, 89–101. [Google Scholar] [CrossRef]
- Turley, A.P.; Moreira, L.A.; O’Neill, S.L.; McGraw, E.A. Wolbachia infection reduces blood-feeding success in the dengue fever mosquito, Aedes aegypti. PLoS Negl. Trop. Dis. 2009, 3, e516. [Google Scholar] [CrossRef] [PubMed]
- Bian, G.; Xu, Y.; Lu, P.; Xie, Y.; Xi, Z. The endosymbiotic bacterium Wolbachia induces resistance to dengue virus in Aedes Aegypti. PLoS Pathog. 2010, 6, e1000833. [Google Scholar] [CrossRef]
- Yeap, H.L.; Mee, P.; Walker, T.; Weeks, A.R.; O’Neill, S.L.; Johnson, P.; Ritchie, S.A.; Richardson, K.M.; Doig, C.; Endersby, N.M. Dynamics of the ‘popcorn’ Wolbachia infection in outbred Aedes aegypti informs prospects for mosquito vector control. Genetics 2011, 187, 583–595. [Google Scholar] [CrossRef] [PubMed]
- United Nations, Human Birth and Death Rates. Available online: https://population.un.org/wpp/Download/Standard/Population/ (accessed on 12 December 2022).
- Khan, M.A.; Fatmawati, C. Dengue infection modeling and its optimal control analysis in East Java, Indonesia. Heliyon 2021, 7, e06023. [Google Scholar] [CrossRef]
- Liang, X.; Liu, J.; Bian, G.; Xi, Z. Wolbachia Inter-strain competition and inhibition of expression of cytoplasmic incompatibility in the mosquito. Front Microbiol. 2020, 11, 1638. [Google Scholar] [CrossRef] [PubMed]

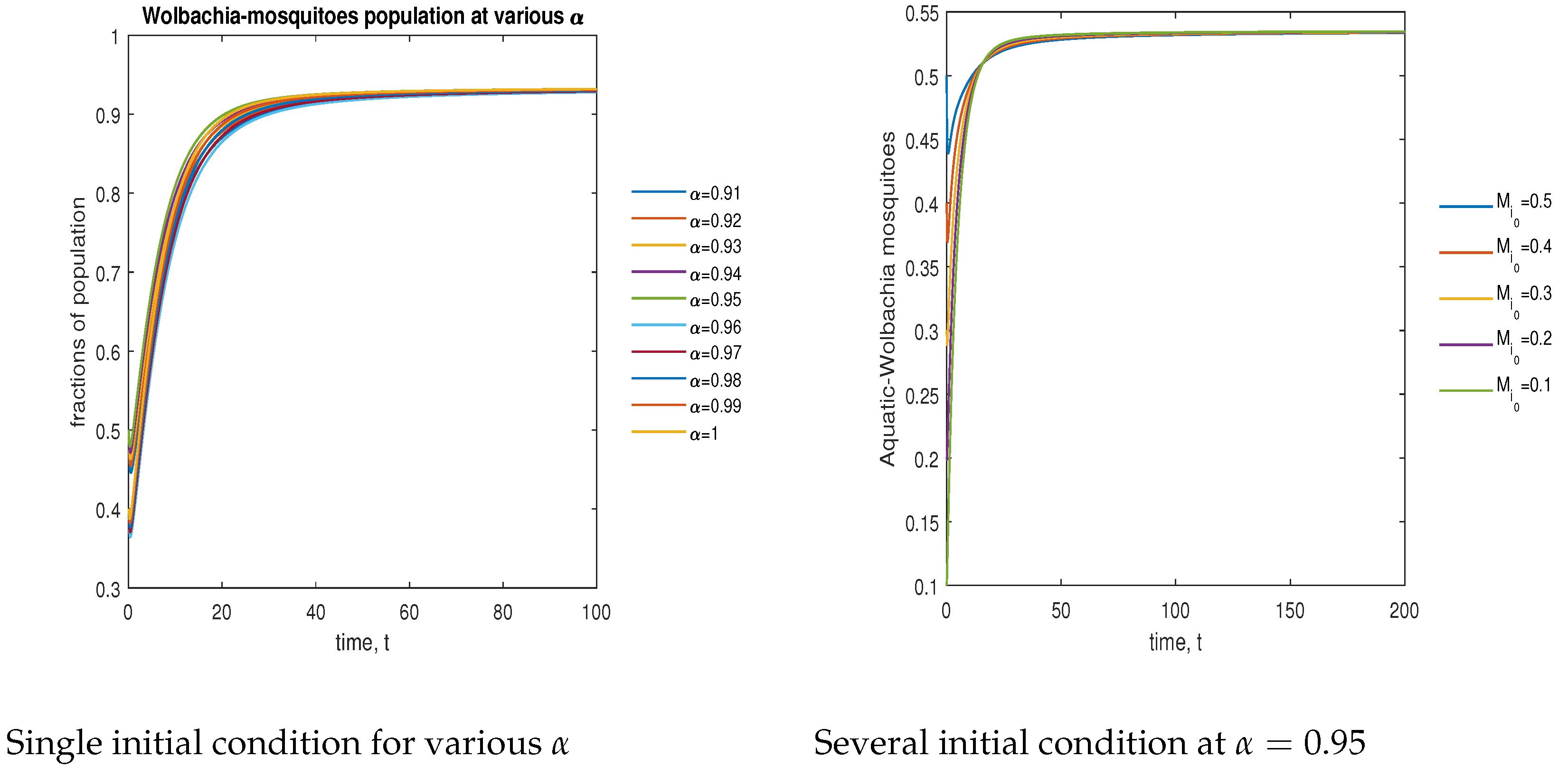

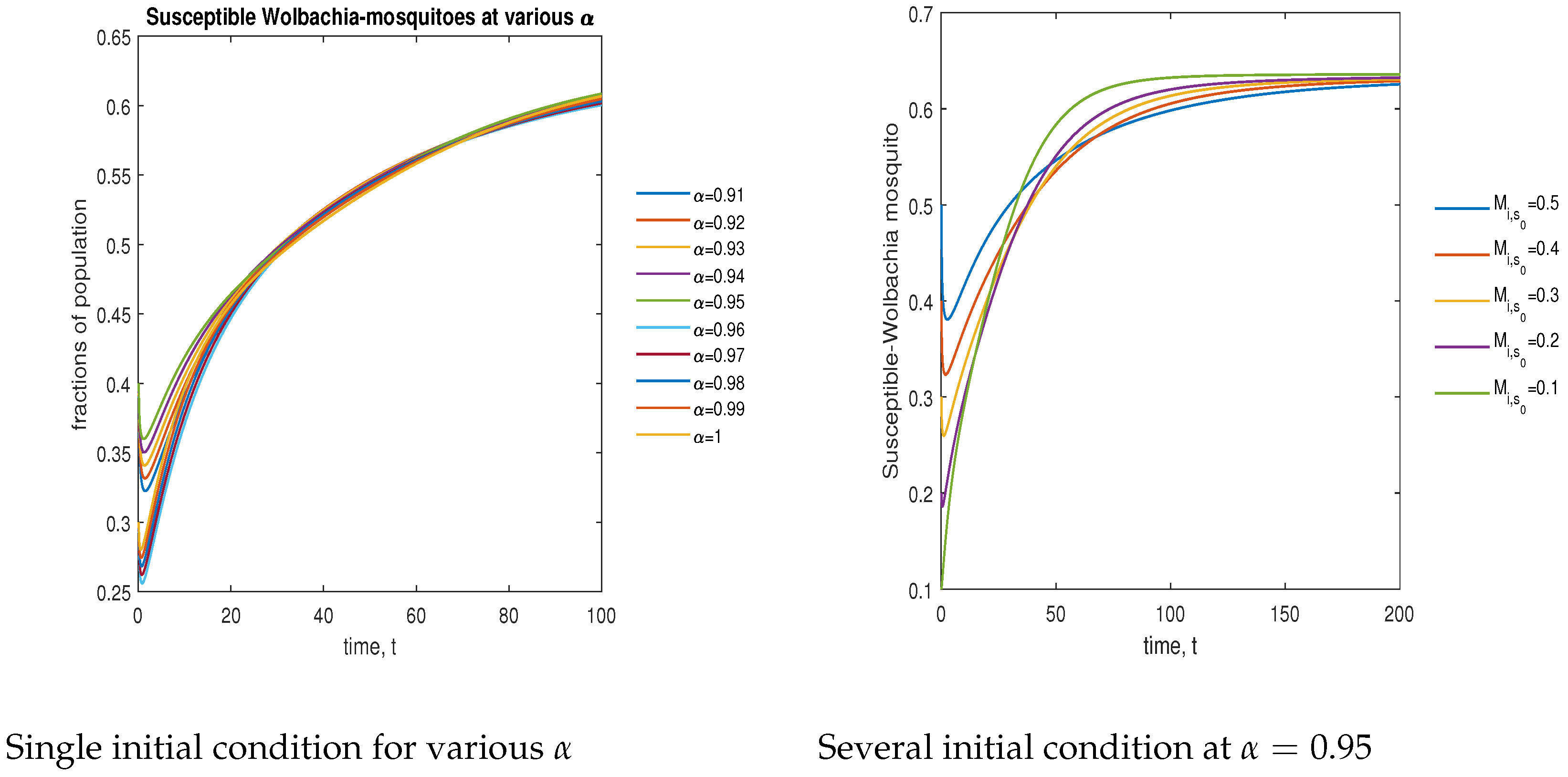
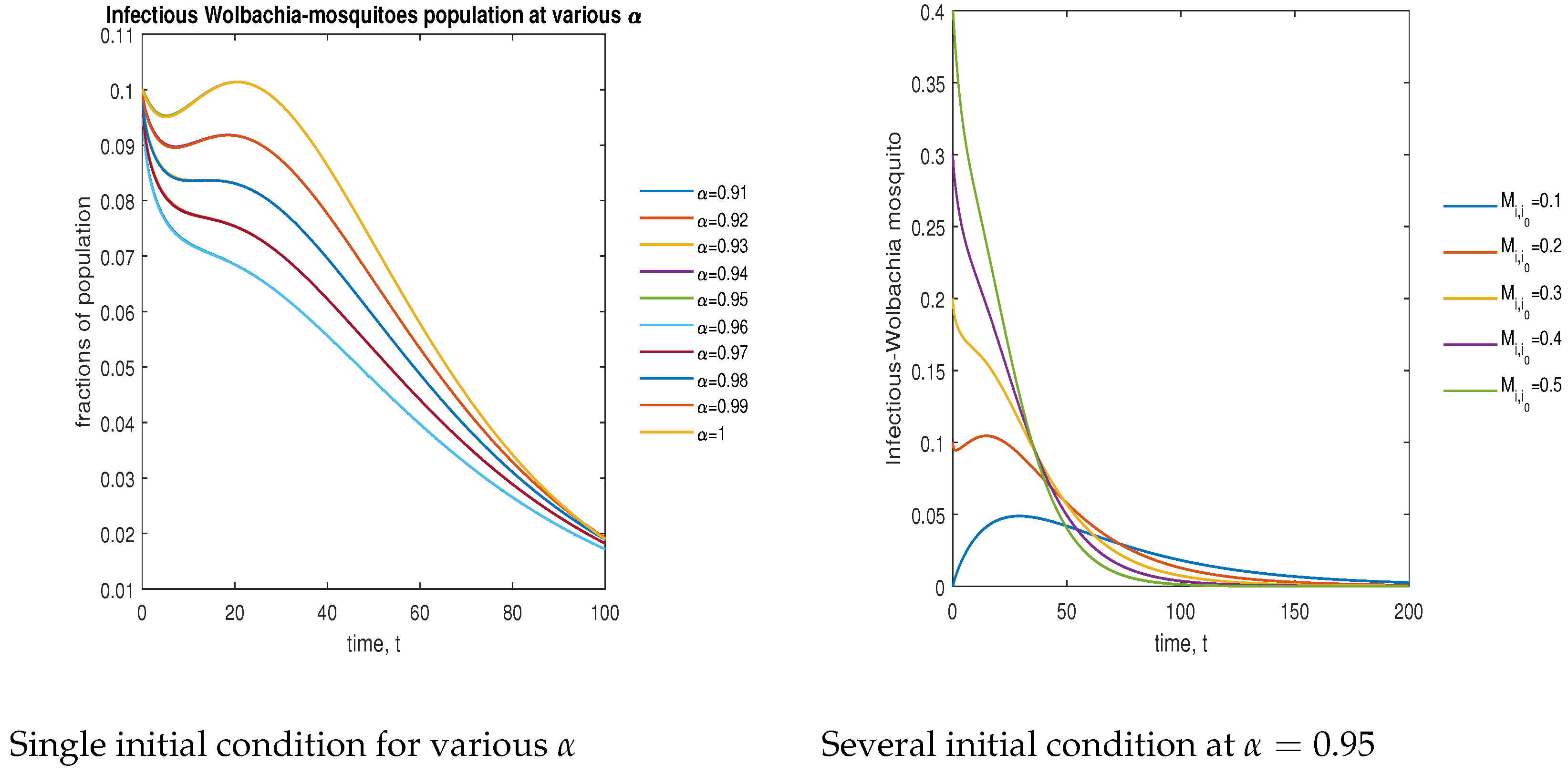
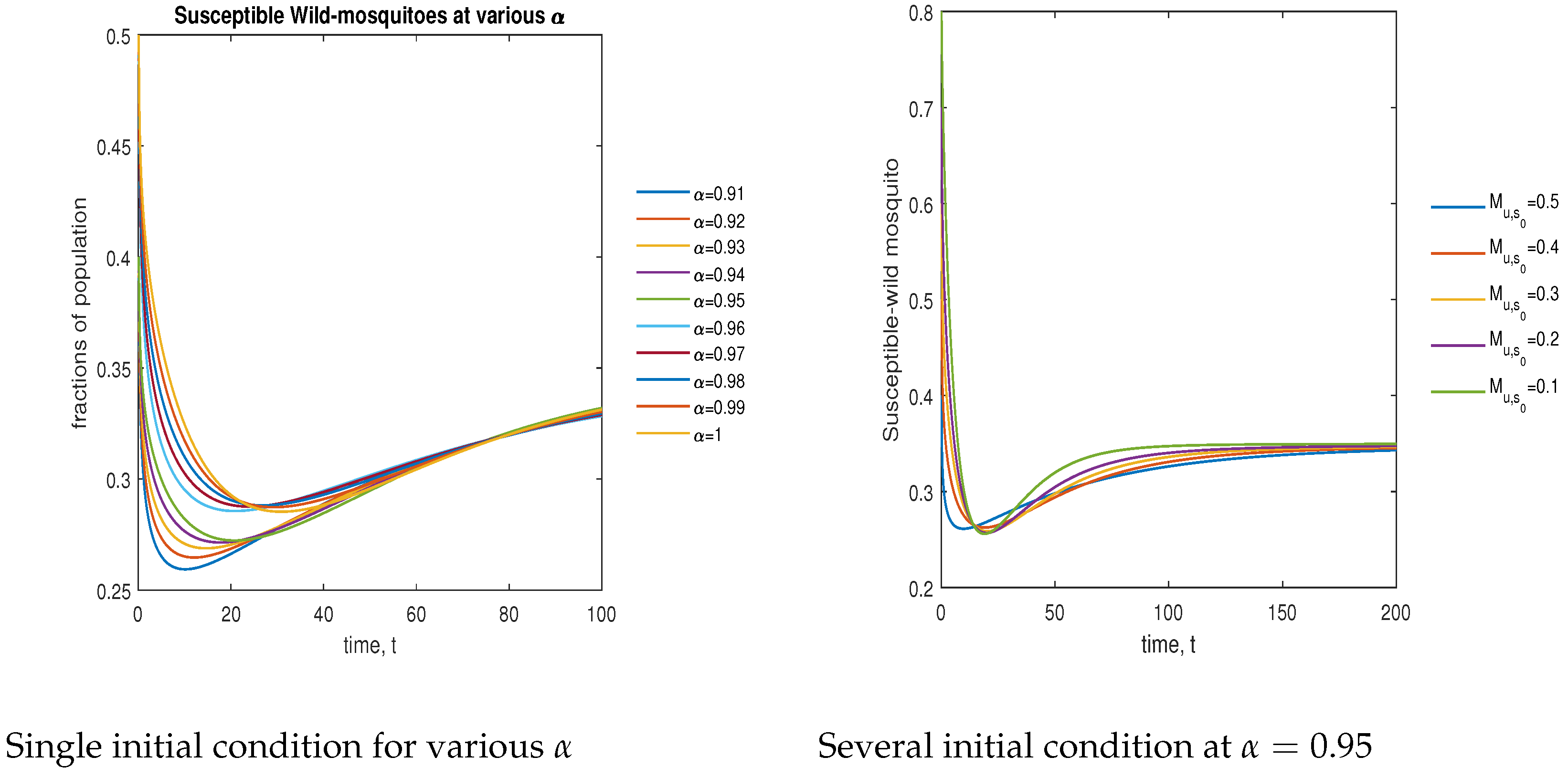




| Variables | Description |
|---|---|
| The number of -infected mosquitoes at time ‘t’ | |
| The number of -infected mosquitoes susceptible | |
| to Dengue virus at a time ‘t’ | |
| The number of -infected mosquitoes infected by | |
| Dengue virus at time ‘t’ | |
| The number of non- mosquitoes at time ‘t’ | |
| The number of non- mosquitoes susceptible to | |
| Dengue virus at time ‘t’ | |
| The number of non- mosquitoes infected by | |
| Dengue virus at time ‘t’ | |
| The number of the susceptible human population at a time ‘t’ | |
| The number of the infectious human population at a time ‘t’ | |
| The number of hospitalized human population at a time ‘t’ | |
| The number of recovered human population at a time ‘t’ |
| Parameters | Description | Values | Unit | Source |
|---|---|---|---|---|
| Reproduction rate of mosquitoes | 1/day | [38] | ||
| Reproduction rate of wild mosquitoes | 1/day | [38] | ||
| Reproduction rate of mosquitoes | 1/day | [56] | ||
| Reproduction rate of mated female mosquitoes | 1/day | [39] | ||
| fraction of produced offspring having infection | NA | [39] | ||
| Fraction of produced offspring not having infection | NA | [39] | ||
| Natural death rate of aquatic mosquitoes | 1/day | [39] | ||
| Density-dependent death rate of aquatic mosquitoes | 1/day | |||
| Natural death rate of non- aquatic mosquitoes | 1/day | [57] | ||
| Density dependent death rate of non- aquatic mosquitoes | 1/day | |||
| Maturation rate of aquatic stage mosquitoes from which adult mosquitoes emerge | 1/day | [57] | ||
| The average bitting rate of non- mosquitoes | 1/day | [58] | ||
| Average bitting rate of mosquitoes | 1/day | [59] | ||
| Probability virus transmission from infected human to and non- mosquitoes | NA | [39] | ||
| Virus transmission probability from infected mosquitoes to susceptible human | NA | [60] | ||
| Virus transmission probability from infected non- mosquitoes to susceptible human | NA | [39] | ||
| Mortality rate of non- adult mosquitoes | 1/day | [57] | ||
| Mortality rate of adult mosquitoes | 1/day | [56,61] | ||
| Birth rate of human | 1/day | [62] | ||
| Natural death rate of human population | 1/day | [62] | ||
| Hospitalization rate of identified infected human | 1/day | [63] | ||
| The rate of natural recovery of infected human due to immunity | 1/day | [63] | ||
| The rate of recovery due to hospitalization | 1/day | [63] |
| S. No | Strain | CI |
|---|---|---|
| 1. | wMelCS | 0.20–0.83 |
| 2. | wAlbB | 0.20–0.88 |
| 3. | wMel | 0.826–2.516 |
| 4. | wPip | 0.367–0.681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joseph, D.; Ramachandran, R.; Alzabut, J.; Jose, S.A.; Khan, H. A Fractional-Order Density-Dependent Mathematical Model to Find the Better Strain of Wolbachia. Symmetry 2023, 15, 845. https://doi.org/10.3390/sym15040845
Joseph D, Ramachandran R, Alzabut J, Jose SA, Khan H. A Fractional-Order Density-Dependent Mathematical Model to Find the Better Strain of Wolbachia. Symmetry. 2023; 15(4):845. https://doi.org/10.3390/sym15040845
Chicago/Turabian StyleJoseph, Dianavinnarasi, Raja Ramachandran, Jehad Alzabut, Sayooj Aby Jose, and Hasib Khan. 2023. "A Fractional-Order Density-Dependent Mathematical Model to Find the Better Strain of Wolbachia" Symmetry 15, no. 4: 845. https://doi.org/10.3390/sym15040845
APA StyleJoseph, D., Ramachandran, R., Alzabut, J., Jose, S. A., & Khan, H. (2023). A Fractional-Order Density-Dependent Mathematical Model to Find the Better Strain of Wolbachia. Symmetry, 15(4), 845. https://doi.org/10.3390/sym15040845







