Analytical Solutions of Peristalsis Flow of Non-Newtonian Williamson Fluid in a Curved Micro-Channel under the Effects of Electro-Osmotic and Entropy Generation
Abstract
:1. Introduction
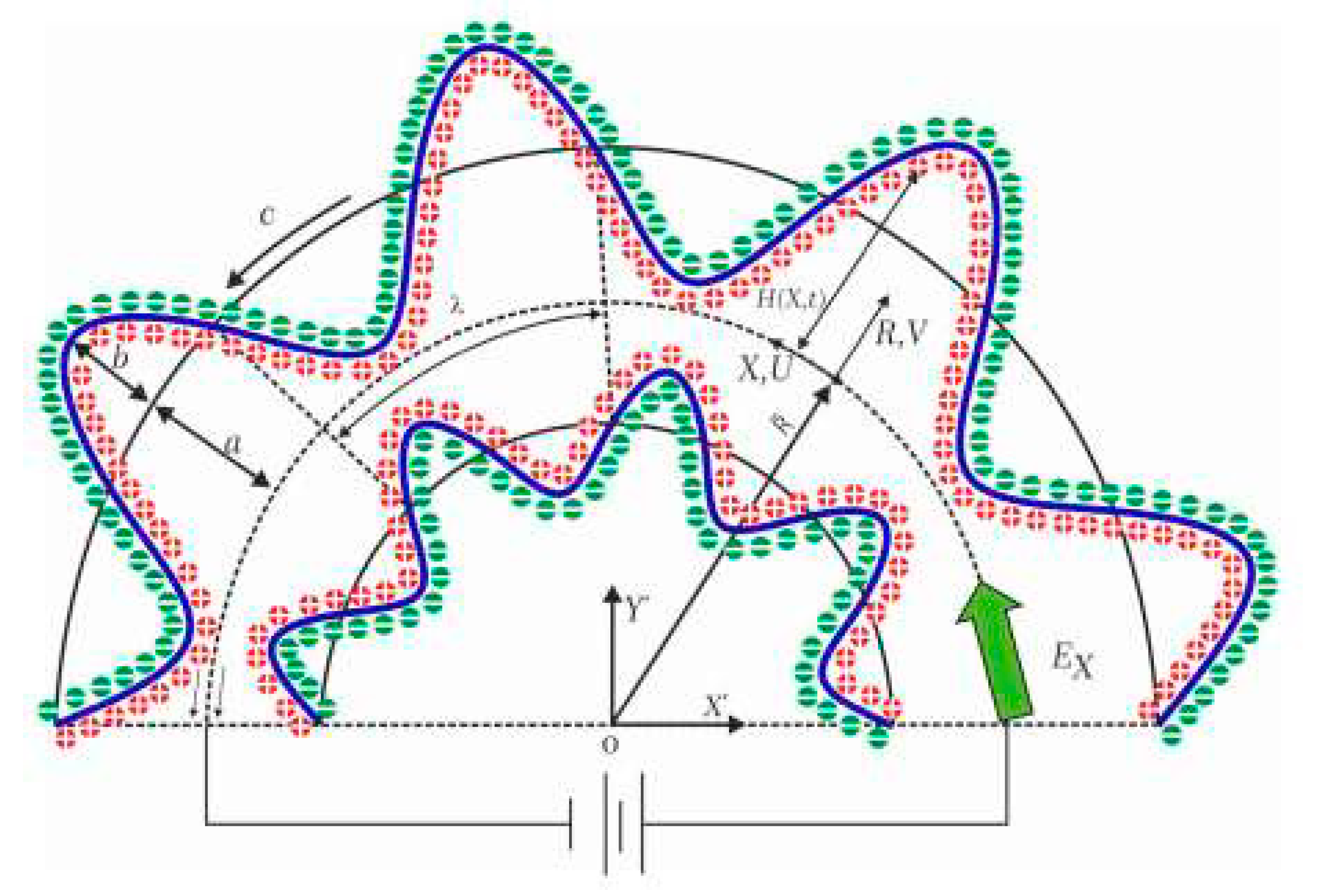
2. Problem Formulation
3. Method of Solution
Entropy
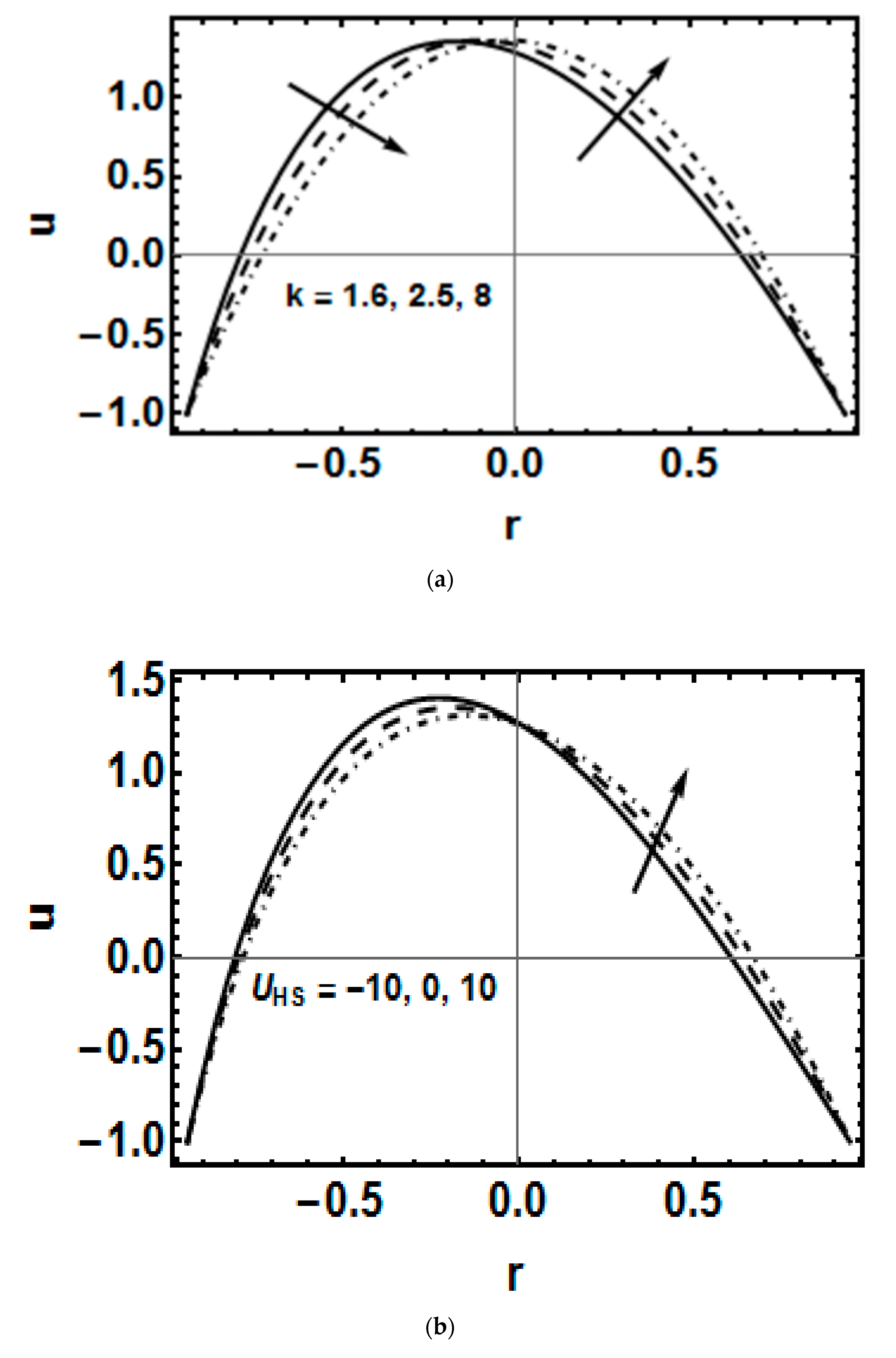
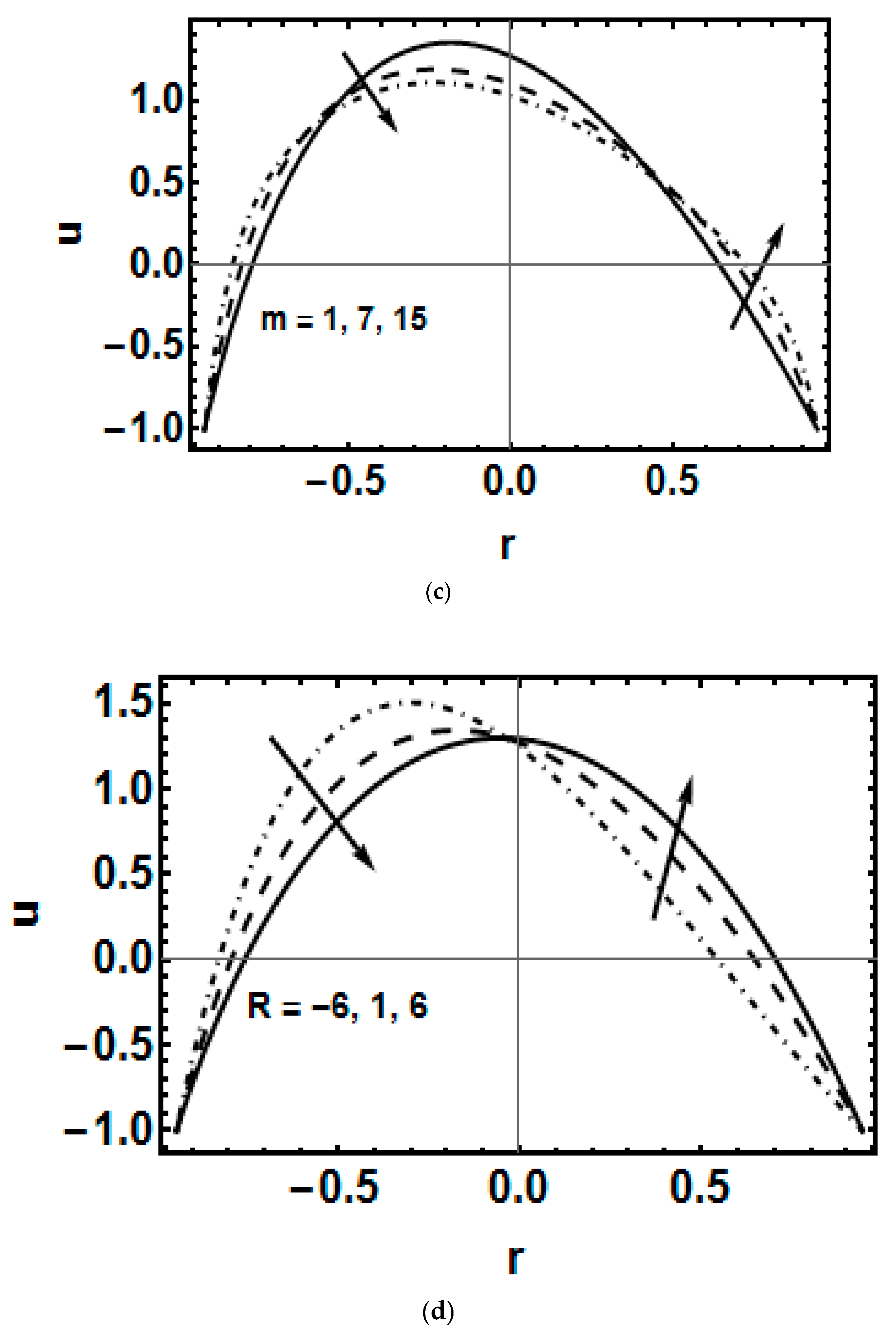
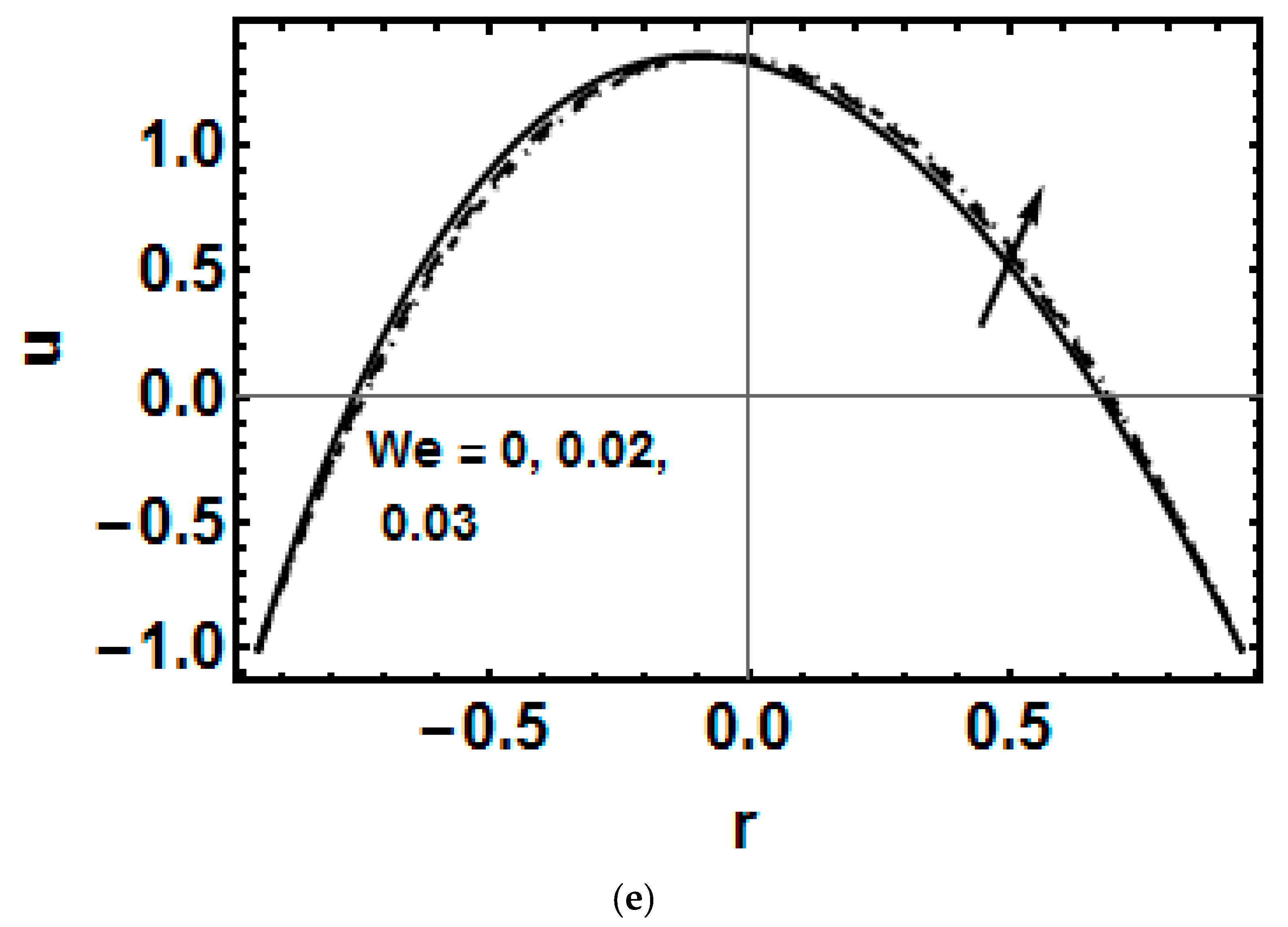
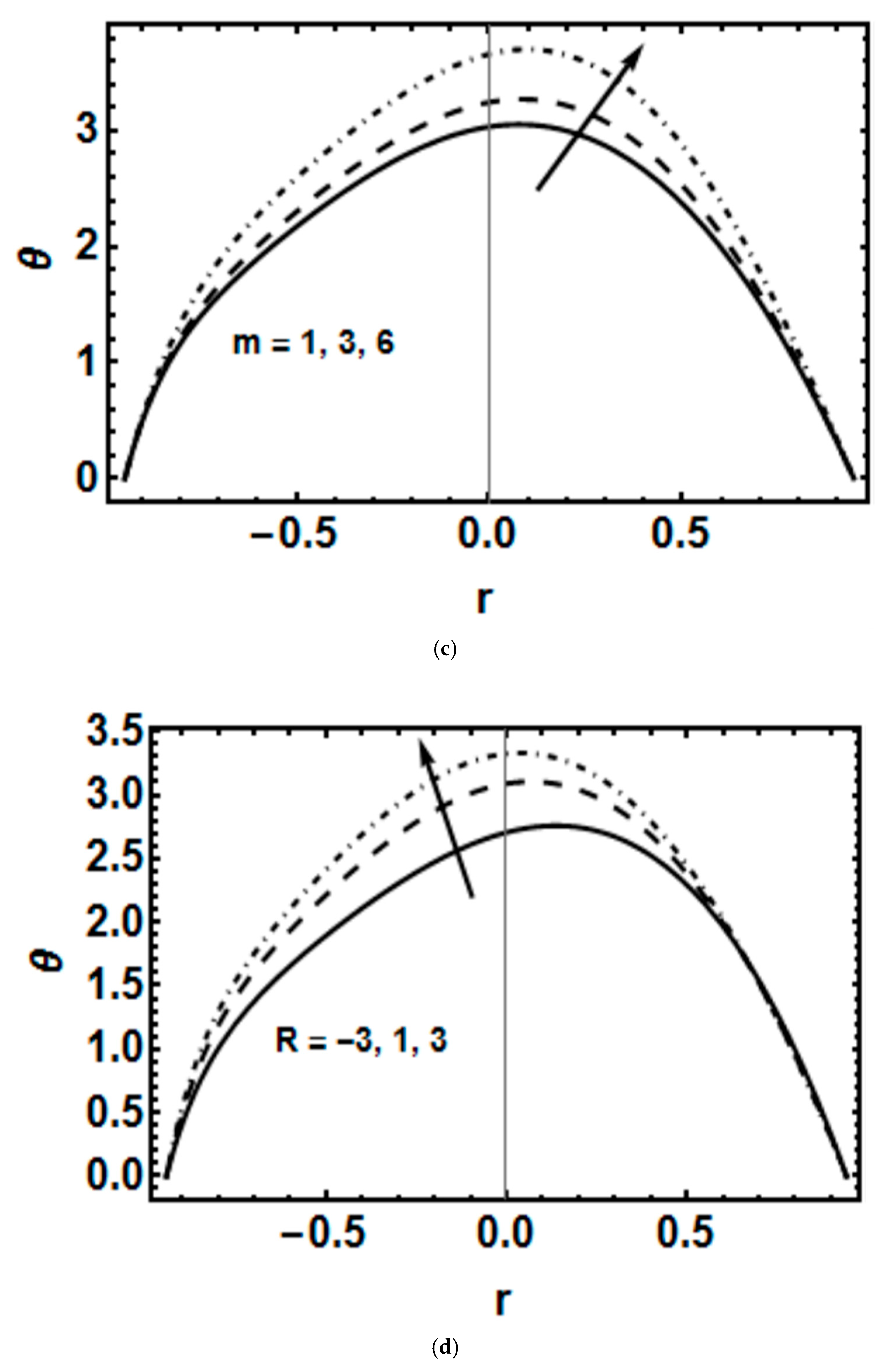
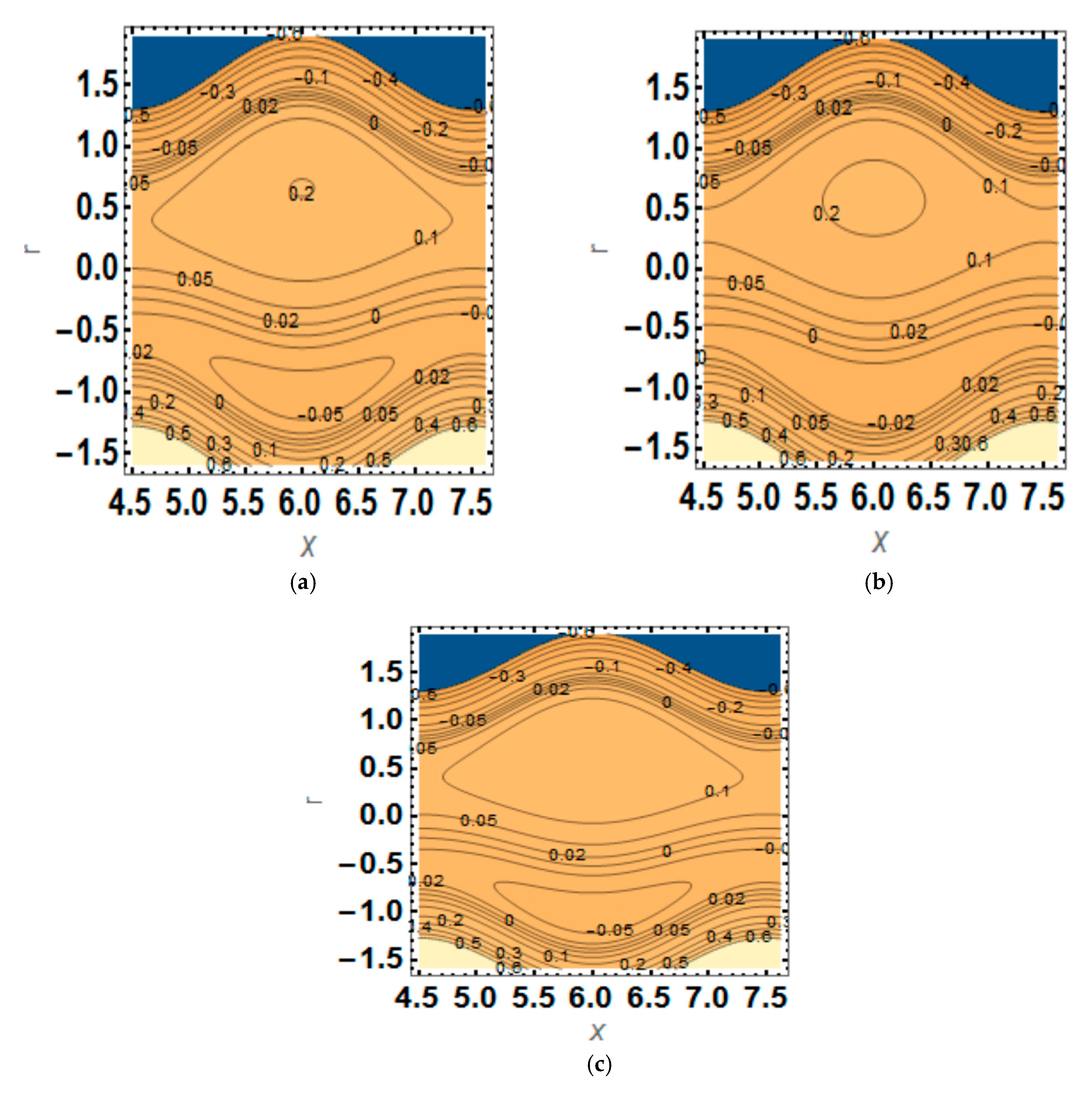
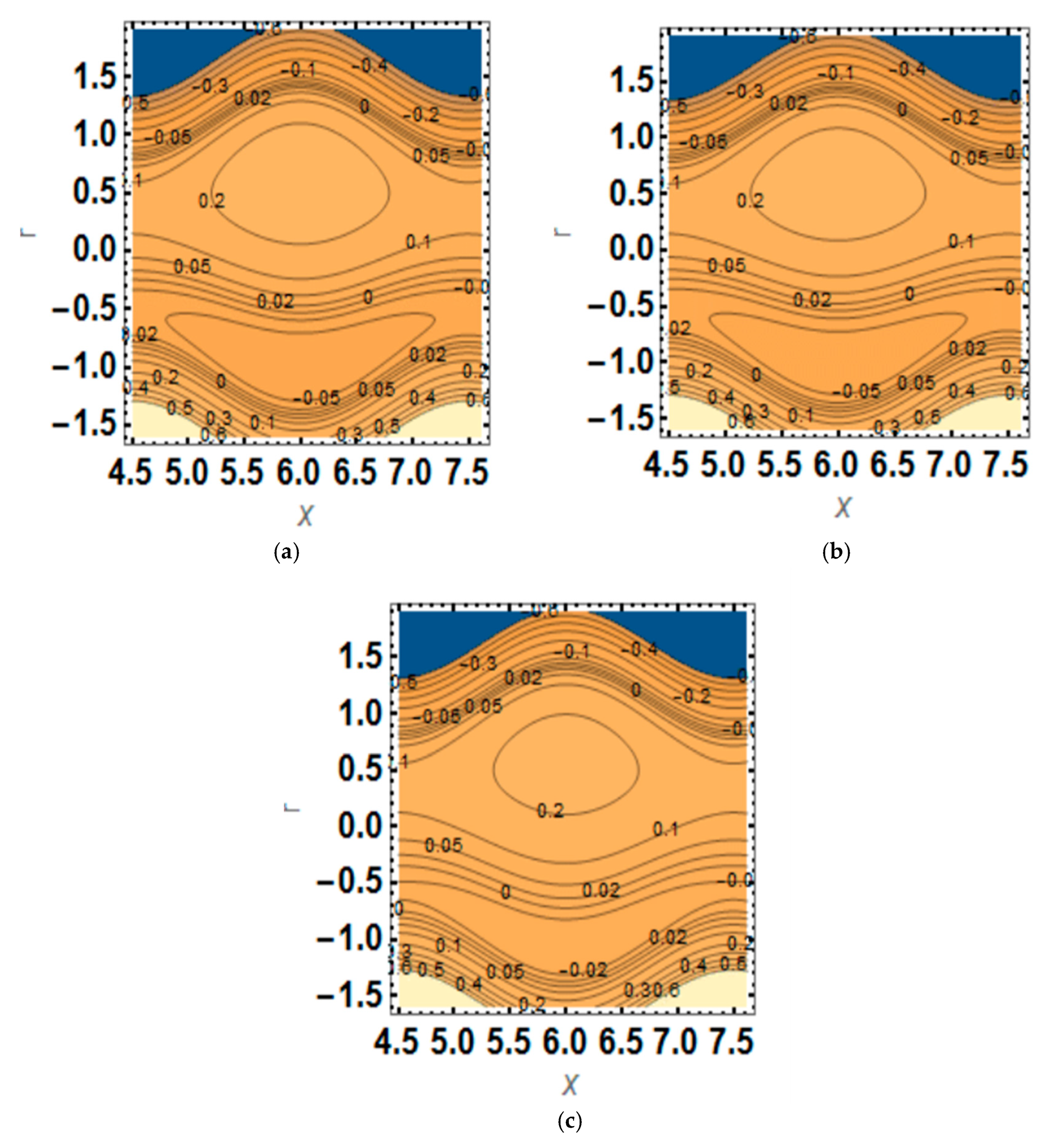
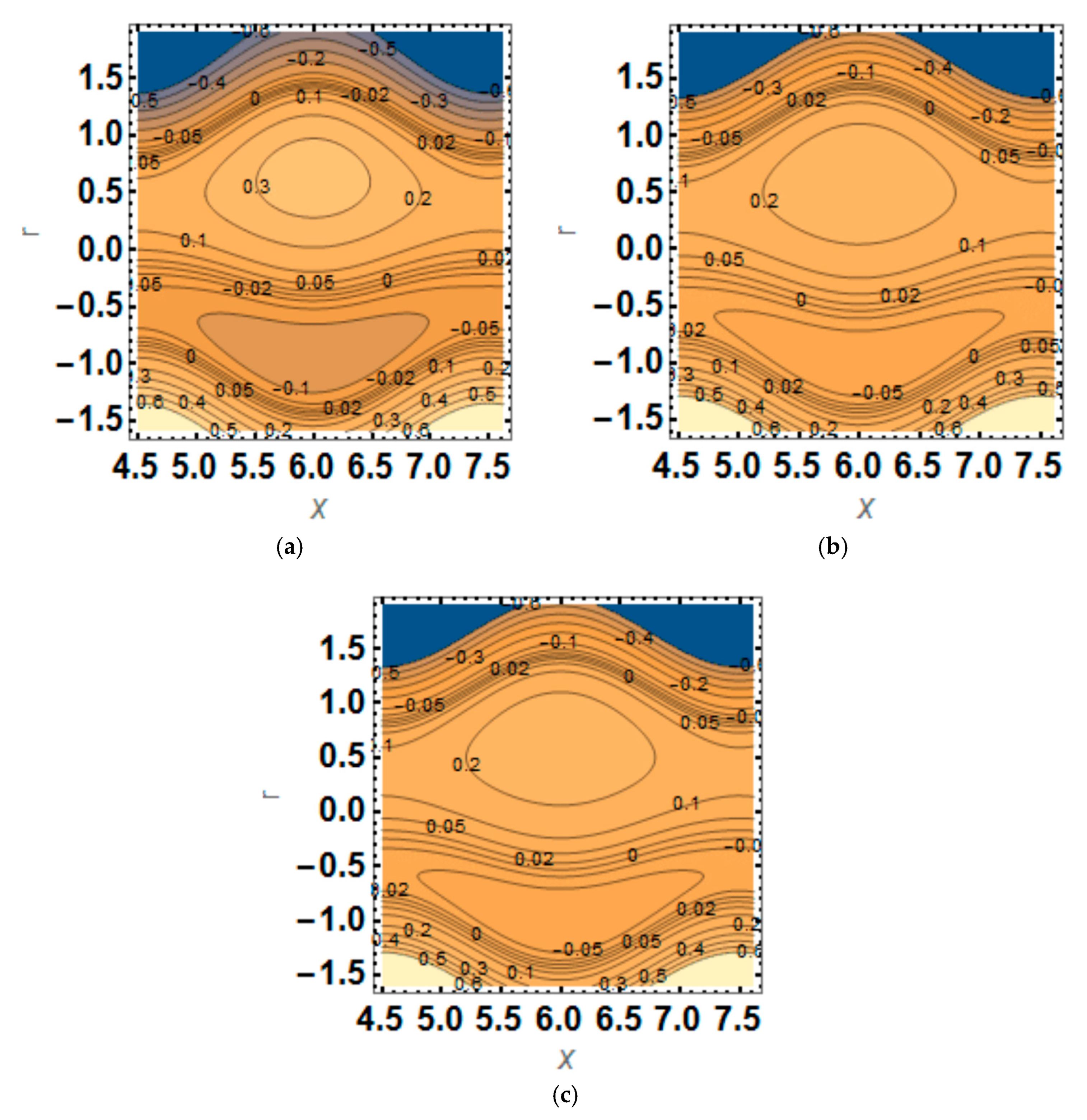
4. Results and Discussion
5. Conclusions
- The temperature rises for the thickness parameter.
- A rise in temperature is observed in the curved channel than the straight channel.
- Using the process of electro-osmosis, we can control the flow of fluid.
- The bolus size increases with the EDL thickness.
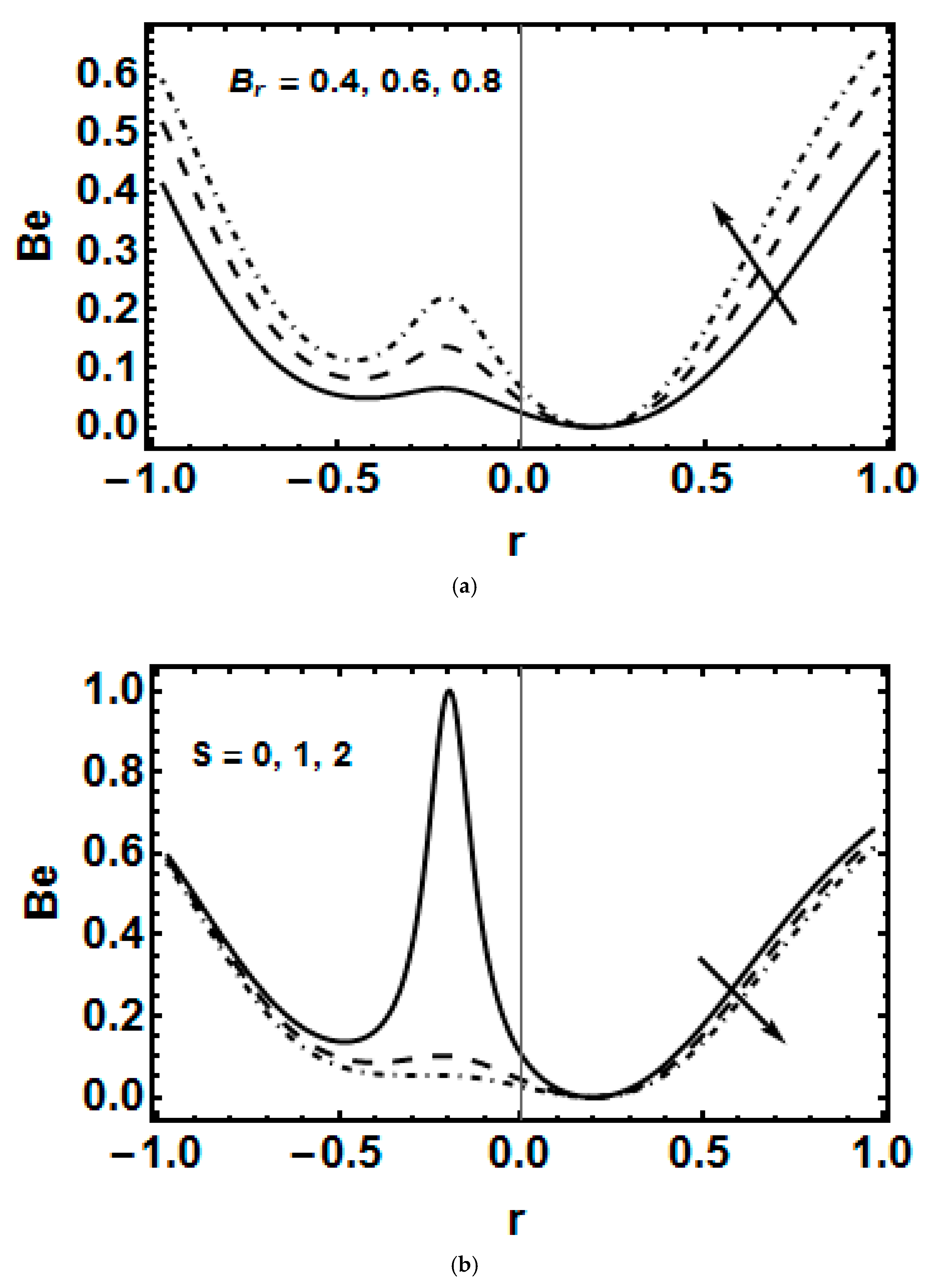
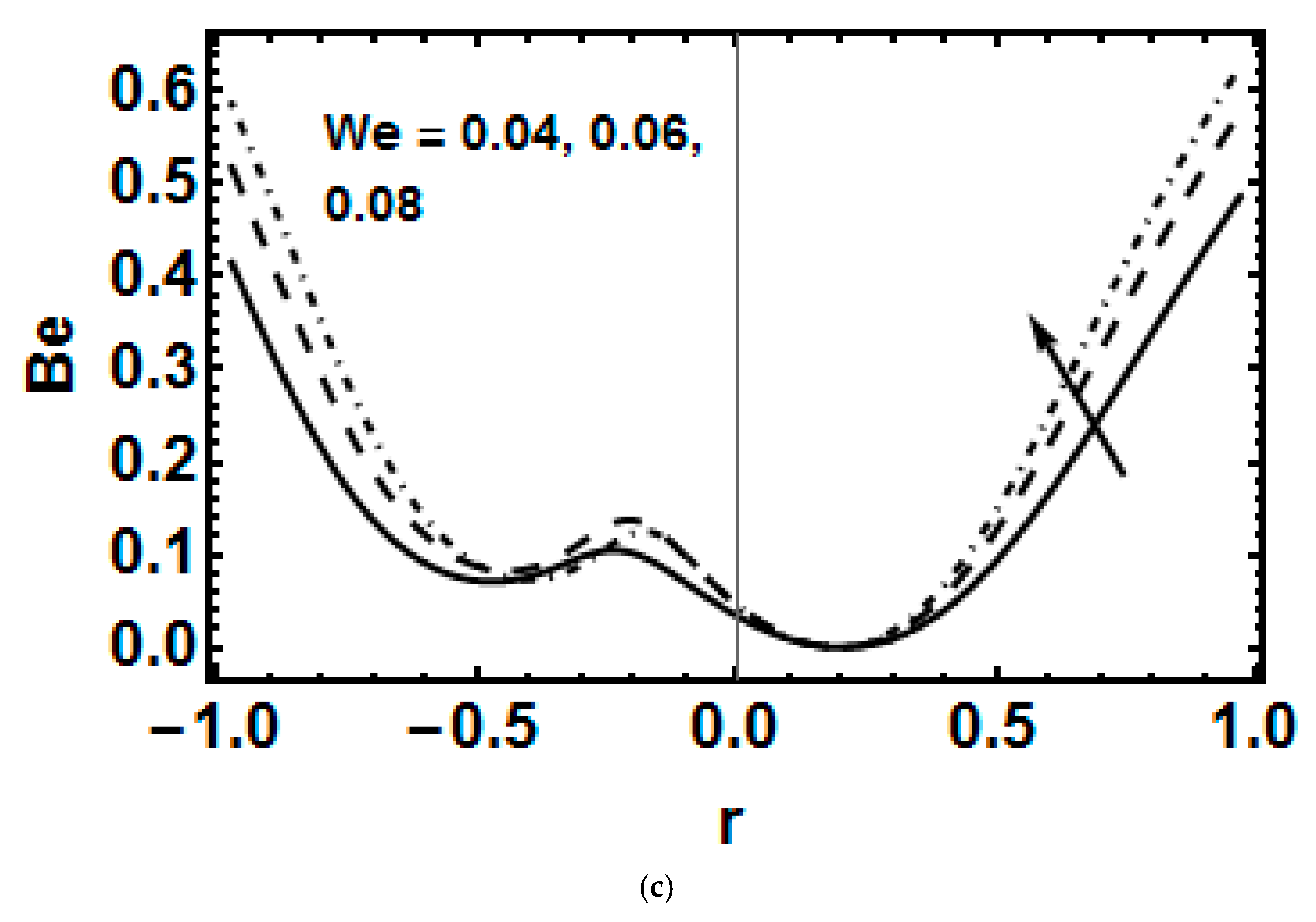
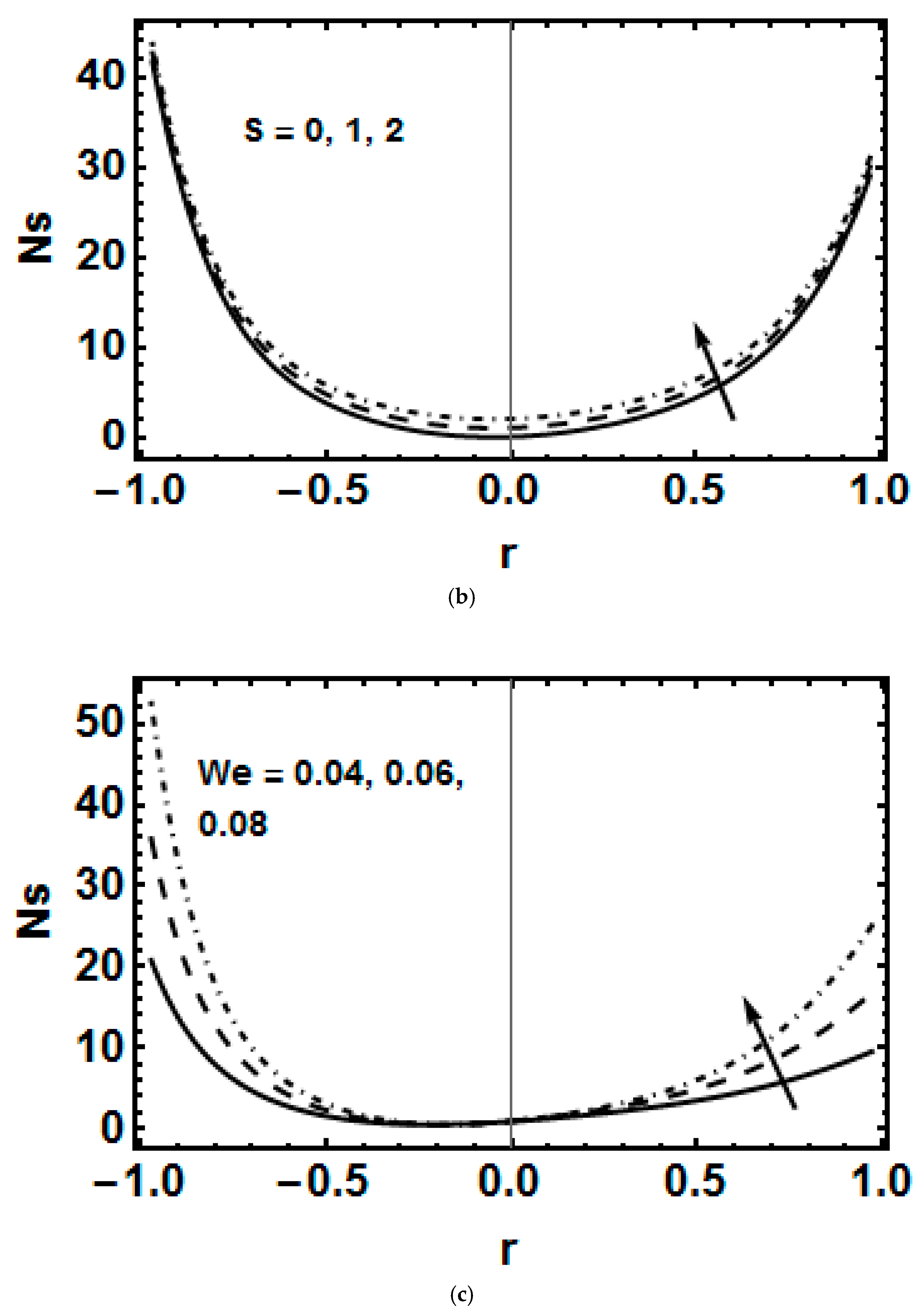
- The Bejan number enhances with both the Brickman number and the Weissenberg number.
- Using the process of electro-osmosis, the flow of fluid can be controlled easily.
- The current study has revealed some intriguing aspects of the curved micro-channel that are relevant to bio-microfluidic devices. Alternative rheological models, such as fourth grade fluid, may be considered in future studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Velocity of the fluid along radial direction (m/s). | |
| Velocity of the fluid along axial direction (m/s). | |
| Electric field (V/m). | |
| Pressure (Pa). | |
| Number densities of p-ions (cm−3). | |
| Ionic valence (mol m3). | |
| Specific heat generation (J/(kg K)). | |
| Thermal conductivity (W/mK). | |
| Absolute temperature (°C). | |
| Ionic species diffusivity (m2/s). | |
| Boltzmann constant (J/K). | |
| Velocity components (m/s). | |
| Velocity components (m/s). | |
| Wave speed (m/s). | |
| Hemholtz-Smoluchowski velocity. | |
| Reynolds number. | |
| Peclet number. | |
| Brinkman number. | |
| Weissenberg number. | |
| Joule heating parameter (Nm). | |
| Prandtl number. | |
| Temperature of fluid (°C). | |
| Greek Symbol | |
| Net charge density (C/m3). | |
| Viscosity (kg·m−1·s−1) | |
| Density (kg/m3). | |
| Electrical conductivity of fluid ions (S/m). | |
| Electric potential function (V). | |
| Permittivity constant (F/m). | |
| Dimensionless temperature. | |
References
- Latham, T.W. Fluid Motions in a Peristaltic Pump. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Jaffrin, M.Y.; Shapiro, A.H. Peristaltic pumping. Annu. Rev. Fluid Mech. 1971, 3, 13–37. [Google Scholar] [CrossRef]
- Srivastava, L.M.; Srivastava, V.P. Peristaltic transport of blood: Casson model-II. J. Biomech. 1984, 17, 821–829. [Google Scholar] [CrossRef] [PubMed]
- Raju, K.K.; Devanathan, R. Peristaltic motion of a non-Newtonian fluid. Rheol. Acta 1972, 11, 170–178. [Google Scholar] [CrossRef]
- Sharifah, E.A.; Ali, I.; Muhammad, A.; Mazhar, A.; Weaam, A.; Haneen, H.; Awatif, A.; Asif, W. Thermal convection in nanofluids for peristaltic flow in a nonuniform channel. Sci. Rep. 2022, 12, 12656. [Google Scholar]
- Nawaz, S.; Hayat, T.; Alsaedi, A. Analysis of entropy generation in peristalsis of Williamson fluid in curved channel under radial magnetic field. Comput. Methods Programs Biomed. 2019, 180, 105013. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Rajanikanth, K.; Lee, C. Peristaltic transport of a Williamson fluid in asymmetric channels with permeable walls. Nonlinear Analysis: Real World Appl. 2012, 13, 2804–2822. [Google Scholar] [CrossRef]
- Riaz, A.; Zeeshan, A.; Bhatti, M.M.; Ellahi, R. Peristaltic propulsion of Jeffrey nano-liquid and heat transfer through a symmetrical duct with moving walls in a porous medium. Phys. A Stat. Mech. Its Appl. 2020, 545, 123788. [Google Scholar] [CrossRef]
- Chakraborty, S. Augmentation of peristaltic microflows through electro-osmotic mechanisms. J. Phys. D Appl. Phys. 2006, 39, 5356. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, A.; Bég, O.A. Electrothermal transport of nanofluids via peristaltic pumping in a finite micro-channel: Effects of Joule heating and Helmholtz-Smoluchowski velocity. Int. J. Heat Mass Transfer. 2017, 111, 138–149. [Google Scholar] [CrossRef]
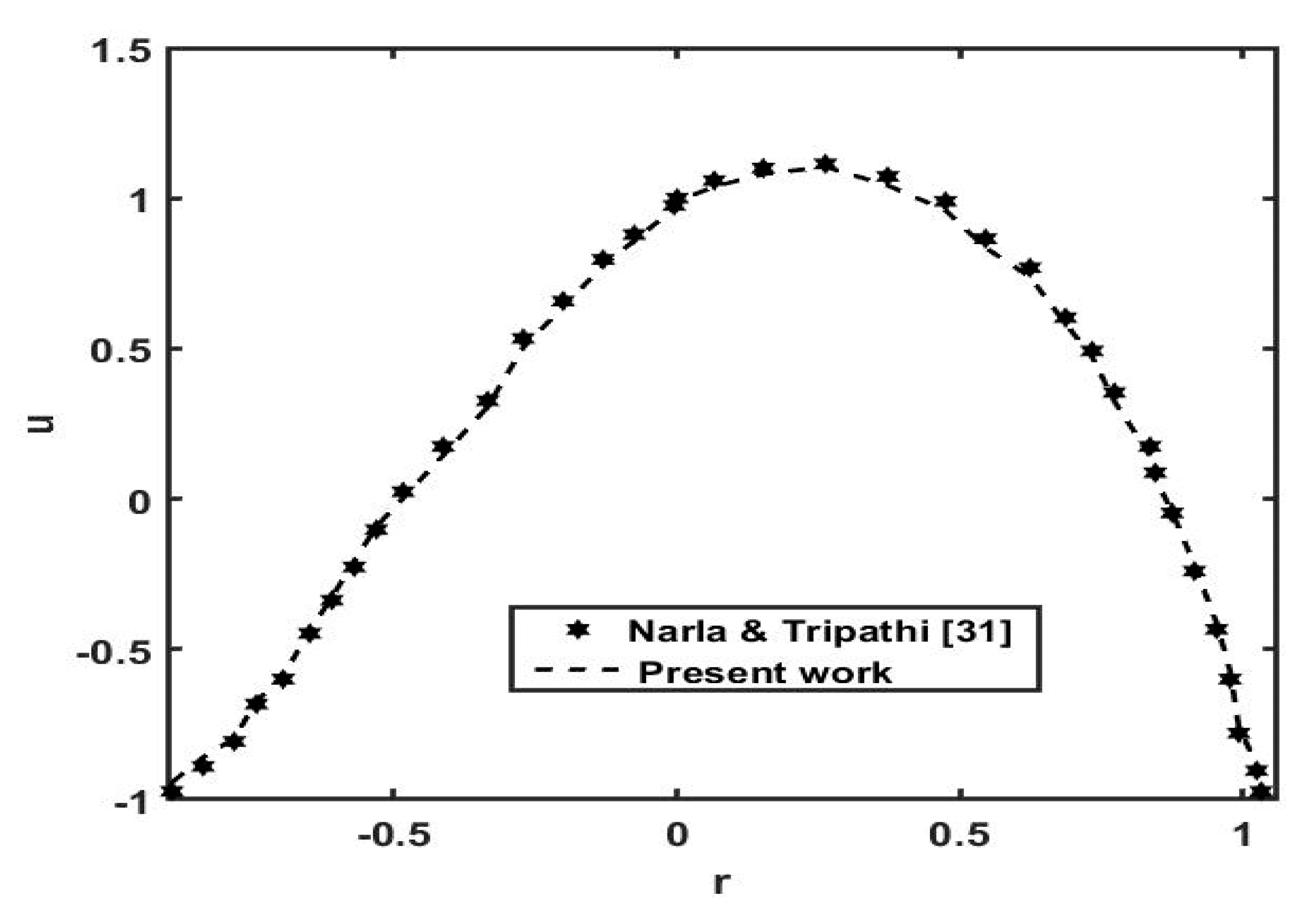
- Narla, V.K.; Tripathi, D.; Bég, O.A. Electro-osmotic nanofluid flow in a curved microchannel. Chin. J. Phys. 2020, 67, 544–558. [Google Scholar] [CrossRef]
- Ambreen, A.K.; Kaenat, A.; Akbar, Z.; Anwar, B.; Tasveer, A.B. Electro-osmotic peristaltic flow and heat transfer in an ionic viscoelastic fluid through a curved micro-channel with viscous dissipation. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 1080–1092. [Google Scholar]
- Ramesh, K.; Prakash, J. Thermal analysis for heat transfer enhancement in electroosmosis-modulated peristaltic transport of Sutterby nanofluids in a microfluidic vessel. J. Therm. Anal. Calorim. 2019, 138, 1311–1326. [Google Scholar] [CrossRef]
- Akram, J.; Akbar, N.S.; Maraj, E.N. A comparative study on the role of nanoparticle dispersion in electroosmosis regulated peristaltic flow of water. Alex. Eng. J. 2020, 59, 943–956. [Google Scholar] [CrossRef]
- Tripathi, D.; Yadav, A.; Bég, O.A. Electro-kinetically driven peristaltic transport of viscoelastic physiological fluids through a finite length capillary: Mathematical modeling. Math. Biosci. 2017, 283, 155–168. [Google Scholar] [CrossRef]
- Tanveer, A.; Mahmood, S.; Hayat, T.; Alsaedi, A. On electroosmosis in peristaltic activity of MHD non-Newtonian fluid. Alexandria Eng. J. 2021, 60, 3369–3377. [Google Scholar] [CrossRef]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite Time Processes; CRC Press: Boca Raton, NY, USA, 2013; p. 23. [Google Scholar]
- Jhorar, R.; Tripathi, D.; Bhatti, M.M.; Ellahi, R. Electro osmosis modulated biomechanical transport through asymmetric microfluidics channel. Indian J. Phys. 2018, 92, 1229–1238. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical simulation and mathematical modeling of electroosmotic Couette-Poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, M.M.; Yousif, M.A.; Mishra, S.R.; Shahid, A. Simultaneous influence of thermo-diffusion and diffusion-thermo on non-Newtonian hyperbolic tangent magnetised nanofluid with Hall current through a nonlinear stretching surface. Pramana 2019, 93, 88. [Google Scholar] [CrossRef]
- Gholamalipour, P.; Siavashi, M.; Doranehgard, M.H. Eccentricity effects of heat source inside a porous annulus on the natural convection heat transfer and entropy generation of Cu-water nanofluid. Int. Commun. Heat Mass Transfer. 2019, 109, 104367. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An analytical treatment for the exact solutions of MHD flow and heat over two–three dimensional deforming bodies. Int. J. Heat Mass Transfer. 2015, 90, 781–789. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.M.; Marin, M.; Mekheimer, K.S. Entropy analysis on the blood flow through anisotropically tapered arteries filled with magnetic zinc-oxide (ZnO) nanoparticles. Entropy 2020, 22, 1070. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Nayak, A.K. Influence of varying zeta potential on non-Newtonian flow mixing in a wavy patterned microchannel. J. Non-Newton. Fluid Mech. 2019, 269, 17–27. [Google Scholar] [CrossRef]
- Rostamzadeh, A.; Razavi, S.E.; Mirsajedi, S.M. Towards multidimensional artificially characteristic-based scheme for incompressible thermo-fluid problems. Mechanics 2017, 23, 826–834. [Google Scholar] [CrossRef] [Green Version]
- Trabzon, L.; Karimian, G.; RKhosroshahi, A.; Gül, B.; Gh Bakhshayesh, A.; Koçak, A.F.; Aldi, Y.E. High-throughput nanoscale liposome formation via electrohydrodynamic-based micromixer. Phys. Fluids 2022, 34, 102011. [Google Scholar] [CrossRef]
- Sharma, B.K.; Kumar, A.; Gandhi, R.; Bhatti, M.M.; Mishra, N.K. Entropy Generation and Thermal Radiation Analysis of EMHD Jeffrey Nanofluid Flow: Applications in Solar Energy. Nanomaterials 2023, 13, 544. [Google Scholar] [CrossRef]
- Gandhi, R.; Sharma, B.K.; Mishra, N.K.; Al-Mdallal, Q.M. Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations. Nanomaterials 2023, 13, 652. [Google Scholar] [CrossRef]
- Sridhar, V.; Ramesh, K.; Gnaneswara Reddy, M.; Azese, M.N.; Abdelsalam, S.I. On the entropy optimization of hemodynamic peristaltic pumping of a nanofluid with geometry effects. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Narla, V.K.; Tripathi, D. Electroosmosis modulated transient blood flow in curved microvessels: Study of mathematical model. Microvasc. Res. 2019, 123, 25–34. [Google Scholar] [CrossRef]
- Rashid, M.; Ansar, K.; Nadeem, S. Effects of induced magnetic field for peristaltic flow of Williamson fluid in a curved channel. Phys. A Stat. Mech. Its Appl. 2020, 553, 123979. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Riaz, A.; Zhang, L.; Sait, S.M.; Ellahi, R. Biologically inspired thermal transport on the rheology of Williamson hydromagnetic nanofluid flow with convection: An entropy analysis. J. Therm. Anal. Calorim. 2021, 144, 2187–2202. [Google Scholar] [CrossRef]
- Ghorbani, G.; Moghadam, A.J.; Emamian, A.; Ellahi, R.; Sait, S.M. Numerical simulation of the electroosmotic flow of the Carreau-Yasuda model in the rectangular microchannel. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 2240–2259. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.A.; Zahra, B.; Ellahi, R.; Sait, S.M. Analytical Solutions of Peristalsis Flow of Non-Newtonian Williamson Fluid in a Curved Micro-Channel under the Effects of Electro-Osmotic and Entropy Generation. Symmetry 2023, 15, 889. https://doi.org/10.3390/sym15040889
Khan AA, Zahra B, Ellahi R, Sait SM. Analytical Solutions of Peristalsis Flow of Non-Newtonian Williamson Fluid in a Curved Micro-Channel under the Effects of Electro-Osmotic and Entropy Generation. Symmetry. 2023; 15(4):889. https://doi.org/10.3390/sym15040889
Chicago/Turabian StyleKhan, Ambreen A., B. Zahra, R. Ellahi, and Sadiq M. Sait. 2023. "Analytical Solutions of Peristalsis Flow of Non-Newtonian Williamson Fluid in a Curved Micro-Channel under the Effects of Electro-Osmotic and Entropy Generation" Symmetry 15, no. 4: 889. https://doi.org/10.3390/sym15040889





