Cell-Dependent Mechanical Properties of Asymmetric Crosslinked Metallic Wire Mesh with Hybrid Patterns Based on Arbitrary Poisson’s Ratio
Abstract
1. Introduction
2. Theoretical Representation of Metallic Wire Mesh
3. Materials and Methods
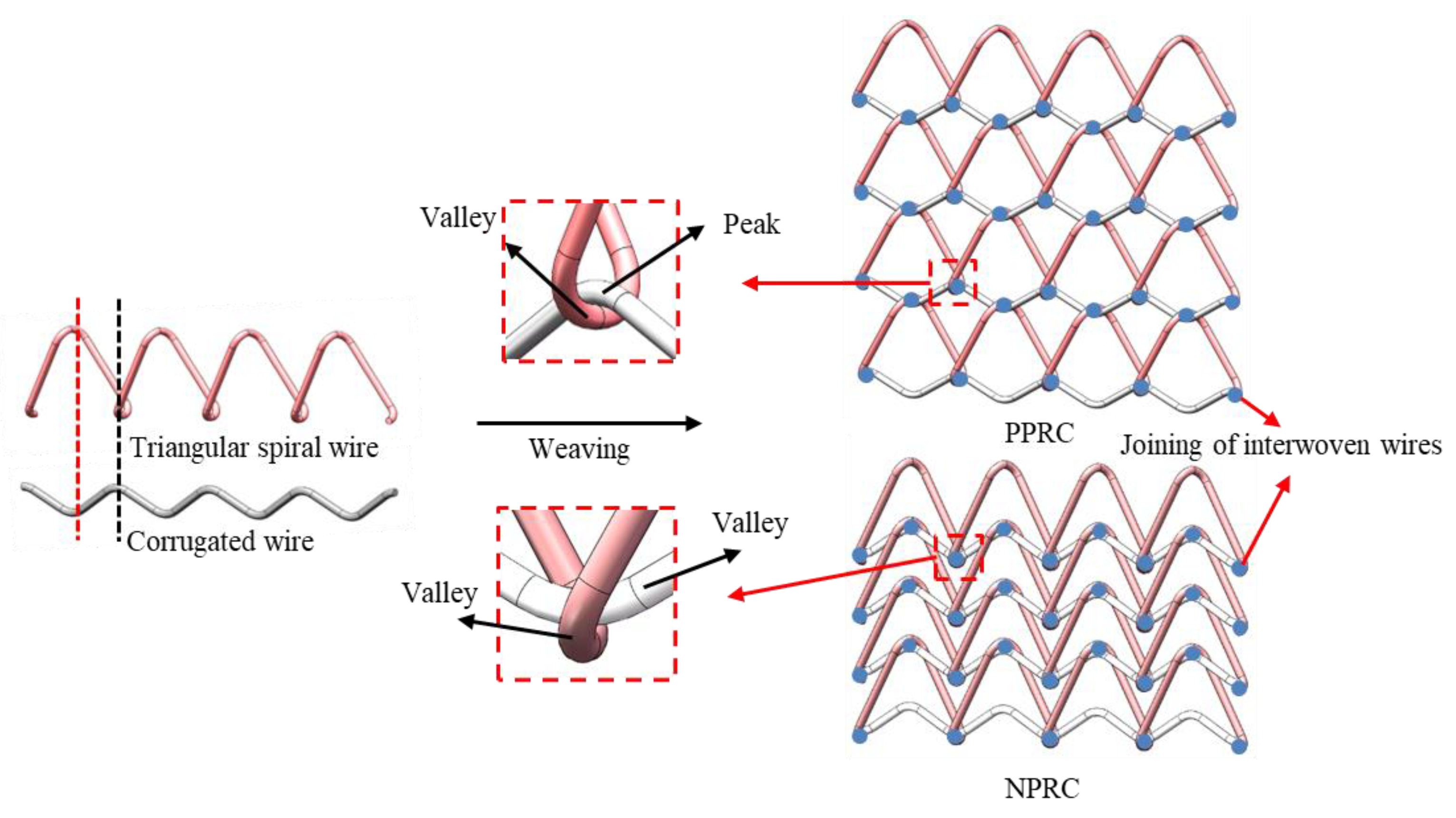
3.1. Structural Design of Asymmetric Crosslinked Metallic Wire Mesh
3.2. Experimental Procedures
3.2.1. Fabrication of Asymmetric Crosslinked Metallic Wire Mesh
3.2.2. Uniaxial Tensile Test
3.2.3. Three-Point Bending
3.3. Finite Element Analysis
3.3.1. Numerical Modeling
3.3.2. Preliminary Results of Numerical Simulation
4. Results and Discussion
4.1. Influence of Cell Beam Angle on the Poisson’s Ratio
4.2. Effects of Hybrid Cell Pattern on Macroscopic Poisson’s Ratio
4.3. Influence of Interwoven Joint on Elastic Bending Property
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yang, G.; Xu, R.; Wang, Y.; Zhu, Y.; Ren, F.; Li, C.; Wu, J. Pore-scale numerical simulations of flow and convective heat transfer in a porous woven metal mesh. Chem. Eng. Sci. 2022, 256, 117696. [Google Scholar] [CrossRef]
- Joo, J.-H.; Kang, K.-J.; Kim, T.; Lu, T. Forced convective heat transfer in all metallic wire-woven bulk Kagome sandwich panels. Int. J. Heat Mass Transf. 2011, 54, 5658–5662. [Google Scholar] [CrossRef]
- Iwaniszyn, M.; Sindera, K.; Gancarczyk, A.; Korpys, M.; Jedrzejczyk, R.J.; Kolodziej, A.; Jodłowski, P.J. Experimental and CFD investigation of heat transfer and flow resistance in woven wire gauzes. Chem. Eng. Process. 2021, 163, 108364. [Google Scholar] [CrossRef]
- Wang, G.S.; Sun, Y.H.; Zhang, A.; Zheng, L.; Lv, Y.Z.; Wu, H.J.; Yang, Y. Study on the Impact Resistance of Metal Flexible Net to Rock fall. Shock Vib. 2020, 2020, 9612405. [Google Scholar] [CrossRef]
- Trad, A.; Limam, A. Load testing and simulation of asymmetric cable-net used for flexible rockfall protection barriers. Eur. J. Environ. Civ. Eng. 2021, 25, 7685–7702. [Google Scholar] [CrossRef]
- Escallon, J.P.; Boetticher, V.; Wendeler, C.; Chatzi, E.; Bartelt, P. Mechanics of chain-link wire nets with loose connections. Eng. Struct. 2015, 101, 68–87. [Google Scholar] [CrossRef]
- Santos, L.; Izzuddin, B.A.; Macorini, L. Gradient-based optimisation of rectangular honeycomb core sandwich panels. Struct. Multidiscip. Optim. 2022, 65, 242. [Google Scholar] [CrossRef]
- Shuang, L.; Yang, J.S.; Rudiger, S.; Wu, L.Z.; Schroder, K.U. Compression and hysteresis responses of multilayer gradient composite lattice sandwich panels. Mar. Struct. 2021, 75, 102845. [Google Scholar] [CrossRef]
- Borges, H.; Martínez, G.; Graciano, C. Impact response of expanded metal tubes: A numerical investigation. Thin-Walled Struct. 2016, 105, 71–80. [Google Scholar] [CrossRef]
- Nedoushan, R.J. Improvement of energy absorption of expanded metal tubular structures under compressive loads. Thin-Walled Struct. 2020, 157, 107058. [Google Scholar] [CrossRef]
- Zhang, C.P.; Khan, A.; Cai, J.X.; Liang, C.W.; Liu, Y.J.; Deng, J.H.; Huang, S.; Li, G.; Li, W.-D. Stretchable Transparent Electrodes with Solution-Processed Regular Metal Mesh for an Electroluminescent Light-Emitting Film. ACS Appl. Mater. Interfaces 2018, 10, 21009–21017. [Google Scholar] [CrossRef]
- Stolbchenko, M.; Makeieva, H.; Grydin, O.; Ya, F.; Schaper, M. Strain parameters at hot rolling of aluminum strips reinforced with steel netting. J. Sandw. Struct. Mater. 2020, 22, 2009–2029. [Google Scholar] [CrossRef]
- Yang, T.; Yang, P.; Zou, Z.Y.; Ma, P. Mechanical properties of warp-knitted metal mesh fabric under biaxial tension loading. Text. Res. J. 2021, 91, 1368–1379. [Google Scholar] [CrossRef]
- Kang, K.-J. Wire-woven cellular metals: The present and future. Prog. Mater. Sci. 2015, 69, 213–307. [Google Scholar] [CrossRef]
- Lee, K.W.; Park, J.-S.; Jeon, I.; Kang, K.-J. Equivalent material properties of a wire-woven cellular core. Mech. Mater. 2013, 57, 1–14. [Google Scholar] [CrossRef]
- Xue, X.; Wu, F.; Zheng, C.; Wei, Y.; Chen, X.; Bai, H. Research progress of flexible sandwich structure materials with metal-rubber damping core. Mater. Rep. 2022, 36, 22040029-11. [Google Scholar]
- Albrecht, V.B.; Axel, V. Numerical modeling of chain-link steel wire nets with discrete elements. Can. Geotech. J. 2019, 56, 398–419. [Google Scholar]
- Zhang, Q.; Jiang, W.C.; Zhang, Y.T.; Luo, Y.; Tu, S.-T. Effective elastic constants of wire mesh material studied by theoretical and finite element methods. Compos. Struct. 2017, 184, 474–483. [Google Scholar] [CrossRef]
- Li, T.J.; Jiang, J.; Shen, T.T.; Wang, Z.W. Analysis of mechanical properties of wire mesh for mesh reflectors by fractal mechanics. Int. J. Mech. Sci. 2015, 92, 90–97. [Google Scholar] [CrossRef]
- Yang, H.; Ma, L. Impact resistance of additively manufactured 3D double-U auxetic structures. Thin-Walled Struct. 2021, 169, 108373. [Google Scholar] [CrossRef]
- Xue, X.; Shen, G.J.; Wu, X.Q.; Xiong, Y.L.Z.; Liao, J.; Bai, H.B. Thermo-mechanical performances of elastic–porous materials with metallic wire mesh structures. Compos. Struct. 2022, 297, 115918. [Google Scholar] [CrossRef]
- Wu, F.; Xiao, X.; Yang, J.; Gao, X.D. Quasi-static axial crushing behaviour and energy absorption of novel metal rope crochet-sintered mesh tubes. Thin-Walled Struct. 2018, 127, 120–134. [Google Scholar] [CrossRef]
- Dong, J.H.; Wang, Y.J.; Jin, F.N.; Fan, H.L. Crushing behaviours of buckling-induced metallic meta-lattice structures. Def. Technol. 2022, 18, 1301–13010. [Google Scholar] [CrossRef]
- Formisano, A.; Durante, M.; Viscusi, A.; Garrino, L.G. Mechanical behaviour and collapse mechanisms of innovative aluminum foam-based sandwich panels under three-point bending. Int. J. Adv. Manuf. Technol. 2021, 112, 1301–1310. [Google Scholar] [CrossRef]
- Xue, X.; Lin, C.C.; Wu, F.; Li, Z.; Liao, J. Lattice structures with negative Poisson’s ratio: A review. Mater. Today Commun. 2023, 34, 105132. [Google Scholar] [CrossRef]
- Magalhaes, R.; Subramani, P.; Lisner, T.; Rana, S.; Ghiassi, B.; Fangueiro, R.; Oliveira, D.V.; Lourenco, P.B. Development, characterization and analysis of auxetic structures from braided composites and study the influence of material and structural parameters. Compos. Part A Appl. Sci. Manuf. 2016, 87, 86–87. [Google Scholar] [CrossRef]
- Paglioccaa, N.; Uddin, K.Z.; Anni, I.A.; Shen, C.; Youssef, G.; Koohbor, B. Flexible planar metamaterials with tunable Poisson’s ratios. Mater. Des. 2022, 215, 110446. [Google Scholar] [CrossRef]
- Yao, J.F.; Su, Y.F.; Scarpa, F.; Li, Y. An optimization approach to design deformation patterns in perforated mechanical metamaterials using distributions of Poisson’s ratio-based unit cells. Compos. Struct. 2022, 281, 115015. [Google Scholar] [CrossRef]
- Wang, M.Z.; Wu, H.Z.; Yang, L.; Chen, A.; Chen, P.; Wang, H.; Chen, Z.; Yan, C. Structure design of arc-shaped auxetic metamaterials with tunable Poisson’s ratio. Mech. Adv. Mater. Struct. 2022, 30, 1426–1436. [Google Scholar] [CrossRef]
- Desu, R.K.; Krishnamurthy, H.N.; Balu, A.; Gupta, A.K.; Singh, S.K. Mechanical properties of Austenitic Stainless Steel 304L and 316L at elevated temperatures. J. Mater. Res. Technol. 2016, 5, 13–20. [Google Scholar] [CrossRef]


















| Elastic Modulus (MPa) | Density (g/mm3) | Poisson’s Ratio | Strain Hardening Exponent (n) | Strength Coefficient (K) |
|---|---|---|---|---|
| 1.9 × 105 | 7.8 × 10−3 | 0.3 | 0.45 | 1400 |
| Geometric Parameters | l/mm | b/mm | θ1 | θ2 |
|---|---|---|---|---|
| Value | 6 | 5.8 | 60° | 30° |
| Sample Number | l/mm | b/mm | |θ1| | |θ2| |
|---|---|---|---|---|
| Model 1 | 6 | 5.8 | 60° | 20° |
| Model 2 | 6 | 5.8 | 60° | 30° |
| Model 3 | 6 | 5.8 | 60° | 40° |
| Model 4 | 6 | 5.8 | 50° | 30° |
| Model 5 | 6 | 5.8 | 70° | 30° |
| l/mm | b/mm | |θ1| | |θ2| |
|---|---|---|---|
| 12 | 1.5 | 60° | 30° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Li, Z.; Lin, C.; Ge, S.; Xue, X. Cell-Dependent Mechanical Properties of Asymmetric Crosslinked Metallic Wire Mesh with Hybrid Patterns Based on Arbitrary Poisson’s Ratio. Symmetry 2023, 15, 941. https://doi.org/10.3390/sym15040941
Wu F, Li Z, Lin C, Ge S, Xue X. Cell-Dependent Mechanical Properties of Asymmetric Crosslinked Metallic Wire Mesh with Hybrid Patterns Based on Arbitrary Poisson’s Ratio. Symmetry. 2023; 15(4):941. https://doi.org/10.3390/sym15040941
Chicago/Turabian StyleWu, Fang, Zeyu Li, Congcong Lin, Shaoxiang Ge, and Xin Xue. 2023. "Cell-Dependent Mechanical Properties of Asymmetric Crosslinked Metallic Wire Mesh with Hybrid Patterns Based on Arbitrary Poisson’s Ratio" Symmetry 15, no. 4: 941. https://doi.org/10.3390/sym15040941
APA StyleWu, F., Li, Z., Lin, C., Ge, S., & Xue, X. (2023). Cell-Dependent Mechanical Properties of Asymmetric Crosslinked Metallic Wire Mesh with Hybrid Patterns Based on Arbitrary Poisson’s Ratio. Symmetry, 15(4), 941. https://doi.org/10.3390/sym15040941








