Spot–Ladder Selection of Dislocation Patterns in Metal Fatigue
Abstract
1. Introduction
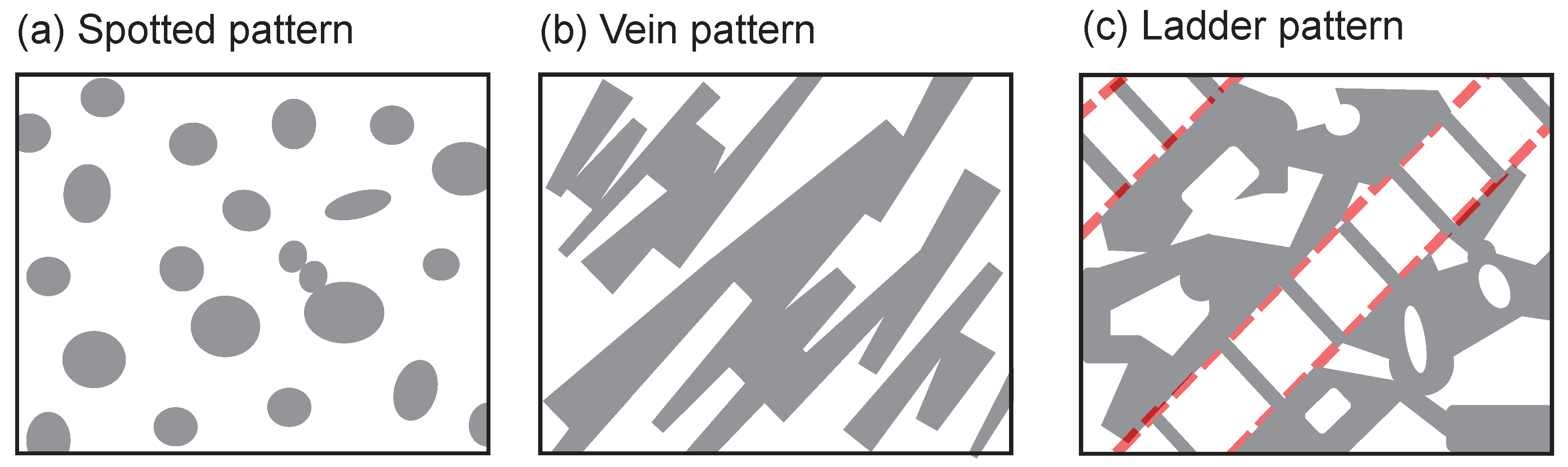
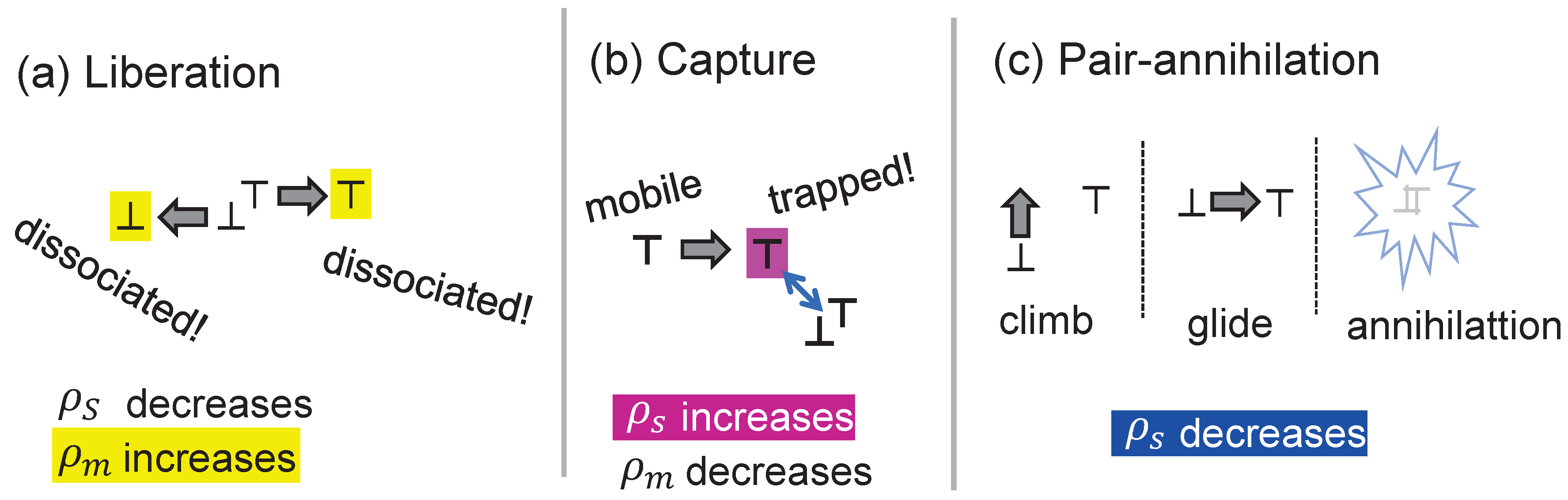
2. Dislocation Patterning and Its Microscopic View
3. Linear Stability Analysis
3.1. Reaction–Diffusion Dynamics
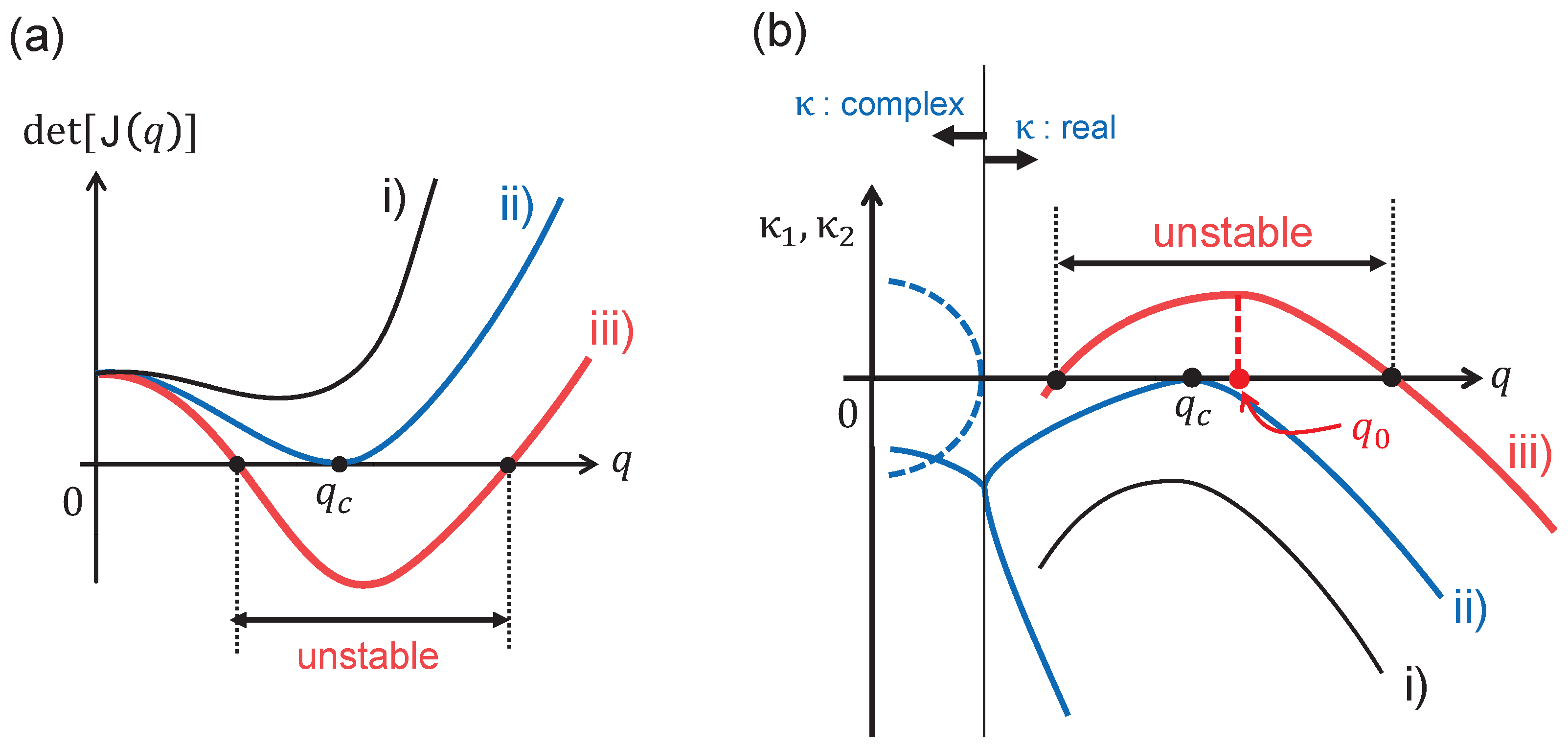
3.2. Occurrence Condition for Diffusion-Induced Instability
4. Weakly Nonlinear Analysis
4.1. Defining the Reaction Terms for Dislocation Systems
4.2. Defining the Nonlinear Vector–Matrix Equation
4.3. Nonlinearity Effect on the Growth in Amplitude
4.4. Time Evolution of the Amplitude
5. Spot–Ladder Selection Rule
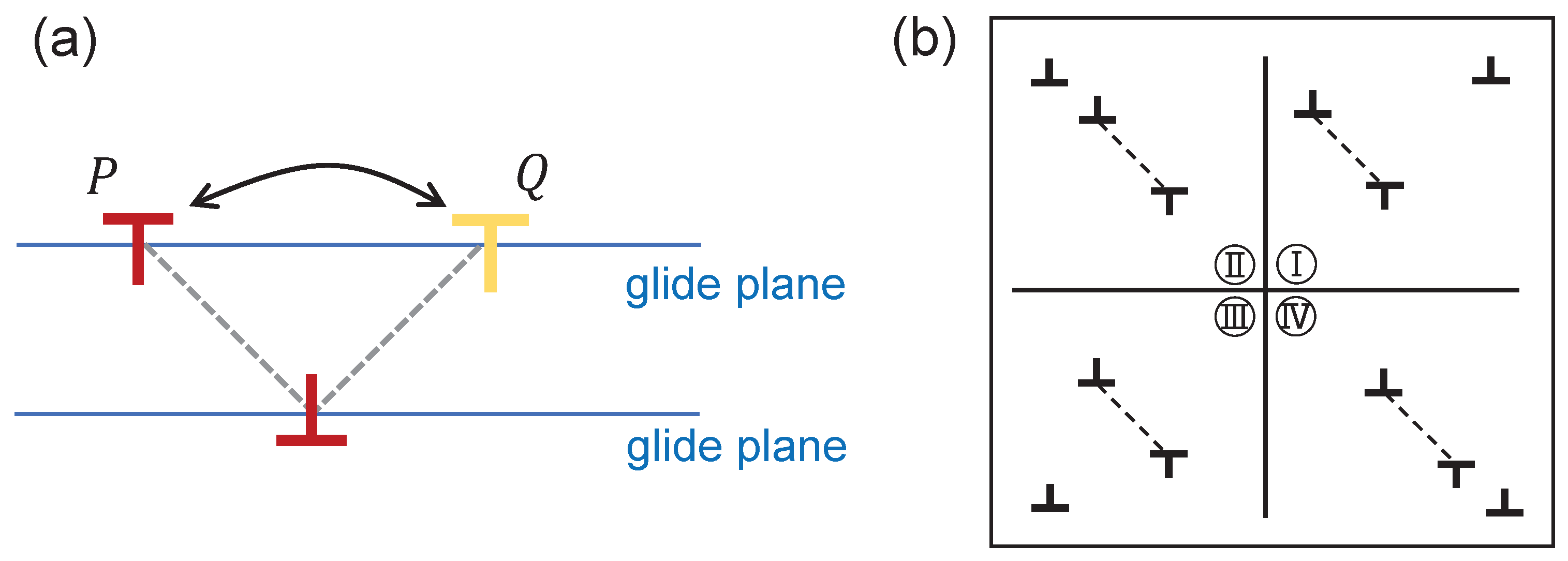
5.1. Condition for a “Ladder” Pattern to Appear
5.2. Condition for a “Spotted” Pattern to Appear
6. Selection Rule for “Spot vs. Ladder” Patterns
7. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Sj and Tj (j = 1, 2)
Appendix B. Trigonometric Formula
References
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Turing, A. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Greif, H.; Kubiak, A.; Stacewicz, P. Turing’s biological philosophy: Morphogenesis, mechanisms and organicism. Philosophies 2023, 8, 8. [Google Scholar] [CrossRef]
- Gierer, A.; Meinhardt, H. A theory of biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Landge, A.N.; Jordan, B.M.; Diego, X.; Muller, P. Pattern formation mechanisms of self-organizing reaction-diffusion systems. Dev. Biol. 2020, 460, 2–11. [Google Scholar] [CrossRef]
- Kondo, S.; Miura, T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science 2010, 329, 1616–1620. [Google Scholar] [CrossRef]
- Maini, P.K.; Painter, K.J.; Chau, H.N.P. Spatial pattern formation in chemical and biological systems. J. Chem.-Soc.-Faraday Trans. 1997, 93, 3601–3610. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Nakamasu, A.M. Correspondences Between Parameters in a Reaction-Diffusion Model and Connexin Functions During Zebrafish Stripe Formation. Front. Phys. 2022, 9, 805659. [Google Scholar] [CrossRef]
- Morita, W.; Morimoto, N.; Otsu, K.; Miura, T. Stripe and spot selection in cusp patterning of mammalian molar formation. Sci. Rep. 2022, 12, 9149. [Google Scholar] [CrossRef]
- Toxvaerd, S. The emergence of the bilateral symmetry in animals: A review and a new hypothesis. Symmetry 2021, 13, 261. [Google Scholar] [CrossRef]
- Castets, V.V.; Dulos, E.; Boissonade, J.; De Kepper, P. Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Phys. Rev. Lett. 1990, 64, 2953–2956. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Q.; Swinney, H.L. Transition from a uniform state to hexagonal and striped Turing patterns. Nature 1991, 352, 610–612. [Google Scholar] [CrossRef]
- Horváth, J.; Szalai, I.; De Kepper, P. An experimental design method leading to chemical Turing patterns. Science 2009, 324, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Saleem, M.T. Spatiotemporal dynamics of reaction-diffusion system and its application to Turing pattern formation in a Gray-Scott model. Mathematics 2023, 11, 1459. [Google Scholar] [CrossRef]
- Fang, A.; Adamo, C.; Jia, S.; Cava, R.J.; Wu, S.C.; Felser, C.; Kapitulnik, A. Bursting at the seams: Rippled monolayer bismuth on NbSe2. Sci. Adv. 2018, 4, eaaq0330. [Google Scholar] [CrossRef] [PubMed]
- Fuseya, Y.; Katsuno, H.; Behnia, K.; Kapitulnik, A. Nanoscale Turing patterns in a bismuth monolayer. Nat. Phys. 2021, 17, 1031. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Khatun, T.; Banerjee, T. Quantum Turing bifurcation: Transition from quantum amplitude death to quantum oscillation death. Phys. Rev. E 2021, 104, 024214. [Google Scholar] [CrossRef]
- Kato, Y.; Nakao, H. Turing instability in quantum activator-inhibitor systems. Sci. Rep. 2022, 12, 15573. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Metals; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Li, P.; Li, S.X.; Wang, Z.G.; Zhang, Z.F. Fundamental factors on formation mechanism of dislocation arrangements in cyclically deformed fcc single crystals. Prog. Mater. Sci. 2011, 56, 328–377. [Google Scholar] [CrossRef]
- Deng, X.; Xiao, Y.; Ma, Y.; Huang, B.; Hu, W. The microstructural evolution of nickel single crystal under cyclic deformation and hyper-gravity conditions: A molecular dynamics study. Metals 2022, 12, 1128. [Google Scholar] [CrossRef]
- Cleja-Ţigoiu, S. Differential Geometry Approach to Continuous Model of Micro-Structural Defects in Finite Elasto-Plasticity. Symmetry 2021, 13, 2340. [Google Scholar] [CrossRef]
- Lazar, M. Displacements and Stress Functions of Straight Dislocations and Line Forces in Anisotropic Elasticity: A New Derivation and Its Relation to the Integral Formalism. Symmetry 2021, 13, 1721. [Google Scholar] [CrossRef]
- Polák, J. Role of persistent slip bands and persistent slip markings in fatigue crack initiation in polycrystals. Crystals 2023, 13, 220. [Google Scholar] [CrossRef]
- Ananthakrishna, G. Current theoretical approaches to collective behavior of dislocations. Phys. Rep. 2007, 440, 113–259. [Google Scholar] [CrossRef]
- Sumigawa, T.; Uegaki, S.; Yukishita, T.; Arai, S.; Takahashi, Y.; Kitamura, T. FE-SEM in situ observation of damage evolution in tension-compression fatigue of micro-sized single-crystal copper. Mater. Sci. Eng. A 2019, 764, 138218. [Google Scholar] [CrossRef]
- Winter, A.T. A model for the fatigue of copper at low plastic strain amplitudes. Philos. Mag. 1974, 30, 719–738. [Google Scholar] [CrossRef]
- Mughrabi, H. The cyclic hardening and saturation behaviour of copper single crystals. Mater. Sci. Eng. 1978, 33, 207–223. [Google Scholar] [CrossRef]
- Differt, K.; Essmann, U. Dynamical model of the wall structure in persistent slip bands of fatigued metals I. Dynamical model of edge dislocation walls. Mater. Sci. Eng. A 1993, 164, 295–299. [Google Scholar] [CrossRef]
- Essmann, U.; Differt, K. Dynamic model of the wall structure in persistent slip bands of fatigued metals II. The wall spacing and the temperature dependence of the yield stress in saturation. Mater. Sci. Eng. A 1996, 208, 56–68. [Google Scholar] [CrossRef]
- Kroupa, F. Dislocation Dipoles and Dislocation Loops. J. Phys. 1966, 27, 154–167. [Google Scholar] [CrossRef]
- Neumann, P.D. The interactions between dislocations and dislocation dipoles. Acta Metall. 1971, 19, 1233–1241. [Google Scholar] [CrossRef]
- Siddique, A.B.; Lim, H.; Khraishi, T.A. The Effect of Multipoles on the Elasto-Plastic Properties of a Crystal: Theory and Three-Dimensional Dislocation Dynamics Modeling. J. Eng. Mater. Technol. 2022, 144, 011016. [Google Scholar] [CrossRef]
- Feltner, C.E. A debris mechanism of cyclic strain hardening for F.C.C. metals. Philos. Mag. 1965, 12, 1229–1248. [Google Scholar] [CrossRef]
- Erel, C.; Po, G.; Crosby, T.; Ghoniem, N. Generation and interaction mechanisms of prismatic dislocation loops in FCC metals. Comput. Mater. Sci. 2017, 140, 32–46. [Google Scholar] [CrossRef]
- Torrisi, M.; Tracinà, R. Symmetries and Solutions for Some Classes of Advective Reaction-Diffusion Systems. Symmetry 2022, 14, 2009. [Google Scholar] [CrossRef]
- Shao, S.; Du, B. Global Asymptotic Stability of Competitive Neural Networks with Reaction-Diffusion Terms and Mixed Delays. Symmetry 2022, 14, 2224. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Shah, R.; Iqbal, N.; Aly, S.; Nonlaopon, K. Fractional Series Solution Construction for Nonlinear Fractional Reaction-Diffusion Brusselator Model Utilizing Laplace Residual Power Series. Symmetry 2022, 14, 1944. [Google Scholar] [CrossRef]
- Trochidis, A.; Douka, E.; Polyzos, B. Formation and evolution of persistent slip bands in metals. J. Mech. Phys. Solids 2000, 48, 1761–1775. [Google Scholar] [CrossRef]
- Aoyagi, Y.; Kobayashi, R.; Kaji, Y.; Shizawa, K. Modeling and simulation on ultrafine-graining based on multiscale crystal plasticity considering dislocation patterning. Int. J. Plast. 2013, 47, 13–28. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. Dislocation Patterning in Fatigued Metals as a Result of Dynamical Instabilities. J. Appl. Phys. 1985, 58, 688–691. [Google Scholar] [CrossRef]
- Ermentrout, B. Stripes or spots? Nonlinear effects in bifurcation of reaction-diffusion equations on the square. Proc. R. Soc. Lond. Ser. A 1991, 434, 413–417. [Google Scholar] [CrossRef]
- Lyons, M.J.; Harrison, L.G. Stripe selection: An intrinsic property of some pattern-forming models with nonlinear dynamics. Dev. Dyn. 1992, 195, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Barrio, R.A.; Varea, C.; Aragon, J.L.; Maini, P.K. A two-dimensional numerical study of spatial pattern formation in interacting Turing systems. Bull. Math. Biol. 1999, 61, 483–505. [Google Scholar] [CrossRef]
- Shoji, H.; Iwasa, Y.; Kondo, S. Stripes, spots, or reversed spots in two-dimensional Turing systems. J. Theor. Biol. 2003, 224, 339–350. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On the Formation and Stability of Dislocation Patterns.1. One-Dimensional Considerations. Int. J. Eng. Sci. 1985, 23, 1351–1358. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On the Formation and Stability of Dislocation Patterns.2. Two-Dimensional Considerations. Int. J. Eng. Sci. 1985, 23, 1359–1364. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On the Formation and Stability of Dislocation Patterns.3. 3-Dimensional Considerations. Int. J. Eng. Sci. 1985, 23, 1365–1372. [Google Scholar] [CrossRef]
- Schiller, C.; Walgraef, D. Numerical-Simulation of Persistent Slip Band Formation. Acta Metall. 1988, 36, 563–574. [Google Scholar] [CrossRef]
- Pontes, J.; Walgraef, D.; Aifantis, E.C. On dislocation patterning: Multiple slip effects in the rate equation approach. Int. J. Plast. 2006, 22, 1486–1505. [Google Scholar] [CrossRef]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Umeno, Y.; Kawai, E.; Kubo, A.; Shima, H.; Sumigawa, T. Inductive determination of rate-reaction equation parameters for dislocation structure formation using artificial neural network. Materials 2023, 16, 2108. [Google Scholar] [CrossRef]
- Shima, H.; Umeno, Y.; Sumigawa, T. Analytic formulation of elastic field around edge dislocation adjacent to slanted free surface. R. Soc. Open Sci. 2022, 9, 220151. [Google Scholar] [CrossRef] [PubMed]
- Shima, H.; Sumigawa, T.; Umeno, Y. Nonsingular stress distribution of edge dislocations near zero-traction boundary. Materials 2022, 15, 4929. [Google Scholar] [CrossRef] [PubMed]

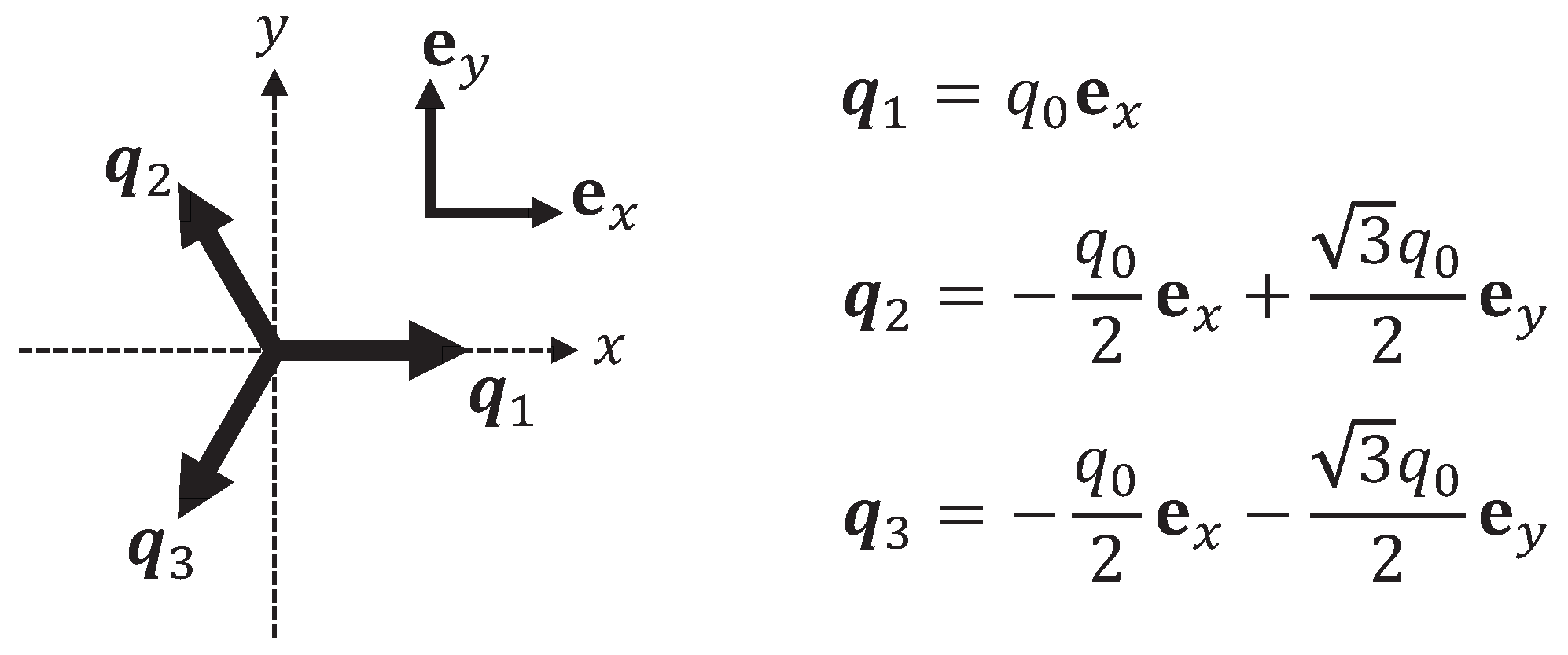

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shima, H.; Umeno, Y.; Sumigawa, T. Spot–Ladder Selection of Dislocation Patterns in Metal Fatigue. Symmetry 2023, 15, 1028. https://doi.org/10.3390/sym15051028
Shima H, Umeno Y, Sumigawa T. Spot–Ladder Selection of Dislocation Patterns in Metal Fatigue. Symmetry. 2023; 15(5):1028. https://doi.org/10.3390/sym15051028
Chicago/Turabian StyleShima, Hiroyuki, Yoshitaka Umeno, and Takashi Sumigawa. 2023. "Spot–Ladder Selection of Dislocation Patterns in Metal Fatigue" Symmetry 15, no. 5: 1028. https://doi.org/10.3390/sym15051028
APA StyleShima, H., Umeno, Y., & Sumigawa, T. (2023). Spot–Ladder Selection of Dislocation Patterns in Metal Fatigue. Symmetry, 15(5), 1028. https://doi.org/10.3390/sym15051028






