Application of Explicit Symplectic Integrators in the Magnetized Reissner–Nordström Spacetime

Abstract

In recent works by Wu and Wang a class of explicit symplectic integrators in curved spacetimes was presented. Different splitting forms or appropriate choices of time-transformed Hamiltonians are determined based on specific Hamiltonian problems. As its application, we constructed a suitable explicit symplectic integrator for surveying the dynamics of test particles in a magnetized Reissner–Nordström spacetime. In addition to computational efficiency, the scheme exhibits good stability and high precision for long-term integration. From the global phase-space structure of Poincaré sections, the extent of chaos can be strengthened when energy E, magnetic parameter B, or the charge q become larger. On the contrary, the occurrence of chaoticity is weakened with an increase of electric parameter Q and angular momentum L. The conclusion can also be supported by fast Lyapunov indicators.

1. Introduction

In recent years, Einstein’s theory of general relativity has been confirmed by a number of detections, such as the gravitational wave event [1], images from supermassive black holes (M87* [2,3], and SgrA* [4]). The highly nonlinear systems in curved spacetime enrich the content of chaotic dynamics [5,6,7,8]. However, not all relativistic gravitational systems are non-integrable and chaotic. Classical black holes, including Schwarzschild [9], Reissner–Nordström [10,11], and Kerr [12], are integrable. This integrability is due to the existence of four conserved quantities [13,14]. Chaos may occur when the black holes are embedded in an external magnetic field [15,16,17,18,19,20]. Moreover, there is chaos found in relativistic systems [21,22].

However, detecting chaotic behavior requires a reliable result. To conserve the physical and geometric properties, symplectic algorithms are regarded as the most appropriate solvers for long-time evolution. Unlike the manifold correction methods [23,24,25,26,27] that exactly preserve the energy, symplectic algorithms not only achieve good long-term stability, but also the structural features, including symplecticity, volume preservation, time symmetry, and conservation of first integrals. If a Hamiltonian can separate into two parts, with analytical solutions as explicit functions of time, explicit symplectic schemes can be established [28,29]. The general second-order leapfrog methods are also applied to multi-part splits [30,31], and higher-order integrators can be easily constructed according to the Yoshida method [32]. Furthermore, other composition methods of high-order explicit operators were designed for many problems [33,34] In general, not all Hamiltonian systems, such as the compact binary Hamiltonian system [35], can be decomposed onto explicitly integrable pieces. Instead, implicit symplectic methods [36,37], or implicit and explicit mixed symplectic methods [38,39,40], are always available. Of course, they are more expensive in computations than same-order explicit integrators.

To take advantage of the higher computational efficiency of explicit methods, Pihajoki [41] proposed a symplectic-like method for inseparable Hamiltonian systems. After variables are doubled in the phase space, explicit symplectic methods are applied to the two sub-Hamiltonians. Namely, similar operations of symplectic methods are repeated during the integrating processes. Many references [6,42,43] proved that extended phase-space methods can maintain long-term stability in energy errors. Unfortunately, mixing or projecting maps, such as midpoint permutations [44], inevitably destroy the symplectic properties. The canonical relationship is artificially missed because one sub-Hamiltonian is combined with old coordinates mixing new momenta and the other is combined with new coordinates mixing old momenta. The expanded phase-space method is not symplectic in the original phase space and extended phase space.

Recently, Wang et al. [45,46,47] designed a class of explicit symplectic schemes by dividing Hamiltonians of non-rotating black holes into multiple parts, where analytical solutions can be expressed as explicit functions of proper time. Zhou et al. [48] found that there are various choices for specific problems, and the best integrator construction and splitting method are not universal. Furthermore, to deal with the dragging effects caused by a rotating black hole, Wu et al. [14] provided a time-transformed method [49] to the Kerr spacetime and successfully obtained the explicit symplectic integrators. Undoubtedly, Wu et al. [50] brought a great extension to the application of explicit symplectic integrators in curved spacetimes. Such explicit symplectic integrators with fixed or adaptive time steps have been used widely in many curved spacetimes [8,14,16,17,18,19,20].

One of the main purposes of this paper was to construct a suitable explicit symplectic integrator for the Reissner–Nordström spacetime. The rest of this paper is organized as follows. A Hamiltonian system of test particles moving in the magnetized Reissner–Nordström spacetime is introduced in Section 2. With the time-transformed method, we propose two fourth-order explicit symplectic integrators for this Hamiltonian system. The symplectic integrator S4 achieves the best performance in long-term evolution. In Section 3, two useful techniques, the Poincaré section and the fast Lyapunov indicators [51,52], are employed to investigate how the chaotic dynamics depend on the responding parameters. Finally, the main results are presented in Section 4.

2. Construction of Explicit Symplectic Integrators in a Magnetized Reissner–Nordström Spacetime

In this section, we introduce a Hamiltonian to a magnetized Reissner–Nordström black hole. Then explicit symplectic integrators are constructed.

2.1. Magnetized Reissner–Nordström Black Hole

Ernst obtained an axisymmetric and static solution in the specific Ernst-potential framework [53]. In spherical-like coordinates $(t,r,\theta ,\varphi )$, the magnetized Reissner–Nordström black hole can be written as

$$\begin{array}{ccc}\hfill d{s}^2& =& g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }\hfill \\ & =& {|\Lambda |}^2\left[-(1-2M/r+Q^2/r^2)d{t}^2+{(1-2M/r+Q^2/r^2)}^{-1}d{r}^2+r^{2}d{\theta }^2\right]\hfill \\ & +& {|\Lambda |}^{-2}{r}^2{sin}^2\theta {(d\varphi -\omega dt)}^2\hfill \\ & =& -d{\tau }^2,\hfill \end{array}$$

(1)

where M and Q are the mass and charge of the black hole, respectively, and geometric units are given to the speed of light and the constant of gravity, i.e., $c=G=1$. Obviously, the metric has covariant nonzero components

$$\begin{array}{ccc}\hfill g_{tt}& =& -{|\Lambda |}^2(1-2M/r+Q^2/r^2)+{\omega }^2{r}^2{sin}^2\theta /{|\Lambda |}^2,\hfill \\ \hfill g_{t\varphi }& =& -\omega r^2{sin}^2\theta /{|\Lambda |}^2=g_{\varphi t},\hfill \\ \hfill g_{rr}& =& {|\Lambda |}^2/(1-2M/r+Q^2/r^2),\hfill \\ \hfill g_{\theta \theta }& =& {|\Lambda |}^2{r}^2,\hfill \\ \hfill g_{\varphi \varphi }& =& r^2{sin}^2\theta /{|\Lambda |}^2.\hfill \end{array}$$

Moreover, the functions in the metric assume the following expressions:

$$\begin{array}{ccc}& \Lambda & =1+\frac{1}{4}{B}^2(r^2{sin}^2\theta +Q^2{cos}^2\theta )-iBQcos\theta ,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& \omega & =-2BQ/r+B^{3}Qr+\frac{1}{2}{B}^3{Q}^3/r-\frac{1}{2}{B}^{3}Q/r(r^2-2Mr+Q^2){sin}^2\theta +const.\hfill \end{array}$$

(3)

Parameter B is the strength of the external magnetic field, where the vacuum solution of Einstein’s field equations is immersed in. When the parameter in Equation (3) takes the value of $B=0$, the metric refers to a classical Reissner–Nordström black hole if it is satisfied as $const=0$. After taking the following operations: $\tau \to \tau M$, $t\to tM$, $r\to rM$, $Q\to QM$, and $B\to B/M$, we obtain a dimensionless Lagrangian to describe the motion of a test particle around the magnetized Reissner–Nordström black hole

$$\begin{array}{ccc}\hfill \mathcal{L}& =& \frac{1}{2}{\left(\frac{ds}{d\tau }\right)}^2=\frac{1}{2}{g}_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }.\hfill \end{array}$$

(4)

For a time-like particle, the four-velocity $\dot{x_{\mu }}=(\dot{t},\dot{r},\dot{\theta },\dot{\varphi })$ satisfies the identical relation as follows

$$\begin{array}{c}\hfill g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=-1.\end{array}$$

(5)

We define a covariant generalized momentum as

$$\begin{array}{c}\hfill P_{\mu }=\partial \mathcal{L}/\partial {\dot{x}}^{\mu }=g_{\mu \nu }{\dot{x}}^{\nu }.\end{array}$$

(6)

According to the classical mechanics, we have the Hamiltonian of a neutral particle

$$\begin{array}{c}\hfill H=P_{\mu }{\dot{x}}^{\mu }-\mathcal{L}=\frac{1}{2}{g}^{\mu \nu }{P}_{\mu }{P}_{\nu },\end{array}$$

(7)

where the nonzero components of contravariant metric $g^{\mu \nu }$ are

$$\begin{array}{ccc}\hfill g^{tt}& =& \frac{g_{\varphi \varphi }}{g_{tt}{g}_{\varphi \varphi }-g_{t\varphi }^2},\hfill \\ \hfill g^{t\varphi }& =& -\frac{g_{t\varphi }}{g_{tt}{g}_{\varphi \varphi }-g_{t\varphi }^2}=g^{\varphi t},\hfill \\ \hfill g^{rr}& =& \frac{1}{g_{rr}},\hfill \\ \hfill g^{\theta \theta }& =& \frac{1}{g_{\theta \theta }},\hfill \\ \hfill g^{\varphi \varphi }& =& \frac{g_{tt}}{g_{tt}{g}_{\varphi \varphi }-g_{t\varphi }^2}.\hfill \end{array}$$

The Hamiltonian does not explicitly contain the coordinates t and $\varphi$; therefore, the axially symmetric system has two conserved quantities, i.e., energy E and angular momentum L:

$$\begin{array}{ccc}\hfill P_t& =& g_{tt}\dot{t}+g_{t\varphi }\dot{\varphi }=-E,\hfill \\ \hfill P_{\varphi }& =& g_{\varphi \varphi }\dot{\varphi }+g_{t\varphi }\dot{t}=L.\hfill \end{array}$$

(8)

In terms of the two constants, the Hamiltonian can be simplified as

$$\begin{array}{ccc}\hfill H& =& \frac{1}{2}{g}^{tt}{E}^2+\frac{1}{2}{g}^{\varphi \varphi }{L}^2-g^{t\varphi }EL+\frac{1}{2}{g}^{rr}{p}_r^2+\frac{1}{2}{g}^{\theta \theta }{p}_{\theta }^2.\hfill \end{array}$$

(9)

In addition, this Hamiltonian strictly equals the Lagrangian. That means that the Hamiltonian itself also remains at

$$\begin{array}{c}\hfill H=-\frac{1}{2}.\end{array}$$

(10)

The authors of [54] have provided an expression for the four-vector potential for a black hole immersed in an external uniform magnetic field. This magnetized Reissner–Nordström black hole has two nonzero covariant components:

$$\begin{array}{c}\hfill A_t=\frac{B}{2}{g}_{t\varphi }-\frac{Q}{2}{g}_{tt}-\frac{Q}{2},A_{\varphi }=\frac{B}{2}{g}_{\varphi \varphi }-\frac{Q}{2}{g}_{t\varphi }.\end{array}$$

(11)

If a test particle with a charge q moves around this magnetized black hole, it should have the momentum $p_{\mu }=P_{\mu }+q{A}_{\mu }$. Therefore, the Hamiltonian for the charged particle motion is determined by

$$\begin{array}{c}\hfill \mathbb{H}=\frac{1}{2}{g}^{\mu \nu }(p_{\mu }-q{A}_{\mu })(p_{\nu }-q{A}_{\nu }).\end{array}$$

(12)

Two conserved quantities, energy E and angular momentum L, are also contained in the axially symmetric system:

$$\begin{array}{ccc}\hfill p_t& =& P_t+q{A}_t=-E,\hfill \\ \hfill p_{\varphi }& =& P_{\varphi }+q{A}_{\varphi }=L.\hfill \end{array}$$

(13)

In terms of the two constants, the Hamiltonian can be simplified as

$$\begin{array}{ccc}\hfill \mathbb{H}& =& \frac{1}{2}{g}^{tt}{(E+q{A}_t)}^2+\frac{1}{2}{g}^{\varphi \varphi }{(L-q{A}_{\varphi })}^2-g^{t\varphi }(E+q{A}_t)(L-q{A}_{\varphi })+\frac{1}{2}{g}^{rr}{p}_r^2+\frac{1}{2}{g}^{\theta \theta }{p}_{\theta }^2.\hfill \end{array}$$

(14)

To make the system (14) dimensionless, we take the scale transformations of $\mathbb{H}\to m^2\mathbb{H}$, $E\to mE$, $p_r\to m{p}_r$, $p_{\theta }\to mM{p}_{\theta }$, $L\to mML$, and $q\to mq$, where m is the mass of the test particle. Due to the four-velocity or rest mass condition, the Hamiltonian also remains at

$$\begin{array}{c}\hfill \mathbb{H}=-\frac{1}{2}.\end{array}$$

(15)

2.2. Construction of Explicit Symplectic Integrators

In the section above, we introduced a Hamiltonian to a magnetized Reissner–Nordström black hole. This Hamiltonian system has four phase-space variables $(r,\theta ;p_r,p_{\theta })$. Since four Hamilton canonical equations can be acquired correspondingly, the Hamiltonian system is solvable. However, it is difficult to give an analytic solution to such a nonlinear system. Numerical methods are still necessary and useful to study the dynamics of the particles in a relativistic spacetime. For a long-term evolution in curved geometry, symplectic integrators are always prior choices. In addition to the conservation properties, explicit symplectic methods also have better computational efficiency than same-order implicit ones. Wang et al. [45,46,47] successfully constructed explicit symplectic integrators by splitting the Hamiltonians into several parts. However, they are not suited for this Hamiltonian system. Fortunately, following the previous works of Wu et al. [14,50], we use a time transformation

$$\begin{array}{c}\hfill d\tau =g(r,\theta )dw,\end{array}$$

(16)

$$\begin{array}{c}\hfill g(r,\theta )={|\Lambda |}^2.\end{array}$$

(17)

where the proper time $\tau$ and new coordinate time w are different from the original coordinate time t. As a new coordinate $q_0=\tau$, it has a corresponding momentum $p_0=-\mathbb{H}=1/2$. Therefore, the four phase-space variables $(r,\theta ;p_r,p_{\theta })$ of the Hamiltonian (14) are extended to $(r,\theta ,q_0;p_r,p_{\theta },p_0)$. Then, we obtain an extended phase-space Hamiltonian:

$$\begin{array}{ccc}\hfill \mathcal{H}& =& g(r,\theta )(\mathbb{H}+p_0)\hfill \\ & =& {|\Lambda |}^2[\frac{1}{2}{g}^{tt}{(E+q{A}_t)}^2+\frac{1}{2}{g}^{\varphi \varphi }{(L-q{A}_{\varphi })}^2-g^{t\varphi }(E+q{A}_t)(L-q{A}_{\varphi })+p_0]\hfill \\ & +& \frac{1}{2}{p}_r^2-\frac{1}{r}{p}_r^2+\frac{Q^2}{2r^2}{p}_r^2+\frac{1}{2r^2}{p}_{\theta }^2.\hfill \end{array}$$

(18)

Now, we can split the time-transformed Hamiltonian into multiple parts in the following way:

$$\begin{array}{c}\hfill \mathcal{H}={\mathcal{H}}_1+{\mathcal{H}}_2+{\mathcal{H}}_3+{\mathcal{H}}_4+{\mathcal{H}}_5,\end{array}$$

(19)

where sub-Hamiltonians are

$$\begin{array}{ccc}\hfill {\mathcal{H}}_1& =& {|\Lambda |}^2[\frac{1}{2}{g}^{tt}{(E+q{A}_t)}^2+\frac{1}{2}{g}^{\varphi \varphi }{(L-q{A}_{\varphi })}^2-g^{t\varphi }(E+q{A}_t)(L-q{A}_{\varphi })+p_0],\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_2& =& \frac{1}{2}{p}_r^2,\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_3& =& -\frac{1}{r}{p}_r^2,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_4& =& \frac{Q^2}{2r^2}{p}_r^2,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_5& =& \frac{1}{2r^2}{p}_{\theta }^2.\hfill \end{array}$$

(24)

For the sub-Hamiltonian ${\mathcal{H}}_1$, the equations of motion can be written with the new coordinate time as

$$\begin{array}{ccc}\hfill \frac{d\tau }{dw}& =& g(r,\theta ),\hfill \\ \hfill \frac{dr}{dw}& =& \frac{d{\mathcal{H}}_1}{d{p}_r}=0,\hfill \\ \hfill \frac{d\theta }{dw}& =& \frac{d{\mathcal{H}}_1}{d{p}_{\theta }}=0,\hfill \\ \hfill \frac{d{p}_0}{dw}& =& 0,\hfill \\ \hfill \frac{d{p}_r}{dw}& =& -\frac{d{\mathcal{H}}_1}{dr}=\Re (r,\theta ),\hfill \\ \hfill \frac{d{p}_{\theta }}{dw}& =& -\frac{d{\mathcal{H}}_1}{d\theta }=\Theta (r,\theta ).\hfill \end{array}$$

(25)

Similarly, we can obtain the equations of motion for the other sub-Hamiltonians

$$\begin{array}{ccc}\hfill {\mathcal{H}}_2:\frac{dr}{dw}& =& p_r;\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_3:\frac{dr}{dw}& =& -\frac{2p_r}{r},\frac{d{p}_r}{dw}=-\frac{p_r^2}{r^2};\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_4:\frac{dr}{dw}& =& \frac{Q^2}{r^2}{p}_r,\frac{d{p}_r}{dw}=\frac{Q^2}{r^3}{p}_r^2;\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\mathcal{H}}_5:\frac{d\theta }{dw}& =& \frac{1}{r^2}{p}_{\theta },\frac{d{p}_{\theta }}{dw}=\frac{p_{\theta }^2}{r^3}.\hfill \end{array}$$

(29)

where h is a time step. When the coordinate time goes from $w_0$ to $w=w_0+h$, the values of phase-space variables $(r_0,{\theta }_0,{\tau }_0,p_{r0},p_{\theta 0})$ turn out to be $(r,\theta ,\tau ,p_r,p_{\theta })$. The operators for these canonical equations correspond to explicit solutions

$$\begin{array}{ccc}\hfill e^{h{\mathcal{H}}_1}:& & \tau ={\tau }_0+g(r,\theta )h,\hfill \\ & & p_r=p_{r0}+h\Re (r_0,{\theta }_0),\hfill \\ & & p_{\theta }=p_{\theta 0}+h\Theta (r_0,{\theta }_0);\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill e^{h{\mathcal{H}}_2}:& & r=r_0+h{p}_{r0};\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill e^{h{\mathcal{H}}_3}:& & r={[{(r_0^2-3h{p}_{r0})}^2/r_0]}^{1/3},\hfill \\ & & p_r=p_{r0}{(1-3h{p}_{r0}/r_0^2)}^{1/3};\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill e^{h{\mathcal{H}}_4}:& & r={(r_0^2+\frac{2h{Q}^2{p}_{r0}}{r_0})}^{1/2},\hfill \\ & & p_r=p_{r0}{(1+\frac{2h{Q}^2{p}_{r0}}{r_0^3})}^{1/2};\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill e^{h{\mathcal{H}}_5}:& & \theta ={\theta }_0+h{p}_{\theta 0}/r_0^2,\hfill \\ & & p_r=p_{r0}+h{p}_{\theta 0}^2/r_0^3.\hfill \end{array}$$

(34)

All of the analytical solutions are indeed explicit functions of the coordinate time step h. With the aid of a combination of these solutions, we obtain two first-order approximations to the Hamiltonian

$$\begin{array}{ccc}\hfill {\chi }_h& =& e^{h{\mathcal{H}}_5}\times e^{h{\mathcal{H}}_4}\times e^{h{\mathcal{H}}_3}\times e^{h{\mathcal{H}}_2}\times e^{h{\mathcal{H}}_1},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\chi }_h^{*}& =& e^{h{\mathcal{H}}_1}\times e^{h{\mathcal{H}}_2}\times e^{h{\mathcal{H}}_3}\times e^{h{\mathcal{H}}_4}\times e^{h{\mathcal{H}}_5}.\hfill \end{array}$$

(36)

Usually, a general second-order symplectic integrator can be constructed as

$$\begin{array}{c}\hfill S2(h)={\chi }_{h/2}\times {\chi }_{h/2}^{*}.\end{array}$$

(37)

According to Yoshida [32], we can easily obtain a fourth-order symplectic integrator

$$\begin{array}{c}\hfill S4(h)=S2(z_{1}h)\times S2(z_{2}h)\times S2(z_{1}h),\end{array}$$

(38)

where $z_1=\frac{1}{1-2^{1/3}}$ and $z_2=1-2z_1$. Unlike the extended phase-space method EP4 [45,46], this integrator is symplectic. Using both maps, ${\chi }_h$ and ${\chi }_h^{*}$, we can also yield a fourth-order optimal explicit symplectic $PRK$ method:

$$\begin{array}{ccc}\hfill PR{K}_{6}4=& & {\chi }_{{\beta }_{12}h}\times {\chi }_{{\beta }_{11}h}^{*}\times {\chi }_{{\beta }_{10}h}\times {\chi }_{{\beta }_{9}h}^{*}\times {\chi }_{{\beta }_{8}h}\times {\chi }_{{\beta }_{7}h}^{*}\hfill \\ & & \times {\chi }_{{\beta }_{6}h}\times {\chi }_{{\beta }_{5}h}^{*}\times {\chi }_{{\beta }_{4}h}\times {\chi }_{{\beta }_{3}h}^{*}\times {\chi }_{{\beta }_{2}h}\times {\chi }_{{\beta }_{1}h}^{*},\hfill \end{array}$$

(39)

where the coefficients are ${\beta }_1={\beta }_{12}=0.079203696431196$, ${\beta }_2={\beta }_{11}=0.130311410182166$, ${\beta }_3={\beta }_{10}=0.222861495867608$, ${\beta }_4={\beta }_9=-0.366713268047426$, ${\beta }_5={\beta }_8=0.324648188689706$, ${\beta }_6={\beta }_7=0.109688477876750$ [33,48]. They are also exactly symmetric.

2.3. Investigation Methods

Clearly, the Hamiltonian is a conservative system with two degrees of freedom, i.e., r and $\theta$. To describe the phase-space structure vividly, Poincaré sections can be employed. When an orbit crosses a two-dimensional surface in the phase space, a point on the surface is obtained each time. These points form a Poincaré section. A smooth curve on the surface, which is known as the Kolmogorov–Arnold–Moser (KAM) torus, indicates a regular quasi-periodic orbit. If an area is densely and randomly filled with discrete points, it can be regarded as the characteristic of chaos.

Unlike the Poincaré section, the fast Lyapunov indicator (FLI) is widely used and suitable for any dimension. With the distance evolution of two nearby orbits [8,51,52], the FLI is defined as follows:

$$\begin{array}{c}\hfill FLI=lo{g}_{10}\frac{d(\tau )}{d(0)}.\end{array}$$

(40)

where $d(0)$ is the proper distance of the phase space $(r,\theta ;p_r,p_{\theta })$ between two nearby orbits at the beginning of the proper time, and $d(\tau )$ is the distance at the proper time $\tau$. The FLI increases in an exponential law with time, indicating that the bounded orbit is chaotic. A power law growth of FLI is consistent with a regular orbit. In general, all FLIs that are no less than 4.5 correspond to the appearance of chaotic motion. Moreover. chaos becomes stronger as the value of the FLI increases. It is an effective method to distinguish chaos from order.

2.4. Performance Evaluation of the Explicit Symplectic Integrators

Taking the parameters $E=0.9900,Q=1\times {10}^{-4},B=1\times {10}^{-3},L=4.0$, and time step $h=1$, we choose a test orbit with initial conditions $r=20,\theta =\pi /2,p_r=0$, and the starting value of $p_{\theta }(>0)$ determined by Equations (9) and (10). Hamiltonian errors $\mathsf{\Delta }H=H-(-1/2)$ are obtained after the integration time ${10}^8$. As described in Figure 1a, Hamiltonian errors of the fourth order Runge–Kutta method accumulate fast with time. It is generally believed that the Runge–Kutta method is not suitable for long-time evolution. An explicit symplectic method $PR{K}_{6}4$ has good stability and can reach an order of ${10}^{-8}$, as plotted in Figure 1b. However, it is still several orders of magnitude larger than the other explicit symplectic integrator S4, whose Hamiltonian errors can remain bounded in an order of ${10}^{-11}$, as listed in

Table 1. Performances for all algorithms in Figure 1. The maximum Hamiltonian errors and computational costs of the algorithms are considered for the same time step $h=1$. The test orbit is orderly, and the integration time of each algorithm reaches $\tau ={10}^8$.

Algorithm	S4	$\mathit{RK}4$	${\mathit{PRK}}_{6}4$	EP4
Hamiltonian errors	$0.5\times {10}^{-11}$	$1.4\times {10}^{-8}$	$4\times {10}^{-8}$	$0.7\times {10}^{-11}$
CPU times (seconds)	4278	4002	5118	5127

. It can be attributed to different constructions of the methods. The number of calculation steps should be as small as possible to reduce round-off errors. As far as the CPU times in Table 1 are concerned, S4 yields the best computational efficiency and is slightly better than the extended phase-space method EP4. Figure 1c describes the evolution of r with time for massive particles. The blue line corresponds to the evolution of r with proper time $\tau$, obtained from method EP4 by solving the original Hamiltonian system. The red dot corresponds to the evolution of r with the new coordinate time w, provided by the algorithm S4 integrating the time-transformed Hamiltonian. It shows that they fit in well with each other. However, the symplectic-like method (EP4) has no advantage in terms of counting steps. Moreover, mixing or projecting maps may also destroy the flow of a relativistic system. To construct a symplectic method, it is not unique for a Hamiltonian system to choose a time-transformation function. This has been demonstrated in many research studies [14,16,17,20]. From Figure 1d, we can realize the relationship between the new coordinate time w and proper time $\tau$ for $S4$ is $g(r,\theta )\doteq 1$ over the whole integration time. This guarantees the conservation of physical and geometric properties, as well as Hamiltonians. Poincaré sections of a chaotic orbit, with the same initial parameters $E=0.9920,L=3.7,Q=1\times {10}^{-4},B=9\times {10}^{-4},q=0$, and $r=10$, are plotted in Figure 1e. The points obtained by the non-symplectic algorithm RK4 are less than those of the S4 method, although at first, they coincide with each other. From the different FLI growths in Figure 1f, we can see that the symplectic method S4 remains bounded until the integration time ${10}^6$. However, the computing process of RK4 has to be interrupted because the data gradually become divergent. Based on the computational accuracy and symplectic conservation, the symplectic method S4 is an appropriate design for the long-time evolution in the curved spacetime.

3. Investigations of the Orbital Dynamics

Considering the excellent performance, we select S4 as a numerical tool in our later discussions and provide some insight into the orbital dynamics of orbits in system (9) for neutral particles and system (14) for charged particles. In what follows, two useful techniques, the Poincaré section and the fast Lyapunov indicator (FLI), are provided to investigate how chaotic behaviors depend on different parameters.

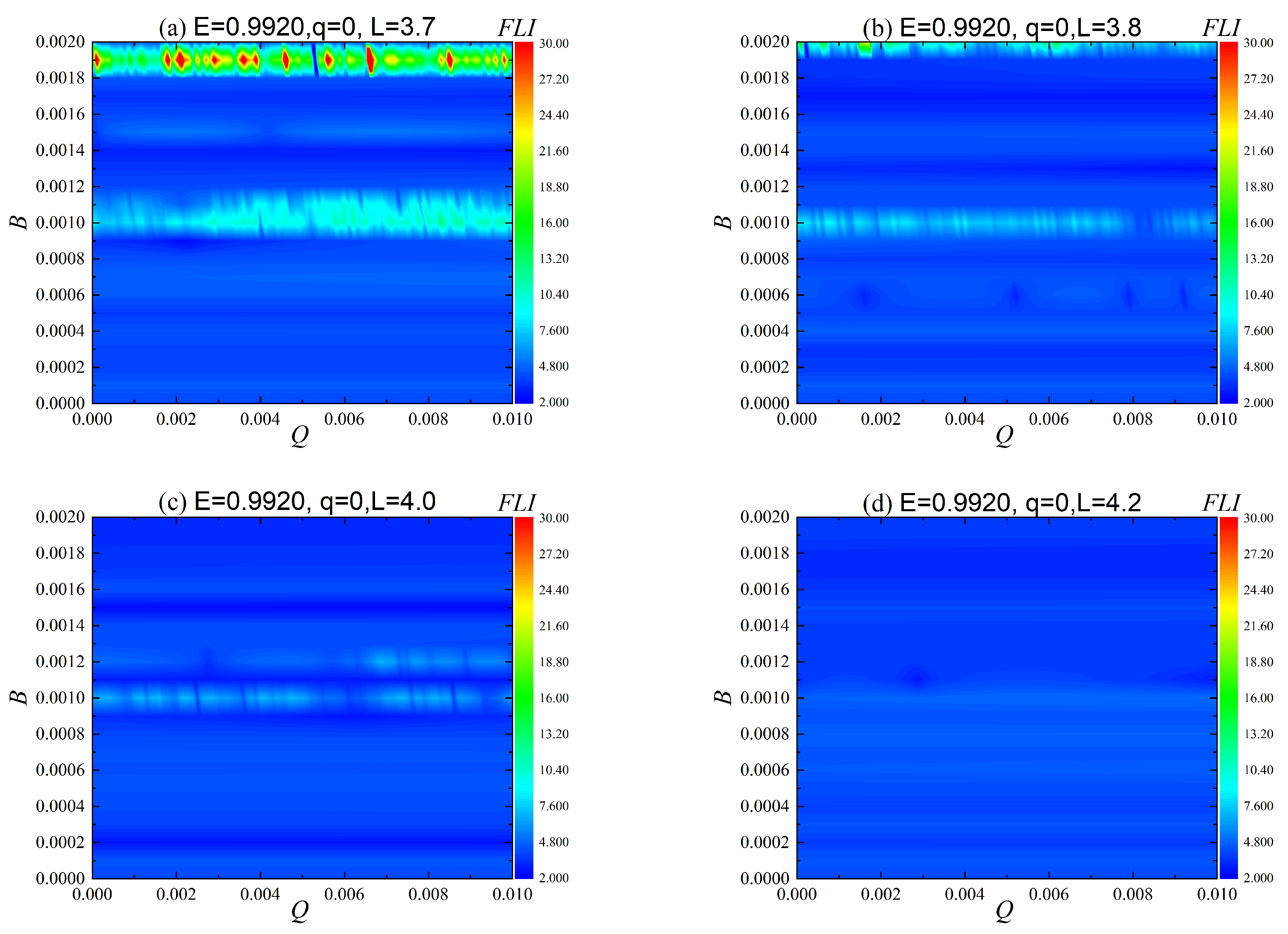
3.1. Order or Chaotic Motion of Orbits

Firstly, let us focus on how the orbital dynamics of the neutral particle depend on the parameters. In Figure 2, Poincaré sections are plotted to explore the order or chaotic motion influenced by different values of the external magnetic parameter B. The same parameters are $E=0.9920,L=4.0,Q=1\times {10}^{-4}$ and $q=0$. Initial orbits are $r=5,10,30,50,60,70$, respectively. When the positive values of the external magnetic field are given as $B=5\times {10}^{-4}$, all Kolmogorov–Arnold–Moser (KAM) tori in Figure 2a prove the regularity of the orbits. If the magnetic parameter becomes a little large, e.g., $B=9\times {10}^{-4}$, many discrete points become densely and randomly distributed. This indicates that two orbits turn out to be chaotic in panel (b). With a further increase in the magnetic parameter, many more orbits become chaotic, as shown in panels (c) and (d). Certainly, the extent of chaos can also be strengthened. Although an increase in the magnetic parameter brings more orbits with stronger chaoticity, it does not mean that a given orbit always remains chaotic.

Regarding the effect of the electric parameter on the orbital dynamics, we will fix the parameters $E=0.9945,L=4.0,B=4.5\times {10}^{-4},q=0$. Initial orbits are $r=5,10,30,60,90$. Figure 3a–d indicate that the cases respond to the electric parameters Q = 1 $\times {10}^{-4}$, 5 $\times {10}^{-4}$, 1 $\times {10}^{-2}$, and $1\times {10}^{-1}$. It has been found that three chaotic orbits always survive. A closer look reveals that chaotic motions are slightly weakened as the charge Q of the black hole increases.

Many references [6,15,16,17,18,19,20] have shown that chaos can become more popular in some circumstances when there is a minor increase in energy E. Figure 4a–d describe that chaos is strengthened when the energy gradually increases from $E=0.9935$ to $0.9950$. The fixed parameters are $Q=1\times {10}^{-4},B=5\times {10}^{-4},q=0$, and $L=4.0$. The initial orbits are the same as those in Figure 3. Obviously, chaotic motion is enhanced as energy increases. This conclusion can also be supported by Figure 5. Here, the FLI for a given orbit $r=5$ is obtained after the integration time $w=1\times {10}^6$. By scanning two-parameter spaces, e.g., (B, Q), under different energy circumstances, we can clearly understand how small changes in multiple parameters act on the dynamics of test particles. Chaos is strengthened as the magnetic field parameter B increases. A similar result is also suitable when the particle energy E increases. However, it seems that electric parameters bring little perturbations to the distributions of FLIs.

In Figure 6a–d, the dependence of chaos on the particle angular momentum is discussed. The fixed parameters are $E=0.9920,Q=1\times {10}^{-4},B=5\times {10}^{-4},q=0$, and the initial orbits are $r=10,30,50,60,70$. With an increase in the angular momentum from $L=3.7,3.8,4.0$ to $4.2$, chaotic motion is somewhat weakened. Taking a given orbit $r=10$, for instance, we can obtain similar results in Figure 7. This is consistent with some conclusions shown in Figure 5.

Finally, let us investigate the chaotic motion of the charged particle influenced by the charge q. The same parameters are given as $E=0.9920,Q=1\times {10}^{-4},$ $B=9\times {10}^{-4},L=3.8$, and the charge of the test particle increases from $q=0$ (neutral particle) to $1\times {10}^{-3},2\times {10}^{-3}$, and $5\times {10}^{-3}$. The orbits are $r=10,30,50,55,70$, respectively. The Poincaré sections in Figure 8a–d show that chaos is slightly strengthened as the charge Q increases. By scanning some different initial orbits, order and chaotic motions can also be distinguished with the distribution of FLIs, as plotted in Figure 9a–d. They fit well with Figure 8.

3.2. Dependence of the Orbital Dynamics

Such a general relative system is highly nonlinear. It is suitable to study the chaotic dynamics. How to explore the chaotic motion depends on the parameters mentioned above. The effective potential can provide important insight into dynamical information, such as stable circular orbits on the equatorial plane $\theta =\pi /2$ [17,18,19,55]. Different types of motion near a weakly magnetized Schwarzschild black hole are illustrated in [56]. The authors of [57] studied quasi-harmonic oscillatory motion. They found that the Larmor frequency is related exclusively to the magnetic field. Reference [58] suggests that the chaotic character increases with the inclination angle of the magnetic field lines to the Keplerian disk. The charged particle dynamics in a combined gravo-magnetic field were discussed in [59]. Due to the chaotic scattering, accelerated motion can be allowed.

Let $p_r=p_{\theta }=0$; we can easily obtain the effective potential, i.e., the expression of energy from Equations (14) and (15):

$$\begin{array}{c}\hfill V=E=\frac{g^{t\varphi }(L-q{A}_{\varphi })-\sqrt{{[g^{t\varphi }(L-q{A}_{\varphi })]}^2-g^{tt}[g^{\varphi \varphi }{(L-q{A}_{\varphi })}^2+1]}}{g^{tt}}-q{A}_t.\end{array}$$

(41)

Then we can study the effect of a small change in different parameters on the effective potential. Figure 10a shows that the shape of the effective potential shifts toward the observer with an increase in the magnetic parameter. Namely, the radius of the circular orbit, corresponding with the local extremum value of the effective potential, becomes large when the magnetic parameter B increases. The magnetic parameter appearing in the metric can bring a tiny change to the space-time structure. As a result, it should stand for an outward gravitational-like force acting on the neutral particle; thus, the effective potential for a larger value of B is always over that of a smaller one. Therefore, the magnetic parameter can considerably affect the motion of the test particle and induce the occurrence of chaos. Similar cases are presented when the electric parameter Q or angular momentum L increase, as shown in Figure 10b,c. The electric parameter Q should be described as a gravitationally repulsive force, which can directly act on the neutral particles (so does the centrifugal force responding to angular momentum L). Undeniably, the effect of angular momentum L is more explicit than that of electric parameter Q. How will the effective potential vary if the test particle is charged? The effective potential plotted in Figure 10d becomes lower as the particle charge q increases. This case is more complicated than that of a neutral particle. Now the charged particle suffers from two external forces. Different from the repulsive Coulomb force, the Lorenz force is attractive toward the black hole. Precisely speaking, a slight change in those parameters can bring about a small additional perturbation to the gravitational attraction of the central object, and induce a substantial effect on the chaotic behavior.

4. Summary

Calculations are useful as they can help us to trace the orbital dynamical evolution of the nonlinear general relativistic system. Symplectic integrators are more suitable for long-term integrations. Generally, explicit symplectic integrators should be developed as much as possible. The construction of such integrators requires the time-transformed Hamiltonian to be separated into five explicitly integrable pieces. Numerical tests show that the explicit symplectic integrator $S4$, yielded with a fourth-order construction of Yoshida, has the best computational accuracy and efficiency.

Therefore, the explicit symplectic integrator $S4$ is applied to investigate the dynamics of test particles moving around the magnetized Reissner–Nordström black hole. The Poincaré section and FLIs are used to show how chaos depends on the parameters. Chaotic motion occurs easily when the charged particle is given higher energy E. The extent of chaos can also be strengthened when the magnetic parameter B or the charge q increases. On the contrary, the chaoticity of orbit weakens with the increase of electric parameter Q and angular momentum L. With the aid of effective potentials, we can understand how the parameters affect the orbital dynamics. That is, a slight change in these parameters can correspond to an influence of the force acting on the test particles. The chaotic behavior can be changed by a small additional perturbation to the gravitational attraction of the central object.