On the Jacobi Stability of Two SIR Epidemic Patterns with Demography

Abstract

In the present work, two SIR patterns with demography will be considered: the classical pattern and a modified pattern with a linear coefficient of the infection transmission. By reformulating of each first-order differential systems as a system with two second-order differential equations, we will examine the nonlinear dynamics of the system from the Jacobi stability perspective through the Kosambi–Cartan–Chern (KCC) geometric theory. The intrinsic geometric properties of the systems will be studied by determining the associated geometric objects, i.e., the zero-connection curvature tensor, the nonlinear connection, the Berwald connection, and the five KCC invariants: the external force ${\epsilon }^i$—the first invariant; the deviation curvature tensor $P_j^i$—the second invariant; the torsion tensor $P_{jk}^i$—the third invariant; the Riemann–Christoffel curvature tensor $P_{jkl}^i$—the fourth invariant; the Douglas tensor $D_{jkl}^i$—the fifth invariant. In order to obtain necessary and sufficient conditions for the Jacobi stability near each equilibrium point, the deviation curvature tensor will be determined at each equilibrium point. Furthermore, we will compare the Jacobi stability with the classical linear stability, inclusive by diagrams related to the values of parameters of the system.

1. Introduction

Mathematical patterns that do not involve births and deaths in population evolution are usually called epidemic patterns without demography. These models are suitable for epidemics with a short time evolution, such as influenza. Omitting population change implies that the disease develops in a shorter time than the period when important changes in population size may occur (such as births and deaths). This is true for quick illnesses such as childhood illnesses and the flu. However, there are slow diseases, such as HIV, tuberculosis and hepatitis C. These diseases evolve over a long period of time, even at the individual level. For these illnesses, the total population changes considerably over time, and the population’s demographic cannot be neglected [1,2,3].

The main goal of the present paper is to study the Jacobi stability for two SIR models with demography: the classical SIR model and a modified SIR model with a variable transmission coefficient of the infection. These two types of SIR (susceptible, infected, and removed individuals) epidemic models represent two classical patterns for the spread of an epidemic. The second model is a natural generalization of the first model by changing the constant coefficient of the transmission of the infection $\beta$ with a variable coefficient of transmission of the infection. More precisely, for the second model, this coefficient is a linear function of the number of infected individuals I, which means $\beta$ is replaced by $\beta (1+\nu I)$, where $\nu$ is a real positive parameter. Consequently, the transmission coefficient of infection and the contact rate will increase with the number of infectious individuals, and new infections occur much faster in comparison with the classical pattern. The local and global dynamics of this modified pattern are much more complicated compared to the simple model. For example, for the second model, it is possible to have two endemic equilibrium points and a Hopf bifurcation can occur near one of the equilibrium points. In this case, although the two endemic equilibrium points check a property of symmetry related to their coordinates (they are symmetrical with respect to a straight line), from the point of view of the local dynamics of the dynamical system, we have no symmetry property.

The classical stability (linear stability or Lyapunov stability) of different kinds of SIR epidemic models without or with demography was widely studied in recent decades [1,2,3,4,5,6]. In this paper, we will approach a new type of stability for these models, namely Jacobi stability. Classical approaches of these models can be found in [1,2,3,4]. Generally, the study of mathematical deterministic models for the spread of diseases, or for the interaction between prey–predator-type populations, is performed only for positive values of the variables, where they have an ecological, biological, or epidemiological meaning [4,5,6,7,8,9].

The Jacobi stability is a natural generalization of the geometric approaches related to the stability of the geodesic flow, from a Riemannian manifold of a Finslerian manifold to a manifold with no metric [10,11,12,13,14,15]. More exactly, the Jacobi stability is an indicator of the vigour of a dynamical system given by a system of second-order differential equations (SODE or semi-spray), where this vigour represents the adaptation and the conservation of the basis behaviour to both the changes of the internal parameters of the system and the influences from the external environment. The local behavior of dynamical systems from the perspective of Jacobi stability, by using the Kosambi–Cartan–Chern (KCC) theory, has recently been addressed in [11,12,16,17,18,19,20,21,22,23,24,25,26]. So, the local behaviour of the dynamical system is studied through the use of the geometrical objects associated with the system of the second-order differential equations (SODE), which is the system obtained from the system of first-order differential equations [27,28,29].

The main aim of KCC theory is the investigation of the deviation of neighboring integral curves, which allows us to estimate the perturbation allowed near the equilibrium points of the system of second-order differential equations. In the beginning, this study was related to the study of the variation equations (or Jacobi field equations) corresponding to the geometry of the smooth manifold. More precisely, P. L. Antonelli, R. Ingarden, and M. Matsumoto began the study of the Jacobi stability for the geodesics associated with a Riemann metric or Finsler metric by deviating the geodesics and through the help of the KCC covariant derivative for the differential system in variations [10,11,12]. Consequently, the second KCC invariant was obtained, called the deviation curvature tensor, which is fundamental for the study of the Jacobi stability for geodesics and for the integral curves corresponding to a system of second-order differential equations. In the framework of differential geometry, a system of second-order differential equations (SODE) is called semi-spray. Starting with a semi-spray, we can define a nonlinear connection on the manifold, and, conversely, by using a nonlinear connection, we can define a semi-spray. Therefore, to any semi-spray (or SODE) we can associate a geometry on the manifold by the corresponding geometric objects [13,30,31,32]. Conversely, these geometric objects are invariant relative to local coordinate changes, which means that they are tensors that can satisfy the conditions of symmetry or skew-symmetry or neither, depending on the form of the system of second-order differential equations (SODE).

Because the roots of the KCC theory come from the papers of D. D. Kosambi [27], E. Cartan [28], and S. S. Chern [29], the abbreviation KCC (Kosambi–Cartan–Chern) appears natural and this geometric theory can be successfully used in many research domains, such as engineering, physics, chemistry, and biology [16,19,21,23,24,33]. Moreover, recent and very interesting approaches to the KCC theory in gravitation and cosmology were carried out in [34,35]. Furthermore, in [18], C.G. Boehmer, T. Harko, and S.V. Sabau made a methodological analysis of the Jacobi stability and its relations with the Lyapunov stability for dynamical systems that model the phenomena based on gravitation and astrophysics. In [36], a comprehensive study of the Jacobi stability for predator–prey models of Holling’s type II and III can be found.

The present manuscript is a purely mathematical investigation, founded on the theoretical tools of dynamical systems theory and the corresponding geometric objects of Kosambi–Cartan–Chern (KCC) theory, by studying the behavior around equilibrium points and obtaining the properties of local dynamics from the Jacobi stability point of view. The biological motivation for this study is given by the fact that these SIR patterns (classical or modified) were intensively studied in past decades in order to model the spread of epidemics in a population or for the study of interactions between species (prey–predator models). The novelty of this study is the use of the geometric tools of KCC theory for obtaining new results about the local dynamics of the dynamical systems that models infectious diseases or the interaction between species.

The obtained results for both patterns are related to the basic reproduction number ${\mathcal{R}}_0$ [2,3,5]. This number is crucial for the determination of the duration of the epidemic period or for the peak of the epidemic. Furthermore, the obtained results about the Jacobi stability near the endemic equilibrium can show us the sufficient and necessary conditions to avoid critical situations during an epidemic, such as the presence of some attractive sets, periodic trajectories, or isolated cycles. More exactly, the Jacobi stability in a neighborhood of an equilibrium point implies that this equilibrium point is a stable focus or an unstable focus. Then, Hopf-type bifurcations can occur, together with possible limits cycles.

After the introduction section, in Section 2, an overview of the classical SIR epidemic model with demography will be presented, and the basic results of the local and global stability of this system will be highlighted. Next, in Section 3, a reformulation of the classical SIR epidemic model with demography (3) as a system of second-order differential equations (SODE) will be developed, and the five geometrical invariants for this system will be obtained. The results relative to the Jacobi stability of this system around the equilibrium points will be obtained and presented in Section 4. More exactly, we will obtain the necessary and sufficient conditions for the Jacobi stability of the system around each equilibrium point. Then, if these conditions are fulfilled, it is not possible to have a chaotic behavior for the classical SIR epidemic model with demography. Additionally, at the end of Section 4, we will find the deviation equations around each equilibrium point and the curvature of the deviation vector; moreover, we will develop an analysis of the Jacobi stability and the classical (linear or Lyapunov) stability to compare these two approaches. Using the same approach, in Section 5 we will obtain similar results for a classical SIR epidemic model with demography and vaccination.

Further, a modified SIR epidemic model with demography with a linear transmission coefficient of infection is presented in Section 6 (see also [1]). After a second-order reformulation of this modified SIR model in the Section 7, the Jacobi stability analysis of this system is carried out in Section 8. Conclusions and possible future research are presented in the last section.

Finally, in Appendix A is presented an overview of the main notions and basic tools of the KCC geometric theory that are strictly needed for the study of the Jacobi stability of dynamical systems. More precisely, the five invariants of the theory and the notion of Jacobi stability are presented. As usual in differential geometry, the sum over the crossed repeated indices is understood.

2. A Classical SIR Epidemic Pattern with Demography

A classical SIR epidemic model for the spread of diseases supposes that the whole population $N\left(t\right)$ at a time t is split into three categories: $S\left(t\right)$ is the number of individuals who are susceptible at the moment t, $I\left(t\right)$ is the number of the infected individuals at t and $R\left(t\right)$ represents the number of removed individuals at the time t (by a removed individual, we mean individuals who either recovered from the illness or diad after infection) [1,2,3,4,5,6]. An SIR model without demography means that the total number of individuals $N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)$ is constant, i.e., no births, no immigration, no deaths and no emigration. However, in practice, this reality is not possible and different SIR models were considered with demography, for which $N\left(t\right)$ is not constant. In order to include the demography in this classical SIR epidemic model, we suppose that each individual is born susceptible [1]. Individuals from every category go out at a death rate $\mu$, per capita, and then the total death rate in the susceptible category is $\mu S$, while in the infectious category it is $\mu I$, and in the removed category it is $\mu R$. If we denote by $\alpha$ the recovery rate, then the rate of the recoveries in the infected people is $\alpha I$. Then, like for the SIR model without demography, if we denote by $\beta$ the transmission coefficient of the infection, then we can consider the next classical SIR model with demography:

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta IS-\mu S\hfill \\ \hfill I^{\prime }& =& \beta IS-\alpha I-\mu I\hfill \\ \hfill R^{\prime }& =& \alpha I-\mu R\hfill \end{array}\right.$$

(1)

where $\Lambda$ is the total birth rate (measured in number of people born per unit of time) and $S^{\prime }=S^{\prime }\left(t\right)$, $I^{\prime }=I^{\prime }\left(t\right)$, and $R^{\prime }=R^{\prime }\left(t\right)$ denote the derivatives with respect to time t, or the rates of changes of these quantities in a short period of time.

Let us remark that the third equation of system (1) was added in order to obtain the next differential equation for the total population $N\left(t\right)$:

$$N^{\prime }\left(t\right)=\Lambda -\mu N\left(t\right),$$

with the unique solution $N\left(t\right)=N\left(0\right)e^{-\mu t}+{\displaystyle \frac{\Lambda }{\mu }}\left(1-e^{-\mu t}\right)$. Therefore, the population size is not constant, but this is asymptotically constant, since $N\left(t\right)\to {\displaystyle \frac{\Lambda }{\mu }}$ when $t\to \infty$.

Obviously, we can observe that the first two equations in (1) are independent of the third, and then we can we can study only the two-dimensional autonomous system of first-order differential equations:

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta IS-\mu S\hfill \\ \hfill I^{\prime }& =& \beta IS-(\alpha +\mu )I\hfill \end{array}\right.$$

(2)

where $R\left(t\right)=N\left(t\right)-S\left(t\right)-I\left(t\right)$.

This is compared to $\beta$, the transmission coefficient of the infection, which has the unit [number of people × time]${}^{-1}$, $\alpha$, the recovery rate, and $\mu$, the death rate, which have the units [unit of time]${}^{-1}$. So, it is better to consider $\tau =(\alpha +\mu )t$ and then $\tau$ is a dimensionless quantity. If we denote $I\left(t\right)=I\left(\frac{\tau }{\alpha +\mu }\right)=\widehat{I}\left(\tau \right)$ and $S\left(t\right)=S\left(\frac{\tau }{\alpha +\mu }\right)=\widehat{S}\left(\tau \right)$, then we have $\frac{d\widehat{S}}{d\tau }=\frac{1}{\alpha +\mu }\frac{dS}{dt}$ and $\frac{d\widehat{I}}{d\tau }=\frac{1}{\alpha +\mu }\frac{dI}{dt}$, by using the chain rule. After resizing the variables $\widehat{S}$ and $\widehat{I}$ with the total limiting population size $\frac{\Lambda }{\mu }$, we obtain the new variables $x\left(\tau \right)=\frac{\mu \widehat{S}}{\Lambda }$ and $y\left(\tau \right)=\frac{\mu \widehat{I}}{\Lambda }$, which are also dimensionless quantities.

Consequently, system (2) has the next form [1]:

$$\left\{\begin{array}{ccc}\hfill x^{\prime }& =& \rho (1-x)-{\mathcal{R}}_{0}xy\hfill \\ \hfill y^{\prime }& =& ({\mathcal{R}}_{0}x-1)y\hfill \end{array}\right.$$

(3)

where $\rho ={\displaystyle \frac{\mu }{\alpha +\mu }}$ and ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{\mu (\alpha +\mu )}}$ are both dimensionless parameters.

Therefore, we can say that system (2) was transformed into a system with a dimensionless form (3), which is equivalent to the original system, because the solutions of the two systems have the same long-term behaviour. Moreover, the number of parameters was reduced from four to two. The notation ${\mathcal{R}}_0$ is not chosen randomly, but because this dimensionless quantity is exactly the reproduction number or the basic reproduction number for this mathematical epidemiological pattern [1,5,6].

Because it is impossible to solve the first-order differential system associated with this SIR pattern with demography by analytical methods, it remains only to find details about the behaviour of the solutions, especially because we want to know what will happen to the illness in the long term: will it go extinct, or will it become established in the population and become endemic? So, the long-term dynamics of the solutions are crucial from an epidemiological perspective [1,2,3].

It is clear that the model has relevance when $x\ge 0$, $y\ge 0$, and then the solutions of system (3) are in the first quadrant ${\Sigma }_{+}^0=\left\{(x,y)\in {\mathbf{R}}^2\mid x\ge 0,y\ge 0\right\}$. Moreover, the lines $\{x=0\}$ and $\{y=0\}$ are invariant manifolds with respect to the flow of the system, which means any integral curve starting from a point from ${\Sigma }_{+}=\left\{(x,y)\in {\mathbf{R}}^2\mid x>0,y>0\right\}$ remains in ${\Sigma }_{+}$. So, the integral curves cannot cross any of these two invariant lines and then the study of the system is well-defined from the epidemiological point of view, i.e., an integral curve starting from a zone with epidemiological relevance does not enter a zone without epidemiological relevance.

However, it is very important to study the local dynamics of the system with the classical tools of dynamical systems as well as with the geometrical tools of the Kosambi–Cartan–Chern (KCC) theory. First of all, we must determine the equilibrium points of the epidemic given by dynamical system (3), by solving the system:

$$\left\{\begin{array}{ccc}\rho (1-x)-{\mathcal{R}}_{0}xy\hfill & =& \hfill 0\\ ({\mathcal{R}}_{0}x-1)y\hfill & =& \hfill 0\end{array}\right.$$

giving us two equilibrium points $E_0(1,0)$, the so-called disease-free equilibrium, and $E_1\left(\frac{1}{{\mathcal{R}}_0},\rho \left(1-\frac{1}{{\mathcal{R}}_0}\right)\right)$, the so-called endemic equilibrium.

Let us remark that the endemic equilibrium exists if and only if the basic reproduction number ${\mathcal{R}}_0>1$. Else, if ${\mathcal{R}}_0=1$, then $E_1$ coincides with $E_0$, or, if ${\mathcal{R}}_0<1$, then $E_1$ is a virtual equilibrium point, i.e., $E_1$ does not belongs to ${\Sigma }_{+}^0$ and $E_1$ is irrelevant.

According to the Hartman–Grobman theorem, it is known that the local stability of a hyperbolic equilibrium’s points is given by the signs of the real part of eigenvalues of the Jacobi matrix at each equilibrium point. Since the Jacobi matrix of (3) at a point $(x,y)$ is

$$A=\left(\begin{array}{cc}-\rho -{\mathcal{R}}_{0}y& -{\mathcal{R}}_{0}x\\ {\mathcal{R}}_{0}y& {\mathcal{R}}_{0}x-1\end{array}\right),$$

the results show that:

• For the disease-free equilibrium $E_0(1,0)$, the Jacobi matrix is $A=\left(\begin{array}{cc}-\rho & -{\mathcal{R}}_0\\ 0& {\mathcal{R}}_0-1\end{array}\right)$ with eigenvalues ${\lambda }_1=-\rho$, ${\lambda }_2={\mathcal{R}}_0-1$. Then $E_0$ is unstable (saddle point) if and only if ${\mathcal{R}}_0>1$, and $E_0$ is locally asymptotically stable (stable node) if and only if ${\mathcal{R}}_0<1$. If ${\mathcal{R}}_0=1$, then $E_0$ is a non hyperbolic equilibrium point and we cannot apply the Hartman–Grobman theorem for the local behavior study.
• For the endemic equilibrium $E_1\left(\frac{1}{{\mathcal{R}}_0},\rho \left(1-\frac{1}{{\mathcal{R}}_0}\right)\right)$, the Jacobian $A=\left(\begin{array}{cc}-\rho {\mathcal{R}}_0& -1\\ \rho ({\mathcal{R}}_0-1)& 0\end{array}\right)$ with characteristic polynomial ${\lambda }^2+\rho {\mathcal{R}}_0\lambda +\rho ({\mathcal{R}}_0-1)=0$ and eigenvalues ${\lambda }_{1,2}={\displaystyle \frac{1}{2}}\left(-\rho {\mathcal{R}}_0\pm \sqrt{\rho (\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4)}\right)$. Since ${\mathcal{R}}_0>1$, we have that ${\lambda }_1+{\lambda }_2=-\rho {\mathcal{R}}_0<0$ and ${\lambda }_1{\lambda }_2=\rho ({\mathcal{R}}_0-1)>0$, which means that, if it exists, the endemic equilibrium $E_1$ is always locally asymptotically stable (stable node or stable focus). More precisely, $E_1$ is a stable node if and only if $\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4\ge 0$, and $E_1$ is a stable focus if and only if $\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4<0$.

In conclusion, the basic reproduction number ${\mathcal{R}}_0$ of the disease modelled by (3) plays a threshold role [1,5,6]:

• If ${\mathcal{R}}_0<1$, then there is only the disease-free equilibrium point, which is an attractive equilibrium (stable node), i.e., any trajectory of the dynamical system (3) starting near to $E_0$ converges at this equilibrium when time tends to infinity, and the illness disappears from the population.
• If ${\mathcal{R}}_0>1$, then two equilibrium points appear: the disease-free equilibrium point and the endemic equilibrium point. The disease-free equilibrium is not attractive (unstable, a saddle point), in the sense that there exist trajectories of system (3) that start very close to $E_0$, but tend to go away. Instead, the endemic equilibrium is attractive (stable node or stable focus), which means any orbit of system (3) starting near to $E_1$ converges to $E_1$ when time goes to infinity. In this situation, the illness remains endemic in the population.

Related to the global stability, an equilibrium point is said to be globally stable if it is stable for almost all initial conditions, not only for initial conditions that are near to this point. For this classical SIR system, the following results are known [1,5] (see also the Dulac–Bendixson theorem).

Theorem 1.

(a) 

For ${\mathcal{R}}_0<1$, the disease-free equilibrium point $E_0$ is globally stable.

(b) 

For ${\mathcal{R}}_0>1$, system (3) has no periodic orbits.

(c) 

For ${\mathcal{R}}_0>1$, the endemic equilibrium point $E_1$ is globally stable whenever $y\left(0\right)>0$.

In conclusion, we collect the obtained results for the local stability in

Table 1. The equilibrium points in the closed first quadrant ${\Sigma }_{+}^0$ for the classical SIR model.

Case	Conditions	Equilibrium Points Type
1	${\mathcal{R}}_0>1$, $\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4\ge 0$	$E_0$ saddle point, $E_1$ stable node
2	${\mathcal{R}}_0>1$, $\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4<0$	$E_0$ saddle point, $E_1$ stable focus
3	${\mathcal{R}}_0=1$	$E_0=E_1$ non hyperbolic
4	${\mathcal{R}}_0<1$	$E_0$ stable node, $E_1\notin {\Sigma }_{+}^0$

.

In the following sections, our approach will be focused on the study of the Jacobi stability for clarifying the behavior of the SIR system and to highlight the properties of the geometric objects corresponding to this system of ordinary differential equations.

3. SODE Formulation of the Classical SIR Pattern with Demography

We consider the classical SIR model with demography (3). For the sake of simplicity, the derivative with respect to time will be denoted with a dot over the variable and we prefer to denote t instead of $\tau$. Then, system (3) can be written in the form

$$\left\{\begin{array}{ccc}\hfill \dot{x}& =& \rho (1-x)-{\mathcal{R}}_{0}xy\hfill \\ \hfill \dot{y}& =& ({\mathcal{R}}_{0}x-1)y\hfill \end{array}\right.$$

(4)

where $\rho ={\displaystyle \frac{\mu }{\alpha +\mu }}\in (0,1)$ and ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{\mu (\alpha +\mu )}}>0$.

By using the derivative relative to the time t for the equations of system (4), we obtain the next system of second-order differential equations:

$$\left\{\begin{array}{ccc}\ddot{x}+(\rho +{\mathcal{R}}_{0}y)\dot{x}+{\mathcal{R}}_{0}x\dot{y}\hfill & =& \hfill 0\\ \ddot{y}-{\mathcal{R}}_{0}y\dot{x}+(1-{\mathcal{R}}_{0}x)\dot{y}\hfill & =& \hfill 0\end{array}\right.$$

In order to use the rule of the crossed repeated indices from differential geometry formalism, we will use the following notations for the variables:

$$x=x^1,\dot{x}=y^1,y=x^2,\dot{y}=y^2$$

Then, the above system of second-order differential equations (SODE) can be written:

$$\left\{\begin{array}{ccc}{\ddot{x}}^1+(\rho +{\mathcal{R}}_0{x}^2)y^1+{\mathcal{R}}_0{x}^1{y}^2\hfill & =& \hfill 0\\ {\ddot{x}}^2-{\mathcal{R}}_0{x}^2{y}^1+(1-{\mathcal{R}}_0{x}^1)y^2\hfill & =& \hfill 0\end{array}\right.$$

(5)

or, equivalently,

$$\left\{\begin{array}{ccc}{\displaystyle \frac{d^2{x}^1}{d{t}^2}}+(\rho +{\mathcal{R}}_0{x}^2)y^1+{\mathcal{R}}_0{x}^1{y}^2\hfill & =& \hfill 0\\ {\displaystyle \frac{d^2{x}^2}{d{t}^2}}-{\mathcal{R}}_0{x}^2{y}^1+(1-{\mathcal{R}}_0{x}^1)y^2\hfill & =& \hfill 0\end{array}\right.$$

(6)

where ${\displaystyle \frac{d{x}^i}{dt}}=y^i$, $i=1,2$.

Therefore, system (6) represents a SODE (or semi-spray) from the KCC theory:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}^1}{d{t}^2}}+2G^1(x^1,x^2,y^1,y^2)=0\\ {\displaystyle \frac{d^2{x}^2}{d{t}^2}}+2G^2(x^1,x^2,y^1,y^2)=0\end{array}\right.$$

(7)

where

$$\begin{array}{ccc}{G}^1(x^i,y^i)\hfill & =& {\displaystyle \frac{1}{2}}\left[(\rho +{\mathcal{R}}_0{x}^2)y^1+{\mathcal{R}}_0{x}^1{y}^2\right],\hfill \\ G^2(x^i,y^i)\hfill & =& {\displaystyle \frac{1}{2}}\left[-{\mathcal{R}}_0{x}^2{y}^1+(1-{\mathcal{R}}_0{x}^1)y^2\right].\hfill \end{array}$$

(8)

The zero-connection curvature $Z_j^i=2{\displaystyle \frac{\partial G^i}{\partial x^j}}$ is given by the next coefficients:

$$\left\{\begin{array}{ccc}\hfill Z_1^1& =& {\mathcal{R}}_0{y}^2\hfill \\ \hfill Z_2^1& =& {\mathcal{R}}_0{y}^1\hfill \\ \hfill Z_1^2& =& -{\mathcal{R}}_0{y}^2\hfill \\ \hfill Z_2^2& =& -{\mathcal{R}}_0{y}^1\hfill \end{array}\right.$$

(9)

The associated nonlinear connection N has the following components:

$$\left\{\begin{array}{ccc}\hfill N_1^1& =& {\displaystyle \frac{\partial G^1}{\partial y^1}}={\displaystyle \frac{1}{2}}\left(\rho +{\mathcal{R}}_0{x}^2\right)\hfill \\ \hfill N_2^1& =& {\displaystyle \frac{\partial G^1}{\partial y^2}}={\displaystyle \frac{1}{2}}{\mathcal{R}}_0{x}^1\hfill \\ \hfill N_1^2& =& {\displaystyle \frac{\partial G^2}{\partial y^1}}=-{\displaystyle \frac{1}{2}}{\mathcal{R}}_0{x}^2\hfill \\ \hfill N_2^2& =& {\displaystyle \frac{\partial G^2}{\partial y^2}}={\displaystyle \frac{1}{2}}\left(1-{\mathcal{R}}_0{x}^1\right)\hfill \end{array}\right.$$

(10)

Consequently, all components of the associated Berwald connection $G_{jk}^i=\frac{\partial N_j^i}{\partial y^k}$ are null and the components of the first invariant of the KCC theory ${\epsilon }^i=-\left(N_j^i{y}^j-2G^i\right)$ are:

$$\left\{\begin{array}{ccc}\hfill {\epsilon }^1& =& {\displaystyle \frac{1}{2}}(\rho +{\mathcal{R}}_0{x}^2)y^1+{\displaystyle \frac{1}{2}}{\mathcal{R}}_0{x}^1{y}^2\hfill \\ \hfill {\epsilon }^2& =& -{\displaystyle \frac{1}{2}}{\mathcal{R}}_0{x}^2{y}^1+{\displaystyle \frac{1}{2}}(1-{\mathcal{R}}_0{x}^1)y^2\hfill \end{array}\right.$$

(11)

Let us observe that ${\epsilon }^i=G^i$ for $i=1,2$, i.e., $\frac{\partial G^i}{\partial y^j}{y}^j=1·G^i$ for $i=1,2$. That means that the functions $G^i$ are homogeneous of degree 1 relative to $y^i$.

Next, according to (A10), we have the coefficients of the second invariant of the Kosambi–Cartan–Chern theory:

$$P_j^i=-2{\displaystyle \frac{\partial G^i}{\partial x^j}}-2G^l{G}_{jl}^i+y^l{\displaystyle \frac{\partial N_j^i}{\partial x^l}}+N_l^i{N}_j^l.$$

Then, the components of deviation curvature tensor for the classical SIR model with demography (4) are given by:

$$\begin{array}{ccc}\hfill P_1^1& =& -{\displaystyle \frac{1}{2}}{\mathcal{R}}_0{y}^2+{\displaystyle \frac{1}{4}}{\left(\rho +{\mathcal{R}}_0{x}^2\right)}^2-{\displaystyle \frac{1}{4}}{\mathcal{R}}_0^2{x}^1{x}^2\hfill \\ \hfill P_2^1& =& -{\displaystyle \frac{1}{2}}{\mathcal{R}}_0{y}^1+{\displaystyle \frac{1}{4}}{\mathcal{R}}_0{x}^1\left(\rho +1+{\mathcal{R}}_0{x}^2-{\mathcal{R}}_0{x}^1\right)\hfill \\ \hfill P_1^2& =& {\displaystyle \frac{1}{2}}{\mathcal{R}}_0{y}^2-{\displaystyle \frac{1}{4}}{\mathcal{R}}_0{x}^2\left(\rho +1+{\mathcal{R}}_0{x}^2-{\mathcal{R}}_0{x}^1\right)\hfill \\ \hfill P_2^2& =& {\displaystyle \frac{1}{2}}{\mathcal{R}}_0{y}^1+{\displaystyle \frac{1}{4}}{\left(1-{\mathcal{R}}_0{x}^1\right)}^2-{\displaystyle \frac{1}{4}}{\mathcal{R}}_0^2{x}^1{x}^2\hfill \end{array}$$

(12)

If we remember that the trace and the determinant of the deviation curvature tensor

$$P=\left(\begin{array}{cc}{P}_1^1& P_2^1\\ P_1^2& P_2^2\end{array}\right)$$

are tr $P=P_1^1+P_2^2$ and $detP=P_1^1{P}_2^2-P_1^2{P}_2^1$, then, by following Theorem A2, we can write the following result:

Theorem 2. 

All the roots of the characteristic polynomial of P are negative or have negative real parts (that means Jacobi stability) if and only if

$$trP=P_1^1+P_2^2<0\mathit{and}detP=P_1^1{P}_2^2-P_1^2{P}_2^1>0.$$

Taking into account that $P_{jk}^i={\displaystyle \frac{1}{3}}\left({\displaystyle \frac{\partial P_j^i}{\partial y^k}}-{\displaystyle \frac{\partial P_k^i}{\partial y^j}}\right)$, $P_{jkl}^i={\displaystyle \frac{\partial P_{jk}^i}{\partial y^l}}$, $D_{jkl}^i={\displaystyle \frac{\partial G_{jk}^i}{\partial y^l}}$, we obtain the third, fourth, and fifth invariants of the classical SIR model with demography (4):

Theorem 3. 

All eight components of the torsion tensor $P_{jk}^i$, the third invariant of KCC theory, are equal to zero, i.e.,

$$P_{jk}^i=0,\forall i,j,k.$$

(13)

All sixteen components of the Riemann–Christoffel curvature tensor $P_{jkl}^i$, the fourth invariant of KCC theory, are equal to zero, i.e.,

$$P_{jkl}^i=0,\forall i,j,k,l.$$

(14)

All sixteen components of the Douglas tensor $D_{jkl}^i$, the fifth invariant of KCC theory, are equal to zero, i.e.,

$$D_{jkl}^i=0,\forall i,j,k,l.$$

(15)

4. Jacobi Stability Analysis of the Classical SIR Pattern with Demography

In the present section, the first two geometric invariants at each equilibrium point of the SIR model with demography (4) will be computed and, consequently, the Jacobi stability conditions of the system around each equilibrium point will be determined.

Further, for equilibrium points $E_0(1,0)$ and $E_1\left(\frac{1}{{\mathcal{R}}_0},\rho \left(1-\frac{1}{{\mathcal{R}}_0}\right)\right)$ of the initial SIR model with demography (4), we have the corresponding equilibrium points $E_0(1,0,0,0)$ and $E_1\left(\frac{1}{{\mathcal{R}}_0},\rho \left(1-\frac{1}{{\mathcal{R}}_0}\right),0,0\right)$ for the semi-spray (6).

For $E_0(1,0,0,0)$, the first invariant of the theory has all coefficients equal to zero, i.e., ${\epsilon }^1={\epsilon }^2=0$, and the next matrix contains the coefficients of the second invariant:

$$P=\left(\begin{array}{cc}{\displaystyle \frac{1}{4}}{\rho }^2& {\displaystyle \frac{1}{4}}{\mathcal{R}}_0\left(\rho +1-{\mathcal{R}}_0\right)\\ 0& {\displaystyle \frac{1}{4}}{\left(1-{\mathcal{R}}_0\right)}^2\end{array}\right).$$

Since $\mathrm{tr}P={\displaystyle \frac{1}{4}}{\rho }^2+\frac{1}{4}{\left(1-{\mathcal{R}}_0\right)}^2>0$ and $detP={\displaystyle \frac{1}{16}}{\rho }^2{\left(1-{\mathcal{R}}_0\right)}^2>0$, by using Theorem 2, we obtain the next result:

Theorem 4. 

The disease-free equilibrium point $E_0$ is always Jacobi unstable.

For $E_1\left(\frac{1}{{\mathcal{R}}_0},\rho \left(1-\frac{1}{{\mathcal{R}}_0}\right),0,0\right)$ the first invariant of the KCC theory has all coefficients equal to zero, i.e., ${\epsilon }^1={\epsilon }^2=0$, and the next matrix contains the coefficients of the second invariant:

$$P=\left(\begin{array}{cc}{\displaystyle \frac{1}{4}}\rho \left(\rho {\mathcal{R}}_0^2-{\mathcal{R}}_0+1\right)& {\displaystyle \frac{1}{4}}\rho {\mathcal{R}}_0\\ -{\displaystyle \frac{1}{4}}{\rho }^2{\mathcal{R}}_0\left({\mathcal{R}}_0-1\right)& -{\displaystyle \frac{1}{4}}\rho \left({\mathcal{R}}_0-1\right)\end{array}\right).$$

Since $\mathrm{tr}P=\frac{1}{4}\rho \left(\rho {\mathcal{R}}_0^2-2{\mathcal{R}}_0+2\right)$ and $detP=\frac{1}{16}{\rho }^2{\left({\mathcal{R}}_0-1\right)}^2>0$, by using Theorem 2, we obtain the following result:

Theorem 5. 

The endemic equilibrium point $E_1$ is Jacobi-stable if and only if $\rho {\mathcal{R}}_0^2-2{\mathcal{R}}_0+2<0$.

Remark 1. 

Whenever $E_1$ exists and is Jacobi-stable, a chaotic behavior of the SIR system in a small enough neighborhood of this point is not possible.

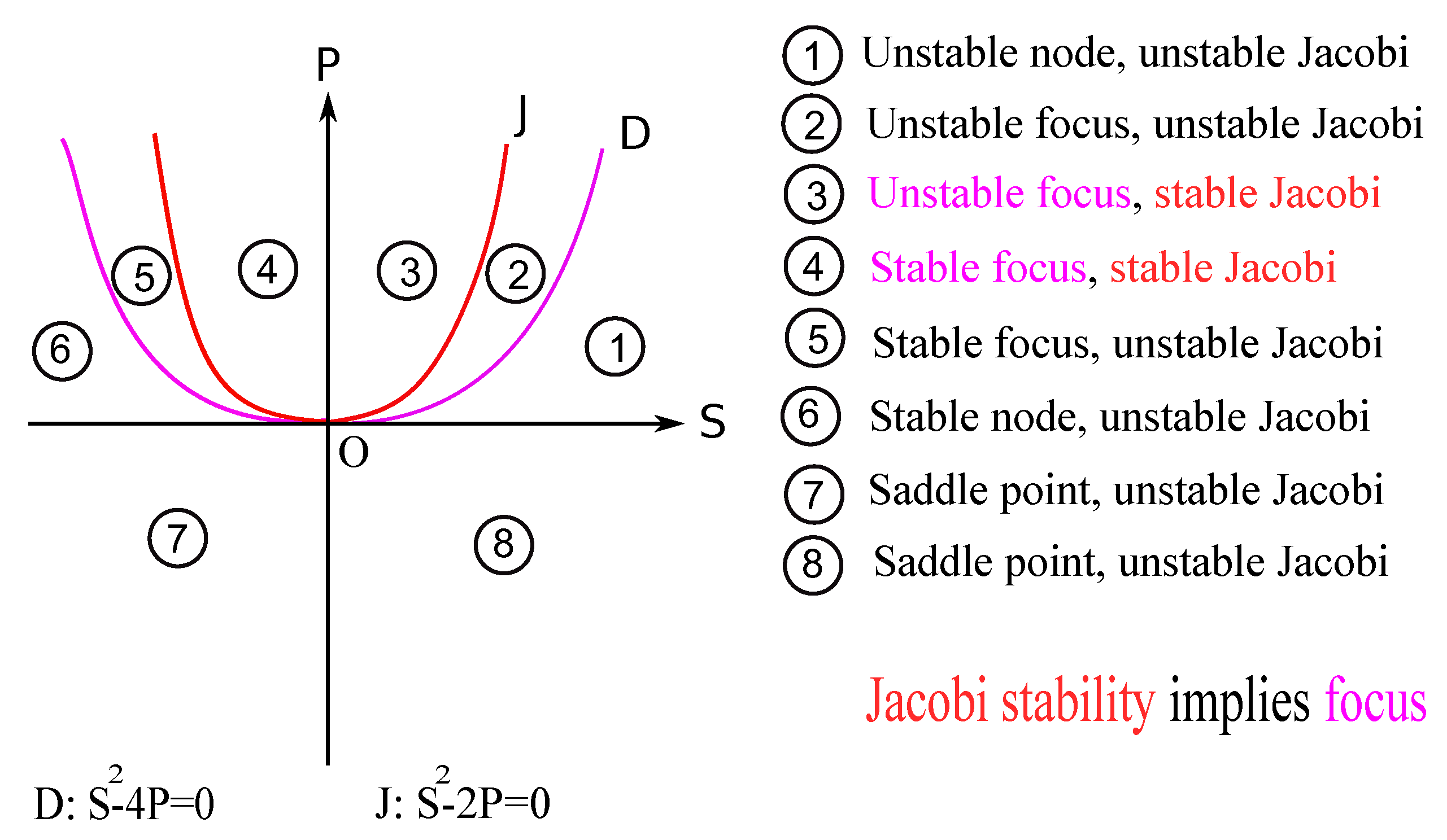
In order to clarify the relation between the classical (Lyapunov or linear) stability and the Jacobi stability for this SIR system, we will present the next diagram relative to the system’s parameters $\rho$ and ${\mathcal{R}}_0$ (see Figure 1):

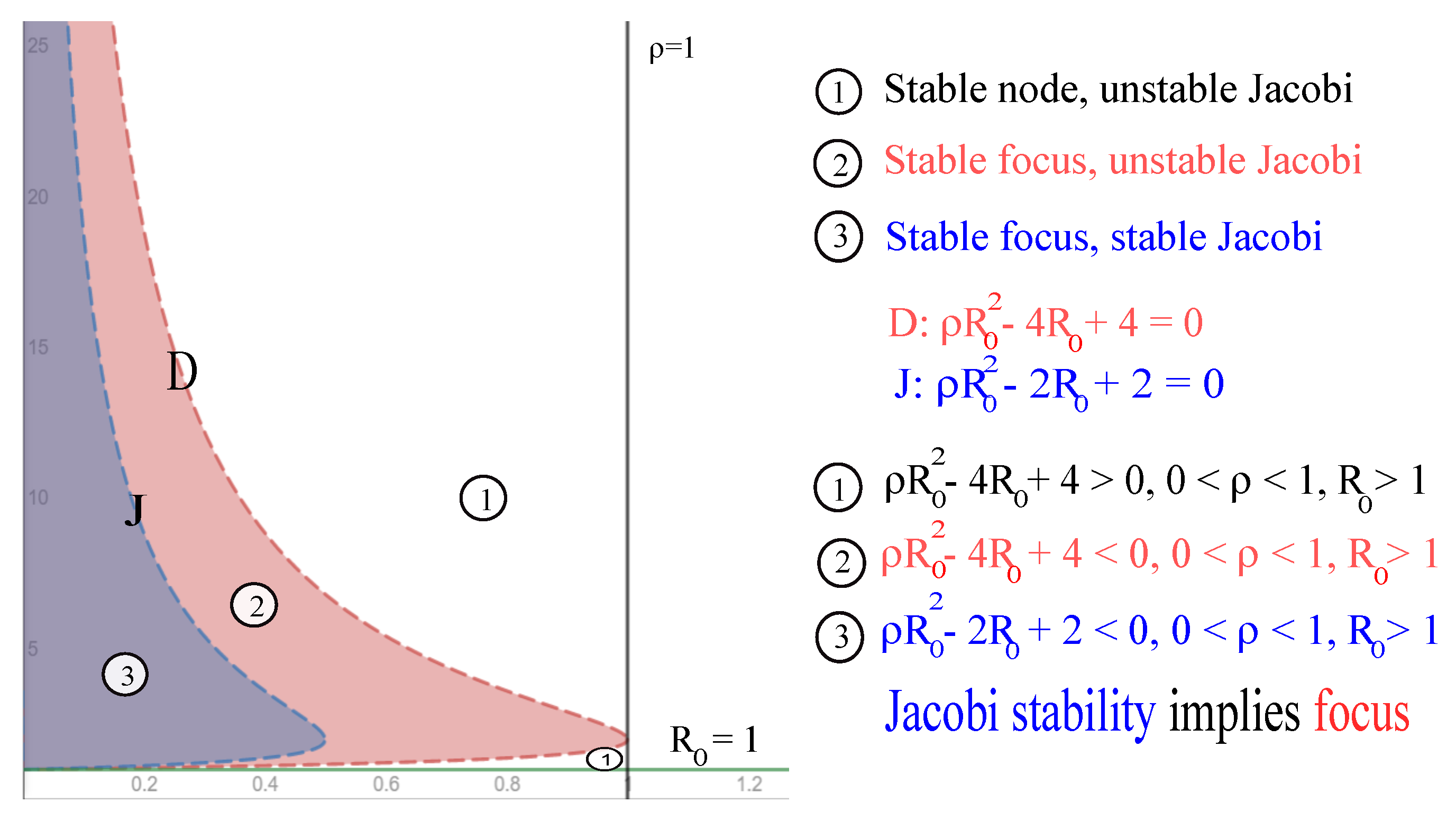
Taking into account that $\rho ={\displaystyle \frac{\mu }{\alpha +\mu }}$, ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{\mu (\alpha +\mu )}}$ and according to Theorem 5, we obtain the following result:

Theorem 6. 

If the endemic equilibrium point $E_1$ exists, then $E_1$ is Jacobi-stable if and only if the reproduction number ${\mathcal{R}}_0$ satisfies the conditions:

$$1+\frac{\alpha }{\mu }-\sqrt{\frac{{\alpha }^2}{{\mu }^2}-1}<{\mathcal{R}}_0<1+\frac{\alpha }{\mu }+\sqrt{\frac{{\alpha }^2}{{\mu }^2}-1}.$$

Proof. 

By using the Jacobi stability condition $\rho {\mathcal{R}}_0^2-2{\mathcal{R}}_0+2<0$ from Theorem 5, and the study of the sign of the second order function in ${\mathcal{R}}_0$, $\mu {\mathcal{R}}_0^2-2(\alpha +\mu ){\mathcal{R}}_0+2(\alpha +\mu )$, with the discriminant equal to $4({\alpha }^2-{\mu }^2)$, the theorem is proved. □

According to the expression of the characteristic polynomial at the endemic equilibrium point $E_1$, we obtain the next result regarding the local linear stability of the endemic equilibrium point.

Theorem 7. 

If it exists, the endemic equilibrium $E_1$ is a stable focus if and only if the reproduction number ${\mathcal{R}}_0$ satisfies the conditions:

$$2\left(1+\frac{\alpha }{\mu }-\sqrt{\frac{{\alpha }^2}{{\mu }^2}+\frac{\alpha }{\mu }}\right)<{\mathcal{R}}_0<2\left(1+\frac{\alpha }{\mu }+\sqrt{\frac{{\alpha }^2}{{\mu }^2}+\frac{\alpha }{\mu }}\right).$$

Otherwise, the endemic equilibrium $E_1$ is a stable node.

Proof. 

Because the discriminant associated with the characteristic polynomial at $E_1$ is equal to $\rho (\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4)$, it is necessary to study the sign of the second order function in ${\mathcal{R}}_0$, $\mu {\mathcal{R}}_0^2-4(\alpha +\mu ){\mathcal{R}}_0+4(\alpha +\mu )$. □

Let us remark that apart from the reproduction number ${\mathcal{R}}_0$, the parameter $\alpha$ is the most important parameter of this epidemic model. Only if $\alpha >\mu$ (i.e., $\rho <\frac{1}{2}$), the endemic equilibrium (if it exists) can be stable from the Jacobi perspective. Therefore, the recovery rate from illness $\alpha$ plays an unexpectedly crucial role both for classical stability and for Jacobi stability of this classical SIR system.

In order to obtain characterizations of the local behaviour of the endemic equilibrium point $E_1$ related to the parameter $\beta$, the transmission coefficient of the infection, the next results are obtained:

Theorem 8. 

If the endemic equilibrium point $E_1$ exists, then $E_1$ is Jacobi-stable if and only if the transmission coefficient β satisfies the conditions:

$${\displaystyle \frac{\alpha +\mu }{{\Lambda }_{\infty }}}\left(1+\frac{\alpha }{\mu }-\sqrt{\frac{{\alpha }^2}{{\mu }^2}-1}\right)<\beta <{\displaystyle \frac{\alpha +\mu }{{\Lambda }_{\infty }}}\left(1+\frac{\alpha }{\mu }+\sqrt{\frac{{\alpha }^2}{{\mu }^2}-1}\right),$$

where ${\Lambda }_{\infty }={\displaystyle \frac{\Lambda }{\mu }}$ is the limit size of the entire population.

Proof. 

By replacing both dimensionless parameters $\rho$ and ${\mathcal{R}}_0$ with the four parameters of the initial system (1), and using the Jacobi stability condition from Theorem 5, the theorem is proved by following the sign of the second order function in $\beta$, ${\Lambda }^2{\beta }^2-2\Lambda {(\alpha +\mu )}^2\beta +2\mu {(\alpha +\mu )}^3$, with the discriminant equal to $4{\Lambda }^2{(\alpha +\mu )}^2({\alpha }^2-{\mu }^2)$. □

Theorem 9. 

If it exists, the endemic equilibrium $E_1$ is a stable focus if and only if the transmission coefficient β satisfies the conditions:

$${\displaystyle \frac{2(\alpha +\mu )}{{\Lambda }_{\infty }}}\left(1+\frac{\alpha }{\mu }-\sqrt{\frac{{\alpha }^2}{{\mu }^2}+\frac{\alpha }{\mu }}\right)<\beta <{\displaystyle \frac{2(\alpha +\mu )}{{\Lambda }_{\infty }}}\left(1+\frac{\alpha }{\mu }+2\sqrt{\frac{{\alpha }^2}{{\mu }^2}+\frac{\alpha }{\mu }}\right),$$

where ${\Lambda }_{\infty }={\displaystyle \frac{\Lambda }{\mu }}$ is the limit size of the entire population.

Otherwise, the endemic equilibrium $E_1$ is a stable node.

Proof. 

Because the discriminant associated with the characteristic polynomial at $E_1$ is equal to $\rho (\rho {\mathcal{R}}_0^2-4{\mathcal{R}}_0+4)$, it is necessary to study the sign of the second order function in $\beta$, ${\Lambda }^2{\beta }^2-4\Lambda {(\alpha +\mu )}^2\beta +4\mu {(\alpha +\mu )}^3$. □

If the mortality rate is known at a value ${\mu }_0$, in order to obtain threshold values for the parameter $\alpha$, the recovery rate, it is enough to replace $\rho$ with ${\displaystyle \frac{{\mu }_0}{\alpha +{\mu }_0}}$ in Theorem 5 and it results:

Theorem 10.

(a) 

If the endemic equilibrium point $E_1$ exists, then it is Jacobi-stable if and only if the recovery rate α fulfills the condition:

$$\alpha >{\alpha }_J={\mu }_0{\displaystyle \frac{{({\mathcal{R}}_0-1)}^2+1}{2({\mathcal{R}}_0-1)}}.$$

(b) 

If it exists, the endemic equilibrium $E_1$ is a stable focus if and only if the recovery rate α fulfills the condition:

$$\alpha >{\alpha }_F={\mu }_0{\displaystyle \frac{{({\mathcal{R}}_0-2)}^2}{4({\mathcal{R}}_0-1)}}.$$

Otherwise, the endemic equilibrium $E_1$ is a stable node.

Let us remark that ${\alpha }_J=2{\alpha }_F+{\mu }_0$, i.e., ${\alpha }_J>{\alpha }_F$ because the Jacobi stability of an equilibrium point implies that this equilibrium is a focus.

Conversely, if we fixed the value of the recovery rate $\alpha$ at the value ${\alpha }_0$, then we obtain the following threshold values for the mortality rate $\mu$:

Theorem 11.

(a) 

If the endemic equilibrium point $E_1$ exists, then $E_1$ is Jacobi-stable if and only if the mortality rate μ fulfills the condition:

$$\mu <{\mu }_J={\alpha }_0{\displaystyle \frac{2({\mathcal{R}}_0-1)}{{({\mathcal{R}}_0-1)}^2+1}}.$$

(b) 

If it exists, the endemic equilibrium $E_1$ is a stable focus if and only if the mortality rate μ fulfills the condition:

$$\alpha <{\mu }_F={\alpha }_0{\displaystyle \frac{4({\mathcal{R}}_0-1)}{{({\mathcal{R}}_0-2)}^2}}.$$

Otherwise, the endemic equilibrium $E_1$ is a stable node.

Of course, ${\mu }_J<{\mu }_F$ because ${\mu }_F-{\mu }_J=2{\alpha }_0{\displaystyle \frac{{\mathcal{R}}_0^2({\mathcal{R}}_0-1)}{{({\mathcal{R}}_0-2)}^2({({\mathcal{R}}_0-1)}^2+1)}}>0$.

4.1. Dynamics of the Deviation Vector for the Classical SIR Pattern with Demography

Because the deviation vector ${\xi }^i$, $i=1,2$ gives us the behaviour of the integral curves of the dynamical system around any equilibrium point, it is important to study the time evolution of this deviation vector, described by the system of deviation Equation (A8), also called Jacobi equations, or by the system of equations in covariant form (A9).

For this classical SIR system with demography, the deviation equations become:

$$\left\{\begin{array}{ccc}\frac{d^2{\xi }^1}{d{t}^2}+\left(\rho +{\mathcal{R}}_0{x}^2\right)\frac{d{\xi }^1}{dt}+{\mathcal{R}}_0{x}^1\frac{d{\xi }^2}{dt}+{\mathcal{R}}_0{y}^2{\xi }^1+{\mathcal{R}}_0{y}^1{\xi }^2\hfill & =& \hfill 0\\ \frac{d^2{\xi }^2}{d{t}^2}-{\mathcal{R}}_0{x}^2\frac{d{\xi }^1}{dt}+\left(1-{\mathcal{R}}_0{x}^1\right)\frac{d{\xi }^2}{dt}-{\mathcal{R}}_0{y}^2{\xi }^1-{\mathcal{R}}_0{y}^1{\xi }^2\hfill & =& \hfill 0\end{array}\right.$$

(16)

The length of the deviation vector $\xi \left(t\right)=\left({\xi }^1\left(t\right),{\xi }^2\left(t\right)\right)$ is defined by

$$∥\xi \left(t\right)∥=\sqrt{{\left({\xi }^1\left(t\right)\right)}^2+{\left({\xi }^2\left(t\right)\right)}^2}.$$

In the following, we will present the deviation equations around the equilibrium points for the classical SIR system with demography. Therefore, the time evolution of the deviation vector close to the disease-free equilibrium point $E_0(1,0,0,0)$ is carried out by the next SODE:

$$\left\{\begin{array}{ccc}\frac{d^2{\xi }^1}{d{t}^2}+\rho \frac{d{\xi }^1}{dt}+{\mathcal{R}}_0\frac{d{\xi }^2}{dt}\hfill & =& \hfill 0\\ \frac{d^2{\xi }^2}{d{t}^2}+\left(1-{\mathcal{R}}_0\right)\frac{d{\xi }^2}{dt}\hfill & =& \hfill 0\end{array}\right.$$

(17)

The time evolution of the deviation vector close to the endemic equilibrium point $E_1\left(\frac{1}{{\mathcal{R}}_0},\rho \left(1-\frac{1}{{\mathcal{R}}_0}\right),0,0\right)$ is carried out by the next SODE:

$$\left\{\begin{array}{ccc}\frac{d^2{\xi }^1}{d{t}^2}+\rho {\mathcal{R}}_0\frac{d{\xi }^1}{dt}+\frac{d{\xi }^2}{dt}\hfill & =& \hfill 0\\ \frac{d^2{\xi }^2}{d{t}^2}+\rho \left(1-{\mathcal{R}}_0\right)\frac{d{\xi }^1}{dt}\hfill & =& \hfill 0\end{array}\right.$$

(18)

Taking into account the differential geometry’s approach for the plane curves [19], the curvature $\kappa \left(t\right)$ of the trajectory $\xi \left(t\right)=\left({\xi }^1\left(t\right),{\xi }^2\left(t\right)\right)$ associated with the deviation Equation (16) is a quantitative description of the dynamics of the deviation vector ${\xi }^i$, given by:

$$\kappa \left(t\right)=\frac{{\dot{\xi }}^1\left(t\right){\ddot{\xi }}^2\left(t\right)-{\ddot{\xi }}^1\left(t\right){\dot{\xi }}^2\left(t\right)}{{\left[{\left({\dot{\xi }}^1\left(t\right)\right)}^2+{\left({\dot{\xi }}^2\left(t\right)\right)}^2\right]}^{3/2}}$$

(19)

where ${\dot{\xi }}^i\left(t\right)={\displaystyle \frac{d{\xi }^i}{dt}}$, ${\ddot{\xi }}^i\left(t\right)={\displaystyle \frac{d^2{\xi }^i}{d{t}^2}}$, $i=1,2$.

5. A Simple SIR Epidemic Pattern with Demography and Vaccination

In this section, we propose a classical and simple SIR model with vaccination as in [37]. Furthermore, a very interesting four-dimensional model with vaccination was studied recently in [38]. Next, we will reconsider the classical SIR model with demography (1) and we will assume that a part of the susceptible individuals are vaccinated with the rate of vaccination p. According to the classical SIR model, this vaccination rate is measured in [unit of time]${}^{-1}$. If we will suppose that all vaccinated individuals will not be infected and that they can be considered to belong to the category of removed individuals, then the model (1) will be written in the form:

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta IS-\mu S-pS\hfill \\ \hfill I^{\prime }& =& \beta IS-\alpha I-\mu I\hfill \\ \hfill R^{\prime }& =& \alpha I-\mu R+pS\hfill \end{array}\right.$$

(20)

Let us observe that the first two equations of system (20) are independent of the third equation, because we can obtain the removed population by using $R\left(t\right)=N\left(t\right)-S\left(t\right)-I\left(t\right)$ and due to the fact that the total population $N\left(t\right)$ can be obtained from the next differential equation:

$$N^{\prime }\left(t\right)=\Lambda -\mu N\left(t\right),$$

with the unique solution $N\left(t\right)=N\left(0\right)e^{-\mu t}+{\displaystyle \frac{\Lambda }{\mu }}\left(1-e^{-\mu t}\right)$.

Obviously, as for the classical model (1), the population number is not constant, but it is asymptotically constant, because $N\left(t\right)\to {\displaystyle \frac{\Lambda }{\mu }}$ when $t\to \infty$.

Taking into account all these proposals, we can consider the two-dimensional autonomous system of first-order differential equations:

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta IS-(\mu +p)S\hfill \\ \hfill I^{\prime }& =& \beta IS-(\alpha +\mu )I\hfill \end{array}\right.$$

(21)

By applying similar techniques as in Section 2 and by changing the time and variables, $\tau =(\alpha +\mu )t$, $x\left(\tau \right)=\frac{p+\mu }{\Lambda }\widehat{S}\left(\tau \right)$, $y\left(\tau \right)=\frac{p+\mu }{\Lambda }\widehat{I}\left(\tau \right)$, where $\widehat{S}\left(\tau \right)=S\left(\frac{\tau }{\alpha +\mu }\right)$, $\widehat{I}\left(\tau \right)=I\left(\frac{\tau }{\alpha +\mu }\right)$, we obtain the equivalent dimensionless form of (21):

$$\left\{\begin{array}{ccc}\hfill x^{\prime }& =& \rho (1-x)-{\mathcal{R}}_{0}xy\hfill \\ \hfill y^{\prime }& =& {\mathcal{R}}_{0}xy-y\hfill \end{array}\right.$$

(22)

where $\rho ={\displaystyle \frac{p+\mu }{\alpha +\mu }}$ and ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{(p+\mu )(\alpha +\mu )}}$ are both dimensionless parameters.

Let us remark that system (22) is exactly the dimensionless system (3) obtained for the classical SIR model in Section 2. Therefore, all obtained results remain available also for this SIR epidemic model with demography and vaccination. Only interpretations can be different because the dimensionless parameters $\rho$ and ${\mathcal{R}}_0$ are different. Of course, ${\mathcal{R}}_0$ is the basic reproduction number for this pattern. Moreover, the number of parameters was reduced from five to two.

According to the expressions of $\rho >0$ and ${\mathcal{R}}_0>0$, it is clear that $\rho <1$ if and only if $\alpha >p$ and $\rho <\frac{1}{2}$ if and only if $\alpha >2p+\mu$. So, if we take account of the results presented in Figure 1, for this model, the endemic equilibrium $E_1$ can be a stable focus only if the recovery rate $\alpha$ is greater than the vaccination rate p and $E_1$ can be Jacobi-stable only if the recovery rate $\alpha$ is greater than $2p+\mu$.

6. A Modified SIR Epidemic Pattern with Demography

Taking into account that for the classical SIR model (1), we have no periodic orbits, and then Hopf bifurcations do not occur; next, we will consider a modified SIR system. More exactly, we will suppose that the coefficient of transmission of the infection $\beta$ is not constant, but it is a linear function of the number of infected individuals, which means $\beta$ is replaced by $\beta (1+\nu I)$, where $\nu$ is a real positive parameter [1,39]. This implies that the transmission coefficient of infection and also the contact rate increase with the number of infected individuals and new infections occur much faster in comparison with the classical model [1]. Of course, the local and global dynamics of this modified pattern is much more complicated compared to the classical pattern. This model is a natural generalization and if $\nu =0$, we come back to the first classical model.

Therefore, the model becomes:

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta (1+\nu I)IS-\mu S\hfill \\ \hfill I^{\prime }& =& \beta (1+\nu I)IS-(\alpha +\mu )I\hfill \\ \hfill R^{\prime }& =& \alpha I-\mu R\hfill \end{array}\right.$$

(23)

Let us remark that the total population size $N=S+I+R$ satisfies $N^{\prime }\left(t\right)=\Lambda -\mu N\left(t\right)$ and then we can omit the third equation for recovered individuals R. It follows that it is necessary and sufficient to study the two-dimensional autonomous system of first-order differential equations:

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta (1+\nu I)IS-\mu S\hfill \\ \hfill I^{\prime }& =& \beta (1+\nu I)IS-(\alpha +\mu )I\hfill \end{array}\right.$$

(24)

where $R\left(t\right)=N\left(t\right)-S\left(t\right)-I\left(t\right)$.

In order to obtain the dimensionless version of the system, using similar techniques as for the classical system (2), after changing the time variable t by $\tau =(\alpha +\mu )t$ and rescaling the variables $\widehat{S}=S\left(\frac{\tau }{\alpha +\mu }\right)$, $\widehat{I}=I\left(\frac{\tau }{\alpha +\mu }\right)$ with the total limiting population number ${\Lambda }_{\infty }=\frac{\Lambda }{\mu }$, we obtain the new variables $x\left(\tau \right)=\frac{\widehat{S}}{{\Lambda }_{\infty }}$, $y\left(\tau \right)=\frac{\widehat{I}}{{\Lambda }_{\infty }}$, which are dimensionless quantities. Consequently, if we denote $\omega =\nu {\Lambda }_{\infty }$, then system (24) becomes:

$$\left\{\begin{array}{ccc}\hfill x^{\prime }& =& \rho (1-x)-{\mathcal{R}}_0(1+\omega y)xy\hfill \\ \hfill y^{\prime }& =& {\mathcal{R}}_0(1+\omega y)xy-y\hfill \end{array}\right.$$

(25)

where $\rho ={\displaystyle \frac{\mu }{\alpha +\mu }}$ and ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{\mu (\alpha +\mu )}}$ are both dimensionless parameters.

Therefore, we can say that system (24) is transformed into a dimensionless-form system (25), which is equivalent to the original system, because the long-term dynamics of the solutions are the same. Moreover, the number of parameters was reduced from five ($\Lambda$, $\beta$, $\nu$, $\mu$, and $\alpha$) to three ($\rho$, ${\mathcal{R}}_0$, and $\omega$), all being strictly positive real numbers. Of course, ${\mathcal{R}}_0$ represent the reproduction number for this modified SIR model and $0<\rho <1$.

Further, our study for this modified SIR model has relevance when $x\ge 0$, $y\ge 0$, i.e., on the first quadrant ${\Sigma }_{+}^0=\left\{(x,y)\in {\mathbf{R}}^2\mid x\ge 0,y\ge 0\right\}$ or even on the open first quadrant ${\Sigma }_{+}=\left\{(x,y)\in {\mathbf{R}}^2\mid x>0,y>0\right\}$.

The Jacobian matrix of system (25) at a point $(x,y)$ is

$$A=\left(\begin{array}{cc}-\rho -{\mathcal{R}}_0(1+\omega y)y& -{\mathcal{R}}_{0}x-2{\mathcal{R}}_0\omega xy\\ {\mathcal{R}}_0(1+\omega y)y& {\mathcal{R}}_{0}x+2{\mathcal{R}}_0\omega xy-1\end{array}\right)$$

In order to determine the equilibrium points of (25), by investigating the system

$$\left\{\begin{array}{ccc}\rho (1-x)-{\mathcal{R}}_0(1+\omega y)xy\hfill & =& \hfill 0\\ {\mathcal{R}}_0(1+\omega y)xy-y\hfill & =& \hfill 0\end{array}\right.$$

we obtain at most three equilibrium, as follows:

For $y=0$, $E_0(1,0)$, the disease-free equilibrium point, with Jacobian $A=$$\left(\begin{array}{cc}-\rho & -{\mathcal{R}}_0\\ 0& {\mathcal{R}}_0-1\end{array}\right)$ and eigenvalues ${\lambda }_1=-\rho$, ${\lambda }_2={\mathcal{R}}_0-1$. Then, $E_0$ is locally asymptotically stable (stable node) if and only if ${\mathcal{R}}_0<1$, or $E_0$ is unstable (saddle point) if and only if ${\mathcal{R}}_0>1$. For ${\mathcal{R}}_0=1$, $E_0$ is a non-hyperbolic equilibrium point because ${\lambda }_2=0$.

For $y\ne 0$, we have ${\mathcal{R}}_0(1+\omega y)x=1$, and then $\rho \left(1-\frac{1}{{\mathcal{R}}_0\left(1+\omega y\right)}\right)-y=0$. Because $\rho \left(1-\frac{1}{{\mathcal{R}}_0\left(1+\omega y\right)}\right)-y=\frac{\rho {\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega y-\rho -{\mathcal{R}}_{0}y-{\mathcal{R}}_0{y}^2\omega }{R\left(1+\omega y\right)}$, the roots of second order algebraic equation in y are

$$-\omega {\mathcal{R}}_0{y}^2+{\mathcal{R}}_0(\omega \rho -1)y+\rho ({\mathcal{R}}_0-1)=0,$$

(26)

$$y_1=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right),y_2=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right),$$

where $\Delta ={\mathcal{R}}_0^2{(\omega \rho +1)}^2-4{\mathcal{R}}_0\omega \rho$ is the discriminant of the second order Equation (26).

If we denote by $f\left(y\right)=-\omega {\mathcal{R}}_0{y}^2+{\mathcal{R}}_0(\omega \rho -1)y+\rho ({\mathcal{R}}_0-1)$, the second order function associated with the Equation (26), then we have the following three cases:

Case 1. If $f\left(0\right)=\rho ({\mathcal{R}}_0-1)>0$, i.e., ${\mathcal{R}}_0>1$, then only the second root $y_2$ is strictly positive and we have only one endemic equilibrium point $E\left(x,y\right)$, with coordinates

$$x=\frac{2}{{\mathcal{R}}_0(1+\omega \rho )+\sqrt{\Delta }},y=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right).$$

(27)

Let us remark that $\Delta >0$, because $\Delta ={\mathcal{R}}_0^2{(\omega \rho +1)}^2-4{\mathcal{R}}_0\omega \rho >{\mathcal{R}}_0^2\left({(\omega \rho +1)}^2-4\omega \rho \right)>{(\omega \rho +1)}^2-4\omega \rho ={(\omega \rho -1)}^2$, for any positive parameters $\omega$ and $\rho$.

Then, taking into account that ${\mathcal{R}}_0(1+\omega y)x=1$, the Jacobi matrix at the only one endemic equilibrium point $E\left(x,y\right)$ is

$$A=\left(\begin{array}{cc}-\rho -{\mathcal{R}}_0\left(1+\omega y\right)y& -{\mathcal{R}}_0\omega xy-1\\ {\mathcal{R}}_0\left(1+\omega y\right)y& {\mathcal{R}}_0\omega xy\end{array}\right),$$

(28)

where the trace is $\mathrm{tr}A={\lambda }_1+{\lambda }_2=-\rho -{\mathcal{R}}_0\left(1+\omega y\right)y+{\mathcal{R}}_0\omega xy$ and the determinant is $detA={\lambda }_1{\lambda }_2=-\rho {\mathcal{R}}_0\omega xy+{\mathcal{R}}_0\left(1+\omega y\right)y$, where ${\lambda }_1$, ${\lambda }_2$ are eigenvalues of A.

By replacing x and y from (27),

$$\mathrm{tr}A=-\frac{1}{4}\frac{\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)}{{\mathcal{R}}_0\omega \left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}$$

and

$$detA=\frac{1}{4}\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)\frac{{\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }\right)}{{\mathcal{R}}_0\omega \left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}.$$

Due to $y>0$ and ${\mathcal{R}}_0>1$, $detA>0$ for any positive values of parameters. Therefore, the endemic equilibrium $E\left(x,y\right)$ is local asymptotically stable (stable node or stable focus) if and only if $\mathrm{tr}A<0$, i.e.,

$$\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)>0.$$

Otherwise, the endemic equilibrium E is unstable (unstable node or unstable focus) if and only if $\mathrm{tr}A>0$, i.e.,

$$\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)<0.$$

Let us point out that if $\mathrm{tr}A=0$ (i.e., ${\lambda }_1=-{\lambda }_2$), then ${\lambda }_{1,2}$ are pure imaginary roots of the characteristic polynomial at E, with Re ${\lambda }_{1,2}=0$. In this case, it is possible to have Hopf bifurcations along the curve tr $A=0$, i.e.,

$$\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)=0.$$

Case 2. If $f\left(0\right)=\rho ({\mathcal{R}}_0-1)=0$, i.e., ${\mathcal{R}}_0=1$, then $\Delta ={(\omega \rho -1)}^2\ge 0$ and the roots of Equation (26) are $y_1=0$ and $y_2=\frac{\omega \rho -1}{\omega }$. Then we have that the first endemic equilibrium $E_1\left(x_1,y_1\right)$ coincides with $E_0(1,0)$, and so this equilibrium point is non hyperbolic, but the second endemic equilibrium becomes $E_2\left(x_2,y_2\right)$, with coordinates $x_2=\frac{1}{\omega \rho }$, $y_2=\frac{\omega \rho -1}{\omega }$.

Obviously, $E_2\in {\Sigma }_{+}$ if and only if $\omega \rho -1>0$. The Jacobian at $E_2$ is $A=$$\left(\begin{array}{cc}-{\rho }^2\omega & -\frac{2\rho \omega -1}{\rho \omega }\\ \left(\rho \omega -1\right)\rho & \frac{\rho \omega -1}{\rho \omega }\end{array}\right)$, with eigenvalues ${\lambda }_{1,2}=\frac{1}{2\rho \omega }\left(\rho \omega -1-{\rho }^3{\omega }^2\pm \sqrt{{\Delta }_1}\right)$, where ${\Delta }_1={\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2-4{\rho }^2\omega {\left(\rho \omega -1\right)}^2$.

Taking into account that $\mathrm{tr}A={\lambda }_1+{\lambda }_2=-\frac{{\rho }^3{\omega }^2-\rho \omega +1}{\rho \omega }$ and $detA={\lambda }_1{\lambda }_2$$=\frac{{\left(\rho \omega -1\right)}^2}{\omega }>0$, the results show that $E_2$ is local asymptotically stable (stable node or stable focus) if and only if $\mathrm{tr}A<0$, i.e., ${\rho }^3{\omega }^2-\rho \omega +1>0$. Else, $E_2$ is unstable (unstable node or unstable focus) if and only if $\mathrm{tr}A>0$, i.e., ${\rho }^3{\omega }^2-\rho \omega +1<0$.

Let us point out that if $\mathrm{tr}A=0$ (i.e., ${\lambda }_1=-{\lambda }_2$), then ${\Delta }_1=-4{\rho }^2\omega {\left(\rho \omega -1\right)}^2<0$, i.e., ${\lambda }_{1,2}$ are pure imaginary roots with Re ${\lambda }_{1,2}=0$. In this case, it is possible to have Hopf bifurcations along the curve ${\rho }^3{\omega }^2-\rho \omega +1=0$. More exactly, for $\omega =\frac{1\pm \sqrt{1-4\rho }}{2{\rho }^2}$ and $0<\rho <\frac{1}{4}$.

If $\frac{1}{4}<\rho <1$, then ${\rho }^3{\omega }^2-\rho \omega +1>0$. For $\rho =\frac{1}{4}$, ${\rho }^3{\omega }^2-\rho \omega +1>0$ for any $\omega \ne \frac{1}{8}$ and ${\rho }^3{\omega }^2-\rho \omega +1=0$ only for $\omega =\frac{1}{8}$.

Case 3. If $f\left(0\right)=\rho ({\mathcal{R}}_0-1)<0$, i.e., ${\mathcal{R}}_0<1$, then we have two endemic equilibrium points $E_1\left(x_1,y_1\right)$ and $E_2\left(x_2,y_2\right)$, with positive coordinates given by

$$x=\frac{1}{{\mathcal{R}}_0(1+\omega y)}\mathrm{and}-\omega {\mathcal{R}}_0{y}^2+{\mathcal{R}}_0(\omega \rho -1)y+\rho ({\mathcal{R}}_0-1)=0$$

if and only if $\Delta ={\mathcal{R}}_0^2{(\omega \rho +1)}^2-4{\mathcal{R}}_0\omega \rho >0$, which means $\frac{4\omega \rho }{{(\omega \rho +1)}^2}<{\mathcal{R}}_0<1$.

More exactly, this two equilibrium points has the following coordinates:

$$x_1=\frac{2}{{\mathcal{R}}_0(1+\omega \rho )-\sqrt{\Delta }},y_1=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)$$

(29)

and, respectively,

$$x_2=\frac{2}{{\mathcal{R}}_0(1+\omega \rho )+\sqrt{\Delta }},y_2=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right).$$

(30)

Let us remark that $\omega \rho -1>0$, because $\frac{y_1+y_2}{2}=\frac{\omega \rho -1}{2\omega }>0$.

For the first endemic equilibrium $E_1\left(x_1,y_1\right)$, taking into account that ${\mathcal{R}}_0(1+\omega y_1)x_1$$=1$, the results show that the Jacobian matrix is

$$A=\left(\begin{array}{cc}-\rho -{\mathcal{R}}_0\left(1+\omega y_1\right)y_1& -{\mathcal{R}}_0\omega x_1{y}_1-1\\ {\mathcal{R}}_0\left(1+\omega y_1\right)y_1& {\mathcal{R}}_0\omega x_1{y}_1\end{array}\right)$$

with $\mathrm{tr}A={\lambda }_1+{\lambda }_2=-\rho -{\mathcal{R}}_0\left(1+\omega y_1\right)y_1+{\mathcal{R}}_0\omega x_1{y}_1$ and $detA={\lambda }_1{\lambda }_2=-{\mathcal{R}}_0\omega x_1{y}_1\rho +{\mathcal{R}}_0\left(1+\omega y_1\right)y_1$, where ${\lambda }_1$, ${\lambda }_2$ are the eigenvalues of A.

By replacing $x_1$ and $y_1$ from (29), the results show that

$$\mathrm{tr}A=-\frac{1}{4}\frac{\left({\left(\rho {\mathcal{R}}_0\omega -\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega -\sqrt{\Delta }\right)-4{\mathcal{R}}_0\omega \left(\rho \omega {\mathcal{R}}_0-{\mathcal{R}}_0-\sqrt{\Delta }\right)}{{\mathcal{R}}_0\omega \left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega -\sqrt{\Delta }\right)}$$

and

$$detA=\frac{1}{4}\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)\frac{{\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)-\sqrt{\Delta }\right)}{{\mathcal{R}}_0\omega \left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega -\sqrt{\Delta }\right)}.$$

Because $y_1=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)>0$ and ${\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega -\sqrt{\Delta }>0$, the results show that the sign of $detA$ is given by ${\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)-\sqrt{\Delta }\right)$. Since $\frac{4\omega \rho }{{(\omega \rho +1)}^2}<{\mathcal{R}}_0<1$, we have $\rho \omega ({\mathcal{R}}_0-1)-\sqrt{\Delta }<0$ and then the expression ${\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)-\sqrt{\Delta }\right)$ can be negative. Indeed, if we use the identity

$$\begin{array}{ccc}\hfill {\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)-\sqrt{\Delta }\right)& =& {\left(1+\rho \omega \right)}^2\left({\mathcal{R}}_0-\frac{4\omega \rho }{{(\omega \rho +1)}^2}\right)\left({\mathcal{R}}_0-\frac{2\sqrt{\Delta }}{\omega \rho +1}\right)\hfill \\ & +& \Delta -\frac{8\rho \omega \sqrt{\Delta }}{1+\omega \rho }\hfill \end{array}$$

and we observe that ${\mathcal{R}}_0-\frac{2\sqrt{\Delta }}{\omega \rho +1}<0$$\left(\mathrm{due} \mathrm{to} {\mathcal{R}}_0>\frac{4\omega \rho }{{(\omega \rho +1)}^2}\right)$, $\Delta -\frac{8\rho \omega \sqrt{\Delta }}{1+\omega \rho }<0$ for ${\mathcal{R}}_0<1$ and $\omega \rho >1$ (because ${(\omega \rho +1)}^2<64{\omega }^2{\rho }^2+4\omega \rho$ for $\omega \rho >1$), it result that

$${\left({\mathcal{R}}_0(\omega \rho -1)-\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)-\sqrt{\Delta }\right)<0\mathrm{for}\mathrm{any}{\mathcal{R}}_0\in \left(\frac{4\omega \rho }{{(\omega \rho +1)}^2},1\right).$$

Therefore, the first endemic equilibrium $E_1$ is unstable (a saddle point) because $detA<0$.

For the second endemic equilibrium $E_2\left(x_2,y_2\right)$, taking into account that ${\mathcal{R}}_0(1+\omega y_2)x_2=1$, the Jacobian matrix is

$$A=\left(\begin{array}{cc}-\rho -{\mathcal{R}}_0\left(1+\omega y_2\right)y_2& -{\mathcal{R}}_0\omega x_2{y}_2-1\\ {\mathcal{R}}_0\left(1+\omega y_2\right)y_2& {\mathcal{R}}_0\omega x_2{y}_2\end{array}\right)$$

with $\mathrm{tr}A={\lambda }_1+{\lambda }_2=-\rho -{\mathcal{R}}_0\left(1+\omega y_2\right)y_2+{\mathcal{R}}_0\omega x_2{y}_2$ and $detA={\lambda }_1{\lambda }_2=-{\mathcal{R}}_0\omega x_2{y}_2\rho +{\mathcal{R}}_0\left(1+\omega y_2\right)y_2$, where ${\lambda }_1$, ${\lambda }_2$ are the eigenvalues of A.

By replacing $x_2$ and $y_2$ from (30), the results show that

$$\mathrm{tr}A=-\frac{1}{4}\frac{\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)-4{\mathcal{R}}_0\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)}{{\mathcal{R}}_0\omega \left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}$$

and

$$detA=\frac{1}{4}\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)\frac{{\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }\right)}{{\mathcal{R}}_0\omega \left({\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}.$$

Since $y_2=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)>0$ and ${\mathcal{R}}_0+\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }>0$, we have that the sign of $detA$ is given by ${\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }\right)$. From $\frac{4\omega \rho }{{(\omega \rho +1)}^2}<{\mathcal{R}}_0<1$, we have $\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }$ can be negative and also the expression ${\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }\right)$ can be negative. However, if we use the identity

$$\begin{array}{ccc}\hfill {\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }\right)& =& {\left(1+\rho \omega \right)}^2\left({\mathcal{R}}_0-\frac{4\omega \rho }{{(\omega \rho +1)}^2}\right)\left({\mathcal{R}}_0+\frac{2\sqrt{\Delta }}{\omega \rho +1}\right)\hfill \\ & +& \Delta +\frac{8\rho \omega \sqrt{\Delta }}{1+\omega \rho }\hfill \end{array}$$

we obtain that ${\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right)}^2+4{\mathcal{R}}_0\left(\rho \omega ({\mathcal{R}}_0-1)+\sqrt{\Delta }\right)>0$ for any ${\mathcal{R}}_0\in \left(\frac{4\omega \rho }{{(\omega \rho +1)}^2},1\right)$.

Then $detA>0$ and the second endemic equilibrium $E_2$ is locally asymptotically stable (stable node or stable focus) if and only of $\mathrm{tr}A<0$, i.e.,

$$\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)>0.$$

Otherwise, the endemic equilibrium $E_2$ is unstable (unstable node or unstable focus) if and only if $\mathrm{tr}A<0$, i.e.,

$$\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)<0.$$

Let us point out that if $\mathrm{tr}A=0$ (i.e., ${\lambda }_1=-{\lambda }_2$), then ${\lambda }_{1,2}$ are pure imaginary roots of the characteristic polynomial at $E_2$, with Re ${\lambda }_{1,2}=0$. In this case, it is possible to have Hopf bifurcations along the curve tr $A=0$, i.e

$$\left({\left(\rho {\mathcal{R}}_0\omega +\sqrt{\Delta }\right)}^2+{\mathcal{R}}_0(4\rho \omega -{\mathcal{R}}_0)\right)\left({\mathcal{R}}_0+\rho R\omega +\sqrt{\Delta }\right)-4R\omega \left(\rho {\mathcal{R}}_0\omega -{\mathcal{R}}_0+\sqrt{\Delta }\right)=0.$$

If $\Delta =0$, i.e., ${\mathcal{R}}_0=\frac{4\omega \rho }{{(\omega \rho +1)}^2}$, then there is an unique endemic equilibrium point $E\left(x,y\right)$, with $x=\frac{\rho \omega +1}{2\omega \rho }$ and $y=\frac{\omega \rho -1}{2\omega }$. The Jacobian at this $E\left(x,y\right)$ is

$$A=\left(\begin{array}{cc}-2{\rho }^2\frac{\omega }{\rho \omega +1}& -2\rho \frac{\omega }{\rho \omega +1}\\ \frac{\rho }{\rho \omega +1}\left(\rho \omega -1\right)& \frac{1}{\rho \omega +1}\left(\rho \omega -1\right)\end{array}\right),$$

with eigenvalues ${\lambda }_1=0, {\lambda }_2=\frac{-2{\rho }^2\omega +\rho \omega -1}{\rho \omega +1}$, which means that this endemic equilibrium point E is a non hyperbolic equilibrium.

If $\Delta <0$, i.e., ${\mathcal{R}}_0<\frac{4\omega \rho }{{(\omega \rho +1)}^2}$, then there is no endemic equilibrium.

In conclusion, we collect the obtained results in

Table 2. The equilibrium points in the closed first quadrant ${\Sigma }_{+}^0$ for the modified SIR model.

Case	Conditions	Equilibrium Points Type
1	${\mathcal{R}}_0>1$	$E_0$ saddle point, $E_1\notin {\Sigma }_{+}^0$, $E_2$ attractor or repeller
2	${\mathcal{R}}_0=1$, $\omega \rho >1$	$E_0=E_1$ non hyperbolic, $E_2$ attractor or repeller
3	${\mathcal{R}}_0=1$, $\omega \rho =1$	$E_0=E_1=E_2$ non hyperbolic
4	${\mathcal{R}}_0=1$, $\omega \rho <1$	$E_0=E_1$ non hyperbolic, $E_2\notin {\Sigma }_{+}^0$
5	$\frac{4\omega \rho }{{(\omega \rho +1)}^2)}<{\mathcal{R}}_0<1$	$E_0$ stable node, $E_1$ saddle point, $E_2$ attractor or repeller
6	${\mathcal{R}}_0=\frac{4\omega \rho }{{(\omega \rho +1)}^2)}$	$E_0$ stable node, $E_1=E_2$ non hyperbolic,
7	$0<{\mathcal{R}}_0<\frac{4\omega \rho }{{(\omega \rho +1)}^2)}$	$E_0$ stable node, $E_1$, $E_2$ do not exists

.

Remark 2. 

Following the ideas and the same techniques as in Section 5, if we will consider the modified SIR model with demography and vaccination,

$$\left\{\begin{array}{ccc}\hfill S^{\prime }& =& \Lambda -\beta (1+\nu I)IS-\mu S-pS\hfill \\ \hfill I^{\prime }& =& \beta (1+\nu I)IS-(\alpha +\mu )I\hfill \\ \hfill R^{\prime }& =& \alpha I-\mu R+pS\hfill \end{array}\right.$$

(31)

then, after changing of time and variables, we will obtain the same dimensionless system (25), where $\rho ={\displaystyle \frac{p+\mu }{\alpha +\mu }}$, ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{(p+\mu )(\alpha +\mu )}}$ and $\omega =\nu \frac{\Lambda }{p+\mu }$. All results obtained remains available also for this SIR epidemic model with demography and vaccination. Only the interpretations can be different because the dimensionless parameters ρ and ${\mathcal{R}}_0$ are different.

7. SODE Formulation of the Modified SIR Pattern with Demography

We consider the modified SIR model with demography (25). For the sake of simplicity, the derivative with respect to time will be denote with a dot over the variable and we prefer to denote t instead of $\tau$. Then, system (25) can be written in the form

$$\left\{\begin{array}{ccc}\hfill \dot{x}& =& \rho (1-x)-{\mathcal{R}}_0(1+\omega y)xy\hfill \\ \hfill \dot{y}& =& {\mathcal{R}}_0(1+\omega y)xy-y\hfill \end{array}\right.$$

(32)

where $\rho ={\displaystyle \frac{\mu }{\alpha +\mu }}\in (0,1)$, $\omega =\nu \frac{\Lambda }{\mu }>0$, ${\mathcal{R}}_0={\displaystyle \frac{\Lambda \beta }{\mu (\alpha +\mu )}}>0$.

By using of the derivative relative to the time t for the equations of system (32), we obtain the next system of second-order differential equations:

$$\left\{\begin{array}{ccc}\ddot{x}+\left[\rho +{\mathcal{R}}_0(1+\omega y)y\right]\dot{x}+\left[{\mathcal{R}}_0\omega xy+{\mathcal{R}}_0(1+\omega y)x\right]\dot{y}\hfill & =& \hfill 0\\ \ddot{y}-{\mathcal{R}}_0(1+\omega y)y\dot{x}+\left[1-{\mathcal{R}}_0\omega xy-{\mathcal{R}}_0(1+\omega y)x\right]\dot{y}\hfill & =& \hfill 0\end{array}\right.$$

In order to use the rule of the crossed repeated indices from differential geometry formalism, we will use the following notations for the variables:

$$x=x^1,\dot{x}=y^1,y=x^2,\dot{y}=y^2$$

Then, the above system of second-order differential equations (SODE) can be written:

$$\left\{\begin{array}{ccc}{\ddot{x}}^1+\left[\rho +{\mathcal{R}}_0(1+\omega x^2)x^2\right]y^1+\left[{\mathcal{R}}_0\omega x^1{x}^2+{\mathcal{R}}_0(1+\omega x^2)x^1\right]y^2\hfill & =& \hfill 0\\ {\ddot{x}}^2-{\mathcal{R}}_0(1+\omega x^2)x^2{y}^1+\left[1-{\mathcal{R}}_0\omega x^1{x}^2-{\mathcal{R}}_0(1+\omega x^2)x^1\right]y^2\hfill & =& \hfill 0\end{array}\right.$$

(33)

or, equivalently,

$$\left\{\begin{array}{ccc}\frac{d^2{x}^1}{d{t}^2}+\left[\rho +{\mathcal{R}}_0(1+\omega x^2)x^2\right]y^1+\left[{\mathcal{R}}_0\omega x^1{x}^2+{\mathcal{R}}_0(1+\omega x^2)x^1\right]y^2\hfill & =& \hfill 0\\ \frac{d^2{x}^2}{d{t}^2}-{\mathcal{R}}_0(1+\omega x^2)x^2{y}^1+\left[1-{\mathcal{R}}_0\omega x^1{x}^2-{\mathcal{R}}_0(1+\omega x^2)x^1\right]y^2\hfill & =& \hfill 0\end{array}\right.$$

(34)

where $\frac{d{x}^i}{dt}=y^i$, $i=1,2$.

Therefore, system (34) represents a SODE (or semi-spray) from the KCC theory:

$$\left\{\begin{array}{c}\frac{d^2{x}^1}{d{t}^2}+2G^1(x^1,x^2,y^1,y^2)=0\\ \frac{d^2{x}^2}{d{t}^2}+2G^2(x^1,x^2,y^1,y^2)=0\end{array}\right.$$

(35)

where

$$\begin{array}{ccc}{G}^1(x^i,y^i)\hfill & =& \frac{1}{2}\left[\rho y^1+{\mathcal{R}}_0\left(1+\omega x^2\right)x^2{y}^1+{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1{y}^2\right],\hfill \\ G^2(x^i,y^i)\hfill & =& \frac{1}{2}\left[-{\mathcal{R}}_0(1+\omega x^2)x^2{y}^1+y^2-{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1{y}^2\right].\hfill \end{array}$$

(36)

The zero-connection curvature $Z_j^i=2\frac{\partial G^i}{\partial x^j}$ is given by the next coefficients:

$$\begin{array}{ccc}\hfill Z_1^1& =& {\mathcal{R}}_0{y}^2+2{\mathcal{R}}_0\omega x^2{y}^2\hfill \\ \hfill Z_2^1& =& {\mathcal{R}}_0{y}^1+2{\mathcal{R}}_0\omega (x^2{y}^1+x^1{y}^2)\hfill \\ \hfill Z_1^2& =& -{\mathcal{R}}_0{y}^2-2{\mathcal{R}}_0\omega x^2{y}^2\hfill \\ \hfill Z_2^2& =& -{\mathcal{R}}_0{y}^1-2{\mathcal{R}}_0\omega (x^2{y}^1+x^1{y}^2)\hfill \end{array}$$

The nonlinear connection N has the coefficients $N_j^i=\frac{\partial G^i}{\partial y^j}$:

$$\left\{\begin{array}{ccc}\hfill N_1^1& =& \frac{1}{2}\left[\rho +{\mathcal{R}}_0\left(1+\omega x^2\right)x^2\right]\hfill \\ \hfill N_2^1& =& \frac{1}{2}{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1\hfill \\ \hfill N_1^2& =& -\frac{1}{2}{\mathcal{R}}_0\left(1+\omega x^2\right)x^2\hfill \\ \hfill N_2^2& =& \frac{1}{2}\left[1-{\mathcal{R}}_0\left(1+\omega x^2\right)x^1\right]\hfill \end{array}\right.$$

(37)

Consequently, all components of the Berwald connection $G_{jk}^i=\frac{\partial N_j^i}{\partial y^k}$ are null and the coefficients of the first invariant, ${\epsilon }^i=-\left(N_j^i{y}^j-2G^i\right)$, are the following:

$$\left\{\begin{array}{ccc}\hfill {\epsilon }^1& =& \frac{1}{2}\rho y^1+\frac{1}{2}{\mathcal{R}}_0\left(1+\omega x^2\right)x^2{y}^1+\frac{1}{2}{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1{y}^2,\hfill \\ \hfill {\epsilon }^2& =& \frac{1}{2}{y}^2-\frac{1}{2}{\mathcal{R}}_0(1+\omega x^2)x^2{y}^1-\frac{1}{2}{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1{y}^2.\hfill \end{array}\right.$$

(38)

Let us observe that ${\epsilon }^i=G^i$ for $i=1,2$, i.e., $\frac{\partial G^i}{\partial y^j}{y}^j=1·G^i$ for $i=1,2$. That means that the functions $G^i$ are homogeneous to degree 1 relative to $y^i$.

Then, by using (A10), the components of deviation curvature tensor for the classical SIR model with demography (32) are given by:

$$\begin{array}{ccc}\hfill P_1^1& =& -\frac{1}{2}{\mathcal{R}}_0\left(1+2\omega x^2\right)y^2+\frac{1}{4}{\left[\rho +{\mathcal{R}}_0\left(1+\omega x^2\right)x^2\right]}^2-\frac{1}{4}{\mathcal{R}}_0^2\left(1+\omega x^2\right)\left(1+2\omega x^2\right)x^1{x}^2\hfill \\ \hfill P_2^1& =& -\frac{1}{2}{\mathcal{R}}_0{y}^1-{\mathcal{R}}_0\omega (x^2{y}^1+x^1{y}^2)+\frac{1}{4}{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1\left[\rho +1+{\mathcal{R}}_0\left(x^2-x^1+\omega {\left(x^2\right)}^2-2\omega x^1{x}^2\right)\right]\hfill \\ \hfill P_1^2& =& \frac{1}{2}{\mathcal{R}}_0\left(1+2\omega x^2\right)y^2-\frac{1}{4}{\mathcal{R}}_0\left(1+\omega x^2\right)x^2\left[\rho +1+{\mathcal{R}}_0\left(x^2-x^1+\omega {\left(x^2\right)}^2-2\omega x^1{x}^2\right)\right]\hfill \\ \hfill P_2^2& =& \frac{1}{2}{\mathcal{R}}_0{y}^1+{\mathcal{R}}_0\omega (x^2{y}^1+x^1{y}^2)-\frac{1}{4}{\mathcal{R}}_0^2\left(1+\omega x^2\right)\left(1+2\omega x^2\right)x^1{x}^2+\frac{1}{4}{\left[1-{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1\right]}^2\hfill \end{array}$$

(39)

If we recall that the trace and the determinant of the deviation curvature tensor

$$P=\left(\begin{array}{cc}{P}_1^1& P_2^1\\ P_1^2& P_2^2\end{array}\right)$$

are tr $P=P_1^1+P_2^2$ and $detP=P_1^1{P}_2^2-P_1^2{P}_2^1$, then, by following Theorem A2, we can write the following result:

Theorem 12. 

All the roots of the characteristic polynomial of P are negative or have negative real parts (that means Jacobi stability) if and only if

$$trP=P_1^1+P_2^2<0\mathit{and}detP=P_1^1{P}_2^2-P_1^2{P}_2^1>0.$$

Taking into account that $P_{jk}^i={\displaystyle \frac{1}{3}}\left({\displaystyle \frac{\partial P_j^i}{\partial y^k}}-{\displaystyle \frac{\partial P_k^i}{\partial y^j}}\right)$, $P_{jkl}^i={\displaystyle \frac{\partial P_{jk}^i}{\partial y^l}}$, $D_{jkl}^i={\displaystyle \frac{\partial G_{jk}^i}{\partial y^l}}$, we obtain the third, fourth, and fifth invariants of the modified SIR model with demography (32):

Theorem 13. 

All eight components of the torsion tensor $P_{jk}^i$, the third invariant of KCC theory, are equal to zero, i.e.,

$$P_{jk}^i=0,\forall i,j,k.$$

(40)

All sixteen components of the Riemann–Christoffel curvature tensor $P_{jkl}^i$, the fourth invariant of KCC theory, are equal to zero, i.e

$$P_{jkl}^i=0,\forall i,j,k,l.$$

(41)

All sixteen components of the Douglas tensor $D_{jkl}^i$, the fifth invariant of KCC theory, are equal to zero, i.e.,

$$D_{jkl}^i=0,\forall i,j,k,l.$$

(42)

8. Jacobi Stability Analysis of the Modified SIR Pattern with Demography

In the present section, the first two geometric invariants at each equilibrium point of the modified SIR model with demography (32) will be computed and, consequently, the Jacobi stability conditions of the system around each equilibrium point will be determined.

For the disease-free equilibrium point $E_0(1,0)$, we have the corresponding equilibrium point $E_0(1,0,0,0)$ of SODE (34) and the results are the same as for the classical model. So, the first invariant has all components null, ${\epsilon }^1={\epsilon }^2=0$, and the matrix with the coefficients of the second invariant is:

$$P=\left(\begin{array}{cc}\frac{1}{4}{\rho }^2& \frac{1}{4}{\mathcal{R}}_0\left(\rho +1-{\mathcal{R}}_0\right)\\ 0& \frac{1}{4}{\left(1-{\mathcal{R}}_0\right)}^2\end{array}\right).$$

Since $\mathrm{tr}P=\frac{1}{4}{\rho }^2+\frac{1}{4}{\left(1-{\mathcal{R}}_0\right)}^2>0$, $detP=\frac{1}{16}{\rho }^2{\left(1-{\mathcal{R}}_0\right)}^2>0$, we obtain the next result:

Theorem 14. 

The disease-free equilibrium point $E_0$ of (32) is always Jacobi unstable.

Using (38) and taking into account that an endemic equilibrium point $E(x,y)$ of (25) have the corresponding equilibrium point $E_0(x,y,0,0)$ of SODE (34), the results show that the first invariant of the geometric theory has all null coefficients, i.e., ${\epsilon }^1={\epsilon }^2=0$, for any endemic equilibrium.

Further, we will made a study of the Jacobi stability for endemic equilibrium points following three cases: ${\mathcal{R}}_0>1$, ${\mathcal{R}}_0=1$ and $0<{\mathcal{R}}_0<1$.

8.1. Jacobi Stability near to Endemic Equilibrium for ${\mathcal{R}}_0>1$

If ${\mathcal{R}}_0>1$ then there is only one endemic equilibrium $E\left(x,y\right)$ in ${\Sigma }_{+}$, where

$$x=\frac{2}{{\mathcal{R}}_0(1+\omega \rho )+\sqrt{\Delta }}\mathrm{and}y=\frac{1}{2{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0(\omega \rho -1)+\sqrt{\Delta }\right),$$

where $\Delta ={\mathcal{R}}_0^2{(\omega \rho +1)}^2-4{\mathcal{R}}_0\omega \rho$.

Using (39), with $x^1=x$, $x^2=y$, $y^1=0$, $y^2=0$, and taking into account that ${\mathcal{R}}_0(1+\omega y)x=1$, the results show that the coefficients of second invariant of KCC theory (the curvature deviation tensor) at E are the following:

$$\begin{array}{ccc}\hfill P_1^1& =& \frac{1}{4}{\left(\rho +\frac{y}{x}\right)}^2-\frac{1}{4}{\mathcal{R}}_0(1+2\omega y)y\hfill \\ \hfill P_2^1& =& \frac{1}{4}{\mathcal{R}}_0\left(\rho +1\right)(1+2\omega y)x+\frac{1}{4}{\mathcal{R}}_0(1+2\omega y)y-\frac{1}{4}{\mathcal{R}}_0^2{(1+2\omega y)}^2{x}^2\hfill \\ \hfill P_1^2& =& -\frac{1}{4}\left(\rho +1\right)\frac{y}{x}-\frac{1}{4}\frac{y^2}{x^2}+\frac{1}{4}{\mathcal{R}}_0(1+2\omega y)y\hfill \\ \hfill P_2^2& =& -\frac{1}{4}{\mathcal{R}}_0(1+2\omega y)y+\frac{1}{4}{\left(1-{\mathcal{R}}_0(1+2\omega y)x\right)}^2\hfill \end{array}$$

Then

$$\mathrm{tr}P=P_1^1+P_2^2=\frac{1}{4}{\left(\rho +\frac{y}{x}\right)}^2-\frac{1}{2}{\mathcal{R}}_0(1+2\omega y)y+\frac{1}{4}{\left(1-{\mathcal{R}}_0(1+2\omega y)x\right)}^2$$

or

$$4x^2\mathrm{tr}P=x^4{\left(1+2\omega y\right)}^2{\mathcal{R}}_0^2-2x^2\left(y+x\right)\left(1+2\omega y\right){\mathcal{R}}_0+{\rho }^2{x}^2+2\rho xy+y^2+x^2,$$

and

$$detP=P_1^1{P}_2^2-P_2^1{P}_1^2=\frac{{\left(-\rho x+\rho x^2{\mathcal{R}}_0+2\rho x^2{\mathcal{R}}_0\omega y-y\right)}^2}{16x^2}>0.$$

Therefore, following Theorem 12, we obtain:

Theorem 15. 

The endemic equilibrium point E of (32) is Jacobi-stable if and only if $\mathit{tr}P<0$.

Using the identity

$$\mathrm{tr}P={\left(\frac{1+2\omega y}{2}\right)}^2\left({\mathcal{R}}_0-\frac{y+x-\sqrt{2xy-{\rho }^2{x}^2-2\rho xy}}{x^2\left(1+2\omega y\right)}\right)\left({\mathcal{R}}_0-\frac{y+x+\sqrt{2xy-{\rho }^2{x}^2-2\rho xy}}{x^2\left(1+2\omega y\right)}\right),$$

which results in

Corollary 1. 

If $2xy-{\rho }^2{x}^2-2\rho xy>0$, then the endemic equilibrium point E of (32) is Jacobi-stable if and only if

$$\frac{y+x-\sqrt{2xy-{\rho }^2{x}^2-2\rho xy}}{x^2\left(1+2\omega y\right)}<{\mathcal{R}}_0<\frac{y+x+\sqrt{2xy-{\rho }^2{x}^2-2\rho xy}}{x^2\left(1+2\omega y\right)}$$

or, equivalently,

$$y+x-\sqrt{2xy-{\rho }^2{x}^2-2\rho xy}<{\mathcal{R}}_0{x}^2\left(1+2\omega y\right)<y+x+\sqrt{2xy-{\rho }^2{x}^2-2\rho xy}.$$

Otherwise, if $2xy-{\rho }^2{x}^2-2\rho xy\le 0$, then the endemic equilibrium E is Jacobi unstable.

In order to deepen the study of the sign of $\mathrm{tr}P$, we replace x, y from (27), the result of which is

$$\begin{array}{ccc}\hfill P_1^1& =& \frac{1}{4}{\left(\rho +\frac{1}{4{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\left({\mathcal{R}}_0\left(1+\omega \rho \right)+\sqrt{\Delta }\right)\right)}^2\hfill \\ \hfill & & -\frac{1}{8\omega }\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\left(1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\right)\hfill \\ \hfill P_2^1& =& \frac{1}{2}{\mathcal{R}}_0\left(\rho +1\right)\frac{1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)}{{\mathcal{R}}_0\left(1+\omega \rho \right)+\sqrt{\Delta }}\hfill \\ \hfill & & +\frac{1}{8\omega }\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\left(1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\right)-{\mathcal{R}}_0^2\frac{{\left(1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\right)}^2}{{\left({\mathcal{R}}_0\left(1+\omega \rho \right)+\sqrt{\Delta }\right)}^2}\hfill \\ \hfill P_1^2& =& -\frac{1}{16}\frac{\rho +1}{{\mathcal{R}}_0\omega }\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\left({\mathcal{R}}_0\left(1+\omega \rho \right)+\sqrt{\Delta }\right)\hfill \\ \hfill & & -\frac{1}{64{\mathcal{R}}_0^2{\omega }^2}{\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)}^2{\left({\mathcal{R}}_0\left(1+\omega \rho \right)+\sqrt{\Delta }\right)}^2\hfill \\ & & +\frac{1}{8\omega }\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\left(1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\right)\hfill \\ \hfill P_2^2& =& -\frac{1}{8\omega }\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\left(1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)\right)\hfill \\ & & +\frac{1}{4}{\left(1-2{\mathcal{R}}_0\frac{1+\frac{1}{{\mathcal{R}}_0}\left({\mathcal{R}}_0\left(\omega \rho -1\right)+\sqrt{\Delta }\right)}{{\mathcal{R}}_0\left(1+\omega \rho \right)+\sqrt{\Delta }}\right)}^2\hfill \end{array}$$

(43)

Then

$$\begin{array}{c}16{\mathcal{R}}_0\omega {\left({\mathcal{R}}_0(1+\rho \omega )+\sqrt{\Delta }\right)}^2\mathrm{tr}P={\mathcal{R}}_0\omega {\rho }^2{\left({\mathcal{R}}_0(1+\rho \omega )+\sqrt{\Delta }\right)}^4\\ -4{\left({\mathcal{R}}_0(1+\rho \omega )+\sqrt{\Delta }\right)}^2\left({\mathcal{R}}_0(\rho \omega -1)+\sqrt{\Delta }\right)\left({\mathcal{R}}_0\rho \omega +\sqrt{\Delta }\right)+4{\mathcal{R}}_0\omega {\left({\mathcal{R}}_0(\rho \omega -1)+\sqrt{\Delta }\right)}^2\end{array}$$

and we obtain the next result:

Theorem 16. 

The endemic equilibrium point E of (32) is Jacobi-stable if and only if

$$\begin{array}{c}{\mathcal{R}}_0\omega {\rho }^2{\left({\mathcal{R}}_0(1+\rho \omega )+\sqrt{\Delta }\right)}^4+4{\mathcal{R}}_0\omega {\left({\mathcal{R}}_0(\rho \omega -1)+\sqrt{\Delta }\right)}^2\\ <4{\left({\mathcal{R}}_0(1+\rho \omega )+\sqrt{\Delta }\right)}^2\left({\mathcal{R}}_0(\rho \omega -1)+\sqrt{\Delta }\right)\left({\mathcal{R}}_0\rho \omega +\sqrt{\Delta }\right).\end{array}$$

8.2. Jacobi Stability near to Endemic Equilibrium for ${\mathcal{R}}_0=1$

For ${\mathcal{R}}_0=1$ and $\omega \rho -1>0$, we have two so called endemic equilibrium points: $E_1(1,0)$ and $E_2(x,y)$ in ${\Sigma }_{+}$, with coordinates $x=\frac{1}{\omega \rho }$, $y=\frac{\omega \rho -1}{\omega }$. However, because $E_1$ coincides with $E_0$, remains to study the Jacobi stability only for $E_2$. Then, we have computed the coefficients of second invariant of KCC theory (the curvature deviation tensor) at $E_2$:

$$\begin{array}{ccc}\hfill P_1^1& =& \frac{1}{4}\frac{{\rho }^4{\omega }^3+3\omega \rho -2{\rho }^2{\omega }^2-1}{\omega }\hfill \\ \hfill P_2^1& =& \frac{1}{4}\left(-1+2\omega \rho \right)\frac{-\omega \rho +{\rho }^3{\omega }^2+1}{{\rho }^2{\omega }^2}\hfill \\ \hfill P_1^2& =& -\frac{1}{4}\left(\omega \rho -1\right)\frac{-\omega \rho +{\rho }^3{\omega }^2+1}{\omega }\hfill \\ \hfill P_2^2& =& -\frac{1}{4}\left(\omega \rho -1\right)\frac{-{\rho }^2\omega +2{\rho }^3{\omega }^2-\omega \rho +1}{{\rho }^2{\omega }^2}\hfill \end{array}$$

Then, the results show that

$$\mathrm{tr}P=P_1^1+P_2^2=\frac{1}{4}\frac{{\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2-2{\rho }^2\omega {\left(\rho \omega -1\right)}^2}{{\rho }^2{\omega }^2}$$

and

$$detP=P_1^1{P}_2^2-P_2^1{P}_1^2=\frac{1}{16}\frac{{\left(\omega \rho -1\right)}^4}{{\omega }^2}>0,\mathrm{for}\mathrm{any}\mathrm{parameter}’\mathrm{s}\mathrm{value}.$$

Theorem 17. 

The endemic equilibrium $E_2$ of (32) is Jacobi-stable if and only if the following condition is satisfied

$${\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2<2{\rho }^2\omega {\left(\rho \omega -1\right)}^2,$$

or, equivalently,

$$-\rho \sqrt{2\omega }\left(\rho \omega -1\right)\le {\rho }^3{\omega }^2-\rho \omega +1\le \rho \sqrt{2\omega }\left(\rho \omega -1\right).$$

Let us remark that $E_2$ is focus (stable or unstable) if and only if the following condition is satisfied

$${\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2<4{\rho }^2\omega {\left(\rho \omega -1\right)}^2,$$

or, equivalently,

$$-2\rho \sqrt{\omega }\left(\rho \omega -1\right)\le {\rho }^3{\omega }^2-\rho \omega +1\le 2\rho \sqrt{\omega }\left(\rho \omega -1\right).$$

If we denote by $S=\mathrm{tr}A$ and $P=detA$, then

$$S^2-4P=\frac{{\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2-4{\rho }^2\omega {\left(\rho \omega -1\right)}^2}{{\rho }^2{\omega }^2}$$

and

$$S^2-2P=\frac{{\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2-2{\rho }^2\omega {\left(\rho \omega -1\right)}^2}{{\rho }^2{\omega }^2}.$$

Consequently, we have $S^2-4P<0$ if and only if ${\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2-4{\rho }^2\omega {\left(\rho \omega -1\right)}^2<0$ and $S^2-2P<0$ if and only if ${\left({\rho }^3{\omega }^2-\rho \omega +1\right)}^2-2{\rho }^2\omega {\left(\rho \omega -1\right)}^2<0$.

Therefore, it is confirmed once again that the Jacobi stability of an equilibrium point implies that this equilibrium point is a focus (stable or unstable); see Figure A1. More that, we can claim that the Jacobi stability near to an equilibrium point not allows a chaotic behavior of the dynamical system around this equilibrium point.

8.3. Jacobi Stability near to Endemic Equilibrium for ${\mathcal{R}}_0<1$

In this case, and for $\Delta ={\mathcal{R}}_0^2{(\omega \rho +1)}^2-4{\mathcal{R}}_0\omega \rho >0$, which means $\frac{4\omega \rho }{{(\omega \rho +1)}^2}<{\mathcal{R}}_0<1$, we have two endemic equilibrium points $E_1\left(x_1,y_1\right)$ and $E_2\left(x_2,y_2\right)$, with positive coordinates given by (29), and, respectively, (30). Because the first endemic equilibrium $E_1\left(x_1,y_1\right)$ is a saddle point, the results show that we have no Jacobi stability at $E_1$. Instead, for the second endemic equilibrium $E_2\left(x_2,y_2\right)$, we will obtain the same results about Jacobi stability as for the endemic equilibrium from the case ${\mathcal{R}}_0>1$ (see Section 8.1).

Obviously, when $\Delta =0$, i.e., ${\mathcal{R}}_0=\frac{4\omega \rho }{{(\omega \rho +1)}^2}$, we have no Jacobi stability at this non-hyperbolic equilibrium point.

Remark 3. 

Similarly with Section 4.1, near every equilibrium point, the dynamics of the deviation vector for this modified SIR system with demography can be obtained from the deviation Equation (A8) as follows:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{d^2{\xi }^1}{d{t}^2}}+\left[\rho +{\mathcal{R}}_0\left(1+\omega x^2\right)x^2\right]{\displaystyle \frac{d{\xi }^1}{dt}}+{\mathcal{R}}_0\left(1+2\omega x^2\right)x^1{\displaystyle \frac{d{\xi }^2}{dt}}\hfill & +& \\ \left[{\mathcal{R}}_0{y}^2+2{\mathcal{R}}_0\omega x^2{y}^2\right]{\xi }^1+\left[{\mathcal{R}}_0{y}^1+2{\mathcal{R}}_0\omega (x^2{y}^1+x^1{y}^2)\right]{\xi }^2\hfill & =& \hfill 0,\\ {\displaystyle \frac{d^2{\xi }^2}{d{t}^2}}-{\mathcal{R}}_0\left(1+\omega x^2\right)x^2{\displaystyle \frac{d{\xi }^1}{dt}}+\left[1-{\mathcal{R}}_0\left(1+\omega x^2\right)x^1\right]{\displaystyle \frac{d{\xi }^2}{dt}}\hfill & -& \\ \left[{\mathcal{R}}_0{y}^2+2{\mathcal{R}}_0\omega x^2{y}^2\right]{\xi }^1-\left[{\mathcal{R}}_0{y}^1+2{\mathcal{R}}_0\omega (x^2{y}^1+x^1{y}^2)\right]{\xi }^2\hfill & =& \hfill 0.\end{array}\right.$$

(44)

9. Conclusions

The fundamental aim of this work is to study the Jacobi stability of two SIR models with demography for the spread of diseases by using the geometric tools of the Kosambi–Cartan–Chern (KCC) theory for the classical SIR model with demography (and vaccination) and a modified SIR model with demography (and vaccination), and with a linear coefficient of the transmission of infection. First of all, we presented the classical local dynamics around equilibrium points for every pattern, and then we rewrote each system of first-order nonlinear differential equations as an equivalent system of second-order differential equations (SODE) for determining the five invariants of the geometric theory. We have determined the first invariant and the second invariant of the Kosambi–Cartan–Chern (KCC) geometric theory, and we found that the third, fourth, and fifth invariants have all components equal to zero. Moreover, the Berwald connection has all null components. Furthermore, we have computed the components of the zero-connection curvature tensor and the components of the nonlinear connection defined by the semi-spray (SODE), and we have determined the deviation curvature tensor in order to find the conditions for Jacobi stability near every equilibrium point.

Furthermore, in order to make a comparison between these two approaches, a comprehensive analysis of the Jacobi stability and the classical (Lyapunov or linear) stability near every equilibrium point was conducted. Moreover, the deviation equations around each equilibrium point were determined. A future approach of this researches could be to perform a computational investigation on the time variation of the deviation vector and its curvature in order to obtain additional information about the behavior of the SIR systems near each equilibrium point.