On the Splitting Tensor of the Weak f-Contact Structure
Abstract
:1. Introduction
2. Preliminaries
3. Results
3.1. Geometry of Weak f-Contact Manifolds
- (a)
- (b)
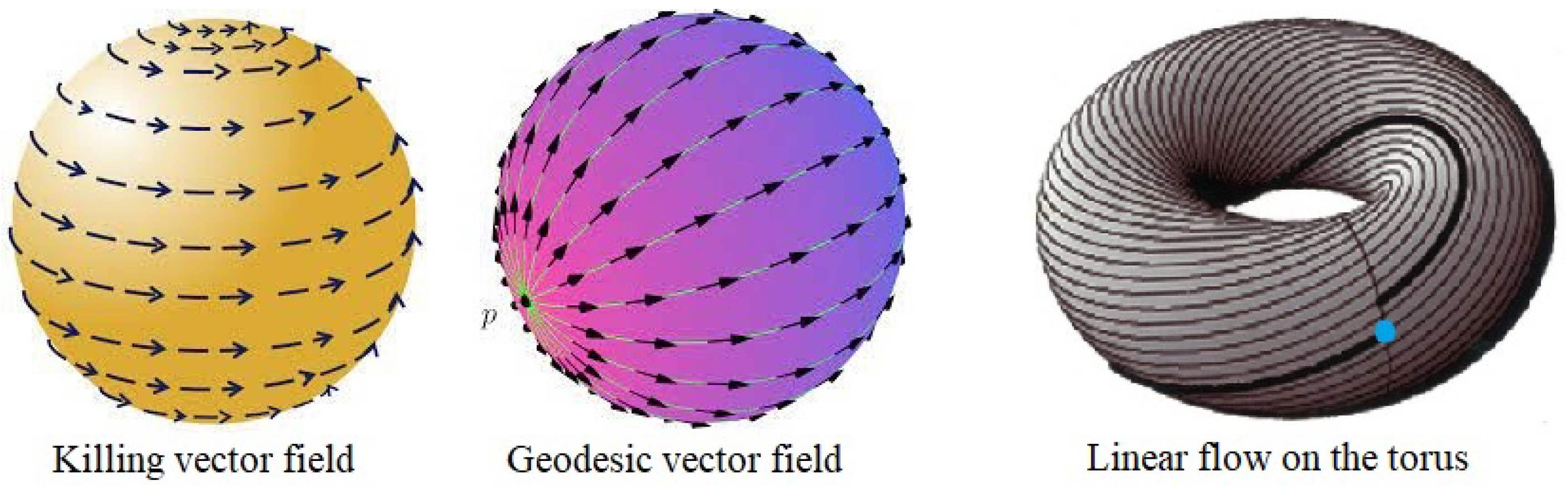
- For a weak f-contact manifold, the tensors and vanish; moreover, vanishes if and only if is a Killing vector field, see ([24], Theorem 2.2).
3.2. The Splitting Tensor of a Weak f-Contact Manifold
3.3. Integral Formulas on Closed Weak f-Contact Manifolds
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boothby, W.M.; Wang, H.C. On contact manifolds. Ann. Math. 1958, 68, 721–734. [Google Scholar] [CrossRef]
- Blair, D.E. Riemannian Geometry of Contact and Symplectic Manifolds, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Blair, D.E. Geometry of manifolds with structural group U(n) × O(s). J. Differ. Geom. 1970, 4, 155–167. [Google Scholar] [CrossRef]
- Brunetti, L.; Pastore, A.M. Curvature of a class of indefinite globally framed f-manifolds. Bull. Math. Soc. Sci. Math. Rouman. 2008, 51, 183–204. [Google Scholar]
- Duggal, K.; Ianus, S.; Pastore, A. Maps interchanging f-structures and their harmonicity. Acta Appl. Math. 2001, 67, 91–115. [Google Scholar] [CrossRef]
- Falcitelli, M.; Ianus, S.; Pastore, A. Riemannian Submersions and Related Topics; World Scientific: Singapore, 2004. [Google Scholar]
- Goldberg, S.I.; Yano, K. On normal globally framed f-manifolds. Tohoku Math. J. 1970, 22, 362–370. [Google Scholar] [CrossRef]
- Di Terlizzi, L.; Pastore, A.M.; Wolak, R. Harmonic and holomorphic vector fields on an f-manifold with parallelizable kernel. Anal. Stii. Univ. Al Cuza Iausi Ser. Noua Mat. 2014, 60, 125–144. [Google Scholar] [CrossRef] [Green Version]
- Yano, K.; Kon, M. Structures on Manifolds; Series in Pure Math; World Scientific Publ. Co.: Singapore, 1985; Volume 3. [Google Scholar]
- Yano, K. On a Structure f Satisfying f3 + f = 0; Technical Report No. 12; University of Washington: Washington, DC, USA, 1961. [Google Scholar]
- Blair, D.E.; Ludden, G.D. Hypersurfaces in almost contact manifolds. Tohoku Math. J. 1969, 21, 354–362. [Google Scholar] [CrossRef]
- Nakagawa, H. f-Structures induced on submanifolds in spaces, almost Hermitian or Kählerian. Kodai Math. Sem. Rep. 1966, 18, 161–183. [Google Scholar] [CrossRef]
- Duggal, K. Lorentzian geometry of globally framed manifolds. Acta Appl. Math. 1990, 19, 131–148. [Google Scholar] [CrossRef]
- Alekseevsky, D.; Michor, P. Differential geometry of g-manifolds. Differ. Geom. Appl. 1995, 5, 371–403. [Google Scholar] [CrossRef] [Green Version]
- Cairns, G. A general description of totally geodesic foliations. Tohoku Math. J. 1986, 38, 37–55. [Google Scholar] [CrossRef]
- Goertsches, O.; Loiudice, E. On the topology of metric f-K-contact manifolds. Monatsh. Math. 2020, 192, 355–370. [Google Scholar] [CrossRef] [Green Version]
- Goertsches, O.; Loiudice, E. How to construct all metric f-K-contact manifolds. Adv. Geom. 2021, 21, 591–598. [Google Scholar] [CrossRef]
- Duggal, K.; Sharma, R. Symmetries of Spacetimes and Riemannian Manifolds; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1999. [Google Scholar]
- Brunetti, L.; Pastore, A.M. S-manifolds versus indefinite S-manifolds and local decomposition theorems. Int. Electron. J. Geom. 2016, 9, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, G.; De, U.C. Generalized Ricci soliton on K-contact manifolds. Math. Sci. Appl. E-Notes 2020, 8, 165–169. [Google Scholar] [CrossRef]
- Rovenski, V.; Walczak, P.G. Progress in Mathematics. In Extrinsic Geometry of Foliations; Birkhäuser: Cham, Switzerland, 2021; Volume 339. [Google Scholar]
- Rovenski, V. Integral formulas for almost product manifolds and foliations. Mathematics 2022, 10, 3645. [Google Scholar] [CrossRef]
- Andrzejewski, K.; Walczak, P. The Newton transformation and new integral formulae for foliated manifolds. Ann. Glob. Anal. Geom. 2010, 37, 103–111. [Google Scholar] [CrossRef]
- Rovenski, V. On the geometry of a weakened f-structure. arXiv 2022, arXiv:2205.02158. [Google Scholar]
- Rovenski, V.; Wolak, R. New metric structures on g-foliations. Indag. Math. 2022, 33, 518–532. [Google Scholar] [CrossRef]
- Dajczer, M.; Tojeiro, R. Submanifold Theory. Beyond an Introduction; Series: Universitext; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Berger, M. A Panoramic View of Riemannian Geometry; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Rovenski, V. Integral formulae for a Riemannian manifold with two orthogonal distributions. Cent. Eur. J. Math. 2011, 9, 558–577. [Google Scholar] [CrossRef]
- Walczak, P. An integral formula for a Riemannian manifold with two orthogonal complementary distributions. Colloq. Math. 1990, 58, 243–252. [Google Scholar] [CrossRef]
- Brînzanescu, V.; Slobodeanu, R. Holomorphicity and the Walczak formula on Sasakian manifolds. J. Geom. Phys. 2006, 57, 193–207. [Google Scholar] [CrossRef] [Green Version]
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | |
| 1 | 3 | 1 | 7 | 1 | 3 | 1 | 8 | 1 | 3 | 1 | 7 | 1 | 3 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rovenski, V. On the Splitting Tensor of the Weak f-Contact Structure. Symmetry 2023, 15, 1215. https://doi.org/10.3390/sym15061215
Rovenski V. On the Splitting Tensor of the Weak f-Contact Structure. Symmetry. 2023; 15(6):1215. https://doi.org/10.3390/sym15061215
Chicago/Turabian StyleRovenski, Vladimir. 2023. "On the Splitting Tensor of the Weak f-Contact Structure" Symmetry 15, no. 6: 1215. https://doi.org/10.3390/sym15061215






